Геомагнетизм и аэрономия, 2019, T. 59, № 5, стр. 607-617
Особенности распределений холловских токов и магнитного поля пульсаций диапазона Рс4
А. В. Петленко *
Санкт-Петербургский филиал института земного магнетизма,
ионосферы и распространения радиоволн им. Н.В. Пушкова РАН (СПбФ ИЗМИРАН)
г. Санкт-Петербург, Россия
* E-mail: petlenko.58@mail.ru
Поступила в редакцию 16.11.2018
После доработки 08.02.2019
Принята к публикации 23.05.2019
Аннотация
Распределения интенсивностей и направлений холловских токов в ионосфере определены по заданным значениям координат и интенсивностей продольных токов. На примере распределений, вычисленных для трех продольных токов, показано, что совпадение вблизи точек их проекций особенностей поля холловских токов и магнитного поля на поверхности Земли объясняется индукционным характером формирования холловских токов. Это позволяет оценивать число, положение и интенсивности продольных токов по экспериментально построенным распределениям поля магнитных пульсаций при условии, что расстояния между источниками больше высоты ионосферы. Приведенное решение уравнений силовых линий и изолиний интенсивности холловских токов показывает, что локально дуги этих кривых порождаются парой эквивалентных продольных токов.
1. ВВЕДЕНИЕ
Известно, что высокоширотные магнитные пульсации на поверхности Земли возникают в результате возбуждения ионосферных холловских токов магнитосферными продольными токами, которые образуются при высыпаниях заряженных частиц. Представления о возбуждении холловских токов в тонкой однородно проводящей ионосфере изложены в работе [Kato and Tamao, 1956]. На основе этих представлений, по распределению продольных токов можно восстановить конфигурацию ионосферных холловских, и, пользуясь законом Био–Савара–Лапласа, найти мгновенное распределение компонент поля геомагнитных пульсаций.
Практический интерес, как правило, вызывает решение обратной задачи, когда по измеренной последовательности распределений магнитного поля, требуется найти изменения интенсивностей и положений продольных токов. Так, согласно [Копытенко и Распопов, 1968] положение продольных токов геомагнитных пульсаций позволяет оценить границы области значительного градиента концентрации частиц внутренней магнитосферы – плазмопаузы. В рамках представлений о модуляции инкрементов нарастания ионно-циклотронных волн геомагнитными пульсациями Рс4 [Ляцкий и Плясова-Бакунина, 1986] выяснение причин интенсификации пульсаций Рс1 связано с определением положения и режима колебаний продольных токов Рс4. Однако не ясно, как влияют неоднородности намагниченности земной коры на распределение областей высыпания магнитосферных заряженных частиц [Петленко и др., 2011а]. В данной работе основное внимание уделяется аспектам решения прямой задачи в постановке, близкой представлениям [Roldugin and Roldugin, 2008].
В модели поля геомагнитных пульсаций [Ролдугин и др., 1971] эквивалентный источник рассматривается в виде скрещенных диполей, помещенных на высоте ионосферы. В поздней модификации [Roldugin and Roldugin, 2008] модель была представлена асимметричными диполями. Если отвлечься от процесса становления холловских токов со скоростями распространения БМЗ-волн в ионосфере и рассматривать токовую конфигурацию в каждый момент времени как квазистатическую (какой она выглядит в диапазоне измерений поля магнитных пульсаций), то асимметрию диполей можно объяснить различиями интенсивности и взаимной удаленности продольных токов. Следуя [Kato and Tamao, 1956], положим, что интенсивность холловского тока определяется величиной магнитного давления, или модулем магнитного поля, созданного продольными токами. Задавая их распределение, представим в аналитической форме распределения интенсивностей и направлений холловских токов, что позволяет рассчитать индуцированное магнитное поле на поверхности Земли.
При условии, что расстояние между точками проекций продольных токов превышает высоту Е-слоя ионосферы, выполненном для пульсаций Pс4 и Pi2 в диапазоне периодов >100 с, сопоставим распределения поля холловских токов и магнитного поля пульсаций, вычисленные при фиксированных параметрах продольных токов. Цель работы состоит в том, чтобы показать, что положения некоторых особенностей этих распределений совпадают с положениями точек проекций продольных токов, что объясняется индуктивным типом ионосферных источников пульсаций в окрестности этих точек и позволяет оценивать положения и интенсивности продольных токов по экспериментально построенным распределениям магнитного поля пульсаций.
Актуальность определяется аналитическим представлением областей локализации особенностей поля холловских токов, обеспечивающим их визуализацию и способствующим интерпретации поля магнитных пульсаций. На примере поля, инициированного тремя продольными токами, будет получено решение уравнений силовых линий и изолиний интенсивности холловских токов. Приведенная в приложении методика решения показывает, что локально дуги этих кривых порождаются парой эквивалентных продольных токов – в рассматриваемом примере положения этих токов согласованы с центрами кривизны этих дуг.
2. РАСЧЕТ РАСПРЕДЕЛЕНИЯ ПОЛЯ ГЕОМАГНИТНЫХ ПУЛЬСАЦИЙ
Поле высокоширотных геомагнитных пульсаций формируется в тонкой однородно проводящей ионосфере системой холловских токов ${{{\mathbf{j}}}_{H}},$ инициируемых магнитосферными продольными токами ${{j}_{{||}}}.$ Пусть заданы число продольных токов K, их интенсивности ${{{\iota }}_{k}}$ и координаты проекций на ионосферу ${{{\mathbf{r}}}_{k}} = ({{x}_{k}},{{y}_{k}}).$ Магнитное поле в точке ${{{\mathbf{r}}}_{{m,n}}} = ({{x}_{m}},{{y}_{n}})$ на поверхности Земли рассчитывается как ${\mathbf{\tilde {B}}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right) = \iint_{\left\{ {\mathbf{r}} \right\}} {d{\mathbf{r}}}\left[ {{{{\mathbf{j}}}_{H}}\left( {\mathbf{r}} \right) \times \left( {{\mathbf{r}} - {{{\mathbf{r}}}_{{m,n}}}} \right)} \right]{{R}^{{ - 3}}},$ R = $ = \sqrt {{{{\left( {{\mathbf{r}} - {{{\mathbf{r}}}_{{m,n}}}} \right)}}^{2}} + {{h}^{2}}} ,$ $h$ – высота ионосферы. Компоненты холловских токов, инициируемых током ${{j}_{{||,k}}},$ в точке ${\mathbf{r}} = \left( {x,y} \right)$ считаем пропорциональными компонентам его магнитного поля ${{j}_{{x,k}}} \propto - \left( {y - {{y}_{k}}} \right)\rho _{k}^{{ - 2}},$ ${{j}_{{y,k}}} \propto \left( {x - {{x}_{k}}} \right)\rho _{k}^{{ - 2}},$ $\rho _{k}^{2}$ = $ = {{\left( {x - {{x}_{k}}} \right)}^{2}}$ + ${{\left( {y - {{y}_{k}}} \right)}^{2}},$ и его интенсивности. В силу принципа суперпозиции ${{{\mathbf{j}}}_{H}}\left( {\mathbf{r}} \right) = \sum\nolimits_k^K {{{{\mathbf{j}}}_{{H,k}}}} \left( {\mathbf{r}} \right),$ ${{{\mathbf{j}}}_{{H,k}}}$ = (${{j}_{{x,k}}},$ ${{j}_{{y,k}}}$), для произвольно заданного числа продольных токов конфигурация холловских токов а, следовательно, и распределение ${\mathbf{\tilde {B}}}\left( {\mathbf{r}} \right)$ имеет алгебраическое представление. Действительно, записывая компоненты ${{{\mathbf{j}}}_{H}}$ как ${{j}_{x}} \propto - \sum\nolimits_k^K {{{{\iota }}_{k}}} \left( {y - {{y}_{k}}} \right)$ × × ${{\prod\nolimits_k^K {\rho _{{\hat {k}}}^{{ - 2}}} } \mathord{\left/ {\vphantom {{\prod\nolimits_k^K {\rho _{{\hat {k}}}^{{ - 2}}} } {\prod\nolimits_k^K {\rho _{k}^{{ - 2}}} }}} \right. \kern-0em} {\prod\nolimits_k^K {\rho _{k}^{{ - 2}}} }}$ и ${{j}_{y}} \propto \sum\nolimits_k^K {{{{\iota }}_{k}}} \left( {x - {{x}_{k}}} \right)$ × × ${{\prod\nolimits_k^K {\rho _{{\hat {k}}}^{{ - 2}}} } \mathord{\left/ {\vphantom {{\prod\nolimits_k^K {\rho _{{\hat {k}}}^{{ - 2}}} } {\prod\nolimits_k^K {\rho _{k}^{{ - 2}}} }}} \right. \kern-0em} {\prod\nolimits_k^K {\rho _{k}^{{ - 2}}} }},$ где символ $\hat {k}$ указывает на пропуск множителя с индексом k, находим, что линии постоянного уровня интенсивности ${{{\iota }}_{L}} = \sqrt {j_{x}^{2} + j_{y}^{2}} = {{\beta }^{{ - 1}}}$ определяются как решение алгебраического уравнения степени $2K$ в переменных x, y, коэффициенты которого определяются параметрами ${{{\mathbf{r}}}_{k}},$ ${{{\iota }}_{k}}$ и $\beta .$
Возможность решения этого уравнения при произвольных значениях $\beta $ позволяет определить особенности функции распределения ${{{\iota }}_{L}}\left( {\mathbf{r}} \right)$ и произвести их сопоставление с особенностями распределения магнитного поля ${\mathbf{\tilde {B}}}\left( {\mathbf{r}} \right),$ вычисленного при известных значениях параметров ${{{\mathbf{r}}}_{k}}$ и ${{{\iota }}_{k}}.$ Этим обеспечивается возможность решения обратной задачи, в которой по особенностям экспериментально построенного ${\mathbf{B}}\left( {\mathbf{r}} \right)$ требуется найти координаты, интенсивности и число продольных токов, инициирующих наблюдаемое в конкретный момент времени распределение поля магнитных пульсаций.
Точность построения ${\mathbf{B}}\left( {\mathbf{r}} \right)$ определяется условиями эксперимента – пороговой чувствительностью магнитометров и расстоянием между ними. Поэтому, вычисляя магнитное поле ${\mathbf{\tilde {B}}}\left( {\mathbf{r}} \right)$ в пределах некоторой ограниченной области ${\Omega ,}$ можно ограничить размеры области интегрирования $\left\{ {\mathbf{r}} \right\} \supset {\Omega ,}$ используя в качестве ограничителя линию уровня ${{{\iota }}_{L}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }_{H}},$ где ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }_{H}}$ – минимальное значение тока, различимое магнитометром на расстоянии h. Использование линий уровня ${{{\iota }}_{L}}$ позволяет устранить возможные сингулярности ${{{\mathbf{j}}}_{H}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right)$ в узлах координатной сети ${{{\mathbf{r}}}_{{m,n}}}$ при случайном расположении точек ${{{\mathbf{r}}}_{k}}$. Чтобы избежать их проявления в компонентах ${\mathbf{\tilde {B}}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right),$ распределение ${{{\mathbf{j}}}_{H}}$ регуляризуют, вводя ограничения на уровень ${{\hat {j}}_{{H,k}}}$ допустимых значений холловских токов и сохраняя ориентацию ${{{\mathbf{\hat {j}}}}_{H}}$ и ${{{\mathbf{j}}}_{H}}$ там, где $\left| {{{{\hat {j}}}_{{H,k}}}} \right| \ll \left| {{{j}_{H}}} \right|.$ Таким образом, верхние ${{\hat {j}}_{{H,k}}}$ и нижний ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }_{H}}$ уровни интенсивности холловских токов фактически определяют внутренние и внешнюю границы области $\left\{ {\mathbf{r}} \right\}.$
Так как магнитное поле холловских токов быстро затухает с расстоянием, а порог чувствительности регистрирующих магнитометров ограничен, то на измерения поля оказывают влияние лишь конечное число продольных токов. Ограничимся случаем $K$ = 3 для иллюстрации решения прямой задачи вычисления ${\mathbf{\tilde {B}}}\left( {\mathbf{r}} \right)$ по заданным значениям ${{{\iota }}_{k}}$ и ${{{\mathbf{r}}}_{k}}$. Будем полагать, что проекции токов ${{j}_{{||,k}}}$ расположены в пределах области ${\Omega }{\text{.}}$ Покажем, что изолинии ${{{\iota }}_{L}}$ замкнуты. При специальном выборе (центрировании) координат $\sum\nolimits_k^K {{{{\mathbf{r}}}_{k}}} = 0$ уравнение ординаты линии уровня ${{{\iota }}_{L}}~ = {{\beta }^{{ - 1}}}$ имеет вид
Так как можно построить контуры произвольного уровня ${{{\iota }}_{L}}$ в диапазоне [${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }_{H}},{\text{\;}}{{\hat {j}}_{H}}$], где ${{\hat {j}}_{H}} = {\text{ma}}{{{\text{x}}}_{{k \in 1..3}}}\left( {{{{\hat {j}}}_{{H,k}}}} \right),$ то ${\mathbf{\tilde {B}}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right)$ представляется интегралом Лебега по совокупности контуров в виде:
(2)
$\begin{gathered} {\mathbf{\tilde {B}}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right) = \int\limits_{{{{\hat {j}}}_{H}}}^{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }}_{H}}} {d{{{\iota }}_{L}}} \int\limits_0^{2\pi } {d\varphi } \left( {{\mathbf{r}},{{{\mathbf{r}}}_{{m,n}}}} \right) \times \\ \times \,\,\left[ {{{{\mathbf{j}}}_{L}}\left( {{\mathbf{r}}\left( \varphi \right)} \right) \times \left( {{\mathbf{r}}\left( \varphi \right) - {{{\mathbf{r}}}_{{m,n}}}} \right)} \right]R{{\left( {{\mathbf{r}}\left( \varphi \right),{{{\mathbf{r}}}_{{m,n}}}} \right)}^{{ - 3}}}. \\ \end{gathered} $В случае $K$ = 3 запишем ${{j}_{y}}\left( {x,~y} \right)$ в виде многочлена, упорядоченного по степеням x, коэффициенты которого имеют вид полинома от y, в котором ${{p}_{{{\mu },{\nu }}}}$ зависят от ${{x}_{k}},$ ${{y}_{k}}$ и ${{{\iota }}_{k}}.$ Так в выражении
(3б)
$\begin{gathered} {{p}_{0}} = \sum\limits_{k = 1}^3 {{{{\iota }}_{k}}} ,\,\,\,\,{{p}_{1}} = \sum\limits_{k = 1}^3 {{{{\iota }}_{k}}{{x}_{k}}} - 2\sum\limits_{k = 1}^3 {{{{\iota }}_{k}}} \sum\limits_{k = 1}^3 {{{x}_{k}},} \\ {{p}_{{2.0}}} = 2{{p}_{0}},\,\,\,\,{{p}_{{2.1}}} = - 2\sum\limits_{k = 1}^3 {{{{\iota }}_{k}}} \left( {{{y}_{{\overbrace {k + 1}^{}}}} + {{y}_{{\overbrace {k + 2}^{}}}}} \right), \\ \end{gathered} $Дифференциальное уравнение (ДУ) силовой линии операторными методами [Айнс, 1939] приводится к виду алгебраического уравнения. В случае $K$ = 3 получаем уравнение 6-й степени, решение которого представляет силовую линию как функцию $y\left( x \right).$ Постоянная интегрирования определяется координатами точки (на контуре ${{{\iota }}_{L}}$), через которую проходит ${{{\iota }}_{F}}.$ Через каждую точку проходит одна силовая линия, при этом вещественными являются кратное двум число ветвей решения алгебраического уравнения – то есть силовые линии ${{{\iota }}_{F}},$ так же как и линии постоянного уровня ${{{\iota }}_{L}},$ образуют систему замкнутых контуров. Число точек пересечения ${{{\iota }}_{F}}$ с изолинией ${{{\iota }}_{L}}$ также кратно 2. Если контуры ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ имеют только две общие точки, то в этих точках они соприкасаются. В таких точках касательная ${{{\mathbf{j}}}_{{\tau }}}$ контура ${{{\iota }}_{L}}$ равна ${{{\mathbf{j}}}_{H}},$ а нормальная составляющая ${{{\mathbf{j}}}_{n}}$ = 0. Критерием определения точек касания ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ является коллинеарность ${{{\mathbf{j}}}_{{\tau }}}$ и ${{{\mathbf{j}}}_{H}},$ или ${{{\mathbf{j}}}_{{\tau }}}$ × $~{{{\mathbf{j}}}_{H}}$ = 0, то есть эти точки тоже находятся из решения соответствующего алгебраического уравнения.
Параметр $\beta $ является критическим для условия касания ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ – при малом изменении $\beta $ фиксированная силовая линия либо не имеет общих точек с ${{{\iota }}_{L}} = {{\beta }^{{ - 1}}},$ либо пересекается дважды с ${{{\iota }}_{L}}$ в малой окрестности точки касания. Поэтому общее число точек касания ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ является множеством меры 0 [Арнольд, 1978] на множестве их всевозможных пересечений и представляется конечным числом кривых на плоскости. Следовательно, ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ образуют сеть почти всюду трансверсальных замкнутых кривых, причем, если ${{{\iota }}_{F}},$ касается к линии фиксированного уровня, то пересечения этой ${{{\iota }}_{F}}$ с другими изолиниями задают узлы ${{{\mathbf{r}}}_{{L,F}}}$ сети, по которым можно производить интегрирование (2). В узлах, принадлежащих линии уровня ${\beta ,}$ модуль вектора ${{{\mathbf{j}}}_{L}}\left( {{{{\mathbf{r}}}_{{L,F}}}} \right)$ равен ${{{\iota }}_{L}},$ направление определяется уравнением силовой линии, а вклад в магнитное поле токов на элементе дуги $d{{{\iota }}_{L}}$ тем больше, чем выше плотность пересекающихся с ним линий ${{\iota }_{F}}$ [Тамм, 2003], то есть, чем выше плотность узлов.
Построим изолинии ${{{\iota }}_{L}},$ проследим за тем, как меняется конфигурация ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ при изменении интенсивностей ${{{\iota }}_{k}}$ и выделим основные особенности распределения холловских токов. Рассчитаем магнитное поле ${\mathbf{\tilde {B}}}$ этих токов в ограниченной области ${\Omega ,}$ в пределах которой локализуются основные особенности распределения поля ${{{\mathbf{j}}}_{H}}.$ Сопоставим положение особенностей распределений ${\mathbf{\tilde {B}}}$ и ${{{\mathbf{j}}}_{H}}$ в случае, когда число продольных токов $K$ в ${\Omega }$ равно 3.
3. РАСПРЕДЕЛЕНИЕ ХОЛЛОВСКИХ ТОКОВ В ПЛОСКОЙ ИОНОСФЕРЕ
Пусть в области ${\Omega }$ заданы проекции продольных токов ${{{\mathbf{r}}}_{k}},$ обозначенные закрашенными ромбиками и пронумерованные цифрами 1, 2, 3 на рис. 1б. Центр треугольника с вершинами в точках ${{{\mathbf{r}}}_{k}}$ совмещен с началом координат в центре ${\Omega }{\text{.}}$ Не придавая определенных значений ни размерам ${\Omega }$, ни интенсивностям ${{{\iota }}_{k}}$, будем полагать ${{{\iota }}_{1}} = $ 1, так что ${{{\iota }}_{2}}$ и ${{{\iota }}_{3}}$ представлены как отношения ${{{\iota }}_{2}}$ : ${{{\iota }}_{3}}:{{{\iota }}_{1}}.$ ${{{\iota }}_{3}}$ = 1.4 и ${{{\iota }}_{2}}$ = +1.1 на рис. 1б будут соответствовать однонаправленным с ${{{\iota }}_{1}}$ токам. ${{{\iota }}_{2}}$ = –1.1 на рис. 1а соответствует току, имеющему противоположную направленность, Очевидно, что при $K$ = 3 случай однонаправленных ${{j}_{{||,k}}}$ и случай, когда только два тока протекают в одинаковом направлении, исчерпывают всевозможные варианты выбора знаков ${{{\iota }}_{k}}.$
Рис. 1.
Покрытие области $\Omega $ изолиниями ${{{\iota }}_{L}}{\text{:}}$ (а) ${{{\iota }}_{2}}$ = –1.1, ${{{\iota }}_{3}}$ = 1.4; (б) ${{{\iota }}_{2}}$ = 1.1, ${{{\iota }}_{3}}$ = 1.4. Цифрами нумерованы проекции продольных токов (ромбики). Буквами индексированы значения параметров уровня $\beta .$ Внешний контур линии ${{{\iota }}_{L}} = \beta _{{\text{G}}}^{{ - 1}}$ на (б) расположен за пределами области ${{\Omega }_{1}}$ вдвое больших, чем $\Omega $ линейных размеров.
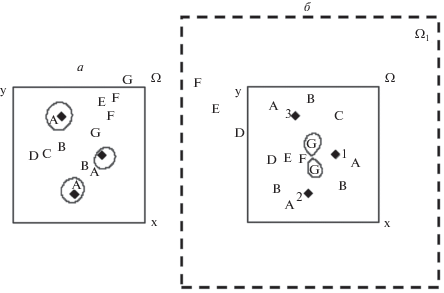
Для обоих случаев нанесем линии постоянных уровней интенсивности ${{{\iota }}_{L}} = {{\beta }^{{ - 1}}},$ найденные как решения уравнения (1) при разных значениях ${\beta }$, индексированных на рис. 1 заглавными латинскими буквами. Так, на рис. 1а ${{\beta }_{{\text{A}}}}$ = 0.07, ${{\beta }_{{\text{B}}}}$ = 0.10, ${{\beta }_{{\text{C}}}} = {\text{0}}{\text{.12,}}$ ${{\beta }_{{\text{D}}}} = {\text{0}}{\text{.17,}}$ ${{\beta }_{{\text{E}}}} = {\text{\;0}}{\text{.22,}}$ ${{\beta }_{{\text{F}}}}$ = 0.27, ${{\beta }_{{\text{G}}}}$ = = 0.32. На рис. 1б ${{\beta }_{{\text{A}}}}$ = 0.07, ${{\beta }_{{\text{B}}}}$ = 0.12, ${{\beta }_{{\text{C}}}}$ = 0.15, ${{\beta }_{{\text{D}}}}$ = 0.17, ${{\beta }_{{\text{E}}}}$ = 0.22, ${{\beta }_{{\text{F}}}}$ = 0.27, ${{\beta }_{{\text{G}}}}$ = 0.42. При малых значениях $\beta $ решение (1) образует три несвязных замкнутых контура, каждый из которых охватывает одну и только одну точку ${{{\mathbf{r}}}_{k}},$ формируя внутренние границы области $\left\{ {\mathbf{r}} \right\}.$ При возрастании $\beta $ размеры областей, ограниченных линиями ${{{\iota }}_{L}},$ возрастают так, что уже при ${{\beta }_{{\text{B}}}}$ = 0.10 (рис. 1а) эти области сливаются. Число контуров, удовлетворяющих решению (1), сокращается до одного при $\beta = {{\beta }_{{\text{C}}}},$ а при дальнейшем увеличении $\beta = {{\beta }_{{\text{F}}}}$ (рис. 1а), $\beta = {{\beta }_{{\text{D}}}}$ (рис. 1б) вновь начинает увеличиваться. Формируется внешний и вложенный в него контуры, при этом область, ограниченная внутренним контуром $\beta = {{\beta }_{{\text{G}}}},$ принадлежит области, ограниченной внутренним контуром $\beta = {{\beta }_{{\text{F}}}},$ тогда как для областей, ограниченных внешними контурами ${{\beta }_{{\text{G}}}}$ и ${{\beta }_{{\text{F}}}},$ отношение вложенности строго противоположное (рис. 1а). На рис. 1б видны два изолированных внутренних контура $\beta = {{\beta }_{{\text{G}}}},$ их внешний контур (не показан) находится за пределами области ${{{\Omega }}_{1}},$ вдвое превышающей линейные размеры области ${\Omega }{\text{.}}$ Этот контур мало отличается от контура ${{{\iota }}_{L}},$ формируемого одиночным продольным током интенсивности $\sum\nolimits_k^3 {{{{\iota }}_{k}}} ,$ помещенным в начало координат. А большим значениям $\beta $ соответствуют внешние границы области $\left\{ {\mathbf{r}} \right\}.$
На рисунке 2 показаны изменения 2D функции распределения ${{{\iota }}_{L}}\left( {x,y} \right)$ при изменениях величины и направления тока ${{{\iota }}_{2}}$ и фиксированных значениях ${{{\iota }}_{1}} = 1$ и ${{{\iota }}_{3}}$ = 1.9. Представленные распределения позволяют понять, что отношения вложенности областей, ограниченных линиями уровней ${{{\iota }}_{L}} = {{\beta }^{{ - 1}}},$ формируют структуру токов ${{{\mathbf{j}}}_{H}},$ покрывающую как область ${\Omega ,}$ так и вмещающую ее область $\left\{ {\mathbf{r}} \right\}.$ Изменения отношения вложенности при различных значениях $\beta $ проявляют наличие двух типов особенностей функции ${{{\iota }}_{L}}\left( {x,y} \right),$ первый из которых включает локальные максимумы интенсивности ${{{\mathbf{j}}}_{H}},$ второй – минимумы. Наличие локального минимума интенсивности ${{{\iota }}_{L}}$ можно наблюдать в случае пары продольных токов (когда ${{{\iota }}_{2}} = \pm 0.1 \ll {{{\iota }}_{1}},$ ${{{\iota }}_{3}}$). С другой стороны, соответствующие распределения (рис. 2) показывают, что даже если значение одного из токов ${{j}_{{||,k}}}$ на порядок меньше интенсивности двух других, изолинии ${{{\iota }}_{L}}$ в его ближайшей окрестности реагируют на него заметным изменением кривизны.
Рис. 2.
Функция распределения интенсивнои холловских токов ${{{\iota }}_{L}}\left( {x,~y} \right)$ при различных значениях продольного тока ${{{\iota }}_{2}}.$

Распределение направлений ${{{\mathbf{j}}}_{H}}$ представлено на рис. 3 силовыми линиями поля холловских токов (нарисованы стрелками), построенными по вычисленным распределениям ${{j}_{x}}\left( {x,~y} \right)$ и ${{j}_{y}}\left( {x,~y} \right).$ Конфигурация на рис. 3а соответствует распределению продольных токов разной, на рис. 3б – одинаковой направленности. Серым цветом на рис. 3а показан контур, найденный как решение ДУ силовой линии. В качестве начального условия использованы координаты точки на контуре ${{{\iota }}_{L}},$ построенном как линия криволинейной сетки (тонкие сплошные линии для обеих конфигураций силовых линий). Ориентированные по и против часовой стрелки векторы ${{{\mathbf{j}}}_{H}}$ в окрестности точек проекций ${{j}_{{||,k}}}$ позволяют отслеживать направление продольного тока. Вблизи как внутренних, так и внешних границ областей $\left\{ {\mathbf{r}} \right\}$ направления ${{{\mathbf{j}}}_{H}}$ не слишком сильно уклоняются от направлений касательных к линиям ${{{\iota }}_{L}}$ векторов ${{{\mathbf{j}}}_{{\tau }}}.$
Рис. 3.
Силовые линии (стрелки) и линии уровня (сплошные) для продольных токов ${{j}_{{||,k}}}$ разных (а), (б) – одинакового направлений. Серым цветом выделен контур ${{{\iota }}_{F}},$ построенный как решение ДУ силовой линии. Серая точка на контуре ${{{\iota }}_{L}}$ выбрана начальным условием ДУ.

Возможность объединения линий ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ в криволинейную координатную сеть, покрывающую области ${\Omega }$ и $\left\{ {\mathbf{r}} \right\},$ позволяет представить магнитное поле холловских токов (2) в виде
(4)
$\begin{gathered} {\mathbf{\tilde {B}}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right) = \int\limits_{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }}_{H}}}^{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{j} }}_{H}}} {d{{j}_{L}}} \int\limits_0^{2\pi } {d\varphi } \left( {{{{\mathbf{r}}}_{{L,F}}}} \right) \times \\ \times \,\,\left[ {{{j}_{L}}\left( {{{{\mathbf{r}}}_{{L,F}}}} \right) \times \left( {{{{\mathbf{r}}}_{{L,F}}} - {{{\mathbf{r}}}_{{m,n}}}} \right)} \right]R{{\left( {{{{\mathbf{r}}}_{{L,F}}},{{{\mathbf{r}}}_{{m,n}}}} \right)}^{{ - 3}}}, \\ \end{gathered} $На рисунке 4а воспроизведена функция ${{s}_{L}}\left( \beta \right).$ Маркерами отмечены значения ${{s}_{L}}\left( {{{\beta }_{{\text{А}}}}} \right),$ … ${{s}_{L}}\left( {{{\beta }_{{\text{G}}}}} \right),$ соответствующие линиям ${{{\iota }}_{L}}$ рис. 1б. Заметим, что функция ${{s}_{L}}\left( \beta \right)$ практически линейна как при малых, так и при больших значениях ${\beta }{\text{.}}$ Вблизи внешних границ области $\left\{ {\mathbf{r}} \right\}$ такую же зависимость будут иметь контуры ${{{\iota }}_{L}},$ инициируемые одиночным продольным током, помещенным в начало координат. Холловские токи при этом будут ориентированы строго по направлениям касательных ${{{\mathbf{j}}}_{{\tau }}},$ и формируемое ими магнитное поле можно рассматривать как поле индукционного источника. Интенсивность ${{{\mathbf{j}}}_{H}}$ на линии ${{{\iota }}_{L}}$ обратно пропорциональна ее общей длине. На внутренних и внешнем контурах линии она одинакова. Из непрерывности тока следует возможность представления интенсивностей ${{{\iota }}_{L}},$ или ${{j}_{L}}\left( {{{{\mathbf{r}}}_{{L,F}}}} \right)$ в терминах ${{{\iota }}_{k}}$ и отношения холловской и педерсеновской проводимостей ионосферы.
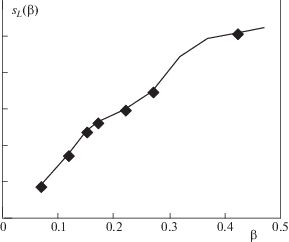
Рис. 4.
Зависимость длины ${{s}_{L}}$ от параметра $\beta $ для линий уровня ${{{\iota }}_{L}}$ на рис. 1б. Значения ${{s}_{L}}\left( {{{\beta }_{{\text{А}}}}} \right),$..${{s}_{L}}\left( {{{\beta }_{{\text{G}}}}} \right)$ отмечены ромбиками. При $\beta $ $ \lesssim $ 0.1 и $\beta $ $ \gtrsim $ 0.4 функция ${{s}_{L}}\left( \beta \right)$ практически линейна.
Неравномерность распределения узлов ${{{\mathbf{r}}}_{{L,F}}}$ вдоль линий ${{{\iota }}_{L}}$ видна на рис. 3, на котором также хорошо просматриваются ячейки криволинейной сети, образованные линиями ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}.$ Можно заметить, что чем выше кривизна силовых линий ${{{\iota }}_{F}},$ пересекающих линию уровня ${{{\iota }}_{L}},$ тем плотнее на ${{{\iota }}_{L}}$ располагаются узлы ${{{\mathbf{r}}}_{{L,F}}}.$ На практике такой способ определения плотности узлов более удобен, чем способ, указанный в разделе 2. Зная поведение ${{j}_{L}}\left( {{{{\mathbf{r}}}_{{L,F}}}} \right)$ и $\varphi \left( {{{{\mathbf{r}}}_{{L,F}}}} \right),$ можно рассчитать распределение магнитного поля холловских токов ${\mathbf{\tilde {B}}}\left( {{{{\mathbf{r}}}_{{m,n}}}} \right)$ в области ${\Omega ,}$ выполняя интегрирование как по узлам сети ${{{\mathbf{r}}}_{{m{\text{,}}n}}}$ области больших (в 1.5 раза линейных) размеров, так и по узлам ${{{\mathbf{r}}}_{{L,F}}}$ криволинейной координатной сети ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}.$ Высоту ионосферы примем равной 0.12–0.15 линейных размеров ${\Omega }{\text{.}}$
На рисунке 5а показано векторное поле холловских токов, инициируемых распределением двух вытекающих (${{{\iota }}_{1}} = 1,$ ${{{\iota }}_{3}} = 1.9$) и втекающего (${{{\iota }}_{2}}$ = –1.4) токов ${{j}_{{||}}},$ проекции которых обозначены закрашенными и незакрашенным ромбиками. Векторное поле горизонтальной составляющей магнитного поля ${\mathbf{\tilde {H}}}$ на поверхности Земли представлено на рис. 5б. Рисунок 5в отображает распределение вертикальной $\tilde {Z},$ рис. 5г – распределение модуля горизонтальной составляющей $\left| {{\mathbf{\tilde {H}}}} \right| = \sqrt {{{{\tilde {X}}}^{2}} + {{{\tilde {Y}}}^{2}}} $ магнитного поля. При увеличении линейных размеров области интегрирования в два раза точность представления $\tilde {Z}$ и $\left| {{\mathbf{\tilde {H}}}} \right|$ возрастает на 3% и соответствует точности интегрирования в криволинейной системе координат с верхним пределом $\beta ~$ ~ 0.5 и числом узлов ${{{\mathbf{r}}}_{{L,F}}},$ составляющим ∼60% от числа ${{{\mathbf{r}}}_{{m,n}}}.$
Рис. 5.
Распределение (а) поля холловских токов ${{{\mathbf{j}}}_{H}};$ (б) полной горизонтальной составляющей вычисленного магнитного поля ${\mathbf{\tilde {H}}};$ (в) вертикальной и (г) модуля полной горизонтальной компонент поля ${\mathbf{\tilde {B}}}.$ Закрашенными ромбиками показаны проекции вытекающих токов ${{j}_{{||,k}}},$ незакрашенным – втекающего. Штриховым овалом отмечена область влияния второго типа особенностей распределения интенсивности холловских токов ${{{\iota }}_{L}}\left( {x,~y} \right).$
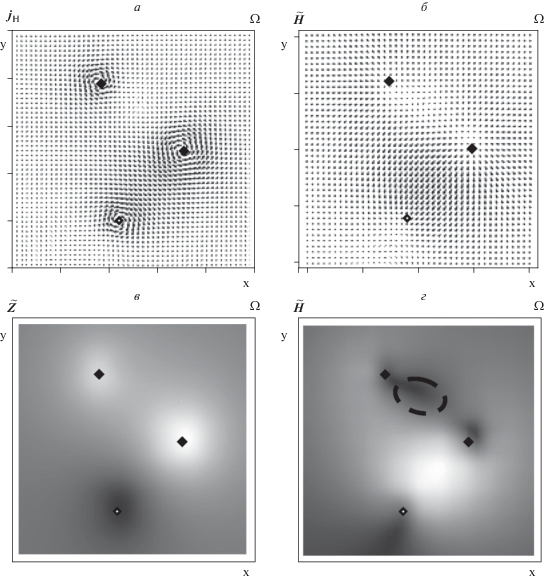
Распределение $\left| {{\mathbf{\tilde {H}}}} \right| \equiv \tilde {H}\left( {x,y} \right)$ на рис. 5г и распределение направлений векторов ${\mathbf{\tilde {H}}}$ на рис. 5б в целом неплохо согласуется с результатами моделирования магнитного поля пульсаций полем асимметричных диполей, помещенных на высоте ионосферы [Roldugin and Roldugin, 2008]. Однако, представленная нами модель учитывает заметные возмущения ${\mathbf{\tilde {H}}}{\text{,}}$ связанные с наличием особенностей типа 2 в распределениях поля холловских токов. На рисунке 5г область локализации этих возмущений обведена овалом, нарисованным жирной штриховой линией. Распределение $\tilde {Z}\left( {x,y} \right)$ на рис. 5в вполне согласуется с наблюдением [Петленко и др., 2011б] о совпадении локальных экстремумов вертикальной компоненты магнитного поля с положениями локальных ионосферных источников иррегулярных магнитных пульсаций типа Pi2.
4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Совпадение локальных экстремумов распределения $\tilde {Z}\left( {x,y} \right)$ и областей локализации особенностей типа 1 в распределениях ${{{\iota }}_{L}}\left( {x,y} \right)$ свидетельствуют о почти индукционном возмущении магнитного поля токами ${{{\mathbf{j}}}_{H}}$ в окрестности точек проекций ${{j}_{{||,k}}}$ на ионосферу, что подтверждается как линейностью ${{s}_{L}}\left( \beta \right)$ при малых значениях $\beta $ (рис. 4), так и почти совпадающими направлениями векторов ${{{\mathbf{j}}}_{H}}$ с касательными ${{j}_{{\tau }}}$ к линиям ${{{\iota }}_{L}}$ (рис. 3) вблизи внутренних границ области $\left\{ {\mathbf{r}} \right\}.$ Асимметричная форма контуров ${{{\iota }}_{L}},$ соответствующих малым значениям $\beta $, видна на рис. 1 и меняется при разных соотношениях интенсивностей продольных токов (рис. 2). Эта асимметрия присуща и распределению $\tilde {H}\left( {x,y} \right)$ на рис. 5г. Два локальных максимума и минимум $\tilde {Z}\left( {x,y} \right)$ на рис. 5в соответствуют двум вытекающим и втекающему токам ${{j}_{{||,k}}}.$ Отношения экстремальных значений $\tilde {Z},$ равные ∼1.8 и –1.3, примерно совпадают с заданными отношениями интенсивностей ${{{\iota }}_{k}}.$ То есть построенное по экспериментальным данным распределение вертикальной компоненты магнитного поля $Z$ позволяет оценить положения, интенсивности и направления продольных токов.
Алгебраические уравнения линий ${{{\iota }}_{F}}$ и ${{{\iota }}_{L}}$ решаются аналитически при $K$ = 4, 5 [Тюрин, 1989а]. Также как и в рассмотренном случае $K$ = 3 окрестности внутренних границ области $\left\{ {\mathbf{r}} \right\}$ можно рассматривать как локальные ионосферные источники магнитных пульсаций индукционного типа. При этом распределение вертикальной компоненты магнитного поля $\tilde {Z}$ имеет локальные экстремумы вблизи точек проекций ${{j}_{{||,k}}},$ а, следовательно, число локальных особенностей $Z$-компоненты измеренного поля равно количеству продольных токов, влияющих на измерения. Для последовательности измеренных распределений поля магнитных пульсаций в диапазоне периодов Pc4, Pi2 наблюдаются пульсирующие квазипериодические изменения интенсивности локальных ионосферных источников, практически не меняющих положения в течение нескольких полупериодов колебаний [Петленко и др., 2011б].
Такая стабильность хорошо согласуется с представлением о сбалансированном магнитном давлении установившихся холловских токов вдоль каждого ${{j}_{{||,k}}}.$ Изменение равновесия при смещении ${{j}_{{||,k}}}$ в $\left( {x,y} \right)$ плоскости обеспечивает устойчивость 3D токовой системы и центра тяжести линий ${{{\iota }}_{L}}$ при произвольных отношениях интенсивностей продольных токов ${{{\iota }}_{k}}.$ Центр тяжести силовых линий меняет положение при относительных изменениях ${{{\iota }}_{k}},$ что приводит к изменениям в распределениях как направлений, так и интенсивностей векторов ${{{\mathbf{j}}}_{H}}.$ В частности, меняются форма, размеры и положение областей локализации особенностей ${{{\iota }}_{L}}\left( {x,y} \right)$ типа 2. Идентификация этих особенностей по принадлежности к модели с тем, или иным числом $K$ позволяет визуализовать внешнюю границу области влияния $\left\{ {\mathbf{r}} \right\}$ наблюдаемой совокупности ионосферных источников пульсаций и отследить относительные изменения ${{{\iota }}_{k}}$ за ее пределами.
Если расстояния между точками проекций ${{j}_{{||,k}}}$ примерно совпадают с высотой ионосферы, то радиусы кривизны линий ${{{\iota }}_{L}}$ и ${{{\iota }}_{F}}$ могут оказаться меньше h. Тогда в вычисленном по формулам (2), или (4) распределении ${\mathbf{\tilde {B}}}\left( {\mathbf{r}} \right)$ могут появиться мелкомасштабные особенности, смещенные относительно особенностей ${{{\iota }}_{L}}\left( {\mathbf{r}} \right).$ При измерениях на не слишком плотной сети магнитометров такие особенности не всегда проявляются в распределениях ${\mathbf{B}}\left( {\mathbf{r}} \right),$ что может приводить к значительным ошибкам определения положений и интенсивностей ионосферных источников пульсаций в отдельные моменты времени и существенно затрудняет интерпретацию последовательности распределений ${\mathbf{B}}\left( {\mathbf{r}} \right).$
5. ВЫВОДЫ
На примере трех продольных токов, координаты точек проекций и интенсивности которых предполагаются известными, показан способ построения распределений интенсивности, направления холловских токов и магнитного поля, индуцированного ими на поверхности Земли. Показано, что особенности распределений интенсивности холловских токов подразделяются на два типа так, что в области локализации особенностей первого типа попадают точки проекций продольных токов и локальные экстремумы вертикальной компоненты магнитного поля. Вытекающим токам соответствуют максимумы, втекающим – минимумы вертикальной компоненты, экстремальные значения магнитного поля пропорциональны их интенсивностям, что объясняется тем, что холловские токи вблизи точек проекций продольных формируют в ионосфере источник индукционного типа.
Установленное соответствие положений особенностей позволяет оценивать количество, положения, интенсивности и направления продольных токов, инициирующих наблюдаемые распределения поля магнитных пульсаций. Наиболее достоверные оценки получаются для магнитных пульсаций типа Pi2, Pc4 (и более длиннопериодных пульсаций), расстояния между ионосферными источниками которых превышают высоту ионосферы.
Список литературы
− Айнс Э.Л. Обыкновенные дифференциальные уравнения. Харьков: ОНТИ. 719 с. 1939.
− Арнольд В.И. Дополнительные главы теории обыкновенных дифференциальных уравнений. М.: Наука. 304 с. 1978.
− Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М.: Наука. 336 с. 1989.
− Копытенко Ю.А., Распопов О.М. Некоторые особенности в распределении концентрации плазмы и поля альвеновских скоростей в магнитосфере Земли // Космич. исслед. Т. 6. С. 611–616. 1968.
− Ляцкий В.Б., Плясова-Бакунина Т.А. О влиянии геомагнитных пульсаций Рс4 на пульсации Рс1 // Геомагнетизм и аэрономия. Т.26. С. 802–806. 1986.
− Петленко А.В., Копытенко Ю.А., Петрова А.А., Петрищев М.С. и рабочая группа BEAR. О возможном влиянии поля региональных магнитных аномалий на положение локальных источников геомагнитных пульсаций // Материалы V всероссийской школы-семинара им. М.Н. Бердичевского и Л.Л. Ваньяна по электромагнитным зондированиям Земли – ЭМЗ-2011. Книга 1. – СПб.: СПбГУ. С. 279–281. 2011а.
− Петленко А.В., Копытенко Ю.А., Мартинес В.А., Пилипенко В.А., Исмагилов В.С. Тонкая структура геомагнитных пульсаций типа Pi2 // Геомагнетизм и аэрономия. Т. 51. С. 592–607. 2011б.
− Ролдугин В.К., Беленькая Б.Н., Мальцева Н.Ф. Электрические поля в ионосфере во время пульсирующих сияний // Геомагнетизм и аэрономия. Т. 11. С. 813–818. 1971.
− Тамм И.Е. Основы теории электричества. М.: ФИЗМАТЛИТ. 616 с. 2003.
− Тюрин А.Н. Дополнение Г. В книге Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М.: Наука. С. 320–324. 1989а.
− Тюрин А.Н. Дополнение В. Там же. С. 301–319. 1989б.
− Чеботарев Н.Г. Теория алгебраических функций. М.: ОГИЗГИТТЛ. 396 с. 1948.
− Чеботарев Н.Г. Теория Галуа. М.: Книжный дом ЛИБРОКОМ. 152 с. 2009.
− Coble A.B. An application of Moore’s cross-ratio group to the solution of the sextic equation // Trans. Am. Math. Soc. V. 12. P. 311–325. 1911.
− Kato Y., Tamao T. Hydromagnetic oscillations in a conducting medium with Hall conductivity under the uniform magnetic field // Sci. Rept. Tohoku Univ. Ser. 5, Geophys. V. 7. P. 147–164.1956.
− Klein F. Über die Auflӧsung der allgemeinen Gleichungen fünften und sechsten Grades // Math. Ann. V. 61. P. 50–71. 1905.
− Roldugin V.C., Roldugin A.V. Pc5 pulsations on the ground, in the magnetosphere and in the electron precipitation: Event of 19 January 2005 // J. Geophys. Res. V. 90. P. A04222–A04227. 2008.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


