1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 59, № 3, 2019

Геомагнетизм и аэрономия, 2019, T. 59, № 3, стр. 364-373

Эффект анизотропии ионосферных неоднородностей при регистрации сбоев фазовых измерений ГНСС

И. В. Безлер 1, 2, *, А. Б. Ишин 3, **, Е. В. Конецкая 1, 2, ***, М. В. Тинин 1, 2, ****

1 Иркутский государственный университет (ИГУ)
г. Иркутск, Россия

2 Институт солнечно-земной физики СО РАН (ИСЗФ СО РАН)
г. Иркутск, Россия

3 Иркутский национальный исследовательский технический университет (ИрНИТУ)
г. Иркутск, Россия

* E-mail: bezlerbl@mail.ru
** E-mail: ishin@iszf.irk.ru
*** E-mail: cpb7.12.2010@gmail.com
**** E-mail: mtinin@api.isu.ru

Поступила в редакцию 13.04.2016
После доработки 14.05.2018
Принята к публикации 24.01.2019

Полный текст (PDF)

Аннотация

При прохождении сигнала глобальной навигационной спутниковой системы через анизотропную случайно неоднородную ионосферу появляются фазовые и амплитудные флуктуации (мерцания). При этом проявляется двойное влияние магнитного поля Земли: не только на показатель преломления ионосферной плазмы, но и на форму ионосферных неоднородностей, обусловливая их “вытянутость” вдоль силовых линий. Это наблюдается в пространственно-временнóм распределении сбоев измерений, связанных с фазовыми мерцаниями. Ранее была показана зависимость плотности сбоев сопровождения фазы несущей частоты системы GPS от угла между лучом спутник−приемник и направлением магнитного поля на высоте ионосферы в возмущенных условиях. В настоящей статье эти исследования дополнены сравнением с измерениями в спокойных условиях и исследованиями ракурсных зависимостей плотности сбоев в системе GPS. Кроме того, проведенное численное моделирование эффекта анизотропии ионосферных неоднородностей не только показало хорошее качественное согласие с экспериментальными данными, но и позволило определить факторы, маскирующие эффекты анизотропии.

1. ВВЕДЕНИЕ

Как известно [Klobuchar and Kunches, 2003], ионосфера оказывает существенное влияние на работу глобальных навигационных спутниковых систем (ГНСС), таких, например, как ГЛОНАСС и GPS. К сожалению, изменчивость ионосферы затрудняет коррекцию ионосферных ошибок путем моделирования. Более точный подход использует зависимость ионосферной ошибки от частоты. Если ограничиться рассмотрением фазовых измерений, как более точных по сравнению с измерениями временнóй задержки сигнала (кодовыми измерениями), то для фазового пути φ( f) из первого приближения геометрической оптики имеем [Grewal et al., 2007; Xu, 2007]

(1)
$\varphi (f) = D - \frac{{40.3}}{{{{f}^{2}}}}{{I}_{{1g}}} + ...\,\,.$

Здесь в D входят кроме расстояния между спутником и наземным наблюдателем все другие поправки к фазовому пути, не зависящие от частоты (например, задержка в тропосфере);

(2)
${{I}_{{1g}}} = \int\limits_{{{z}_{0}}}^{{{z}_{t}}} {N(z{\text{'}})dz{\text{'}}} $
− интеграл от электронной плотности N(r) по прямой, соединяющей наземный приемник со спутником, называемый полным электронным содержанием (ПЭС); f − частота излучения. Поправка первого порядка, второе слагаемое в (1), пропорциональное f −2, описывает влияние ионосферной плазмы на распространение сигнала ГНСС в пренебрежении дифракционными эффектами, эффектом геомагнитного поля (поправкой второго порядка) и отклонением луча от прямой (поправкой третьего порядка).

Измеряя фазу на двух частотах из соотношения (1) получаем систему для двух неизвестных D и I1g, решая которую получаем результат двухчастотных измерений (см., например, [Grewal et al., 2007; Xu, 2007]):

(3)
$D \approx {{D}^{{(2)}}} = \frac{{{{\varphi }_{1}}f_{1}^{2} - {{\varphi }_{2}}f_{2}^{2}}}{{f_{1}^{2} - f_{2}^{2}}},$
(4)
${{I}^{{(2)}}} = \frac{{f_{1}^{2}f_{2}^{2}}}{{40.3}}\frac{{{{\varphi }_{1}} - {{\varphi }_{2}}}}{{f_{1}^{2} - f_{2}^{2}}}.$

Выражения (3) и (4) – так называемые свободная от ионосферы и свободная от геометрии комбинации наблюдения соответственно [Beutler et al., 1996].

Многие исследователи (см., например, [Bassiri and Hajj, 1993; Hoque and Jakowski, 2008] изучали возможность повышения точности двухчастотных измерений путем исследования отброшенной в выражении (1) поправки второго порядка, учитывающей влияние геомагнитного поля на показатель преломления ионосферы, и, следовательно, на фазовую скорость сигнала ГНСС. В исследованиях [Тинин и Конецкая, 2013; Kedar et al., 2003; Kim and Tinin, 2011; Tinin and Konetskaya, 2014 и цитированных там статьях] изучена возможность повышения точности в приближении тонкого слоя, погрешность которого 1−2 мм [Bassiri and Hajj, 1993; Hoque and Jakowski, 2008; Тинин и Конецкая, 2013], поправка второго порядка выражается через поправку первого порядка, и при известной модели геомагнитного поля ее можно вычислить [Bassiri and Hajj, 1993; Hoque and Jakowski, 2008; Kedar et al., 2003] или учесть непосредственно в двухчастотных измерениях путем модификации свободной от ионосферы комбинации (3) [Тинин и Конецкая, 2013; Kim and Tinin, 2011; Tinin and Konetskaya, 2014]. После учета остаточной ошибки второго порядка дальнейшее повышение точности связано с учетом ошибки третьего порядка. В геометрооптическом приближении эта ошибка, пропорциональная f −4, в основном, связана с отклонением траектории от прямой линии и может быть устранена в трехчастотных измерениях [Ким и Тинин, 2007]. Однако это возможно, когда масштабы ионосферных неоднородностей (например, регулярной, фоновой неоднородности ионосферного слоя) превышают радиус первой зоны Френеля и можно использовать геометрооптическое приближение. Присутствие в ионосфере неоднородностей с масштабами меньше первой зоны Френеля приводит к тому, что это приближение становится неприменимым, и ионосферные ошибки из-за дифракционных эффектов приобретают более сложную зависимость от частоты. В силу этого, в трехчастотных измерениях по сравнению с двухчастотными измерениями уменьшается только средняя ошибка, а дисперсия случайной ошибки не только не уменьшается, но и возрастает [Kim and Tinin, 2011; Tinin, 2015а]. Пространственная обработка сигнала ГНСС в виде френелевской инверсии позволяет устранить дифракционные эффекты и уменьшить ошибку третьего порядка [Tinin, 2015а, b].

Вышеприведенные результаты повышения точности двухчастотных ГНСС измерений получены при наличии измерений фазы на двух частотах. Однако на процесс измерения фазы сигналов в приемниках ГНСС значительное влияние оказывают различные факторы космической погоды: всплески солнечного радиоизлучения, возмущения в магнитном поле Земли, регулярная структура и динамика ионосферы, неоднородности ионосферной плазмы. Все эти факторы могут приводить к искажению ГНСС сигнала и затруднять проведение фазовых измерений. Есть много работ, посвященных срывам фазовых измерений во время геомагнитных возмущений (см., например, [Skone, 2001; Skone and Jong, 2000; Афраймович и Перевалова, 2006; Афраймович и др., 2002]). При этом на стабильность функционирования системы ГНСС оказывают существенное влияние фазовые мерцания при прохождении ГНСС сигнала через случайные ионосферные неоднородности [Skone et al., 2001; Knepp, 2004; Hofmann-Wellenhof et al., 2008], что особенно актуально для высоких и низких широт [Wernik et al., 2004]. Связаны эти эффекты со сложной динамикой ионосферы в авроральной зоне и регионе действия экваториальной аномалии. Однако в отдельных случаях на сетях станций ГНСС регистрируются нарушения функционирования системы, вызванные крупномасштабными ионосферными неоднородностями, и на средних широтах. Так, в статье [Ma and Maruyama, 2006] авторы указывают на большие градиенты полного электронного содержания, регистрируемые одновременно с многочисленными сбоями сопровождения фазы несущей на частоте L2 системы GPS. По мнению авторов это показательный пример проявления “ионосферного пузыря” (super bubble) − вытянутой вдоль магнитного поля области пониженной электронной концентрации, заполненной случайными неоднородностями.

Срыв сопровождения фазы (сбой) часто связывают с превышением флуктуации фазового пути целого числа циклов [Hofmann-Wellenhof et al., 2008], что может быть связано с “нефизичными значениями” скорости изменения ПЭС [Захаров и др., 2017]. Анизотропия ионосферных неоднородностей приводит к анизотропии рассеяния, что в свою очередь проявляется в зависимости сбоев ГНСС измерений от ориентации LOS спутник−наблюдатель относительно силовой линии магнитного поля Земли. Таким образом, наблюдение за этой зависимостью может дать ценную информацию об анизотропии ионосферных неоднородностей. В статье [Afraimovich et al., 2011] с помощью сети GEONET было проведено исследование наблюдавшегося над территорией Японии крупного “пузыря” электронной концентрации 12 февраля 2000 г. Анализ сбоев, наблюдаемых на частоте L2 GPS, показал, что плотность сбоев достигает максимума на лучах, направленных вдоль магнитного поля на ионосферных высотах. Отсюда был сделан вывод о вытянутости мелкомасштабной структуры наблюдаемого “пузыря” вдоль магнитного поля. К сожалению, в работе [Afraimovich et al., 2011] не было показано, насколько регулярно наблюдается такая ситуация, связано ли это с “пузырем”, и каковы будут угловые характеристики плотности сбоев при отсутствии подобных крупномасштабных неоднородностей.

Настоящая работа посвящена развитию исследований, начатых в статье [Ишин и др., 2016], посвященных связи сбоев ГНСС измерений с ориентацией неоднородностей вдоль геомагнитного поля путем численного моделирования и привлечения большего числа измерений.

2. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

В качестве экспериментальных данных нами были использованы данные двухчастотных геодезических приемников GPS, входящих в японскую сеть GEONET [http://mekira.gsi.go.jp]. Анализу подвергались сбои на дополнительной частоте L2. Частота L2 оказывается гораздо более чувствительным индикатором фазовых сбоев, что обусловлено характеристиками передатчиков на спутниках GPS. Отношение сигнал/шум на частоте L2 меньше, чем на частоте L1, из-за того, что мощность передатчика L2 спутника GPS на 6 Дб меньше, чем передатчика основной частоты L1 [Hofmann-Wellenhof et al., 2008]. Достоверность определения различных параметров сигнала (число циклов фазы, доплеровское смещение частоты, соотношение сигнал/шум и др.) указывается в выходном файле приемника. Общепринятым стандартом для хранения и передачи данных системы GPS является формат RINEX. В нем, в частности, есть специальные флаги, указывающие на срыв сопровождения фазы несущей конкретно на дополнительной частоте. Однако внутренние алгоритмы приемника не являются открытыми. Из-за этого сложно установить наличие события сбоя сопровождения фазы в течение тридцатисекундного интервала времени. В нашей работе мы вычисляем относительное число сбоев сопровождения фазы на частоте L2 для всех спутников и всех приемников в текущий момент времени. Эту величину мы называем “плотность сбоев”.

2.1. Сбои по данным сети GEONET

Для обеспечения значительной статистики нами обработаны данные плотной японской сети GEONET (рис. 1а) за 100 дней 2008 г. Лучше было бы обработать данные соседних дней, однако, к сожалению, они доступны только за отдельную плату. В состав сети входит более чем 1200 станций с приемниками GPS. В каждый конкретный момент приемник осуществляет слежение за сигналами не менее чем шести навигационных спутников. Для рассмотрения были взяты только спутники с углом места более 5° над горизонтом. Нам были доступны данные измерений радионавигационных параметров, зафиксированные один раз в 30 с. Таким образом, нами было обработано более чем 2 × 109 измерений.

Рис. 1.

Расположение станций GPS сети GEONET в Японии − черные точки (a), треки ионосферных точек за сутки для одной станции − 37.6° N, 140.6° W (б).

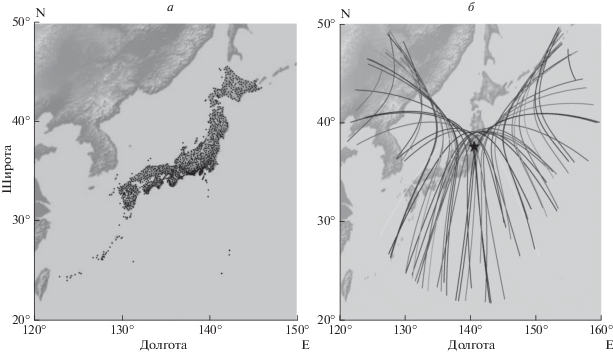
При использовании такой плотной сети станций мы смогли в течение 100 дней сканировать значительную область ионосферы: порядка 40° по широте и долготе (рис. 1б). Весь купол неба был разбит на азимутальные секторы по 45° с центральным направлением по азимутам: 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°. Для этих секторов получены зависимости плотности сбоев сопровождения фазы на частоте L2 от угла места спутника (рис. 2, 3).

Рис. 2.

Зависимости плотности сбоев сопровождения фазы несущей от угла места спутника для сети GEONET (верхняя панель). Зависимости количества наблюдений от угла места (нижняя панель). Данные приведены для азимутальных секторов с центрами 315°, 0° и 45° (штрихпунктирной, тонкой сплошной и штриховой линиями соответственно). Модельные расчеты сбоев (серая сплошная линия) проводились без учета магнитоориентированности неоднородностей.

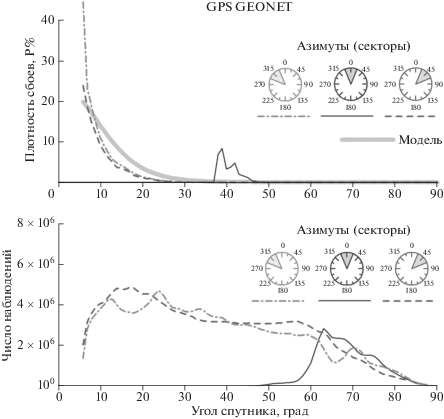
Рис. 3.

Зависимости плотности сбоев сопровождения фазы несущей от угла места спутника для сети GEONET (верхняя панель). Зависимости количества наблюдений от угла места (нижняя панель). Данные приведены для азимутальных секторов с центрами 225°, 180° и 135 (штрихпунктирной, тонкой сплошной и штриховой линиями соответственно). Модельные расчеты сбоев (серая сплошная линия) проводились без учета магнитоориентированности неоднородностей.

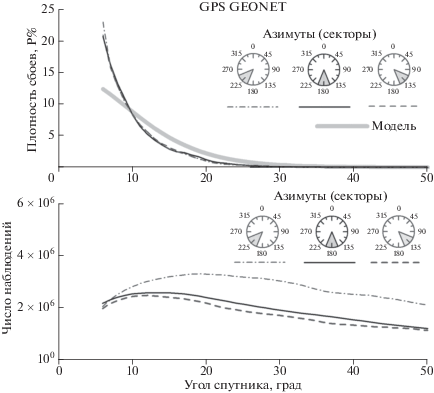
Для северного сектора на низких углах места спутники не появляются (рис. 2, нижняя панель, сплошная тонкая линия). Это видно по положению ионосферных точек (рис. 1б). Именно с этим связано увеличение плотности сбоев на углах ~40° (рис. 2, тонкая сплошная линия). Для остальных секторов (рис. 2, 3) наблюдается рост плотности фазовых сбоев L2 с уменьшением угла места (при угле возвышения 6° относительное число сбоев достигает значения 20–30%). Учитывая анизотропию рассеяния на ионосферных неоднородностях, следовало бы ожидать увеличение плотности сбоев в южном секторе (секторе с азимутом 180) и углах места 25°−30°, при коллинеарности луча “спутник−приемник” и направления магнитного поля на высоте ионосферы. Однако мы не наблюдаем ожидаемого эффекта (рис. 3, тонкая сплошная линия). В указанном секторе характер зависимостей плотности сбоев от угла места спутника такой же, как и в остальных секторах (рис. 2, 3). Таким образом, можно сделать вывод, что максимум плотности сбоев на низких углах связан исключительно с увеличением эффективной толщины ионосферы с уменьшением угла места спутника.

2.2. Сбои по данным сети GEONET в присутствии ионосферного “пузыря”

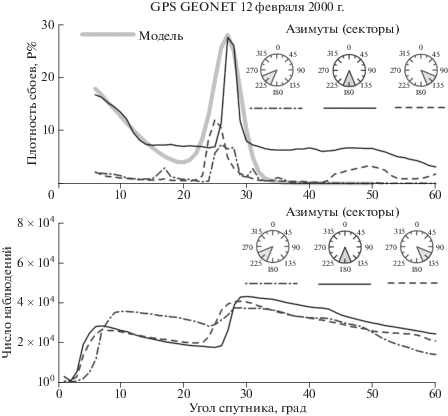
Для поиска ожидаемых эффектов, вызванных манитоориентированностью мелкомасштабной структуры ионосферной неоднородности нами были построены аналогичные зависимости отдельно для 12 февраля 2000 г. (рис. 4). Как и ожидалось, эффект магнитной ориентации неоднородностей действительно проявился для южного сектора (рис. 4, тонкая сплошная линия), где наблюдается соответствующее увеличение плотности более 25% для углов места 26°−30°. Для южного сектора именно на углах 25°−30° наблюдаются условия параллельности луча “спутник−приемник” и силовой линии на высоте ионосферы. Для секторов с азимутами 135° и 225° (рис. 4, штриховая и штрихпунктирная линии соответственно) также наблюдается увеличение плотности сбоев, хотя и меньшее по значению (до 8−12%). Для остальных секторов характер зависимости 12 февраля 2000 г. незначительно отличается от накопленных данных (рис. 2, 3), поэтому они не были представлены в настоящей статье.

Рис. 4.

Зависимости плотности сбоев сопровождения фазы несущей от угла места спутника для сети GEONET (верхняя панель) для 12 февраля 2000 г. Зависимости количества наблюдений от угла места (нижняя панель). Данные приведены для азимутальных секторов с центрами 225°, 180° и 135 (штрихпунктирной, тонкой сплошной и штриховой линиями-соответственно). Модельные расчеты сбоев проводились с учетом магнитоориентированности неоднородностей.

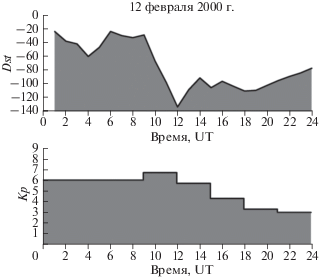
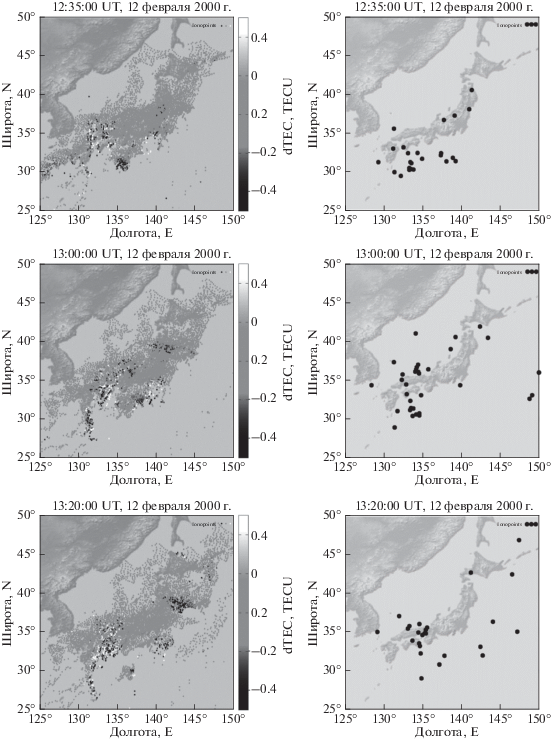
Нами была проверена гипотеза о взаимосвязи возникновения сбоев сопровождения фазы с большими градиентами ПЭС. Для этого были построены карты ПЭС с положениями ионосферных точек измерений (рис. 5, левые панели) и карты ионосферных точек для лучей со сбоями (рис. 5, правые панели). Ряды полного электронного содержания, получаемые из измерений на одном приемнике при пролете одного спутника, фильтровались для удаления тренда скользящим средним с окном 0−10 мин. Оттенками серого указано значение вариаций ПЭС для данного луча “спутник−приемник” в указанный на рисунке момент времени. Видно, что на южном направлении для целого ряда станций наблюдались значительные вариации ПЭС (амплитудой до 1 TECU). Кроме того, на ближайших ионосферных точках (разнесенных на единицы километров) могли быть противоположные отклонения (см. рис. 5, левые панели). Это свидетельствует о больших градиентах ПЭС и о наличии мелкомасштабной структуры наблюдаемой неоднородности. При сравнении левой и правой панелей рис. 5 видно, что наибольшее число сбоев наблюдается именно в тех регионах, где присутствуют максимальные градиенты ПЭС, т.е. на лучах, проходящих через возмущенную область. Нужно отметить, что указанные эффекты наблюдались на фоне возмущенной геомагнитной обстановки. В рассматриваемый день регистрировалась умеренная геомагнитная буря: индекс Kp достигал значений 6.6, Dst достигал −130 (рис. 6).

Рис. 5.

Положение ионосферных точек для всех спутников и всех приемников над территорией Японии (левые панели) в отдельные моменты времени и соответствующие этим точкам амплитуды вариаций ПЭС. Положение ионосферных точек, для которых регистрировались сбои сопровождения фазы несущей на дополнительной частоте GPS (правые панели), в эти же моменты времени.

Рис. 6.

Геомагнитные условия во время эксперимента.

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Для исследования связи наблюдавшихся зависимостей сбоев сопровождения от угла места было проведено численное моделирование. Ввиду отсутствия достаточной информации о параметрах ионосферы во время получения экспериментальных данных, параметры при моделировании выбирались для согласия экспериментальных и модельных данных. При этом полагалось [Hofmann-Wellenhof et al., 2008], что сбои обусловлены флуктуациями фазы 2πfφ/c (c − скорость света) и вероятность сбоя равна вероятности превышения флуктуацией фазы некоторого порога, который был взят равным π. Выбор порога в данном случае всего лишь вопрос нормировки, и он не влияет на качественную картину моделирования условий, приводящих к появлению сбоев. Таким образом, моделируя вероятность превышения флуктуации фазы, мы считали, что указанная вероятность и есть вероятность сбоя. Учитывая, что при большом пути распространения сигнала в случайно неоднородной ионосфере флуктуации фазы распределены по нормальному закону [Rytov et al., 1989], для вероятности сбоя получаем

(5)
$P = \left( {1 - {\text{Erf}}\left( {\frac{\pi }{{\sqrt {2{{\sigma }^{2}}} }}} \right)} \right) \times 100\% .$
Здесь σ2 − дисперсия флуктуаций фазы; Erf(x) − интеграл вероятностей [Абрамовиц и Стиган, 1979]. Случайные флуктуации фазы в геометрооптическом приближении находятся из выражений (1)−(2), после учета того, что электронная плотность $N(r) = \bar {N}(r) + \tilde {N}(r)$ ионосферной плотности включает в себя детерминированную $\bar {N}(r)$ и случайную $\tilde {N}(r)$ составляющие. Аналогично тому, как сделано в работах [Briggs and Parkin, 1963; Wheelon, 2004], получаем
(6)
$\begin{gathered} {{\sigma }^{2}} = \frac{{{{{(k40.3)}}^{2}}2\sqrt \pi {\kern 1pt} \Gamma ({p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2})}}{{{{f}^{{{\kern 1pt} 4}}}\Gamma ({{(p - 3)} \mathord{\left/ {\vphantom {{(p - 3)} {2)({p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2} - 1)}}} \right. \kern-0em} {2)({p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2} - 1)}}}}\frac{{\alpha {{l}_{ \bot }}}}{{\sqrt {{{{\cos }}^{2}}\theta + {{\alpha }^{2}}{{{\sin }}^{2}}\theta } }} \times \\ \times \,\,\int\limits_{{{z}_{0}}}^{{{z}_{t}}} {\sigma _{N}^{2}(z{\text{'}})dz{\text{'}}} . \\ \end{gathered} $
Здесь θ – угол между волновым вектором и вектором геомагнитного поля; $\sigma _{N}^{2}(r)$ – дисперсия электронной плотности; p = 11/3; α = l⊥/lz, l⊥ = = lx = ly и lz – соответственно поперечные и продольные масштабы случайных неоднородностей, спектр которых в отличие от гауссова закона, использованного Briggs and Parkin [1963], задан степенным законом

(7)
$\begin{gathered} {{\Phi }_{N}}(\chi ,r) = \frac{{l_{ \bot }^{2}{{l}_{z}}\Gamma ({p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2})\sigma _{N}^{2}(r)}}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\Gamma ({{(p - 3)} \mathord{\left/ {\vphantom {{(p - 3)} 2}} \right. \kern-0em} 2})}} \times \\ \times \,\,{{[1 + \chi _{1}^{2}l_{1}^{2} + l_{ \bot }^{2}(\chi _{x}^{2} + \chi _{y}^{2})]}^{{{{ - p} \mathord{\left/ {\vphantom {{ - p} 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $

На первой стадии моделирования полагалось, что σN(r) пропорциональна фоновой плотности $\bar {N}(r)$

(8)
${{\sigma }_{N}}(r) = {{\sigma }_{0}}\bar {N}(r).$

В качестве модели ионосферы (зависимость фоновой электронной плотности $\bar {N}(z)$ от высоты z) был взят Чепменовский слой:

(9)
$\begin{gathered} \bar {N}(z) = {{N}_{{\max }}} \times \\ \times \,\,\exp \left[ {{{\left( {1 - \frac{{z - {{z}_{{\max }}}}}{{{{h}_{m}}}} - \exp \left[ { - \frac{{z - {{z}_{{\max }}}}}{{{{h}_{m}}}}} \right]} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \frac{{z - {{z}_{{\max }}}}}{{{{h}_{m}}}} - \exp \left[ { - \frac{{z - {{z}_{{\max }}}}}{{{{h}_{m}}}}} \right]} \right)} 2}} \right. \kern-0em} 2}} \right]. \\ \end{gathered} $

Здесь hm – полутолщина слоя; Nmax = ${{f_{c}^{{\text{2}}}} \mathord{\left/ {\vphantom {{f_{c}^{{\text{2}}}} {{\text{8}}0.{\text{6}}}}} \right. \kern-0em} {{\text{8}}0.{\text{6}}}}$ – электронная плотность в максимуме zmax; fc – критическая частота ионосферного слоя. В качестве модели магнитного поля Земли была выбрана модель IGRF [Mandea and Macmillan, 2000]. Задавались географические координаты приемника, азимут и угол места спутника.

На рисунках 2, 3 (сплошная серая линия) представлены результаты моделирования вероятности сбоев ГНСС как функции угла возвышения для фоновой ионосферы с изотропными неоднородностями (α = 1). Параметры ионосферы были выбраны: zmax = 320 км, hmax= 50 км и критическая частота fc = 12 MHz. Полученный результат демонстрирует монотонное падение вероятности сбоя фазы с увеличением угла возвышения спутника, что обусловлено уменьшением толщины ионосферного слоя и соответствующим уменьшением числа неоднородностей на пути распространения сигнала от спутника к приемнику для модели (8)–(9). В целом, рис. 2, 3 демонстрируют хорошее качественно совпадение модельных и экспериментальных данных.

Особенный интерес представляет исследование появления второго максимума плотности сбоев на рис. 4. Для этого было проведено моделирование случая, когда фоновые неоднородности вытянуты вдоль магнитных силовых линий (α < 1) при тех же остальных ионосферных параметрах, что и на рис. 2, 3. Моделирование проводилось для географических координат наблюдателя 34.4° N и 134.7° E (Япония), как и в работе [Afraimovich et al., 2011]. Однако при моделировании не удалось обнаружить резкий рост плотности сбоев на углах 26°–30°. Таким образом, присутствие второго максимума не может быть объяснено анизотропией неоднородностей ионосферы при использовании модели (8).

Следуя выводам работы [Afraimovich et al., 2011], для объяснения этого эффекта к модели ионосферы с изотропными неоднородностями была добавлена модель анизотропного “пузыря” электронной концентрации. “Пузырь” задавался вытянутой вдоль геомагнитного поля гауссовой областью, содержащей анизотропные неоднородности [Wernik et al., 2004]. Остальные ионосферные параметры и географические координаты наблюдателя были взяты такими же, как и для рис. 2, 3. Степень вытянутости была задана равной α = 0.33, центр “пузыря” был расположен на высоте 500 км, вертикальный размер был выбран 100 км, степень вытянутости “пузыря” также взята равной 0.33. Расчеты производились для азимута 180°, совпадающего с азимутом центра “пузыря”. Интенсивность в центре “пузыря” была 0.33Nmax. В зависимости вероятности сбоев от угла возвышения (серая кривая на рис. 4) видны два максимума. Первый обусловлен увеличением длины участка траектории в среде со случайными изотропными неоднородностями при уменьшении угла возвышения, как наблюдалось ранее на рис. 2, 3. Второй максимум связан с дополнительным влиянием ориентации траектории относительно неоднородностей, вытянутых вдоль геомагнитного поля, которое обусловлено увеличением рассеяния при уменьшении угла между направлениями луча и геомагнитной силовой линией. Кроме того, сказывается увеличение пути сигнала через вытянутую область “пузыря”. Положение второго максимума и его параметры зависят от координат приемника, азимута, положения и параметров “пузыря” ионизации. В целом, сравнение рис. 2, 3 и рис. 4 демонстрируют хорошее совпадение результатов наблюдений и моделирования.

4. ВЫВОДЫ

Сравнение результатов наблюдения и моделирования показало, что появление двух областей повышения сбоев в работе ГНСС, наблюдавшееся Afraimovich et al. [2011], связано с влиянием двух факторов на флуктуации фазы. Первый фактор, связанный с увеличением дисперсии фазы с уменьшением угла возвышения, обусловлен увеличением числа неоднородностей на траектории при увеличении участка траектории внутри неоднородного слоя (т.е. с увеличением “эффективной толщины” ионосферы). Второй фактор связан с анизотропией рассеяния на неоднородностях, вытянутых вдоль силовых линий геомагнитного поля. В результате в зависимости сбоев от угла возвышения появляется максимум, соответствующий траектории, направление которой наиболее близко к направлению силовой линии геомагнитного поля. Это проявляется в виде анизотропии наблюдаемых сбоев. Кроме того, моделирование показало, что анизотропия существенна при достаточно малых углах между направлением распространения сигнала и магнитным полем Земли, что затрудняет обнаружение таких эффектов на практике.

Однако эффект анизотропии может усилиться при неоднородном распределении случайных неоднородностей в ионосфере. В частности, во время умеренной магнитной бури это наблюдалось 12 февраля 2000 г. По-видимому, это событие связано с пришедшим с нижних широт “пузырем”, наполненным турбулентными неоднородностями меньших масштабов. Анизотропия сбоев в этом случае связана не только с анизотропией мелкомасштабного наполнения, но и с анизотропией “пузыря” [Wernik et al., 2004]. На это указывает распределение положения сбоев и областей с максимальными градиентами ПЭС (см. рис. 5).

Стоит также отметить, что при статистической обработке длинных рядов данных (100 дней) обнаружить сколько-нибудь заметного влияния магнитоориентированных неоднородностей на лучи вблизи магнитного зенита не удалось. Это указывает на то, что появление пузыря в ионосфере над Японией − явление достаточно редкое.

Для исследования возможности прогнозирования сбоев и их использования в мониторинге неоднородной ионосферы необходимо дальнейшее изучение связи сбоев с параметрами комплексной модели анизотропного “пузыря” электронной плотности с мелкомасштабным анизотропным заполнением на фоне слабоанизотропной турбулентной ионосферной плазмы.

Приведенные в работе исследования влияния анизотропии ионосферных неоднородностей на сбои в работе ГНСС с помощью численного моделирования были выполнены И.В. Безлер, Е.В. Конецкой и М.В. Тининым при поддержке Российского научного фонда (проект № 14-37-00027), приведенные экспериментальные данные получены Ишиным А.Б. рамках базового финансирования программы ФНИ II.16.

Список литературы

  1. − Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука. 832 с. 1979.

  2. − Афраймович Э.Л., Лесюта О.С., Ушаков И.И. Геомагнитные возмущения и функционирование навигационной системы GPS // Геомагнетизм и аэрономия. Т. 42. № 2. С. 220−227. 2002.

  3. − Афраймович Э.Л., Перевалова Н.П. GPS-мониторинг верхней атмосферы Земли. Иркутск: изд-во ГУ НЦ РВХВ СНЦ СО РАМН. 480 с. 2006.

  4. − Захаров В.И., Ясюкевич Ю.В., Пронин В.Е. Метод статистического определения уровня сбоев полной электронной концентрации по данным GPS наблюдений // Учен. зап. физич. фак. Московского ун-та. № 1. С. 171 901. 2017.

  5. − Ишин А.Б., Тинин М.В., Безлер И.В., Конецкая Е.В. Влияние анизотропии ионосферных неоднородностей на работу ГНСС // Изв. вузов. Физика. Т. 59. С. 88−92. 2016.

  6. − Ким Б.-Ч., Тинин М.В. Влияние ионосферных неоднородностей на точность двухчастотных систем GPS // Геомагнетизм и аэрономия. Т. 47. № 2. С. 254−259. 2007.

  7. − Тинин М.В., Конецкая Е.В. Влияние геомагнитного поля на ионосферную ошибку спутниковых навигационных систем // Геомагнеизм и аэрономия. Т. 53. № 6. С. 788–796. 2013.

  8. − Afraimovich E.L., Ishin A.B., Tinin M.V., Yasyukevich Yu.V., Jin S.G. First evidence of anisotropy of GPS phase slips caused by the mid-latitude field-aligned ionospheric irregularities // Adv. Space Res. V. 47. P. 1674–1680. 2011.

  9. − Bassiri S., Hajj G.A. Higher order ionospheric effects on global positioning system observables and means of modeling them // Manuscripta Geodaetica. № 18. P. 280–289. 1993.

  10. − Briggs B.H., Parkin I.A. On the variation of radio star and satellite scintillations with zenith angle // J. Atmos. Terr. Phys. V. 25. P. 339–365. 1963.

  11. − Beutler G., Brockmann E., Fankhauser S., Gurtner W., Johnson J., Mervart L., Rothacher M., Schaer S., Springer T., Weber R. Bernese GPS Software Version 4.0. Bern: University of Berne. 1996.

  12. − Grewal M.S., Weill L.R., Andrews A.P. Global Positioning Systems, Inertial Navigation, and Integration. N.Y.: Wiley. 525 p. 2007.

  13. − Hoque M.M., Jakowski N. Estimate of higher order ionospheric errors in GNSS positioning // Radio Sci. V. 43. № 5. 2008. https://doi.org/10.1029/2007RS003817

  14. − Hofmann-Wellenhof B., Lichtenegger H., Wasle E. GNSS – Global Navigation Satellite Systems. GPS, GLONASS, Galileo, and more. Wien: Springer-Verlag. 2008.

  15. − Kedar S., Hajj G.A., Wilson B.D., Heflin M.B. The effect of the second order GPS ionospheric correction on receiver positions // Geophys. Res. Lett. V. 30. № 16. P. 1829–1832. 2003. https://doi.org/10.1029/2003GL017639

  16. − Kim B.C., Tinin M.V. Potentialities of multifrequency ionospheric correction in Global Navigation Satellite Systems // J. Geodesy. V. 85. P. 159–169. 2011. https://doi.org/10.1007/s00190-010-0425-z

  17. − Knepp D. L. Effects of ionospheric scintillation on Transit satellite measurement of total electron content // Radio Sci. V. 39. RS1S11. 2004. https://doi.org/10.1029/2002RS002825

  18. − Klobuchar J.A., Kunches J.M. Comparative range delay and variability of the Earth’s troposphere and ionosphere // GPS Solut. V. 7. № 1. P. 55–58. 2003.

  19. − Ma G., Maruyama T. A super bubble detected by dense GPS network at east Asian longitudes // Geophys. Res. Lett. L21103. 2006. doi 33https://doi.org/10.1029/2006GL027512

  20. − Mandea M., Macmillan S. International Geomagnetic Reference Field the eighth generation // Earth Planets Space. V. 52. № 12. P. 1119–1124. 2000.

  21. − Rytov S.M., Kravtsov Yu. A., Tatarskii V.I. Introduction to statistical radiophysics. Wave propagation through random media. V. 4. N.Y.: Springer-Verlag. 1989.

  22. − Skone S.H. The impact of magnetic storms on GPS receiver performance // J. Geodesy. V. 75. № 9–10. P. 457–468. 2001. https://doi.org/10.1007/ S001900100198

  23. − Skone S., de Jong M. The impact of geomagnetic substorms on GPS receiver performance // Earth Planets Space. V. 52. P. 1067–1071. 2000.

  24. − Skone S., Knudsen K., de Jong M. Limitations in GPS reciever tracking performance under ionospheric scintillation conditions // Phys. Chem. Earth (A). V. 26. № 6–8. P. 613−621. 2001.

  25. − Tinin M.V., Konetskaya E.V. Eliminating the second-order ionospheric error in dual-frequency global navigation satellite systems // J. Atmos. Solar-Terr. Phys. V. 107. № 1. P. 99−103. 2014.

  26. − Tinin M.V. Eliminating diffraction effects during multi-frequency correction in global navigation satellite systems // J. Geodesy. V. 89. P. 491–503. 2015a. https://doi.org/10.1007/s00190-015-0794-4

  27. − Tinin M.V. Influence of Ionospheric Irregularities on GNSS remote sensing// Adv. Meteorol. ID 532015. 2015b. http://dx.doi.org/https://doi.org/10.1155/2015/532015

  28. − Wernik A.W., Alfonsi L., Materassi M. Ionospheric irregularities, scintillation and its effect on systems // Acta Geophys. Pol. V. 52. № 2. 2004.

  29. − Wheelon A.D. Electromagnetic Scintillation // Geometrical optics. V. 1. Cambridge: Cambridge University Press. 2004.

  30. − Xu G. GPS Theory, algorithms and applications. 2nd ed. Springer: N.Y. 340 p. 2007. http://mekira.gsi.go.jp

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал