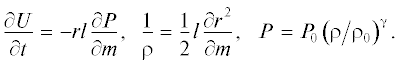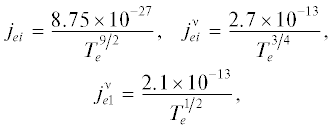Геомагнетизм и аэрономия, 2019, T. 59, № 3, стр. 340-363
Динамика плазменного сгустка на начальной и последующей стадии движения в разреженном газе
С. Г. Баннов 1, А. М. Житлухин 2, А. А. Моторин 4, *, Е. Л. Ступицкий 3, 4, **, А. С. Холодов 4, В. Е. Черковец 2
1 Научно-испытательный центр ракетно-космической промышленности (ФКП “НИЦ РКП”)
г. Пересвет (Московская обл.), Россия
2 Государственный науный центр Российской Федерации Троицкий институт инновационных
и термоядерных исследований (АО “ГНЦ РФ ТРИНИТИ”)
г. Москва, г. Троицк, Россия
3 Московский физико-технический университет (МФТИ)
г. Москва, Россия
4 Институт автоматизации проектирования РАН (ИАП РАН)
г. Москва, Россия
* E-mail: vansp91@gmail.com
** E-mail: stup@bk.ru
Поступила в редакцию 07.01.2018
После доработки 05.09.2018
Принята к публикации 24.01.2019
Аннотация
Выполнены физические и подробные численные исследования генерации плазменных сгустков высокой удельной энергии с помощью плазменной пушки. Рассчитаны параметры плазменного сгустка на выходе из плазменного ускорителя и при распространении в ионосфере (h > 200 км) на значительные расстояния (≈100 км). Представлен специальный численный алгоритм по определению результатов воздействия разреженного высокоскоростного газового потока (v ∼ 5 × 107 см/с) на поверхность кристаллических и аморфных твердых тел.
1. ВВЕДЕНИЕ
В настоящее время исследования, направленные на разработку и использование плазменных пушек, активно развиваются. В России большой цикл экспериментальных работ выполнен в ТРИНИТИ и посвящен как разработке генераторов плазменных сгустков высокой удельной энергии, так и исследованию их импульсного воздействия на твeрдотельную мишень [Степанов и Сиднев, 1989; Польский и др., 1984; Архипов и др., 1985; Сиднев и Скворцов, 1987; Борисов и др., 1994]. В США по данной теме также был выполнен ряд работ с целью издания импульсного плазменного генератора с наиболее высокими энергетическими и динамическими характеристиками [Hartman and Hammer, 1982; Degnan et al., 1993; Hussey et al., 1993]. Достаточно содержательной и, вместе с тем, краткий обзор работ ведущих плазменных лабораторий США по данному направлению сделан в статье [Degnan et al., 1993]. Основные экспериментальные результаты данной работы посвящены исследованиям на установке MARAUDER и были направлены на анализ процесса генерации компактного плазменного тороида (СТ) высокой удельной энергии и оценке характеристик высокотемпературной плазменной области, образующейся при взаимодействии падающего и отраженного от твердотельной мишени потоков непосредственно при выходе СТ из генератора, поперечные и продольные масштабы которого порядка метров.
Отличительная и практически важная особенность работ [Степанов и Сиднев, 1989; Польский и др., 1984; Архипов и др., 1985; Сиднев и Скворцов, 1987; Борисов и др., 1994] заключаeтся, прежде всего, в значительно меньших масштабах самого генератора, что может сделать область его применения достаточно широкой. При движении плазменного сгустка в вакууме или сильно разреженном газе увеличиваются его масштабы, уменьшаются плотность, температура и степень ионизации, а, следовательно, и характер взаимодействия с окружающей разреженной газовой средой и геомагнитным полем. Исследование этих процессов важно для решения целого ряда фундаментальных и прикладных вопросов физики плазмы [Дьяченко и др., 1969; Филипп и др., 1986; Операция “Аргус”, 1960; Операция “Морская звезда”, 1964; Галеев и Сагдеев, 1964; Koopman and Gotorth, 1974; Ананьин и др., 1985; Brunetkin et al., 1992; Алипченков, 1978]. Так как масштабы сгустка при этом существенно возрастают, и он перестает быть компактным, то в дальнейшем будем называть его ТПС (тороидальный плазменный сгусток).
В работах [Ступицкий и Репин, 1996; Репин и Ступицкий, 2004; Репин и др., 2004; Ступицкий, 2006] был разработан двумерный численный алгоритм, на основе которого исследовалась самая начальная стадия динамики тороидального плазменного сгустка при выходе из генератора и движении в вакууме, а также взаимодействие взаимопроникающих падающего и отраженного от преграды потоков, с определением параметров генерируемого при этом электромагнитного возмущения.
В связи с созданием компактных плазменных генераторов, естественно, существенно расширяется область их практического использования, прежде всего, обусловленная возможностью распространения сгустка на значительные расстояния в разреженной атмосфере. В связи с этим подобные устройства часто называют плазменной пушкой.
Работа космической техники в околоземном космическом пространстве (ОКП) в значительной степени основана на использовании оптико-электронных средств (ОЭС). Как в самих ОЭС, так и в средствах их защиты используются диэлектрические материалы типа стекол, обладающих высокой степенью прозрачности.
Таким образом, анализ возможного использования плазменных пушек для исследований научных и прикладных вопросов динамики плазменных сгустков в ионосфере включает в себя последовательное решение трех основных задач:
− формирование ТПС и его движение на начальной стадии – сразу же после выхода из генератора, когда определяющее влияние на его структуру оказывает внутренний тороидальный ток и генерируемое им полоидальное магнитное поле;
− численное исследование движения частично-ионизованного ТПС в разреженной ионосфере, когда внутренний ток уже мал и определяющее влияние на его структуру и движение оказывают процессы столкновительного взаимодействия плазмы сгустка с разреженным окружающим газом при их взаимопроникновении в результате высокоскоростного относительного движения;
− численное исследование воздействия разреженного газового потока, образованного ТПС, на поверхность прозрачного диэлектрика.
Цель данной работы состоит в математическом моделировании начальной и последующей стадии движения ТПС в разреженном газе, а также воздействие высокоскоростного потока на поверхность твердого тела.
2. ФИЗИЧЕСКАЯ КАРТИНА ФОРМИРОВАНИЯ И ДИНАМИКИ ТОРОИДАЛЬНОГО ПЛАЗМЕННОГО СГУСТКА
Электромагнитные ударные трубы, которые используются для создания интенсивных ударных волн, известны достаточно давно. В основе их действия используются эффекты нагревания газа электрическим разрядом и ускорения его под действием магнитных сил. Разрядный ток течет в радиальном направлении между электродами, одним из которых служит стержень, расположенный на оси трубки, а другим – цилиндр вблизи поверхности трубки. Радиальный ток разряда взаимодействует с концентрическим магнитным полем самого тока и тока, текущего по центральному электроду. Пондеромоторная сила направлена вдоль оси трубки и ускоряет плазму в этом направлении. Физически ясный анализ таких устройств и соответствующие оценки кратко изложены в известной монографии [Зельдович и Райзер, 2008]. Дальнейшее развитие работ в этом направлении было связано с созданием плазменных пушек. Важной отличительной особенностью плазменных пушек является наличие мощного тороидального тока в вылетающим из генератора торообразном плазменном сгустке. Как показано в работе [Degnan et al., 1993] радиальное магнитное поле, формирующее тороидальный ток, создаeтся специальным токовым витком, помещенным в начальной части канала. При движении СТ в этом поле тороидальный ток создает собственное полоидальное магнитное поле, которое оказывает определяющее влияние на сохранение компактной структуры плазменного сгустка на начальной стадии его движения, после вылета из генератора.
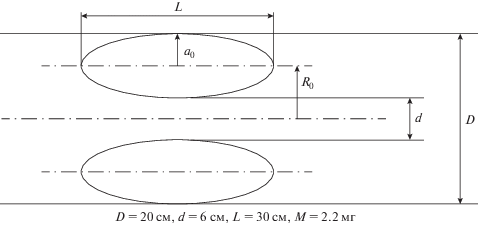
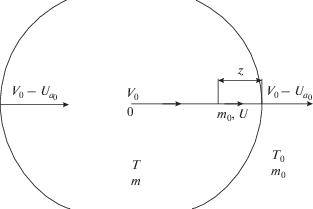
В работе [Degnan et al., 1993] основное внимание уделено исследованию электродинамики сгустка при его движении в генераторе, поэтому были получены приближенные значения основных параметров разряда в процессе формирования СТ. Эти значения совершенно необходимы для прогнозирования дальнейшего поведения СТ после выхода из генератора. К сожалению, во многих, имеющихся по данному вопросу работах, достаточно определенно известны лишь некоторые интегральные характеристики плазменного сгустка: масса и скорость направленного движения. Что касается его внутренних параметров: электронной и ионной температуры, тороидального тока внутри СТ и соответственно величины магнитного поля, то их в этом случае, по-видимому, можно оценить лишь на основе физических представлений, основанных, в определенной степени, на конкретном эксперименте. Так, электронная и ионная температуры, определяемые развитием самого разряда внутри генератора и ускорением в сходящемся канале, по оценкам работ ТРИНИТИ [Степанов и Сиднев, 1989; Польский и др., 1984; Архипов и др., 1985; Сиднев и Скворцов, 1987; Борисов и др., 1994] на выходе из канала составляют величины порядка 10 и 40 эВ соответственно. Геометрия плазменного сгустка на выходе импульсного плазменного ускорителя имеет примерно следующие характеристики, показанные на рис. 1.
Рассматривается водородная плазма с массой сгустка $M = 2.2\quad\,\,{\text{м г }}.$ Использование реальной геометрии сечения тора, с $L > 2{{a}_{0}},$ по-видимому, дает возможность определить концентрацию частиц плазмы, близкую к эксперименту, однако существенно усложняет расчет полоидального магнитного поля. Если принять, что объем плазмы равен $V = 2\pi {{R}_{0}}2{{a}_{0}}L,$ где ${{R}_{0}} = \frac{{D + d}}{4} = 6.5$ см; ${{a}_{0}} = \frac{{D - d}}{4} = 3.5$ см для указанных D, d, L, M получаем: общее число ионов водорода N = = $\frac{M}{{{{m}_{i}}}} = 1.31 \times {{10}^{{21}}};$ объем ${{V}_{0}} = 8573$ см3 и концентрация ионов ${{n}_{0}} = \frac{N}{{{{V}_{0}}}} = 1.5 \times {{10}^{{17}}}$ см–3. Как показали расчеты [Ступицкий, 2006а], сразу после вылета из генератора геометрические характеристики торового кольца быстро меняются под действием полоидального магнитного поля и внутреннего давления. В соответствии с принципом минимума магнитной части потенциальной энергии существует тенденция к сокращению длины силовых линий поля, и можно полагать, что огибающая поперечного сечения тора быстро приобретет форму, близкую к окружности. Если положить, что площадь поперечного сечения $S = \pi a_{0}^{2},$ где ${{a}_{0}} = \frac{{D - d}}{4} = 3.5$ см, ${{R}_{0}} = \frac{{D + d}}{4} = 6.5\quad$ см, то ${{V}_{0}} = 2\pi {{R}_{0}}\pi a_{0}^{2} = 1570$ см3 и соответственно n0 = = $8.3 \times {{10}^{{17}}}$ см–3, т.е. примерно в 5−6 раз выше, чем по экспериментальным оценкам. Если использовать ${{n}_{0}} = 1.5 \times {{10}^{{17}}}$ см–3, то для этого необходимо изменить ${{R}_{0}} = 11.5$ см и ${{a}_{0}} = 6.2$ см, т.е. значительно изменить начальную геометрию вылетающего из генератора тора, что может существенно изменить начальную картину его развития, поэтому в расчетах принималось ${{a}_{0}} = 3.5\quad\,\,{\text{с м }},$ ${{R}_{0}} = 6.5\,\,\quad{\text{с м }}.$
В данной работе создан математический алгоритм определения параметров тороидального плазменного сгустка (ТПС), применимый для достаточно широкого спектра начальных условий. Поэтому для предварительных исследований начальные данные выбирались из физических соображений, примерно соответствующих экспериментально допускаемым значениям.
Будем предполагать, что тороидальный ток в ТПС, определяется радиальной составляющей магнитного поля ${{B}_{r}},$ создаваемой витком с током ${{I}_{k}} \cong 5$ кА и с расстоянием от витка до поверхности ТПС $\delta \cong 1{\kern 1pt} - {\kern 1pt} 3$ см, тогда радиальную составляющую магнитного поля в области внутри ТПС можно оценить как
(1)
${{B}_{r}} = \frac{1}{{2{{a}_{0}}}}\int\limits_{\delta }^{2{{a}_{0}}} {\frac{{{{\mu }_{0}}{{I}_{k}}}}{{2\pi r}}dr} = \frac{{{{\mu }_{0}}{{I}_{k}}}}{{4\pi {{a}_{0}}}}\ln \left( {\frac{{2{{a}_{0}}}}{\delta }} \right),$(2)
$\sigma = \frac{3}{{4\sqrt {2\pi m} }}\quad\,\frac{{{{{\left( {k{{T}_{e}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{{e}^{2}}\bar {z}{{L}_{k}}\left( {{{1 + {{\nu }_{{e0}}}} \mathord{\left/ {\vphantom {{1 + {{\nu }_{{e0}}}} {{{\nu }_{{ei}}}}}} \right. \kern-0em} {{{\nu }_{{ei}}}}}} \right)}}.$Можно полагать для отношения частот столкновений ${{{{\nu }_{{e0}}}} \mathord{\left/ {\vphantom {{{{\nu }_{{e0}}}} {{{\nu }_{{ei}}}}}} \right. \kern-0em} {{{\nu }_{{ei}}}}} = 0;$ $\bar {z} = 1.$ Для кулоновского логарифма имеем:
Как известно, измерения электронной и ионной температуры в плазменных потоках, движущихся с большой скоростью, представляют серьезные трудности. Оценим время электрон-ионного энергообмена:
(4)
${{\tau }_{{ei}}} = \frac{{3.15 \times {{{10}}^{8}}\mu T_{{{\text{э В }}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}{{{{n}_{i}}{{z}^{2}}{{L}_{k}}}}.$Для $T = 10$ эВ; ${{n}_{i}} = 8.3 \times {{10}^{{17}}}$ см–3, $\mu = 1;$ $z = 1$ получим ${{L}_{k}} = 6.3$ и ${{\tau }_{{ei}}} = 1.9 \times {{10}^{{ - 9}}}$ с. Для $T = 35$ эВ; ${{n}_{i}} = 1.5 \times {{10}^{{17}}}$ см–3, получаем ${{L}_{k}} = 9$ и τei = = $2.8 \times {{10}^{{ - 8}}}$ с. Вместе с тем характерное время развития и движения разряда в генераторе длиною порядка 1 м со скоростью $\sim {\kern 1pt} 3 \times {{10}^{7}}$ см/с составляет $\sim {\kern 1pt} 3 \times {{10}^{{ - 6}}}$ с, т.е. на 2−3 порядка больше. Поэтому можно считать, что в вылетающем из генератора плазменном сгустке ${{T}_{e}} = {{T}_{i}},$ т.е. плазма однотемпературная. Тогда, полагая в (2), (3) ${{T}_{e}} = 10$ эВ; ${{n}_{i}} = 8.3 \times {{10}^{{17}}}$ см–3; $\bar {z} = 1,$ получаем для проводимости $\quad\sigma \,\,\quad{\text{в }}\,\,\left( {\frac{{{\text{С м }}}}{{\text{м }}}} \right)$
(5)
$\sigma = 0.97 \times {{10}^{4}}\frac{{T_{{e,{\text{э В }}}}^{{\frac{3}{2}}}}}{{\bar {z}{{L}_{k}}}}\quad\quad\quad = 4.87 \times {{10}^{4}}\quad{\text{.}}$Тогда тороидальный ток можно оценить как $I = S\sigma U{{B}_{r}}.$ Полагая $S = \pi a_{0}^{2} = 3.85 \times {{10}^{{ - 3}}}$ м2; $U = 3 \times {{10}^{5}}$ м/с; ${{B}_{r}} = 0.013$ Тл, получим $I \cong 0.7$ МА. Такой ток создает на поверхности тороида полоидальное магнитное поле ${{{{B}_{{\varphi }}} \approx {{\mu }_{0}}I} \mathord{\left/ {\vphantom {{{{B}_{{\varphi }}} \approx {{\mu }_{0}}I} {2\pi {{a}_{0}} \cong 4}}} \right. \kern-0em} {2\pi {{a}_{0}} \cong 4}}$ Тл.
Таким образом, начальное распределение энергии в кДж в ТПС при выходе из генератора примерно следующее:
Ионизационная энергия ${{E}_{i}}$ и тепловая ${{E}_{T}}$ значительно меньше кинетической энергии направленного движения, где $\mathcal{T} = 13.6\quad\quad{\text{э В }}.$
Как показал проведенный анализ, для расчета начальной стадии ТПС после выхода из генератора, когда на его параметры определяющее влияние оказывает магнитное поле, создаваемое тороидальным током, можно принять следующие, достаточно согласованные, исходные параметры: ${{I}_{0}} = 0.7$ МА; ${{a}_{0}} = 3.5$ см; ${{R}_{0}} = 6.5$ см; ${{T}_{{e0}}} = {{T}_{{i0}}} = $ = 10 эВ; ${{n}_{{i0}}} = 8.3 \times {{10}^{{17}}}$ см–3; ${{U}_{0}} = 3 \times {{10}^{7}}$ см/с.
Дальнейшее изменение геометрических и внутренних характеристик ТПС будет происходить самосогласованно и определяться, прежде всего, внутренним тепловым давлением и магнитным полем, пока масса захватываемого сильно разреженного окружающего газа будет значительно меньше массы ТПС. По мере движения, в результате действия внутреннего омического сопротивления величина тороидального тока будет уменьшаться, а, следовательно, будет уменьшаться действие магнитного поля на изменение геометрических характеристик ТПС. Если бы разлет происходил в вакуум, то в отсутствии поля изменение ТПС имело бы чисто газодинамический характер. Однако при движении в разреженном газе необходимо учитывать взаимодействие с ним, которое происходит в процессе взаимопроникновения плазмы и газа, что существенно усложняет математический анализ последующей стадии ТПС. Для более всестороннего понимания эволюции ТПС в процессе движения в данной работе происходила постепенная детализация и уточнение поставленной задачи.
3. ПРИБЛИЖЕННЫЙ ЧИСЛЕННЫЙ АНАЛИЗ ПОВЕДЕНИЯ ТОРОИДАЛЬНОГО ГАЗОВОГО СГУСТКА В ОТСУТСТВИИ МАГНИТНОГО ПОЛЯ. МОДЕЛЬНАЯ ЗАДАЧА
Вначале рассмотрим поведение однородного цилиндрического газового слоя, в одномерном цилиндрическом приближении. Газ предполагается идеальным. Тогда исходная система уравнений относительно $U,$ $\quad\rho ,$ $P,$ r в лагранжевых координатах имеют вид:
Пусть начальные параметры ${{a}_{0}},$ ${{R}_{0}},$ ${{T}_{0}},$ ${{\rho }_{0}},$ где ${{a}_{0}},$ ${{R}_{0}}$ – внутренний и внешний радиусы цилиндрического слоя; ${{T}_{0}},$ ${{\rho }_{0}}$ – начальная температура и плотность газа. В качестве характерных значений для обезразмеривания системы используем: ${{R}_{x}} = {{R}_{0}};$ ${{U}_{x}} = \sqrt {{{\gamma k{{T}_{0}}} \mathord{\left/ {\vphantom {{\gamma k{{T}_{0}}} m}} \right. \kern-0em} m}} ;$ ${{t}_{x}} = {{{{R}_{x}}} \mathord{\left/ {\vphantom {{{{R}_{x}}} {{{U}_{x}}}}} \right. \kern-0em} {{{U}_{x}}}};$ ${{\rho }_{x}} = {{\rho }_{0}};$ ${{P}_{x}} = {{\rho }_{x}}U_{x}^{2} = \gamma {{P}_{0}};$ $\gamma = {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}.$ В безразмерных величинах вид системы (6)–(9) не меняется, уравнение для давления будет $\bar {P} = {{{{{\bar {\rho }}}^{{\gamma }}}} \mathord{\left/ {\vphantom {{{{{\bar {\rho }}}^{{\gamma }}}} {\gamma }}} \right. \kern-0em} {\gamma }}.$ Тогда краевые условия будут иметь вид:
Начальные координаты границ лагранжевых ячеек определялись выражением
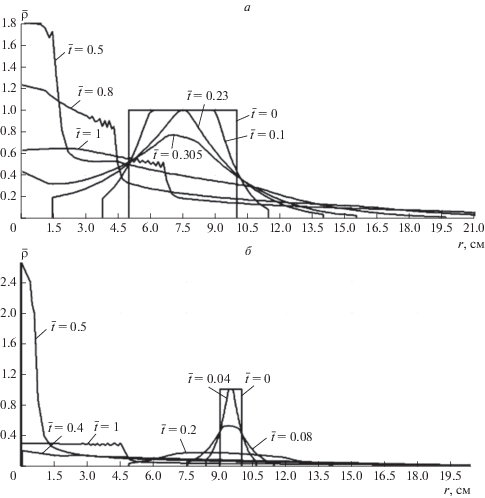
Для расчета использовалась разностная схема Броуда [Броуд, 1971] с искусственной вязкостью Неймана. Как следует из безразмерных уравнений и начальных условий, единственным параметром, определяющим развитие течения, является ${{\bar {a}}_{0}}.$ Как следует из расчетов (рис. 2а, 2б для ${{\bar {a}}_{0}} = 0.5$ и $0.9$ соответственно), при любых ${{\bar {a}}_{0}}$ внутренний фронт волны разрежения, имеющий отрицательную скорость, доходит до центра, где происходит сжатие газа и фронт сжатия начинает распространяться от центра вслед за фронтом внешней волны разрежения.
Рис. 2.
Распределение плотности по радиусу при различной начальной толщине цилиндра (а) $\quad{{a}_{0}}$ = 5 см; (б) ${{a}_{0}}$ = 9 см.
Так как в реальных условиях начальная длина цилиндра ${{l}_{0}}$ всегда конечна, то следовало оценить влияние ухода массы через торцы цилиндра на радиальное движение газа. Использовалась квазидвумерная постановка, в предположении, что длина цилиндра меняется по закону l(t) = = ${{l}_{0}} + \frac{2}{{\gamma - 1}}{{c}_{0}}t,$ где ${{c}_{0}}$ – скорость звука в газе при $t = 0.$ Тогда уравнения будут:
На рисунке 3а показаны результаты расчета для плотности в строго одномерной и квазидвумерной постановке. Хотя плотность во втором случае, естественно, падает значительно быстрее, однако положение фронтов волн разрежения практически совпадает.
Рис. 3.
Сравнение распределений плотности для строго одномерной и квазиодномерной задачи для случая ${{a}_{0}}$ = 5 см (а). Структура кольца, имеющего начальную скорость $\bar {U} = 2.2\quad$ (б).
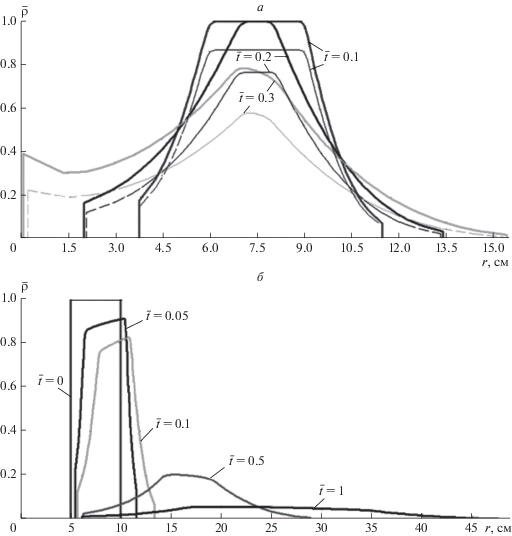
Таким образом, представленные результаты, полученные при нулевом значении начальной скорости газа, и отсутствии каких-либо внешних сил, действующих внутри кольца тороида и направленных по радиусу от центра, показали, что кольцеобразная структура быстро схлопывается в расширяющийся сплошной диск при любых начальных значениях ${{a}_{0}},$ от которого зависит только время схлопывания. Однако дальнейшие расчеты показали, что если принять начальную радиальную скорость тороида $\bar {U}\left( {\bar {t} = 0} \right) \geqslant 2,$ то внутренняя волна разрежения не достигает центра и кольцеобразное расширение будет продолжаться по времени (рис. 3б). Отметим, что это значение $\bar {U} = 2$ меньше максимального значения $\bar {U} = {2 \mathord{\left/ {\vphantom {2 {\left( {\gamma - 1} \right)}}} \right. \kern-0em} {\left( {\gamma - 1} \right)}} = 3$ для фронта плоской волны разрежения, т. к. в данном случае движение цилиндрическое и не автомодельное.
4. ФИЗИКО-МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ О НАЧАЛЬНОЙ СТАДИИ ДИНАМИКИ ТОРОИДАЛЬНОГО ПЛАЗМЕННОГО СГУСТКА
Динамика ТПС описывается изменением двух главных параметров $R\left( t \right)$ и $a\left( t \right).$ Изменение $R\left( t \right)$ определяется радиальной силой растяжения, создаваемой давлением магнитного поля внутри торового кольца и пропорциональным квадрату силы тока ${{I}^{2}},$ протекающему внутри тора, а также действием внутреннего давления внутри ТПС. Выражение для обоих составляющих силы были получены в работах [Осовец и Щедрин, 1958; Голант и др., 1972; Арцимович и Сагдеев, 1972]. Используя их, уравнение для $R\left( t \right)$ можно приближенно записать в виде:
(11)
${{M}_{0}}\frac{{{{d}^{2}}R}}{{d{{t}^{2}}}} = 2{{\pi }^{2}}{{a}^{2}}\bar {P} + \frac{{{{I}^{2}}}}{{2{{c}^{2}}}}\frac{{\partial L}}{{\partial R}}.$Здесь $\bar {P} = nkT + {{n}_{e}}k{{T}_{e}}$ – среднее давление плазмы внутри ТПС; $L = 2\pi R\left[ {\ln \left( {\frac{R}{a}} \right) + 0.25} \right]$ – индуктивность тора.
Для расчета изменения $a\left( t \right)$ пренебрегаем разницей давлений на внутренней и внешней огибающей границе тора и используем уравнение для плазменного цилиндра с продольным током; для скорости внутри него имеем:
(12)
$\rho \frac{{dU}}{{dt}} = - \frac{{\partial P}}{{\partial r}} + \frac{1}{c}{{\left[ {{\mathbf{j}} \times {\mathbf{B}}} \right]}_{z}}.$Учитывая, что 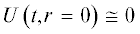 и то, что со временем магнитное давление на границе падает, будем приближенно полагать,
что скорость меняется линейно по радиусу:
и то, что со временем магнитное давление на границе падает, будем приближенно полагать,
что скорость меняется линейно по радиусу:
Тогда в пределах $0 \leqslant r \leqslant a$ получаем:
Магнитная сила связана только с наличием полоидального поля ${{B}_{{\theta }}} = B,$ а ток – только по оси тора ${{j}_{z}} = j.$ Тогда из уравнений Максвелла:
Получим ${{j}_{z}} = j = \frac{c}{{4\pi r}}\frac{{\partial Br}}{{\partial r}},$ и для магнитной силы, направленной по радиусу $a,$ имеем:
Тогда уравнение (12) можно переписать в виде:
(13)
$4\pi \rho {{r}^{3}}\frac{{\ddot {a}}}{a} = - 4\pi {{r}^{2}}\frac{{\partial P}}{{\partial r}} - Br\frac{{\partial Br}}{{\partial r}}.$Если проинтегрировать это уравнение от $r = 0$ до $r = a,$ то
Тогда из (13) получаем:
(14)
$\frac{{\ddot {a}}}{a}\int\limits_0^a {4\pi \rho {{r}^{3}}dr} = 4\pi {{a}^{2}}\bar {P} - \frac{{{{B}^{2}}\left( a \right){{a}^{2}}}}{2}.$В рамках принятых приближений можно полагать, что плотность $\rho $ мало меняется по сечению тора, тогда из (14) получаем:
(15)
$\frac{{\bar {\rho }{{a}^{2}}}}{4}\quad\frac{{\ddot {a}}}{a} = \bar {P} - \frac{{{{B}^{2}}\left( a \right)}}{{8\pi }},$Тогда из (15) окончательно получим:
(16)
$M\left( t \right)\ddot {a} = 4\pi a\left( {\bar {P} - \frac{{{{B}^{2}}\left( a \right)}}{{8\pi }}} \right),$Давление:
(18)
$\begin{gathered} \quad\bar {P} = k\left( {{{n}_{i}} + {{n}_{0}}} \right){{T}_{i}} + k{{n}_{e}}{{T}_{e}} = \\ = kn{{T}_{i}} + k{{n}_{e}}{{T}_{e}} = k\left( {{{T}_{i}} + \alpha {{T}_{e}}} \right)n, \\ \end{gathered} $(19)
$\bar {P} = \frac{{k\left( {{{T}_{i}} + \alpha {{T}_{e}}} \right)}}{{2{{\pi }^{2}}{{a}^{2}}R}}\frac{{{{M}_{0}}}}{m}$Изменение тока в торе после выхода из генератора можно получить из закона электромагнитной индукции:
так как ${{\varepsilon }_{i}} = I{{R}_{c}};$ ${\Phi } = \frac{1}{c}LI,$ где ${{R}_{c}} = \frac{1}{\sigma }\frac{{2\pi R}}{{\pi {{a}^{2}}}}$ – сопротивление торового кольца; $L = 2\pi R\left[ {\operatorname{l} {{nR} \mathord{\left/ {\vphantom {{nR} {a + \frac{1}{4}}}} \right. \kern-0em} {a + \frac{1}{4}}}} \right]$ – его индуктивность. Тогда из (20) получаем:
Откуда получаем дифференциальное уравнение для тока:
(22)
$\frac{{dI}}{{dt}} = - I\frac{{{{c}^{2}}{{R}_{c}} + \dot {L}}}{L}\,\,\,\,{\text{и л и }}\,\,\,\,\quad\frac{{dI}}{{dt}} = - \frac{I}{\tau },$(23)
$I = {{I}_{0}}{\text{exp}}\left[ { - \mathop \smallint \limits_0^t \frac{{dt{\text{'}}}}{{\tau (t{\text{'}})}}} \right],$Из (21) также можно получить решение и в другом виде:
(25)
$I = {{I}_{0}}\frac{{{{L}_{0}}}}{L}{\text{exp}}\left[ { - \int\limits_0^t {\frac{{dt{\kern 1pt} {\text{'}}}}{{\tau (t{\text{'}})}}} } \right].$Тогда $\tau (t{\text{'}}) = \frac{L}{{{{c}^{2}}{{R}_{c}}}}$ – такое же выражение как в работе [Ступицкий, 2006а].
Как из (23) так и из (25) видно, что учет изменений индуктивности во времени должен приводить к более быстрому падению тока. Индуктивность определяется геометрическими характеристиками торового кольца. Отметим, что при численном решении задачи удобно пользоваться уравнением (22) с $\tau ,$ определенным (24). Интегральные выражения иногда удобны для грубых качественных оценок.
Таким образом, динамическая часть уравнений, определяющих $R\left( t \right),$ $a\left( t \right),$ ${{U}_{R}}\left( t \right),$ ${{U}_{a}}\left( t \right),$ $I\left( t \right)$ имеет вид:
(27)
${{M}_{0}}\frac{{d{{U}_{R}}}}{{dt}} = 2{{\pi }^{2}}{{a}^{2}}P + \frac{{\pi {{I}^{2}}}}{{{{c}^{2}}}}\left[ {\ln \frac{R}{a} + \frac{5}{4}} \right],$(31)
$M\left( t \right) = {{{{M}_{0}}} \mathord{\left/ {\vphantom {{{{M}_{0}}} {2\pi R}}} \right. \kern-0em} {2\pi R}},\,\,\,\,\tau = \frac{L}{{{{c}^{2}}{{R}_{c}} + \dot {L}}},\,\,\,\,\dot {L} = {{dL} \mathord{\left/ {\vphantom {{dL} {dt}}} \right. \kern-0em} {dt}},$Для определения $P\left( t \right)$ и $\sigma \left( t \right)$ необходимо знать поведение во времени средних по объему ТПС значений ${{T}_{e}}\left( t \right),$ $T\left( t \right),$ $\alpha \left( t \right).$ Входящая в $\sigma \left( t \right)$ частота столкновений ${{\nu }_{e}}$ в общем случае зарядового состава плазмы определяется выражением:
(36)
${{\nu }_{{e0}}} = \frac{4}{3}{{\sigma }_{{e0}}}\overline {{{V}_{e}}} {{n}_{0}},\,\,\,\,\overline {{{V}_{e}}} = \sqrt {\frac{{8k{{T}_{e}}}}{{\pi {{m}_{e}}}}} \quad{\text{,}}$(37)
${{\nu }_{{ei}}} = \frac{{4\sqrt {2\pi } {{e}^{4}}{{L}_{k}}}}{{3\sqrt {{{m}_{e}}} {{{\left( {k{{T}_{e}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\quad\quad\sum {{{z}^{2}}{{n}_{z}}} .$Для движения плазмы в канале в выражении (2) для проводимости мы полагали $\frac{{{{\nu }_{{e0}}}}}{{{{\nu }_{{ei}}}}} = 0.$ После выхода из канала температура падает и в результате рекомбинации могут возникнуть нейтральные атомы водорода. Тогда из общей формулы (2) получаем
(38)
$\sigma = 8.73 \times {{10}^{{13}}}\frac{{T_{e}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}{{\bar {z}{{L}_{k}}\left( {1 + \delta } \right)}},\,\,\,\,\quad\frac{1}{c}.$Полагая для сечения ${{\sigma }_{{e0}}} = {{10}^{{ - 15}}}$ см2; $\bar {z} = 1;$ ${{L}_{k}} = 6.3$ получаем окончательно
(39)
$\sigma = 1.4 \times {{10}^{{13}}}\frac{{T_{e}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}{{1 + \delta }},$(40)
$\delta = {{{{\nu }_{{e0}}}} \mathord{\left/ {\vphantom {{{{\nu }_{{e0}}}} {{{\nu }_{{ei}}}}}} \right. \kern-0em} {{{\nu }_{{ei}}}}} = 4.9 \times {{10}^{{ - 3}}}T_{e}^{2}{{\left( {1 - \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \alpha } \right)} \alpha }} \right. \kern-0em} \alpha },$Среди кинетических процессов главную роль играет ионизация атомов водорода и возбуждение их электронных состояний. Так как плазма оптически тонкая даже для резонансных переходов, то возбуждение электронных состояний нейтральных атомов, концентрация которых по мере расширения и охлаждения плазмы будет возрастать, может сказываться на снижении электронной температуры. Для оценки роли этого процесса достаточно учесть возбуждения на второй электронный уровень. Для концентрации тяжелых частиц $n = {{n}_{0}} + {{n}_{i}}$ выполняется уравнение неразрывности. Поэтому уравнения кинетики для относительных концентраций электронов $\alpha = {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} n}} \right. \kern-0em} n}$ и возбужденных атомов ${{\alpha }_{1}} = {{{{n}_{1}}} \mathord{\left/ {\vphantom {{{{n}_{1}}} n}} \right. \kern-0em} n}$ имеют вид:
(41)
$n\frac{{d\alpha }}{{dt}} = \left( {{{n}_{0}}{{n}_{e}} - n_{e}^{3}{{j}_{{ei}}} - n_{e}^{2}j_{{ei}}^{{\nu }}} \right),$(42)
$\begin{gathered} n\frac{{d{{\alpha }_{1}}}}{{dt}} = \left( {{{n}_{e}}{{n}_{0}}{{j}_{{01}}} - {{n}_{e}}{{n}_{1}}{{j}_{{10}}}} \right) - \\ - \,\,\left( {{{n}_{e}}{{n}_{1}}{{j}_{{1e}}} - n_{e}^{3}{{j}_{{e1}}} - n_{e}^{2}j_{{e1}}^{{\nu }}} \right) - {{A}_{{10}}}{{n}_{1}}. \\ \end{gathered} $Здесь полагаем ${{n}_{1}} \ll {{n}_{i}},\quad{{n}_{0}};$ ${{n}_{i}} = {{n}_{e}}.$
Константы скоростей процессов:
При быстром расширении возможен отрыв температуры тяжелых частиц от температуры электронов, поэтому задача рассматривалась в двухтемпературном приближении ${{T}_{e}} \ne {{T}_{i}} = {{T}_{0}} = T{\text{:}}$
(43)
$\begin{gathered} \frac{3}{2}{{n}_{e}}\frac{{d{{T}_{e}}}}{{dt}} + {{n}_{e}}{{T}_{e}}{\text{div}}{\mathbf{U}} = - \left( {J + \frac{3}{2}{{T}_{e}}} \right) \times \\ \times \,\,{{n}_{e}}{{j}_{{ei}}}\left( {{{n}_{0}}K - n_{e}^{2}} \right) - {{E}_{{01}}}{{n}_{e}}\left( {{{n}_{0}}{{j}_{{01}}} - {{n}_{1}}{{j}_{{10}}}} \right) - \\ - \,\,\left( {{{J}_{1}} + \frac{3}{2}{{T}_{e}}} \right){{n}_{e}}{{j}_{{e1}}}\left( {{{n}_{1}}{{K}_{1}} - n_{e}^{2}} \right) + \\ + \,\,{{T}_{e}}\left( {\frac{3}{2} - F} \right)n_{e}^{2}j_{{ei}}^{{\nu }} - S_{e}^{{\nu }} + {{Q}_{{e0}}} + {{Q}_{{ei}}} + {{Q}_{g}}, \\ \end{gathered} $Из уравнения непрерывности $\frac{{\partial n}}{{\partial t}} + n{\text{div}}{\mathbf{U}} = 0$ для члена, описывающего адиабатическое расширение, получаем:
где $V = 2\pi R\pi {{a}^{2}}$ – объем тора.Входящие в правые части (43), (44) функции имеют вид:
(46)
${{Q}_{{e0}}} = \frac{3}{2}{{n}_{e}}\frac{{T - {{T}_{e}}}}{{{{\tau }_{{e0}}}}},\,\,\,\,{{Q}_{{ei}}} = \frac{3}{2}{{n}_{e}}\frac{{T - {{T}_{e}}}}{{{{\tau }_{{ei}}}}},$Для джоулева разогрева электронов можно использовать приближенное выражение:
(47)
${{Q}_{g}} = \frac{{{{I}^{2}}{{R}_{c}}}}{{Vk}} = \frac{{{{I}^{2}}}}{{\sigma {{\pi }^{2}}{{a}^{4}}k}}\,\,\quad\frac{{{\text{э В }}}}{{{\text{с }}{{{\text{м }}}^{{\text{3}}}}\,{\text{с }}}}.$Так как пространственное изменение параметров внутри тора не рассматривается, то для решения первой части общей задачи о параметрах сгустка при движении в вакууме требовалось определить изменение во времени следующих характеристик: $a\left( t \right),$ $R\left( t \right),$ $\alpha \left( t \right),$ $I\left( t \right),$ ${{T}_{e}}\left( t \right),$ $T\left( t \right).$ В этом приближении для решения наиболее сложных уравнений для ${{T}_{e}}\left( t \right)$ и $T\left( t \right)$ удобно использовать метод расщепления по физическим процессам [Ступицкий и др., 1985]. Так как изменение температур связано с одной стороны с адиабатическим расширением, и с другой – с внутренними процессами, то делая замену:
и подставляя ее в уравнения (43), (44), записанные в общем виде:Используя (45), из (48) получаем:
(51)
$\frac{{{{T}_{g}}}}{{{{n}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}} = {\text{const,}}$Данная задача, даже без учета внутренних распределений параметров, достаточно сложна как в математическом, так и особенно в физическом отношении. Представленные уравнения при некоторых условиях представляют собой систему жестких обыкновенных дифференциальных уравнений и требуют использования специальных численных алгоритмов. Насыщенность взаимосвязанными физическими процессами требует специального анализа для адекватного понимания роли каждого из них в общем поведении ТПС. Поэтому имело смысл последовательное численное решение задачи с постепенным подключением физических процессов. В первом разделе была рассмотрена простейшая газодинамическая задача, в следующем разделе рассматривается задача с учетом магнитного поля, но без учета внутренних кинетических процессов и джоулева подогрева, т.е. в адиабатическом приближении. Такая постановка дает в первом приближении представление о взаимосвязи геометрических характеристик ТПС с током и магнитным полем.
Тогда ${{T}_{e}} = {{T}_{i}} = T;$ ${{y}_{e}} = {{y}_{i}} = 1;$ $\alpha = {{\alpha }_{0}};$ P0 = $ = {{n}_{0}}k{{T}_{0}}\left( {1 + {{\alpha }_{0}}} \right)$ и система (26)–(35) будет иметь вид:
(54)
$\frac{{d{{U}_{a}}}}{{dt}} = \frac{{2\pi R}}{{{{M}_{0}}}}\left[ {4\pi a{{P}_{0}}{{{\left( {\frac{{{{V}_{0}}}}{V}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} - \frac{{2{{I}^{2}}}}{{{{c}^{2}}a}}} \right],$(56)
$\frac{{d{{U}_{R}}}}{{dt}} = \frac{1}{{{{M}_{0}}}}\left[ {2{{\pi }^{2}}{{a}^{2}}{{P}_{0}}{{{\left( {\frac{{{{V}_{0}}}}{V}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + \frac{{\pi {{I}^{2}}}}{{{{c}^{2}}}}\left( {\ln \frac{R}{a} + \frac{5}{4}} \right)} \right].$В уравнениях (26), (27) принималось:
(57)
$P = {{P}_{0}}{{\left( {\frac{{{{V}_{0}}}}{V}} \right)}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} = {{P}_{0}}{{\left( {\frac{{{{a}_{0}}{{R}_{0}}}}{{aR}}} \right)}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}.$Из (24) для характерного времени спада тока получаем:
(58)
$\begin{gathered} \tau = \frac{L}{{{{c}^{2}}{{R}_{c}} + \dot {L}}} = \frac{L}{{{{c}^{2}}{{R}_{c}}\left( {{{1 + \dot {L}} \mathord{\left/ {\vphantom {{1 + \dot {L}} {{{c}^{2}}{{R}_{c}}}}} \right. \kern-0em} {{{c}^{2}}{{R}_{c}}}}} \right)}} = \\ = \frac{{\pi \sigma {{a}^{2}}}}{{{{c}^{2}}}}\frac{{\left( {\ln \frac{R}{a} + \frac{1}{4}} \right)}}{{1 + \Delta }}, \\ \end{gathered} $При выходе ТПС из генератора его состояние определялось границей корпуса, и равновесное условие $\beta = \frac{{\bar {P}}}{{{{{{B}^{2}}} \mathord{\left/ {\vphantom {{{{B}^{2}}} {8\pi }}} \right. \kern-0em} {8\pi }}}} = 1$ при $a = {{a}_{0}}$ могло не выполняться. В частности при ${{T}_{{e0}}} = {{T}_{{i0}}} = 10$ эВ; ${{n}_{0}} = 8.3 \times {{10}^{{17}}}$ см–3, $\alpha = 1$ и ток $I = 0.7$ МА, полоидальное поле ${{B}_{\varphi }} \approx 4\quad\,\,{\text{Т л ,}}$ внутреннее давление $\bar {P} = 2.66 \times {{10}^{7}}$ Дн/см2; магнитное давление ${{{{B}^{2}}} \mathord{\left/ {\vphantom {{{{B}^{2}}} {8\pi }}} \right. \kern-0em} {8\pi }} = 6.37 \times {{10}^{7}}$ Дн/см2 т.е. $\beta = 0.42.$ Поэтому в расчетах представляло интерес рассматривать некоторый диапазон изменения начальных определяющих параметров по току ${{I}_{0}}$ и температуре ${{T}_{0}}.$ Для удобства анализа результатов на рис. 4 в плоскости ${{T}_{0}},$ ${{I}_{0}}$ показана кривая $\beta = 1,$ для ${{n}_{0}} = 8.3 \times {{10}^{{17}}}$ см–3:
(59)
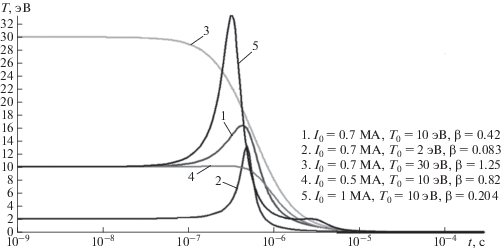
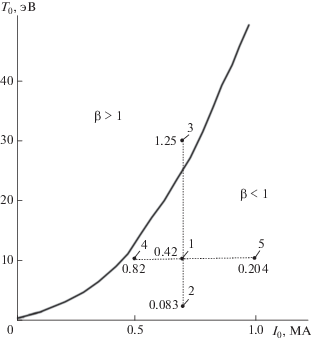
$\begin{gathered} \beta \left( {t = 0} \right) = \\ = \frac{{{{{\bar {P}}}_{0}}}}{{{{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {8\pi }}} \right. \kern-0em} {8\pi }}}} = \frac{{2\pi k{{T}_{0}}{{n}_{0}}\left( {1 + {{\alpha }_{0}}} \right){{c}^{2}}a_{0}^{2}}}{{I_{0}^{2}}} = 0.0204\frac{{{{T}_{{0\,\,{\text{э В }}}}}}}{{I_{{0\,\,{\text{MА }}}}^{2}}}. \\ \end{gathered} $Рис. 4.
Зависимость β(t = 0) = 1 в плоскости $\quad{{T}_{0}}$, ${{I}_{0}}$. Варианты: 1. ${{I}_{0}}$ = 0.7 МА, $\quad{{T}_{0}}$ = 10 эВ; 2. ${{I}_{0}}$ = 0.7 МА, $\quad{{T}_{0}}$ = 2 эВ; 3. ${{I}_{0}}$ = 0.7 МА, $\quad{{T}_{0}}$ = 30 эВ; 4. $\quad{{I}_{0}}$ = 0.5 МА, $\quad{{T}_{0}}$ = 10 эВ; 5. ${{I}_{0}}$ = 1 МА, ${{T}_{0}}$ = 10 эВ.
Итак, искомыми величинами являются $a,$ $R,$ ${{U}_{a}},$ ${{U}_{R}},$ $I,$ $n,$ $\tau ,$ $T$ в зависимости от $t.$ Для обезразмеривания системы выберем следующие масштабы величин:
Тогда безразмерные переменные и функции определяются следующим образом: $\bar {t} = {t \mathord{\left/ {\vphantom {t {{{t}_{x}}}}} \right. \kern-0em} {{{t}_{x}}}};$ $\bar {a} = {a \mathord{\left/ {\vphantom {a {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}};$ $\bar {R} = {R \mathord{\left/ {\vphantom {R {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}};$ $\bar {I} = {I \mathord{\left/ {\vphantom {I {{{I}_{x}}}}} \right. \kern-0em} {{{I}_{x}}}};$ $\bar {\tau } = {\tau \mathord{\left/ {\vphantom {\tau {{{t}_{x}}}}} \right. \kern-0em} {{{t}_{x}}}};$ $\bar {n} = {n \mathord{\left/ {\vphantom {n {{{n}_{x}}}}} \right. \kern-0em} {{{n}_{x}}}};$ ${{\bar {U}}_{a}} = {{{{U}_{a}}} \mathord{\left/ {\vphantom {{{{U}_{a}}} {{{V}_{x}}}}} \right. \kern-0em} {{{V}_{x}}}};$ ${{\bar {U}}_{R}} = {{{{U}_{R}}} \mathord{\left/ {\vphantom {{{{U}_{R}}} {{{V}_{x}}}}} \right. \kern-0em} {{{V}_{x}}}}.$
Начальные условия задавались в виде:
5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА, ВЫПОЛНЕННЫХ В АДИАБАТИЧЕСКОМ ПРИБЛИЖЕНИИ
Рассмотренное ранее решение модельной газодинамической задачи о поведении торообразного газового кольца дало представление о влиянии его начальных скоростных и геометрических характеристик на дальнейшую эволюцию его структуры.
Главная цель решения задачи о поведении ТПС с начальным внутренним током в адиабатическом приближении состояла в том, чтобы, учитывая изменения индуктивности, и, в первом приближении (без учета изменения $\alpha (t)$) проводимости, исследовать взаимодействие тока, магнитного поля и геометрических характеристик ТПС.
Для решения обыкновенных дифференциальных уравнений использовалась явная схема. Для расчета тока использовалась полунеявная схема Эйлера [Калиткин, 2000]. Как будет показано ниже, в зависимости от начальных условий, возможно возникновение автоколебаний $a(t).$ Для того, чтобы убедиться, что эти колебания не связаны с разбалтыванием схемы, а имеют физическую природу были выполнены расчеты методом Гира, который показывает, что разбалтывание схемы не происходит, а при определенных начальных условиях, реализуется автоколебательный режим.
Выполненные расчеты показали, что поведение $a\left( t \right),$ ${{U}_{a}}\left( t \right),$ $T\left( t \right),$ $n\left( t \right)$ существенно зависит от соотношения между тепловым давлением внутри тора и магнитным давлением, создаваемым током внутри тора, т.е. от $\beta \left( {t = 0} \right).$ Расчеты выполнены для различных ${{T}_{0}},$ ${{I}_{0}}$ таким образом, чтобы были реализованы различные значения $\beta \left( {t = 0} \right)$ и в то же время оставались в рамках возможных экспериментальных значений. Некоторые значения $\beta \left( {t = 0} \right)$ указаны на рис. 4. Следует подчеркнуть, что главные начальные параметры, определяющие поведение ТПС, после выхода из генератора – ${{T}_{0}},$ ${{I}_{0}}$ не связаны непосредственно друг с другом, так как ${{T}_{0}}$ определяется мощностью разряда, а ${{I}_{0}}$ определяется прежде всего наличием радиальной составляющей магнитного поля, каким-либо образом создаваемого в генераторе. Поэтому, прежде всего исследовались влияние ${{T}_{0}},$ ${{I}_{0}}$ на изменение характеристик ТПС непосредственно после выхода из генератора.
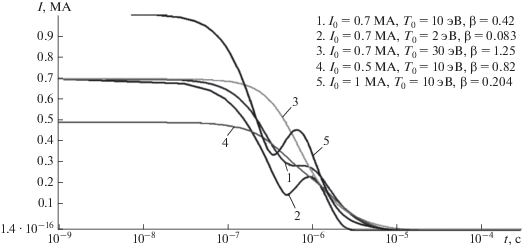
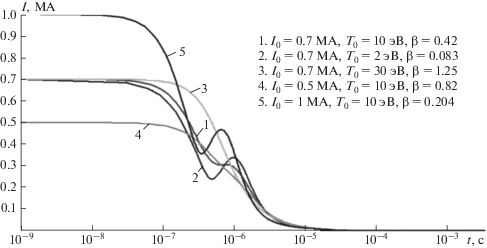
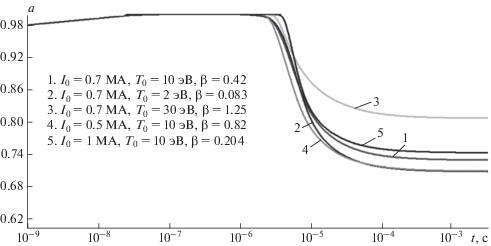
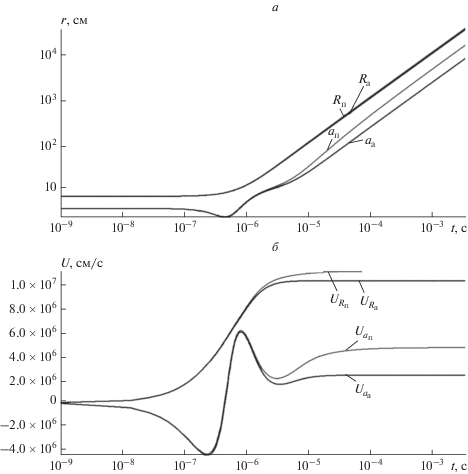
На рисунках 5–8 показано изменение во времени основных параметров ТПС для некоторых начальных значений ${{I}_{0}}$ и ${{T}_{0}}.$ Эти значения соответствуют $\beta \left( {t = 0} \right) = 0.41{\kern 1pt} - {\kern 1pt} 1.25{\;\;}$ (рис. 4). Из рисунка 5 следует, что существенное изменение $R\left( t \right),$ $a\left( t \right)$ начинаются при $t \geqslant {{10}^{{ - 7}}}$ c когда скорости ${{U}_{a}},$ ${{U}_{R}}$ уже достигают достаточно заметных величин (рис. 6). При этом $R\left( t \right)$ и ${{U}_{R}}{\;}\left( t \right),$ монотонно возрастают, а $a\left( t \right)$ и ${{U}_{a}}\left( t \right)$ при определенных ${{I}_{0}}$ и ${{T}_{0}}$ совершают колебания. Возрастание скорости ${{U}_{R}}\left( t \right)$ и колебания $a\left( t \right)$ и ${{U}_{a}}\left( t \right)$ заканчиваются практически после полного падения температуры и тока (рис. 7, 8). Монотонный рост $R\left( t \right)$ обусловлен тем, что как тепловое так и магнитное давления направлены по радиусу от центра тора. Для $a\left( t \right)$ магнитное и тепловое давления имеют противоположные направления, чем и обусловлены колебания $a\left( t \right)$ и ${{U}_{a}}{\;}\left( t \right),$ т.к. $\beta \left( {t = 0} \right) \ne 1$ и начальное состояние динамически неравновесно. При $\beta \left( {t = 0} \right)$ близком к единице (варианты 3, 4) колебаний не возникает. Так как колебания возникают в отсутствии внешнего периодического воздействия и их характер определяется исключительно самой системой, то их можно отнести к определенному классу нелинейных автоколебаний [Ланда, 1983].
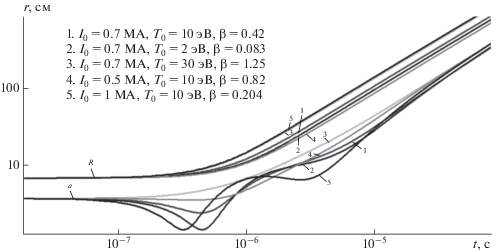
Рис. 5.
Зависимость радиуса торового кольца R (см) и торового сечения а (см) от времени для различных начальных условий (адиабатическое приближение).
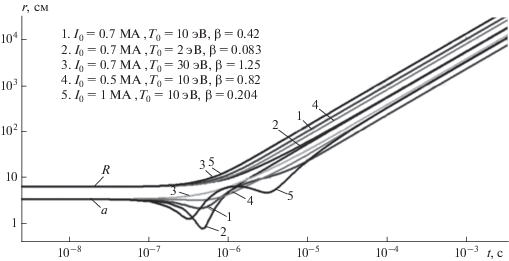
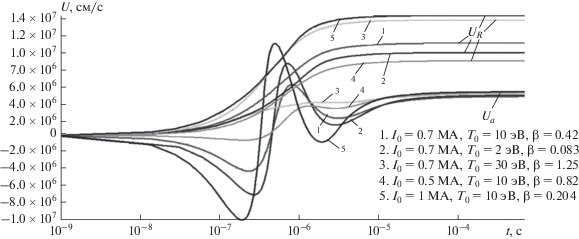
Рис. 6.
Зависимость скорости разлета торового кольца ${{U}_{R}}$ (см/c) и скорости разлета торового сечения ${{U}_{a}}$ (см/c) от времени для различных начальных условий (адиабатическое приближение).
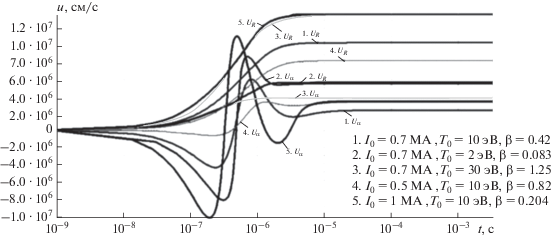
На время $\sim {\kern 1pt} {{10}^{{ - 5}}}{\;с }$ скорости ${{U}_{a}},$ ${{U}_{R}}$ выходят на асимптотически постоянные значения, и радиусы $R$ и $a$ линейно возрастают со временем. Чем больше ${{T}_{0}},$ тем выше ${{U}_{{a\infty }}}$ и ${{U}_{{R\infty }}}$ за счет накопленной в начале тепловой энергии. Увеличение ${{I}_{0}}$ в меньшей степени влияет на повышение ${{U}_{{a\infty }}}$ и ${{U}_{{R\infty }}}.$
При малых начальных $\beta \left( {t = 0} \right)$ (варианты 1, 2, 5) магнитное поле, сразу после выхода из генератора ($t\sim {{10}^{{ - 7}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 6}}}\quad\,\,{\text{с }}$), приводит к сжатию сечения тора (уменьшению $a\left( t \right),$ рис. 5), что приводит к росту температуры (рис. 7) и соответственно проводимости плазмы. Это приводит к немонотонному поведению тока (рис. 8). Вместе с тем характерное время спада тока, при высоких начальных ${{T}_{0}}$ меняется мало ($\sim {\kern 1pt} {{10}^{{ - 5}}}$ с).
Вариация ${{T}_{0}}$ при заданном ${{I}_{0}}$ (для определенности принималось ${{I}_{0}} = 0.7$ МА) показало что, если ${{T}_{0}} < 1.95$ эВ, то скорость ${{U}_{a}}$ очень быстро превосходит ${{U}_{R}}$ и тор схлопывается в сплошной диск, аналогично тому, как это происходит в модельной задаче при малых начальных скоростях его радиального расширения (рис. 9). Принципиальное отличие в том, что в данном случае радиальная скорость расширения формируется не только тепловым давлением, но и магнитным полем. При ${{T}_{0}} > 1.95$ эВ и ${{I}_{0}} = 0.7$ МА магнитное давление позволяет поддерживать торообразную структуру, как следует из рассматриваемого адиабатического приближения, по крайней мере на начальной стадии динамики ТПС. Отметим, что под начальной стадией понимается тот период времени, после выхода ТПС из генератора, когда магнитное поле полоидального тока оказывает существенное влияние на структуру ТПС. Если принять время релаксации тока $\sim {\kern 1pt} 5 \times {{10}^{{ - 5}}}$ с, а скорость направленного движения ТПС ${{V}_{0}} = 3 \times {{10}^{7}}$ см/с, то за это время он пролетит $L \cong 1.5 \times {{10}^{3}}$ см. При этом (для варианта 1) его размеры будут $R = 630$ см, $a = 140\,\,\quad{\text{с м }}{\text{.}}$ Получим оценку сверху для количества массы воздуха, который подмешивается в тор, в предположении, что он сгребает воздух как снежный плуг. Полагая $R\left( t \right) = {{R}_{0}}\left( {{{1 + t} \mathord{\left/ {\vphantom {{1 + t} \tau }} \right. \kern-0em} \tau }} \right);$ $a\left( t \right) = {{a}_{0}}\left( {{{1 + t} \mathord{\left/ {\vphantom {{1 + t} \tau }} \right. \kern-0em} \tau }} \right)$ и площадь с которой воздух попадает в тор S(t) = $ = 2\pi R2a = 4\pi {{a}_{0}}{{R}_{0}}{{\left( {{{1 + t} \mathord{\left/ {\vphantom {{1 + t} \tau }} \right. \kern-0em} \tau }} \right)}^{2}}$ получаем:
(60)
$M = \int\limits_0^t {{{\rho }_{0}}{{V}_{0}}S\left( t \right)dt{\kern 1pt} {\text{'}}} = \frac{4}{3}\pi {{a}_{0}}{{R}_{0}}{{V}_{0}}\tau {{\rho }_{0}}\left[ {{{{\left( {1 + \frac{t}{\tau }} \right)}}^{3}} - 1} \right].$Рис. 9.
Зависимости радиусов (а) и скоростей (б) от времени для начальных условий ${{I}_{0}}$ = 0.7 MA и ${{T}_{0}}$ = 1.5 эВ.
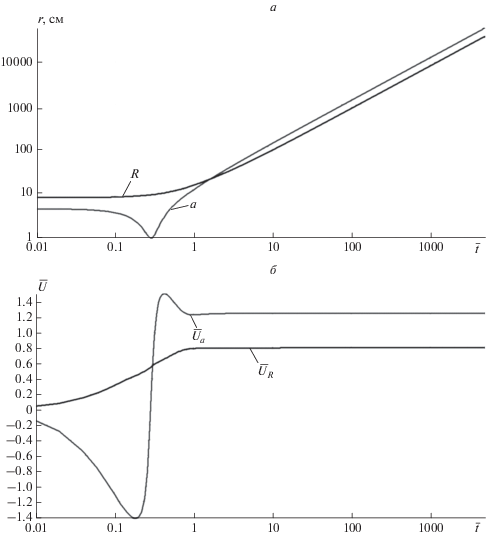
Полагая ${{V}_{0}} = 3 \times {{10}^{7}}$ м/с, $\tau = 0.69 \times {{10}^{{ - 6}}}$ с (здесь $\tau $ аппроксимационная постоянная), $t = 5 \times {{10}^{{ - 5}}}\,\,\quad{\text{с }}$ получаем $M\left( {\text{г }} \right) = 7.3 \times {{10}^{8}}{{\rho }_{0}}\,\,({{\text{г }} \mathord{\left/ {\vphantom {{\text{г }} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}).$ Для грубой оценки можно предположить, что влияние воздуха на движение ТПС можно не учитывать, если его, возмущенная движением масса $M \ll {{M}_{0}}$ [Ступицкий, 2006б]. Это условие выполняется, если ${{\rho }_{0}} \ll 3 \times {{10}^{{ - 12}}}\quad\,\,{{\text{г }} \mathord{\left/ {\vphantom {{\text{г }} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}},$ т.е. на высотах в атмосфере $h > 150\,\,\quad{\text{к м }}.$ Такими образом на начальной стадии влияние воздуха можно не учитывать если эксперимент проводится в верхней атмосфере.
6. РАСЧЕТ НАЧАЛЬНОЙ СТАДИИ ДИНАМИКИ ТПС В ПОЛНОЙ ПОСТАНОВКЕ. СРАВНЕНИЕ С АДИАБАТИЧЕСКИМ ПРИБЛИЖЕНИЕМ
Учет ионизации, возбуждения, различия ${{T}_{e}}$ и ${{T}_{i}}$ создает целый ряд дополнительных каналов обмена энергией внутри системы между различными степенями свободы, и, соответственно, к расширению возможности генерации различного рода колебательных процессов. Важно при этом иметь в виду, что внутренние степени свободы имеют свои характерные времена, что может отражаться на амплитудно-частотных колебаниях параметров ТПС.
В полной рассматриваемой задаче можно выделить следующие основные характерные времена:
− время релаксации тока $\left( {\beta \to \infty } \right);$
− время релаксации ионизационной и температурной неравновесности;
− время достижения полного взаимопроникновения частиц воздуха через ТПС при его направленном движении;
− время торможения ТПС в разреженной атмосфере.
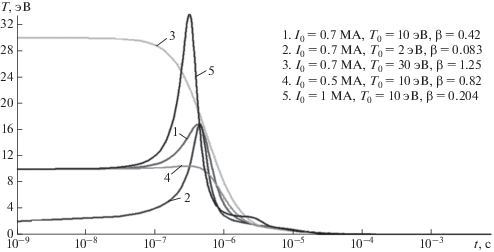
В данном разделе приведены результаты расчетов начальной стадии динамики ТПС с учетом неравновесных процессов (первые два из указанных временных диапазонов). Главная отличительная особенность полной постановки задачи о начальной стадии ТПС – это достаточно полный учет внутренней энергии в плазме: кроме тепловой, учитывается энергия ионизации, возбуждения и джоулев разогрев. Причем, как показали расчеты, относительный вклад этих составляющих в температуру зависит от ${{T}_{0}},$ ${{I}_{0}}$. Из рисунка 10 следует, что наибольший положительный вклад в ${{T}_{e}}$ в области наибольших временных градиентов дает джоулев разогрев и рекомбинация. Излучение не играет существенной роли.
Рис. 10.
Вклад во внутреннюю энергию различных процессов на начальной стадии ее динамики для различных начальных условий: (a) I0 = 0.7 МА, T0 = 10 эВ; (б) I0 = 0.7 МА, T0 = 30 эВ; (в) I0 = 1 МА, T0 = 10 эВ.
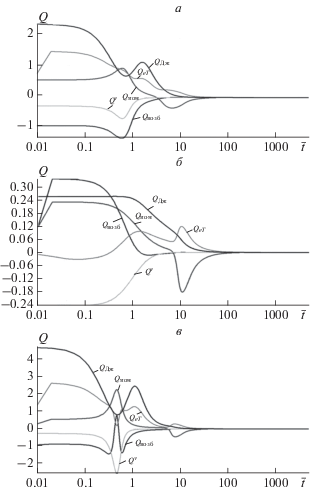
На рисунках 11–16 показано поведение основных рассчитываемых параметров. В целом, поведение геометрических параметров $R,$ $a,$ ${{U}_{R}},$ ${{U}_{a}},$ температуры $T$ и тока $I$ по форме аналогичны результатам полученным в адиабатическом приближении. За счет джоулевой и рекомбинационной энергии асимптотические значения ${{U}_{{R\infty }}}$ и ${{U}_{{a\infty }}}$ примерно на 20% выше, чем в адиабатике. Несколько дольше происходит основное падение тока и температуры ($\sim {\kern 1pt} 3 \times {{10}^{{ - 5}}}$ c).
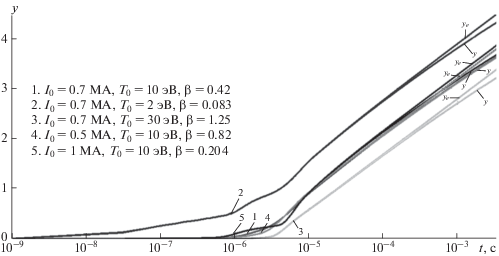
Однако полная постановка позволила выяснить два важных эффекта. Так как с течением времени концентрация частиц быстро падает, то замедляется скорость рекомбинации и реализуется режим близкий к закалке степени ионизации, причем асимптотические значения ${{\alpha }_{\infty }}$ достаточно велики (70–75%, рис. 15). Следовательно, проводимость плазмы сгустка остается высокой на протяжении дальнейшего движения ТПС, что и определяет его взаимодействие с геомагнитным полем. Однако, как показано в работе [Ступицкий и др., 1985], полной закалки не происходит. В данных расчетах об этом свидетельствует рост кинетических температур ${{y}_{e}}$, $y$ на $t \geqslant {{10}^{{ - 5}}}{\;с }$, что в дальнейшем замедляет темп падения ${{T}_{e}}$ и $T,$ причем на $t \geqslant 3 \times {{10}^{{ - 4}}}\,\,{\text{с }}$ столкновения уже не обеспечивают выравнивание температур, и ${{T}_{e}} > T,$ хотя превышения незначительные.
Наиболее четко различие между адиабатической и полной постановкой видно из рис. 17 для основного (“базового”) варианта начальных условий ${{T}_{0}} = 10\,\,\quad{\text{э В }};$ ${{I}_{0}} = 0.7\quad\,\,{\text{М А }}.$ Сравнение подтверждает данное выше общее объяснение такого различия.
Отметим, что понижение начальной энергии ТПС – уменьшение ${{T}_{0}}$ или ${{I}_{0}},$ приводит, через определенное время, к схлопыванию тора в диск, как это было отмечено в адиабатическом приближении. Расчеты в полной постановке показали, что во всем диапазоне рассматриваемых токов ${{I}_{{0{\text{к р }}}}} = 0.5{\kern 1pt} - {\kern 1pt} 1\quad\,\,{\text{М А ,}}$ при ${{T}_{{0{\text{к р }}}}} \approx 0.6\quad\,\,{\text{э В }}$ происходит схлопывание тора в сплошной диск. Снижение ${{T}_{{0{\text{к р }}}}}$ по сравнению с адиабатикой связано с выделением ионизационной энергии.
7. ИССЛЕДОВАНИЕ РАСПРОСТРАНЕНИЯ ТПС В РАЗРЕЖЕННОЙ ВЕРХНЕЙ АТМОСФЕРЕ
Динамика, летящего в разреженной верхней атмосфере и расширяющегося ТПС, зависит от характера его взаимодействия с геомагнитным полем и воздухом. Так как градиент плотности воздуха в атмосфере не совпадает с направлением магнитного поля, и, по мере разрежения сгустка, становится возможным взаимопроникновение плазмы и воздуха, то численное моделирование такой трехмерной задачи представляет собой чрезвычайно сложную проблему. Чтобы понять возможные пути упрощения ее решения и получить приближенные качественные результаты необходимо достаточно подробно проанализировать те процессы, которые сопровождают распространение ТПС в ионосфере.
Оценим влияние геомагнитного поля на движение сгустка, пренебрегая пока взаимодействием с воздухом. Будем предполагать, что скорость движения сгустка $V$ перпендикулярна силовым линиям поля, а, так как проводимость плазмы достаточно высока, то его диффузией в плазму можно пренебречь. Тогда:
где $S\left( t \right) = 4\pi R\left( t \right)a\left( t \right)$ – площадь взаимодействия сгустка с полем растет со временем. Анализ представленных выше расчетных результатов начальной стадии показал, что при выходе на асимптотический режим можно приближенно принять $R = {{R}_{0}}\left( {{{1 + t} \mathord{\left/ {\vphantom {{1 + t} \tau }} \right. \kern-0em} \tau }} \right);$ $a = {{a}_{0}}\left( {{{1 + t} \mathord{\left/ {\vphantom {{1 + t} \tau }} \right. \kern-0em} \tau }} \right).$ Весь анализ процесса торможения ТПС в этом разделе будем проводить для наиболее характерных (типовых) начальных условий ${{T}_{0}} = 10\,\,\quad{\text{э В ;}}$ ${{I}_{0}} = 0.7\,\,\quad{\text{М А }};$ ${{R}_{0}} = 6.5\,\,\quad{\text{с м }};$ ${{a}_{0}} = 3.5\quad\,\,{\text{с м }};$ ${{V}_{0}} = 3 \times {{10}^{7}}\,\,\quad{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}.$ В этом случае $\tau = 0.69 \times {{10}^{{ - 6}}}\quad\,\,{\text{c}}{\text{.}}$ Тогда, интегрируя (61), получаем:(62)
$V\left( t \right) = {{V}_{0}}\left\{ {1 - \omega \left[ {{{{\left( {1 + \frac{t}{\tau }} \right)}}^{3}} - 1} \right]} \right\},$(63)
$L\left( {{{t}_{k}}} \right) = {{V}_{0}}{{t}_{k}}\left[ {\left( {1 + \omega } \right) - \frac{\omega }{4}{{{\left( {\frac{{{{t}_{k}}}}{\tau }} \right)}}^{3}}} \right],$Из (62) время торможения $\frac{{{{t}_{k}}}}{\tau } = \sqrt[3]{{\frac{1}{\omega } + 1}}$ –$ - \,\,1 \approx 4.66 \times {{10}^{3}},$ т.е. ${{t}_{k}} = 3.2 \times {{10}^{{ - 3}}}\quad\,\,{\text{c}}{\text{.}}$ Расстояние на котором произойдет торможение магнитным полем из (63) получаем ${{L}_{k}} = L\left( {{{t}_{k}}} \right) \cong \frac{3}{4}{{V}_{0}}{{t}_{k}} = 720\quad\,\,{\text{м }}.$
Следует отметить, что при торможении в плазме может развиваться релей-тейлоровкая неустойчивость [Ступицкий, 2006б] и вся структура ТПС может развалиться еще раньше. Ясно, что при движении ТПС под углом к полю картина будет еще более сложной и неоднозначной из-за неустойчивости. Поэтому для анализа влияния разреженной ионосферы на движение ТПС можно рассматривать его движение вдоль силовых линий поля. В этом случае поле может повлиять лишь на поперечное расширение тора, уменьшая ${{U}_{R}}\left( t \right).$ Возникающую при этом необходимость учета неоднородности ионосферы не сложно сделать в приближенном алгоритме расчета торможении ТПС.
Однако наиболее важным является тот факт, что, как было показано выше, в результате быстрого расширения и закалки рекомбинации, около 25% плазменного потока будут представлять нейтральные атомы. А так как основное время движения (см. ниже) ТПС будет происходить в режиме взаимопроникновения, то именно поток нейтральных частиц, на который не действует геомагнитное поле, и будет определять дальность распространения и взаимодействие на преграду.
Взаимодействие летящего ТПС с разреженной ионосферой может носить различный характер. Если плотность ТПС при выходе из генератора достаточно высока, то в самом начале на некоторое время может возникнуть его обтекание воздухом в свободно молекулярном режиме или в режиме сплошной среды, в зависимости от плотности окружающего воздуха. Ясно, что оба этих режима возможны, если в переднем слое сгустка, толщиной порядка длины свободного пробега $\lambda $, возможен быстрый рост концентрации частиц, обеспечивающий отражение вновь налетающих молекул. Если концентрация частиц водорода:
(64)
${{n}_{p}} = \frac{N}{{2{{\pi }^{2}}R{{a}^{2}}}} = \frac{N}{{2{{\pi }^{2}}{{R}_{0}}a_{0}^{2}{{{\left( {1 + \frac{t}{\tau }} \right)}}^{3}}}}\quad,$(65)
${{n}_{{\Phi }}} = \frac{{{{n}_{0}}{{V}_{0}}St}}{{S\lambda }} = {{n}_{0}}{{V}_{0}}n\sigma t\quad{\text{,}}$Рассмотрим движение молекулы воздуха после того, как на нее налетает плазменный сгусток. Уравнения движения молекулы воздуха можно записать в виде [Ступицкий, 2006а]:
(66)
${{m}_{0}}\frac{{dU}}{{dt}} = \frac{{\mu \sigma {{U}_{T}}}}{{\sqrt \pi }}n\left( {V - U} \right){{F}_{0}}\left( \chi \right),$$\mu = {{m{{m}_{0}}} \mathord{\left/ {\vphantom {{m{{m}_{0}}} {\left( {m + {{m}_{0}}} \right)}}} \right. \kern-0em} {\left( {m + {{m}_{0}}} \right)}},$ где $m$ – масса молекулы водорода;
$n$ – концентрация частиц ТПС;
${{U}_{T}} = \sqrt {{{{{2kT} \mathord{\left/ {\vphantom {{2kT} {m + 2n{{T}_{0}}}}} \right. \kern-0em} {m + 2n{{T}_{0}}}}} \mathord{\left/ {\vphantom {{{{2kT} \mathord{\left/ {\vphantom {{2kT} {m + 2n{{T}_{0}}}}} \right. \kern-0em} {m + 2n{{T}_{0}}}}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}} ;$
$V$ – скорость частиц ТПС в инерциальной системе;
$\chi = {{\left| {V - U} \right|} \mathord{\left/ {\vphantom {{\left| {V - U} \right|} {{{U}_{T}}}}} \right. \kern-0em} {{{U}_{T}}}};$ ${{F}_{0}}\left( \chi \right)$ – безразмерная функция [Ступицкий, 2006а], имеющая асимптоты:
Анализ показал, что в прикладном отношении наибольший интерес представляет использование ТПС в диапазоне высот $h \cong 200{\kern 1pt} - {\kern 1pt} 300\,\,\quad{\text{к м }},$ где диапазон изменения основных параметров атмосферы приведен в таблице 1.
Таблица 1.
Основные параметры атмосферы
| $h,$ км | $n,$ см3 | ${{{\text{N}}}_{2}}$ | ${{{\text{O}}}_{2}}$ | ${\text{O}}$ | ${\text{N}}$ | ${{n}_{e}}$ | $T,$ К | ${{T}_{e}},$ К | ${{\alpha }_{{\text{в }}}}$ | ${{m}_{0}}$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 200 | $8.3 \times {{10}^{9}}$ | $2.6 \times {{10}^{9}}$ | $2.1 \times {{10}^{8}}$ | $5.5 \times {{10}^{9}}$ | $3.2 \times {{10}^{7}}$ | $5.1 \times {{10}^{5}}$ | 859 | 2150 | $6.1 \times {{10}^{{ - 5}}}$ | 20.1 |
| 300 | $8.5 \times {{10}^{8}}$ | $8.6 \times {{10}^{7}}$ | $4.3 \times {{10}^{6}}$ | $7.5 \times {{10}^{8}}$ | $8.0 \times {{10}^{6}}$ | $1.6 \times {{10}^{6}}$ | 973 | 2980 | $1.9 \times {{10}^{{ - 3}}}$ | 16.5 |
Как показано выше, степень ионизации в сгустке после закалки достигает значительной величины. Концентрация же ионов в воздухе очень мала ${{\alpha }_{{\text{в }}}}\sim {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 5}}}.$ Поэтому столкновения атомов и ионов водорода с нейтральными молекулами и атомами воздуха, в отличие от столкновений заряженных частиц, можно описать некоторым средним сечением, которое по порядку величины равно $\sigma = {{10}^{{ - 15}}}\,\,{\text{с }}{{{\text{м }}}^{2}}.$ Среднее значение ${\mu \mathord{\left/ {\vphantom {\mu {{{m}_{0}} \approx 0.05}}} \right. \kern-0em} {{{m}_{0}} \approx 0.05}}.$
Схема динамики молекулы воздуха внутри тора показана на рис. 18, где $\left| {{{U}_{{{{a}_{0}}}}}} \right| < \left| {{{V}_{0}}} \right|.$
Траектория частицы описывается уравнением:
Для оценки общего характера взаимодействия сгустка с молекулой воздуха полагаем ${{V}_{0}} = {\text{const,}}$ ${{U}_{{{{a}_{0}}}}} = {\text{const}}{\text{.}}$ Тогда скорость вдоль диаметра сгустка, где рассматривается захваченная молекула воздуха, будет:
(68)
$V\left( t \right) = {{V}_{0}} + {{U}_{{{{a}_{0}}}}}\left( {1 - \frac{{z\left( t \right)}}{{a\left( t \right)}}} \right).$Определяющим параметром, от которого зависит характер взаимодействия ТПС с сильно разреженным воздухом, является средняя концентрация частиц внутри тора. На первом этапе динамики тора, когда концентрация частиц плазмы внутри нее еще достаточна велика, он работает как снежный плуг, и все налетающие молекулы воздуха остаются внутри него. Тогда общее количество частиц внутри ТПС приближенно определяется уравнением:
(69)
$\frac{{dN}}{{dt}} = {{n}_{0}}\left( {{{V}_{0}} + {{U}_{{{{a}_{0}}}}}} \right)S\left( t \right),$(70)
$N\left( t \right) = {{N}_{0}} + \frac{4}{3}\pi {{R}_{0}}{{a}_{0}}\left( {{{V}_{0}} + {{U}_{{{{a}_{0}}}}}} \right){{n}_{0}}\tau \left[ {{{{\left( {1 + \frac{t}{\tau }} \right)}}^{3}} - 1} \right],$Для того чтобы определить момент перехода к режиму полного взаимопроникновения рассматривались частицы, захваченные последовательно в моменты ${{t}_{{01}}},$ ${{t}_{{02}}},$ …, отсчитываемые от выхода ТПС из генератора. Как показали расчеты, захваченные в начальный момент (${{t}_{0}} = 0$) молекулы воздуха, на глубине $z = 0.1\,\,\quad{\text{с м }}$ (около 4 длин свободного пробега) уже приобретают скорость, равную скорости движения водородного сгустка. Таким образом концентрация частиц внутри сгустка пополняется молекулами воздуха. Отметим, что полная энергия, которую приобретают молекулы воздуха при прохождении сгустка, зависит от интеграла концентрации по траектории движения молекул. Поэтому приближенно при определении $U\left( t \right)$ можно использовать среднее значение концентрации частиц по объему тора $n\left( t \right) = {{n}_{p}}\left( t \right) + {{n}_{{\Phi }}}\left( t \right),$ где ${{n}_{p}},$ ${{n}_{{\Phi }}}$ средние концентрации водорода и воздуха.
Если бы на всем протяжении движения тора молекулы воздуха оставались внутри него и их полного взаимопроникновения не было, то концентрация внутри него выходила бы на константу:
Однако расчеты по представленной упрощенной модели показали, что с увеличением времени сгусток быстро просветляется, еще до того, как воздух будет давать заметный вклад в его концентрацию. Момент времени ${{t}_{{0*}}},$ после которого в момент ${{t}_{*}}$ молекула выйдет из ТПС, определялось соотношением $z{{({{t}_{*}})} \mathord{\left/ {\vphantom {{({{t}_{*}})} {2a({{t}_{*}})}}} \right. \kern-0em} {2a({{t}_{*}})}} = 1.$ После просветления количество входящего и выходящего из ТПС воздуха практически одинаково и он, двигаясь со скоростью $U\left( t \right),$ практически не влияет на движение последующих молекул воздуха внутри ТПС. На рисунке 19 показано изменение скорости молекул воздуха захваченных в различные моменты ${{\bar {t}}_{0}} = {{{{t}_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}} \tau }} \right. \kern-0em} \tau }$ сгустком. С течением времени ${{t}_{0}}$ воздух все слабее увлекается плазмой сгустка и скорость $U$ падает. При выходе из сгустка скорость молекулы воздуха остается постоянной. Поэтому зависимость $z\left( t \right)$ переходит в линейную при $t > {{t}_{*}}.$ Естественно на периферии сгустка просветление наступает раньше. Однако, так как основная масса воздуха проходит через осевую область, то приближенно можно полагать, что до момента времени ${{t}_{*}}$ весь воздух по сечению $4\pi Ra$ захватывается ТПС.
Рис. 19.
Изменение скоростей молекул воздуха, захваченные в различные моменты времени ${{\bar {t}}_{0}} = {t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-0em} \tau }$ плазменным тором.
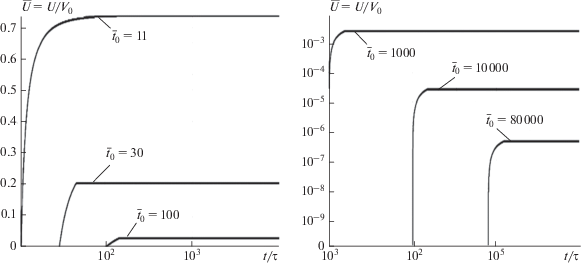
Расчеты без учета подмешивания воздуха и с учетом подмешивания показали, что просветление ТПС наступает на ранее время ${{t}_{0}},$ когда подмешанный воздух не дает заметного вклада в общую концентрацию сгустка. На рисунке 20 показано изменение ${z \mathord{\left/ {\vphantom {z {2a\left( t \right)}}} \right. \kern-0em} {2a\left( t \right)}}.$ При ${{{{t}_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}} {\tau \leqslant 10}}} \right. \kern-0em} {\tau \leqslant 10}}$ молекула воздуха не доходит до противоположной границы сгустка и остается в плазме. При ${{{{t}_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}} {\tau \geqslant 11{\kern 1pt} - {\kern 1pt} 13}}} \right. \kern-0em} {\tau \geqslant 11{\kern 1pt} - {\kern 1pt} 13}}$ постепенно наступает просветление и при ${{{{t}_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}} {\tau > 20{\kern 1pt} - {\kern 1pt} 50}}} \right. \kern-0em} {\tau > 20{\kern 1pt} - {\kern 1pt} 50}}$ оно уже становится четко выраженным. Такие же значения следуют из грубых аналитических оценок (${{{{t}_{{0*}}}} \mathord{\left/ {\vphantom {{{{t}_{{0*}}}} {\tau \approx 15}}} \right. \kern-0em} {\tau \approx 15}}$), при этом $n = 2 \times {{10}^{{14}}}\,\,{\text{с }}{{{\text{м }}}^{{ - 3}}},$ $2a \cong 120\quad\,\,{\text{с м }}.$ Учитывая, что момент выхода молекулы ТПС ${{t}_{*}} > {{t}_{{0*}}},$ то из анализа, представленных на рис. 20 результатов можно принять, что при ${{{t \mathord{\left/ {\vphantom {t {\tau > {{t}_{*}}}}} \right. \kern-0em} {\tau > {{t}_{*}}}}} \mathord{\left/ {\vphantom {{{t \mathord{\left/ {\vphantom {t {\tau > {{t}_{*}}}}} \right. \kern-0em} {\tau > {{t}_{*}}}}} \tau }} \right. \kern-0em} \tau }$ = $32\left( {{{{{t}_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}} \tau }} \right. \kern-0em} \tau } = 20} \right)$ ТПС становится прозрачным (напомним $\tau = 0.69 \times {{10}^{{ - 6}}}\,\,{\text{с }}$).
Рис. 20.
Реализация условия полного взаимопроникновения молекул воздуха через ТПС, захваченных в различные моменты времени.
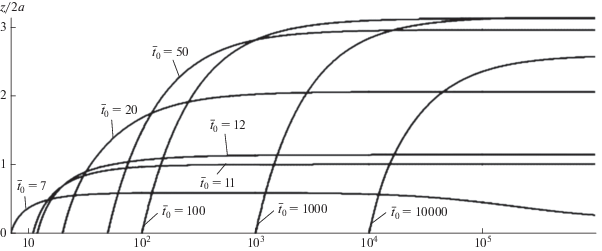
В рамках принятых приближений проанализируем динамику ТПС в направлении его начальной скорости ${{V}_{0}} = 3 \times {{10}^{7}}\,\,{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}$ (ось Х). Тогда дифференциальное уравнение движения [Ступицкий, 2006а, б] имеет вид:
(71)
$mn\frac{{dV}}{{dt}} = - \frac{{\mu \sigma {{U}_{T}}}}{{\sqrt \pi }}{{n}_{0}}n\left( {V - U} \right){{F}_{0}},$Тогда интегрируя (71) по объему и учитывая, что в данном случае $m \cong \mu ,$ получим систему уравнений, определяющих торможение ТПС из-за его взаимодействия с воздухом в режиме полного взаимопроникновения:
(72)
$\frac{{dV}}{{dt}} = - \frac{\sigma }{N}\int\limits_{{{V}_{{{\text{о б }}}}}} {{{n}_{0}}n{{{\left( {V - U} \right)}}^{2}}d{{V}_{{{\text{о б }}}}}} ,$Численные исследования данной системы и описанный выше анализ указали на возможность ее аналитического решения с приемлемой точностью. До начала основного режима движения – стадии полного взаимопроникновения (просветление ТПС) количество подмешенного воздуха мало по сравнению с количеством плазмы. Так на ${{{{t}_{{0*}}}} \mathord{\left/ {\vphantom {{{{t}_{{0*}}}} \tau }} \right. \kern-0em} \tau } = 20$ (${{{{t}_{*}}} \mathord{\left/ {\vphantom {{{{t}_{*}}} \tau }} \right. \kern-0em} \tau } = 32$):
(76)
$V\left( t \right) = \frac{{{{V}_{{0*}}}}}{{1 + {{V}_{{0*}}}\sigma {{n}_{0}}\left( {t - {{t}_{*}}} \right)}},$Так как к моменту просветления относительная масса подмешенного воздуха очень мала, то можно полагать ${{V}_{{0*}}} = {{V}_{0}} = 3 \times {{10}^{7}}\,\,{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}.$ Тогда из формулы (76) характерное время торможения ТПС, то есть время, за которое его скорость уменьшается вдвое будет ${{\tau }_{T}} = {1 \mathord{\left/ {\vphantom {1 {{{V}_{0}}\sigma {{n}_{0}}}}} \right. \kern-0em} {{{V}_{0}}\sigma {{n}_{0}}}} \cong 4 \times {{10}^{{ - 3}}}\,\,{\text{c}}$ для $h = 200\,\,\quad{\text{к м }}.$ За это время ТПС пролетит расстояние:
При этом будет иметь размеры ${{R}_{T}} \approx 380\,\,\quad{\text{м }},$ ${{a}_{T}} \approx 200\,\,\quad{\text{м }}$ и концентрацию атомов и ионов водорода внутри него будет $n = {N \mathord{\left/ {\vphantom {N {2{{\pi }^{2}}{{R}_{T}}a_{T}^{2}}}} \right. \kern-0em} {2{{\pi }^{2}}{{R}_{T}}a_{T}^{2}}}$ ≈ $ \approx 4 \times {{10}^{6}}\,\,{\text{с }}{{{\text{м }}}^{{ - 3}}}.$
8. ОЦЕНКА ВОЗДЕЙСТВИЯ РАЗРЕЖЕННОГО ВЫСОКОСКОРОСТНОГО ПОТОКА ЧАСТИЦ НА ПОВЕРХНОСТЬ ТВЕРДОГО ТЕЛА
В работе [Смирнов и Ступицкий, 2010] на основе метода молекулярной динамики был разработан эффективный численный алгоритм расчета воздействия отдельных высокоэнергетических частицы разреженного плазменного потока на поверхность, кристаллических и аморфных тел. Определены размеры и характер образующихся дефектов. Показано, что они могут существенно влиять на оптические свойства прозрачных тел типа стекла. Показано, что возникающие даже при непродолжительном воздействии дефекты в приповерхностном слое стекла, служащим защитой для многих чувствительных элементов космических аппаратов, существенно снижают его прозрачность даже при очень большом расстоянии от источника плазмы.
Для воздействия на открытые поверхности практический интерес представляют энергии атомов водорода $\sim {\kern 1pt} 0.1{\kern 1pt} - {\kern 1pt} 10\,\,\quad{\text{к э В }}$ [Смирнов и Ступицкий, 2010]. По представленным оценкам при ${{V}_{0}} = 3 \times {{10}^{7}}{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}},$ энергия ${{\varepsilon }_{0}} \approx 0.47\,\,\quad{\text{к э В }},$ и, соответственно, на расстоянии ${{L}_{T}}$ $\varepsilon \approx 0.1\,\,\quad{\text{к э В }},$ а плотность потока для h = 200 км ${{j}_{T}} = 6.2 \times {{10}^{{13}}}\,\,{1 \mathord{\left/ {\vphantom {1 {{\text{с }}{{{\text{м }}}^{2}}{\text{ с }}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{2}}{\text{ с }}}}$ и полный поток ${{{\Phi }}_{T}} = 1.2 \times {{10}^{{11}}}\,\,\quad{1 \mathord{\left/ {\vphantom {1 {{\text{с }}{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{2}}}}}}.$ Для $h = 300\,\,\quad{\text{к м }}$ соответственно ${{n}_{T}} = 4.2 \times {{10}^{3}}\,\,\quad{1 \mathord{\left/ {\vphantom {1 {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}},$ ${{j}_{T}} = 6.2 \times {{10}^{{10}}}\,\,{1 \mathord{\left/ {\vphantom {1 {{\text{с }}{{{\text{м }}}^{{\text{2}}}}{\text{ с }}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{2}}}}{\text{ с }}}}$ и ${{{\Phi }}_{T}} = 1.2 \times {{10}^{9}}\,\,{1 \mathord{\left/ {\vphantom {1 {{\text{с }}{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{2}}}}}}.$ Здесь учитывался как заряженный, так и нейтральный компоненты.
Отметим, что при распространении ТПС вдоль силовых линий магнитного поля его радиальное расширение будет ограничено примерно теми же масштабами, которые следуют из оценок по уравнению (61): ${{R}_{{{\text{max}}}}} \approx 700{\kern 1pt} - {\kern 1pt} 800\quad\,\,{\text{м }}.$ В результате ограничения радиального движения тор превратится в диск с плотностью примерно на порядок меньший, чем полученная выше для торможения на $h = 200\,\,\quad{\text{к м }}$ $\left( {\sim {\kern 1pt} 4 \times {{{10}}^{5}}\,\,{{\quad1} \mathord{\left/ {\vphantom {{\quad1} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}} \right).$ Дальнейшее его движение, колимированное магнитным полем, будет определяться главным образом разреженным воздухом.
В работе [Смирнов и Ступицкий, 2010] создана уникальная программа расчета дефектов в кристаллических и аморфных структурах под действием частиц высокой энергии. При полном потоке Ф ~ 1012–1013 1/см2 в образующуюся полость могут последовательно попадать несколько частиц и существенно расширять ее объем, как показано на рис. 21 (а, б, в). Как показали оценки такое изменение поверхностного слоя прозрачного диэлектрика приводят к рассеиванию порядка 50% световой энергии, которая переносит информацию на КА.
9. ЗАКЛЮЧЕНИЕ
В работе дано достаточно подробное численное исследование параметров ТПС на его начальной стадии движения и при дальнейшем разлете и взаимодействии с сильно разреженным воздухом. Дальность движения зависит от плотности воздуха и в верхней ионосфере может достигать десятков километров.
В данной работе также показано, что активно разрабатываемые в настоящее время плазменные пушки могут служить эффективным средством поражения стеклозащитных покрытий. Дальнейшая теоретическая и экспериментальная работа в данном направлении позволит выбрать оптимальные параметры как плазменного устройства, так и самой плазмы. Выполненные исследования, в частности, показали, что наряду с высокой скоростью плазменного потока необходимо добиться, чтобы степень его ионизации была минимальной, что обеспечит минимальное тормозящее действие геомагнитного поля на его динамику.
Предварительные расчеты так же показали, что в области распространения ТПС может существенно повышаться степень ионизации ионосферы. В настоящее время такие исследования ведутся в достаточно подробной постановке.
Список литературы
− Алипченков В.М. // Физика плазмы. Т. 4. № 5. С. 1051– 1055. 1978.
− Ананьин О.Б., Быковский Ю.А., Ступицкий Е.Л. и др. // Препр. № 012–85. МИФИ, 32 с. 1985.
− Архипов Н.И., Жилтухин А.М., Софронов В.М. и др. Температура ионов в потоках мощных электродинамических ускорителей // Физика плазмы. Т. 11. № 2. С. 201–205. 1985.
− Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков. М.: Атомиздат, 317 с. 1972.
− Борисов И.И., Васильев В.И., Житлухин Н.Р. и др. Спектроскопия взаимодействия импульсных плазменных потоков с поверхностью на установках МКТ // Физика плазмы. Т. 20. № 1. С. 81–83. 1994.
− Броуд Г.Л. Действие ядерного взрыва. М.: Мир, 310 с. 1971.
− Галеев А.А., Сагдеев Р.З. Модель ударной волны в плазме солнечного ветра // ЖЭТФ. Т. 57. № 3(а). С. 1047–1053. 1964.
− Голант В.Е., Жилинский А.П., Сахаров С.А. Основы физики плазмы. М.: Атомиздат, 384 с. 1972.
− Дьяченко В.Ф., Имшенник В.С., Полейчик В.В. К вопросу о движении межзвездной среды под действием оболочки новой и сверхновой // Астрон. журн. Т. 46. № 4. С. 739−744. 1969.
− Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука. Изд-е 3-е. 656 с. 2008.
− Калиткин Н.Н. Численные методы. М.: Наука, 592 с. 2000.
− Ланда П.С. Автоколебания в распределенных системах. М.: Наука, 320 с. 1983.
− Операция “Аргус”. М.: Атомиздат, 118 с. 1960.
− Операция “Морская звезда”. М.: Атомиздат. 288 с. 1964.
− Осовец С.М., Щедрин Н.Н. Плазменный виток при наличии активной индукции // Физика плазмы и проблема УТС. Т. III. М.: АНСССР. 110 с. 1958.
− Польский В.И., Калин Б.А., Карцев П.И. и др. Повреждение поверхности конструкционных материалов при воздействии плазменных сгустков // Атомная энергия. Т. 50. № 2. С. 83–88. 1984.
− Репин А.Ю., Ступицкий Е.Л. Динамика и взаимодействие с преградой тороидального плазменного сгустка. Динамика тороидального плазменного сгустка в вакууме // Теплофизика высоких температур. Т. 42. № 1. С. 31–37. 2004.
− Репин А.Ю., Ступицкий Е.Л. Динамика и взаимодействие с преградой тороидального плазменного сгустка. Взаимодействие падающего и отраженного потоков // Теплофизика высоких температур. Т. 42. № 3. С. 364–373. 2004.
− Репин А.Ю., Ступицкий Е.Л., Шапранов А.В. Динамика и взаимодействие с преградой тороидального плазменного сгустка. Ионизационно-динамические характеристики и электромагнитное излучение // Теплофизика высоких температур. Т. 42. № 4. С. 523−537. 2004.
− Сиднев В.В., Скворцов Ю.В. Динамика взаимодействия сверхзвукового плазменного потока с твердотельной мишенью // Физика плазмы. Т. 13. № 5. С. 632–634. 1987.
− Смирнов Е.В., Ступицкий Е.Л. Численное моделирование воздействия разреженного плазменного потока на поверхность твердого тела // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. № 11. С. 102–112. 2010.
− Степанов А.Е., Сиднев В.В. Об условии преобразования кинетической энергии сверхзвукового плазменного потока в мягкое рентгеновское излучение // Физика плазмы. Т. 5. № 8. С. 1000–1007. 1989.
− Ступицкий Е.Л. Динамика мощных импульсных излучений и плазменных образований. М.: Физматлит. 280 с. 2006а.
− Ступицкий Е.Л. Особенности плазменных течений взрывного типа в околоземном космическом пространстве // Геомагнетизм и аэрономия. Т. 46. № 1. С. 21–43. 2006б.
− Ступицкий Е.Л., Любченко О.С., Худавердян А.М. Неравновесные процессы при разлете высокотемпературного плазменного сгустка // Квантовая электроника. Т. 12. № 5. С. 1038–1049. 1985.
− Ступицкий Е.Л., Репин А.Ю. Численное моделирования процесса взаимодействия сгустков плазмы с помощью метода крупных частиц // Тр.VI Международной конференции: “Метод крупных частиц: теория и приложения”. С. 70–82. 1996.
− Филипп Н.Д., Ораевский В.Н., Блаунштейн Н.Ш., Ружин Ю.Я. Эволюция искусственных плазменных неоднородностей в ионосфере Земли. Кишинев: Штиинца. 246 с. 1986.
− Brunetkin B.A., Stupitsky E.L., Repin A.Yu. et al. // J. Phys. D.: Appl. Phys. V. 25. P. 1583–1590. 1992.
− Brunetkin B.A., Stupitsky E.L., Repin A.Yu. et al. Laser – produced plasma expansion in a uniform magnetic field // Laser and Particle Beams. V. 10. № 4. P. 723–735. 1992.
− Brunetkin B. A., Stupitsky E. L., Repin A. Yu. et al. // Proc. 10-th International Colloquium on UV and X-Ray Spectroscopy of Astrophysical and Laboratory Plasmas. – University of California, Berceley, February, 1992.
− Degnan J.H. Compact toroid formation, compression and acceleration // Phys. Fluids. № 5. P. 2938–2959. 1993.
− Hartman C.W., Hammer J.H. // Phys. Rev. Lett. V. 48. P. 929. 1982.
− Hussey T.W. Theoretical modeling of pulsed-power driven flux compression systems at the Phillips Laboratory // Report Phillips Laboratory, High Energy Plasma Division, Kirtland AFB. № M87117–6008. 1993.
− Koopman D.W., Gotorth R.R. // Phys. Fluids. V. 17. P. 1560. 1974.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия