Физика Земли, 2023, № 2, стр. 49-61
Гравитационная неустойчивость вязкоупругой земной коры
Б. И. Биргер *
Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
* E-mail: birgerbor@mail.ru
Поступила в редакцию 10.01.2022
После доработки 31.08.2022
Принята к публикации 31.08.2022
- EDN: LHOUUE
- DOI: 10.31857/S0002333723020059
Аннотация
Методом линейной теории для малых возмущений исследуется неустойчивость тяжелого включения в верхних слоях Земли. Существование такого рода включений с повышенной плотностью связано с химической неоднородностью или фазовыми переходами. Вязкоупругость геоматериала описывается реологической моделью Максвелла. Рассмотрены два варианта расположения включения с повышенной плотностью. Тяжелое включение в холодном верхнем упругом слое коры не меняет своего расположения при малых возмущениях, т.е. является устойчивым по линейной теории. Тяжелое включение, которое расположено в горячем вязком слое коры, подстилающем верхний холодный слой, является неустойчивым (медленно погружается в лежащие ниже вязкие слои мантии).
ВВЕДЕНИЕ
Анализ неустойчивости, основанный на линейной теории для малых возмущений, т.е. теорией Ляпунова, является локальным, поскольку проблема устойчивости существенно нелинейна. Состояние системы, которое по линейной теории считается устойчивым, может оказаться неустойчивым при достаточно больших возмущениях. Поэтому линейная теория дает только достаточное условие неустойчивости. При глобальном анализе устойчивости величина рассматриваемых возмущений не ограничена. Глобальный анализ использует энергетический метод, который, как правило, дает только достаточное условие устойчивости, а следовательно, метод линейной теории и энергетический метод дополняют друг друга при исследовании устойчивости [Джозеф, 1981]. Энергетический метод успешно применяется при рассмотрении гравитационной устойчивости упругих слоев Земли в работах [Мухамедиев и др., 2016; Рыжак и др., 2016; Рыжак, Синюхина, 2019], в которых авторам удается получить не только достаточные, но и необходимые условия устойчивости.
Однако линейный анализ устойчивости имеет свои преимущества. Глобальный анализ дает критерий устойчивости рассматриваемой системы, но не прослеживает эволюцию того или иного начального возмущения. В частности, такой анализ не учитывает вязкость, которая характеризует исследуемую систему, поскольку устойчивость (или неустойчивость) системы не зависит от вязкости. Вязкость определяет скорость возвращения системы в начальное состояние после возмущения (если система устойчива) или скорость, с которой система удаляется от начального состояния после возмущения (если система неустойчива). Для геофизических приложений важно знать характерное время развития неустойчивости. Если система обладает огромной вязкостью, что характерно для верхних слоев Земли, может оказаться, что в глобально неустойчивой системе неустойчивость заметно развивается только на временах, сравнимых со временем существования самой системы (несколько миллиардов лет для Земли). Линейная теория прослеживает эволюцию начальных возмущений той или иной пространственной формы. Поэтому линейная теория позволяет говорить об устойчивости системы к возмущениям определенного типа, что не имеет смысла в рамках глобального анализ. Согласно линейной теории, система устойчива, если она устойчива к малым возмущениям любого типа, и неустойчива, если она неустойчива хотя бы к одному типу малых возмущений.
В геодинамике при рассмотрении медленных процессов, связанных с гравитационной неустойчивостью,
обычно рассматриваются только малые начальные возмущения, а развитие возмущения представляется
в виде $a{{e}^{{{{\lambda }}t}}}$, где $a$ начальное возмущение, а λ – комплексный инкремент. Если действительная часть λ отрицательна,
имеет место устойчивость, а если положительна – неустойчивость. Когда начальное возмущение
мало, а 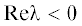 (устойчивость) линейная теория полностью описывает эволюцию начального малого возмущения.
Когда
(устойчивость) линейная теория полностью описывает эволюцию начального малого возмущения.
Когда 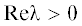 (неустойчивость), линейная теория описывает эволюцию возмущения только на не слишком
больших временах, при которых возмущение остается малым.
(неустойчивость), линейная теория описывает эволюцию возмущения только на не слишком
больших временах, при которых возмущение остается малым.
В настоящее время принята такая реологическая модель земной коры, в которой эффективная вязкость уменьшается с глубиной на несколько порядков, что вызвано ростом температуры [Karato, 2008; Birger, 2013]. Поэтому верхняя кора, где вязкость очень велика, ведет себя как упругая среда при не слишком высоких сдвиговых напряжениях (при достаточно больших напряжениях – как хрупко-упругая), а подстилающие ее слои нижней коры и мантийной литосферы, ведут себя как вязкие при медленных течениях и как упругие при быстрых. Тяжелые включения в коре могут вызвать гравитационную неустойчивость, при которой возникают медленные течения, представляющие интерес для геологии.
В настоящей работе методом линейной теории исследуется неустойчивость тяжелого включения в земной коре. Существование такого рода включений с повышенной плотностью связано с химической неоднородностью или фазовыми переходами. Будет исследована неустойчивость для двух вариантов расположения тяжелого включения: тяжелое упругое включение в верхнем холодном упругом слое коры и тяжелое вязкое включение в более глубоко расположенных горячих и вязких слоях Земли.
ПОСТАНОВКА ЗАДАЧИ
Рассматривается двухслойная модель. Нижний слой представлен как полупространство. Начало координат помещено на нижней поверхности верхнего слоя, а ось z направлена вертикально вверх. Слой (0 < z < d) моделирует верхнюю упругую кору, а полупространство (z < 0) – подстилающую литосферу и мантию. Начальное состояние в решаемой задаче – это литостатическое равновесие. В этом состоянии отсутствуют девиаторные напряжения, а давление связано с плотностью уравнением
где: $g$ – ускорение силы тяжести, а плотность определена какВ состоянии литостатического равновесия Земля испытывает огромное давление, вызванное гравитацией. Еще Рэлей ввел представление, согласно которому напряжение в Земле складывается из литостатического давления и небольшого добавочного напряжения, которое связано с деформациями, отсчитываемыми от равновесного состояния, обычными соотношениями линейной теории упругости или вязкоупругости. Это представление, широко используемое в современной геофизике, применяется и в данной статье.
Уравнения, описывающие возмущения литостатического равновесия несжимаемой среды, записываются в виде:
(2)
$ - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {{\sigma }_{{xx}}}}}{{\partial x}} + \frac{{\partial {{\sigma }_{{xz}}}}}{{\partial z}} = \rho \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{u}_{x}},$(3)
$ - \frac{{\partial p}}{{\partial z}} + \frac{{\partial {{\sigma }_{{xz}}}}}{{\partial x}} + \frac{{\partial {{\sigma }_{{zz}}}}}{{\partial z}} = \rho \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{u}_{z}},$(5)
${{\varepsilon }_{{xx}}} = \frac{{\partial {{u}_{x}}}}{{\partial x}},~\,\,\,\,{{\varepsilon }_{{zz}}} = \frac{{\partial {{u}_{z}}}}{{\partial z}},~\,\,\,\,~{{\varepsilon }_{{xz}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{x}}}}{{\partial z}} + \frac{{\partial {{u}_{z}}}}{{\partial x}}} \right)~.~$Уравнения (1)–(5) справедливы и для верхнего, и для нижнего слоя, моделированного как полупространство. Однако плотности и реологические свойства слоев отличаются. Чтобы учесть скачок плотности на границе между слоями необходимо ввести граничные условия.
На верхней деформируемой границе слоя обращается в нуль сила, действующая на единицу площади поверхности, откуда следует, что на недеформированной верхней границе $\left( {z = d} \right)$ выполняются условия
(6)
$\sigma _{{xz}}^{{\left( 2 \right)}} = 0,\,\,\,\, - {{p}^{{\left( 2 \right)}}} + \sigma _{{zz}}^{{\left( 2 \right)}} + {{\rho }^{{\left( 2 \right)}}}gu_{z}^{{\left( 2 \right)}} = 0.$Индекс 1 относится к нижнему слою (полупространству), индекс 2 – к верхнему. Вывод уравнений (6) приведен в Приложении 1. На границе ($z = 0)$ между верхним слоем и полупространством непрерывны смещения
(7)
$\begin{gathered} \sigma _{{xz}}^{{\left( 2 \right)}} = \sigma _{{xz}}^{{\left( 1 \right)}}, \\ - {{p}^{{\left( 2 \right)}}} + \sigma _{{zz}}^{{\left( 2 \right)}} + ({{\rho }^{{\left( 2 \right)}}} - {{\rho }^{{\left( 1 \right)}}})g{{u}_{z}} = - {{p}^{{\left( 1 \right)}}} + \sigma _{{zz}}^{{\left( 1 \right)}}. \\ \end{gathered} $На нижней границе полупространства ($z = - \infty $) наложено условие ограниченности вертикальных и горизонтальных смещений.
Вертикальное смещение представим в виде:
(8)
${{u}_{z}}\left( {x,z,t} \right) = {{U}_{z}}\left( z \right)\exp \left( {\lambda t} \right)\cos \left( {kx} \right),\,\,\,k > 0,$Для среды Максвелла уравнение состояния (реологическое соотношение) имеет вид:
(9)
${{\sigma }_{{ij}}} + \frac{\eta }{\mu }\frac{d}{{dt}}{{\sigma }_{{ij}}} = 2\eta \frac{d}{{dt}}{{\varepsilon }_{{ij}}},\,\,\,\,i,j = 1,2,$(10)
${{\sigma }_{{ij}}} + \frac{\eta }{\mu }\lambda {{\sigma }_{{ij}}} = 2\eta \lambda {{\varepsilon }_{{ij}}}.$Как следует из уравнения (10), если вязкость η очень велика $\left( {\frac{\eta }{\mu }\left| \lambda \right| \gg 1} \right)$ , уравнение Максвелла вырождается в уравнение состояния для упругой среды
а если упругий модуль сдвига µ очень велик $\left( {\frac{\eta }{\mu }\left| \lambda \right| \ll 1} \right)$, уравнение Максвелла вырождается в реологическое соотношение для вязкой ньютоновской жидкостиВ рамках линейной теории устойчивости скорости связаны со смещениями простым соотношением ${{v}_{i}} = \lambda {{u}_{i}}$, поэтому уравнения, описывающие движения упругой среды, и уравнения, описывающие течения вязкой среды, имеют аналогичный вид. Из уравнений для упругой среды, в которые входят смещения ${{u}_{i}}$ и модуль сдвига μ, сразу получаются уравнения для вязкой среды, если заменить ${{u}_{i}}$ на ${{v}_{i}}$, а μ на $\eta $. Записывая уравнения для вязкой среды не в скоростях, а в смещениях, следует ввести эффективный модуль сдвига вязкой среды ${{\mu }_{{eff}}} = \lambda \eta $.
Вязкость геоматериала сильно зависит от температуры, которая в Земле быстро растет с глубиной. Поэтому верхняя кора обладает очень высокой вязкостью и ведет себя как упругая среда, а более глубокие слои Земли, где вязкость значительно ниже, ведут себя как вязкая среда.
Медленные безынерционные течения, которые называют ползущими, характеризуют геологические движения, возникающие при тепловой конвекции и при восстановлении изостазии. В настоящей работе рассматриваются ползущие геологические течения, вызываемые возмущениями плотности земной коры. В правой части уравнения (2) стоит инерционный член $\rho {{\lambda }^{2}}{{U}_{x}}$, а левая часть этого уравнения в случае упругой среды содержит член $\mu {{k}^{2}}{{U}_{x}}$. Аналогичная ситуация и в уравнении (3), которое содержит члены $\rho {{\lambda }^{2}}{{U}_{z}}$ и $\mu {{k}^{2}}{{U}_{z}}$. Следовательно, для пренебрежения инерционностью упругой среды, необходимо выполнение условия
(13)
$\left| \lambda \right| \ll k\sqrt {{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }} .$Сжимаемостью упругой среды можно пренебречь при условии
(14)
$\mu \ll K,\,\,\,\,\,\nu = \frac{{3K - 2\mu }}{{2\left( {3K + \mu } \right)}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$Эти условия можно получить из требований (13) и (14) для упругой среды, подставив $\lambda \eta $ вместо упругого модуля сдвига μ.
Подставляя (8) в уравнения (2)–(5) и накладывая на величину инкремента ограничение (13), которое позволяет пренебречь инерционными членами в уравнениях (2) и (3), выражаем все физические переменные через вертикальное смещение:
(17)
${{u}_{x}}\left( {x,z,t} \right) = \frac{1}{k}D{{U}_{z}}\left( z \right)\exp \left( {\lambda t} \right)\sin \left( {kx} \right),$(18)
$p\left( {x,z,t} \right) = \mu \left( { - D + \frac{{{{D}^{3}}}}{{{{k}^{2}}}}} \right){{U}_{z}}\left( z \right)\exp \left( {\lambda t} \right)\cos \left( {kx} \right),$(19)
$\begin{gathered} {{\sigma }_{{zz}}}\left( {x,z,t} \right) = - {{\sigma }_{{xx}}}\left( {x,z,t} \right) = \\ = 2\mu D{{U}_{z}}\left( z \right)\exp \left( {\lambda t} \right)\cos \left( {kx} \right), \\ \end{gathered} $(20)
$\begin{gathered} {{\sigma }_{{xz}}}\left( {x,z,t} \right) = \\ = \mu \frac{1}{k}\left( {{{D}^{2}} + {{k}^{2}}} \right){{U}_{z}}\left( z \right)~\exp \left( {\lambda t} \right)\sin \left( {kx} \right), \\ \end{gathered} $Уравнения (17)–(21), в которых введен дифференциальный оператор $D = {d \mathord{\left/ {\vphantom {d {dz}}} \right. \kern-0em} {dz}}$, записаны для упругого верхнего слоя. Чтобы рассматривать вязкую среду, подстилающую упругий слой, в уравнения (18)–(20) следует вместо упругого модуля сдвига µ подставить ${{\mu }_{{eff}}} = \lambda \eta $.
Уравнение (21) имеет общее решение:
(22)
${{U}_{z}} = {{e}^{{kz}}}{{C}_{1}} + z{{e}^{{kz}}}{{C}_{2}} + {{e}^{{ - kz}}}{{C}_{3}} + z{{e}^{{ - kz}}}{{C}_{4}},\,\,\,0 \leqslant z \leqslant 1.$(23)
${{U}_{z}} = {{e}^{{kz}}}{{B}_{1}} + z{{e}^{{kz}}}{{B}_{2}},\,\,\, - \infty \leqslant z \leqslant 0,$Коэффициент вязкости земных недр оценивается как $\eta \approx 4 \times {{10}^{{19}}}\,\,{\text{Па}} \cdot {\text{с}}$ [Cathles, 1975]. Упругий модуль сдвига и плотность недр можно оценить как $\mu \approx 6 \times {{10}^{{10}}}\,\,{\text{Па}}$, $\rho \approx 3 \times {{10}^{3}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$. Все дальнейшие соотношения будут выписаны для безразмерных физических переменных, для которых сохраняем те же самые обозначения, что и для размерных. В качестве масштаба длины использована толщина верхнего упругого слоя коры, которая оценивается как d = 10 км, масштаб напряжения – упругий модуль сдвига μ, масштаб времени ${\eta \mathord{\left/ {\vphantom {\eta \mu }} \right. \kern-0em} \mu }$, где η коэффициент вязкости для глубоких слоев Земли. В приповерхностном слое вязкость выше на несколько порядков, и этот слой ведет себя как упругий даже на временах, сравнимых с возрастом Земли. Время ${\eta \mathord{\left/ {\vphantom {\eta \mu }} \right. \kern-0em} \mu }$, выбранное в качестве масштабного, называется временем Максвелла. Согласно приведенным оценкам, получаем масштаб времени ${\eta \mathord{\left/ {\vphantom {\eta \mu }} \right. \kern-0em} \mu } \approx 6 \times {{10}^{{\text{8}}}}\,\,{\text{с}} \approx 20~\,\,{\text{лет}}$. После введения масштаба времени можно сказать, что глубокие слои Земли ведут как вязкая среда, если $\left| \lambda \right| \ll 1$. Нет смысла рассматривать возмущения, длина волны которых $\frac{{2\pi }}{k}$ превышает 1000 км. Такое ограничение, наложенное на длину волны, приводит к ограничению $k > 6 \times {{10}^{{ - 2}}}$, наложенному на безразмерное волновое число. При этом из условия (16) следует ограничение $\left| \lambda \right| \ll 2$, наложенное на безразмерный инкремент, а условия (13) и (15) приводят к значительно более слабому ограничению $\left| \lambda \right| \ll 1.5 \times {{10}^{7}}$. Таким образом, при выполнении условия $\left| \lambda \right| \ll 1$ слои Земли, подстилающие верхнюю упругую кору, можно рассматривать как вязкую среду, пренебрегая инерционностью и сжимаемостью.
На всех графиках в этой статье представлены безразмерные инкременты λ и безразмерные волновые числа k. При выбранных масштабах длины и времени волновое число k измеряется в масштабе обратной длины ${{10}^{{ - 4}}}\,\,{{{\text{м}}}^{{ - 1}}}$, а инкремент λ – в масштабе обратного времени $1.7 \times {{10}^{{ - 9}}}\,\,{{{\text{с}}}^{{ - 1}}}$. В этих масштабах построены все графики в статье. Расчеты, в результате которых получены эти графики, проведены для безынерционной несжимаемой среды, т.е. заранее предполагается, что $\left| \lambda \right| \ll 1$. Если бы какой-нибудь расчет давал безразмерный инкремент, не удовлетворяющий требованию $\left| \lambda \right| \ll 1$, это означало бы только то, что в этом случае не появляется ползущее безынерционное течение. Однако ни в одном из случаев, которые будут рассмотрены далее, такая ситуация не возникает.
Для устойчивой системы ($\lambda < 0$), используемая линейная теория справедлива на любых временах, поскольку возмущение, зависящее от времени как $\exp \left( {\lambda t} \right)$, остается малым. Когда рассматриваемая система неустойчива $(\lambda > 0$), использование линейной теории перестает быть законным, когда $\lambda t \gg 1$. Поэтому в случае неустойчивости результаты линейного анализа устойчивости справедливы только на временах $t \leqslant {1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0em} \lambda }$, но это ограничение не является сильным в случае, когда $\lambda \ll 1$.
Учитывая соотношения (18)–(19) и вводя безразмерные переменные, уравнения (6) и (7) перепишем в виде:
(24)
$\left( {{{D}^{2}} + {{k}^{2}}} \right)U_{z}^{{\left( 2 \right)}} = 0,\,\,\,\,\left( {3D - \frac{{{{D}^{3}}}}{{{{k}^{2}}}} + \varphi } \right)U_{z}^{{\left( 2 \right)}} = 0,$(25)
$\begin{gathered} \left( {{{D}^{2}} + {{k}^{2}}} \right)U_{z}^{{\left( 2 \right)}} = \lambda \left( {{{D}^{2}} + {{k}^{2}}} \right)U_{z}^{{\left( 1 \right)}}, \\ \left( {3D - \frac{{{{D}^{3}}}}{{{{k}^{2}}}}} \right)U_{z}^{{\left( 2 \right)}} + RU_{z}^{{\left( 2 \right)}} = \lambda \left( {3D - \frac{{{{D}^{3}}}}{{{{k}^{2}}}}} \right)U_{z}^{{\left( 1 \right)}}. \\ \end{gathered} $В уравнениях (24) и (25) введены безразмерные параметры $\varphi = \frac{{{{\rho }^{{\left( 2 \right)}}}gd}}{\mu }$, $R = \frac{{\Delta \rho gd}}{\mu }$, где $\Delta \rho = {{\rho }^{{\left( 2 \right)}}} - {{\rho }^{{\left( 1 \right)}}}$ – скачок плотности на границе между верхним слоем и полупространством. Если считать, что плотность верхнего слоя выше, чем плотность подстилающего полупространства, перепад плотности $~\Delta \rho $ и параметр $R~$ положительны. Поскольку в недрах Земли перепады плотности малы, $\frac{R}{\varphi } = \frac{{\Delta \rho }}{\rho } \ll 1$.
Итак, решается краевая задача: обыкновенное дифференциальное уравнение четвертого порядка (21) имеет общее решение, в которое входят 8 произвольных констант (по 4 для верхнего и нижнего слоев). Граничных условий тоже 8. На верхней свободно деформируемой границе $\left( {z = 1} \right)$ наложены условия (24). На границе между слоями $\left( {z = 0} \right)$ наложены условия (25) и условия непрерывности горизонтальных и вертикальных смещений. В силу (17) и (20) условия непрерывности горизонтального смещения и касательного напряжения сводятся к условиям непрерывности первой и второй производной вертикального смещения ${{U}_{z}}$ по z. На нижней границе нижнего слоя $z = - \infty $ наложено условие ограниченности смещений. Из этого условия следует равенство нулю двух произвольных констант нижнего слоя, что учтено в уравнении (23). Краевые условия, как и само уравнение, записаны в терминах функции ${{U}_{z}}\left( z \right)$.
При такой постановке задачи исследуется устойчивость бесконечного горизонтального слоя к возмущениям, характеризуемым любыми волновыми числами k. Однако постановку задачи можно интерпретировать по-другому. Пусть в верхней коре имеется возмущение плотности (тяжелое включение), охватывающее область с горизонтальном размером $L$. Вертикальный размер d этой аномальной области выбран в качестве масштаба длины и, следовательно, равен 1. Такое возмущение плотности создает возмущение гравитационной силы, которое вызывает течение. Возможность перехода от рассмотрения возмущения с горизонтальным размером L к периодическому по горизонтали возмущению связана с тем, что первая гармоника $\cos \left( {\frac{{2\pi }}{L}x} \right)$ дает основной вклад в разложение Фурье возмущения с горизонтальным размером L [Cathles, 1975; Биргер, 2016; 2017]. Волновое число k, характеризующее периодичность по горизонтали, связано с горизонтальным размером аномальной области как $k = \frac{{2\pi }}{L}$. При периодическом движении среда, неограниченная по горизонтали, разбивается на бесконечный набор вертикальных столбов. Движение в одном из вертикальных столбов $\left( {0 < x < L} \right)$ моделирует движение, которое возникает в случае, когда возмущение плотности происходит в области с горизонтальном размером $L$. В столбе $\left( {0 < x < L} \right)$ вертикальное смещение зависит от горизонтальной координаты как $\cos \left( {\frac{{2\pi }}{L}x} \right)$, а горизонтальное смещение – как $\sin \left( {\frac{{2\pi }}{L}x} \right)$. Поэтому на боковых краях столба ($x = 0,~~x = L$) горизонтальное смещение отсутствует, а вертикальное смещение максимально и направлено вверх, а в центре ($x = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$) столба вертикальное смещение имеет ту же величину, но направлено вниз.
УСТОЙЧИВОСТЬ ТЯЖЕЛОГО УПРУГОГО СЛОЯ
В случае упругого тяжелого слоя на вязком полупространстве граничные условия приводят к системе из шести однородных уравнений для шести произвольных констант:
(26)
$\begin{gathered} k{{e}^{k}}{{C}_{1}} + \left( {1 + k} \right){{e}^{k}}{{C}_{2}} + k{{e}^{{ - k}}}{{C}_{3}} + \left( { - 1 + k} \right){{e}^{{ - k}}}{{C}_{4}} = 0, \\ \left( {\varphi + 2k} \right){{e}^{k}}({{C}_{1}} + {{C}_{2}}) + \left( {\varphi - 2k} \right){{e}^{{ - k}}}({{C}_{3}} + {{C}_{4}}) = 0, \\ {{C}_{1}} + {{C}_{3}} - {{B}_{1}} = 0, \\ k{{C}_{1}} + {{C}_{2}} - k{{C}_{3}} + {{C}_{4}} - k{{B}_{1}} - {{B}_{2}} = 0, \\ k{{C}_{1}} + {{C}_{2}} + k{{C}_{3}} - {{C}_{4}} - \lambda k{{B}_{1}} - \lambda {{B}_{2}} = 0, \\ \left( {R + 2k} \right){{C}_{1}} + \left( {R - 2k} \right){{C}_{3}} - 2\lambda k{{B}_{1}} = 0. \\ \end{gathered} $Приравнивая нулю определитель этой системы линейных уравнений (если определитель отличен от нуля, все константы равны нулю), получаем биквадратное уравнение
где:Решая уравнение (27), находим два значения инкремента $\lambda $ и зависимость каждого значения инкремента $\lambda $ от k при различных значениях параметра $R = \frac{{\Delta \rho gd}}{\mu }$ и фиксированном значении параметра $\varphi = \frac{{\rho gd}}{\mu } \approx 0.005$ (такая оценка соответствует верхнему слою земной коры толщиной порядка 10 км). Безразмерный параметр $\frac{{\Delta \rho }}{\rho }$, где $\rho $ – плотность тяжелого верхнего слоя, лежит в интервале $0 < \frac{{\Delta \rho }}{\rho } < 1$. Этот параметр равен единице только в случае, когда плотность нижнего слоя равна нулю. Поскольку $\frac{R}{\varphi } = \frac{{\Delta \rho }}{\rho }$, параметр $R$ может изменяться в интервале $0 < R < \varphi $.
Когда $R < \varphi $, уравнение (27) имеет два действительных отрицательных корня λ, зависимость которых от R и от k представлена на рис. 1 и рис. 2.
Рис. 1.
Зависимость инкремента ${{\lambda }}$ от параметра R при ${{\varphi }} = 0.005$ и фиксированном волновом числе k = 0.1. На этом рисунке, как и на всех последующих, безразмерный инкремент λ измеряется в масштабе $1.7 \times {{10}^{{ - 9}}}\,\,{{{\text{с}}}^{{ - 1}}}$.
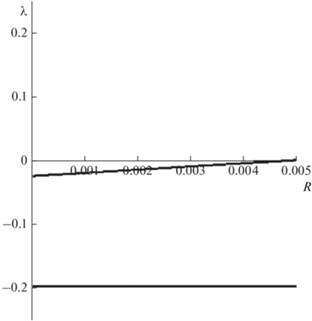
Рис. 2.
Зависимость инкремента $\lambda $ от волнового числа k при фиксированном значении параметров ${{\varphi }} = 0.005$, $R = 0.01{{\varphi }}$. На этом рисунке, как и на всех последующих, безразмерное волновое число k измеряется в масштабе ${{10}^{{ - 4}}}\,\,{{{\text{м}}}^{{ - 1}}}$.

Таким образом, тяжелое включение в верхнем упругом слое земной коры устойчиво. Эта устойчивость обеспечивает восстановление изостатического равновесия: земная поверхность, возмущенная в начальный момент, со временем возвращается в исходное равновесное состояние даже при наличии тяжелого включения в верхней коре. Примером восстановления изостазии является процесс послеледниковых поднятий земной поверхности [Cathles, 1975; Биргер, 2016; 2017]. Расчеты показывают, что неустойчивость могла бы возникнуть только в том случае, когда параметры $\varphi = \frac{{\rho gd}}{\mu }$ и $\frac{{\Delta \rho }}{\rho }$ на несколько порядков превышают их оценки для земной коры, т.е. при нереально малом модуле упругости и при нереально большом перепаде плотности. Например, если принять $\varphi = 5$, $R = 4$, получаем неустойчивость, при которой зависимость $\lambda $ от k показана на рис. 3.
Рис. 3.
Зависимость инкремента ${{\lambda }}$ от волнового числа k при фиксированном значении параметров ${{\varphi }} = 5$, $R = 4$.
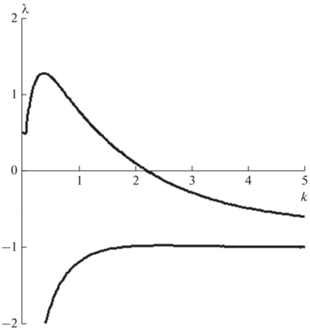
Результаты анализа устойчивости тяжелого упругого слоя, лежащего на упругом полупространстве, представлены в Приложении 2.
НЕУСТОЙЧИВОСТЬ ТЯЖЕЛОГО ВЯЗКОГО СЛОЯ
В случае тяжелого включения в вязком слое $(0 < z < 1)$, лежащем на вязком полупространстве, граничные условия приводят к системе однородных уравнений:
(28)
$\begin{gathered} k{{e}^{k}}{{C}_{1}} + \left( {1 + k} \right){{e}^{k}}{{C}_{2}} + k{{e}^{{ - k}}}{{C}_{3}} + \left( { - 1 + k} \right){{e}^{{ - k}}}{{C}_{4}} = 0, \\ \left( {\varphi + 2\lambda k} \right){{e}^{k}}({{C}_{1}} + {{C}_{2}}) + \left( {\varphi - 2\lambda k} \right){{e}^{{ - k}}}({{C}_{3}} + {{C}_{4}}) = 0, \\ {{C}_{1}} + {{C}_{3}} - {{B}_{1}} = 0, \\ k{{C}_{1}} + {{C}_{2}} - k{{C}_{3}} + {{C}_{4}} - k{{B}_{1}} - {{B}_{2}} = 0, \\ k{{C}_{1}} + {{C}_{2}} + k{{C}_{3}} - {{C}_{4}} - k{{B}_{1}} - {{B}_{2}} = 0, \\ \left( {R + 2\lambda k} \right){{C}_{1}} + \left( {R - 2\lambda k} \right){{C}_{3}} - 2\lambda k{{B}_{1}} = 0. \\ \end{gathered} $Приравнивая определитель этой системы линейных уравнений нулю, находим для $\varphi = 0.005$ и $R = 0.001$ зависимость λ от k, показанную на рис. 4. В случае, когда $R = 0$, т.е. когда нет скачка плотности, верхняя кривая на рис. 4 исчезает, а оставшаяся нижняя кривая показывает устойчивость, которая приводит к восстановлению изостатического равновесия.
Рис. 4.
Зависимость λ от k при фиксированных параметрах ${{\varphi }} = 0.005$ и $R = 0.001$ для тяжелого вязкого включения.
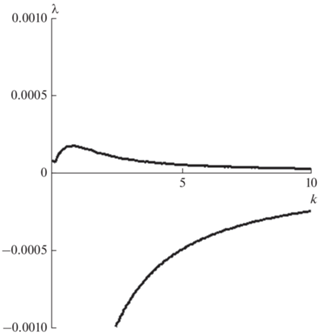
Зависимость λ от параметра $R$ при $k = 1$ показана на рис. 5. Вязкий тяжелый слой, подстилаемый вязким полупространством с тем же самым коэффициентом вязкости, неустойчив при $\Delta \rho > 0$, т.е. при сколь угодно малом перепаде плотности. Такая неустойчивость, называемая неустойчивостью Рэлея–Тейлора, хорошо известна в гидродинамике и геофизике [Теркот, Шуберт, 1985].
Рис. 5.
Зависимость инкремента λ от параметра $R$ при фиксированном волновом числе $k = 1$ для тяжелого вязкого включения.
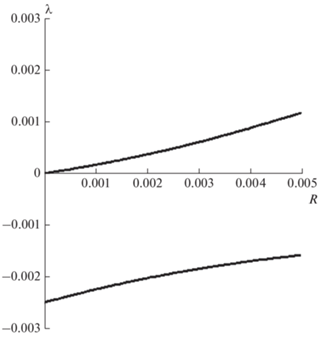
Однако задача о тяжелом вязком слое, подстилаемым вязким слоем с меньшей плотностью, не соответствует реальной ситуации в Земле, где холодный верхний слой ведет себя как упругая среда даже на очень больших временах. Чтобы учесть влияние верхнего упругого слоя, можно моделировать этот слой как тонкую упругую пластину. Тогда на верхней поверхности (z = 1) должны выполняться граничные условия, определяемые силовым воздействием упругой пластины:
(29)
$\frac{2}{{\left( {1 - \nu } \right)}}\frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{x}^{2}}}} + \frac{1}{{\mu {{h}_{{el}}}}}{{\sigma }_{{xz}}} = 0,$(30)
$N\frac{{{{\partial }^{4}}{{u}_{z}}}}{{\partial {{x}^{4}}}} + \rho g{{u}_{z}} + {{\sigma }_{{zz}}} - p = 0,$(32)
$\begin{gathered} \left( {1 + \frac{1}{{\left( {1 - \nu } \right)}}k} \right)k{{e}^{k}}{{C}_{1}} + \left( {1 + \frac{1}{{\left( {1 - \nu } \right)}}k} \right)\left( {1 + k} \right){{e}^{k}}{{C}_{2}} + \\ + \,\,\left( {1 - \frac{1}{{\left( {1 - \nu } \right)}}k} \right)k{{e}^{{ - k}}}{{C}_{3}} + \\ + \,\,\left( {1 - \frac{1}{{\left( {1 - \nu } \right)}}k} \right)\left( { - 1 + k} \right){{e}^{{ - k}}}{{C}_{4}} = 0, \\ \end{gathered} $(33)
$\begin{gathered} \left( {\varphi + \frac{1}{{6\left( {1 - \nu } \right)}}{{k}^{4}} + 2\lambda k} \right){{e}^{k}}({{C}_{1}} + {{C}_{2}}) + \\ + \,\,\left( {\varphi + \frac{1}{{6\left( {1 - \nu } \right)}}{{k}^{4}} - 2\lambda k} \right){{e}^{{ - k}}}({{C}_{3}} + {{C}_{4}}) = 0. \\ \end{gathered} $Приравнивая нулю определитель полученной системы уравнений, находим зависимость λ от R при фиксированных значениях $\varphi = 5 \times {{10}^{{ - 3}}}$ и $k = 1$, показанную на рис. 6. Сравнение рис. 6 с рис. 5 показывает, что учет самого верхнего упругого слоя, моделируемого как тонкая пластина, снижает значения инкрементов $\lambda $, т.е. снижает неустойчивость.
Рис. 6.
Зависимость положительного инкремента λ от параметра R в случае, когда верхний упругий слой моделируется как тонкая пластина.
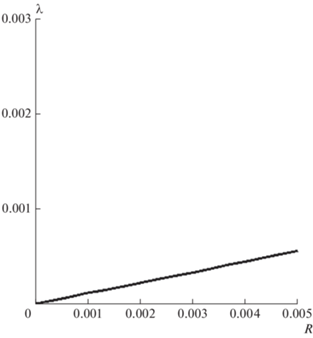
Фиксируя $\varphi = 5 \times {{10}^{{ - 3}}}$ и $R = 5 \times {{10}^{{ - 5}}}$, находим зависимость λ от k, которая показана на рис. 7а. На рис. 7б показана та же самая зависимость в другом масштабе.
Рис. 7.
(а) – Зависимость инкремента λ от волнового числа k при фиксированных параметрах ${{\varphi }} = 5 \times {{10}^{{ - 3}}}$ и $R = 5 \times {{10}^{{ - 5}}}$ в случае, когда верхний упругий слой моделируется как тонкая пластина; (б) – та же самая зависимость, что и на рис. 7а, при малых значениях инкремента λ.
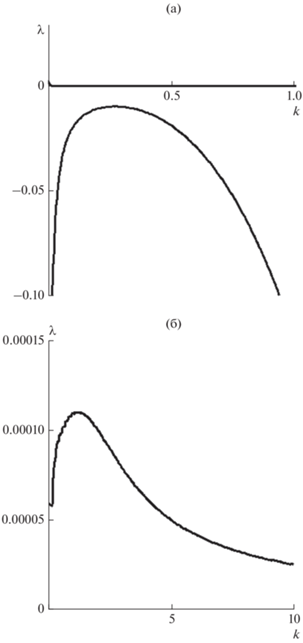
Приближение тонкой пластины применимо в случае, когда рассматриваются возмущения с длиной волны, значительно превышающей толщину слоя. Этому условию удовлетворяют только возмущения с волновыми числами $k \ll \pi $. Кроме того, приближение тонкой пластины не учитывает вес упругого слоя. Поэтому приходится применять трехслойную модель, рассматривая упругий верхний слой $(1 \leqslant z \leqslant 2$) с плотностью ρ. Под этим упругим слоем находится тяжелый вязкий слой $(0 \leqslant z \leqslant 1$) с плотностью $\rho + \Delta \rho $. Под тяжелым вязким слоем находится слой, который моделируется как полупространство $\left( { - \infty \leqslant z \leqslant 0} \right)$ с плотностью ρ. На верхней границе $z = 2$ (земная поверхность) отсутствуют нормальные и касательные напряжения, т.е. наложены граничные условия (23) и (24). На внутренних границах $z = 1$ и $z = 0$ выполняются условия непрерывности смещений и напряжений. Распределение вертикальных смещений в верхнем слое имеет вид:
(34)
$\begin{gathered} {{U}_{z}} = {{e}^{{kz}}}{{A}_{1}} + z{{e}^{{kz}}}{{A}_{2}} + {{e}^{{ - kz}}}{{A}_{3}} + z{{e}^{{ - kz}}}{{A}_{4}}, \\ 1 \leqslant z \leqslant 2, \\ \end{gathered} $(35)
$\begin{gathered} k{{e}^{{2k}}}{{A}_{1}} + \left( {1 + 2k} \right){{e}^{{2k}}}{{A}_{2}} + k{{e}^{{ - 2k}}}{{A}_{3}} + \\ + \,\,\left( { - 1 + 2k} \right){{e}^{{ - 2k}}}{{A}_{4}} = 0, \\ \left( { - 1 + 2k} \right){{e}^{{ - 2k}}}{{A}_{1}} + \left( {\varphi + 4k} \right){{e}^{{2k}}}{{A}_{2}} + \\ + \,\,\left( {\varphi - 2k} \right){{e}^{{ - 2k}}}{{A}_{3}} + \left( {\varphi - 4k} \right){{e}^{{ - 2k}}}{{A}_{4}} = 0, \\ {{e}^{k}}{{A}_{1}} + {{e}^{k}}{{A}_{2}} + {{e}^{{ - k}}}{{A}_{3}} + {{e}^{{ - k}}}{{A}_{4}} - {{e}^{k}}{{C}_{1}} - {{e}^{k}}{{C}_{2}} - \\ - \,\,{{e}^{{ - k}}}{{C}_{3}} - {{e}^{{ - k}}}{{C}_{4}} = 0, \\ k{{e}^{k}}{{A}_{1}} + \left( {1 + k} \right){{e}^{k}}{{A}_{2}} - k{{e}^{{ - k}}}{{A}_{3}} + \left( {1 - k} \right){{e}^{{ - k}}}{{A}_{4}} - \\ - \,\,k{{e}^{k}}{{C}_{1}} - \left( {1 + k} \right){{e}^{k}}{{C}_{2}} + \\ + \,\,k{{e}^{{ - k}}}{{C}_{3}} + \left( {k - 1} \right){{e}^{{ - k}}}{{C}_{4}} = 0, \\ k{{e}^{k}}{{A}_{1}} + \left( {1 + k} \right){{e}^{k}}{{A}_{2}} + k{{e}^{{ - k}}}{{A}_{3}} + \left( {k - 1} \right){{e}^{{ - k}}}{{A}_{4}} - \\ - \,\,\lambda k{{e}^{k}}{{C}_{1}} - \lambda \left( {1 + k} \right){{e}^{k}}{{C}_{2}} - \lambda k{{e}^{{ - k}}}{{C}_{3}} - \\ - \,\,\lambda \left( {k - 1} \right){{e}^{{ - k}}}{{C}_{4}} = 0, \\ (2k{{e}^{k}} - R)({{A}_{1}} + {{A}_{2}}) - (2k{{e}^{k}} + R)\left( {{{A}_{3}} + {{A}_{4}}} \right) - \\ - \,\,2\lambda k{{e}^{k}}({{C}_{1}} + {{C}_{2}}) + 2\lambda k{{e}^{{ - k}}}\left( {{{C}_{3}} + {{C}_{4}}} \right) = 0, \\ {{C}_{1}} + {{C}_{3}} - {{B}_{1}} = 0, \\ k{{C}_{1}} + {{C}_{2}} - k{{C}_{3}} + {{C}_{4}} - k{{B}_{1}} - {{B}_{2}} = 0, \\ k{{C}_{1}} + {{C}_{2}} + k{{C}_{3}} - {{C}_{4}} - k{{B}_{1}} - {{B}_{2}} = 0, \\ \left( {R + 2\lambda k} \right){{C}_{1}} + \left( {R - 2\lambda k} \right){{C}_{3}} - 2\lambda k{{B}_{1}} = 0. \\ \end{gathered} $Приравняв нулю определитель системы уравнений (35) и решив полученное уравнение 3-го порядка по λ, получаем зависимость корней λ от волнового числа $k$. На рис. 8 представлена зависимость положительного корня λ от волнового числа при фиксированных значениях $\varphi = 5 \times {{10}^{{ - 3}}}$ и $R = 5 \times {{10}^{{ - 5}}}$.
Рис. 8.
Зависимость инкремента λ от волнового числа $k$ при фиксированных значениях параметров ${{\varphi }} = 5 \times {{10}^{{ - 3}}}$ и $R = 5 \times {{10}^{{ - 5}}}$ в случае трехслойной модели.
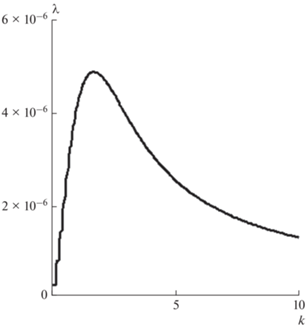
Как видно из рис. 8, наиболее неустойчивой является мода, для которой $~k \approx 1.8$. Таким образом, при фиксированном вертикальном размере $~d = 10{\text{\;км}}$ тяжелого включения, наиболее неустойчиво включение с горизонтальным размером $\frac{{2\pi }}{k}d \approx 35{\text{\;км}}$. Для волнового числа $k \approx 1.8$ значение безразмерного инкремента $\lambda \approx 5 \times {{10}^{{ - 6}}}$. Возмущение развивается во времени как $\exp \left( {\lambda t} \right)$. Поскольку был введен масштаб времени $\frac{\eta }{\mu } \approx 20\,\,~{\text{лет}}$, характерное время развития возмущения, т.е. время, за которое возмущение возрастает в $e \approx 2.7$ раз, составляет 4 миллиона лет.
ЗАКЛЮЧЕНИЕ
Цель проведенного исследования состоит в том, чтобы установить при каких условиях возмущения плотности коры вызывают медленные (ползущие) течения в недра Земли, изменяющие рельеф земной поверхности в геологических масштабах времени. Ползущие течения являются безынерционными и характеризуются малыми значениями инкрементов и волновых чисел. Возникновение ползущих течений связано с крупномасштабными возмущениями плотности земной коры. Показано, что тяжелое включение, которое расположено в вязком горячем слое коры, подстилающем верхний холодный упругий слой, является неустойчивым (медленно погружается в лежащие ниже вязкие слои мантии).
Кроме того, показано, что тяжелое включение в холодном верхнем слое коры является
устойчивым. Именно упругость холодного верхнего слоя определяет устойчивость, препятствуя
погружению тяжелого включения в подстилающие вязкие слои. Материал земной коры, как
и любой поликристаллический материал, обладает не только упругостью, но и ползучестью,
которая определяется имеющимися дефектами в идеально правильной кристаллической структуре.
Упруго – ползучая реология хорошо описывается моделью Максвелла, которая представляет
полную деформацию в виде суммы упругой деформации и вязкой деформации. Ползучесть
геоматериала, конечно, не описывается вязкой ньютоновской моделью, однако можно ввести
эффективную ньютоновскую вязкость, зависящую от характерной продолжительности рассматриваемого
процесса. Материал, описываемый моделью Максвелла, ведет себя как вязкий при медленных
процессах, характерное время которых значительно превышает время Максвелла, представляющее
собой отношение коэффициента вязкости к упругому модулю сдвига. В процессах с характерным
временем, значительно более коротким, чем время Максвелла, материал ведет себя как
упругий. При линейном анализе устойчивости зависимость от времени задается в виде
${{e}^{{\lambda t}}}$, а характерное время процесса определяется как $\frac{1}{{{\lambda }}}$. Вязкость геоматериала сильно зависит от температуры, которая в Земле быстро растет
с глубиной. Поэтому верхняя кора обладает очень высокой вязкостью и может вести себя
как упругая среда в то время, когда более глубокие слои Земли, где вязкость значительно
ниже, ведут себя как вязкая среда. Однако при очень малом инкременте λ (сверхмедленный
процесс) холодный верхний слой коры ведет себя как вязкий, и имеет место неустойчивость
Рэлея – Тейлора, при которой включение с повышенной плотностью в верхнем вязком слое
погружается в подстилающую вязкую среду при любом (даже очень малым) перепаде плотности.
Таким образом, можно утверждать, что тяжелое включение в верхней коре всегда неустойчиво,
хотя движение, вызванное неустойчивостью, происходит крайне медленно. Сделанное выше
утверждение о том, что тяжелое включение в верхнем холодном слое коры является устойчивым,
подразумевает только невозможность наблюдать такой медленный процесс на ограниченном
промежутке времени. Эффективная вязкость верхнего слоя на несколько порядков выше,
чем вязкость подстилающих слоев. На рис. 9 представлены результаты расчетов, выполненных для случая, когда верхний слой с тяжелым
включением $\left( {\frac{{\Delta \rho }}{\rho } = 0.01} \right)$ имеет вязкость на 4 порядка выше, чем вязкость 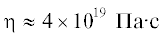 подстилающего слоя, который моделируется как полупространство.
подстилающего слоя, который моделируется как полупространство.
Рис. 9.
Зависимость инкремента от волнового числа в случае, когда вязкость верхнего холодного слоя на 4 порядка выше, чем вязкость подстилающих горячих слоев.
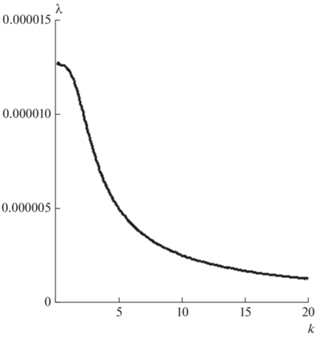
Как видно из рис. 9, наиболее неустойчивым является тяжелое включение, которому соответствует безразмерное волновое число $k \approx 1.5$ и безразмерный инкремент $\lambda \approx {{10}^{{ - 5}}}$. Поскольку масштаб длины – $d = 10{\text{\;м}}$ (толщина верхнего слоя), такое включение имеет горизонтальный размер $\frac{{2\pi }}{k}d \approx 40\,\,~{\text{км}}$. В качестве масштаба времени принято отношение коэффициента вязкости верхнего слоя к упругому модулю сдвига $\mu \approx 6 \times {{10}^{{10}}}\,\,{\text{Па}}$. Безразмерному инкременту ${{\lambda }} \approx {{10}^{{ - 5}}}$ соответствует огромное характерное время развития неустойчивости $\frac{{{\eta }}}{{{{\lambda \mu }}}} \approx 2 \times {{10}^{{10}}}\,\,{\text{лет}}$, которое значительно превосходит возраст Земли. Если верхний холодный слой коры рассматривается как упругий, ему приписывается бесконечно большая вязкость, при которой тяжелые включения в этом слое устойчивы. Однако вязкость этого слоя хотя и велика, но не бесконечна. Поэтому тяжелые включения в этом верхнем слое коры неустойчивы, но эта неустойчивость развивается так медленно, что тяжелые включения в верхнем слое коры практически не меняют своего положения за период времени, сравнимый с возрастом Земли.
Список литературы
Биргер Б.И. Динамика литосферы Земли. М.: Ленанд. 2016. 256 с.
Биргер Б.И. Восстанавливающие изостазию течения в литосфере // Геофизические исследования. 2017. № 4. С. 17–31.
Джозеф Д. Устойчивость движений жидкости. М.: Мир. 1981. 638 с.
Мухамедиев Ш.А., Рыжак Е.И., Синюхина С.В. Об устойчивости двуслойной системы неоднородных тяжелых сжимаемых жидкостей // Прикладная математика и механика. 2016. Т. 80. Вып. 3. С. 375–385.
Рыжак Е.И., Мухамедиев Ш.А., Синюхина С.В. Условия и механизмы возникновения гравитационной неустойчивости слоистых объемно-упругих геомассивов // Физика Земли. 2016. № 6. С. 4–20.
Рыжак Е.И., Синюхина С.В. Об устойчивости стратифицированных упругих геосистем в поле силы тяжести // Докл. РАН. 2019. Т. 489. № 3. С. 298–302.
Теркот Д., Шуберт Дж. Геодинамика. Геологические приложения физики сплошных сред. М.: Мир. 1985. 730 с.
Birger B.I. Temperature-dependent transient creep and dynamics of cratonic lithosphere // Geophys. J. Inter. 2013. V. 195. P. 695–705.
Karato S. Deformation of Earth Materials. An Introduction to the Rheology of Solid Earth. Cambridge university press. 2008. 463 p.
Cathles L.M. The viscosity of the Earth’s mantle. Princeton university press. 1975. 386 p.
Дополнительные материалы отсутствуют.


