Журнал физической химии, 2020, T. 94, № 9, стр. 1427-1431

Вопрос о необходимости явного учета межатомных колебаний в жидкости рассмотрен в работе [1] на примере инертного газа. Одна из проблем расчета термодинамических функций жидкого состояния простых веществ и смесей – проблема учета влияния межмолекулярных колебаний молекул. В жидкой фазе все частицы находятся в связанном состоянии, и колебания – один из видов их теплового движения. Их следует учитывать при интерпретации спектров инфракрасных и комбинационного рассеяния, при анализе динамических задач об элементарных реакциях в жидкой фазе и процессов массопереноса и теплопереноса. Экспериментальные данные о спектрах колебательного движения могут служить независимым источником информации о межмолекулярных взаимодействиях, и, естественно, необходимы для расчета и интерпретации термодинамических функций.

Данный вопрос возник в связи с учетом реальных времен релаксаций для процессов переноса массы и импульса в системах любой плотности. Лимитирующим является процесс установления равновесия по массе, тогда как локальное равновесие по импульсу всегда подстраивается под распределение массы. Это означает, что колебательные движения, отражающие импульсную часть свободной энергии, строго равновесны для любого локального состояния связанных частиц, как в паре, так и в жидкости. Традиционная процедура парожидкостных систем в теории неидеальных газов Урселла–Майера [2, 3] и в цепочке уравнений Боголюбова–Борна–Грина–Кирквуда–Ивона (ББГКИ) [4–6] исходит из существования только поступательных движений отдельных частиц и их межчастичного взаимодействия. Связанные состояния отдельных групп молекул отражаются только через ее потенциальную энергию, а колебательные движения в этих группах отсутствуют. Тем не менее, везде утверждается [7, 8], что в теории жидкости на основе цепочки ББГКИ учитываются (неявным образом) колебательные движения. Еще раньше этот же вопрос возник в теории неидеальных газов в работах [9–11] (см. также [12]), и он не был решен, за исключением димера [12, 13]. В [1] показано, что главная проблема обсуждаемой задачи связана с тем, что колебательные движения явным образом влияют на вероятность реализации локальных конфигураций. Это резко усложняет анализ конфигурационных состояний системы, так как необходимо переходить к кластерному рассмотрению пространственного распределения частиц.

В данном сообщении уравнения дискретно-континуальной теории [1] (в рамках модели решеточного газа (МРГ) [12, 14]) использованы как в дискретном, так и континуальном описаниях распределения молекул по ячейкам, на которые разбивается полный объем системы в МРГ. Теория учитывает как потенциальную энергию взаимодействия между атомами, так и их колебания в связанных состояниях, начиная от изолированного димера до плотной фазы. Межчастичные взаимодействия описываются потенциалом Леннард–Джонса [14–17], а локальные частоты атомов рассчитываются в квазидимерной модели колебательного движения [14]. Центр масс частицы в континуальной версии не локализован в центре ячейки, как в дискретной версии, а смещается внутри нее (плотность вероятности для нахождения молекулы внутри ячейки есть непрерывная функция ее координаты) [1].

В обоих случаях использовано квазихимическое приближение (КХП) учета межчастичных взаимодействий, учитывающее прямые корреляции взаимодействующих молекул. Расчеты проведены с учетом взаимодействия только между ближайшими соседями. Для континуального описания это означает, что учитываются все взаимодействия между двумя соседними частицами А, находящимися в различных положениях внутри этих двух ячеек. Естественно, что при этом расстояния между частицами АА могут быть больше, чем параметр дискретной модели равный 2^1/2 σ, где σ – параметр потенциала Леннард–Джонса, отвечающей твердой сфере частицы, ограничивающей сближение двух частиц АА.

Для расчета использован разработанный алгоритм решения системы интегральных уравнений относительно парной функции распределения [18]. Суть данной реализации состоит в том, что любое смещение частица от центра рассматривается как квази-сорт исходной частицы. Ячейка МРГ равномерно делится на микроячейки. В результате задача сводится к многосортной смеси, для которой в КХП существуют методы существенного понижения размерности системы уравнений [19–21]. В итоге, редуцированная система уравнений имеет ту же размерность, что и число микроячеек в каждой ячейке. Это позволило исследовать влияния континуального описания распределения частиц на концентрационные зависимости основных термодинамических функций, и дать объяснение концентрационной зависимости эффективного параметра латерального взаимодействия [18]. Однако, при учете локальных кластерных конфигураций традиционная процедура редуцирования усложняется за счет необходимости рассмотрения каждого из неприводимых типов конфигураций [22] (детали расчета будут опубликованы позже).

Ниже для простоты рассматривается одномерная система (в ней нет фазовых переходов). Одновременно с учетом колебаний в расчетах отражается также поступательное движение частиц. (В плотных фазах пара и жидкости традиционные представления об индивидуальных движениях частиц, как в разреженном газе, являются приближенными и неоднозначным [1].) В одномерной системе исключаются вращательные движения, и можно обсуждать выражения для статсумм поступательного Q_tran и колебательного Q_vib движений. Это позволяет проиллюстрировать разные предположения об отдельных типах движения молекул в плотных фазах, которые часто обсуждаются в разных модельных построениях в теории растворов (такие же обсуждения составляют часть теории абсолютных скоростей реакций в плотных фазах и в задачах расчета коэффициентов самодиффузии и сдвиговой вязкости) [14–17].

Поступательная статсумма запишется как ${{Q}_{{{\text{tr}}}}} = {{({{[2\pi m{{k}_{{\text{B}}}}T]}^{{1/2}}}\lambda t_{{fg}}^{{AV}}{\text{/}}h)}^{{b(k)}}}$. Здесь m – масса частицы, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, Т – температура, λ – параметр ячейки, h – постоянная Планка, b(k) – число степеней свободы поступательного движения для конфигурации с числом ближайших соседей равных k (k = 0, 1, 2). Эти значения равны соответственно 1 (нет препятствия движению), 1/2 (движение в одну сторону) и нулю (отсутствие движения из-за блокировки соседями). Кроме того, чтобы в данной модели реализовалось поступательное движение, центр масс должен покинуть данную ячейку. Это возможно только, если рядом есть вакантный узел, описываемый сомножителем $t_{{fg}}^{{AV}}$ – условная вероятность того, что рядом с занятым узлом f есть свободных узел g.

Колебательные движения аппроксимируются квазидимерной моделью [14, 23], в которой частота колебаний центральной частицы в поле неподвижных соседей $\nu _{{f\{ g\} }}^{{A\{ i\} }}$ выражается как $\nu _{{f\{ g\} }}^{{A\{ i\} }} = $ $ = \frac{6}{\pi }{{\left[ {\frac{{K_{{f\{ g\} }}^{{A\{ i\} }}}}{{d(\theta )\mu _{{f\{ g\} }}^{{A\{ i\} }}}}} \right]}^{{1/2}}}$, где символы {i} и {g} обозначают локальную конфигурацию с числом k соседних частиц А по отношению к центральной частице А на узле f, находящихся на множестве соседних узлов с номерами {g}, т.е. между символами {i} и {g} и k для каждого узла f имеется однозначная связь. Здесь $K_{{f\{ g\} }}^{{A\{ i\} }} = U_{{f\{ g\} }}^{{A\{ i\} }}{\text{/}}{{\lambda }^{2}}$, где $U_{{f\{ g\} }}^{{A\{ i\} }} = \sum\nolimits_{k = 1}^z {\varepsilon _{{f{{g}_{k}}}}^{{A{{i}_{k}}}}} $ – потенциальная энергия центральной частицы А в поле соседей, $K_{{f\{ g\} }}^{{A\{ i\} }}$ – аналог второй производной от потенциальной энергии $U_{{f\{ g\} }}^{{A\{ i\} }}$ по параметру решетки; $\mu _{{f\{ g\} }}^{{A\{ i\} }}$ – приведенная масса эффективного димера, состоящего из центральной частицы А и его ближайших соседей, формирующих вторую частицу димера; ${{(\mu _{{f\{ g\} }}^{{A\{ i\} }})}^{{ - 1}}} = {{(m_{f}^{A})}^{{ - 1}}} + {{\left( {\sum\nolimits_{k = 1}^z {m_{{{{g}_{k}}}}^{{A{{i}_{k}}}}} } \right)}^{{ - 1}}}$, $d(\theta ) = 1 + t_{{fg}}^{{AA}}$ – аппроксимационная функция, связывающая свойства выделенного димера (центральная частица А в узле f и один из его соседей в узле g) от изолированного состояния в газе до плотной фазы флюида (подробнее см. [14, 23]). Колебательная статсумма рассчитывается как $Q_{{f\{ g\} }}^{{A\{ i\} }}(vib) = {{\left( {2\sinh \left[ {\frac{h}{{2{{k}_{{\text{B}}}}T}}\nu _{{f\{ g\} }}^{{A\{ i\} }}} \right]} \right)}^{{ - \varphi (k)}}}$. Для континуальной версии [18] вместо частицы А в центре микроячейки находится квазисорт  j. В остальном структура уравнений для статсумм сохраняется.

Для одномерной структуры реализуются значения φ(k), равные нулю для k = 0 (отсутствие соседей исключает колебания), 1/2 для k = 1 (наличие одного соседа) и 1 для k = 2 (наличие двух соседей). Отметим, что здесь рассматриваются не изолированные молекулы в газовой фазе, как в механике молекул, а фрагменты фазы. В целом, для одномерной системы естественно выполняется баланс количества степеней свободы для каждой частицы b(k) + φ(k) = 1.

Ниже приводится пример влияния учета поступательного и колебательного движений атомов аргона на равновесные характеристики паро-жидкостной системы: рассчитана величина химического потенциала как функция плотности флюида θ_А. Рассматривались следующие варианты, обсуждаемые в литературе: 1) традиционный вид допущений о полном отделении внутренних статсумм в МРГ от конфигурационных вкладов при описании любых растворов, что формально эквивалентно случаю отсутствия всех внутренних движений из-за сдвига химпотенциала на некоторую постоянную величину; 2) учет только поступательного движения при условии фиксированности полного числа степеней свободы (учет b(k) при φ(k) = 0); 3) учет только колебательного движения без учета трансляций (т.е. учет φ(k) при b(k) = 0); 4) совместный согласованный учет поступательного и колебательного движений при b(k) + φ(k) = 1; 5) учет только колебательного движения без учета трансляций и без изменения числа колебательных степеней свободы от плотности (т.е. φ(k) = 1 при b(k) = 0); 6) учет только поступательного движения без учета колебаний и без изменения числа поступательных степеней свободы от плотности (т.е. b(k) = 1 при φ(k) = 0).

Результаты расчетов изотерм (или зависимость химического потенциала μ от плотности) в виде a₀P(θ_A) = exp(μ(θ_A)) представлены на рис. 1 для дискретной (а) и континуальной (б) версий теории. Распределение центров масс соседних частиц в континуальной версии теории приводит к разным взаимодействиям частиц на разных расстояниях, что отражается на среднем значении их взаимодействия, равное [14, 18] ${{\varepsilon }_{{eff}}} = {{{{{\left\langle {{{\varepsilon }_{{AA}}}{{\theta }_{{AA}}}} \right\rangle }}_{{{\text{micro}}}}}} \mathord{\left/ {\vphantom {{{{{\left\langle {{{\varepsilon }_{{AA}}}{{\theta }_{{AA}}}} \right\rangle }}_{{{\text{micro}}}}}} {{{\theta }_{{AA}}}}}} \right. \kern-0em} {{{\theta }_{{AA}}}}}$, где, например, для малых плотностей θ_AA = = ${{\theta }_{A}}^{2}\exp [\beta {{\varepsilon }_{{AA}}}({{r}_{0}})]$, r₀ – среднее расстояние между частицами в дискретной модели, и ${{\left\langle {{{\varepsilon }_{{AA}}}{{\theta }_{{AA}}}} \right\rangle }_{{{\text{micro}}}}}$ = $\sum\nolimits_{f,g}^{} {\int_{\Delta (f)}^{} {\int_{\Delta (g)}^{} {\varepsilon _{{fg}}^{{AA}}(r_{f}^{A},r_{g}^{A})} } } \theta _{f}^{A}(r_{f}^{A})\theta _{g}^{A}(r_{g}^{A})\, \times $ $ \times \;\exp [\beta \varepsilon _{{fg}}^{{AA}}(r_{f}^{A},r_{g}^{A})]dr_{f}^{A}dr_{g}^{A}$. На рис. 1в показаны эффективные энергии латерального взаимодействия между соседями в соответствующих вариантах движений частицы как функции плотности системы.

Рис. 1.

Изотермы, связывающие химический потенциал атомов аргона с плотностью флюида во всем диапазоне плотности, при βε = 2 в дискретной (а) и континуальной (б) версиях теории, а также эффективные энергии латерального взаимодействия между соседями (в). Номер кривой соответствует номеру варианта расчета.

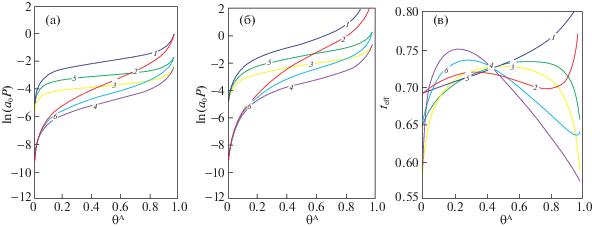
Для дискретного варианта верхняя кривая 1 отвечает первому варианту, затем идет учет только колебаний (5). Самая нижняя кривая 4 отвечает учету взвешенных вкладов поступательного и колебательного движений. Она во многом аналогична кривой 1 со сдвигом вниз на четыре единицы по ln(а₀Р) для малых плотностей и на две единицы для больших плотностей. Для континуального варианта кривые при высоких плотностях идут выше, чем соответствующие кривые для дискретного варианта. В остальном порядок расположения кривых для разных вариантов движений аналогичен.

Из рис. 1 следует, что учет колебаний смещает величину химпотенциала к меньшим значениям при постоянной величине плотности системы. Это отвечает более выгодному состоянию системы. Эффективный параметр ${{\varepsilon }_{{{\text{eff}}}}}$ всегда меньше величины параметра ${{\varepsilon }_{{AAf}}}$ латерального взаимодействия, используемого в обычной модели МРГ. Здесь он меняется в диапазоне от 0.6 до 0.8 доли от значений исходного параметра ${{\varepsilon }_{{AAf}}}$. Ход кривой зависит от способа учета внутренних движений частиц.

Внутренние движения меняют ход распределений центра масс внутри ячейки. Результаты расчета распределения центра масс были проиллюстрированы в работе [18]. На рис. 2 представлены аналогичные для распределения центра масс в зависимости от типа движений частиц (номера кривых совпадают с номером варианта).

Рис. 2.

Распределение центра масс в ячейке (а–в), г – условный парный коррелятор t^AV(r) для континуальной модели при βε = 4 и θ_А = 0.2 (а), 0.5 (б, г), 0.8 (в). Номера кривых совпадают с номером варианта учета движений частиц.

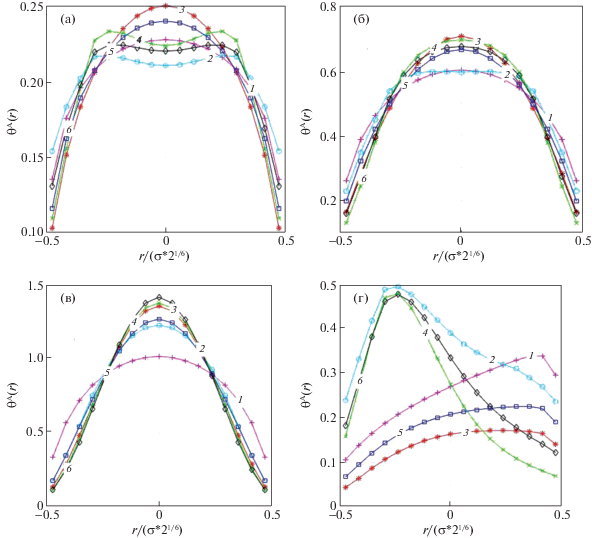
Распределения центра масс частиц А при плотностях θ_А = 0.2 (а), 0.5 (б), 0.8 (в) показывают заметную зависимость распределения от типа движений. При малых плотностях возможно даже появление минимума в центре ячейки. Отмечено, что колебательные движения стабилизируют купол кривых распределений, тогда как поступательное движение размывает его. Эту тенденцию также показывает поле (г), на котором представлена условная вероятность нахождения частицы рядом с вакансией: поступательное движение смещает кривые в сторону свободной ячейки, тогда как колебательные движения смещают кривые – в противоположную сторону от свободной ячейки.

Таким образом, иллюстрация влияния внутренних статсумм на значение химического потенциала и характер распределения центра масс позволяет сделать вывод о необходимости более детального учета движений частиц во всех концентрационных областях парожидкостной системы. При этом учет должен быть самосогласованным в отношении вкладов поступательного и колебательного движений. Использованные ранее в литературе допущения об учете только поступательного движения [14–17] без колебательного или одного колебательного без поступательного движения не соответствуют их корректному учету. Точно также в теориях неидеальных газов и теории интегральных уравнений для жидкости отсутствует учет колебательных вкладов для разных связанных состояний флюида от пара до жидкости.

Результаты расчета показывают, что в общем случае влияние вклада поступательного движения превышает влияние вклада колебательного движения в концентрационное изменение химического потенциала. Учет одного колебательного движения (кривая 5) ранее обсуждался только для двух предельных ситуаций в плотной жидкости и для димеров. В данной работе впервые проведен самосогласованный расчет поступательного и колебательного движений в полной концентрационной области флюида (вариант 4). Он отвечает минимальному значению химического потенциала при любых плотностях. Этот эффект не зависит от типа модели (дискретной или континуальной) при одинаковом использовании КХП учета взаимодействия ближайших соседей в одномерной системе. Кривые 4 и 6 дают оценку систематических отклонений в классических подходах для парожидкостных систем [2–10] и при учете связанных состояний, присутствующих в этих же системах.

Включение в теорию учета связанных состояний частиц делает ее более последовательной и точной, и должно приводить к расширению возможности теории для предсказания разных термодинамических и кинетических характеристик. Теория допускает расширение на смеси и на неоднородные системы.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта № 18-03-00030а).