Журнал физической химии, 2020, T. 94, № 8, стр. 1232-1241
Влияние изоморфных примесей на эластопроводимость хиральных углеродных нанотрубок
О. С. Лебедева a, b, *, Н. Г. Лебедев a, И. А. Ляпкосова b
a Волгоградский государственный университет
Волгоград, Россия
b Волгоградский государственный аграрный университет
Волгоград, Россия
* E-mail: lebedeva_os@volsu.ru
Поступила в редакцию 13.09.2019
После доработки 13.09.2019
Принята к публикации 12.11.2019
Аннотация
Представлены результаты теоретического исследования пьезорезистивных свойств хиральных углеродных нанотрубок с разным типом проводимости, как идеальных, так и допированных точечными дефектами замещения различной концентрации, однородно распределенными в кристаллической решетке. В качестве донорной и акцепторной примеси выбирались атомы бора и азота соответственно. В рамках модели Хаббарда и Андерсона с использованием метода функций Грина проведены моделирование зонной структуры исследуемых наночастиц и аналитический расчет продольной компоненты тензора эластопроводимости, а также исследована его зависимость от диаметра нанотрубок, величины относительной деформации продольного сжатия и растяжения, концентрации примесей. Дано физическое обоснование полученных результатов, проведено их сравнение с литературными данными.
Углеродные нанотрубки (УНТ) [1] являются одной из аллотропных форм углерода и визуализируются как протяженный поверхностный объект цилиндрической формы нанометрового диаметра и микронной длины. Физические свойства их зависят от их электронного строения, геометрической структуры и диаметра [1].
Электронные характеристики УНТ достаточно чувствительны по отношению к механическому воздействию [2]. Изменение энергетической щели и проводимости деформированных полупроводниковых углеродных наночастиц приводит к эффекту пьезосопротивления, который количественно характеризуется пьезорезистивными константами, такими как, тензор эластосопротивления, тензор пьезосопротивления, тензор эластопроводимости и калибровочный фактор [3]. Эффект пьезосопротивления лег в основу разработки и развития MEMS [4] – технологии интеграции механических элементов и датчиков на кремниевом субстрате. Высокая чувствительность проводящих свойств углеродных нанотрубок по отношению к механическим деформациям интенсивно исследуется, как экспериментально, так и теоретически, на протяжении последних десятилетий и открывает новые перспективы использования деформированных нанотрубок как основного структурного элемента пьезорезистивных сенсоров и датчиков давления [5]. Количественная калибровка таких приборов основывается на использовании значений пьезорезистивных констант, аналитический расчет которых проводится в данной работе.
Кроме того, эффект пьезосопротивления лежит в основе сформировавшегося недавно нового научного направления – стрейнтроники [6], использующий эффекты в твердых телах, обусловленные деформациями и приводящие к изменению зонной структуры, проводящих и магнитных свойств материалов. Подобные эффекты позволяют реализовать новое поколение устройств информационных и сенсорных технологий. Например, в работе [7] анонсирована разработка на базе графена транзистора, использующего деформационное изменение баллистической проводимости (эффект пьезопроводимости).
В работах [8–11] построена математическая модель электронного строения зигзагообразных и кресельных ахиральных углеродных нанотрубок, деформированных объемным расширением (сжатием) и осевым растяжением (сжатием), как идеальных, так и с акцепторными и донорными точечными дефектами замещения, а также с учетом поперечной деформации, в линейном приближении по деформационному потенциалу на основе метода сильной связи в рамках модели Хаббарда. Проведен теоретический расчет продольной компоненты тензора эластопроводимости [3] углеродных нанотрубок как функции относительной деформации объемного расширения (сжатия) и осевого растяжения (сжатия). Показана ее монотонная нелинейная зависимость для углеродных нанотрубок всех типов от величины относительной деформации и от диаметра полупроводниковых углеродных нанотрубок и независимость пьезорезистивной константы проводящих нанотрубок от их диаметра.
Полный теоретический обзор пьезорезистивных свойств углеродных наночастиц невозможен без изучения пьезопроводимости хиральных УНТ, которые имеют спиральную симметрию и названы хиральными в соответствии с химической номенклатурой [1]. Моделирование электронного спектра таких деформированных трубок, которое имеет свою специфику в силу винтовой симметрии их структуры и, вследствие этой особенности, представляет определенную сложность, обусловленную изменением валентных углов в результате искажения решетки, осуществлено в работе [12]. Авторами показано, что изменение проводимости хиральных УНТ, которое происходит под действием деформаций, зависит от наличия примесей в кристаллической структуре и их концентрации, варьируя которую, можно эффективно управлять пьезорезистивными свойствами исследуемых наночастиц.
В данной работе представлены результаты теоретического исследования пьезорезистивных свойств примесных хиральных УНТ. Моделирование электронного строения деформированных углеродных наноструктур осуществляется с помощью введения деформационного потенциала, учитывающего варьирование длин межатомных связей и валентных углов.
МОДЕЛЬ ЭЛЕКТРОННОГО СТРОЕНИЯ ДЕФОРМИРОВАННЫХ ПРИМЕСНЫХ ХИРАЛЬНЫХ УГЛЕРОДНЫХ НАНОТРУБОК
Моделирование электронного строения деформированных идеальных хиральных УНТ наглядно описано в работе [12]. Поэтому здесь кратко приводятся теоретические основы модели для логического построения всей статьи.
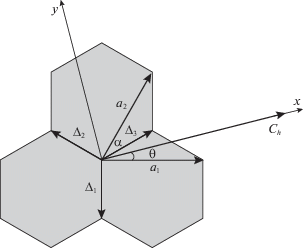
В качестве геометрической модели хиральных УНТ выбирался двумерный гексагональный графеновый слой. Фрагмент такой графеновой кристаллической структуры изображен на рис. 1, на котором обозначены хиральный вектор Сh = na1 + + ma2, угол α между векторами основных трансляций a1 и a2 (a1 = a2 = a) и вектора межатомных расстояний Δi. Ось Оx выбрана параллельно вектору Сh, который отмеряет ширину ленты, задающей диаметр трубки, а ось Оy направлена вдоль оси УНТ, получающейся после сворачивания графеновой ленты в цилиндр.
Рис. 1.
Фрагмент структуры хиральной УНТ, с выбранной системой координат, Δ1, Δ2, Δ3 – вектора расстояний между ближайшими соседями, a1, a2 – вектора трансляций, α – угол между векторами трансляций, θ – хиральный угол, Сh – хиральный вектор.
Математическая модель электронного строения недеформированных хиральных УНТ строится, исходя из их геометрического строения и зонной структуры графенового слоя с использованием метода сворачивающихся зон [1]. Общий вид зонной структуры в рамках метода сильной связи в приближениях Хюккеля и ближайших соседей можно представить в виде [1]:
(1)
$\begin{gathered} \varepsilon ({\mathbf{k}}) = \pm {{\gamma }_{0}}\left\{ {{\text{3 + 2cos}}\left( {{\mathbf{k}}{{{\mathbf{a}}}_{1}}} \right){\text{ + 2cos}}\left( {{\mathbf{k}}{{{\mathbf{a}}}_{2}}} \right)} \right. + \\ {{\left. { + \;2{\text{cos}}\left( {{\mathbf{k}}\left( {{{{\mathbf{a}}}_{1}} - {{{\mathbf{a}}}_{2}}} \right)} \right)} \right\}}^{{{\text{1/2}}}}} = \\ = \; \pm {\kern 1pt} {{\gamma }_{0}}\left\{ {{\text{1 + 4cos}}\left( {\frac{{{\mathbf{k}}\left( {{{{\mathbf{a}}}_{1}} + {{{\mathbf{a}}}_{2}}} \right)}}{{\text{2}}}} \right){\text{cos}}\left( {\frac{{{\mathbf{k}}\left( {{{{\mathbf{a}}}_{1}} - {{{\mathbf{a}}}_{2}}} \right)}}{{\text{2}}}} \right)} \right. + \\ {{\left. { + \;{\text{4co}}{{{\text{s}}}^{{\text{2}}}}\left( {\frac{{{\mathbf{k}}\left( {{{{\mathbf{a}}}_{1}} - {{{\mathbf{a}}}_{2}}} \right)}}{{\text{2}}}} \right)} \right\}}^{{{\text{1/2}}}}}, \\ \end{gathered} $Для хиральных трубок справедливо условие квантования волнового вектора k вдоль направления хирального вектора Сh [1]:
(2)
${\mathbf{k}}{{{\mathbf{C}}}_{{\mathbf{h}}}} = 2\pi q,\quad {\text{где}}\quad q = 1,2, \ldots \,.$Компоненты волнового вектора kx и ky целесообразно выбрать вдоль вектора Сh и оси УНТ соответственно, т.е. kx↑↑Сh и ky⊥Сh. Модуль хирального вектора недеформированных УНТ можно представить, исходя из его определения, в следующем известном виде [1]:
(3)
$\begin{gathered} \left| {{{{\mathbf{C}}}_{{{\mathbf{h}}0}}}} \right| = \sqrt {n{\mathbf{a}}_{{_{1}}}^{2} + m{\mathbf{a}}_{{_{2}}}^{2} + 2nm{{{\mathbf{a}}}_{1}}{{{\mathbf{a}}}_{2}}} = \\ = a\sqrt {{{n}^{2}} + {{m}^{2}} + nm} . \\ \end{gathered} $С помощью (3) и условий (2) можно получить явное выражение условия квантования поперечной компоненты волнового вектора:
(4)
$\begin{gathered} {{k}_{x}}a = \frac{{2\pi q}}{{\sqrt {{{n}^{2}} + {{m}^{2}} + nm} }}, \\ q = 1,2,\; \ldots ,\;[\sqrt {{{n}^{2}} + {{m}^{2}} + nm} ]. \\ \end{gathered} $(5)
$\begin{gathered} \frac{{{\mathbf{k}}({{{\mathbf{a}}}_{1}} + {{{\mathbf{a}}}_{2}})}}{2} = \left( {\frac{1}{{\sqrt {{{n}^{2}} + {{m}^{2}} + nm} }}} \right. \times \\ \times \;\left. {\left( {\frac{{3\pi q(n + m)}}{{2\sqrt {{{n}^{2}} + {{m}^{2}} + nm} }} + \frac{{\sqrt 3 {{k}_{y}}a(n - m)}}{4}} \right)} \right), \\ \frac{{{\mathbf{k}}({{{\mathbf{a}}}_{1}} - {{{\mathbf{a}}}_{2}})}}{2} = \left( {\frac{1}{{\sqrt {{{n}^{2}} + {{m}^{2}} + nm} }}} \right. \times \\ \times \;\left. {\left( {\frac{{\pi q(n - m)}}{{2\sqrt {{{n}^{2}} + {{m}^{2}} + nm} }} - \frac{{\sqrt 3 {{k}_{y}}a(n + m)}}{4}} \right)} \right). \\ \end{gathered} $В результате выражение (1) и соотношения (5) полностью определяют энергетический спектр электронов недеформированных хиральных УНТ. Согласно теории электронного строения УНТ [1], набор дисперсионных кривых электронного спектра, нумеруемых целым числом q, образуется путем пересечения двумерной энергетической поверхности графена параллельными плоскостями, соответствующими непрерывной компоненте волнового вектора, и положение которых относительно зоны Бриллюэна задается значением дискретной kx-компоненты волнового вектора согласно условию квантования (2). Кроме того, если разность хиральных индексов n – m = 3d, где d – целое, то такие УНТ характеризуются металлическим типом проводимости, а если n – m = 3d + 1 или n – m = 3d + 2, то УНТ имеют соответственно широкую или узкую энергетическую щель и проявляют полупроводниковый тип проводимости.
Деформированное состояние кристаллита в общем случае характеризуется тензором дисторсии ${{u}_{{\alpha \beta }}} = {{\partial }_{\beta }}{{({\mathbf{r}}{\text{'}} - {\mathbf{r}})}_{\alpha }}$, (α, β = x, y, z), где r и r' – радиус-векторы начального и конечного положения некоторой точки кристаллита [13]. Диагональные элементы тензора характеризуют относительное удлинение образца вдоль соответствующего направления, недиагональные элементы задают угол поворота линейного элемента при деформации.
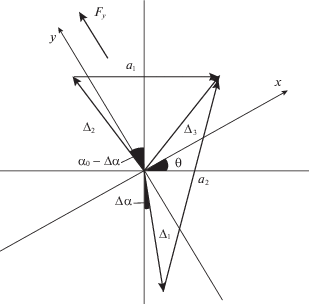
Исходя из определения тензора дисторсии вывод энергетического спектра деформированных хиральных УНТ основывается на модификации аргументов тригонометрических функций в выражении (1). Изменение элементарной ячейки УНТ под действием деформации растяжения показано на рис. 2. Рисунок демонстрирует модельные представления о том, что вследствие деформации происходит изменение не только длин межатомных связей Δi = R0(1 + δ) на величину их относительного удлинения δ = ΔR/R0, но и угла между векторами трансляций α = α0 + Δα (α0 = = π/3 – угол между векторами трансляций в недеформированной решетке), а, следовательно, проекций векторов трансляций a1 и a2 на оси Оx и Оy выбранной системы координат.
Рис. 2.
Положения межатомных векторов Δ1, Δ2, Δ3 после деформации растяжения (сжатия) с учетом их поворота на угол Δα.
В результате геометрических преобразований (рис. 2) электронный спектр деформированных хиральных УНТ примет вид:
(6)
$\begin{gathered} \varepsilon ({\mathbf{k}}) = \pm \gamma (1 + 4\cos [\pi n{{A}_{1}} + {{B}_{1}}] \times \\ \times \;\cos [\pi n{{A}_{2}} - {{B}_{2}}] + 4{{\cos }^{2}}[\pi n{{A}_{2}} - {{B}_{2}}]{{)}^{{1/2}}}, \\ \end{gathered} $(7)
$\begin{gathered} {{A}_{1}} = \frac{{F\cos \alpha + G\sin \alpha }}{{A\cos \alpha + B\sin \alpha }}, \\ {{B}_{1}} = {{k}_{y}}{{R}_{0}}(1 + \delta )( - G\cos \alpha + F\sin \alpha ), \\ {{A}_{2}} = \frac{{ - E\cos \alpha }}{{A\cos \alpha + B\sin \alpha }}, \\ {{B}_{2}} = {{k}_{y}}{{R}_{0}}(1 + \delta )E\sin \alpha , \\ \end{gathered} $(8)
$E = \sin \theta \sin \left( {\frac{{{{\alpha }_{0}}}}{2}} \right) + \cos \theta \cos \left( {\frac{{{{\alpha }_{0}}}}{2}} \right),$Изменение поперечных размеров (диаметра) УНТ в результате деформации учитывается путем модификации модуля хирального вектора Ch, который, исходя из определения коэффициента Пуассона и прямой пропорциональности основных геометрических размеров нанотрубок параметрам решетки, можно рассчитать по следующей формуле:
где ν – коэффициент Пуассона, значение которого для УНТ в соответствии с экспериментальными данными [2] варьируется в пределах ν = 0.19–0.27.Соотношение (9) и выбранная геометрическая модель деформированных хиральных УНТ позволяют определить угол α между векторами трансляций в деформированной гексагональной решетке, входящий в выражения для коэффициентов (7) спектра УНТ (6):
(10)
$\sin \alpha = \frac{{BC + A\sqrt {{{B}^{2}} - {{C}^{2}} + {{A}^{2}}} }}{{{{A}^{2}} + {{B}^{2}}}},$Методика вычисления зависимости прыжкового интеграла γ(δ) от относительной деформации УНТ наглядно описана в работах [8–11].
Наличие донорных и акцепторных примесей (точечных дефектов замещения) в кристаллической структуре хиральных УНТ может существенным образом влиять на их пьезопроводимость, как показано на примере ахиральных нанотрубок в работе [10]. Для описания электронного строения примесных нанотрубок использовалась периодическая модель Андерсона [14]. Эту модель, как правило, применяют для описания электронных состояний кристалла с малыми концентрациями дефектов, взаимодействие которых мало по сравнению с энергией электронов невозмущенного кристалла. Она заключается в отдельном рассмотрении двух групп электронов: коллективизированных (π-электронов) и локализованных, взаимодействие между которыми осуществляется посредством потенциала гибридизации. Электрон-фононное взаимодействие в модели не учитывается. Модель успешно адаптирована для изучения влияния точечных дефектов (в том числе адсорбированных атомов) на зонную структуру углеродных нанотрубок [10, 11, 15, 16].
Электронный спектр УНТ в рамках модели Андерсона имеет следующий вид [10]:
(11)
$E({\mathbf{k}}) = \frac{1}{2}\left[ {{{\varepsilon }_{l}} + {{\varepsilon }_{k}} \pm \sqrt {{{{({{\varepsilon }_{l}} - {{\varepsilon }_{k}})}}^{2}} + 36{{{\left| {{{V}_{{CD}}}} \right|}}^{2}}x} } \right],$В качестве примера акцепторной и донорной примесей выбирались атомы бора и азота соответственно. Величина энергии электрона на дефекте (атоме азота) вычислялась как разность потенциалов ионизации (работ выхода электронов) атомов азота и углерода:
Параметр потенциала гибридизации VCD вычислялся по формуле резонансного интеграла в рамках квантово-химического полуэмпирического метода MNDO [17]:
(12)
$\begin{gathered} {{V}_{{lj}}} = \left\langle {{{\psi }_{l}}\left| { - \frac{{{{\hbar }^{2}}}}{{2m}}{{\nabla }^{2}} + {{V}_{l}} + {{V}_{j}}} \right|{{\psi }_{j}}} \right\rangle \approx \\ \approx \frac{1}{2}({{\beta }_{C}} + {{\beta }_{D}}){{S}_{{CD}}}, \\ \end{gathered} $(13)
$\begin{gathered} {{S}_{{CD}}} \equiv {{S}_{{pp}}} = \int {{{\Psi }_{{2{{p}_{z}}}}}({{{\mathbf{R}}}_{D}} - {\mathbf{r}})} {{\Psi }_{{2{{p}_{z}}}}}({\mathbf{r}})d{\mathbf{r}}, \\ {{\Psi }_{{{{p}_{z}}}}}({\mathbf{r}}) = \frac{1}{{4\sqrt {2\pi } }}{{\left( {\frac{Z}{{{{a}_{0}}}}} \right)}^{{3/2}}}{\mathbf{\rho }}\exp ( - {\mathbf{\rho }}{\text{/}}2)\cos \phi , \\ \end{gathered} $ЭЛАСТОПРОВОДИМОСТЬ ХИРАЛЬНЫХ УГЛЕРОДНЫХ НАНОТРУБОК
Расчет пьезорезистивных констант (продольной компоненты тензора эластопроводимости) хиральных УНТ осуществлялся по методике, подробно описанной в работах [8–10]. Исходя из определения тензора эластопроводимости [3] его продольная компонента для одномерных структур может быть выражена следующей формулой:
где M = mzzzz – продольная компонента тензора 4-го ранга эластопроводимости, Δσ = σ – σ0 – изменение продольной компоненты тензора удельной проводимости вследствие деформации кристаллита, σ и σ0 – продольные компоненты σzz тензора 2-го ранга удельной проводимости деформированного и недеформированного кристалла соответственно.Продольная компонента тензора удельной бесфононной проводимости УНТ вычислялась в рамках теории Кубо–Гринвуда с помощью метода функций Грина и использованием модельного гамильтониана сильной связи [19]. Окончательное выражение для продольной удельной проводимости УНТ, использованное в расчетах константы M, имеет следующий вид [10]:
(15)
$\begin{gathered} \sigma = 2\frac{{i\pi {{e}^{2}}}}{{{{k}_{{\text{B}}}}TV}}\sum\limits_{{\mathbf{k}},\alpha } {\sum\limits_{{\mathbf{q}},\beta } {{v}({\mathbf{k}})} } {v}({\mathbf{q}})\left\langle {{{n}_{{{\mathbf{k}}\alpha }}}} \right\rangle \times \\ \times \;\left[ {\left\langle {{{n}_{{{\mathbf{q}}\beta }}}} \right\rangle + {{\delta }_{{{\mathbf{kq}}}}}{{\delta }_{{\beta \alpha }}}\left( {1 - \left\langle {{{n}_{{{\mathbf{k}}\alpha }}}} \right\rangle } \right)} \right], \\ \end{gathered} $Поскольку многочисленные исследования транспортных свойств углеродных нанотрубок свидетельствуют о баллистическом (бесфононном) характере электронной проводимости [20], то использование модели сильной связи, не учитывающей электрон-фононное взаимодействие, является оправданным.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА
Для теоретических расчетов в работе использованы следующие значения относительной деформации растяжения (сжатия) δ = ±0.035, ±0.069, ±0.104, 0.25, соответствующие длинам межатомных связей R = 1.49, 1.54, 1.59, 1.8 Å в случае растяжения и R = 1.39, 1.34, 1.29 Å в случае сжатия. Электронный спектр деформированных (δ = 0.035) хиральных УНТ с учетом поперечных деформаций изображен на рис. 3 для ряда УНТ (3, 1), (7, 3) и (7, 4) разного диаметра и типа проводимости: полупроводник с широкой щелью, полупроводник с узкой щелью и проводник соответственно.
Рис. 3.
Зонная структура деформированных 3.5%-м растяжением хиральных УНТ: а – (3, 1), б – (7, 3), в – (7, 4).
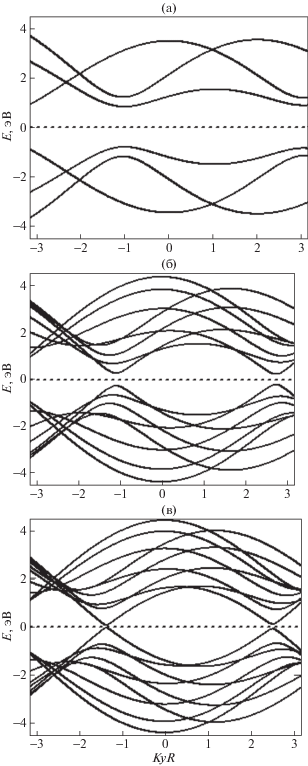
Принципиальных качественных различий полученных зонных структур по сравнению с энергетическим спектром недеформированных хиральных УНТ не наблюдается. Количественный анализ показывает увеличение наклона дисперсионных кривых к оси абсцисс и сужение зоны проводимости (ЗП) и валентной зоны (ВЗ), приводящее к увеличению плотности электронных состояний, в случае сжатия и, наоборот, увеличение наклона кривых и уширение ЗП и ВЗ (уменьшение плотности состояний) при деформации растяжения. Подобный эффект наблюдался и в случае деформации ахиральных (кресельных и зигзагообразных) УНТ [11].
Важным следствием влияния деформаций на электронный спектр хиральных УНТ, на наш взгляд, является, например, уменьшение ширины запрещенной зоны полупроводниковых УНТ при растяжении и увеличение при сжатии. Этот эффект принципиально отличается от случая деформации полупроводниковых ахиральных (зигзагообразных) УНТ [11], и связан с тем, что в результате деформаций растяжения (сжатия) модифицируется также (сжимается и растягивается) и двумерная расширенная зона Бриллюэна (ЗБ), представляющая собой шестиугольник (гексагон) в пространстве волновых векторов [1]. Причем изменение последней происходит вдоль линий непрерывной ky-компоненты волнового вектора, положение которых в зоне Бриллюэна определяется квантованием kx-компоненты. Учет поперечной деформации УНТ приводит соответственно к растяжению (сжатию) ЗБ в направлении оси x. В результате такой несимметричной деформации линии непрерывного волнового вектора приближаются к особым K-точкам (точки Дирака [1]) зоны Бриллюэна, в которых пересекаются ВЗ и ЗП графена, или удаляются от них в зависимости от величины деформации δ. Последнее и приводит к уменьшению (увеличению) запрещенной зоны (рис. 3б). Анализ электронных спектров показывает, что подобное поведение характерно для всех рассмотренных хиральных УНТ, для которых выполняется условие n – m = = 3d + 1, например, трубка (7, 3) (рис. 3б).
Что касается зонной структуры деформированных полупроводниковых хиральных УНТ, чьи индексы хиральности удовлетворяют условию n – ‒ m = 3d + 2, например, (3, 1) (рис. 3а), то ее качественная модификация аналогична изменению электронного спектра полупроводниковых зигзагообразных нанотрубок. То есть наблюдается уменьшение (увеличение) наклона дисперсионных кривых к оси абсцисс и сужение (уширение) ЗП и ВЗ в случае растяжения (сжатия), приводящее к увеличению (уменьшению) плотности электронных состояний на границах зон.
В случае проводящих хиральных УНТ, например, (7, 4) продольное растяжение (сжатие) также изменяет их зонную структуру вышеописанным способом и принципиально отличает их от кресельных и проводящих зигзагообразных нанотрубок. А именно, деформация зоны Бриллюэна ведет, наоборот, к удалению линий непрерывной компоненты волнового вектора от вершинных K‑точек, вследствие чего в электронном спектре появляется запрещенная щель (рис. 3в), меняющая электронные свойства трубки. Этот эффект наблюдается только в металлических хиральных УНТ и отсутствует в ахиральных нанотрубках, в которых не появляется энергетическая щель в спектре благодаря деформации растяжения (сжатия).
Необходимо отметить, что проводимость деформированных хиральных УНТ, как и недеформированных, зависит от их диаметра и хиральности, что проявляется в увеличении числа квантовых состояний электрона вдоль окружности нанотрубки. В этом случае даже малая деформация ЗБ вдоль направления непрерывной компоненты волнового вектора может приводить к смещению линий квантования поперечной компоненты, приближению (или удалению) их к дираковским точкам и появлению (или исчезновению) энергетической щели в спектре. Поэтому для хиральных трубок возможны переходы моттовского типа “проводник–полупроводник” и “полупроводник–проводник”, обусловленные осевыми деформациями растяжения (сжатия).
Как и в случае ахиральных УНТ [11], введение в структуру кристаллита точечного акцепторного дефекта замещения (атома бора) способствует появлению примесной зоны и энергетической щели на уровне Ферми в спектре проводящих и полупроводниковых нанотрубок (рис. 4а). С увеличением относительной деформации сжатия (растяжения) происходит последовательное расширение (сужение) запрещенной щели в примесной зоне, а плотность состояний в ЗП при этом уменьшается (увеличивается). Это связано с изменением прыжкового интеграла (энергии электронов) и потенциала гибридизации, которое приводит к усилению (ослаблению) взаимодействия примесей с кристаллитом соответственно. Следствием последнего является увеличение (уменьшение) расщепления примесного уровня.
Рис. 4.
Зонная структура УНТ (6, 2), содержащей: а) 100 акцепторных дефектов (атомов бора) и б) 100 донорных дефектов (атомов азота).
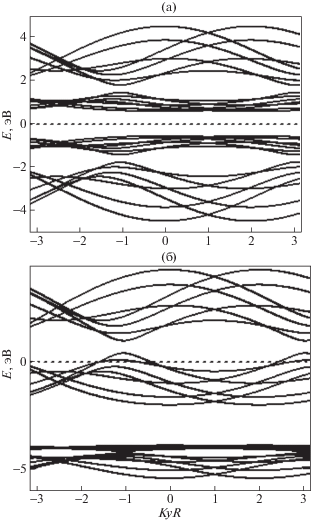
Донорные примеси формируют примесную зону в окрестности уровня дефекта εl, который при выбранных выше параметрах модели расположен в ВЗ (рис. 4б). Это изменяет всю зонную структура хиральных нанотрубок. Увеличение концентрации донорных примесей, как и следовало ожидать, при любой деформации ведет к уменьшению запрещенной зоны полупроводникового кристаллита. Деформация растяжения (сжатия) при любых концентрациях дефектов приводит к увеличению (уменьшению) запрещенной зоны допированных УНТ. Донорные примеси также изменяют зонную структуру и “металлических” углеродных нанотрубок при любой относительной деформации, однако это не приводит к каким-либо качественным изменениям физических свойств. Изменяется только плотность электронных состояний вблизи уровня дефекта.
Подробный анализ результатов расчета продольной компоненты M тензора эластопроводимости идеальных хиральных УНТ представлен в работе [12]. Здесь представим сокращенный вариант обсуждения данных результатов.
Зависимость компоненты M от относительной деформации δ (= –0.104, –0.069, –0.035, 0.035, 0.069, 0.104, 0.25) для хиральных УНТ разного диаметра и типа проводимости (3, m), (6, m), (7, m), где m = 1, …, n – 1, представлена на рис. 5. Численные результаты получены при температуре Т = 300 K. Для наглядного изображения тенденции изменения константы M расчетные точки соединены сплошными линиями. При этом надо понимать, что точка δ = 0 не определена.
Рис. 5.
Продольная компонента М тензора эластопроводимости хиральных УНТ как функция относительной деформации осевого растяжения и сжатия δ: а) (3, m), б) (6, m), в) (7, m). На всех кривых точка δ = 0 не определена.
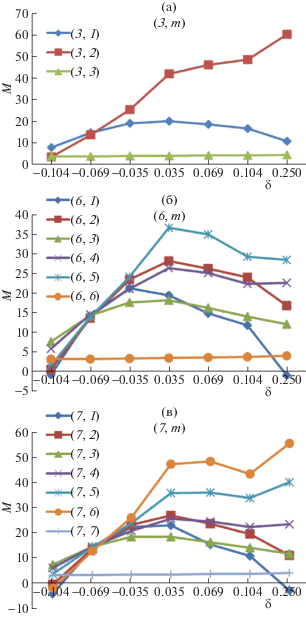
Общей закономерностью для большинства рассмотренных хиральных УНТ, существенно отличающей их от ахильных нанотрубок, является монотонное уменьшение константы М с ростом относительной деформации растяжения (сжатия) δ. Такое поведение обусловлено качественным и количественным изменением плотности состояний вблизи уровня Ферми и ширины запрещенной зоны вследствие деформации зоны Бриллюэна. Модификация электронного спектра ведет к изменению удельной проводимости, учитывающей все возможные заполненные электронные состояния, а, следовательно, к уменьшению компоненты M с ростом и уменьшением величины δ. Уменьшение компоненты M и в случае растяжения, и в случае сжатия обусловлено тем, что в результате деформации кристаллита линии разрешенных значений kx-компоненты приближаются к одним K-точкам ЗБ, а от других удаляются. В результате ширина запрещенной зоны уменьшается при любом типе деформации.
Исключением является трубка (3, 2), а также и некоторые другие трубки малого диаметра, например, (4, 2) и т.д., которая ведет себя как проводящие кресельные УНТ [11]. Это связано с тем, что ее хиральный угол близок к 30°, как у “arm-chair” нанотрубок, поэтому при деформации расширения (сжатия) линии разрешенных значений kx-компоненты волнового вектора удаляются (приближаются) к K-точкам ЗБ.
Для трубок большого диаметра, таких как (7, 5) и (7, 6), при осевом растяжении наблюдается осциллирующая зависимость величины M от δ, также соответствующая особенностям зонной структуры деформированных хиральных УНТ.
Как видно из рис. 5, исключением из общего поведения компоненты M является предельно допустимая деформация δend = 0.25, которая приводит к росту пьезорезистивной константы при сильном растяжении (сжатии).
Зависимость компоненты тензора М для ряда хиральных УНТ, например, (6, m) (рис. 5б) и (7, m) (рис. 5в) от их диаметра (индекса m) при заданном значении δ немонотонная (осциллирующая), что напрямую связано с зависимостью электронного спектра таких трубок от хирального угла (хиральный эффект) [1]. Изменение угла означает поворот таких линий и приближение к (или удаление от) точкам Дирака.
Описанные выше результаты находятся в хорошем согласии с литературными данными по пьзорезистивным свойствам углеродных структур. Например, в работе [21] экспериментально получены зависимости относительного изменения сопротивления ΔR/R образцов тонких пленок из углеродных нанотрубок от величины относительной деформации удлинения δ, показан монотонный нелинейный характер данной зависимости.
Оценка значения ΔR/R с помощью рассчитанной в данной работе продольной компоненты M для УНТ (3, 1) по формуле:
при выбранных значениях относительной микродеформации δ = 0.001 показала результаты (ΔR/R)теор ≈ 0.020, близкие к экспериментальному значению (ΔR/R)экс ≈ 0.013 и сохраняющие тенденцию монотонного нелинейного роста. Разница в результатах, на наш взгляд, объясняется наличием взаимодействия между УНТ в пленках и другими видами деформаций, которые в модельных расчетах не учитывались.В обзоре [5] представлены результаты теоретических расчетов калибровочного фактора K ряда однослойных углеродных нанотрубок с использованием стандартного активационного выражения для удельной проводимости полупроводников. Оценка фактора по формуле:
дает значение K = –18.96 при δ = 0.01 и K = –12.31 при δ = 0.035 для УНТ (15, 4), что находится в хорошем соответствии с указанной работой, где также отмечено, что калибровочный фактор такой нанотрубки медленно возрастает с ростом величины относительной деформации.Пьезорезистивные константы M примесных хиральных УНТ рассчитывались на основе формулы (14) с учетом (11) и (15), в которую входит выражение для их зонной структуры (6). Наличие донорных и акцепторных дефектов замещения в кристаллической решетке нанотрубок модифицирует энергетический спектр УНТ в соответствии с дисперсионным соотношением (6). Данные расчета пьезорезистивных констант хиральных примесных УНТ (3, 1), (6, 2), (6, 3) и (7, 5) с добавленными в кристаллическую решетку акцепторными и донорными примесями (атомами бора и азота) соответственно, как функций относительной деформации растяжения и сжатия представлены на рис. 6 и 7.
Рис. 6.
Продольная компонента М тензора эластопроводимости хиральных УНТ как функция концентрации x акцепторных дефектов Nd (атомов бора) и величины относительной деформации растяжения и сжатия δ: а) x = 0.001 и б) x = 0.1.
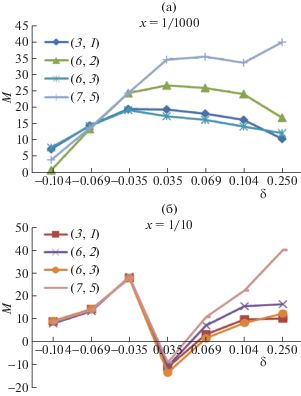
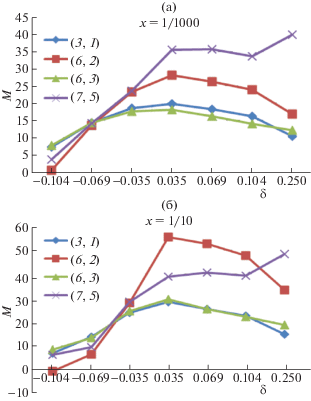
Рис. 7.
Продольная компонента М тензора эластопроводимости хиральных УНТ как функция концентрации x донорных дефектов Nd (атомов азота) и величины относительной деформации растяжения и сжатия δ: а) x = 0.001 и б) x = 0.1.
Как следует из анализа результатов расчета, частично представленных на рисунках, малые добавки акцепторных примесей Nd = 1, 10, 100, приходящиеся на N = 100 000 элементарных ячеек в кристалле, оказывают слабое влияние на компоненту М, которая незначительно (во втором, третьем значащем знаке) уменьшается (увеличивается) при деформации растяжения (сжатия) с ростом концентрации акцепторных примесей по сравнению с идеальными структурами (рис. 6).
В случае же донорных примесей (атомов азота) наблюдается незначительный (в третьем знаке) рост пьезорезистивной константы для каждой заданной деформации δ для малых концентраций x (рис. 7). Подобное поведение пьезопроводимости хирального кристаллита аналогично описанному в работе [10] изменению величины М ахиральных УНТ и связано с возникновением энергетической щели в электронном спектре в окрестности уровня дефекта, влияющей на заполнение электронами зоны проводимости нанотрубки при конечной температуре, и изменением плотности состояний вблизи уровня Ферми.
Как показали расчеты, с ростом относительной деформации δ кристаллической решетки величина М ведет себя так же, как и для идеальных структур, т.е. убывает при растяжении (сжатии) для обоих типов дефектов. Данный эффект связан с изменением самой зонной структуры УНТ: увеличением (уменьшением) наклона дисперсионных кривых вблизи минимума и уширением (сужением) ЗП при деформации растяжения (сжатия), т.е. уменьшением (увеличением) плотности электронных состояний, которые при конечной температуре заполняются согласно распределению Ферми–Дирака и дают вклад в проводимость системы.
Увеличение концентрации акцепторных примесей до значения x = 0.1 меняет как величину М, так и характер ее зависимости от δ (рис. 6б). Наблюдается ее возрастание с ростом деформации δ для всех рассмотренных УНТ. Подобное поведение связано с тем, что заданная концентрация акцепторных дефектов увеличивает щель в примесной зоне и уменьшает плотность состояний в окрестности уровня Ферми независимо от типа УНТ.
ЗАКЛЮЧЕНИЕ
На основе проведенного теоретического исследования можно сформулировать его основные результаты и выводы.
1. Построена модель электронного строения хиральных углеродных нанотрубок, деформированных растяжением и сжатием, как идеальных, так и с донорными и акцепторными примесями в рамках метода сильной связи.
2. Показано, что под влиянием деформаций сжатия и растяжения происходит модификация зонной структуры полупроводниковых хиральных УНТ с последующей вариацией ширины запрещенной зоны и плотности состояний, что косвенно отражается в изменении проводимости рассматриваемых нанотрубок и приводит к возникновению переходов моттовского типа “проводник-полупроводник” и “полупроводник-проводник”.
3. Исследованы пьезорезистивные свойства хиральных УНТ разного диаметра и типа проводимости, как идеальных, так и с донорными и акцепторными примесями в кристаллической решетке. Рассчитаны продольные компоненты тензора эластопроводимости хиральных УНТ, исследована их зависимость от величины относительной деформации и ее типа. Изучено влияние концентрации примесей на пьезорезистивные константы, приведено физическое обоснование полученных результатов.
4. Исследование пьезорезистивных свойств хиральных УНТ позволяет получить полное представление об изменении проводимости углеродных нанотрубок, обусловленном деформацией осевого растяжения (сжатия).
5. Полученные результаты также можно адаптировать для электромеханических наносенсорных разработок, в основе работы которых лежит эффект пьезосопротивления, а основным структурным элементом выступают хиральные УНТ.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований и Администрации Волгоградской области в рамках научного проекта № 18-42-343004.
Список литературы
Saito R., Dresselhaus M.S., Dresselhaus G. Physical properties of carbon nanotubes. London: Imperial College Press, 1999. 251 p.
Rafii–Tabar H. Computation physics of carbon nanotubes. New York: Cambridge University Press, 2008. 493 p.
Бир Г.Л., Пикус Г.Е. Симметрия и деформационные эффекты в полупроводниках. М.: Наука, 1972. 584 с.
Востриков М.В. // Наукоемкие технологии. МГТУ имени Н.Э. Баумана. 2007. С. 223.
Obitayo W., Liu T. // J. Sensors. 2012. V. 2012. P. 652438.
Бухараев А.А., Звездин А.К., Пяток А.П., Фетисов Ю.К. // УФН. 2018. Т. 188. № 12(12). С. 1288.
McRae A.C., Wei G., Champagne A.R. // Physical Review Applied. 2019. V. 11. P. 054019.
Ляпкосова О.С., Лебедев Н.Г. // Физика твердого тела. 2012. Т. 54. № 7. С. 1412.
Лебедева О.С., Лебедев Н.Г. // Научно-технические ведомости СПбГПУ. Серия “Физико-математические науки”. 2014. Т. 189. № 1. С. 26.
Лебедева О.С., Лебедев Н.Г. // Научно-технические ведомости СПбГПУ. 2014. Т. 195. № 2. С. 149.
Лебедева О.С., Лебедев Н.Г. // Химическая физика. 2014. Т. 33. № 10. С. 73.
Lebedeva O.S., Lebedev N.G., Lyapkosova I.A. // Математическая физика и компьютерное моделирование. 2018. Т. 21. № 1. С. 53.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VII. Теория упругости. М.: ФИЗМАТЛИТ, 2003. 264 с.
Изюмов Ю.А., Чащин Н.И., Алексеев Д.С. Теория сильно коррелированных систем. Метод производящего функционала. М.: Изд-во “Регулярная и хаотическая динамика“, 2006. 384 с.
Пак А.В., Лебедев Н.Г. // Химическая физика. 2012. Т. 31. № 3. С. 82.
Пак А.В., Лебедев Н.Г. // Журн. физ. химии. 2013. Т. 87. С. 994.
Степанов Н.Ф. Квантовая механика и квантовая химия. М.: Мир, 2001. 519 с.
Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.: Наука, 1975. 632 с.
Квасников И.А. Термодинамика и статистическая физика. Т. 4: Квантовая статистика. Москва: КомКнига, 2005. 352 с.
Елецкий А.В. // УФН. 2009. Т. 179. № 3. С. 225.
Li Y., Wang W., Liano K., Hu C. // Chinese Science Bulletin. 2003. V. 48. № 2. P. 125.
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии


