1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 94, № 8, 2020

Журнал физической химии, 2020, T. 94, № 8, стр. 1228-1231

О пороге перколяции в полимерных нанокомпозитах

В. И. Иржак a, *

a Российская академия наук, Институт проблем химической физики
142400 Черноголовка, Московской области, Россия

* E-mail: irzhak@icp.ac.ru

Поступила в редакцию 22.08.2019
После доработки 15.01.2020
Принята к публикации 21.01.2020

Полный текст (PDF)

Аннотация

Проанализирована простая модель J. Li расчета величины порога перколяции в полимерных нанокомпозитах. Показано, что ее можно использовать, но с существенными поправками: во-первых, необходимо учитывать результат решения задачи об узлах на кубической решетке; во-вторых, более корректно усреднять ориентацию анизодиаметричных наночастиц.

Ключевые слова: полимерные нанокомпозиты, наночастицы, порог перколяции, ориентация анизодиаметричных наночастиц

Полимерные композиты, содержащие анизодиаметрические наночастицы (НЧ), обычно рассматривают как дисперсные твердоподобные системы. При низких концентрациях в сдвиговом потоке НЧ ориентируются, что приводит к снижению вязкости, как было показано для расплава полипропилена, наполненного многослойными углеродными нанотрубками (МСУНТ) [1, 2]. Увеличение концентрации НЧ приводит к росту вязкости вследствие образования упругой сетки [3]. Формирование сетки проявляется также в механических, электрофизических и других свойствах композитов [4–8]. Для этих свойств формирование сетки формулируется как перколяция.

Теория перколяции [9, 10] основана на идее, что при увеличении объемной концентрации φ НЧ объединяются в постоянно увеличивающиеся кластеры и, когда достигается определенное значение φс, образуют бесконечную структуру, называемую перколяционным кластером. Значение φс является порогом перколяции. Если НЧ способны проводить электричество, а именно при φ ≥ φс, электропроводность σ композита увеличивается на порядки величины. Изменение σ проявляется в виде резкого увеличения в узком диапазоне концентраций НЧ. Это позволяет рассматривать перколяционный переход изолятор-проводник как фазовый переход второго рода.

Все кластеры имеют фрактальную структуру. “Путешествие” по связям, соединяющим НЧ в конечном кластере (φ < φс), неизбежно приводит к терминальным ветвям (“хвостам”). Перколяционный кластер (φ ≥ φс) соединяет противоположные границы образца, хотя число “хвостов” в его структуре может быть большим. Порог перколяции определяется соотношениями:

(1)
$\sigma \propto \left\{ \begin{gathered} 0,\quad \varphi < {{\varphi }_{C}}, \hfill \\ {{(\varphi - {{\varphi }_{C}})}^{\beta }},\quad \varphi \geqslant {{\varphi }_{C}}. \hfill \\ \end{gathered} \right.$

Существует множество подходов к объяснению перколяционного поведения проводящих композитов, главным образом, основанных на вычислительных моделях [11–14], но ни одной из них не удалось объяснить все различные экспериментальные результаты, поскольку в таких системах играют роль многие факторы, в частности, межфазный слой [15, 16]. В настоящей работе проведен анализ простейшего аналитического подхода к вычислению порогового значения перколяции.

МОДЕЛЬ ПЕРКОЛЯЦИИ LI

Модель J. Li и J.-K. Kim [17] заключается в следующем. Весь объем системы делится на кубические элементы с длиной ребра L. Каждый куб содержит одну проводящую НЧ. Общее число кубических элементов равно общему количеству НЧ.

(2)
$\varphi = \frac{{{{V}_{{NP}}}}}{{{{L}^{3}}}},$
где VNP объем НЧ.

Если L равно сумме геометрического размера частицы (например, диаметра шара D) и толщины слоя δ матрицы, который обеспечивает туннельную передачу заряда, то весь объем станет проводящим. Согласно [17] это порог перколяции:

(3)
${{\varphi }_{{\text{c}}}} = \frac{{{{V}_{{NP}}}}}{{{{{(D + \delta )}}^{3}}}}.$
Порог перколяции ${{\varphi }_{{{\text{c}}3}}}$ 3-мерных проводящих сферических НЧ равен [17, 18]:
(3a)
${{\varphi }_{{{\text{c}}3}}} = \frac{{\pi {{D}^{3}}}}{{6{{{(D + \delta )}}^{3}}}} \to \frac{\pi }{6} \cong 0.523,$
при D $ \gg $ δ.

Двумерные НЧ, содержащиеся в полимерных нанокомпозитах, моделировали в виде тонкой круглой пластинки толщиной t и диаметром D, диспергированной матрице [13, 14]. Если дробь D/t = χ, представляющее собой аспектное отношение, больше 1, необходимо учитывать ориентацию НЧ.

Порог перколяции φс2 двумерных НЧ определится как:

(4)
${{\varphi }_{{{\text{с2}}}}} = \frac{{\pi {{D}^{2}}t}}{{4{{{\left( {\left\langle {{{{\cos }}^{2}}\theta } \right\rangle (D + \delta )} \right)}}^{3}}}} \to \frac{{27\pi }}{{4\chi }} = \frac{{21.2}}{\chi },$
где θ – угол между направлениями ориентации НЧ и образца, угловые скобки $\left\langle \, \right\rangle $ обозначают усреднение; в трехмерном пространстве для случайного распределения ориентации 〈cos2 θ〉 = 1/3.

Итак, φc2 обратно пропорционально аспектному отношению χ.

Одномерные НЧ, содержащиeся в полимерных нанокомпозитах, моделировали в виде тонкого стержня с толщиной d и длиной l [19]. Порог перколяции, φc1, определяется:

(5)
${{\varphi }_{{{\text{с1}}}}} = \frac{{\pi {{d}^{2}}l}}{{4{{{\left( {\left\langle {{{{\cos }}^{2}}\theta } \right\rangle (l + \delta )} \right)}}^{3}}}} \to \frac{{27\pi }}{{4{{\chi }^{2}}}}.$

Итак, φc1 обратно пропорционально χ2, где χ = l/d.

M.R. Loos и I. Manas-Zloczower [20] со ссылкой на [21] принимают φc1 = $\frac{{0.5}}{\chi }$. Однако в [21] высказано мнение, что φc1 ∝ χ–1 при χ ≤ 15, в случае бóльших значений χ φc1 ∝ χ–2.

Естественно, порог перколяции зависит от структурных характеристик НЧ. Улучшения в дисперсности НЧ в полимерной матрице могут снизить значение порога перколяции. На рис. 1 представлены данные, полученные J. Li и др. [22] о влиянии степени дисперсности и аспектного отношения χ частиц на величину φc1. Эти авторы рассмотрели поведение цилиндрических НЧ по модифицированным (учет агрегации) формулам (3а) и (5): предполагалось, что агрегированные НЧ образуют сферические клубки. Это приближение является упрощением экспериментально наблюдаемых агломератов и не учитывает факты изогнутости и наличия трехмерной сетки УНТ. Однако ранее такую модель успешно применяли для изучения влияния сферических включений на упругие свойства композитов, армированных УНТ [23].

Рис. 1.

Связь значений порога перколяции φc с параметрами χ и ε. Кривые – расчет по (6), точки – эксперимент для МСУНТ; ε = (1) 0.01, (2) 0.05, (3) 0.1, (4) 0.2 и (5) 0.4. См текст для объяснений. Данные [22].

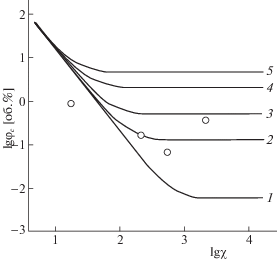
Итак, если объемная доля ε цилиндрических наполнителей включена в сферические агломераты, то:

(6)
${{\varphi }_{{\text{c}}}} = {\text{\;}}0.523\varepsilon {\text{\;}} + (1 - \varepsilon )\frac{{21.2}}{{{{\chi }^{2}}}}.$

Как видно, с ростом χ φc достигает плато, и только агрегация становится решающим фактором. Чем меньше степень агрегации ε, то есть чем выше дисперсность НЧ, тем ниже порог перколяции. В то же время значение φc нечувствительно к размеру агрегатов при χ < 10. Представленные на рис. 1 данные эксперимента относятся к НЧ, различающихся как по аспектному отношению, так и по способу смешивания, следствием чего является разная степень агрегирования.

КОРРЕКЦИЯ МОДЕЛИ

На первый взгляд, экспериментальные результаты согласуются с расчетными. Однако, если сравнить то, что дает теория, с данными компьютерного моделирования, увидим, что предложенная модель дает преувеличенные значения φс. Например, для однородного композита, содержащего случайно расположенные наполнители сферической формы и аналогичного размера, значение φс приблизительно равно 0.16 [10]. В то же время формула (3а) дает величину 0.523.

Дело в том, что модель требует, по существу, чтобы для перколяции все элементарные объемы стали проводящими. Между тем, для ее осуществления достаточно иметь относительно небольшую долю. Так, в рамках задачи узлов11 на кубической решетке эта доля примерно равна 0.31 [10]. Учитывая это обстоятельство, получаем: 0.523 × ×  0.31 = 0.162, т.е. совпадение с данными компьютерного моделирования.

Итак, каждое рассчитанное в соответствии с моделью значение порога перколяции должно быть умножено на 0.31.

С учетом вышеприведенной поправки

(4a)
${{\varphi }_{{{\text{с2}}}}} = {\text{\;}}\frac{{6.57}}{\chi },$
(5a)
${{\varphi }_{{{\text{c1}}}}} = \frac{{6.57}}{{{{\chi }^{2}}}}.$

Кроме этого, метод усреднения вызывает сомнения. В работе [17], на которую ссылаются авторы, проведено усреднение по углам ориентации НЧ, отсюда коэффициент 1/3. Но логичнее было бы получить среднее значение порога перколяции, имея в виду прямую зависимость последнего от ориентации НЧ [24–26], т.е. φc1 = = f(lθ), а φc2 = f(Dθ). Поэтому метод усреднения должен учитывать это обстоятельство. Например, таким образом:

(7)
${{\varphi }_{{{\text{c}}1\theta }}} = \frac{{\pi {{d}^{2}}l}}{{4{{{({{l}_{\theta }} + \delta )}}^{3}}}} \to \frac{\pi }{{4{{\chi }^{2}}}}\frac{1}{{{{{\cos }}^{{\text{3}}}}\theta }},$
где lθ/l = cos θ.

(7a)
${{\varphi }_{{{\text{c}}1\theta }}}{{\cos }^{3}}\theta {\text{\;}} = \frac{\pi }{{{\text{\;}}4{{\chi }^{2}}}}.$

Соответственно,

(8)
${{\varphi }_{{{\text{c1}}}}} = \left\langle {{{\varphi }_{{{\text{c1}}\theta }}}{{{\cos }}^{3}}\theta } \right\rangle = B\frac{\pi }{{{\text{\;}}4{{\chi }^{2}}}}.$

Аналогичное соотношение получается для дисков:

(9)
${{\varphi }_{{{\text{c2}}}}} = \left\langle {{{\varphi }_{{{\text{c2}}\theta }}}{{{\cos }}^{3}}\theta } \right\rangle = B\frac{\pi }{{4\chi }},$
где cos θ = Dθ/D.

В свете вышесказанного формула (6) примет вид:

(6a)
${{\varphi }_{{\text{c}}}} = 0.162\varepsilon + (1 - \varepsilon )B\frac{\pi }{{4{{\chi }^{2}}}}.$

Вычислить коэффициент В можно, опираясь на данные зависимости φc1 = f(lθ). Например, в работе [24] получена связь величины порога перколяции со степенью ориентации цилиндрических частиц cos θ (табл. 1)

(10)
$\begin{gathered} {{\varphi }_{{{\text{c1}}}}} = \left\langle {{{\varphi }_{{{\text{c1}}\theta }}}{{{\cos }}^{3}}\theta } \right\rangle = \frac{{\mathop \sum \nolimits_\theta {{\varphi }_{{{\text{c1}}\theta }}}{{{\cos }}^{3}}\theta }}{{\mathop \sum \nolimits_\theta {{{\cos }}^{3}}\theta }} = \\ = \frac{{4\frac{\pi }{{{\text{\;}}4{{\chi }^{2}}}}}}{{1.774}} = 2.25\frac{\pi }{{{\text{\;}}4{{\chi }^{2}}}}. \\ \end{gathered} $
Таблица 1.  

Зависимость порога перколяции от степени ориентации НЧ [24]

θ° cos θ φc, об. %
0 1 16.05 ≤ φc ≤ 20.53
30 0.866 1.00 ≤ φc ≤ 1.99
60 0.5 0.75 ≤ φc ≤ 1.49
90 0 0.58 ≤ φc ≤ 1.15

По-видимому, угловая зависимость φс может объяснить результаты экспериментов [27, 28] по влиянию скорости сдвига на порог перколяции (рис. 2). Как показано в таблице 1, высокой степени ориентации (cos θ = 1) соответствует большая величина φс. Снижение ориентации ведет к существенному уменьшению порога перколяции.

Рис. 2.

График проводимости σ нанокомпозита MСУНT/эпоксидная смола как функции массовой доли нанотрубок для различных методов подготовки образца. Скорость перемешивания дисперсии до отверждения в течение 5 мин при 80°С, об./мин: (1) 50, (2) 500 и (3) 2000. Данные [28].

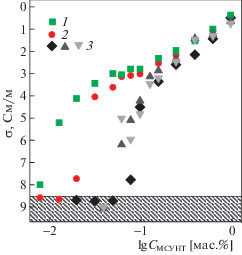
Теоретическое исследование влияния степени ориентации УНТ на сопротивление за счет перколяции с использованием моделирования методом Монте-Карло было опубликовано А. Behnam и др. [26]: минимальное удельное сопротивление имело место для невысокой, а не идеальной степени ориентации пленки нанотрубок.

Итак, простую модель J. Li [17, 22] можно использовать для расчета величины порога перколяции полимерных нанокомпозитов, но с существенными поправками: во-первых, необходимо учитывать результат решения задачи об узлах на кубической решетке [10]; во-вторых, более корректно усреднять ориентацию анизодиаметричных НЧ. Это означает, что расчетные данные рис. 1 сильно завышены, а УНТ агрегированы в большей степени, чем это следует из рисунка.

Список литературы

  1. Teng C.-C., Ma C.-C.M., Huang Y.-W. et al. // Compos. A. 2008. V. 39. № 12. P. 1869.

  2. Pujari S., Rahatekar S.S., Gilman J.W. et al. // J. Chem. Phys. 2009. V. 130. P. 214903.

  3. Hobbie E.K., Fry D.J. // J. Chem. Phys. 2007. V. 126. P. 124907.

  4. Kozlov G.V., Dolbin I.V. // J. Appl. Mech. Techn. Phys. 2018. V. 59. № 4. P. 765.

  5. Козлов Г.В., Долбин И.В. // Изв. вуз. Физика. 2018. Т. 61. № 5. С. 151.

  6. Martin-Gallego M., Bernal M.M., Hernandez M. et al. // Eur. Polym. J. 2013. V. 49. № 6. P. 1347.

  7. Shi B., Dong L., Li M. et al. // Appl. Phys. Lett. 2018. V. 113. № 4. P. 041902.

  8. Marsden A.J., Papageorgiou D.G., Vallés C. et al. // 2D Mater. 2018. V. 5. № 3. P. 032003.

  9. Stauffer D., Aharony A. Introduction to percolation theory. London: Taylor and Francis. 1994.

  10. Эфрос А.Л. Физика и геометрия беспорядка. М.: Наука, 1982.

  11. Spanos P., Elsbernd P., Ward B., Koenck T. // Philos. Transact. Roy. Soc. A. 2013. V. 371. P. 20120494.

  12. Rahaman M., Aldalbahi A., Govindasami P. et al. // Polymers. 2017. V. 9. № 12. P. 527.

  13. Ni X., Hui C., Su N. et al. // Nanotechnol. 2018. V. 29. № 7. P. 075401.

  14. Ni X., Hui C., Su N. et al. // Ibid. 2019. V. 30. № 18. P. 185302.

  15. Wang Y., Yang C., Pei Q.-X., Zhang Y. // ACS Appl. Mater. Interfac. 2016. V. 8. № 12. P. 8272.

  16. Deng H., Wu F., Chen L. et al. // J. Appl. Polym. Sci. 2014. V. 131. № 23. P. 41164.

  17. Li J., Kim J.-K. // Compos. Sci. Technol. 2007. V. 67. № 10. P. 2114.

  18. Zhang B., Yu Y., Liu Y. et al. // Nanoscale. 2013. V. 5. № 5. P. 2100.

  19. Li J., Ma P.C., Sze C.W. et al. // Proceed. 16th Intern. Conf. Compos. Mater. http://hdl.handle.net/1783.1/50129. P. 1.

  20. Loos M.R., Manas-Zloczower I. // Macromol. Theory Simul. 2011. V. 21. № 2. P. 130.

  21. Balberg I., Anderson C.H., Alexander S., Wagner N. // Phys. Rev. B. 1984. V. 30. № 7. P. 3933.

  22. Li J., Ma P.C., Chow W.S. et al. // Adv. Funct. Mater. 2007. V. 17. № 16. P. 3207.

  23. Shi D.L., Feng X.Q., Huang Y.Y. et al. // J. Eng. Mater. Technol. 2004. V. 126. № 3. P. 250.

  24. Celzard A., McRae E., Deleuze C. et al. // Phys. Rev. B. 1996. V. 53. № 10. P. 6209.

  25. Du F., Fischer J.E., Winey K.I. // Phys. Rev. 2005. V. 72. № 12. P. 121404.

  26. Behnam A., Guo J., Ural A. // J. Appl. Phys. 2007. V. 102. № 4. P. 044313.

  27. Kovacs J.Z., Velagala B.S., Schulte K., Bauhofer W. // Compos. Sci. Technol. 2007. V. 67. № 5. P. 922.

  28. Bauhofer W., Kovacs J.Z. // Compos. Sci. Technol. 2009. V. 69. № 10. P. 1486.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал