Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 71-75
ТРЕХМЕРНАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ, ИСКАЖЕННЫХ СМЕШАННЫМ МУЛЬТИПЛИКАТИВНО-АДДИТИВНЫМ ШУМОМ
В. Ф. Кравченко 1, 2, 3, *, В. И. Пономарев 4, **, академик РАН В. И. Пустовойт 2, 3, ***, А. Паласиос-Энрикес 4, ****
1 Институт радиотехники и электроники
им. В.А. Котельникова Российской академии наук
Москва, Россия
2 Научно-технологический центр уникального приборостроения Российской академии наук
Москва, Россия
3 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
4 Национальный политехнический институт Мексики
Мехико, Мексика
* E-mail: kvf-ok@mail.ru
** E-mail: vponomar@ipn.mx
*** E-mail: vlad_pst@yahoo.com
**** E-mail: alfredoepe@yahoo.com.mx
Поступила в редакцию 21.08.2020
После доработки 21.08.2020
Принята к публикации 24.08.2020
Аннотация
Впервые обоснована и реализована процедура фильтрации изображений, искаженных смешанным (мультипликативно-аддитивным) шумом. Новый метод характеризуется следующими этапами: формирование сходных структур в трехмерном пространстве, голоморфное преобразование, фильтрация изображения в трехмерном пространстве дискретного косинусного преобразования (DCT), обратное гомоморфное преобразование и заключительный этап обработки, где корректируются погрешности и восстанавливаются контуры и детали изображений. Дана физическая интерпретация процедуры фильтрации в условиях смешанных шумов и разработана структурная схема фильтрации. Моделирование предложенного метода фильтрации изображений подтвердило преимущество новой схемы фильтрации в терминах общепризнанных критериев: оценки структурного индекса схожести, пикового отношения сигнал/шум, а также при визуальном сравнении профильтрованных изображений.
ВВЕДЕНИЕ
Восстановление и улучшение качества изображений и видеопоследовательностей (ВП) усложнено из-за их искажений в канале передачи информации, а также при их приеме и регистрации вследствие шумов различной природы, смазывании деталей и контуров. Сложная и меняющаяся структура реальных изображений и ВП не позволяет эффективно отфильтровывать и выделять искаженные детали изображений. Это часто приводит к неправильным решениям в приложениях: дистанционное зондирование, распознавание образов, медицина, ультразвуковая диагностика, управление объектами и т.д. Различные шумы, как аддитивные, так и мультипликативные (спекл-шумы), присутствующие в конкретных физических моделях, могут в дальнейшем быть дополнены импульсным шумом. Используемые процедуры подавления шумов часто зависят от приложений, где они применяются, что не позволяет их применение в других условиях. Подавление шумов в изображениях и ВП является обязательным элементом, позволяющим восстановить контуры и детали, а также улучшить структуру и качество изображений [1–12]. Ряд эффективных подходов, применяемых в фильтрации, включает применение стохастических методов [1–8] в сочетании c дисперным представлением изображений или ВП в базисах различных преобразований (вейвлет, контурлет, DCT, др.), позволяющих отличать мелкие детали, контуры, хроматические и структурные характеристики в изображении от зашумленных пикселей [5–12].
В литературе приводится ряд алгоритмов обработки изображений в присутствии шумов различной физической природы, где, как правило, для различных типов шума (мультипликативного, импульсного или аддитивного) используются разные математические методы и подходы, которые не позволяют реализовать эффективную фильтрацию изображений или ВП, искаженных шумом сложной структуры [5–13]. Большинство известных алгоритмов требует априорных статистических данных о шумах, изображениях или ВП.
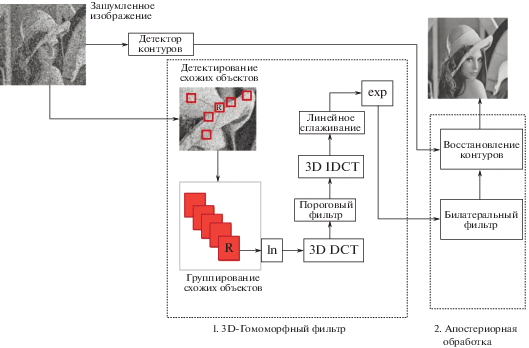
На основе идей, изложенных в работах [1–9, 15], в настоящей работе предложен и обоснован оригинальный подход к фильтрации изображений, искаженных смешанным шумом (смесь мультипликативного и аддитивного). Новый метод сочетает процедуры теории гомоморфной фильтрации и стохастический подход к фильтрации изображения в дисперсном его представлении. Метод содержит два этапа: на первом этапе реализуется поиск объектов со схожими структурными свойствами, которые выделяются на основе выбранного критерия подобия. Каждый выделенный объект подвергается гомоморфному преобразованию (ln), которое формирует новые структуры в 3D. В дальнейшем изображение фильтруется в трехмерном пространстве дискретного косинусного преобразования (DCT), где схожие объекты образуют третью координату в DCT, существенно увеличивая объем выборки и улучшая качество фильтрации. Первый этап обработки завершается линейным сглаживанием и обратным гомоморфным преобразованием (exp). На втором, заключительном этапе обработки изображений проводится фильтрация с целью коррекции погрешностей предыдущих этапов, восстановления контуров и деталей изображений. Критериями, используемыми при сравнении предложенных алгоритмов с известными в литературе, являются пиковое отношение сигнал–шум в децибеллах (PSNR) и оценка структурного индекса схожести (SSIM) [1–5, 8, 14].
Результаты многочисленных численных экспериментов в условиях различных интенсивностей шумов на тестовых изображениях подтверждают эффективность нового метода, позволяющего очистить изображение от cпекл-шума, характеристики которого могут быть неизвестными, восстанавливая мелкомасштабные детали изображений и улучшая их качество.
ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ
Предложенная процедура фильтрации включает в себя два этапа обработки (см. рис. 1).
Регистрируемое искаженное изображение $E(i,j)$ в случае мультипликативного $\varepsilon (i,j)$ и аддитивного ${{n}_{{ad}}}(i,j)$ шумов имеет вид
Оно анализируется с целью обнаружения и формирования групп подобных объектов, используя процесс детектирования схожих блоков (block-matching: BM). Процесс BM позволяет найти похожие структуры путем минимизации критерия подобия SAD
(2)
${\text{SAD}}(i,j) = \sum\limits_{p = 1}^{{{M}_{1}}} {\sum\limits_{q = 1}^{{{N}_{1}}} {\left| {A(i,j) - A(i + p,j + q)} \right|} } ,$(3)
$\begin{gathered} \ln [E(i,j)] \approx \\ \approx \ln [\varepsilon (i,j)] + \ln [e(i,j)] + \left[ {\frac{{{{n}_{{ad}}}(i,j)}}{{\varepsilon (i,j)e(i,j)}}} \right]. \\ \end{gathered} $Таким образом, удается мультипликативную шумовую модель свести к ее аддитивному варианту. В дальнейшем изображение (3) фильтруется в трехмерном пространстве DCT, где схожие объекты формируют третью координату, существенно увеличивая объем выборки и улучшая качество фильтрации (рис. 1).
Преобразование, примененное к 3D-структурам, формирует в пространстве DCT массив данных $S(i,j,L)$, который подвергается пороговой фильтрации. Здесь на основе процедуры сегментации по алгоритму K-средних (K-means) выделяются области с плавным изменением интенсивности (α = 1) и области с границами или мелкими деталями (α = 2). Для каждой структуры 3D производится ограничение коэффициентов (пороговая фильтрация) в пространстве DCT:
(4)
$\hat {S}(i,j,L) = \left\{ {\begin{array}{*{20}{l}} \begin{gathered} S(i,j,L),\quad S(i,j,L) \geqslant T_{\alpha }^{{}}, \hfill \\ \alpha = {\text{1 для сглаживания;}} \hfill \\ \end{gathered} \\ \begin{gathered} 0,\quad S(i,j,L) < {{T}_{\alpha }}; \hfill \\ \alpha = 2{\text{ }}\,{\text{для деталей}}{\text{.}} \hfill \\ \end{gathered} \end{array}} \right.$Затем к массиву данных $\hat {S}(i,j,l)$ применяется обратное 3D-преобразование (IDCT), формируя первую аппроксимацию блоков ${{\hat {A}}_{L}}(i,j)$, $L = 1, \ldots ,K$. Процесс 3D-обработки завершается линейной фильтрацией, которая реализует финальную оценку блоков схожести, используя линейный фильтр с весами, зависящими от дистанции SAD:
(5)
$\begin{gathered} \hat {A}(i,j) = \frac{{\sum\limits_{L = 1}^K {{{{\hat {A}}}_{L}}(i,j)q_{L}^{{}}} }}{{\sum\limits_{L = 1}^K {{{q}_{L}}} }}{\text{,}} \\ {{q}_{L}} = 1 - {\text{SAD}}\left[ {{{A}_{L}}(i,j),{{A}_{1}}(i,j)} \right]. \\ \end{gathered} $Первый этап обработки завершается обратным гомоморфным преобразованием (exp), целью которого является возвратить профильтрованные данные в исходную реальную плоскость изображений.
На следующем этапе фильтрации шумов производится коррекция эффектов, которые внесены на предыдущих этапах. В частности, восстанавливаются сглаженные контуры и мелкие детали изображений с использованием билатеральной фильтрации [11] и восстановления контуров (рис. 1).
Билатеральный фильтр определяется двумя весовыми функциями гауссовского типа, где первая $d(i,j;k,l) = \exp \left[ { - \frac{{{{{(i - k)}}^{2}} + {{{(j - l)}}^{2}})}}{{2\sigma _{D}^{2}}}} \right]$ зависит от геометрического расстояния между пикселями, центральным (i, j), подлежащим фильтрации, и соседним (k, l) в окне обработки, а вторая весовая функция вводит нелинейную обработку с весами, которые зависят от разности радиометрических значений (интенсивностей) пикселей
R[A(i, j); A(k, l)] = $\exp \left[ { - \frac{{{{{[A(i,j) - A(k,l)]}}^{2}}}}{{2\sigma _{g}^{2}}}} \right]$.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Свойства нового метода фильтрации смешанных шумов, названного F-MNSR-DCT, а также известных наилучших по качеству алгоритмов Lee, Frost, Kuan, Anisotropic Diffusion [5–7, 9] были исследованы на основе стандартных численных критериев PSNR и SSIM, а также используя визуальный субъективный анализ профильтрованных изображений. Значения критерия PSNR вычисляются по следующей формуле:
величины SSIM-критерия определяются так:
(7)
${\text{SSIM}}(E,\hat {E}) = \frac{{(2{{\mu }_{E}}{{\mu }_{{\hat {E}}}} + {{C}_{1}})({{\sigma }_{{E,\hat {E}}}} + {{C}_{2}})}}{{(\mu _{E}^{2} + \mu _{{\hat {E}}}^{2} + {{C}_{1}})(\sigma _{E}^{2} + \sigma _{{\hat {E}}}^{2} + {{C}_{2}})}}.$В формуле (7) μE и ${{\mu }_{{\hat {E}}}}$ определяют локальные средние для E и $\hat {E}$ соответственно; $\sigma _{E}^{2}$ и $\sigma _{{\hat {E}}}^{2}$ являются локальными значениями дисперсий для E и $\hat {E}$ и ${{\sigma }_{{E,\hat {E}}}}$ это локальная функция ковариации для E и $\hat {E}$. Константы ${{C}_{n}} \ll 1$ выбираются такими, чтобы избежать нестабильности [14].
Тестовые изображения из базы данных [13] были искажены мультипликативным шумом разной интенсивности (СКО шума $\sigma $: 10–50) и в дальнейшем обработаны фильтрами. Представленные в табл. 1 усредненные по 100 изображениям из базы данных значения PSNR и SSIM в случае применения алгоритмов фильтрации Lee, Frost, Kuan, Anisotropic Diffusion и предложенного алгоритма F-MNSR-DCT, а также визуальный анализ рис. 2 подтверждают, что новый алгоритм превосходит лучшие из известных согласно полученным результатам в широком диапазоне интенсивностей шумов. Эффективная фильтрация изображений pic 015 и pic 091 (Boat), в которых наблюдается много мелких деталей и контуров, и вариации интенсивности, подтверждает робастность предложенного метода для шумов различной интенсивности (рис. 2).
Таблица 1.
Усредненные по 100 изображениям значения PSNR и SSIM из базы данных в случае применения алгоритмов фильтрации Lee, Frost, Kuan, Anisotropic Diffusion и предложенного алгоритма F-MNSR-DCT
| σ | 10 | 20 | 30 | 40 | 50 | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|
| Lee | 31.09 | 29.21 | 25.73 | 19.16 | 14.54 | 0.7308 | 0.7290 | 0.7254 | 0.7200 | 0.7132 |
| Frost | 32.93 | 29.94 | 25.86 | 19.09 | 14.55 | 0.8770 | 0.8589 | 0.8312 | 0.7982 | 0.7434 |
| Kuan | 29.76 | 28.32 | 25.27 | 19.02 | 14.48 | 0.8959 | 0.8098 | 0.7016 | 0.7833 | 0.7431 |
| Anisotropic | 29.88 | 26.38 | 23.63 | 19.81 | 15.40 | 0.8988 | 0.8572 | 0.8393 | 0.7963 | 0.7617 |
| F-MNSR-DCT | 33.80 | 30.19 | 26.61 | 21.48 | 19.76 | 0.9043 | 0.8885 | 0.8414 | 0.8295 | 0.8006 |
Рис. 2.
Профильтрованные изображения и инвертированные ошибки фильтрации разными методами для pic015 и pic091 в случае мультипликативных (спекл) шумов с интенсивностями (СКО = 30 для pic015, СКО = 40 для pic091); а – незашумленные изображения, слева направо: pic015; увеличенное pic015; pic091; увеличенное pic091; б – профильтрованные фильтрами и инвертированные ошибки, слева направо: Lee, pic015; Kuan, pic015; Lee, pic091; Kuan, pic091; в – профильтрованные фильтрами и инвертированные ошибки, слева направо: Anisotropic Diffusion, pic015; F-MNSR-DCT, pic015; Anisotropic Diffusion, pic091; F-MNSR-DCT, pic091.

ВЫВОДЫ
Теоретическое обоснование и анализ физических результатов численного моделирования нового метода фильтрации изображений в условиях их искажений мультипликативным шумом позволяют сделать ряд важных выводов:
1. Предложенный метод, который основан на дисперсном представлении данных с использованием 3D-дискретного косинусного преобразования, эффективно восстанавливает сложные структуры в изображениях.
2. Гомоморфное преобразование сформированной последовательности схожих объектов позволяет реализовать фильтрацию спекл шумов с использованием дисперных методов фильтрации.
3. 3D-фильтрация с весами, зависящими от степени схожести объектов, улучшает качество обработанных изображений.
4. Билатеральная фильтрация совместно с восстановленными контурами изображений, примененная на этапе апостериорной обработки, приводит к улучшению качества восстановления мелких деталей и контуров.
5. Новый метод подтвердил наилучшее качество как в значениях критериeв (PSNR и SSIM), так и при визуальном анализе профильтрованных изображений.
Список литературы
Guan D., Xiang D., Tang X., Kuang G. // IEEE Trans. Geosci. Rem. Sens. 2018. V. 57. № 6. P. 3472–3489.
Huang T., Dong W., Xie X., Shi G., Bai X. // IEEE Trans. Image Proces. 2017. V. 26. № 7. P. 3171–3186.
Rubel O., Lukin V., Egiazarian K. // Elect. Imag. 2019. V. 2019. № 11. P. 1–11.
Wang G., Pan Z., Zhang Z. // Multimedia Tools and App. 2019. V. 78. № 20. P. 29 007–29 019.
Sagheer S.V.M., George S.N., Kurien S.K // Biomed. Signal Proces. Cont. 2019. V. 54. № 101595. P. 1–14.
Кравченко В.Ф., Пономарев В.И., Пустовойт В.И., Паласиос-Энрикес A. // ДАН. 2017. Т. 475. № 6. С. 629–633.
Кравченко В.Ф., Пономарев В.И., Пустовойт В.И. // ДАН. 2018. Т. 481. № 4. С. 375–380.
Palacios-Enriquez A., Ponomaryov V., Reyes-Reyes R., Sadovnychiy S. // Circuits, System & Signal Proces. 2018. V. 37. № 12. P. 5389–5416.
Ponomaryov V., Montenegro H., Gallegos F., Pogrebnyak O., Sadovnychiy S. // Neurocomputing. 2015. V. 155. P. 225–246.
Dabov K., Foi A., Katkovnik V., Egiazarian K. // IEEE Trans. Image Process. 2007. V. 16. № 8. P. 2080–2095.
Zhang Y., Tian X., Ren P. // Neurocomputing. 2014. V. 140. P. 299–316.
Jiang J., Zhang L., Yang J. // IEEE Trans. Image Proces. 2014. V. 23. № 6. P. 2651–2662.
Malinski L., Smolka B. // J. Real-Time Image Proces. 2016. V. 11. № 3. P. 427–444.
Wang Z., Bovik A. // IEEE Signal Process. Mag. 2009. V. 26. № 1. P. 98–117.
Кравченко В.Ф., Кравченко О.В. Конструктивные методы алгебры логики, атомарных функций, вейвлетов, фракталов в задачах физики и техники. Под ред. В.Ф. Кравченко. М.: Техносфера, 2018. 696 с.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления