Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 493, № 1, стр. 86-89

1. В заданном коридоре Y ⊂ ${{\mathbb{R}}^{2}}$, граница ∂Y которого гомеоморфна окружности, движется объект t со скоростным поражающим миниобъектом m, способным двигаться равномерно и прямолинейно. В ${{\mathbb{R}}^{2}}$ зафиксировано множество G, G ∩ Y = ϕ, с кусочно гладкой границей ∂G, являющееся замыканием открытого множества, препятствующее движению и видимости. Наблюдатель f, опасаясь миниобъекта, находится в окрестности угловых точек или выпуклых участков границы ∂G множества G. Скорость ${{{v}}_{m}}$ миниобъекта существенно превосходит скорости ${{{v}}_{f}}$ > 0, ${{{v}}_{t}}$ > 0 наблюдателя и объекта. Траектория объекта – это кривая $\mathcal{T}$ ⊂ Y (маршрут) с заданным скоростным режимом ${{{v}}_{t}}$ на ней. Далее ${{t}_{*}}$ – начальная, t* – конечная точки маршрута.

Задача состоит в выяснении возможности наблюдателя следить за объектом в безопасном для себя режиме, а объекта – уклониться от наблюдения при их одновременном движении. Здесь важное значение имеют позиция наблюдателя и расположение траектории $\mathcal{T}$. В работе характеризуются позиции, для которых объект для любой $\mathcal{T}$ может выбрать режим ${{{v}}_{t}}$, позволяющий уклониться от наблюдения, и позиции, гарантирующие наблюдателю возможность слежения за объектом на части маршрута. В предлагаемой модели объект изображается точкой t, а наблюдатель – кругом V_ε(  f  ) малого радиуса ε > 0, в центре f которого расположено средство наблюдения. Модель с телесным наблюдателем принципиально отличается от модели с точечным наблюдателем (см., например, [1, 2]) по причине повышенной уязвимости наблюдателя (см. также [3]).

2. Если наблюдатель f имеет время τ₀, чтобы уйти из зоны видимости движущегося объекта t, то он может следить в безопасном для себя режиме за объектом при условии, что ||  f – t|| > $\mathcal{R}$, где $\mathcal{R}$ = ${{{v}}_{m}}$τ₀. Пусть t_s ∈ $\mathcal{T}$, ||  f – t_s|| = $\mathcal{R}$. Поэтому далее рассматриваются сформулированные выше задачи применительно к участку маршрута от точки t_s предполагаемого старта миниобъекта до конечной точки t* маршрута. Этот участок маршрута обозначим через $\mathcal{T}$.

Через C обозначается гладкая строго выпуклая связная максимальная по включению дуга, C ⊂ ∂G, без концевых точек. Для любой точки c ∈ C существует единственная опорная к множеству G ∩ ∩ V_δ(c) прямая при малом δ > 0. Точку a ∈ ∂G называем вершиной угла A ⊂ ∂G или угловой, если в ней существует пара односторонне касательных к ∂G ∩ ∂V_δ(a) прямых (см. рис. 1). Выпуклые дуги C и углы A играют одинаковую роль в рассматриваемой задаче, поэтому далее используем запись S ∈ ∈ {A, C}, s ∈ {a ∈ A, c ∈ C} и S называем фрагментом границы множества G.

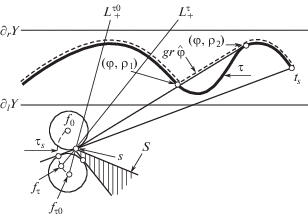
Далее ∂_lY, ∂_r Y – левая и правая границы коридора Y относительно двигающегося по коридору объекта t из начальной ${{t}_{*}}$ в конечную точку t*. Наблюдатель выбирает фрагмент S, расположенный вблизи $\mathcal{T}$, и начальную позицию f₀ так, что прямая L_s = {s + λ(t_s – s), λ ∈ ${{\mathbb{R}}^{1}}$} является опорной к V_δ(s) ∩ S в точке s = L_s ∩ S, круг V_ε(f₀) содержит точку s, и прямая L_s разделяет V_ε(f₀) и S ∩ V_δ(s), и, кроме того, существует $\bar {f}$, для которого V_ε($\bar {f}$) принадлежит конусу co(t_s, S) с вершиной t_s, натянутому на S и касается невидимой из t_s стороны поверхности S. Наблюдатель также выбирает траекторию ${{\mathcal{T}}_{s}}$ движения центра f_τ (0 ≤ τ ≤ τ₀) от f₀ до $\bar {f}$ = ${{f}_{{{{\tau }_{0}}}}}$, $V_{\varepsilon }^{^\circ }$(f_τ) ∩ S = ϕ, где V^{° – внутренность круга. Выбор исходного положения f₀ диктуется желанием видеть весь коридор Y, а ${{\mathcal{T}}_{s}}$ – траектория, по которой наблюдатель должен стартовать из f₀ (одновременно со стартом объекта из t_s по траектории $\mathcal{T}$) в “укрытие”, исключающее возможность попадания миниобъекта m в круг V_ε(f_τ).}

Обозначим через $L_{ + }^{\tau }$ = L₊(f_τ) луч с началом f_τ такой, что прямая L^τ = L^τ(f_τ) ⊃ $L_{ + }^{\tau }$ является опорной к S и разделяет точку f₀ и S, и $L_{ + }^{\tau }$ ∩ S = L^τ ∩ S. Полупространство с границей L^τ, содержащее S, обозначается через P_τ. Наблюдателю f_τ не видны точки из P_τ ∩ Y, но видны точки из (${{\mathbb{R}}^{2}}$\P_τ) ∩ Y. Множество возможных позиций наблюдателя разобьем на две группы I и II, в зависимости от расположения S на левой или правой стороне коридора Y и от направления движения вокруг S по траектории ${{\mathcal{T}}_{s}}$ центра шара f_τ, 0 ≤ τ ≤ τ₀, по или против часовой стрелки:

3. Рассмотрим случай I. Ради определенности будем считать, что ρ(S, ∂_lY) < ρ(S, ∂_rY) и, значит, f_τ движется против часовой стрелки часов. Пусть

есть гладкая кривая, определяющая маршрут, наблюдатель находится в ε-окрестности фрагмента S, который занимает позицию I, t_s ∈ $\mathcal{T}$, ||s – t_s|| = $\mathcal{R}$. Определим полярную систему координат (φ, ρ) с началом в точке s и осью L₊(${{f}_{{{{\tau }_{s}}}}}$) = {s + λ(t_s – s): λ ≥ 0}. При движении наблюдателя по траектории ${{\mathcal{T}}_{s}}$ луч $L_{ + }^{\tau }$ = L₊(f_τ) вращается против стрелки часов от L₊(${{f}_{{{{\tau }_{s}}}}}$) до L₊(${{f}_{{{{\tau }_{0}}}}}$), при этом f_τ не видит точки из P_τ. Поэтому задача объекта t – следовать по $\mathcal{T}$ за лучом $L_{ + }^{\tau }$, находясь в полупространстве P_τ, например, в полупространстве P_{τ – δ} при малом δ > 0.

Пусть границы ∂_lY, ∂_rY и кривая $\mathcal{T}$ представлены в полярной системе координат графиками функций φ = φ_l(ρ), φ = φ_r(ρ), φ = φ(ρ). Ясно, что

Функция

непрерывна и при изменении ρ от $\mathcal{R}$ до нуля возрастает. На участке строгого возрастания функции $\hat {\varphi }$ движение объекта t(τ), следующего по кривой $\mathcal{T}$ за точкой $\mathcal{T}$ ∩ $L_{ + }^{\tau }$, задается соотношением t(τ) = $\mathcal{T}$ ∩ $L_{ + }^{{\tau - \delta }}$. Скорость движения точки t(τ) по такому участку кривой $\mathcal{T}$ определяется величиной производной

Пусть [ρ₁, ρ₂] ⊂ [0, $\mathcal{R}$], ρ₁ < ρ₂ – участок постоянства функции $\hat {\varphi }$(ρ). График функции $\hat {\varphi }$ на этом участке лежит на луче $L_{ + }^{\tau }$ при некотором τ. Чтобы объекту t следовать за лучом $L_{ + }^{{\tau + 0}}$, он должен преодолеть участок графика grφ = $\mathcal{T}$, связывающий точки ($\hat {\varphi }$(ρ_i), ρ_i) (i = 1, 2), с возможно большей скоростью, потратив на это некоторое время δ > 0. В момент прибытия объекта в точку ($\hat {\varphi }$(ρ₁), ρ₁) преследуемый луч займет положение $L_{ + }^{{\tau + \delta }}$. Итак, наблюдатель, опасаясь миниобъекта, вынужден без остановки двигаться по ${{\mathcal{T}}_{s}}$, при этом вращается луч $L_{ + }^{\tau }$. Объект следует за лучом $L_{ + }^{\tau }$ с некоторым отставанием, будучи невидимым для наблюдателя. В конечный момент τ₀ наблюдатель занимает положение ${{f}_{{{{\tau }_{0}}}}}$ и в целях безопасности выключает излучающее устройство, а объект t далее следует по $\mathcal{T}$ в отсутствии наблюдения. Таким образом, указан способ выбора скоростного режима ${v}$(τ) на $\mathcal{T}$ и доказана

Теорема 1. Пусть наблюдатель f располагается в ε-окрестности фрагмента S, который находится в позиции I, $\mathcal{T}$ ⊂ Y – гладкая кривая, соединяющая точки t_s и t*. Тогда существует функция ${{{v}}_{t}}$(τ) скорости передвижения объекта t по кривой $\mathcal{T}$ такая, что

и объект t, начинающий движение из точки t_s одновременно со стартом наблюдателя из точки ${{f}_{{{{\tau }_{s}}}}}$ по траектории ${{\mathcal{T}}_{s}}$, не виден наблюдателем ни в одной точке кривой $\mathcal{T}$.

Замечание. Пусть ${{\varphi }_{{{{\tau }_{0}}}}}$ – угол луча $L_{ + }^{{{{\tau }_{0}}}}$ с осью L₊(${{f}_{{{{\tau }_{s}}}}}$). Если наблюдатель в конечном положении ${{f}_{{{{\tau }_{0}}}}}$ готов продолжить слежение (в безопасном режиме) за объектом t = t(φ, ρ), то это возможно только при φ > ${{\varphi }_{{{{\tau }_{0}}}}}$

Наличие двух наблюдателей в позиции I не исключает для объекта возможности быть незамеченным на траектории. Пусть фрагменты S ⁱ (i = 1, 2) расположены по разные стороны коридора Y в позиции I каждый, $\hat {t}$ = ${{t}_{{{{s}^{1}}{{s}^{2}}}}}$ ⊂ Y, ||$\hat {t}$ – sⁱ|| = $\mathcal{R}$. Одновременное движение наблюдателей f ⁱ по своим траекториям ${{\mathcal{T}}_{{{{s}^{i}}}}}$ порождает два однопараметрических пучка лучей L₊($f_{\tau }^{i}$), ${{\tau }_{{{{s}^{i}}}}}$ ≤ τ ≤ $\tau _{0}^{i}$. Обозначим

Непрерывная кривая

соединяет точки $\hat {t}$ и L₊($f_{{\tau _{0}^{1}}}^{1}$) ∩ L₊($f_{{\tau _{0}^{2}}}^{2}$). Объект t, двигаясь по этой кривой за точкой $\hat {t}$(λ) с малым запаздыванием, при изменении λ от 0 до 1 остается невидимым для обоих наблюдателей.

4. Пусть скорость движения объекта t по $\mathcal{T}$ строго больше нуля. Покажем, что наблюдатель в позиции II всегда имеет возможность отслеживать начальный участок любого маршрута $\mathcal{T}$ от точки t_s ⊂ $\mathcal{T}$, ||s – t_s|| = $\mathcal{R}$. Не ограничивая общности рассуждений, предположим, что

ρ(S, ∂_lY) < ρ(S, ∂_rY).

Для τ ∈ [0, τ₀] наблюдатель, находясь в положении f_τ, видит все точки из Y ∩ (${{\mathbb{R}}^{2}}$\P_τ), а точки из Y ∩ P_τ ему не видны, где P_τ – полупространство с границей L_τ, содержащее множество S. В момент τ = 0 одновременно стартуют объект t по $\mathcal{T}$ из точки t_s и наблюдатель  f по ${{\mathcal{T}}_{s}}$ из точки f₀ по часовой стрелке. Пусть $\tilde {\tau }$ – момент встречи объекта с движущимся ему навстречу лучом $L_{ + }^{\tau }$, и $\tilde {t}$ – точка из $\mathcal{T}$ ∩ $L_{ + }^{{\tilde {\tau }}}$, для которой длина дуги $\mathcal{T}$(t_s, $\tilde {t}$) кривой $\mathcal{T}$ между точками t_s и $\tilde {t}$ минимальна. Двигаясь по дуге $\mathcal{T}$(t_s, $\tilde {t}$), объект находится в поле зрения наблюдателя f_τ(0 ≥ τ ≥ $\tilde {\tau }$). Часть кривой ($\mathcal{T}$\${{P}_{{\tilde {\tau }}}}$)\$\mathcal{T}$(t_s, $\tilde {t}$) преодолевается объектом t движением по $\mathcal{T}$ за лучом $L_{ + }^{\tau }$ (τ ≥ $\tilde {\tau }$) с запаздыванием. Остаток маршрута $\mathcal{T}$ ∩ ${{P}_{{\tilde {\tau }}}}$ объект проходит вне области наблюдения. Наблюдатель в целях безопасности движется до момента τ_s, для которого t_s ∈ $L_{ + }^{{{{\tau }_{s}}}}$. Итак, установ-лена

Теорема 2. Пусть наблюдатель f расположен в ε-окрестности фрагмента S, находящегося в позиции II, $\mathcal{T}$ ⊂ Y – кривая, соединяющая точки t_s и t*. Тогда существует точка $\tilde {t}$ ∈ $\mathcal{T}$, $\tilde {t}$ ≠ t*, $\tilde {t}$ ≠ t_s такая, что для наблюдателя обеспечена возможность проследить движение объекта t на участке кривой $\mathcal{T}$ от точки t_s до $\tilde {t}$, и только на нем.