1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 491, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 82-85

ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ С МЕНЯЮЩИМСЯ НАПРАВЛЕНИЕМ ВРЕМЕНИ

С. В. Попов 1, 2, *

1 Академия наук Республики Саха (Якутия)
Якутск, Россия

2 Северо-Восточный федеральный университет им. М.К. Аммосова
Якутск, Россия

* E-mail: guspopov@mail.ru

Поступила в редакцию 19.02.2019
После доработки 25.02.2020
Принята к публикации 25.02.2020

Полный текст (PDF)

Аннотация

Рассматривается теорема о поведении интеграла типа Коши на концах контура интегрирования и в точках разрыва плотности и ее приложение для краевых задач для 2n-параболических уравнений с меняющимся направлением времени. Теория сингулярных уравнений дает возможность наряду с гладкостью данных задачи указать дополнительно необходимые и достаточные условия, обеспечивающие принадлежность решения гёльдеровским пространствам. Отметим случай n = 3, когда гладкость входных данных с условиями разрешимости определяют принадлежность решения более гладким пространствам вблизи концов по временной переменной.

Ключевые слова: интеграл типа Коши, параболические уравнения с меняющимся направлением времени, условия склеивания, пространство Гёльдера, сингулярное интегральное уравнение

Изучаются параболические уравнения с меняющимся направлением времени с помощью применения теории сингулярных интегральных уравнений с ядром Коши [1–5], а также поведение интеграла типа Коши на концах контура интегрирования и в точках разрыва плотности в пространствах Гёльдера. Известно, что гёльдеровские классы решений параболических уравнений переменного направления времени существенно зависят как от условий склеивания, так и от нецелого показателя пространства Гёльдера.

В области $Q = \Omega \times (0,T)$, $\Omega \equiv \mathbb{R}$ рассматривается параболическое уравнение 2n-го порядка с меняющимся направлением времени

(1)
${\text{sgn}}\,x{{u}_{t}} = {{( - 1)}^{{n + 1}}}\frac{{{{\partial }^{{2n}}}u}}{{\partial {{x}^{{2n}}}}}.$

Решение уравнения (1) ищется из пространства Гёльдера $H_{{x\,\,\,t}}^{{p,p/2n}}({{Q}^{ \pm }})$, $p = 2nl + \gamma $, $0 < \gamma < 1$, $l \geqslant 1$ – целое число. Пусть оно удовлетворяет следующим начальным условиям

(2)
$\begin{gathered} u(x,0) = {{\varphi }_{1}}(x),\quad x > 0, \\ u(x,T) = {{\varphi }_{2}}(x),\quad x < 0, \\ \end{gathered} $
и условиям склеивания

(3)
$\begin{gathered} \frac{{{{\partial }^{k}}u}}{{\partial {{x}^{k}}}}( - 0,t) = \frac{{{{\partial }^{k}}u}}{{\partial {{x}^{k}}}}( + 0,t), \\ 0 < t < T,\quad k = 0,1, \ldots ,2n - 1. \\ \end{gathered} $

Пусть L = ab – гладкая разомкнутая дуга на комплексной плоскости $\mathbb{C}$ и $\varphi (\tau ) \in {{H}^{\lambda }}(L)$, $0 < \lambda < 1$, концы a или b обозначим через c. Будем считать, что положительное направление на $L$ ведет от $a$ к $b$.

Рассмотрим интеграл типа Коши с плотностью, имеющей интегрируемую особенность:

(4)
$\Phi (t) = \frac{1}{{2\pi i}}\int\limits_L \,\frac{{\varphi (\tau )}}{{{{{(\tau - c)}}^{\mu }}(\tau - t)}}d\tau ,$
где $0 < \mu < 1$ и $\varphi (\tau ) \in {{H}^{\lambda }}(L)$ вблизи c, включая c, $0 < \lambda < 1$.

Перепишем формулу (4) в виде

(5)
$\begin{array}{*{20}{c}} {\Phi (t) = \frac{1}{{2\pi i}}\int\limits_L \,\frac{{\varphi (\tau ) - \varphi (c)}}{{{{{(\tau - c)}}^{\mu }}(\tau - t)}}d\tau + } \\ {\, + \frac{{\varphi (c)}}{{2\pi i}}\int\limits_L \,\frac{{d\tau }}{{{{{(\tau - c)}}^{\mu }}(\tau - t)}}d\tau \equiv F(t) + \varphi (c)\Omega (t),} \end{array}$
где $\Omega (t)$ вблизи точки a определяется формулой
(6)
$\begin{gathered} \Omega (t) = \frac{1}{{2\pi i}}\int\limits_L \,\frac{{d\tau }}{{{{{(\tau - a)}}^{\mu }}(\tau - t)}}d\tau = \\ \, = \frac{1}{{2i}}{\text{ctg}}(\mu \pi ){{(t - a)}^{{ - \mu }}} + {{\Omega }_{1}}(t), \\ \end{gathered} $
вблизи точки b – формулой
(7)
$\begin{gathered} \Omega (t) = \frac{1}{{2\pi i}}\int\limits_L \,\frac{{d\tau }}{{{{{(\tau - b)}}^{\mu }}(\tau - t)}}d\tau = \\ \, = - \frac{1}{{2i}}{\text{ctg}}(\mu \pi ){{(t - b)}^{{ - \mu }}} + {{\Omega }_{2}}(t), \\ \end{gathered} $
где функция ${{\Omega }_{1}}(z)$ является аналитической функцией в окрестности точки a, а функции ${{\Omega }_{2}}(z)$ – аналитической функцией в окрестности точки b.

Введем обозначение

(8)
$\Psi (t) = \frac{{{{{(t - c)}}^{\mu }}}}{{2\pi i}}\int\limits_L \,\frac{{\psi (\tau )}}{{{{{(\tau - c)}}^{\mu }}(\tau - t)}}d\tau \equiv {{(t - c)}^{\mu }}F(t),$
где
$\psi (\tau ) = \varphi (\tau ) - \varphi (c) \in {{H}^{\lambda }}(L)$
вблизи c, включая c.

Сформулируем теорему о гёльдеровости функции $\Psi (t)$ для точек контура L в окрестности точки c, включая c.

Теорема 1. Пусть $\psi (t)$ удовлетворяет условию Гёльдера с показателем $\lambda $ вблизи c, $0 < \lambda < 1$, $0 < \mu < 1$. Тогда для точек контура ab интеграл типа Коши $\Psi (t)$ вида (8) удовлетворяет условию Гёльдера вблизи c, включая c, с показателем $\min \{ \lambda ,\mu \} $ при $\lambda \ne \mu $ и условию Гёльдера с показателем $\lambda - \varepsilon $ при $\lambda = \mu $, где $\varepsilon $ – сколь угодно малая положительная постоянная.

Замечание 1. Впервые теорема 1 о гёльдеровости интеграла типа Коши $\Psi (t)$ для точек контура L с точными гёльдеровскими показателями была доказана в работах Р.В. Дудучава [6], А.П. Солдатова [7].

Замечание 2. Теорема Н.И. Мусхелишвили о гёльдеровости интеграла типа Коши $\Psi (t)$ также доказана в работе В.Н. Монахова [4], но в несколько слабой форме и другим методом, чем она доказана в частных случаях теоремы 1, в монографиях Н.И. Мусхелишвили [2], С.А. Терсенова [3].

Замечание 3. Если $\mu = \lambda + \tfrac{1}{2}$, $0 < \lambda < \tfrac{1}{2}$ и $\varphi (t) = O({{(t - c)}^{\lambda }})$ для t близких к c, то $\Psi (t) = O({{(t - c)}^{{\lambda + \frac{1}{2}}}})$ для $t$ близких к c, при этом $\Psi (t)$ удовлетворяет условию Гёльдера вблизи $c$ с показателем $\lambda + \tfrac{1}{2}$.

Справедлива теорема [9, 10].

Теорема 2. Пусть ${{\varphi }_{1}},{{\varphi }_{2}} \in {{H}^{p}}$ $(p = 2nl + \gamma )$. Тогда при выполнении $2[p]\left( {1 - \frac{1}{{2n}}} \right) + 2$ условий

(9)
${{L}_{s}}({{\varphi }_{1}},{{\varphi }_{2}}) = 0,\quad s = 1, \ldots ,2[p]\left( {1 - \frac{1}{{2n}}} \right) + 2$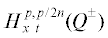
существует единственное решение уравнения (1), удовлетворяющее условиям (2), (3), из пространства .

Методом параболических потенциалов простого слоя, построенных при помощи фундаментального решения и элементарных решений Л. Каттабрига [12, 13], краевая задача (1), (2) при непрерывных условиях склеивания (3) приводится к решению системы сингулярных интегральных уравнений нормального типа

(10)
$A\vec {\beta }(t) - \tfrac{1}{\pi }\int\limits_0^T \,\tfrac{{B(t,\tau )\vec {\beta }(\tau )}}{{\tau - t}}d\tau = \vec {Q}(t).$

В классе функций, ограниченных на концах отрезка (0, T), каноническая функция соответствующей краевой задачи Римана имеет вид

$\chi (z) = {{z}^{{\tfrac{1}{4}}}}{{(z - 1)}^{{\tfrac{3}{4}}}},\quad {\text{если}}\quad n\,\,{\text{нечетно}},$
$\chi (z) = {{z}^{{\tfrac{3}{4}}}}{{(z - 1)}^{{\tfrac{1}{4}}}},\quad {\text{если}}\quad n\,\,{\text{четно}},$
индекс задачи $\varkappa = - 1$. Имеем $min\left\{ {\frac{1}{4},\frac{{1 + \gamma }}{{2n}}} \right\} = \frac{{1 + \gamma }}{{2n}}$ при $n \geqslant 4$. С учетом этого и теоремы 1 количество условий разрешимости можно уменьшить до необходимых и достаточных $2nl$ условий. В случае n = 2 или n = 3 справедливы соответственно 4l, 6l разрешимости при выполнении общих весовых условий склеивания
$\begin{gathered} \frac{{{{\partial }^{k}}u}}{{\partial {{x}^{k}}}}( - 0,t) = {{\sigma }_{k}}\frac{{{{\partial }^{k}}u}}{{\partial {{x}^{k}}}}( + 0,t), \\ 0 < t < T,\quad k = 0, \ldots ,2n - 1, \\ \end{gathered} $
где ${{\sigma }_{k}}$ – действительные постоянные.

При $n = 2$ справедлива теорема [11].

Теорема 3. Пусть ${{\varphi }_{1}},{{\varphi }_{2}} \in {{H}^{p}}$ $(p = 4l + \gamma )$. Тогда при выполнении 4l условий

(12)
${{L}_{s}}({{\varphi }_{1}},{{\varphi }_{2}}) = 0,\quad s = 1, \ldots ,4l,$
существует единственное решение уравнения (1), удовлетворяющее условиям (2), (3) из пространства

1) 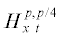, если $0 < \gamma < 1 - 4\theta $;

2) 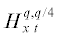, $q = 4l + 1 - 4\theta $, если $1 - 4\theta < \gamma < 1$;

3) 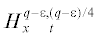, если $\gamma = 1 - 4\theta $, где ε – сколь угодно малая положительная постоянная.

Здесь $\theta = \tfrac{1}{\pi }{\text{arctg}}\left| {\tfrac{a}{b}} \right| < \tfrac{1}{4}$, a = σ0σ1 – σ0σ3 + σ1σ2 ++ $2\sqrt 2 {{\sigma }_{0}}{{\sigma }_{2}}$ – σ2σ3, b = ${{\sigma }_{0}}{{\sigma }_{3}}\, + \,{{\sigma }_{2}}{{\sigma }_{3}}\, + \,{{\sigma }_{1}}{{\sigma }_{2}}$ + $2\sqrt 2 {{\sigma }_{1}}{{\sigma }_{2}}$ – – σ0σ1.

Замечание 4. Если выполнены условия теоремы при $\theta \geqslant \tfrac{1}{4}$, то из теоремы 3 следует существование единственного решения задачи (1)–(3) из пространства 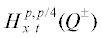при выполнении $6l + 2$ условий вида (12).

Примеры. Для уравнения (1) с начальными условиями (2) рассмотрим условия склеивания при ${{\sigma }_{0}} = 1$, ${{\sigma }_{1}} = - 1$, ${{\sigma }_{2}} = 1$, ${{\sigma }_{3}} = 1$. В этом случае единственное решение исходной задачи существует при выполнении 6l + 2 условий вида (12), если же рассмотрим условия склеивания (3) при σ0 = $\frac{1}{2}$, ${{\sigma }_{1}}$ = –2, ${{\sigma }_{2}} = \tfrac{1}{2}$, ${{\sigma }_{3}}$ = –2, то θ = $\tfrac{1}{\pi }{\text{arctg}}\tfrac{{\sqrt 2 + 4}}{{16\sqrt 2 + 4}} \approx 0.064$ < < 0.25, тогда находимся в условиях теоремы 3 и единственное решение исходной задачи существует при выполнении 4l условий (12).

Рассмотрим случай n = 3:

(13)
${\text{sgn}}\,x{{u}_{t}} - \frac{{{{\partial }^{6}}u}}{{\partial {{x}^{6}}}} = 0.$

Отметим, что в силу замечания 2 к теореме 1

$\begin{gathered} \frac{3}{4} - \frac{{1 + \gamma }}{{2n}} = \frac{1}{2} \Rightarrow 2 < n < 4 \Rightarrow n = 3 \\ {\text{при}}\quad \gamma = \frac{1}{2}. \\ \end{gathered} $

Теорема 4. Пусть ${{\varphi }_{1}},{{\varphi }_{2}} \in {{H}^{p}}$ $(p = 6l + \gamma )$. Тогда при выполнении 10l + 2 условий (9) существует единственное решение уравнения (13), удовлетворяющее условиям (2), (3) из пространства 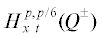. При $\gamma = \tfrac{1}{2}$ вблизи t = 0, T решение принадлежит пространству 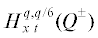, $q = 6l + \tfrac{1}{2} + \varepsilon $, где ε – сколь угодно малая положительная постоянная.

Замечание 5. Аналогичные результаты справедливы и в случае общих $2n$-параболических уравнений с меняющимся направлением времени с произвольными переменными коэффициентами.

Список литературы

  1. Гахов Ф.Д. Краевые задачи. М.: Наука, 1977. 640 с.

  2. Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.: Наука, 1968. 512 с.

  3. Терсенов С.А. Параболические уравнения с меняющимся направлением времени. Новосибирск: Наука, 1985. 105 с.

  4. Монахов В.Н. Краевые задачи со свободными границами для эллиптических систем уравнений. Новосибирск: Наука, 1977. 424 с.

  5. Векуа Н.П. Системы сингулярных интегральных уравнений. М.: Наука, 1968. 380 с.

  6. Дудучава Р.В. О сингулярных интегральных операторах в пространстве Гёльдера с весом // ДАН СССР. 1970. Т. 191. № 1. С. 16–19.

  7. Солдатов А.П. Одномеpные сингуляpные опеpатоpы и кpаевые задачи теоpии функций. М.: Высш. шк., 1991. 266 с.

  8. Попов С.В. О гладкости решений параболических уравнений с меняющимся направлением эволюции // ДАН. 2005. Т.400. № 1. С. 29–31.

  9. Попов С.В. Разрешимость краевых задач для параболического уравнения с меняющимся направлением времени высокого порядка / Ред. журн. “Сиб. мат. журнал”. Новосибирск, 1988. 56 с. Деп. в ВИНИТИ 07.12.88, 8646–Б88.

  10. Попов С.В., Потапова С.В. Гельдеровские классы решений 2n-параболических уравнений с меняющимся направлением эволюции // ДАН. 2009. Т. 424. № 5. С. 594–596.

  11. Попов С.В. Гельдеровские классы решений параболических уравнений четвертого порядка с меняющимся направлением времени с переменными условиями склеивания // Матем. заметки СВФУ. 2014. Т. 21. № 2 (82). С. 81–93.

  12. Cattabriga L. Problemi al contorno per equazioni paraboliche di ordine 2n // Rend. Sem. Mat. Univ. Padova. 1958. V. 28. № 2. P. 376–401.

  13. Cattabriga L. Equazioni paraboliche in due variabili. I // Rend. sem. fac. sc. Univ. Cagliari. 1961. V. 31. № 1–2. P. 48–79; II // Rend. sem. fac. sc. Univ. Cagliari. 1962. V. 32. № 3-4. P. 254–267.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал