Астрономический журнал, 2022, T. 99, № 3, стр. 189-210
Влияние испарения пыли на остаточное магнитное поле молодых звезд и их аккреционных дисков
А. Е. Дудоров 1, 2, С. Н. Замоздра 1, *
1 Челябинский государственный университет
Челябинск, Россия
2 Уральский федеральный университет
Екатеринбург, Россия
* E-mail: sezam@csu.ru
Поступила в редакцию 04.06.2021
После доработки 03.12.2021
Принята к публикации 16.12.2021
- EDN: FOERYR
- DOI: 10.31857/S000462992204003X
Аннотация
Путем сравнения наблюдательных данных с результатами численного моделирования коллапса протозвездных облаков проверяется теория остаточного магнитного поля молодых звезд и их аккреционных дисков. Предложена новая модель испарения пыли, в которой параметром является не толщина мантий, а начальное отношение радиусов ядра и мантии пылинки. Построено полуаналитическое описание эволюции распределения пылинок по радиусам. На его основе рассчитаны изменения относительной концентрации пылинок, а также средних значений радиуса, площади поперечного сечения и массы пылинок. Показано, что на этапе исчезновения ядер пылинок эти средние достигают максимумов, но на взаимодействие пыли с частицами газа это не влияет, поскольку пыли становится мало. На моделях облаков W3 (main), NGC 2024 и DR 21 OH1 продемонстрировано, что пренебрежение испарением пыли занижает остаточное магнитное поле в несколько раз. Подтверждена возможность образования магнитного уплотнения на внешней границе зоны сильной диффузии магнитного поля (мертвой зоны). Сделан вывод, что корректный расчет эволюции пыли, ионизации среды и анизотропии коллапса позволяет согласовать теоретическое и наблюдаемое магнитное поле молодых звезд и их аккреционных дисков.
1. ВВЕДЕНИЕ
Теория происхождения крупномасштабного магнитного поля звезд основана на двух взаимодополняющих концепциях [1–3]: остаточное поле и динамо-поле. В первой концепции магнитное поле является медленно затухающим остатком более сильного поля, возникшего на предыдущих стадиях эволюции звезды либо еще раньше – на стадии звездообразования. Согласно второй концепции, в звезде в наблюдаемую эпоху работает гидромагнитное динамо среднего поля.
Поле, предшествующее остаточному, может создаваться любым механизмом, в том числе и динамо, однако после его выключения все его следы могут исчезнуть в ходе перестройки остаточного поля. Она вызвана стремлением системы к магнитогидродинамическому (МГД) равновесию, а также пересоединением и диффузией поля. Равновесных конфигураций остаточного поля может быть много, и они могут быть очень сложны [2]. Поэтому наблюдательное отделение динамо-поля от остаточного поля по геометрии пока невозможно, но по наличию динамо-цикла возможно.
Быстрым механизмом эволюции крупномасштабного поля является его турбулентная диффузия. Однако, если плотность энергии этого поля выше плотности кинетической энергии турбулентности, то турбулентная диффузия слаба [4], поскольку в сильном поле турбулентность становится волновой. Поэтому концепция остаточного поля используется для объяснения сильного магнитного поля звезд, которое выключило турбулентную диффузию и не было создано динамо, поскольку превышает уровень его нелинейного насыщения [5]. Наоборот, слабое остаточное поле еще более ослабляется турбулентной диффузией и диамагнетизмом в конвективных зонах и, достигнув уровня насыщения динамо, заменяется динамо-полем. Поэтому слабое крупномасштабное поле конвективных зон объясняется работой динамо. Предложены модели динамо и для зон лучистого переноса, использующие магнито-ротационную и тейлеровскую (пинч) неустойчивости для генерации полоидального поля из тороидального [2]. Слабое остаточное поле заменяется динамо-полем бесследно, но остаточное поле промежуточной интенсивности проявляется в пониженной эффективности динамо [6] и укрупнении магнитных структур конвективных зон [7].
Ситуация, когда остаточное поле достаточно сильно, чтобы подавить турбулентную диффузию, конвекцию и динамо, весьма вероятна в протозвездах и молодых звездах, а также их аккреционных дисках, поскольку в процессе их образования работает эффективный механизм усиления магнитного поля – сжатие среды поперек поля (магнитная кумуляция). Действительно, при формировании этих объектов в ходе коллапса и фрагментации протозвездных облаков (гравитационно связанных ядер молекулярных облаков) сочетается сжатие вдоль и поперек крупномасштабного поля. В целом сжатие близко к изотропному. В идеально проводящей среде отношение магнитной индукции $\vec {B}$ к плотности вещества $\rho $ пропорционально векторному элементу длины $\delta \vec {l}$ вещественной линии. При изотропном (сферическом) сжатии среды $\delta l \propto {{\rho }^{{ - 1/3}}}$, поэтому (см. [8])
В процессе звездообразовании концентрация атомов и молекул возрастает с $n \simeq {{10}^{4}}{\kern 1pt} - {\kern 1pt} {{10}^{6}}$ см–3 в протозвездных облаках до $n \simeq {{10}^{{16}}}{\kern 1pt} - {\kern 1pt} {{10}^{{18}}}$ см–3 в основаниях фотосфер молодых звезд (см., напр., [9]), поэтому при выполнении условий соотношения (1) магнитная индукция может вырасти примерно на 8 порядков величины: с ${{10}^{{ - 4}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 3}}}$ Гс в протозвездных облаках (см. [10]) до ${{10}^{4}}{\kern 1pt} - {\kern 1pt} {{10}^{5}}$ Гс в основаниях фотосфер молодых звезд. Такое поле подавит конвекцию, поскольку его плотность энергии на 5 порядков величины больше плотности тепловой энергии. В зонах испарения пыли (температура $T \approx 1500$ К) в экваториальной плоскости дисков звезд типа Т Тельца $n \simeq {{10}^{{16}}}$ см–3 [11], поэтому остаточное поле в этих зонах также может достичь ${{10}^{4}}$ Гс и подавит конвекцию, если выполняется соотношение (1).Наблюдаемая магнитная индукция в фотосферах молодых звезд заметно меньше, чем в приведенных выше оценках: от $B \simeq 10{\kern 1pt} - {\kern 1pt} 100$ Гс у Ae/Be звезд Хербига [12] (масса 2–10 ${{M}_{ \odot }}$) и звезд типа Т Тельца промежуточных масс [13] (1.2–3.8 ${{M}_{ \odot }}$) до ${{10}^{3}}$ Гс у классических звезд типа Т Тельца [14] (0.3–2.3 ${{M}_{ \odot }}$). Единственное, и поэтому ненадежное, измерение магнитного поля аккреционных дисков молодых звезд опубликовано Донати и др. [15]: $B \simeq {{10}^{3}}$ Гс на расстоянии 0.05 а.е. от молодой звезды FU Ori в зоне с $n \simeq {{10}^{{17}}}$ см–3. Оценка магнитной индукции в протосолнечной туманности по остаточной намагниченности хондр дает $0.5 \pm 0.2$ Гс на расстоянии 2 а.е. [16]. Для удаленных от звезд частей дисков получены только верхние оценки: до 30 мГс на высоте 18 а.е. и радиусе 42 а.е. в диске TW Hya [17] и до 10 мГс над диском AS 209 на радиусе 50 а.е. [18].
Таким образом, соотношение (1) завышает магнитную индукцию относительно наблюдаемых значений на 2–3 порядка величины в молодых звездах и на порядок величины на внутренней границе аккреционного диска FU Ori. Тем не менее остается в силе вывод, что плотность магнитной энергии в фотосферах молодых звезд может быть выше плотности тепловой энергии (см., напр., [14]), и магнитное поле, если не подавляет, то существенно модифицирует конвекцию, например, разбивая ее на локализованные горячие плюмы [19].
Построить более ясную картину взаимодействия остаточного поля и конвекции в молодых звездах пока невозможно из-за огромной вычислительной сложности задачи. В идеале необходим сквозной трехмерный расчет от стадии протозвездного облака до стадии термоядерных реакций, причем пространственное разрешение модели должно быть достаточным для выявления конвективной, магнито-ротационной и других крупномасштабных неустойчивостей. А попытки обойти эту проблему, начиная расчеты с более поздних этапов, упираются в проблему реалистичных начальных и граничных условий. Поэтому до сих пор не ясно, возможны ли магнито-ротационная неустойчивость в аккреционных дисках протозвезд [20] и конвективная неустойчивость в протозвездах до зажигания термоядерных реакций [21, 22]. Развитие конвективной неустойчивости в молодых звездах с началом термоядерных реакций предполагается неизбежным, однако границы конвективных зон пока не определены, поскольку они сильно зависят от модели (см., напр., [23]). Расчеты эволюции звезд до главной последовательности (пока одномерные), учитывающие магнитное подавление конвекции, используют предписанную интенсивность магнитного поля (см., напр., [24]).
Тем не менее проработаны элементы теории эволюции магнитного поля в протозвездных облаках до начала термоядерных реакций. В протозвездных облаках с измеренным магнитным полем МГД турбулентность является трансальвеновской [10]. На начальном (почти изотермическом) этапе гравитационного коллапса протозвездные облака лишены значимых источников МГД турбулентности. Поэтому, несмотря на эффекты усиления, она затухает из-за магнитной амбиполярной диффузии (дрейфа заряженных частиц относительно нейтральных частиц) [25, 26] и превращается в крупномасштабные несимметричные возмущения, провоцирующие фрагментацию облака (см., напр., [27]). Турбулентная диффузия крупномасштабного магнитного поля на этом этапе мала, однако другие виды диффузии существенны. С помощью одномерной численной модели коллапса протозвездных облаков, учитывающей кинетику ионизации и испарение пыли, Дудоров и Сазонов [28] показали, что омическая и амбиполярная диффузии ослабляют остаточное поле молодых звезд солнечного типа на 1–2 порядка величины относительно значений, следующих из выражения (1). В двумерных моделях коллапса протозвездных облаков пока не удалось достичь плотности звездных фотосфер, однако установлено [29], что замедление сжатия среды поперек магнитного поля (и сплющивание облака вдоль поля) приводит к соотношению $B \propto {{\rho }^{{1/2}}}$ при $n \simeq {{10}^{4}}{\kern 1pt} - {\kern 1pt} {{10}^{{12}}}$ см–3. Трехмерное моделирование продвинулось дальше. В моделях [30, 31] магнитная индукция при плотности звездных фотосфер снижена на полпорядка величины относительно (1) за счет неизотропности сжатия и еще на 2 порядка величины за счет диффузии магнитного поля. В модели [32] неизотропность сжатия дает аналогичный эффект, но диффузия снижает поле еще сильнее – на 2.5 порядка величины.
Полученное в трехмерных моделях [30–32] снижение магнитной индукции на 2.5–3 порядка величины относительно уровня (1) было бы приемлемым, если бы они стартовали с достаточно сильного магнитного поля. Однако в этих моделях начальное отношение массы облака к магнитному потоку в 4–5 раз выше критического уровня, поэтому магнитная индукция при плотности звездных фотосфер оказывается слишком низкой: 1–10 Гс, что соответствует самым слабым из наблюдаемых полей молодых звезд. Провести расчеты с более сильным начальным полем до плотности звездных фотосфер пока не удается, поскольку тогда шаг по времени значительно уменьшится из-за амбиполярной диффузии.
Еще одной проблемой остается учет эволюции пыли, влияющей на эволюцию магнитного поля в протозвездных облаках прямо и косвенно через множество связей – 1) непрозрачность вещества, 2) адсорбцию и десорбцию атомов и молекул, 3) химические реакции на поверхности, 4) рекомбинацию ионов и электронов, 5) вклад заряженных пылинок в проводимость. Этим факторам посвящено много работ, однако характеристики пыли в них обычно предписываются. Напротив, расчеты эволюции пыли в процессе коллапса протозвездных облаков пока немногочисленны. В частности, Морфилл и др. [33] показали, что коагуляция пылинок без учета дробления (фрагментации) приводит к росту их среднего радиуса в десятки раз, если разность скоростей пылинок вызвана различием сил трения о газ. Гийе и др. [34] показали, что коагуляция пылинок может быть вызвана различием скорости их дрейфа в магнитном поле, а конденсация летучих веществ на пылинках во время почти изотермического коллапса с $T \simeq 10$ K увеличивает массу пыли на четверть. Разрушение пыли в сжимающейся протозвезде при $n \simeq {{10}^{{14}}}$ см–3 за счет термического разложения и химического распыления рассчитано Ленцуни и др. [35]. Для краткости эти процессы названы испарением. Показано, что за счет химического распыления атомами H и молекулами H2O разрушается аморфный и кристаллический углерод при температуре $T = 900{\kern 1pt} - {\kern 1pt} 1100$ К, а за счет термического разложения – силикаты типа (Mg0.5Fe0.5)2SiO4 при $T = 1200{\kern 1pt} - {\kern 1pt} 1300$ К и оксид алюминия Al2O3 при $T = 1600{\kern 1pt} - {\kern 1pt} 1700$ К. Душл и др. [36] обнаружили, что углеродную пыль эффективно разрушают радикалы OH: она исчезает при $T = 950{\kern 1pt} - {\kern 1pt} 1000$ К, даже если распыление атомами H неэффективно.
В моделях [30–32] испарение пыли в протозвезде учтено только через уменьшение непрозрачности. Однако еще желательно учесть, что с исчезновением пыли растет степень ионизации, поскольку прекращается прилипание электронов к пылинкам и рекомбинация ионов на пылинках. Кроме того, степень ионизации растет благодаря тепловой ионизации атомов щелочных металлов, освобожденных из пылинок. Эти эффекты повышают проводимость плазмы. С другой стороны, исчезновение заряженных пылинок снижает проводимость. Таким образом, исчезновение пыли приводит к противоположным эффектам, и пока не ясно, как его учет в моделях эволюции магнитного поля отразится на согласии теории и наблюдений.
Дудоров и Сазонов [28] учли испарение пыли, введя кусочно-линейное снижение коэффициента рекомбинации на пыли с ростом температуры, но пренебрегли вкладом заряженных пылинок в проводимость и рассмотрели только 3 сорта заряженных частиц. Замоздра и Жилкин [37] доработали модель [28], учтя вклад пылинок в проводимость и рассмотрев 14 сортов заряженных частиц. Испарение пыли в [37] описывалось через кусочно-линейное уменьшение радиуса пылинок с ростом температуры. Мершан и др. [38] включили в модель 12 сортов заряженных частиц, предполагая, что есть 3 сорта пылинок: из углерода, силикатов и оксида алюминия, а количество пылинок каждого сорта линейно убывает с ростом температуры в интервалах, полученных Ленцуни и др. [35].
Такой разнобой в учете испарения пыли можно устранить, используя более фундаментальный и перспективный подход – расчет эволюции распределения пылинок по размерам. Поскольку скорость изменения радиуса сферических пылинок при поверхностном разрушении не зависит от самого радиуса [35], то распределение однослойных пылинок по размерам при их испарении сдвигается влево без деформации [36]. Бауэр и др. [39] обобщили эту модель на трехслойные пылинки, предположив, что толщины внешних слоев (СО и H2O) не зависят от радиусов ядер пылинок. В этом случае все пылинки лишаются этих слоев одновременно. В настоящей работе мы строим альтернативное обобщение, предположив, что вначале от радиусов пылинок не зависит отношение радиусов ядра и мантии, т.е. мантии толще у более крупных пылинок. В этом случае у разных по размеру пылинок ледяные мантии испаряются в разное время, которое нам удалось найти аналитически.
Предлагаемая нами модель испарения пылинок в коллапсирующих протозвездных облаках представлена в разделе 2, а роль испарения пыли в эволюции магнитного поля протозвездных облаков исследуется в разделе 3. Выводы сделаны в разделе 4.
2. МОДЕЛЬ ЭВОЛЮЦИИ ПЫЛИ
2.1. Структура и состав пылинок
В начальный момент времени пылинки являются двухслойными шариками: ядро с плотностью ${{\rho }_{{\text{c}}}}$ и радиусом ${{a}_{{\text{c}}}}$ покрыто мантией с плотностью ${{\rho }_{{\text{m}}}}$ и радиусом ${{a}_{{\text{m}}}}$ (измеряемым от центра пылинки), причем отношение ${{a}_{{\text{c}}}}{\text{/}}{{a}_{{\text{m}}}} \equiv k$ не зависит от размера пылинки. Параметр $k$ вычисляется через начальное отношение масс мантии и ядра ${{m}_{{\text{m}}}}{\text{/}}{{m}_{{\text{c}}}}$, а также через их плотности:
(2)
$k = {{\left( {1 + \frac{{{{m}_{{\text{m}}}}}}{{{{m}_{{\text{c}}}}}}\frac{{{{\rho }_{{\text{c}}}}}}{{{{\rho }_{{\text{m}}}}}}} \right)}^{{ - 1/3}}}.$Предполагается, что и форстерит, и водяной лед имеют пористость 20%, поэтому ${{\rho }_{{\text{c}}}} = 2.6$ г/см3, ${{\rho }_{{\text{m}}}} = 0.8$ г/см3. Тогда из (2) следует $k = 0.5$. Поскольку мантии и ядра однородны по составу, то их испаряющаяся поверхность остается сферической. После исчезновения мантий пылинки становятся однослойными шариками.
2.2. Эволюция распределения пылинок по радиусам
Распределение пылинок по радиусам $a$ в момент времени $t$ представлено плотностью $f(a,t)$ – числом пылинок в единичном интервале радиусов в единице массы вещества (размерность $[f] = {{{\text{г}}}^{{ - 1}}}\;{\text{с}}{{{\text{м}}}^{{ - 1}}}$). Такой выбор $f(a,t)$ позволяет легко учесть сжимаемость среды. Начальная функция $f(a,t)$ считается степеннóй:
где $x \equiv a{\text{/}}{{a}_{{01}}}$ – безразмерный радиус пылинок, ${{a}_{{01}}}$ – начальный радиус наименьших пылинок, ${{f}_{{01}}} = f({{a}_{{01}}},0)$ – нормировочный коэффициент. Во всех моделях $q = - 3.5$. Вначале $x \in [1,A]$, где $A = 100$ – начальное отношение максимального и минимального радиусов.Для простоты модели предполагается, что 1) коагуляция и фрагментация пылинок уравновешивают друг друга и не влияют на $f(a,t)$; 2) к начальному моменту времени почти вся вода уже сконденсировалась на мантиях, поэтому ее дальнейшей конденсацией можно пренебречь; 3) почти весь кремний уже находится в форстерите, поэтому рост ядер пылинок после потери мантий пренебрежимо мал; 4) пылинки разрушаются только путем отделения атомов и молекул от внешнего слоя: сначала при сублимации воды, затем при термическом разложении форстерита. Для краткости оба эти процесса называются испарением. Испарение через поры не рассматривается. Также предполагается, что 5) температуры газа и пыли одинаковы, что приемлемо в моделях коллапса протозвездных облаков при $n{{ > 10}^{5}}$ см–3 (см., напр., [42]), кроме случаев, когда пыль проникает внутрь ультракомпактных HII зон возле массивных протозвезд [43]. Считается, что 6) температура среды растет достаточно плавно, чтобы мантии пылинок успевали испариться при $T \approx 130$ К до начала испарения ядер при $T \approx 1150$ К. Это условие может не выполняться на скачках температуры с $ \sim {\kern 1pt} 100$ К до ${{10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{4}}$ К, например, на фронтах ионизации водорода возле массивных протозвезд [43] и на ударных волнах, ограничивающих протозвезды (см. модели с массой 2 и 14 ${{M}_{ \odot }}$ в [22]).
Начальные радиусы ядер наименьших пылинок приравниваются к минимальному радиусу стабильных наночастиц ${{a}_{{\min }}}$, при котором испарение вещества наночастиц еще отличается от их взрывного разрушения, т.е. связи атомов и молекул внутри наночастиц сохраняются. Из этого предположения следует, что ${{a}_{{01}}} = {{a}_{{\min }}}{\text{/}}k$. Считается, что ${{a}_{{\min }}} = 5$ нм, но при более детальном подходе необходимо задавать ${{a}_{{\min }}}$, исходя из состава и структуры ядер (см., напр., [35]).
Темп потери массы пылинки, состоящей из сферических слоев, $\dot {m} = - 4\pi {{a}^{2}}w$, где $w > 0$ – темп потери массы с единицы площади поверхности слоя, являющегося внешним в данный момент. С другой стороны, $\dot {m} = 4\pi {{a}^{2}}\dot {a}\tilde {\rho }$, где $\dot {a}$ – скорость изменения радиуса, $\tilde {\rho }$ – плотность внешнего слоя. Поэтому скорость изменения радиуса пылинки при испарении вещества с ее поверхности не зависит от радиуса явно и определяется только характеристиками внешнего слоя [36]:
Однако $\dot {a}$ зависит от $a$ неявно: и $w$, и $\tilde {\rho }$ меняются скачком, когда текущий радиус пылинки проходит через внутренний радиус слоя, т.е. слой исчезает. В рассматриваемой двухслойной модели пылинок при исчезновении мантии $w$ резко уменьшается, поскольку ядро является менее летучим, а $\tilde {\rho }$ резко увеличивается, поскольку ядро является более плотным, чем мантия.Термическое разложение в отличие от сублимации относится к химическим реакциям, однако темп потери массы при этих процессах может быть рассчитан единым образом с помощью уравнения Герца-Кнудсена, использующего давление насыщенного пара $\tilde {p}$. При температуре интенсивного испарения оно много больше давления ненасыщенного пара, созданного пылинками. Поэтому можно пренебречь последним и записать уравнение Герца-Кнудсена в виде (см., напр., [44])
где $\tilde {v}$ – средний модуль скорости атомов или молекул, образующих пар. Для паров H2O известна простая, но достаточно точная аппроксимация экспериментальных данных [45]:(4)
$\begin{gathered} \tilde {p}({\text{SiO}}{{) = 10}^{6}}\exp ( - 6.28 \times {{10}^{4}}{{T}^{{ - 1}}} + 17.96 + \\ \, + 3.59 \times {{10}^{{ - 4}}}T - 3.72 \times {{10}^{{ - 7}}}{{T}^{2}} + \\ \, + 6.54 \times {{10}^{{ - 11}}}{{T}^{3}})\;{\text{дин/с}}{{{\text{м}}}^{2}}. \\ \end{gathered} $Скорость изменения радиуса пылинки $\dot {a}$ есть скорость ее движения в одномерном пространстве размеров. Когда мантия исчезает, $\dot {a}$ скачком уменьшается, поскольку при характерной температуре испарения воды 130 К функция (4) близка к нулю. Значит, эволюция пылинок, потерявших мантию, приостанавливается до тех пор, пока при $T \approx 1150$ К испарение форстерита не станет заметным. Поскольку начальное отношение радиусов ядра и мантии $k$ одинаково для всех пылинок, толщина мантии у мелких пылинок существенно меньше, чем у крупных (см. рис. 1). Поэтому мелкие пылинки теряют мантию раньше крупных, и делают остановку в пространстве размеров тоже раньше.
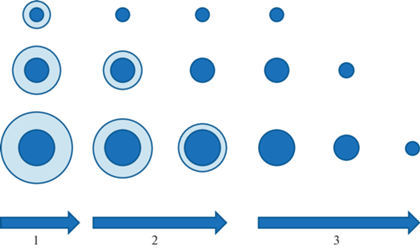
Рис. 1.
Поперечное сечение пылинок трех размеров на трех этапах эволюции: уменьшение мантий (1), уменьшение и исчезновение мантий (2) и уменьшение и исчезновение ядер (3).
Монотонная зависимость начального радиуса ядра от начального радиуса мантии исключает перемешивание пылинок в пространстве размеров в моменты остановок и позволяет описать эволюцию пыли полуаналитическими методами, а именно выразить $f(a,t)$ через элементарные функции и их интегралы по времени.
Пока $\dot {a}$ не зависит от $a$, функция $f(a,t)$ при испарении вещества пылинок смещается влево без деформаций. Смещенная функция (3) имеет вид
(5)
$\begin{gathered} f(a,t) = {{f}_{{01}}}{{(x - \epsilon )}^{q}}, \\ \epsilon = \epsilon (t) \equiv \frac{1}{{{{a}_{{01}}}}}\int\limits_0^t \,\dot {a}dt{\kern 1pt} ' \leqslant 0. \\ \end{gathered} $Предположения о двухслойности пылинок и плавном росте их температуры позволяют описать эволюцию пыли в рамках трех этапов. На рис. 1 схематично показана эволюция пылинок трех размеров и стрелками указаны этапы эволюции. На этапе 1 мантии испаряются у всех пылинок, поэтому в пространстве размеров они движутся все, и справедливо решение (5). Этот этап заканчивается, когда останавливаются наименьшие пылинки: при $\epsilon = k - 1$. На этапе 2 пылинки без мантий стоят, а пылинки с мантиями движутся. Этот этап заканчивается, когда останавливаются наибольшие пылинки: при $\epsilon = A(k - 1)$. На этапе 3 снова движутся все пылинки: их ядра испаряются и, достигнув радиуса ${{a}_{{{\text{min}}}}}$, исчезают. Следовательно, число пылинок в единице массы вещества на этапе 3 уменьшается.
Распределение пылинок по радиусам на этапе 2 состоит из двух частей: левую часть создают пылинки без мантий, а правую часть – пылинки с мантиями. Граница между ними – точка остановки c координатой ${{a}_{{\text{s}}}}$ – постоянно смещается вверх по течению, подобно краю пробки на дороге. Найти закон движения этой границы можно из следующих соображений. Пылинки с начальным радиусом ${{a}_{0}} + d{{a}_{0}}$ облачены в мантию на время $d{{t}_{{\text{s}}}}$ дольше, чем пылинки с начальным радиусом ${{a}_{0}}$, и останавливаются на $d{{a}_{{\text{s}}}}$ правее. Поскольку вначале их разделяет расстояние $d{{a}_{0}}$, то $d{{a}_{{\text{s}}}} = d{{a}_{0}} + \dot {a}d{{t}_{{\text{s}}}}$. С другой стороны, $d{{a}_{0}} = d{{a}_{{\text{s}}}}{\text{/}}k$. Поэтому $d{{a}_{{\text{s}}}} = k\dot {a}d{{t}_{{\text{s}}}}{\text{/}}(k - 1)$. Тогда, приравнивая $d{{t}_{{\text{s}}}}$ к $dt$, находим зависимость безразмерной координаты точки остановки от времени
Деформацию распределения пылинок по радиусам в точке остановки на этапе 2 можно найти из следующих соображений. Пылинки с начальными радиусами ${{a}_{0}}$ и ${{a}_{0}} + d{{a}_{0}}$ после испарения мантий имеют радиусы ${{a}_{{\text{s}}}} = k{{a}_{0}}$ и $a_{{\text{s}}}^{'} = k({{a}_{0}} + d{{a}_{0}})$. Поэтому все пылинки из интервала с начальной шириной $d{{a}_{0}}$ оказываются в более узком интервале с шириной $d{{a}_{{\text{s}}}} = kd{{a}_{0}}$. В терминах лагранжева описания в пространстве размеров это означает, что лагранжев элемент с начальной шириной $d{{a}_{0}}$ сжимается до ширины $kd{{a}_{0}}$. Поскольку число пылинок в этом элементе сохраняется, то лагранжева плотность распределения возрастает в $1{\text{/}}k$ раз.
На этапе 3 все сжатое распределение $f(a,t)$ смещается влево без деформаций и обрезается на границе $a = {{a}_{{\min }}}$. Относительное смещение пылинок в пространстве размеров на этом этапе
Введя переменные ${{x}_{*}} \equiv x{\text{/}}k$ и $\chi \equiv {{x}_{{\text{s}}}}{\text{/}}k = $ ${{x}_{{\text{s}}}} - \epsilon = \epsilon {\text{/}}(k - 1)$, запишем распределение пылинок по радиусам на всех трех этапах эволюции:
(6)
$\begin{gathered} f(a,t) = \\ = {{f}_{{01}}}\left( {\begin{array}{*{20}{l}} {{{{(x - \epsilon )}}^{q}},\;\;0 \leqslant \chi < 1,\;\;1 + \epsilon \leqslant x \leqslant A + \epsilon ,} \\ {x_{*}^{q}{\text{/}}k,\;\;1 \leqslant \chi \leqslant A,\;\;1 \leqslant {{x}_{*}} \leqslant \chi ,} \\ {{{{(x - \epsilon )}}^{q}},\;\;1 \leqslant \chi \leqslant A,\;\;{{x}_{s}} < x \leqslant A + \epsilon ,} \\ {{{{({{x}_{*}} - \delta )}}^{q}}{\text{/}}k,\;\;1 - A < \delta \leqslant 0,\;\;1 \leqslant {{x}_{*}} \leqslant A + \delta ,} \end{array}} \right. \\ \end{gathered} $Нормировочный коэффициент ${{f}_{{01}}}$ вычисляется из условия, что интеграл от начальной массы пылинок по всему распределению (3) должен быть равен начальному отношению массы пыли к массе вещества ${{Y}_{{\text{d}}}}$:
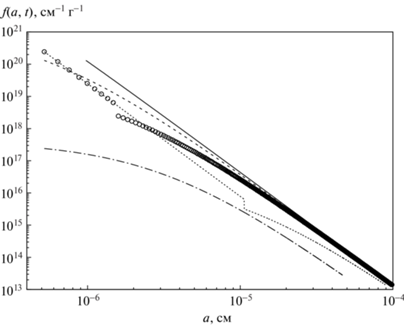
На рис. 2 приведены примеры распределения пылинок по радиусам (6) при нескольких выбранных значениях $\chi $ и $\delta $ (без привязки ко времени). В логарифмическом масштабе прямыми линиями являются графики $f(a,t)$ на старте и на этапе 2 слева от точки остановки (пылинки без мантий). В остальных случаях графики $f(a,t)$ являются выпуклыми кривыми. Видно, что в точке остановки функция $f(a,t)$ терпит разрыв. Постепенно он смещается вправо – вверх по течению частиц в пространстве размеров. Поскольку радиусы пылинок только уменьшаются, все графики $f(a,t)$ сдвигаются влево. Поскольку $k = 0.5$, то $\max [f(a,t)] = 2\max [f(a,0)]$ (этап 2, левая граница: $a = {{a}_{{\min }}}$).
2.3. Интегральные характеристики пыли
В качестве интегральных характеристик пыли рассматриваются радиус $\langle a\rangle $, площадь поперечного сечения $\langle s\rangle $ и масса пылинки $\langle m\rangle $, усредненные по распределению радиусов пылинок; ${{Y}_{{{\text{ev}}}}}$ – отношение испарившейся массы пыли к массе вещества, ${{X}_{{\text{g}}}}$ – отношение концентраций пылинок и частиц газа.
Введем интеграл
Тогда из (6) следуют выражения для средней величины радиуса пылинок(7)
$\langle {{a}^{\nu }}\rangle = a_{{01}}^{\nu }\left\{ \begin{gathered} {{F}_{{\epsilon \nu }}}(1)/{{P}_{0}}(1,A),\quad 0 \leqslant \chi < 1, \hfill \\ \left\{ {{{k}^{\nu }}{{P}_{\nu }}(1,\chi ) + {{F}_{{\epsilon \nu }}}(\chi )} \right\}{\text{/}}{{P}_{0}}(1,A), \hfill \\ 1 \leqslant \chi \leqslant A, \hfill \\ {{k}^{\nu }}{{F}_{{\delta \nu }}}(1 - \delta ){\text{/}}{{P}_{0}}(1 - \delta ,A), \hfill \\ 1 - A < \delta \leqslant 0. \hfill \\ \end{gathered} \right.$(8)
$\langle m\rangle = \frac{4}{3}\pi a_{{01}}^{3}\left( {\begin{array}{*{20}{l}} \begin{gathered} \{ {{k}^{3}}{{\rho }_{{{\text{cm}}}}}{{P}_{3}}(1,A) + {{\rho }_{{\text{m}}}}{{F}_{{\epsilon 3}}}(1)\} {\text{/}}{{P}_{0}}(1,A), \hfill \\ 0 \leqslant \chi < 1, \hfill \\ \end{gathered} \\ \begin{gathered} \{ {{k}^{3}}{{\rho }_{{\text{c}}}}{{P}_{3}}(1,\chi ) + {{k}^{3}}{{\rho }_{{{\text{cm}}}}}{{P}_{3}}(\chi ,A) + \hfill \\ + \;{{\rho }_{{\text{m}}}}{{F}_{{\epsilon 3}}}(\chi )\} {\text{/}}{{P}_{0}}(1,A), \hfill \\ 1 \leqslant \chi \leqslant A, \hfill \\ \end{gathered} \\ \begin{gathered} {{k}^{3}}{{\rho }_{{\text{c}}}}{{F}_{{\delta 3}}}(1 - \delta ){\text{/}}{{P}_{0}}(1 - \delta ,A), \hfill \\ 1 - A < \delta \leqslant 0. \hfill \\ \end{gathered} \end{array}} \right.$(9)
${{Y}_{{{\text{ev}}}}} = \frac{{{{Y}_{{\text{d}}}}}}{{{{\rho }_{{\text{g}}}}}}\left\{ \begin{gathered} {{\rho }_{{\text{m}}}}\{ 1 - {{F}_{{\epsilon 3}}}(1){\text{/}}{{P}_{3}}(1,A)\} ,\quad 0 \leqslant \chi < 1, \hfill \\ {{\rho }_{{\text{m}}}}\{ (1 - {{k}^{3}}){{P}_{3}}(1,\chi ) + {{P}_{3}}(\chi ,A) - \hfill \\ - \;{{F}_{{\epsilon 3}}}(\chi )\} {\text{/}}{{P}_{3}}(1,A),\quad 1 \leqslant \chi \leqslant A, \hfill \\ {{\rho }_{{\text{m}}}}(1\, - \,{{k}^{3}})\, + \,{{k}^{3}}{{\rho }_{{\text{c}}}}\{ 1\, - \,{{F}_{{\delta 3}}}(1\, - \,\delta ){\text{/}}{{P}_{3}}(1,A)\} , \hfill \\ 1 - A < \delta \leqslant 0. \hfill \\ \end{gathered} \right.$Пусть ${{N}_{{\text{g}}}} = {{N}_{{\text{g}}}}(t) = \int \,f(a,t)da$ – число пылинок в единице массы вещества. Тогда отношение концентраций пылинок и частиц газа ${{X}_{{\text{g}}}} = {{N}_{{\text{g}}}}\mu $, где $\mu = 2.3$ а.е. м. – средняя масса частиц газа. На первом и втором этапах эволюции пылинок величина ${{N}_{{\text{g}}}}$ не меняется, но на этапе 3 монотонно уменьшается:
(10)
${{N}_{{\text{g}}}} = {{f}_{{01}}}{{a}_{{01}}}\left( {\begin{array}{*{20}{l}} {{{P}_{0}}(1,A),\quad 0 \leqslant \chi \leqslant A,} \\ {{{P}_{0}}(1 - \delta ,A),\quad 1 - A < \delta \leqslant 0.} \end{array}} \right.$Выражения (7)–(10) протестированы на модели свободного коллапса однородного шарообразного облака из состояния покоя. Движение любой частицы на краю такого облака есть свободное падение в поле с потенциалом $ - GM{\text{/}}R$, где $M$ – масса облака, $R = R(t)$ – его радиус, $G$ – гравитационная постоянная. Поэтому скорость частицы $dR{\text{/}}dt = - \sqrt {2GM({{R}^{{ - 1}}} - R_{0}^{{ - 1}})} $, где ${{R}_{0}} = R(0)$. Переменные $t$ и $R$ в этом уравнении разделяются и
(11)
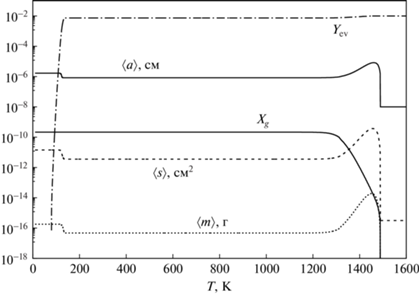
$\begin{gathered} t = - \sqrt {\frac{{R_{0}^{3}}}{{2GM}}} \int\limits_1^{R/{{R}_{0}}} \frac{{dx}}{{\sqrt {1{\text{/}}x - 1} }} = \\ = \sqrt {\frac{{R_{0}^{3}}}{{2GM}}} \left( {\frac{R}{{{{R}_{0}}}}\sqrt {\frac{{{{R}_{0}}}}{R} - 1} + \operatorname{arctg} \sqrt {\frac{{{{R}_{0}}}}{R} - 1} } \right). \\ \end{gathered} $Рис. 3.
Зависимость интегральных характеристик пыли от температуры в модели свободного коллапса: $\langle a\rangle $ – средний радиус, $\langle s\rangle $ – средняя площадь поперечного сечения, $\langle m\rangle $ – средняя масса пылинки, ${{Y}_{{{\text{ev}}}}}$ – отношение испарившейся массы пыли к массе вещества, ${{X}_{{\text{g}}}}$ – отношение концентраций пылинок и частиц газа.
3. ВЛИЯНИЕ ИСПАРЕНИЯ ПЫЛИ НА ЭВОЛЮЦИЮ МАГНИТНОГО ПОЛЯ
3.1. Модель коллапса протозвездного облака
Гравитационный коллапс протозвездного облака моделируется численно в приближении двухкомпонентной магнитной газодинамики. Межзвездная плазма рассматривается как сплошная среда, которая является смесью 1) электрически нейтральных частиц (нейтралов) и 2) электропроводящего компонента, состоящего из электронов, ионов и заряженных пылинок. Исследуются стадии коллапса до температуры существенной тепловой ионизации водорода (10 тыс. К), поэтому считается, что плотность и тепловое давление среды определяются только концентрацией нейтралов ${{n}_{{\text{n}}}}$: $\rho = \mu {{n}_{{\text{n}}}}$, $P = {{n}_{{\text{n}}}}{{k}_{{\text{b}}}}T$, где ${{k}_{{\text{b}}}}$ – постоянная Больцмана. Скорость среды ${\vec {v}}$ приравнивается к скорости нейтралов. Поскольку в численном методе используется лагранжева разностная сетка (движущаяся со скоростью среды), то уравнение движения единицы объема среды записывается через субстанциональную производную $d{\text{/}}dt$:
(12)
$\rho \frac{{d\vec {v}}}{{dt}} = - \nabla P + \rho \vec {g} + \frac{1}{{4\pi }}\left( {\nabla \times \vec {B}} \right) \times \vec {B},$При описании диффузии магнитного поля в коллапсирующих протозвездных облаках можно пренебречь трением проводящих компонентов плазмы друг с другом [46]. Поэтому предполагается, что компонент сорта $\alpha $, состоящий из частиц с массой ${{m}_{\alpha }}$, зарядом $ \pm e$ и концентрацией ${{n}_{\alpha }}$, имеет проводимость ${{\sigma }_{\alpha }} = {{e}^{2}}n_{\alpha }^{2}{\text{/}}{{R}_{{\alpha {\text{n}}}}}$, где ${{R}_{{\alpha {\text{n}}}}} = {{\mu }_{{\alpha {\text{n}}}}}{{n}_{\alpha }}{{n}_{{\text{n}}}}{{\langle sv\rangle }_{{\alpha {\text{n}}}}}$ – коэффициент трения с нейтралами, ${{\mu }_{{\alpha {\text{n}}}}} = \mu {{m}_{\alpha }}{\text{/}}(\mu + {{m}_{\alpha }})$ – приведенная масса, ${{\langle sv\rangle }_{{\alpha {\text{n}}}}}$ – коэффициент замедления. Для ионов ${{\langle sv\rangle }_{{{\text{in}}}}} = 2 \times {{10}^{{ - 9}}}$ см3 с–1 (см. [47, п. 2.2]). Для заряженных пылинок ${{\langle sv\rangle }_{{{{{\text{g}}}_{ + }}{\text{n}}}}} = {{\langle sv\rangle }_{{{{{\text{g}}}_{ - }}{\text{n}}}}} = \langle s\rangle {{v}_{{\text{n}}}}$, где ${{v}_{{\text{n}}}} = \sqrt {8{{k}_{{\text{b}}}}T{\text{/}}\pi \mu } $ – средняя тепловая скорость нейтралов. Коэффициент замедления электронов задается кусочно-степеннóй аппроксимацией табличных данных из [48, с. 393],
Проводимость плазмы $\sigma = \sum \,{{\sigma }_{\alpha }}$, т.е. циклотронное вращение заряженных частиц не учитывается. Коэффициент трения проводящего компонента с нейтралами ${{R}_{{{\text{in}}}}} = \sum\nolimits_\alpha \,{{R}_{{\alpha {\text{n}}}}}$. Магнитная амбиполярная диффузия (дрейф плазмы) – медленное совместное движение всех заряженных частиц относительно нейтралов под действием электромагнитной силы – считается стационарной (см. [47, п. 13.3]), т.е. полагается, что электромагнитная сила уравновешена силой трения
(13)
$0 = \frac{1}{{4\pi }}\left( {\nabla \times \vec {B}} \right) \times \vec {B} - {{R}_{{{\text{in}}}}}({{\vec {v}}_{{\text{i}}}} - \vec {v}),$Для учета магнитной амбиполярной диффузии в уравнении индукции считается, что магнитное поле вморожено в проводящий компонент. В описании омической диффузии магнитного поля пренебрегается производными по координатам от проводимости плазмы. Кроме того, пренебрегается различием субстанциональных производных проводящего компонента и нейтралов. Поэтому уравнение индукции записывается в виде
(14)
$\frac{{d\vec {B}}}{{dt}} = (\vec {B}\nabla ){{\vec {v}}_{{\text{i}}}} - \vec {B}\nabla {{\vec {v}}_{{\text{i}}}} + {{\eta }_{{\text{O}}}}{{\nabla }^{2}}\vec {B},$Турбулентная диффузия магнитного поля не рассматривается, поскольку магнитная амбиполярная диффузия подавляет МГД турбулентность еще вначале коллапса протозвездного облака [25, 26].
В численной модели вращение облака не учитывается, поле скорости и поле плотности считаются сферически симметричными, а магнитное поле – полоидальным. В сферических координатах $(r,\theta ,\phi )$ компоненты магнитного поля представляются в виде ${{B}_{r}} = {{H}_{r}}(r,t)\cos \theta $, ${{B}_{\theta }} = - {{H}_{\theta }}(r,t)\sin \theta $. Это позволяет усреднить по полусферам и электромагнитную силу в (12), (13), и уравнение индукции (14), чтобы получить сферически симметричную модель коллапса [49]. В такой модели $g = GM{\text{/}}{{r}^{2}}$, где $M = M(r)$ – масса внутри сферы с радиусом $r$. На лагранжевой сетке масса $dM$ сферического слоя с объемом $dV$ постоянна, поэтому $\rho = dM{\text{/}}dV$, а $dV$ вычисляется через координаты узлов сетки.
Температура задается кусочно-степеннóй функцией плотности, аппроксимирующей результаты работы [50]. Показатель степени меняется в интервале (0.1, 0.66) и зависит не от плотности, а от самой температуры, поскольку с ее ростом возбуждаются колебательные и вращательные степени свободы молекул водорода, а затем происходит их диссоциация.
3.2. Модель ионизации
Для корректного расчета диффузии магнитного поля в протозвездных облаках необходимо знать концентрации электронов ${{n}_{{\text{e}}}}$, ионов ${{n}_{{\text{i}}}}$ и пылинок ${{n}_{{{{{\text{g}}}_{ - }}}}}$ и ${{n}_{{{{{\text{g}}}_{ + }}}}}$, имеющих заряд $ - e$ и $ + e$ соответственно (см. [38, 46]). Уравнения кинетики ионизации разделены на две системы: первая описывает ионизацию среды космическими лучами и радионуклидами, вторая – ее ионизацию собственным тепловым излучением. В обеих системах учитывается рекомбинация ионов на пылинках.
Считается, что при $T < 575$ K в газовой фазе есть только один вид атомов металлов – Mg, а остальные десорбируются из ядер пылинок при $T > 575$ K – после испарения мало летучей органики [51]. Предполагается, что эти атомы металлов равномерно распределены в верхней трети ядра (по радиусу), и в интервале температур от 575 до 1300 K занимаемая ими область линейно уменьшается по радиусу с ростом $T$. Распространенность таких атомов в газовой фазе пропорциональна изменению занимаемого ими объема пылинок и для каждого элемента ограничена его распространенностью в современной солнечной системе [40]. Такая модель десорбции металлов из пылинок реалистична, но строго не обоснована. Она лишь призвана описать плавный впрыск металлов в газовую фазу, не повышая сложность модели испарения пыли.
Поскольку моделируется коллапс облаков с начальной концентрацией частиц $n \simeq {{10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{6}}$ см–3, то пренебрегается ионизацией среды межзвездным ультрафиолетом, и ион C+ не учитывается, хотя он значим во внешних слоях таких облаков (см. [52]). При наличии мелких (5–10 нм) пылинок на начальной стадии коллапса с $T \approx 10$ K доминирует ион ${\text{H}}_{3}^{ + }$ [53], а в их отсутствие – ион HCO+ [52, 53]. На более теплой стадии коллапса начинается сублимация летучих веществ из мантий пылинок, поэтому доминируют ионы HCO+ и H3O+, независимо от наличия мелких пылинок [53]. Учитывая мелкую пыль, мы рассматриваем только один молекулярный ион – ${\text{H}}_{3}^{ + }$. Пренебрежение ионами HCO+ и H3O+ влияет на остаточное поле незначительно, поскольку в зонах сильной диффузии магнитного поля проводимость определяется именно мелкой пылью [53].
Предполагается, что ионы Mg+ и других металлов образуются в процессе диссоциативной перезарядки иона ${\text{H}}_{3}^{ + }$ с атомами, а также при их фотоионизации тепловым излучением среды на поздних стадиях коллапса. Ион ${\text{H}}_{3}^{ + }$ возникает в результате быстрых реакций, начинающихся с ионизации водорода и гелия космическими лучами и радионуклидами, поэтому темп производства H$_{3}^{ + }$ в единице объема
(15)
${{S}_{{{{{\text{m}}}_{ + }}}}} = (\zeta {{e}^{{ - \tau }}} + {{\zeta }_{1}}{{e}^{{ - t/{{t}_{1}}}}} + {{\zeta }_{2}}{{e}^{{ - t/{{t}_{2}}}}}){{n}_{{\text{n}}}},$Первая система уравнений кинетики ионизации основана на модели Кунца и Мусковиаса [56] и дополнена учетом рекомбинации ионов на пылинках при $T > 575$ K. Эта система состоит из 4 уравнений для расчета ${{n}_{{{{{\text{g}}}_{ - }}}}}$ и ${{n}_{{{{{\text{g}}}_{ + }}}}}$, а также для расчета концентраций ${{n}_{{{{{\text{a}}}_{ + }}}}}$ и ${{n}_{{{{{\text{m}}}_{ + }}}}}$ ионов Mg+ и ${\text{H}}_{3}^{ + }$:
(16)
$\begin{gathered} {{{\dot {n}}}_{{{{{\text{a}}}_{ + }}}}} = {{C}_{{{{{\text{a}}}_{0}}{{{\text{m}}}_{ + }}}}}{{n}_{{{{{\text{m}}}_{ + }}}}}{{n}_{{{{{\text{a}}}_{0}}}}} - \\ - \;\left( {{{C}_{{{{{\text{a}}}_{ + }}{\text{e}}}}}{{n}_{{\text{e}}}} + {{C}_{{{{{\text{a}}}_{ + }}{{{\text{g}}}_{ - }}}}}{{n}_{{{{{\text{g}}}_{ - }}}}} + {{C}_{{{{{\text{a}}}_{ + }}{{{\text{g}}}_{0}}}}}{{n}_{{{{{\text{g}}}_{0}}}}}} \right){{n}_{{{{{\text{a}}}_{ + }}}}}, \\ \end{gathered} $(17)
$\begin{gathered} {{{\dot {n}}}_{{{{{\text{m}}}_{ + }}}}} = {{S}_{{{{{\text{m}}}_{ + }}}}} - \\ - \;\left( {{{C}_{{{\text{dr}}}}}{{n}_{{\text{e}}}} + {{C}_{{{{{\text{m}}}_{ + }}{{{\text{g}}}_{ - }}}}}{{n}_{{{{{\text{g}}}_{ - }}}}} + {{C}_{{{{{\text{m}}}_{ + }}{{{\text{g}}}_{0}}}}}{{n}_{{{{{\text{g}}}_{0}}}}} + {{C}_{{{{{\text{a}}}_{0}}{{{\text{m}}}_{ + }}}}}{{n}_{{{{{\text{a}}}_{0}}}}}} \right){{n}_{{{{{\text{m}}}_{ + }}}}}, \\ \end{gathered} $(18)
${{\dot {n}}_{{{{{\text{g}}}_{ - }}}}} = {{C}_{{{\text{e}}{{{\text{g}}}_{0}}}}}{{n}_{{\text{e}}}}{{n}_{{{{{\text{g}}}_{0}}}}} - \left( {{{C}_{{{\text{g}} \pm }}}{{n}_{{{{{\text{g}}}_{ + }}}}} + \sum\limits_\beta \,{{C}_{{{{\beta }_{ + }}{{{\text{g}}}_{ - }}}}}{{n}_{{{{\beta }_{ + }}}}}} \right){{n}_{{{{{\text{g}}}_{ - }}}}},$(19)
${{\dot {n}}_{{{{{\text{g}}}_{ + }}}}} = {{n}_{{{{{\text{g}}}_{0}}}}}\sum\limits_\beta \,{{C}_{{{{\beta }_{ + }}{{{\text{g}}}_{0}}}}}{{n}_{{{{\beta }_{ + }}}}} - \left( {{{C}_{{{\text{g}} \pm }}}{{n}_{{{{{\text{g}}}_{ - }}}}} + {{C}_{{{\text{e}}{{{\text{g}}}_{ + }}}}}{{n}_{{\text{e}}}}} \right){{n}_{{{{{\text{g}}}_{ + }}}}},$Таблица 1.
Обозначения констант реакций и ссылки на источники
| Обозначение | Реакция | Ссылка |
|---|---|---|
| ${{C}_{{{{{\text{a}}}_{0}}{{{\text{m}}}_{ + }}}}}$ | Диссоциативная перезарядка ${\text{H}}_{3}^{ + }$ с атомом | [57] |
| ${{C}_{{{{{\text{a}}}_{ + }}{\text{e}}}}}$ | Фоторекомбинация атомарного иона | [47] |
| ${{C}_{{{{\beta }_{ + }}{{{\text{g}}}_{ - }}}}}$ | Рекомбинация иона сорта $\beta $ на отрицательных пылинках | [56] |
| ${{C}_{{{{\beta }_{ + }}{{{\text{g}}}_{0}}}}}$ | Рекомбинация иона сорта $\beta $ на нейтральных пылинках | [56] |
| ${{C}_{{{\text{dr}}}}}$ | Диссоциативная рекомбинация ${\text{H}}_{3}^{ + }$ | [57] |
| ${{C}_{{{\text{e}}{{{\text{g}}}_{0}}}}}$ | Захват электрона нейтральной пылинкой | [56] |
| ${{C}_{{{\text{g}} \pm }}}$ | Взаимная нейтрализация пылинок | [56] |
| ${{C}_{{{\text{e}}{{{\text{g}}}_{ + }}}}}$ | Нейтрализация положительной пылинки | [56] |
Вторая система уравнений кинетики ионизации состоит из 10 уравнений для расчета концентраций однозарядных ионов 10 химических элементов: H, Li, Na, Mg, Al, Si, K, Ca, Rb, Cs. В этой системе уравнений в расчет приняты только те атомы Mg, которые десорбированы пылью при $T > 575$ K. Каждое из уравнений второй системы решается только при $T > 575$ K и имеет вид
(20)
$\begin{gathered} {{{\dot {n}}}_{{{{\beta }_{ + }}}}} = \left( {{{P}_{{{{\beta }_{0}}}}} + {{C}_{{{{\beta }_{0}}{{{\text{m}}}_{ + }}}}}{{n}_{{{{{\text{m}}}_{ + }}}}}} \right){{n}_{{{{\beta }_{0}}}}} - \\ \, - \left( {{{C}_{{{{\beta }_{ + }}{\text{e}}}}}{{n}_{{\text{e}}}} + {{C}_{{{{\beta }_{ + }}{{{\text{g}}}_{ - }}}}}{{n}_{{{{{\text{g}}}_{ - }}}}} + {{C}_{{{{\beta }_{ + }}{{{\text{g}}}_{0}}}}}{{n}_{{{{{\text{g}}}_{0}}}}}} \right){{n}_{{{{\beta }_{ + }}}}}, \\ \end{gathered} $(21)
${{P}_{{{{\beta }_{0}}}}} = c\int\limits_{{{\nu }_{\beta }}}^\infty \,{{s}_{\beta }}(\nu )\frac{{{{u}_{\nu }}}}{{h\nu }}d\nu $Поскольку обилие металлов мало, считается, что их фотоионизация не влияет на поле излучения. Зависимости ${{s}_{\beta }}(\nu )$ для разных атомов сильно различаются, однако при исследовании магнитной диффузии достаточно знать пороговые значения ${{s}_{\beta }}({{\nu }_{\beta }})$. Дело в том, что в области эффективной магнитной диффузии $T < 5000$ К и $h\nu {\text{/}}{{k}_{{\text{b}}}}T \gg 1$, поэтому с ростом частоты функция ${{u}_{\nu }}$ настолько быстро убывает, что для всех зависимостей ${{s}_{\beta }}(\nu )$ справедлива следующая аппроксимация интеграла (21) (см. [58]):
Концентрация электронов находится из условия электронейтральности,
где сумма берется по всем ионам, существующим при данной температуре.3.3. Начальные и граничные условия, численные методы
Начальная температура среды ${{T}_{0}}$ постоянна по всему облаку, а распределение плотности вещества и модуля магнитной индукции вычисляется из условия гидростатического равновесия с постоянным отношением магнитного и теплового давлений. Это отношение вычисляется через концентрацию частиц ${{n}_{{{\text{c0}}}}}$ и магнитную индукцию ${{B}_{{{\text{c0}}}}}$ в центре облака (табл. 2). Среда вначале покоится. Поскольку магнитное натяжение в расчете равновесия не учитывается, то начальная равнодействующая сила в каждом слое облака отлична от нуля. Однако она существенно слабее силы тяготения, поэтому скорость коллапса меньше, чем в случае изначально однородного облака.
Таблица 2.
Начальные характеристики моделируемых облаков
| Объект | $M,{{M}_{ \odot }}$ | ${{R}_{0}}$, пк | ${{n}_{{{\text{c0}}}}}$, см–3 | ${{T}_{0}}$, К | ${{B}_{{{\text{c0}}}}}$, мГс | ${{\varepsilon }_{{\text{t}}}}$ | ${{\varepsilon }_{{\text{m}}}}$ |
|---|---|---|---|---|---|---|---|
| W3 (main) | 37 | 0.12 | $5.0 \times {{10}^{5}}$ | 60 | 0.57 | 0.34 | 0.34 |
| NGC 2024 | 10 | 0.20 | $5.5 \times {{10}^{5}}$ | 25 | 0.12 | 0.59 | 0.06 |
| DR 21 OH1 | 8 | 0.05 | $5.5 \times {{10}^{6}}$ | 50 | 1.00 | 0.46 | 0.16 |
Примечание. В столбцах приведены: масса облака $M$, радиус ${{R}_{0}}$, концентрация частиц в центре ${{n}_{{{\text{c0}}}}}$, температура ${{T}_{0}}$, магнитная индукция в центре ${{B}_{{{\text{c0}}}}}$, отношения тепловой и магнитной энергий к модулю гравитационной энергии, ${{\varepsilon }_{{\text{t}}}}$, ${{\varepsilon }_{{\text{m}}}}$.
Начальные характеристики протозвездных облаков (табл. 2) вычисляются на основе наблюдательных данных о столбцовой плотности, радиусе облака и магнитной индукции вдоль луча зрения [10]. Последняя умножается на $\sqrt 2 $, чтобы получить ${{B}_{{{\text{c0}}}}}$. Значение ${{n}_{{{\text{c0}}}}}$ подбирается так, чтобы радиус и столбцовая плотность гидростатически равновесного облака совпали с наблюдаемыми значениями. После этого вычисляется масса облака. Начальные отношения тепловой и магнитной энергий облака к модулю его гравитационной энергии, ${{\varepsilon }_{{\text{t}}}}$ и ${{\varepsilon }_{{\text{m}}}}$, в сумме $ < {\kern 1pt} 1$, поэтому устойчивое гидростатическое равновесие облака недостижимо, и оно, иногда после некоторых колебаний, испытывает гравитационный коллапс.
Граничные условия в центре облака: скорость меняет знак, плотность и магнитное поле непрерывны. На внешней границе облака: скорость среды вычисляется из условия постоянства массы и плотности внешнего сферического слоя, производная скорости проводящего компонента непрерывна, магнитная индукция непрерывна.
Задача с начальными и граничными условиями для одномерных уравнений движения и индукции решается численно методом Лакса-Вендроффа с добавленной искусственной вязкостью. Этот метод достаточно прост в реализации, но, будучи явным, требует слишком малых шагов по времени при сильной диффузии магнитного поля. Основа численного кода разработана Дудоровым и Сазоновым [49] и существенно доработана авторами для включения современных моделей ионизации и испарения пыли.
Для исследования влияния пыли на эволюцию магнитного поля протозвездных облаков рассматривается два варианта моделей, отличающихся параметрами пыли и начальным обилием Mg в газовой фазе ${{X}_{{\text{a}}}}(0)$: 1) мелкая пыль с нормальной массовой долей ${{Y}_{{\text{d}}}}$, приводящая к низкому значению ${{X}_{{\text{a}}}}(0)$, 2) крупная пыль с низкой массовой долей, сохраняющая высокое значение ${{X}_{{\text{a}}}}(0)$ (табл. 3). Такая антикорреляция ${{Y}_{{\text{d}}}}$ и ${{X}_{{\text{a}}}}(0)$ описывает на качественном уровне так называемое вымерзание атомов на пылинках, что означает преобладание их адсорбции над десорбцией.
Таблица 3.
Варианты моделей, отличающиеся параметрами пыли и начальным обилием Mg в газовой фазе ${{X}_{{\text{a}}}}(0)$
| Вариант | Особенности | ${{a}_{{\min }}}$, нм | ${{Y}_{{\text{d}}}}$ | ${{X}_{{\text{a}}}}(0)$ |
|---|---|---|---|---|
| 1 | Мелкая пыль с нормальной массовой долей, мало Mg | 5 | 0.01 | ${{10}^{{ - 8}}}$ |
| 1а | Аналогичен варианту 1, но пыль не испаряется | ″ | ″ | ″ |
| 2 | Крупная пыль с низкой массовой долей, много Mg | $100$ | 0.001 | ${{10}^{{ - 7}}}$ |
Для прояснения роли пыли рассматривается также нереальный, но поучительный вариант 1а без испарения пыли, имеющий те же параметры, что и вариант 1. Десорбция металлов из пылинок при $T > 575$ K в варианте 1а учитывается, чтобы не занижать степень ионизации слишком сильно.
Уравнения (16)–(20) решаются в каждом сферическом слое одномерной модели облака методом Гира 2 порядка точности. Возникающие при этом системы нелинейных уравнений решаются методом Ньютона, а системы линейных уравнений – методом Гаусса.
3.4. Результаты расчетов
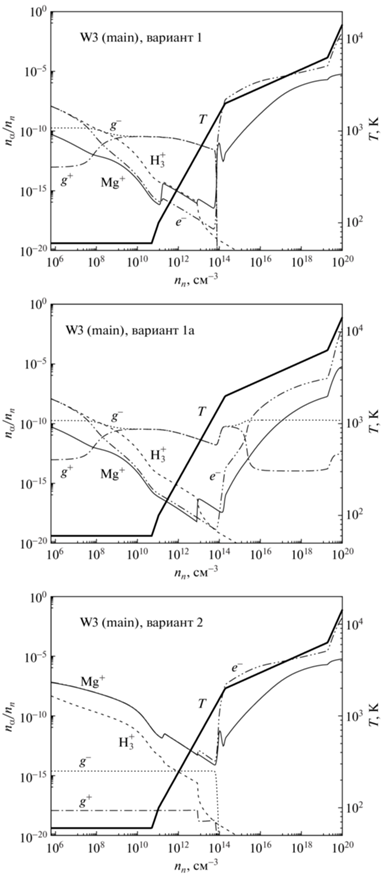
3.4.1. Концентрация заряженных частиц. Рисунок 4 показывает зависимости температуры и относительной концентрации заряженных частиц от концентрации нейтральных частиц в центре облака в трех вариантах модели W3 (main). Пылинки являются доминирующими носителями заряда при $2 \times {{10}^{8}} < {{n}_{{\text{n}}}} < 7 \times {{10}^{{13}}}$ см–3 в варианте 1 и при $2 \times {{10}^{8}} < {{n}_{{\text{n}}}} < 3 \times {{10}^{{15}}}$ см–3 в варианте 1а. В этих случаях ион ${\text{H}}_{3}^{ + }$ доминирует только при ${{n}_{{\text{n}}}}{{ < 10}^{8}}$ см–3. В варианте 2 почти все время доминируют ионы металлов и электроны; лишь при $T \approx 8000$ K их сменяют протоны с электронами; концентрация иона H$_{3}^{ + }$ всюду уступает ионам металлов на порядок величины и более.
Рис. 4.
Зависимость температуры (толстая линия, правая шкала) и относительной концентрации заряженных частиц (тонкие линии, левая шкала) от концентрации нейтральных частиц в центре облака в трех вариантах модели W3 (main).
В варианте 1 испарение ледяных мантий при $T \approx 120$ K вызывает повышение концентраций электронов в 2 раза, а ионов Mg+ в 54 раза, поскольку из-за уменьшения площади поперечного сечения пылинок (в 4 раза) происходит снижение темпа рекомбинации на пыли у доминирующего иона H$_{3}^{ + }$. При $T > 575$ K относительная концентрация иона H$_{3}^{ + }$ быстро снижается из-за диссоциативной перезарядки с атомами металлов, десорбированных из пылинок. При $T \approx 1350$ K пылинки исчезают совсем. Тогда концентрация электронов возрастает на 7 порядков, а ионов Mg+ – на 5 порядков величины.
В варианте 1а резких изменений концентраций всего два: при $T > 575$ K из-за десорбции металлов быстро падает концентрация H$_{3}^{ + }$ и возрастает концентрация Mg+, а при $T > 1300$ K быстро растет относительная концентрация электронов из-за фотоионизации металлов. Резкий спад относительной концентрации Mg+ при $T \approx 1500{\kern 1pt} - {\kern 1pt} 1800$ K в вариантах 1 и 2 вызван усилением рекомбинации из-за быстрого роста концентрации электронов при фотоионизации щелочных металлов. При более высоких температурах начинается интенсивная фотоионизация самих атомов Mg.
Зависимость относительной концентрации протонов и ионов металлов от концентрации нейтральных частиц и температуры в центре облака в варианте 1 модели W3 (main) показана на рис. 5. С началом десорбции металлов из пылинок при $T > 575$ K основным конкурентом Mg+ становится Si+, поскольку Mg и Si близки по распространенности и кинетическим коэффициентам. Концентрация остальных ионов металлов при $T < 1100$ K также соответствует распространенности. Тепловая ионизация сначала заметна у металлов с наименьшей энергией ионизации (Cs, Rb, K при $T \approx 1000$, 1050, 1150 K соответственно), но выйти в лидеры им не удается из-за низкой распространенности. При $T < 1400$ K за счет высокой распространенности доминируют Mg+ и Si+, а затем их сменяют K+, Na+ и Al+. Таким образом, в используемой модели можно пренебречь ионизацией Ca, Li, Rb, Cs.
Рис. 5.
Зависимость относительной концентрации протонов и ионов металлов от концентрации нейтральных частиц при $T > 575$ К (верхняя панель) и зависимость относительной концентрации ионов металлов от температуры в области минимума степени ионизации (нижняя панель) в центре облака в варианте 1 модели W3 (main). При ${{n}_{{\text{n}}}} < 2 \times $ × 1014 см–3 и $T < 2000$ K кривые для Mg+ и Si+ неразличимы.
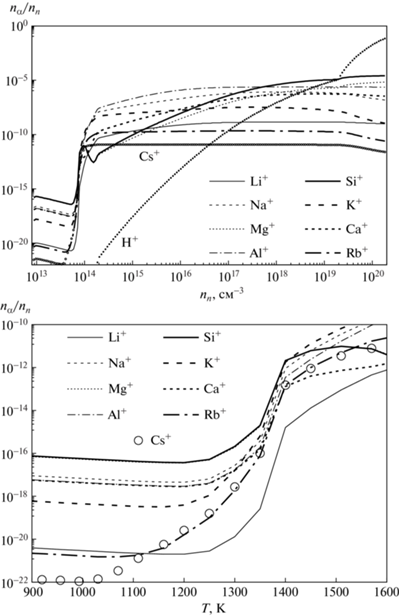
В моделях объектов NGC 2024 и DR 21 OH1 относительные концентрации заряженных частиц зависят от плотности и температуры почти так же, как в модели W3 (main), поскольку и температуры, и ослабление потока космических лучей во всех моделях различаются не сильно.
3.4.2. Коэффициенты диффузии и магнитное число Рейнольдса. Диффузия магнитного поля сильна, если магнитное число Рейнольдса ${{{\text{R}}}_{{\text{m}}}} < 1$. Выбрав радиальную координату $r$ в качестве характерного размера течения, положим ${{{\text{R}}}_{{\text{m}}}} = vr{\text{/}}({{\eta }_{{\text{A}}}} + {{\eta }_{{\text{O}}}})$, где, напомним, ${{\eta }_{{\text{A}}}}$ и ${{\eta }_{{\text{O}}}}$ – коэффициенты амбиполярной и омической диффузии. Магнитная амбиполярная диффузия максимальна там, где минимальна концентрация массивных заряженных частиц с большим сечением рассеяния на нейтралах, т.е. ионов и пылинок. Омическая диффузия магнитного поля максимальна там, где минимальна относительная концентрация легких заряженных частиц, т.е. электронов и ионов. Поэтому зоны эффективной амбиполярной и омической диффузий обычно не совпадают, а испарение пыли существенно влияет на их соотношение.
Рассмотрим финальные зависимости ${{\eta }_{{\text{A}}}}(r)$ и ${{\eta }_{{\text{O}}}}(r)$ в трех вариантах модели W3 (main) (рис. 6). Эти зависимости немонотонны и имеют пики и провалы в зонах испарения мантий пылинок (30–80 а.е.) и ядер пылинок (3–6 а.е.). Во внешних частях облака ($r > 100$ а.е.) во всех вариантах ${{\eta }_{{\text{A}}}} > {{\eta }_{{\text{O}}}}$. Если же пыли мало и она крупная (вариант 2), то ${{\eta }_{{\text{A}}}} > {{\eta }_{{\text{O}}}}$ при $r > 0.3$ а.е., т.е. амбиполярная диффузия доминирует в средних и внешних слоях облака. В варианте 1 глобальные максимумы ${{\eta }_{{\text{A}}}}$ и ${{\eta }_{{\text{O}}}}$ одинаковы по порядку величины, причем в варианте 1а это совпадение сохраняется. Зона высоких значений ${{\eta }_{{\text{A}}}}$ наиболее широка в варианте 2, поскольку сцепление проводящего компонента с нейтралами ослаблено из-за дефицита заряженных пылинок. Зона высоких значений ${{\eta }_{{\text{O}}}}$ наиболее широка в варианте 1а, поскольку концентрации электронов и ионов снижены из-за неослабевающей рекомбинации на пылинках.
Рис. 6.
Зависимость коэффициентов амбиполярной (толстые линии) и омической (тонкие линии) диффузии магнитного поля (верхняя панель) и магнитного числа Рейнольдса ${{{\text{R}}}_{{\text{m}}}}$ (нижняя панель) от радиальной координаты в трех вариантах модели W3 (main) на момент завершения расчетов. Горизонтальные линии разделяют диапазоны ${{{\text{R}}}_{{\text{m}}}}$, где диффузия магнитного поля считается сильной, умеренной и слабой.
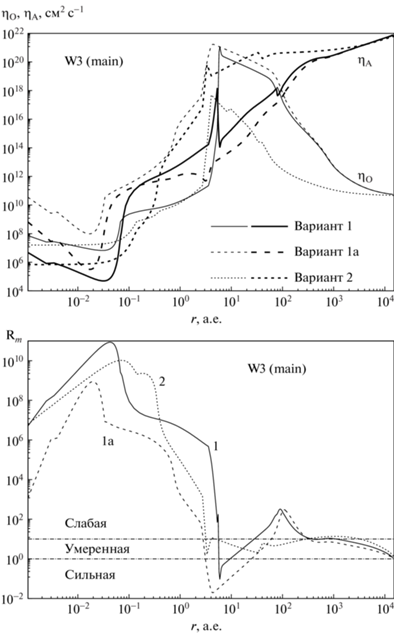
Зависимость магнитного числа Рейнольдса от радиальной координаты в трех вариантах модели W3 (main) на момент завершения расчетов также представлена на рис. 6. Диффузия магнитного поля считается сильной при ${{R}_{{\text{m}}}} < 1$, умеренной при $1 < {{R}_{{\text{m}}}} < 10$ и слабой при ${{R}_{{\text{m}}}} > 10$. Зона сильной диффузии имеет ширину 3 а.е. в варианте 1 и ширину 22 а.е. в варианте 1а, но отсутствует в варианте 2. Зон умеренной диффузии может быть несколько: две в вариантах 1 и 1а, но три в варианте 2. Пренебрежение испарением пыли расширило зону сильной диффузии в 7 раз и умеренной диффузии в 2 раза.
Поведение коэффициентов диффузии и магнитного числа Рейнольдса в моделях NGC 2024 и DR 21 OH1 на качественном уровне такое же, как в модели W3 (main), однако положения и величины экстремумов отличаются. В табл. 4 сравниваются основные показатели моделей: минимальная относительная концентрация электронов в центре облака и соответствующая ей температура $T{\kern 1pt} '$, а также магнитная индукция в центре облака при плотности фотосфер молодых звезд. Кроме того, в табл. 4 указаны границы зоны сильной диффузии магнитного поля (мертвой зоны), в которой должны быть существенно снижены турбулентная вязкость и радиальная диффузия дециметровых твердых тел [60]. Такие тела могут собираться в планетезимали на границах мертвой зоны из-за неустойчивости волн Россби [61], а также внутри этой зоны из-за потоковой неустойчивости [60].
Таблица 4.
Отличия моделей и вариантов по основным показателям
| Модель | Вариант | ${\text{min[}}{{n}_{{\text{e}}}}{\text{/}}{{n}_{{\text{n}}}}]$ | $T{\kern 1pt} '$, K | ${{r}_{{{{{\text{R}}}_{{\text{m}}}} < 1}}}$, а.е. | ${{B}_{{\text{c}}}}$, кГс |
|---|---|---|---|---|---|
| W3 (main) | 1 | $6 \times {{10}^{{ - 19}}}$ | 1200 | 6–9 | 2.3–49.7 |
| 1а | $1 \times {{10}^{{ - 19}}}$ | 1350 | 3–25 | 0.8–19.0 | |
| 2 | $2 \times {{10}^{{ - 14}}}$ | 1240 | нет | 3.3–72.1 | |
| NGC 2024 | 1 | $2 \times {{10}^{{ - 19}}}$ | 1090 | 1–6 | 0.2–3.3 |
| 1а | $4 \times {{10}^{{ - 20}}}$ | 1300 | 0.5–8 | 0.05–1.0 | |
| 2 | $3 \times {{10}^{{ - 15}}}$ | 1210 | нет | 0.6–13.4 | |
| DR 21 OH1 | 1 | $6 \times {{10}^{{ - 19}}}$ | 1170 | 2–10 | 0.7–14.5 |
| 1а | $1 \times {{10}^{{ - 19}}}$ | 1300 | 1–20 | 0.2–5.2 | |
| 2 | $1 \times {{10}^{{ - 14}}}$ | 1240 | нет | 1.4–28.3 |
Примечание. Приведены: минимальная относительная концентрация электронов в центре облака и соответствующая ей температура $T{\kern 1pt} '$, границы зоны сильной диффузии магнитного поля, магнитная индукция в центре облака при концентрации частиц, характерной для оснований фотосфер молодых звезд (${{10}^{{16}}}{\kern 1pt} - {\kern 1pt} {{10}^{{18}}}$ см–3).
Таблица 4 показывает, что минимальные относительные концентрации электронов в центре облака в разных моделях и вариантах отличаются на 5.5 порядков величины, но значения $T{\kern 1pt} '$ различаются всего на $260$ К, поскольку температуры полного испарения пыли и существенной тепловой ионизации металлов тоже близки. В моделях Мершана и др. [38], учитывающих и не учитывающих испарение пыли, минимальные относительные концентрации электронов отличаются на порядок величины, но расположение минимума также почти не меняется. Таким образом, пренебрежение испарением пыли в моделях коллапса протозвездных облаков существенно усиливает диффузию магнитного поля, но сохраняет характерное расстояние от центра до мертвой зоны, 1–10 а.е.
3.4.3. Эволюция магнитного поля. В используемой сферически симметричной модели коллапса [49] сплющивание облака вдоль магнитного поля не учитывается, поэтому зависимость магнитной индукции от плотности ближе к $B \propto {{\rho }^{{2/3}}}$, чем в многомерных моделях. Рассмотрим, например, зависимость магнитной индукции ${{B}_{{\text{c}}}}$ от концентрации частиц ${{n}_{{\text{c}}}}$ в центре облака в модели DR 21 OH1 (рис. 7). В нашей модели амбиполярная диффузия в центре облака неэффективна, поэтому с высокой точностью ${{B}_{{\text{c}}}} \propto n_{{\text{c}}}^{{2/3}}$ при ${{n}_{{\text{c}}}}{{ < 10}^{{12}}}$ см–3 и ${{n}_{{\text{c}}}}{{ > 10}^{{15}}}$ см–3, однако ${{B}_{{\text{c}}}} \propto n_{{\text{c}}}^{{0.45}}$ в условиях сильной омической диффузии при ${{10}^{{13}}} < {{n}_{{\text{c}}}}{{ < 10}^{{14}}}$ см–3. Пренебрежение испарением пыли (вариант 1а) продлевает интервал сильной омической диффузии до ${{n}_{{\text{c}}}} \simeq {{10}^{{15}}}$ см–3, что снижает магнитную индукцию на полпорядка величины. И наоборот, в случае дефицита пыли (вариант 2) обилие электронов достаточно велико, чтобы омическая диффузия была несущественной и лишь чуть понизила ${{B}_{{\text{c}}}}$. В итоге в диапазоне ${{n}_{{\text{c}}}}{{ = 10}^{{16}}}{\kern 1pt} - {\kern 1pt} {{10}^{{18}}}$ см–3, соответствующем основаниям фотосфер молодых звезд, ${{B}_{{\text{c}}}} = 0.7{\kern 1pt} - {\kern 1pt} 14.5$ кГс в варианте 1, $0.2{\kern 1pt} - {\kern 1pt} 5.2$ кГс в варианте 1а, и $1.4{\kern 1pt} - {\kern 1pt} 28.3$ кГс в варианте 2. Таким образом, магнитное поле при фотосферных плотностях ослабло в 3 раза из-за пренебрежения испарением пыли и выросло в 2 раза из-за дефицита пыли.
Рис. 7.
Зависимость магнитной индукции от концентрации частиц в центре облака в трех вариантах модели DR 21 OH1. Вертикальные линии указывают предполагаемый диапазон концентраций частиц в основаниях фотосфер молодых звезд. Зависимость ${{B}_{{\text{c}}}} \propto n_{{\text{c}}}^{{2/3}}$ выполняется при изотропном сжатии идеально проводящей среды, а ${{B}_{{\text{c}}}} \propto n_{{\text{c}}}^{{0.45}}$ в условиях сильной омической диффузии.
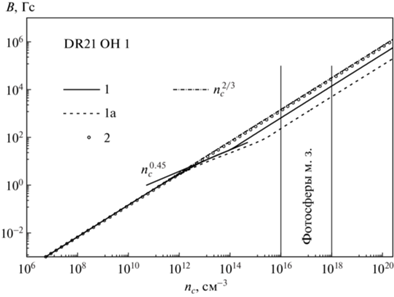
Значения магнитной индукции ${{B}_{{\text{c}}}}$ в центре облака при плотности фотосфер молодых звезд для всех моделей и вариантов собраны в последнем столбце табл. 4. Видно, что ${{B}_{{\text{c}}}}$ варьируется от десятков гаусс до десятков килогаусс и коррелирует с начальным отношением магнитной энергии облака к модулю его гравитационной энергии. В модели W3 (main) поле занижается в 2.6 раза в отсутствие испарения пыли и завышается в 1.5 раза из-за дефицита пыли. В модели NGC 2024, соответственно, в 5 раз и в 4 раза.
Полагая варианты 1 в трех моделях наиболее корректными, получим при плотности фотосфер ${{B}_{{\text{c}}}} = 0.2{\kern 1pt} - {\kern 1pt} 49.7$ кГс, что на полтора порядка величины больше наблюдаемых магнитных полей молодых звезд. Эту нестыковку можно устранить с помощью многомерных моделей коллапса протозвездных облаков, если начинать расчет с достаточно сильным магнитным полем, которое вызывает значительное уплощение облака вдоль поля. Например, Замоздра и Жилкин [37] показали, что переход от одномерных к двумерным моделям привел к снижению ${{B}_{{\text{c}}}}$ на 2 порядка величины в модели W3 (main), на 1.5 порядка величины в модели DR 21 OH1 и на порядок величины в модели NGC 2024, еще до прохождения минимума степени ионизации. В других работах такое сравнение одномерных и двумерных моделей коллапса конкретных протозвездных облаков не выполнялось. Однако более медленный, чем (1), рост магнитного поля с плотностью на начальных стадиях коллапса показывают все многомерные модели, в которых магнитное поле достаточно сильно, чтобы замедлить поперечное сжатие (см., напр., [21, 29–32]).
Поскольку в работах по магнитометрии звезд и околозвездных дисков обычно указывается не плотность вещества, а геометрические характеристики, используем их тоже для проверки теории. На рис. 8 представлены зависимости магнитной индукции от радиальной координаты $B(r)$ в варианте 1 трех моделей, а также в классических звездах типа T Tau (CTTS) [14], аккреционном диске FU Ori [15], оболочках дисков TW Hya [17] и AS 209 [18]. Также показана оценка магнитной индукции в протосолнечной туманности на расстоянии 2 а.е. от Солнца по остаточной намагниченности хондр в LL хондрите Semarkona [16]. Как и в работе [37], ближе всего к точке FU Ori проходит кривая $B(r)$ в модели NGC 2024 с самым слабым начальным полем и самой сильной диффузией, но для прохода через точки CTTS этой кривой необходимо спуститься еще на 1.5 порядка величины. Кривым $B(r)$ в моделях DR 21 OH1 и W3 (main) необходимо спуститься еще ниже: на 2 и 2.5 порядка величины соответственно.
Рис. 8.
Зависимости магнитной индукции от радиальной координаты для варианта 1 трех моделей в сравнении с наблюдательными данными: крестики – классические звезды типа T Tau [14], кружок – внутренняя кромка диска FU Ori [15], окружность – LL хондрит Semarkona [16], стрелки – оболочки дисков TW Hya [17] и AS 209 [18]. Вертикальная штрихпунктирная линия – радиус Солнца.
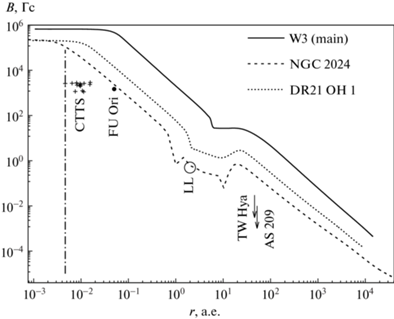
Вероятно, эти различия теории и наблюдений можно почти полностью устранить, перейдя от одномерных к многомерным моделям. Если это снизит остаточное поле на 1–2 порядка величины, как в работе [37], то к данным FU Ori и Semarkona ближе окажется модель DR 21 OH1, а к данным TW Hya и AS 209 – модель NGC 2024.
Заметим, что в [37] не учитывалось химическое распыление графита, поэтому считалось, что он исчезает при $T = 2300$ К. Это приводило к более медленному росту магнитного поля при сжатии среды на расстоянии около 1 а.е. от центра облака. Поэтому на меньших расстояниях кривые $B(r)$ проходили ниже примерно на 50%, чем на рис. 8.
Обратим внимание, что кривые $B(r)$ на рис. 8 имеют локальные минимумы в мертвой зоне ($r \simeq 1{\kern 1pt} - {\kern 1pt} 10$ а.е.), что указывает на формирование магнитного уплотнения (локального максимума) на внешней границе этой зоны. В моделях без испарения пыли это уплотнение более выражено. Вероятно, в трехмерных моделях, учитывающих вращение облака, магнитное уплотнение превращается в магнитную трубку, обнаруженную Вастером и др. [31]. Однако мы предполагаем, что при учете испарения пыли эта трубка не должна быть слишком заметной. Тем не менее такая структура интересна и требует дальнейшего изучения. В отличие от “магнитной стены” из двумерной модели Тассиса и Мусковиаса [62] она создает немонотонную зависимость интенсивности магнитного поля от радиальной координаты.
Наконец отметим, что возможность ослабления магнитного поля в центре облака с ростом плотности [31] наши расчеты не подтверждают, даже в вариантах без испарения пыли. Вероятно, этот эффект вызван ошибками реализации метода сглаженных частиц (SPH) в модели [31], оставшимися от ее предыдущего варианта, в котором не учитывалась диффузия магнитного поля [21]. К такому же выводу приводит сравнение с конкурирующими моделями [30, 32]: в них магнитная индукция в центре облака монотонно растет с плотностью, хотя модель [30] основана на SPH, а модель [32] использует сеточные методы.
4. ВЫВОДЫ
Работа посвящена развитию теории остаточного магнитного поля молодых звезд и их аккреционных дисков, образующихся в процессе коллапса протозвездных облаков. Целью работы была оценка влияния испарения пыли на интенсивность этого поля. Решены две задачи: 1) предложена модель испарения двухслойных пылинок, которая допускает полуаналитическое описание эволюции распределения пылинок по радиусам; 2) модель эволюции пыли встроена в одномерную численную модель коллапса протозвездного облака Дудорова и Сазонова [28, 49] и рассчитана интенсивность остаточного магнитного поля при плотностях и радиусах, характерных для фотосфер молодых звезд и их аккреционных дисков.
В модели предполагалось, что МГД турбулентность в коллапсирующем облаке подавлена магнитной амбиполярной диффузией, поэтому турбулентная диффузия крупномасштабного магнитного поля не рассматривалась. Однако вне мертвых зон в аккреционных дисках молодых звезд МГД турбулентность может генерироваться магнито-ротационной неустойчивостью (см. [20]), и турбулентная диффузия может быть доминирующей.
В отличие от [28] в настоящей работе учтен вклад заряженных пылинок в проводимость плазмы, рассчитана концентрация 11 вместо 2 видов ионов, а изменение интегральных характеристик пыли вычислено через распределение пылинок по радиусам. В отличие от трехмерных моделей [30–32] наша модель не учитывает сплющивание облака вдоль магнитного поля, однако учитывает испарение пыли в кинетике ионизации. В модели [39] внешние слои пылинок (СО и H2O) имеют толщину, которая не зависит от радиусов ядер, поэтому все пылинки лишаются этих слоев одновременно. В нашей модели константой является начальное отношение радиусов ядра и мантии, поэтому более крупные пылинки имеют более толстую мантию и теряют ее позже. Время потери мантии нам удалось найти аналитически.
Модели ионизации в нашей работе и в работах [27, 30–32] сопоставимы по полноте, но значительно уступают специализированным исследованиям ионизационно-химических процессов в протозвездных облаках и дисках (см., напр., [63]). Полнота моделей ионизации наиболее важна в мертвых зонах. Если в них ${{n}_{{\text{n}}}} = {{10}^{{12}}}{\kern 1pt} - {\kern 1pt} {{10}^{{14}}}$ см–3 и $T = 200{\kern 1pt} - {\kern 1pt} 1300$ К, то помимо рассмотренных нами ионов металлов и H$_{3}^{ + }$ в этих зонах могут быть значимы ионы HCO+ и H3O+ (см., напр., [53]). Однако их учет не должен сильно изменить диффузию магнитного поля, поскольку в мертвых зонах она определяется движением мелких заряженных пылинок [53]. Этот вывод подтверждается близостью интенсивностей остаточного поля в данной работе и в работе [37], где вместо иона ${\text{H}}_{3}^{ + }$ рассматривался ион HCO+.
Основные результаты работы таковы.
1. Средние значения радиуса, площади поперечного сечения и массы пылинок на этапе исчезновения ядер достигают максимумов, но на взаимодействие пыли с частицами газа это не влияет, поскольку пыли становится мало.
2. На этапе десорбции металлов из пылинок основными ионами являются Na+, Mg+, Al+, Si+, K+.
3. Пренебрежение испарением пыли расширяет зону сильной диффузии магнитного поля (мертвую зону), но сохраняет характерное расстояние 1–10 а.е. от этой зоны до центра облака.
4. Пренебрежение испарением пыли занижает остаточное магнитное поле молодых звезд и их аккреционных дисков в несколько раз.
5. Возможность ослабления магнитного поля в протозвезде с ростом плотности [31] не подтвердилась, но образование магнитного уплотнения на внешней границе мертвой зоны подтверждено.
6. Сочетание корректных расчетов эволюции пыли, анизотропии коллапса и диффузии магнитного поля позволяет согласовать теорию остаточного поля молодых звезд и их аккреционных дисков с наблюдениями.
Отметим, что полученное нами превышение рассчитанного поля над наблюдаемым не критично для теории остаточного поля молодых звезд, поскольку она учитывает ослабление поля за счет диссипативных процессов на стадии медленного сжатия этих звезд. Тейлер [64] предположил, что высокая поверхностная активность молодых звезд вызвана диссипацией энергии сильного остаточного поля, которое постепенно спадает до уровня насыщения динамо и заменяется динамо-полем. С помощью одномерных расчетов остаточного поля и порядковых оценок динамо-поля Дудоров [65] показал, что внутри и на поверхности звезд типа Т Тельца остаточное поле на порядок величины и более превышает уровень насыщения динамо. Строгих моделей перехода от сильного остаточного поля к слабому динамо-полю пока нет, однако появились наблюдательные подтверждения этого процесса: обнаружена обратная корреляция магнитного поля и возраста звезд солнечного типа [66]. Вместе с этим найдена слабая корреляция магнитного поля и возраста Ae/Be звезд Хербига [12], что может быть признаком динамо в зонах лучистого переноса таких звезд [2].
Далее мы планируем встроить полуаналитические модели испарения пыли в двумерную модель коллапса протозвездного облака, реализованную в программе Enlil. Также планируется увеличить количество слоев в моделях пылинок и детально учесть их распределение по радиусам в расчете проводимости плазмы.
Список литературы
A. E. Dudorov and S. A. Khaibrakhmanov, in Stars: From Collapse to Collapse, Proc. of a conference held at Special Astrophysical Observatory, Nizhny Arkhyz, Russia 3–7 October 2016. Edited by Yu. Yu. Balega, D. O. Kudryavtsev, I. I. Romanyuk, and I. A. Yakunin (San Francisco: Astronomical Society of the Pacific, 2017), p. 114.
J. Braithwaite and H. Spruit, Roy. Society Open Science 4, id. 160271 (2017).
A. S. Brun and M. K. Browning, Liv. Rev. Solar Physics 14, id. 4 (2017).
B. B. Karak, M. Rheinhardt, A. Brandenburg, P. J. Kapyla, and M. J. Kapyla, Astrophys. J. 795, id. 16 (2014).
A. S. Jermyn and M. Cantiello, Astrophys. J. 900, id. 113 (2020).
D. Moss, Astron. and Astrophys. 414, 1065 (2004).
N. A. Featherstone, M. K. Browning, A. S. Brun, and J. Toomre, Astrophys. J. 705, 1000 (2009).
Д. А. Франк-Каменецкий, Лекции по физике плазмы (М.: Атомиздат, 1968).
L. E. Cram, Astrophys. J. 234, 949 (1979).
R. M. Crutcher, Astrophys. J. 520, 706 (1999).
A. E. Dudorov, S. A. Khaibrakhmanov, and A. M. So-bolev, Monthly Not. Roy. Astron. Soc. 487, 5388 (2019).
А. Ф. Холтыгин, О. А. Циопа, E. И. Макаренко, И. М. Туманова, Астрофиз. бюлл. 74, 313 (2019).
F. Villebrun, E. Alecian, G. Hussain, J. Bouvier, et al., Astron. and Astrophys. 622, id. A72 (2019).
C. M. Johns-Krull, Astrophys. J. 664, 975 (2007).
J.-F. Donati, F. Paletou, J. Bouvier, and J. Ferreira, Nature 438, 466 (2005).
J. F. J. Bryson, B. P. Weiss, J. B. Biersteker, A. J. King, and S. S. Russell, Astrophys. J. 896, id. 103 (2020).
W. H. T. Vlemmings, B. Lankhaar, P. Cazzoletti, C. Ceccobello, et al., Astron. and Astrophys. 624, id. L7 (2019).
R. E. Harrison, L. W. Looney, I. W. Stephens, Z.-Y. Li, et al., Astrophys. J. 908, id. 141 (2021).
S. M. Houghton and P. J. Bushby, Monthly Not. Roy. Astron. Soc. 412, 555 (2011).
Y. Kawasaki, S. Koga, and M. N. Machida, Monthly Not. Roy. Astron. Soc. 504, 5588 (2021).
M. R. Bate, T. S. Tricco, and D. J. Price, Monthly Not. Roy. Astron. Soc. 437, 77 (2014).
A. Bhandare, R. Kuiper, T. Henning, C. Fendt, M. Flock, and G.-D. Marleau, Astron. and Astrophys. 638, id. A86 (2020).
G. Wuchterl and W. M. Tscharnuter, Astron. and Astrophys. 398, 1081 (2003).
G. A. Feiden and B. Chaboyer, Astrophys. J. 761, 30 (2012).
A. Hujeirat, P. Myers, M. Camenzind, and A. Burkert, New Astronomy 4, 601 (2000).
С. Н. Замоздра, МГД волны в протозвездных облаках, диссертация … кандидата физ.-мат. наук (Челябинск, 2010).
R. Mignon-Risse, M. Gonzalez, B. Commercon, and J. Rosdahl, Astron. and Astrophys. 652, id. A69 (2021).
А. Е. Дудоров, Ю. В. Сазонов, Научные информации астрон. совета АН СССР 63, 68 (1987).
M. W. Kunz and T. C. Mouschovias, Monthly Not. Roy. Astron. Soc. 408, 322 (2010).
Y. Tsukamoto, K. Iwasaki, S. Okuzumi, M. N. Machida, and S. Inutsuka, Monthly Not. Roy. Astron. Soc. 452, 278 (2015).
J. Wurster, M. R. Bate, and D. J. Price, Monthly Not. Roy. Astron. Soc. 481, 2450 (2018).
N. Vaytet, B. Commercon, J. Masson, M. Gonzalez, and G. Chabrier, Astron. and Astrophys. 615, id. A5 (2018).
G. Morfill, S. Roeser, H. Voelk, and W. Tscharnuter, Moon and Planets 19, 211 (1978).
V. Guillet, P. Hennebelle, G. P. des Forets, A. Marcowith, B. Commercon, and P. Marchand, Astron. and Astrophys. 643, id. A17 (2020).
P. Lenzuni, H.-P. Gail, and T. Henning, Astrophys. J. 447, 848 (1995).
W. J. Duschl, H.-P. Gail, and W. M. Tscharnuter, Astron. and Astrophys. 312, 624 (1996).
S. N. Zamozdra and A. G. Zhilkin, Astron. Astrophys. Trans. 27, 517 (2012).
P. Marchand, J. Masson, G. Chabrier, P. Hennebelle, B. Commercon, and N. Vaytet, Astron. and Astrophys. 592, id. A18 (2016).
I. Bauer, F. Finocchi, W. J. Duschl, H.-P. Gail, and J. P. Schloder, Astron. and Astrophys. 317, 273 (1997).
K. Lodders, Space Sci. Rev. 217, id. 44 (2021).
M. Pontoppidan, C. Salyk, E. A. Bergin, S. Brittain, B. Mar-ty, O. Mousis, and K. I. Oberg, Protostars and Planets VI, 363 (2014), https://hal.archives-ouvertes.fr/hal-01346297.
Я. Н. Павлюченков, А. Г. Жилкин, Э. И. Воробьев, А. М. Фатеева, Астрон. журн. 92, 154 (2015).
H. W. Yorke, Astron. and Astrophys. 80, 308 (1979).
Y. V. Skorov, L. Rezac, P. Hartogh, and H. U. Keller, A-stron. and Astrophys. 600, id. A142 (2017).
F. P. Fanale and J. R. Salvail, Icarus 60, 476 (1984).
T. Nakano, R. Nishi, and T. Umebayashi, Astrophys. J. 573, 199 (2002).
Л. Спитцер, Физические процессы в межзвездной среде (М.: Мир, 1981).
И. С. Григорьев, Е. З. Мейлихов, Физические величины: справочник (М.: Энергоатомиздат, 1991).
А. Е. Дудоров, Ю. В. Сазонов, Научные информации астрон. совета АН СССР 49, 114 (1981).
H. Masunaga and S. Inutsuka, Astrophys. J. 531, 350 (2000).
J. B. Pollack, D. Hollenbach, S. Beckwith, D. P. Simonelli, T. Roush, and W. Fong, Astrophys. J. 421, 615 (1994).
V. I. Shematovich, D. S. Wiebe, B. M. Shustov, and Z.‑Y. Li, Astrophys. J. 588, 894 (2003).
B. Zhao, P. Caselli, and Z.-Y. Li, Monthly Not. Roy. A-stron. Soc. 478, 2723 (2018).
W. R. Webber, Astrophys. J. 506, 329 (1998).
F. Finocchi and H.-P. Gail, Astron. and Astrophys. 327, 825 (1997).
M. W. Kunz and T. C. Mouschovias, Astrophys. J. 693, 1895 (2009).
D. McElroy, C. Walsh, A. J. Markwick, M. A. Cordiner, K. Smith, and T. J. Millar, Astron. and Astrophys. 550, id. A36 (2013).
Я. Б. Зельдович, Ю. П. Райзер, Физика ударных волн и высокотемпературных гидродинамических явлений (М.: Наука, 1966).
К. У. Аллен, Астрофизические величины (М.: Мир, 1977).
C. Yang, M. MacLow, and A. Johansen, Astrophys. J. 868, id. 27 (2018).
W. Lyra, A. Johansen, A. Zsom, H. Klahr, and N. Piskunov, Astron. and Astrophys. 497, 869 (2009).
K. Tassis and T. C. Mouschovias, Astrophys. J. 618, 783 (2005).
D. Semenov and D. Wiebe, Astrophys. J. Suppl. 196, id. 25 (2011).
R. J. Tayler, Monthly Not. Roy. Astron. Soc. 227, 553 (1987).
А.Е. Дудоров, Астрон. журн. 72, 884 (1995).
C. P. Folsom, P. Petit, J. Bouvier, A. Lebre, et al., Monthly Not. Roy. Astron. Soc. 457, 580 (2016).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал