Акустический журнал, 2023, T. 69, № 2, стр. 129-145

2.1. Постановка задачи

Пусть существует двумерная треугольная решетка S, в которой каждый узел определяется парой чисел $m \times n$, где $m,n \in \mathbb{Z}$. Введем координатные оси, как показано на рис. 2. Угол между осями составляет ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$, как показано на рисунке. Зададим на S функцию $u(m,n)$, которая удовлетворяет уравнению Гельмгольца с возмущением в точке $(0,0)$:

где ${{\delta }_{{m,0}}},\,\,{{\delta }_{{n,0}}}$ – символ Кронекера, а дискретный оператор Лапласа ${{\Delta }_{S}}$ на треугольной сетке [19] задан следующим образом:

Уравнение (1) является аналогом непрерывного уравнения Гельмгольца на плоскости

$k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$ – волновое число. Для данного уравнения известно точное аналитическое решение, которое носит название функции Грина [24]: где $H_{0}^{{(1)}}$ – функция Ханкеля первого рода, $r = \sqrt {{{x}^{2}} + {{y}^{2}}} $.

Нетрудно проверить, что при шаге сетки $h$ существует связь между волновым числом $k$ и параметром $K$:

Важной частью постановки задачи математической физики является формулировка условий излучения – аналитических условий, выделяющих единственное решение. Наиболее популярными из них являются условия излучения Зоммерфельда [25], имеющие два представления: дифференциальное и интегральное. В нашем же случае наиболее простым в применении условием излучения является принцип предельного поглощения [26]. Согласно данному принципу, решение в среде без поглощения можно представить в виде предела ограниченного решения в поглощающей среде при стремлении поглощения к нулю. В соответствии с принципом предельного поглощения, пусть $K = {{K}_{1}} + i{{K}_{2}}$, где ${{K}_{1}},{{K}_{2}} \in \mathbb{R}$ и ${{K}_{2}} > 0$, и пусть поле $u(m,n)$ затухает экспоненциально при

После получения ограниченного решения в поглощающей среде получим решение для среды без затухания, устремляя ${{K}_{2}}$ к нулю.

Задачей данного раздела будет нахождение точного решения уравнения (1) и сравнение этого решения с (4).

2.2. Представление поля в виде двойного интеграла

Выпишем пару (прямое и обратное) преобразований Фурье для функции $u(m,n)$:

Для решения уравнения (1) мы воспользуемся прямым преобразованием Фурье. После применения (6) к (1) получаем:

где

Выпишем представление поля в виде прямого преобразования Фурье (7) с учетом решения (8):

Для алгебраизации нашей задачи введем следующую замену переменных:

При этом будем считать, что $x,y \in \mathbb{C}$. В новых переменных выражение $D({{\xi }_{1}},{{\xi }_{2}})$ приобретает вид:

а представление поля в переменных $(x,y)$ будет выглядеть так: где контур $\sigma $ – это единичная окружность с положительным направлением обхода (против часовой стрелки), рис. 3. Обратим внимание, что (13) является представлением функции Грина в виде двойного интеграла от мероморфной функции.

Плоской волной на решетке S будем называть выражение

если $x$ и $y$ подчиняются уравнению

Будем называть уравнение (15) дисперсионным уравнением, так как нетрудно проверить, что если оно выполнено, то плоская волна ${{x}^{m}}{{y}^{n}}$ автоматически удовлетворяет однородному уравнению Гельмгольца:

и, как следствие, может распространяться по сетке S. Обратим внимание, что решением уравнения (15) являются комплексные пары чисел, в общем случае по модулю не равные единице. Поэтому волны такого типа могут иметь затухание.

2.3. Снятие интегрирования по одной переменной

Рассмотрим знаменатель двойного интеграла (13). Заметим, что он обращается в ноль, когда $(x,y)$ удовлетворяют дисперсионному уравнению (12). Дисперсионное уравнение является квадратным уравнением по переменной $x$ при фиксированном $y$ и наоборот. Следовательно, (13) имеет в общем случае два комплексных корня. Найдем решение (12) как функцию $y(x)$. Обозначим это решение как $\Xi (x)$:

Квадратный корень является двузначной функцией. Обозначения $\Xi {{(x)}_{ + }}$ и $\Xi {{(x)}_{ - }}$ выбраны таким образом, чтобы:

Следует также отметить, что данные корни связаны друг с другом соотношением

что также свидетельствует о наличии симметрии отражения, описанной в предыдущем пункте.

Таким образом, интеграл (13) может быть рассмотрен как повторный интеграл по одной из переменных. Его подынтегральное выражение в общем случае имеет два полюса первого порядка. Следовательно, мы можем воспользоваться теорией вычетов для однократного взятия интеграла. При этом, выбор переменной интегрирования ($x$ или $y$) будет зависеть от координаты точки на S: $(m,n)$. Как будет показано ниже, процедура взятия интеграла зависит от положения точки наблюдения относительно оси координат (при переходе из одной полуплоскости относительно оси в другую, подынтегральное выражение меняет набор полюсов). Кроме осей, соответствующих координатам $m$ и $n$, существует еще одна прямая ($m = - n$), которая разделяет плоскость на две полуплоскости, в которых подынтегральное выражение ведет себя аналогично первым двум случаям. Таким образом, возможны шесть различных случаев.

Случай 1: $n \geqslant 0$

В данном случае числитель подынтегрального выражения в (13) гарантированно является аналитической функцией по переменной $y$ внутри контура $\sigma $. По этой причине мы можем применить теорию вычетов к интегралу по переменной $y$. Так как $\left| x \right| = 1$ (контур интегрирования по $x$ – это единичная окружность) и выполняется (18), то

Следовательно, два полюса подынтегральной функции (13) располагаются по разные стороны от контура интегрирования $\sigma $, рис 3.

Таким образом, внутри контура интегрирования оказывается лишь точка ${{\Xi }_{ + }}(x)$, в которой мы и берем вычет:

Учитывая, что

получаем представление поля в виде интеграла по переменной $x$:

Случай 2: $n \leqslant 0$

При $n < 0$ числитель подынтегрального выражения в (13) уже не является аналитической функцией. В этом случае подынтегральное выражение получает еще один полюс в точке $y = 0$ внутри контура σ.

Воспользуемся известной теоремой из ТФКП: если функция аналитична на полной комплексной плоскости за исключением конечного числа полюсов, включая $\infty $, то сумма вычетов во всех полюсах равна нулю. Поэтому сумма вычетов внутри σ равна вычету снаружи контура с обратным знаком:

Случай 3: $m \geqslant 0$

Повторяем процедуру, описанную в случае 1, для взятия интеграла по $x$:

Случай 4: $m \leqslant 0$

Повторяем процедуру, описанную в случае 2, для взятия интеграла по $x$:

Введем замену переменных, которая поможет нам найти вид двух оставшихся представлений:

Новая координата $t$ соответствует координатной оси $m = - n$ на S, рис. 4. Перепишем интеграл (13) с использованием новой координаты $t$:

Случай 5: $m + n \geqslant 0$

Нетрудно убедиться, что если произвести взятие интеграла (25) по переменной $x$, а затем совершить обратную замену переменных ($y \to t$), то полученный результат будет иметь вид:

Случай 6: $m + n \leqslant 0$

Аналогично случаю 5, получаем представление поля для данной области:

Таким образом, мы получили шесть различных представлений (21)–(27) функции Грина для уравнения Гельмгольца на треугольной решетке S. Каждое такое представление описывает поле в соответствующем секторе S, секторы для разных представлений могут пересекаться. На данном этапе задачу можно считать решенной, однако, оказывается, что решения (21)–(27) могут быть сведены к единственному контурному интегралу по комплексному многообразию.

2.4. Представление поля в виде интеграла по комплексному многообразию

Проанализируем интеграл (21). Будем считать, что $x$ и $y$ — комплексные переменные на своих сферах Римана $\bar {\mathbb{C}}$. Так, точка $(x,y)$ лежит на $\bar {\mathbb{C}} \times \bar {\mathbb{C}}$. Определим набор точек $(x,y)$, на котором удовлетворяется (12).

Пусть существует множество точек H, состоящее из всех пар значений $(x,y)$, которые являются решением уравнения (12). Поскольку (12) является дисперсионным уравнением для нашей сетки, будем называть ${\mathbf{H}}$ дисперсионной поверхностью. Пара комплексных точек $(x,y)$ имеет четыре действительных степени свободы, а дисперсионное уравнение можно рассматривать как пару действительных уравнений (действительную и мнимую часть). Таким образом, множество точек H имеет действительную размерность 2 (и комплексную размерность 1), а значит, является поверхностью.

Рассмотрим риманову поверхность $R$ функции $\Xi (x)$, которая является проекцией ${\mathbf{H}}$ на $x$. Зададим отображение $\zeta $: ${\mathbf{H}} \to {\mathbf{R}}$ (проекция на переменную $x$). Также нас будет интересовать обратное отображение ${{\zeta }^{{ - 1}}}:{\mathbf{R}} \to {\mathbf{H}}$, имеющее вид:

$\zeta $ является гомеоморфизмом поверхностей, следовательно, H и R топологически эквивалентны. Рассмотрим подробнее структуру римановой поверхности R, а затем, пользуясь гомеоморфизмом поверхностей R и H, перейдем к изучению H.

Риманова поверхность R состоит из двух листов, так как ветвление обусловлено квадратным корнем, который является двузначной функцией. Назовем их физическим (содержащим контур интегрирования $\sigma $) и не-физическим соответственно. Функция $\Xi (x)$ имеет четыре точки ветвления. Найдем их, приравнивая к нулю подкоренное выражение в (17):

Получаем:

где

Непосредственной проверкой установим, что часть подынтегрального выражения в (21), обозначим ее $\Upsilon (x)$, может быть переписана с использованием точек ветвления. Для $y = \Xi (x)$:

Перечислим все особенности подынтегрального выражения (21), которые имеются на ${\mathbf{R}}$. Будем обозначать точки на римановой поверхности парой чисел $({{x}_{*}},\Xi ({{x}_{*}}))$. Такое обозначение однозначно определяет положение точки на римановой поверхности. На листах ${\mathbf{R}}$ располагаются четыре точки ветвления $B(x,\Xi (x))$:

и шесть точек, в которых $x$ или $y = \Xi (x)$ равны $0$ или $\infty $ (назовем их бесконечностями):

Бесконечности ${{J}_{1}},\;...,\;{{J}_{6}}$ имеют смысл особых точек выражения ${{x}^{m}}{{y}^{n}}$, которое является множителем подынтегрального выражения (21). Так как координаты $m$ и $n$ могут быть как больше, так и меньше нуля, то, очевидно, точки ${{J}_{1}},\;...,\;{{J}_{6}}$ являются особыми точками такого выражения, и, соответственно, полюсами подынтегрального выражения (21). По этой причине, бесконечности стоит рассматривать отдельно.

Четыре точки ветвления ${{B}_{1}},\;...,\;{{B}_{4}}$ на R попарно соединены разрезами, на каждом листе находится по три точки бесконечности. Схема римановой поверхности R показана на рис. 5а.

Вернемся к рассмотрению H. Заменим листы в R на сферы Римана. Аналогично листам R на каждой сфере располагаются две точки ветвления, попарно соединенные разрезами. Склейка берегов разрезов повторяет аналогичную в R. Следовательно, H можно представить в виде пары сфер Римана, соединенных друг с другом двумя “перешейками” (рис. 5б). Предположим, что наши сферы Римана сделаны из эластичного материала, что позволит нам непрерывно деформировать их. Нетрудно видеть, что данная конструкция может быть деформирована в тор (рис. 5в).

Задание локальных координат на многообразии не является однозначным. К примеру, система локальных координат и соответствующих окрестностей на H может быть задана следующим образом:

• $x$ для всех точек за исключением точек ветвления ${{B}_{1}},...,{{B}_{4}}$ и бесконечностей ${{J}_{4}}$ и ${{J}_{5}}$;

• $y$ для точек ветвления ${{B}_{1}},...,{{B}_{4}}$;

• $\frac{1}{x}$ для бесконечностей ${{J}_{4}}$ и ${{J}_{5}}$.

Такая система окрестностей и локальных переменных будет удобна для нас далее. Легко проверить, что в области пересечения любой пары окрестностей выполнено условие биголоморфности, а значит, H является комплексным многообразием.

2.5. Представление поля в инвариантном виде

На данном этапе работы поле $u(m,n)$ описывается шестью разными представлениями в различных областях (21)–(27). Введенные выше понятия позволят нам перейти к инвариантному представлению в виде единственного интеграла, который опишет поле на всей поверхности S.

Определим на H дифференциальную 1-форму:

Заметим, что $\psi $ – часть подынтегрального выражения в (21). Докажем, что дифференциальная форма $\psi $ аналитична на комплексном многообразии ${\mathbf{H}}$. Это тривиальная задача всюду за исключением бесконечностей ${{J}_{1}},...,{{J}_{6}}$ и точек ветвления ${{B}_{1}},...,{{B}_{4}}$, определенных ранее.

Начнем с бесконечностей. Легко показать, что в точках ${{J}_{1}}$ и ${{J}_{2}}$ знаменатель (30) не обращается в ноль, а в точках ${{J}_{3}}$ и ${{J}_{4}}$ дифференциальная форма $\psi $ ведет себя как $ \sim {{x}^{{ - 2}}}$ при $x \to 0$. Замена переменной $x \to \tau = \frac{1}{x}$ показывает регулярность формы. Для окрестностей точек ${{J}_{5}}$ и ${{J}_{6}}$ произведем замену переменных $x \to \varepsilon = \frac{1}{x} + 1$. Такая замена переменной обеспечивает аналитичность формы в данных окрестностях.

Перейдем к рассмотрению окрестностей точек ветвления ${{B}_{1}},...,{{B}_{4}}$. Для них в качестве локальной переменной мы можем выбрать введенную ранее переменную $y$. По теореме о неявной функции:

везде на H. Получаем, что:

Знаменатель правой части (32) не обращается в ноль в окрестностях ${{B}_{1}},...,{{B}_{4}}$. Таким образом, мы доказали, что данная 1-форма аналитична.

Формула (32) устанавливает связь между представлениями (21), (22) и (23). Представление (21) переходит в (22) при переходе с физического листа R на не-физический, это же справедливо и для пар (23)–(24) и (26)–(27). Это значит, что поле на всей поверхности S для любой координаты $(m,n)$ можно описать при помощи единственного интеграла по одной переменной, подставляя для различных частей плоскости различные контуры интегрирования. Обозначим контуры интегрирования, которые переводят представление (21) в представления (23), (24), (26), (27) как ${{\sigma }_{2}}$, ${{\sigma }_{3}}$, ${{\sigma }_{4}}$, ${{\sigma }_{5}}$ и ${{\sigma }_{6}}$ соответственно. Контур $\sigma $ переобозначим как ${{\sigma }_{1}}$. Расположение семейства таких контуров на R показано на рис. 6, а на рис. 7 изображены те же контуры на H.

Как было показано выше, представления поля $u(m,n)$ в виде (21)–(27) могут быть записаны в виде единственного контурного интеграла с различными контурами интегрирования, соответствующими различным областям S. Выпишем данное представление:

где ${{\Psi }_{{m,n}}} = \frac{3}{{4\pi i}}{{x}^{m}}{{y}^{n}}\psi $ – дифференциальная форма, которая, однако, аналитична всюду на H только при $m = n = 0$. Во всех остальных случаях она имеет полюсы в точках бесконечностей. Вычислим условие регулярности формы ${{\Psi }_{{m,n}}}$ для каждой точки ${{J}_{1}},...,{{J}_{6}}$:

Пользуясь условием теоремы Коши для интеграла (33), мы можем деформировать контуры интегрирования в областях, где выполнены условия регулярности формы ${{\Psi }_{{m,n}}}$. Можно заметить, что контуры ${{\sigma }_{1}},...,{{\sigma }_{6}}$ могут быть продеформированы друг в друга в порядке ${{\sigma }_{1}} \to {{\sigma }_{1}},..., \to {{\sigma }_{6}}$ при движении точки наблюдения $(m,n)$ в направлении против часовой стрелки начиная с точки $({{m}_{0}},{{n}_{0}})$, где ${{m}_{0}} > 0$, ${{n}_{0}} > 0$. Или, другими словами, перенос контуров в положительном направлении по тору соответствует перемещению точки наблюдения в плоскости $(m,n)$ против часовой стрелки (в положительном направлении).

2.6. Исследование функции Грина

Произведем численное интегрирование представления (21) функции Грина для треугольной решетки. В качестве контура интегрирования построим единичную окружность на физическом листе Римановой поверхности R. Обход особой точки –1 осуществим при помощи построения вспомогательной полуокружности малого радиуса с центром в точке –1. Обход контура произведем в положительном направлении.

Представление (21) справедливо лишь в полуплоскости $n \geqslant 0$, однако, мы можем получить поле на всей плоскости, воспользовавшись симметрией задачи. Для этого достаточно построить поле в области $n \geqslant 0$, $m \geqslant 0$ и с помощью поворота данного сегмента поля на ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ получить поле на всей плоскости. Интегрирование производится методом трапеций.

Так как в нашем случае шаг сетки $h$ равен единице, выберем для простоты длину волны $\lambda = \pi $. Тогда:

Произведем интегрирование (21) по контуру $\sigma $ при $K = 2$. В данном случае, на одну длину волны приходится около трех точек решетки по каждой из осей. График действительной части поля $u(m,n)$ показан на рис. 8. Увеличим длину волны в 10 раз. Пусть теперь $\lambda = 10\pi $, следовательно, $K = 0.2$. Повторим процедуру для данного значения $K$ и построим аналогичный график, рис. 9. Видно, что в первом случае наблюдается анизотропия, вызванная параметрами решетки. Однако, на втором графике мы видим уже гораздо более изотропную функцию.

Проанализируем поведение поля функции Грина в дальнем поле с помощью метода седловой точки и построим диаграммы направленности для различных $K$. Пусть существует некоторый параметр $N \in \mathbb{Z}$, причем $N \to \infty $. Найдем асимптотику функции $u(mN,nN)$, описываемую интегралом (21). Заметим, что плоская волна (часть подынтегрального выражения в (21)) может быть переписана в виде:

Пользуясь видом (35), найдем выражение для нахождения седловой точки ${{x}_{s}}$:

Решение уравнения (36) может быть найдено численно при помощи метода Ньютона. После нахождения седловой точки ${{x}_{s}}$ мы можем найти асимптотическое представление (21) в приближении дальнего поля:

где ${{y}_{s}} = y({{x}_{s}})$.

3.1. Постановка задачи

Пусть поле $u(m,n)$ удовлетворяет однородному уравнению Гельмгольца на всей треугольной сетке S, за исключением линии $n = 0$, $m \geqslant 0$. Пусть на этой линии задано граничное условие Дирихле (рис. 10):

Пусть на препятствие падает плоская волна, имеющая вид:

где

Введем параметр

где, для удобства, введено обозначение

Параметр ${{\phi }_{{{\text{in}}}}}$ играет роль угла распространения падающей волны. Положим ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2} < {{\phi }_{{{\text{in}}}}} < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$.

Введем понятие рассеянного поля ${{u}_{{{\text{sc}}}}}$ как разность между полным полем $u(m,n)$ и падающей волной ${{u}_{{{\text{in}}}}}(m,n)$:

Рассеянное поле должно удовлетворять принципу предельного поглощения, т.е. ${{u}_{{{\text{sc}}}}}(m,n) \to 0$ при $r = \sqrt {{{m}^{2}} + {{n}^{2}} + mn} \to \infty $.

3.2. Построение разветвленной поверхности S₂

Для преобразования задачи воспользуемся методом Зоммерфельда [1]. Для этого “разрежем” физический лист поверхности S по полупрямой $n = 0$, $m > 0$. Далее, возьмем копию листа (S') и склеим их так, как показано на рис. 11. Стороны, помеченные одной римской цифрой, склеены между собой. Получившуюся разветвленную поверхность будем называть S₂.

Зададим функцию $\tilde {u}(m,n)$, которая будет описывать поле на всей поверхности S₂, и докажем, что данная функция удовлетворяет уравнению Гельмгольца везде на S₂ за исключением точки $m = 0$, $n = 0$. Кроме того, покажем, что условие Дирихле выполнено на полупрямой $n = 0$, $m \geqslant 0$.

Для начала, перейдем в полярную систему координат, которая будет более удобна для дальнейшего описания. Так как наша система координат не ортогональна, преобразование координат имеет не совсем привычный вид:

Очевидно, что пара координат $(r,\phi )$ также является дискретной и взаимно однозначно соответствует $(m,n)$.

Пусть $u(m,n)$ – функция, удовлетворяющая однородному уравнению Гельмгольца на S. Определим функцию $\tilde {u}(m,n)$, которая описывает поле на S₂, следующим образом:

Докажем, что $\tilde {u}(m,n)$, заданная таким образом, удовлетворяет уравнению Гельмгольца на всей поверхности S₂ за исключением точки $(0,0)$. На каждом листе поверхности $\tilde {u}(m,n)$ удовлетворяет уравнению, так как этому же уравнению по условию удовлетворяет функция $u(m,n)$. Таким образом, остается исследовать лишь полупрямую $n = 0$, $m \geqslant 0$. На этой полупрямой оператор Лапласа имеет вид:

Замечаем, что $\tilde {u}(m,n) = - \tilde {u}(m, - n)$ и $\tilde {u}(m,0) = 0$ по определению $\tilde {u}$. Тогда

На поверхности S₂ уже не одна, а две падающих волны, рис. 11. Это волны с направлением волнового вектора $\phi = {{\phi }_{{{\text{in}}}}}$ на S и $\phi = 4\pi - {{\phi }_{{{\text{in}}}}}$ на S'. Каждая из этих волн имеет свою область видимости, которая задается неравенством

Сформулируем дифракционную задачу на разветвленной поверхности S₂:

Найти поле $\tilde {u}$, определенное на S₂, которое удовлетворяет однородному уравнению Гельмгольца на S₂ и равно нулю в начале системы координат $(0,0)$. Рассеянное поле, определяемое разностью $\tilde {u} - {{\tilde {u}}_{{{\text{in}}}}}$ для падающих волн в пределах их областей видимости ${{\phi }_{{{\text{vis}}}}}$, должно экспоненциально затухать при $r \to \infty $.

Главное преимущество такого подхода заключается в отсутствии на разветвленной поверхности рассеивателя. Если поле удовлетворяет поставленной задаче, то условие Дирихле на заданной полупрямой выполняется автоматически.

3.3. Построение интеграла Зоммерфельда

При решении задачи нахождения функции Грина для треугольной решетки было показано, что один обход в положительном направлении по сетке S ($\phi :$ $0 \to 2\pi $) соответствует одному обходу тора H вдоль одной из его направляющих. В случае с S₂ полный обход точки наблюдения состоит из обхода по S ($\phi :$ $0 \to 2\pi $) и затем обхода по S' ($\phi :$ $2\pi \to 4\pi $). Напомним, что $u(r,0) = u(r,4\pi )$. Таким образом, полный обход точки наблюдения по S₂ ($\phi :$ $0 \to 4\pi $) соответствует обходу тора H ($\phi :$ $0 \to 2\pi $), а затем его копии, H' ($\phi :$ $2\pi \to 4\pi $). Поверхность, состоящая из H и H' и соединенная, как показано на рис. 12а, называется двойным накрытием тора, будем обозначать ее H₂. Проекция H₂ на переменную $x$ (риманова поверхность R₂) будет иметь четыре листа, рис. 12б. Такая Риманова поверхность называется абстрактной, так как на данный момент мы не знаем, существует ли такая функция, которая бы определяла R₂ [27]. Далее мы покажем, что такая функция существует и найдем ее. Многообразие H₂ топологически также является тором. Накрытие H₂ имеет 12 точек бесконечности $({{J}_{1}},...,{{J}_{6}},J_{1}^{'},...,J_{6}^{'})$, которые являются прообразами $x = 1,\;x = - 1,\;x = \infty $.

Такой подход является расширением метода А. Зоммерфельда [1], который в своей работе поставил в соответствие разветвленной поверхности распространения волн удвоенную по периоду частотную поверхность. В работе [20] проделана аналогичная процедура для квадратной решетки и показано, что построенная в таком виде поверхность H₂ действительно является дисперсионной поверхностью задачи.

Обобщая метод А. Зоммерфельда [1], будем искать поле $\tilde {u}(m,n)$ в следующем виде:

где $\Upsilon (x)$ задается выражением (29), $A(\tilde {x})$ – трансформанта Зоммерфельда, которая будет найдена позднее. Отметим, что трансформанта является мероморфной функцией на H₂ и может иметь полюс только в точке, соответствующей падающей или отраженной волне. ${{\Gamma }_{i}}$ – система контуров Зоммерфельда. В оригинальной работе определено бесконечное множество контуров интегрирования. Ниже мы покажем, что для нашей задачи хорошо работает дискретный набор контуров интегрирования.

Контуры Зоммерфельда должны удовлетворять следующим требованиям:

1. Для любой точки $(m,n) \in {{{\mathbf{S}}}_{2}}$ должен существовать контур ${{\Gamma }_{i}}$, который бы давал правильный интеграл (49), описывающий поле в точке $(m,n)$ и в шести ее соседях.

2. Если существуют два контура ${{\Gamma }_{i}}$ и ${{\Gamma }_{j}}$, которые описывают поле в точке $(m,n)$, то контуры должны деформироваться друг в друга без прохождения сингулярностей подынтегрального выражения в (49).

Построим “диаграмму аналитичности” бесконечностей, которая поможет нам правильно определить систему контуров для интеграла (49), рис. 13а. Такая диаграмма показывает, при каких углах наблюдения $\phi $ определенная точка бесконечности является полюсом подынтегрального выражения в (49): серым цветом выделены области, в которых точки аналитичны, красным – области, в которых точки являются полюсами. Введем обозначение

Так мы будем обозначать контур, который обходит перечисленные бесконечности. К примеру, на рис. 13б и 14 показано, как выглядит контур $\Gamma = {{J}_{6}}$ + $J_{5}^{'}$ + $J_{4}^{'}$ + $J_{3}^{'}$ + $J_{2}^{'}$ + $J_{1}^{'}$ на H₂ и R₂ соответственно. Выберем контуры интегрирования так, чтобы внутри контура находилось шесть бесконечностей, три из которых являются аналитичными в заданной области. Пользуясь “диаграммой аналитичности”, мы можем определить набор контуров так, чтобы контуры попарно могли бы переходить один в другой в пересечении их областей применимости. Таким образом, мы получим инвариантное представление поля при всех интересующих нас углах наблюдения $\phi $. Ограничимся рассмотрением физической области, т.е. $0 < \phi < 2\pi $. Выпишем набор контуров интегрирования, с помощью которого может быть описано поле $u(m,n)$ в физической области:

• ${{\Gamma }_{1}} = {{J}_{6}}$ + $J_{5}^{'}$ + $J_{4}^{'}$ + $J_{3}^{'}$ + $J_{2}^{'}$ + $J_{1}^{'}$ при ${{ - 2\pi } \mathord{\left/ {\vphantom {{ - 2\pi } 3}} \right. \kern-0em} 3} < \phi < {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-0em} 3}.$

• ${{\Gamma }_{2}} = {{J}_{3}}$ + ${{J}_{2}}$ + ${{J}_{1}}$ + ${{J}_{6}}$ + $J_{5}^{'}$ + $J_{4}^{'}$ при ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3} < \phi < {{5\pi } \mathord{\left/ {\vphantom {{5\pi } 3}} \right. \kern-0em} 3}.$

• ${{\Gamma }_{3}} = {{J}_{1}}$ + ${{J}_{2}}$ + ${{J}_{3}}$ + ${{J}_{4}}$ + ${{J}_{5}}$ + $J_{6}^{'}$ при ${{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3} < \phi < {{8\pi } \mathord{\left/ {\vphantom {{8\pi } 3}} \right. \kern-0em} 3}.$

Легко проверить, что построенная таким способом система контуров удовлетворяют условиям 1) и 2), поставленным выше.

3.4. Деформация контуров интегрирования

Рассмотрим подробнее контур ${{\Gamma }_{1}}$. Данный контур состоит из шести вспомогательных контуров, каждый из которых обходит свою бесконечность, изобразим его на H₂ (рис. 13б) и на R₂ (рис. 14). Пользуясь теоремой Коши для интеграла (49), мы можем деформировать каждую часть контура ${{\Gamma }_{1}}$ до тех пор, пока он не “задевает” особых точек на поверхности. Две части контура взаимно уничтожаются, если они совпадают друг с другом и при этом имеют противоположные направления.

Деформация контура ${{\Gamma }_{1}}$ на многообразии H₂ в два этапа показана на рис. 13в, 13г. На первом этапе увеличиваются радиусы вспомогательных окружностей до их взаимного пересечения, области пересечения взаимно уничтожаются, получаем одну “петлю”, охватывающую шесть точек бесконечностей, рис. 13в. Н втором этапе происходит расширение контура вдоль малой направляющей тора до взаимного уничтожения вытянутых частей контура, в результате получаются две окружности, опоясывающие тор аналогично контуру σ, и вспомогательный контур, отвечающий за обход полюса трансформанты Зоммерфельда.

На многообразии H₂ деформация контуров ${{\Gamma }_{i}}$ имеет довольно наглядный вид, однако в практическом применении используют представление на римановой поверхности R₂. На ней деформированный контур приобретает вид, показанный на рис. 15 .

Подчеркнем, что интегрирование по деформированному контуру ${{\Gamma }_{1}}$ дает такой же результат, что и интегрирование по исходному контуру, так как при деформации не была нарушена теорема Коши. Таким образом, контур ${{\Gamma }_{1}}$ состоит из двух единичных окружностей на листах 2 и 4 римановой поверхности R₂ и полюсного вклада падающей волны на первом листе. Такой контур является куда более простым и удобным в использовании, чем контур до деформации. Аналогичным образом могут быть продеформированы и два других контура.

3.5. Функциональная задача построения трансформанты Зоммерфельда

Задача нахождения трансформанты Зоммерфельда является задачей теории функций. Сформулируем ее:

1. Трансформанта $A(p)$ должна быть мероморфной на H₂.

2. $A(p)$ может иметь простые полюсы в точках H₂, которые соответствуют падающей волне и ее зеркальному отражению ($\phi = 2\pi + {{\phi }_{{{\text{in}}}}}$ и $\phi = 4\pi - {{\phi }_{{{\text{in}}}}}$).

3. Вычеты дифференциальной формы $A(p)\psi $ в этих точках должны соответствовать $ - {{(2\pi i)}^{{ - 1}}}$ и $(2\pi i)$ соответственно.

Рассмотрим четыре точки ${{p}_{1}}(x,y,n),..,{{p}_{4}}(x,y,n)$, которые имеют одинаковое значение $x$ на $\mathbb{C}$, равное ${{x}_{{{\text{in}}}}}$. Для описания этих точек будем использовать следующее обозначение: $p(x,y$, № листа на R₂). Перечислим эти точки:

Можно показать, что точки ${{p}_{1}}$ и ${{p}_{4}}$ соответствуют падающей и отраженной волне. Дело в том, что, как было показано в предыдущем пункте, деформация контуров интегрирования приводит к “задеванию” полюсов соответствующих волн. После деформации всех контуров интегрирования было установлено, что лишь точки ${{p}_{1}}$ и ${{p}_{4}}$ попадают в область деформации, следовательно, являются полюсами подынтегрального выражения. По этой причине функция $A(p)$ должна иметь полюса в этих точках, Так как по условию нашей задачи падающая волна имеет единичную амплитуду, вычет функции $A$ в точках ${{p}_{1}}$ и ${{p}_{4}}$ должен иметь вид

В то же время $A(p)$ должна быть регулярна в точках ${{p}_{2}}$ и ${{p}_{3}}$. Поэтому зададим условие:

Таким образом, проблема нахождения функции $A(p)$ становится проблемой нахождения четырехзначной функции на $\mathbb{C}$, которая также является однозначной на Римановой поверхности R₂ и имеет полюса только в двух точках на заданной поверхности. Можно показать, что такая функция является алгебраической. В данном случае ее достаточно легко построить. Выберем четыре функции на R₂, которые обладают всеми возможными симметриями данной поверхности, связанными с перестановкой ее листов. Эти четыре функции имеют вид:

Представим $A(p)$ как линейную комбинацию функций ${{f}_{0}},...,{{f}_{3}}$, где $R(x)$ – рациональные функции от $x$:

Наша задача найти функции ${{R}_{i}}(x)$.

Обозначим вычеты функций ${{R}_{i}}(x)$ как ${{c}_{i}}$. Используя данное обозначение, запишем вычеты функции $A(p)$ в точках ${{p}_{1}},..,{{p}_{4}}$:

Решаю данную систему, получаем:

Простейшей функцией, которая имеет полюс в заданной точке, является функция вида:

Подставляя (59) и (61) в (54), получаем формулу для трансформанты Зоммерфельда:

3.6. Исследование интеграла Зоммерфельда, сравнение с методом Винера–Хопфа

Деформируя контур $\Gamma $ как показано на рис. 15, мы можем представить (49) в виде:

Функции ${{f}_{i}}$ на контурах $\sigma {\kern 1pt} '$ и 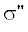различаются только знаком, поэтому возможно преобразовать интеграл по двум контурам к единичному интегралу:

Таким образом:

Представление для рассеянного поля имеет вид:

В работе [19] было получено представление поля для аналогичной задачи методом Винера–Хопфа. Выпишем это решение в используемых нами обозначениях:

Нетрудно видеть, что подстановка (53) и (29) в (65) приводит нас к представлению (66). А значит, наше решение (65) и решение задачи методом Винера–Хопфа (66) эквивалентны.

3.7. Численное исследование интеграла Зоммерфельда

Проинтегрируем полученное в предыдущем пункте решение (64) численно. В качестве контура интегрирования $\sigma {\kern 1pt} '$ будем использовать единичную окружность с обходом особой точки $ - 1$, как в пункте 2.6. На рис. 16 показан график для действительной части полного поля $u(m,n)$ при $K = 0.5$ и ${{\phi }_{{{\text{in}}}}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$. Видно, что полное поле имеет характерные интерференционные области, а на полупрямой $n = 0,\;m \geqslant 0$ выполнено граничное условие Дирихле. Также отчетливо видна теневая зона.