Акустический журнал, 2023, T. 69, № 2, стр. 155-164

ВВЕДЕНИЕ

В авиационной акустике достаточно часто встречаются измерения сигналов с явно выраженными дискретными спектральными составляющими, например, шум винта, шум двигателя, дискретные тона в шуме струи и т.д. В ряде случаев источник двигается, что требует специальных методов обработки сигналов [1–4]. Независимо от вида измерений при обработке данных используется практически один вид анализа – преобразование Фурье. Если обратиться к характеристикам любого измерительного комплекса, то среди его ключевых особенностей обязательно будет присутствовать этот вид узкополосного спектрального анализа, и зачастую количество линий выступает как показатель технического совершенства прибора. Безусловно, спектральный анализ на основе БПФ является мощным инструментом исследователя. Однако необходимо иметь в виду, что любая обработка сигнала вносит погрешность метода, обусловленную выходом за пределы области применимости метода.

Основным источником погрешности методов обработки сигнала, основанных на вычислении дискретного преобразования Фурье, является эффект “растекания” или “утечки” энергии спектральных компонент [5]. Этот эффект наблюдается, если период спектральной составляющей полезного сигнала не кратен периоду дискретизация сигнала. В спектре появляются паразитные компоненты в виде боковых лепестков, а сама спектральная линия уширяется. Применение оконного взвешивания позволяет уменьшить эффект растекания, но возникает ошибка определения амплитуды сигнала, которая зависит от соотношения частоты сигнала и частоты ближайшей линии БПФ. При измерениях, необходимых при валидации расчетов, а также в некоторых других случаях, погрешность при использовании основанных на БПФ методов может маскировать физические эффекты [6, 7]. Гладкая оконная функция существенно снижает уровень боковых лепестков, однако существенно расширяется основной лепесток, что ухудшает разрешающую способность метода по частоте.

Проблема выделения дискретных составляющих и точного определения частоты существует достаточно давно, можно найти большое количество работ по данной проблеме [8–13]. Существуют реализации многих методов и в популярных математических пакетах (например, в Matlab стандартные методы – Burg, Covariance, Modified Covariance, Yule-Walker). Однако данные методы ориентированы на определение доминирующих гармонических составляющих в предположении стационарности сигнала.

Если исключить случай анализа переходных процессов, то для улучшения статистической достоверности данных практически во всех случаях используется усреднение спектров. За счет этого достигается снижение случайной составляющей погрешности измерений. Однако остается вопрос: как повлияет на результат такое усреднение, если сигнал нестационарный? Действительно, при пролете летательного аппарата звуковой сигнал может значительно изменяться даже в пределах одной выборки. При сокращении интервала анализа для смягчения влияния “нестационарности” ошибка оценки спектра становится неприемлемой большой. При последующем усреднении спектров становится непонятно, чему будут соответствуют полученные значения, т.к. за время осреднения действующие значения амплитуды и частоты дискретных составляющих полезного сигнала могут сильно измениться. Налицо противоречие – за малое время анализа ошибка измерения очень большая, а за большое время сам сигнал успевает измениться. Поэтому возникает необходимость построения метода точных измерений амплитуды сигнала, частота которого может плавно меняться. Под плавностью изменения подразумевается, что на интервале нескольких периодов мгновенная частота хорошо описывается линейной по времени функцией, а полное изменение частоты на интервале анализа много меньше номинального значения.

В работе рассматривается метод анализа именно таких слабо нестационарных процессов, представленных в виде равнодистантных по времени измеренных значений физических величин, характеризующих такие процессы. Записи измеренных значений будем называть сигналом $x\left( n \right)$, где $n$ – индекс, дискретное время. При изменении индекса на единицу, физическое время увеличивается на интервал квантования или, по-другому, период квантования $T$. Величина, обратная к периоду квантования, называется частотой дискретизации ${{f}_{d}} = {1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}$. Сами значения сигнала также оцифровываются с разрешающей способностью устройства, измеряющего физическую величину. Обычно шаг амплитудного квантования выбирают существенно меньше как действующего значения сигнала, так и собственных шумов измеряющего устройства, поэтому шумом квантования в большинстве случаев можно пренебречь.

Для стационарных эргодических процессов спектральные оценки ее параметров сколь угодно точно могут быть получены в результате усреднения по времени. В нашем случае параметры системы меняются с течением времени, поэтому существует предел точности, обусловленный ограниченностью выборки, для которой в достаточной мере выполняется свойство эргодичности. Достаточность в данном контексте определяется практической необходимостью. Например, для сигнала с частотой доминантного гармонического сигнала, изменяющейся на 1 Гц за секунду, интуитивный выбор интервала обработки 0.1 с кажется достаточным для обеспечения точности ее отслеживания с погрешностью порядка 0.1 Гц. Таким образом, интервал обработки прямо связан с интервалом регулярности процесса. Термин “интервал регулярности”, а не “интервал стационарности” видится более подходящим для процессов, имеющих “регулярный” дискретный спектральный состав, например, упоминавшийся выше шум винта или шум двигателя. Собственно, для таких задач, связанных с отслеживанием амплитудных значений отдельных спектральных компонент полезного сигнала, и предлагается использовать описанный ниже метод.

МОДЕЛЬ ПОЛЕЗНОГО СИГНАЛА

Будем полагать, что на интервале регулярности опорная частота $f\left( n \right) \simeq {{f}_{o}}$ полезного сигнала $s\left( n \right)$ изменяется незначительно. Тогда, обозначив начало интервала индексом $n = - N$, а его конец индексом $n = N$, можно записать:

где $M$ – количество гармонических компонент в полезном сигнале, действительные коэффициенты ${{A}_{m}}$ определяют амплитуды, а неравные друг другу коэффициенты ${{k}_{m}}$ задают отношение частоты гармоничекой компоненты к значению опорной частоты. Каждая компонента полезного сигнала имеет индивидуальный фазовый сдвиг ${{{{\varphi }}}_{m}}$.

Сам сигнал $x\left( n \right)$ описывается более сложной формулой, учитывающей изменение частоты с течением времени. В первом приближении ограничимся линейным законом ее изменения $f\left( n \right) = {{f}_{o}}\left( {1 + {{\delta }_{f}} + {{\kappa }_{f}}n} \right),$ $N{{\kappa }_{f}} \ll 1,$ ${{\delta }_{f}} \ll 1$. Степень отклонения модели от сигнала будем характеризовать скаляром ${{e}^{2}}$ – суммой квадратов ошибок по всем значениям $n$:

Во втором приближении по порядку малости параметра ${{\delta }_{f}}$ ошибка модели примет вид:

где $a$, $b$ и $c$ — некоторые действительные числа. При фиксированном малом значении ${{\kappa }_{f}}$ минимальное значение ${{e}^{2}}$ будет достигаться при $\delta _{f}^{*} = {{b\kappa _{f}^{2}} \mathord{\left/ {\vphantom {{b\kappa _{f}^{2}} {2a}}} \right. \kern-0em} {2a}}$, т.е. модель (1) будет оптимальной для сигналов с линейным законом изменения частоты следующего вида:

Таким образом, для сигналов с локально-линейным изменением частоты оптимальной моделью будет служить сигнал с опорной частотой, равной опорной частоте сигнала в середине интервала анализа.

МОДЕЛЬ НАБЛЮДЕНИЙ

Обозначим через $y\left( n \right)$ измерения полезного сигнала. Помимо собственно полезного сигнала измерения содержат помеху. Будем выделять две ее составляющих, первая – это совокупность процессов $\xi \left( n \right)$ с нулевым средним, например, неучтенные гармонические составляющие и случайные шумы различной природы. Вторая составляющая – это дрейф “нуля”, которую удобно выразить полиномом невысокого порядка $L$.

Избавившись от фазы в аргументе $\sin \left( \ldots \right)$, получим окончательное выражение для модели наблюдений, линейно зависящей от действительных коэффициентов ${{a}_{m}}$, ${{b}_{m}}$, ${{p}_{l}}$ и нелинейно от опорной частоты ${{f}_{o}}$:

Выделим важный частный случай, когда $M = N$, $L = 0$, ${{f}_{o}} = {{{{f}_{d}}} \mathord{\left/ {\vphantom {{{{f}_{d}}} {2N}}} \right. \kern-0em} {2N}}$и ${{k}_{m}} = m$, т.е.

Формула (7) есть не что иное, как уравнение преобразования Фурье. Моделью сигнала при этом является эквидистантный набор гармонических составляющих, а моделью дрейфа является простой сдвиг, определяемый единственным коэффициентом ${{c}_{0}} = {{p}_{0}}$. Эта модель полезного сигнала будет оптимальной только в случае, когда все частоты его гармонических составляющих будут кратны ${{{{f}_{d}}} \mathord{\left/ {\vphantom {{{{f}_{d}}} {2N}}} \right. \kern-0em} {2N}}$. Такое ограничение весьма жесткое, оно исключает возможность подстройки опорной частоты и понижает качество описания связей спектральных составляющих из-за потери свободы выбора коэффициентов ${{k}_{m}}$. На практике это выражается в неправильном определении амплитуд и частот спектральных компонент полезного сигнала. Другим недостатком столь жесткого ограничения является отсутствие усреднения по интервалу анализа, т.к. в модели Фурье количество неизвестных параметров совпадает с количеством отсчетов на интервале анализа.

ПРИМЕР 1. ОПРЕДЕЛЕНИЕ ДЕЙСТВУЮЩЕГО ЗНАЧЕНИЯ ГАРМОНИЧЕСКОГО СИГНАЛА ПО КОРОТКОЙ ВЫБОРКЕ

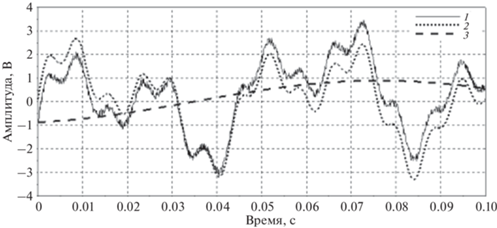
Рассмотрим модельный сигнал, состоящий из смеси гармонических сигналов c частотами 6, 20, 45, 114 и 140 Гц, а также постоянной составляющей и белого шума. Низкочастотные составляющие и шум будем интерпретировать как помеху. Среднеквадратичные значения компонент полезного сигнала составляют 1 В для частот 20, 45 Гц, 0.4 В для частоты 140 Гц и 0.1 В для компоненты с частотой 114 Гц. Короткая выборка такого сигнала с частотой дискретизации 10240 Гц показана на рис. 1.

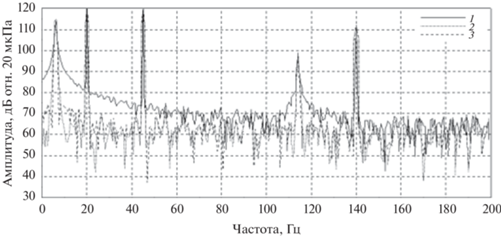
Оценка спектра сигнала по выборке длиной 1024 отсчета показана на рис. 2. Видно, что полученные спектральные составляющие не позволяют раскрыть структуру полезного сигнала. Применение оконных функций не приносит значимого эффекта.

Компонента полезного сигнала с частотой 140 Гц совпала с частотой 14-й линии БПФ, поэтому для нее возможно достаточно точно определить действующее значение, для компонент с частотами 45 и 114 Гц оценка амплитуды сильно осложнена, т.к. эти частоты не совпадают ни с какой частотой линий БПФ. Самая низкочастотная компонента полезного сигнала, 20 Гц, хотя и совпадает по частоте с 2-й линией БПФ, но из-за вклада низкочастотного дрейфа ее амплитуда так же не может быть правильно определена.

Если увеличить длину выборки, то спектральная картина становится четкой, как видно на рис. 3. В этом случае точность определения амплитуды будет определятся степенью близости частоты спектральной составляющей сигнала к частоте ближайшей линии БПФ. На практике длинные выборки для обработки могут быть неудобны по причине нестабильности измеряемых сигналов, за время накопления частоты и амплитуды полезного сигнала могут изменится, что неизбежно приведет к размыванию спектральных компонент и дополнительной потере точности.

Применим для обработки сигнала метод, описанный в предыдущем разделе. На рис. 4 показан сам сигнал и его аппроксимация. Использовалась модель, содержащая четыре гармонических компоненты, дрейф описывался полиномом третьей степени, т.е. число независимых параметров модели равнялось 12.

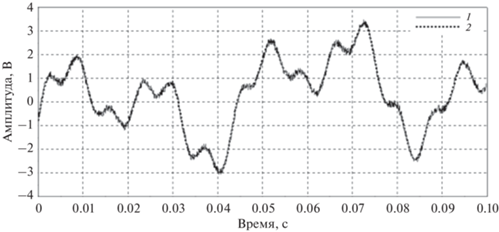
Высокое качество аппроксимации обусловлено эффектом осреднения из-за сильной избыточности, действительно, $12 \ll 1024$, т.е. число свободных параметров модели существенно меньше количества обрабатываемых данных. В данном методе точность определения амплитуды составляющих полезного сигнала в первую очередь зависит от энергии шума измерений, т.е. от стохастической компоненты помехи. Для рассмотренного примера ошибка определения действующих значений гармонических составляющих полезного сигнала лежит в пределах нескольких десятых процента. При уменьшении длины обрабатываемого сигнала ошибка будет расти и достигнет наибольшего значения, когда число свободных параметров модели совпадет с количеством отсчетов в выборке.

Условие равенства длины выборки и количества свободных параметров модели является естественным ограничением на применимость метода. Для практической значимости метода следует использовать выборки сигнала, содержащие хотя бы несколько периодов самой низкочастотной гармонической составляющей полезного сигнала. В приведенном примере на длине выборки 1024 отсчета, что составляет 0.1 с, для самой низкочастотной компоненты укладывается всего два периода.

ПРИМЕР 2. ЭФФЕКТ ДОПЛЕРА ДЛЯ ТОЧЕЧНОГО МОНОХРОМНОГО ИСТОЧНИКА ЗВУКА

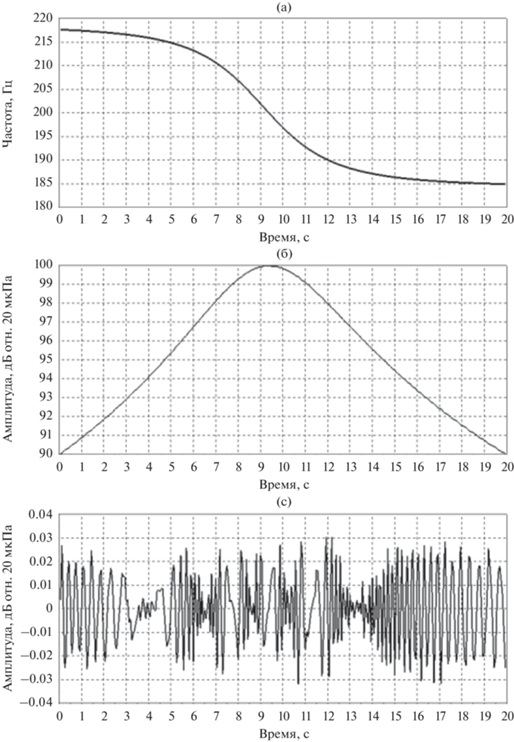
Смоделируем запись шума пролета летательного аппарата, движущегося со скоростью $v = $ 30 м/с на высоте ${{h}_{o}} = $ 100 м. Траектория прямолинейная, проходит непосредственно над точкой измерений. Начало записи соответствует точке траектории, удаленной по горизонтали на ${{l}_{o}} = $ 300 м, а конец – на том же расстоянии в другую сторону. Доминантная звуковая частота составляет $f = $ 200 Гц, что для двухлопастного винта соответствует 6000 об/мин двигателя. Будем считать, что частота дискретизации ${{f}_{d}}$ синтезируемого сигнала равняется 48 кГц.

Мгновенная амплитуда звукового давления от точечного источника, связанного с летательным аппаратом, будет меняться по закону

где $n$ – дискретное время, а ${{A}_{o}}$ – масштабный коэффициент. Условимся считать, что индекс $n = 0$ соответствует моменту, когда звук от летательного аппарата, находившегося в стартовой точке, только что дошел до микрофона, тогда связь момента наблюдения летательного аппарата ${{t}_{n}}$ и дискретного времени $n$ определяется следующим уравнением здесь буквой $c$ обозначена скорость звука, а ${{t}_{b}}$ – коррекция на время, затраченное звуковой волной для преодоления расстояния от стартовой точки до точки измерения. Уравнение (18) имеет два корня. Выбирать следует тот корень, для которого выполняется условие ${{t}_{0}} = {{t}_{b}}$. Сопоставив каждому моменту $n$ дискретного времени значение ${{t}_{n}}$ и воспользовавшись уравнением (17), получим модельный временной ряд для обработки.

На рис. 5 показаны результаты обработки модельных данных. Оценивались текущее значение частоты полезного сигнала и значение его амплитуды. Для этого сигнал был разбит на выборки длиной 3000 отсчетов и шагом 1500 отсчетов. Выборки последовательно обрабатываются начиная с первой. Оптимальное значение частоты подбирается за несколько итераций методом деления отрезка пополам с использованием критерия (16). Полученная зависимость показана на верхнем графике рисунка. Кривая практически неотличима от теоретически предсказанной для эффекта Доплера. Это же утверждение справедливо и для оценки уровня звукового давления. Следящий алгоритм выдает результат, практически совпадающий с теорией. На нижнем графике показана ошибка, видно, что ее значение лежит в сотых долях децибела.

ПРИМЕР 3. СТЕНДОВЫЕ ИЗМЕРЕНИЯ ШУМА ВИНТА БПЛА В БЕЗЭХОВОЙ КАМЕРЕ

В данном примере полезным сигналом будем считать шум пропеллера беспилотного летательного аппарата. Шум высокооборотного электродвигателя и шум, создаваемый динамиком, являются помехой. Двигатель установлен на специальной стойке, расположенной в заглушенной камере “АК-2” ЦАГИ (рис. 6), в которой реализуются условия, близкие к условиям свободного поля. Три микрофона размешены на расстояниях 110, 220 и 440 см от точки крепления винта. Четвертый микрофон расположен на расстоянии 50 см перед винтом, именно его данные используются для отслеживания оборотов двигателя. Для анализа помехозащищенности алгоритма в камере расположен источник белого шума, мощность которого можно регулировать. Сигналы микрофонов регистрируются измерительным модулем Экофизика-500. В процессе регистрации происходит плавное изменение оборотов двигателя.

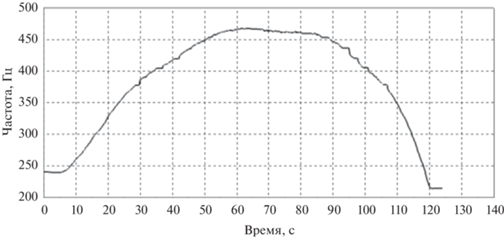
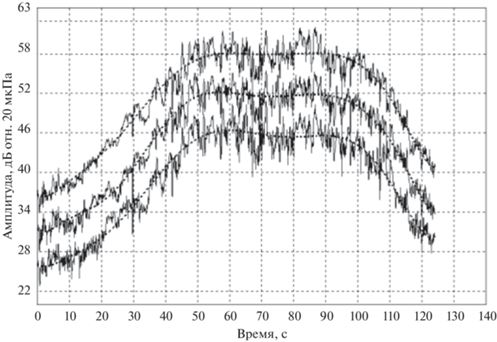
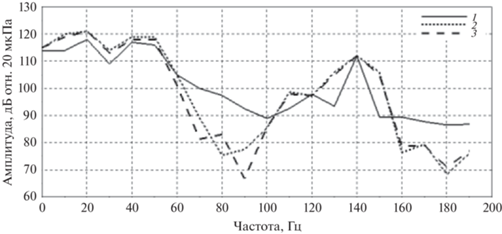
Измеренные сигналы разбиваются на интервалы анализа длительностью 0.2 с, следующие друг за другом с шагом 0.1 с. Лопастная частота оценивается по сигналу с ближайшего к винту микрофона и принимается как опорная. Для обработки сигналов с оставшихся микрофонов принимается модель данных, содержащая 20 первых гармоник опорной частоты и дрейф как полином 4-го порядка. Таким образом, модель данных имеет 45 свободных параметров для аппроксимации выборки, содержащих 6400 отсчетов, что приводит к хорошему осреднению результата. На рис. 7 показано изменение опорной частоты, а на рис. 8 – уровни звукового давления для суммы 20 первых гармоник. Следует отметить, что уровни звукового давления, обусловленные винтом, оказались как минимум на 10 дБ ниже общего уровня звука, включающего широкополосный фоновый шум и шум, создаваемый двигателем и структурной вибрацией. На рис. 8 также представлены линии тренда, как видно, они отстоят друг от друга примерно на 6 дБ, что и должно наблюдаться при заданных расстояниях между микрофонами и выполнении условия свободного поля.

ЗАКЛЮЧЕНИЕ

Предложенный метод аналитической аппроксимации временных выборок определяет амплитуду гармонических составляющих сигнала. При этом обеспечивается точное измерение мгновенных значений амплитуды и частоты, т.е. относящихся к короткому интевалу, порядка нескольких периодов анализируемой составляющей. При этом предполагается, что нам заранее известен диапазон для значения опорной частоты, с которой пропорционально связаны все интересующие нас гармонические составляющие полезного сигнала.

Для полевых измерений метод позволяет с высокой точностью определять доли вклада в общий уровень сигнала различных источников. Метод отлично отслеживает динамику изменения процессов и способен работать в условиях сильных помех.

Для стендовых измерений еще большая точность может быть достигнута за счет использования опорного сигнала, по которому отслеживается главная частота изучаемого процесса. Параметры других, когерентно измеряемых с ним сигналов, хорошо определяются даже при наличии сильных помех, включающих в себя шум, паразитные дискретные компоненты и различного рода дрейфы постоянной составляющей. Высокая степень помехозащищенности обеспечивается присущим методу внутренним механизмом усреднения результата, т.к. число свободных параметров, описывающих модель полезного сигнала, как правило, много меньше количества отсчетов в выборке для анализа. Последовательно перемещая интервал анализа по записи, можно строить зависимости изучаемых параметров от времени. Алгоритм эффективно реализуется на современных вычислительных устройствах, что позволяет проводить обработку параллельно с измерениями и наблюдать изучаемые процессы непосредственно в ходе экспериментов.

Экспериментальная часть работы выполнена на базе УНУ “Заглушенная камера с потоком АК-2” ФАУ "ЦАГИ”, модернизируемой при финансовой поддержке Министерства науки и высшего образования Российской Федерации по соглашению № 075-11-2021-066.