Акустический журнал, 2023, T. 69, № 1, стр. 73-83

ВВЕДЕНИЕ

Для прикладных задач акустики океана весьма актуально [1, 2] рассмотрение эффективности алгоритмов обработки слабых акустических сигналов на фоне помех с использованием протяженных антенных решеток (АР). Оптимальные алгоритмы обработки частично когерентных сигналов хорошо известны (см., например, [3–6]) и требуют лишь адекватных (для конкретных условий распространения звука) моделей корреляционных матриц сигнала и шума на апертуре антенны. Таким образом, для оценки эффективности обнаружения (либо оценки параметров) акустических сигналов необходимы реалистичные теоретические либо эмпирические модели сигналов и помех. Например, теоретическая модель, описывающая когерентные свойства сигнала в океанических волноводах, должна учитывать не только регулярные характеристики волновода, но и эффекты многократного рассеяния акустического поля на ветровом волнении, случайных внутренних волнах, нерегулярном дне и т.д.

На данный момент недостаточная разработка теоретических моделей сигнала и помех связана не столько с ограниченностью методов описания корреляционных характеристик акустического поля в рефракционном волноводе с нерегулярными параметрами, сколько с отсутствием статистических моделей для самих флуктуаций среды. В первую очередь, это относится к случайным внутренним волнам (за исключением модели Гаррета–Манка для глубоководного океана) и нерегулярному дну. В то же время, спектр ветрового волнения изучен относительно хорошо [7] и это позволило оценить влияние эффектов многократного рассеяния акустического поля на эффективность пространственной обработки узкополосных акустических сигналов с использованием горизонтальной АР. Результаты подобных исследований приведены в работах [8–10], где рассматривались такие характеристики, как угловой отклик антенны и коэффициент ее усиления при различных способах обработки сигнала. Следует при этом заметить, что в этих работах использовалась в качестве помехи максимально простая и в общем-то абстрактная модель шума, некоррелированного на элементах АР. Вместе с тем для океанического шума ветрового происхождения (динамического шума) разработаны теоретические модели, позволяющие рассчитывать корреляционную матрицу шумовой помехи на апертуре горизонтальной АР. Первоначально эти результаты были получены применительно к плоскослоистому волноводу для шумового поля, генерируемого равномерно распределенными по свободной поверхности дипольными источниками [11]. Позднее в работах [12, 13] была предложена обобщающая эти результаты теоретическая модель динамического шума в океаническом волноводе, которая учитывает не только генерацию его дипольными источниками, но и эффекты многократного рассеяния на взволнованной морской поверхности. Таким образом, возникает возможность исследования эффективности пространственной обработки сигнала на фоне вполне конкретной океанической помехи, а именно, динамического шума, что и является предметом данной работы. Корреляционные характеристики сигнала и шума рассчитываются путем численного моделирования уравнения переноса для пространственной функции корреляции акустических мод. Основное влияние уделено сравнительному анализу различных методов пространственной обработки сигналов и реалистичным оценкам дополнительного выигрыша АР при использовании оптимальных методов обработки в сравнении со стандартным методом формирования диаграммы направленности (ФАР). С практической точки зрения подобные расчеты представляются полезными для прогнозирования эффективности АР протяженной апертуры в условиях открытых к поверхности звуковых каналов. Наряду с моделированием коэффициентов усиления АР на фоне шума ветрового происхождения проводятся аналогичные расчеты коэффициентов усиления на фоне некоррелированного шума, что позволяет оценить значимость рассматриваемых эффектов. Численное моделирование проделано как для мелкого моря, так и для глубокого океана.

ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим акустическое поле сигнала, генерируемое точечным источником, и акустическое поле динамического шума (т.е. шума ветрового происхождения) в океаническом волноводе со взволнованной свободной поверхностью. Волновод предполагается плоскослоистым с профилем скорости звука c(z), открытым к поверхности, и дном с произвольной многослойной структурой. Для прикладных задач акустики океана наиболее интересен низкочастотный диапазон $f \leqslant 300$ Гц, где затухание звука относительно мало и акустические сигналы могут распространяться на расстояния порядка сотен километров. Будем считать, что сигнал генерируется тональным источником с частотой f₀, лежащей в этом диапазоне. Соответственно, на той же частоте будет рассматриваться и поле ветрового океанического шума, выступающего в качестве помехи при пространственной обработке сигнала.

Для описания низкочастотного акустического поля будем использовать модовое представление, т.е. представим его в виде разложения по ортонормированным собственным функциям плоскослоистого волновода. При этом поле давления для сигнала в дальней зоне имеет вид:

где ${{\varphi }_{n}}\left( z \right)$ и k_n – соответственно, собственные функции и волновые числа мод, a_n – их амплитуды, r – горизонтальное расстояние от источника до точки наблюдения. В отсутствие ветрового волнения коэффициенты разложения a_p с точностью до численного сомножителя имеют вид ${{a}_{n}} = {{\varphi }_{n}}\left( {{{z}_{{\text{И}}}}} \right)$, где z_И – глубина источника. При распространении звука в волноводе со взволнованной свободной поверхностью амплитуды a_n являются случайными функциями горизонтальных координат и времени и, как правило, описываются парными корреляторами $\left\langle {{{a}_{n}}\left( {{{{\mathbf{r}}}_{1}},{{t}_{1}}} \right)\,a_{m}^{*}\left( {{{{\mathbf{r}}}_{2}},{{t}_{2}}} \right)} \right\rangle $. В дальнейшем нас будут интересовать усредненные по интерференционной структуре и поэтому более предсказуемые характеристики акустического поля, для описания которых достаточно анализировать автокорреляторы $\left\langle {{{a}_{n}}\left( {{{{\mathbf{r}}}_{1}},{{t}_{1}}} \right)\,a_{n}^{*}\left( {{{{\mathbf{r}}}_{2}},{{t}_{2}}} \right)} \right\rangle $. Более подробно процедура усреднения по интерференционной структуре обсуждается в работах [14, 15]. Для описания таких функций пространственной когерентности сигнала на входе горизонтальной антенной решетки достаточно рассмотреть автокорреляционные функции мод с поперечным (относительно горизонтальной оси x, соединяющей источник и центр АР) разнесением точек наблюдения ρ:

Для расчета функций (2) в волноводе с нерегулярной свободной границей ранее было получено [15, 16] уравнение переноса, которое описывает эффекты многократного рассеяния акустического поля. В случае ненаправленного (в горизонтальной плоскости) источника и изотропного ветрового волнения оно имеет вид:

Здесь ${{W}_{{mn}}}$ – вероятность перехода между модами, описывающая их взаимный обмен корреляциями (при рассеянии акустической энергии из моды в моду), ${{\gamma }_{n}}$ – декремент затухания когерентной компоненты $\left\langle {{{a}_{n}}} \right\rangle $, $\operatorname{Im} {{k}_{n}}$ – мнимая часть волнового числа, обусловленная потерями энергии в среде распространения. В свою очередь, функции ${{W}_{{mn}}}$ и ${{\gamma }_{n}}$ выражаются через частотный спектр изотропного ветрового волнения:

где g – ускорение свободного падения, ${{k}_{0}} = {{{{{{\omega }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}_{0}}} {c\left( 0 \right)}}} \right. \kern-0em} {c\left( 0 \right)}}$, ${{d{{\varphi }_{n}}} \mathord{\left/ {\vphantom {{d{{\varphi }_{n}}} {dz}}} \right. \kern-0em} {dz}}$ – производная собственной функции при z = 0. Отметим, что приведенное выражение для ${{{{\gamma }}}_{n}}$ учитывает рассеяние данной моды не только во все моды дискретного спектра, но и в моды сплошного спектра, т.е. излучение ее из волновода (см. [15]). Уравнение переноса (2) получено при малых значениях параметра Рэлея, т.е. предполагает малость эффектов однократного рассеяния [17]. При этом оно позволяет описывать эффекты многократного рассеяния, приводящие к декорреляции сигнала на значительном удалении от источника. Оценки показывают, что при скоростях ветра V ≤ 15 м/с и частотах f ≤ 300 Гц параметр Рэлея мал в сравнении единицей. Для частотного спектра развитого волнения при численном моделировании будет использоваться спектр JONSWAP [7], который описывает наблюдаемое в натурных экспериментах превышение спектральной плотности энергии вблизи частотного максимума в сравнении со спектром Пирсона–Московитца: где ${{\Omega }_{m}} = {{0.8g} \mathord{\left/ {\vphantom {{0.8g} V}} \right. \kern-0em} V}$ – частота спектрального максимума (V – скорость ветра). Эмпирические константы ${{\beta }}$ и ${{\gamma }}$ имеют средние значения $\beta = 8 \times {{10}^{{ - 3}}}$, $\gamma = 3.3$. Важно также отметить, что и само уравнение переноса (3) и эмпирические константы, приведенные в спектре (8), предполагают статистическую однородность ветрового волнения, т.е. рассмотрение для открытой акватории вдали от береговой линии.

Приведем теперь основные соотношения для шумового поля, обусловленного ветровым волнением. Будем при этом полагать, что источники динамического шума имеют дипольный характер, однородно распределены на свободной поверхности океанического волновода и пространственно некоррелированы. Кроме того, поскольку нами выбрана изотропная модель ветрового волнения, то и динамический шум будет изотропным (в горизонтальной плоскости). Модель анизотропного шума (см. [12, 13]) здесь не рассматривается, поскольку усложняет рассмотрение интересующих нас эффектов. Поле давления для шума мы также представим в виде разложения по собственным модам плоскослоистого волновода

В дальнейшем нас будет интересовать пространственная функция корреляции шума с горизонтальным разнесением точек наблюдения, которую с учетом статистической однородности и изотропности шумового поля обозначим следующим образом:

где $\rho = \left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right|$. Определим аналогичным образом функцию корреляции амплитуд нормальных мод:

При этом для функций корреляции шума на апертуре АР, расположенной на глубине z_А, имеем:

Нетрудно убедиться, что вычисление пространственной функции корреляции модовых амплитуд в силу изотропности шума сводится к вычислению их интенсивности ${{I}_{n}} = {{R}_{n}}\left( 0 \right)\,$. Для этого воспользуемся представлением функций корреляции ${{R}_{n}}\left( \rho \right)$ через угловой спектр модовых амплитуд ${{\Phi }_{n}}\left( \varphi \right)\,$:

и учтем, что для изотропного спектра ${{\Phi }_{n}}\left( \varphi \right) = {{{{I}_{n}}} \mathord{\left/ {\vphantom {{{{I}_{n}}} {2\pi }}} \right. \kern-0em} {2\pi }}$. В результате, используя известное интегральное представление функции Бесселя ${{J}_{0}}\,\left( x \right)$, для функции корреляции R_n имеем:

Для интенсивности I_n мод шумового поля, возбуждаемого равномерно распределенными источниками дипольного типа, ранее было получено уравнение [12]:

где ${{\tilde {W}}_{{mn}}} \equiv {{W}_{{mn}}}\left( {{{\rho }} = 0} \right)$ и для ${{\gamma }_{n}}$ и ${{W}_{{mn}}}$ имеем те же выражения (4)–(7). Функция Q_n соответствует дипольным источникам шума и выражается через пространственный спектр дипольного момента давления на свободной поверхности [11] ${{\rho }_{{\text{в}}}}$ – плотность воды.

Важно отметить, что уравнение (15) описывает как генерацию шума ветровым волнением, так и дальнейшую трансформацию интенсивности мод шумового поля вследствие эффектов их многократного рассеяния на взволнованной поверхности волновода. Изменение интенсивности мод в зависимости от уровня ветрового волнения приводит, как это следует из формул (12), (14), к изменению и функции пространственной корреляции шумового поля на апертуре АР.

Перейдем далее к анализу характеристик приемной АР в зависимости от выбранного метода обработки сигнала на фоне динамического шума. Будем считать, что АР состоим из M эквидистантных элементов, расположенных в горизонтальной плоскости на глубине ${{z}_{{\text{A}}}}$ и ориентированных под углом β_А к направлению на источник (угол отсчитываем от нормали к антенне). Расстояние между источником и центром АР вдоль оси x обозначим r. Для межэлементного расстояния d будем использовать стандартное значение, равное половине длины волны на частоте f₀.

Основными характеристиками сигнала и шума, используемыми при пространственной обработке, являются их корреляционные матрицы размерности M × M. В дальнейшем будем использовать нормированные матрицы сигнала и шума, которые обозначим, соответственно, N и R. При этом элементы матрицы сигнала N имеют вид:

где для каждой из мод: ${{N}_{p}}\left( {\rho ,r} \right)$ – решение уравнения (3) с начальным условиями, соответствующими точечному источнику, расположенному на глубине ${{z}_{{\text{И}}}}$.

Элементы матрицы шума R представляются аналогичным образом:

где $R_{{mn}}^{p} = {{N}_{p}}{{J}_{0}}\left( {{{k}_{p}}d\left| {m - n} \right|} \right)$, N_p – решение уравнения (15). При этом следует отметить, что элементы корреляционной матрицы шума R_mn не зависят от расстояния r и угла β_А (т.е. ориентации АР) в силу статистической однородности и изотропности шумового поля.

Для количественной оценки эффективности пространственной обработки сигналов выберем коэффициент усиления антенны G, который стандартно определяется как величина выходного отношения сигнал/шум (ОСШ), отнесенная к величине ОСШ на отдельном приемном элементе. Именно эта величина характеризует эффективность АР как пространственного фильтра входных сигналов, повышающего вероятность обнаружения сигнала удаленного источника. Естественно, величина G зависит не только от вида корреляционных матриц сигнала и помехи (в нашем случае ветрового шума), но и метода пространственной обработки. В целях сравнительного анализа мы рассмотрим три известных метода пространственной обработки: 1 – стандартный метод ФАР, компенсированной в направлении на источник сигнала (соответствующий коэффициент усиления обозначим G₀), 2 – метод оптимальной линейной обработки (коэффициент усиления обозначим G₁), 3 – метод оптимальной квадратичной обработки (коэффициент усиления обозначим G₂). Следует отметить, что выражения для коэффициентов усиления ${{G}_{i}}$ будут отличаться от тех, которые использовались в работах [8–10], где рассматривались аналогичные вопросы, но использовалась модель некоррелированного шума. В нашем случае для коэффициента усиления G₀ имеем выражение

где фазовая компенсация для всех мод происходит с одним и тем же волновым числом k₀. Коэффициенты усиления G₁ и G₂ оптимальной обработки выражаются через собственные значения матрицы S = R^–1N, что соответствует дополнительной операции пространственной декорреляции (“выбеливания”) шума [3–5]. Соответствующие выражения имеют вид: где ${{{{\lambda }}}_{i}}$ – собственные значения матрицы S, пронумерованные в порядке их убывания (${{\lambda }_{1}}$ – максимальное из них). В дальнейшем для сравнения будут приводиться и результаты вычисления коэффициентов усиления на фоне некоррелированного шума. В этом случае матрица шума R является единичной, $\sum\nolimits_{mn} {{{R}_{{mn}}}} = M$ и в формулах (21) фигурируют собственные значения матрицы сигнала N.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Ввиду сложности расчета корреляционных матриц сигнала и шума в многомодовом волноводе, интересующие нас эффекты могут быть рассмотрены лишь численными методами. При проведении численного моделирования на основании приведенных выше аналитических результатов использовалась также стандартная модовая программа. При этом очевидно, что в наибольшей степени данные эффекты проявятся в звуковых каналах, открытых к поверхности. Гидрология такого типа возможна как в мелком море, так и в глубоком океане, поэтому мы приведем результаты численных расчетов как для мелкого моря, так и для глубоководного океанического волновода.

Рассмотрим вначале численное моделирование коэффициентов усиления антенны G_i для мелководного звукового канала со слабым положительным градиентом скорости звука, что, например, типично для Баренцева моря в зимний период. При этом для волновода с линейным профилем c(z) выбраны следующие параметры: c(0) = 1490 м/с, c(H) = 1500 м/с, глубина дна H = 200 м. В качестве модели дна рассматривается жидкое полупространство со скоростью звука ${{c}_{l}} = 1800$ м/с, плотностью ρ₀ = 2 г/см³ и коэффициентом затухания δ = 0.2 дБ/км Гц. Предполагается, что источник с частотой излучения f₀= 250 Гц расположен на глубине z_И = 100 м. Горизонтальная АР с числом элементов M = 51 и межэлементным расстоянием d = λ/2 = 3 м расположена вблизи дна на глубине z_A = 197 м. При этом рассматривается антенна, ориентированная либо перпендикулярно к источнику (β_A = 0) либо под углом β_A = 30°. Расчеты проводились для скоростей ветра V = 10 м/с и V = 15 м/с, т.е., согласно принятой терминологии, для умеренного и сильного ветрового волнения. При этом в спектре JONSWAP использовались приведенные выше средние значения эмпирических констант β и γ, соответствующие развитому ветровому волнению. Для того чтобы продемонстрировать специфику обнаружения сигнала на фоне ветрового шума, ниже будут приводиться, для сравнения, и результаты расчетов коэффициентов усиления ${{G}_{i}}$ для тех же условий распространения сигнала, но на фоне некоррелированного шума.

Результаты пространственной обработки зависят от вида коэффициентов корреляции сигнала и динамического шума:

На рис. 1, 2 приведены, в качестве примера, результаты численных расчетов коэффициента корреляции сигнала (на расстоянии r = 200 км от источника) и ветрового шума на глубине расположения антенны. Видно, что при V = 10 м/с уровень остаточной когерентности сигнала на апертуре АР составляет 0.3, т.е. остается достаточно высоким, что важно для эффективности линейной обработки. При сильном ветре он снижается практически до нуля, и в этом случае можно рассчитывать на существенный выигрыш оптимальной квадратичной обработки сигнала. Отметим, что здесь наблюдается более значительная декорреляция сигнала, чем в работе [9]. Это связано с тем, что в предыдущих расчетах использовалось минимальное значение параметра γ = 1 в спектре JONSWAP, а также другое значение глубины источника z_И = 197 м. На рис. 2 приведены, в качестве примера, результаты расчета коэффициента корреляции динамического шума при скорости ветра V = 10 м/с. Функция корреляции является осциллирующей, при этом важно отметить, что нули корреляционной функции являются неэквидистантными, что приводит к достаточно высокому уровню межэлементных корреляций динамического шума на апертуре АР.

Перейдем теперь непосредственно к обсуждению результатов численных расчетов коэффициентов усиления АР при различных способах обработки сигнала. На рис. 3 приведены зависимости от расстояния r коэффициентов усиления G₀, G₁ и G₂ при поперечной ориентации АР для умеренного и сильного ветрового волнения. Здесь же, для сравнения, приводятся и аналогичные зависимости для традиционной модели некоррелированного шума. Нетрудно видеть, что коэффициенты усиления ${{G}_{i}}$, полученные в рамках модели ветрового океанического шума, существенно больше (приблизительно на 2 дБ), чем аналогичные коэффициенты усиления сигнала на фоне некоррелированного шума (при этом модель сигнала и в тех и других расчетах одна и та же). На малом удалении антенны от источника r ≈ 0, когда сигнал на апертуре полностью когерентен, коэффициенты усиления ${{G}_{i}}$ = 51 (17 дБ), т.е. равны числу приемных элементов АР для модели некоррелированного шума, но для модели динамического шума имеют значения ${{G}_{i}}$ ≈ 77 (19 дБ), что значительно превышает значение M. Этот результат может показаться неожиданным, поскольку традиционно считается, что наличие межэлементных корреляций шума снижает коэффициент усиления АР [18], а значение коэффициента усиления, равное M, является максимально возможным. Объяснение приведенных на рис. 3а и 3в результатов связано со специфическим видом корреляционной функции ветрового шума, а именно ее знакопеременным спаданием по ρ и расположением ее нулей. Наиболее наглядно это можно пояснить на примере коэффициента усиления G₀. Учитывая когерентность сигнала при r ≈ 0 и нормировку матричных элементов N_mn и R_mn, для G₀ при β_A = 0 из формулы (20) следует:

где, для наглядности, выделен вклад межэлементных корреляций шума. В случае некоррелированного шума отсюда получаем G₀ = M, в случае монотонного спадания коэффициента корреляции шума отсюда следовало бы, что G₀ < M, но для ветрового шума расчеты показывают, что сумма межэлементных коэффициентов корреляции является отрицательной и вследствие этого значение G₀ > M.

При увеличении расстояния от источника до антенны из-за эффектов многократного рассеяния на ветровом волнении увеличивается декорреляция сигнала на апертуре АР, вследствие чего коэффициенты усиления ${{G}_{i}}$ монотонно уменьшаются. При этом значения G₁ и G₀ практически совпадают и уменьшаются на 4−5 дБ при умеренном волнении и на 6−7 дБ при сильном ветре. Коэффициент усиления при оптимальной квадратичной обработке G₂ спадает более медленно, поскольку эффективность ее в сравнении с оптимальной линейной растет с увеличением декорреляции сигнала. При V = 10 м/с этот выигрыш не столь значим и не превышает одного децибела, но при V = 15 м/с разница значений G₂ и G₁ достигает 3 дБ, что существенно для задач выделения слабых сигналов на фоне помех. Следует также отметить, что качественный характер зависимости от дистанции коэффициентов усиления для двух моделей шума примерно одинаков, но значения ${{G}_{i}}$ для модели динамического шума приблизительно на 2 дБ превышают аналогичные значения, полученные для модели некоррелированного шума и той же модели сигнала.

Рассмотрим теперь результаты численного моделирования для антенны, ориентированной под углом β_A = 30°. На рис. 4 приведены расчетные зависимости от r коэффициентов усиления G_i с использованием двух моделей шума для умеренного и сильного ветрового волнения. Нетрудно видеть, что и в этом случае коэффициенты усиления АР, рассчитанные с использованием модели динамического шума, превышают аналогичные величины, полученные для модели некоррелированного шума, хотя их отличие не столь значительно. Коэффициенты усиления при оптимальной обработке сигнала G₁ и G₂ монотонно уменьшаются с ростом дистанции и этот эффект существенен: например, G₁ уменьшается на 3 дБ при V = 10 м/с и на 4−5 дБ при V = 15 м/с. Сравнение результатов оптимальной квадратичной и оптимальной линейной обработки приводит к тем же выводам: малые их отличия при умеренном ветре и заметный выигрыш квадратичной обработки при сильном ветре. Качественно, по сравнению с перпендикулярно ориентированной антенной, меняется зависимость от дистанции r для G₀, т.е. метода ФАР. Коэффициент усиления G₀ сначала растет с дистанцией и лишь начиная с некоторого удаления от источника (r ~ 50 км при V = 10 м/с, r ~ 20 км при V = 15 м/с) начинает спадать. Этот эффект обусловлен возбуждением широкого спектра мод и различием их волновых чисел. Поскольку фазовая компенсация происходит с опорным волновым числом ${{k}_{{\text{A}}}} = {\omega \mathord{\left/ {\vphantom {\omega {c\left( {{{z}_{{\text{A}}}}} \right)}}} \right. \kern-0em} {c\left( {{{z}_{{\text{A}}}}} \right)}}$ и не учитывает индивидуальные фазовые распределения мод на апертуре АР, значительная часть мод “выпадает” из главного лепестка диаграммы направленности (ДН), что приводит к неэффективности метода ФАР на малых расстояниях. В то же время, оптимальная линейная обработка обеспечивает адаптивное, отвечающее модовому спектру сигнала, смещение угла фазировки на максимум углового отклика АР. В результате оптимизированная ДН учитывает основные энергонесущие моды, что позволяет получить выигрыш линейной обработки сигнала в сравнении с ФАР. С увеличением дистанции модовый спектр сигнала определяется слабозатухающими низшими модами, для которых волновые числа k_p близки к значению k₀ и, соответственно, эффективность метода ФАР растет. При этом G₀ приближается к значениям оптимальной линейной обработки G₁ и в дальнейшем уменьшается с дистанцией вследствие декорреляции сигнала на апертуре АР.

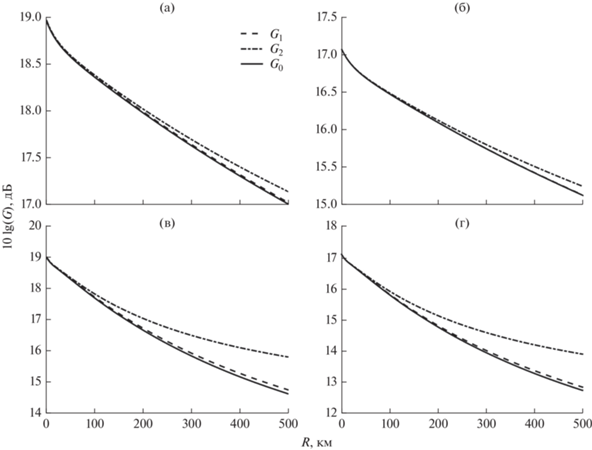
Рассматриваемые нами эффекты могут представлять интерес не только для прикладных задач акустики мелкого моря, но и при рассмотрении эффективности методов пространственной обработки сигналов в глубоком океане, а именно высокоширотных волноводах, где наблюдаются существенные сезонные изменения профиля скорости звука и в зимних условиях формируются звуковые каналы, открытые к поверхности. В качестве примера рассмотрим профиль скорости звука, который наблюдается в Тихом океане в районе полуострова Камчатка (см. рис. 5). Здесь в зимних условиях формируется выраженный приповерхностный звуковой канал шириной приблизительной 200 м, который ниже переходит в линейный с градиентом 0.016 с^–1. Глубина океана H = 2000 м, в качестве модели дна выберем жидкое полупространство со скоростью звука ${{c}_{l}} = 1700$ м/с, плотностью ρ₀ = 2 г/см³ и коэффициентом затухания δ = 0.2 дБ/км Гц. Будем полагать, что АР с теми же параметрами находится на глубине z_A = 10 м (что соответствует модели заглубленной буксируемой антенны) и ориентирована перпендикулярно к источнику. Частота излучения f₀ = 250 Гц, источник расположен посредине канала на глубине z_И = 100 м. Результаты расчетов коэффициентов усиления G_i(r) приведены на рис. 6. Поскольку в глубоком океане затухание звука значительно меньше и практический интерес представляют протяженные акустические трассы, расчеты проделаны для дистанции 0 ≤ r ≤ 500 км. Результаты моделирования показывают, что и в этом случае коэффициенты усиления на фоне динамических шумов ветрового происхождения значительно выше, чем для модели некоррелированного шума. На малом удалении от источника r ≈ 0 имеем значение ${{G}_{i}}$ ≈ 80, т.е. на 2 дБ больше значения ${{G}_{i}}$ = 51, соответствующего некоррелированному шуму. При умеренном волнении все три способа обработки дают практически одинаковые результаты, что свидетельствует о значительной остаточной корреляции сигнала на апертуре антенны. При сильном ветре имеется некоторый выигрыш оптимальной квадратичной обработки, но он меньше, чем в случае мелкого моря и не превышает одного децибела. В то же время уменьшение самих коэффициентов усиления с дистанцией из-за декорреляции сигнала на апертуре АР равно 2 дБ для умеренного ветрового волнения и, соответственно, 4 дБ при сильном волнении, т.е. рассматриваемые эффекты могут иметь определенное значение и для прикладных задач акустики глубокого моря.

Отметим, что приведенные выше результаты о превышении коэффициента усиления АР на фоне динамического шума над аналогичными значениями, полученными для некоррелированного шума, имеют в случае изотропного ветрового волнения достаточно универсальный характер, поскольку обусловлены лишь горизонтальной изотропностью поля динамического шума и его узким модовым спектром. Последнее обстоятельство типично для океанических волноводов, где вследствие рассеяния и затухания в дне “выживают” лишь низшие моды. В то же время для более сложной модели анизотропного динамического шума [12, 13] эти выводы не столь очевидны и требуют дальнейшего изучения.

ЗАКЛЮЧЕНИЕ

В работе продолжено исследование влияния ветрового волнения на эффективность пространственной обработки низкочастотных акустических сигналов в океанических волноводах с использованием горизонтальной антенной решетки (АР). В отличие от предыдущих статей, где в качестве помехи рассматривалась абстрактная модель некоррелированного шума, здесь предлагается достаточно реалистичная модель океанического шума ветрового происхождения (динамический шум). Анализируются три метода пространственной обработки сигнала: формирование диаграммы направленности (ФАР), оптимальная линейная обработка и оптимальная квадратичная обработка. В качестве основной характеристики пространственной обработки рассматривается коэффициент усиления антенны, который анализируется при умеренном и сильном волнении на различном удалении АР от источника. При этом основные характеристики сигнала и шума – матрицы их пространственной корреляции на элементах АР – рассчитываются на основании уравнения переноса для корреляционных функций акустических мод. Ввиду сложности аналитического исследования данной задачи, конкретные результаты получены путем численного моделирования для типичных зимних условий распространения в Баренцевом море и Тихом океане вблизи Камчатки. Параллельно приводятся результаты расчетов коэффициентов усиления АР на фоне некоррелированного шума, что позволяет наглядно оценить значимость модели динамического шума для результатов пространственной обработки сигнала.

Показано, что для антенны, состоящей из 51 элемента со стандартным межэлементным расстоянием, равным половине длины волны, коэффициенты усиления АР на фоне динамического шума существенно (до двух децибел) превышают аналогичные коэффициенты усиления на фоне некоррелированного шума. Приводится физическое объяснение этого, на первый взгляд, неожиданного результата. Обсуждается также уменьшение коэффициентов усиления АР вследствие декорреляции сигнала на апертуре антенны на различном удалении ее от источника. Этот эффект оказался наиболее значим для условий распространения в Баренцевом море. В этом случае для АР с поперечным расположением апертуры коэффициенты усиления G₁ и G₀ практически совпадают и спадают на 4–5 дБ при умеренном волнении (V = 10 м/с) и на 6–7 дБ при сильном ветре V = 15 м/с. Выигрыш оптимальной квадратичной обработки при V = 10 м/с порядка 1 дБ, но при V = 15 м/с достигает 3 дБ. Для антенны, ориентированной под углом 30° (относительно направления на источник), коэффициенты усиления G₁ и G₂ ведут себя аналогичным образом, а метод ФАР значительно проигрывает методу оптимальной линейной обработки, поскольку формирование ДН происходит без учета многомодового характера сигнала. Этот эффект также обсуждается в работе.

Результаты расчетов, проделанных для приповерхностного волновода в Тихом океане на удалении от источника до 500 км, имеют качественно тот же характер. Предполагается при этом, что антенна имеет глубину z_А = 10 м и ориентирована перпендикулярно к направлению на источник (глубина источника z_И = 100 м). Коэффициенты усиления G_i на фоне динамического шума при малом удалении АР от источника в этом случае имеют значение G_i ≈ 80 (19 дБ), т.е. и для данной гидрологии существенно превышают значение M = 51 (17 дБ), полученное для модели некоррелированного шума. Результаты моделирования для оптимальной линейной обработки и метода ФАР практически совпадают. Выигрыш оптимальной квадратичной обработки в сравнении с линейной незначителен при V = 10 м/с и порядка 1 дБ при V = 15 м/с. В то же время спадание коэффициентов усиления с расстоянием из-за декорреляции сигнала на апертуре АР достигает 2 дБ при умеренном волнении и 4 дБ при сильном ветре V = 15 м/с и представляется достаточно значимым для практических приложений. Важно отметить, что значения G_i для динамического шума существенно превышают аналогичные значения для модели некоррелированного шума для всех значений 0 < r ≤ 500 км.

Авторы выражают благодарность А.И. Малеханову за проявленный интерес к работе и полезные замечания.

Данная работа выполнена при поддержке гранта РНФ № 20-19-00383.