1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 68, № 5, 2022

Акустический журнал, 2022, T. 68, № 5, стр. 475-478

Нелинейные локализованные продольные волны в метаматериале, задаваемом как цепочка “масса-в-массе”

В. И. Ерофеев a, *, Д. А. Колесов a, А. О. Мальханов a

a Институт проблем машиностроения РАН – филиал ФГБНУ “Федеральный исследовательский центр Институт прикладной физики Российской академии наук”
603024 Нижний Новгород, ул. Белинского 85, Россия

* E-mail: erof.vi@yandex.ru

Поступила в редакцию 09.03.2022
После доработки 09.03.2022
Принята к публикации 30.03.2022

Полный текст (PDF)

Аннотация

Рассматривается математическая модель акустического (механического) метаматериала, представляющая собой цепочку осцилляторов, состоящую из нелинейно-упругих элементов и масс, каждая из которых содержит внутренний нелинейный осциллятор. Показано, что в длинноволновом приближении полученная система уравнений может быть сведена к нелинейному эволюционному уравнению Бенджамина–Бона–Махони, в рамках которого исследовано взаимодействие трех модулированных квазигармонических волн (волновых пакетов) при выполнении условий фазового синхронизма. Исследовано также формирование связанных трехчастотных солитонов огибающих, т.е. волновых пакетов, сохраняющих свои амплитудно-фазовые профили при распространении в метаматериале благодаря компенсирующему действию нелинейных эффектов. Отмечено, что кроме решений, описывающих квазигармонические процессы, полученное эволюционное уравнение имеет точное аналитическое решение в виде уединенной стационарной волны (солитона). Выявлены различия свойств этого солитона и классического солитона Кортевега–де Вриза.

Ключевые слова: математическое моделирование, нелинейные волны, акустический метаматериал, цепочка “масса-в-массе”, одномерная система

ВВЕДЕНИЕ

Акустические (или механические) метаматериалы, являясь, по сути дела, не материалами, а ячеистыми периодическими конструкциями, в длинноволновом диапазоне ведут себя подобно непрерывным материалам. Изучение особенностей дисперсии, диссипации и проявления нелинейности акустических волн в метаматериалах представляет интерес. Этот интерес обусловлен как фундаментальной значимостью, так и перспективами практических приложений метаматериалов [1–4], среди которых все чаще называют возможность создания на их основе суперпоглотителей звука [5–8].

Руководствуясь математической аналогией между акустическими и электромагнитными волнами, многие исследователи пытались построить континуальные модели механических метаматериалов. Однако большого успеха на этом пути добиться не удалось, поскольку механические аналоги реально существующих материалов с отрицательной диэлектрической проницаемостью представляют собой деформируемые твердые тела, обладающие отрицательной массой, плотностью или отрицательным модулем упругости [9–13]. А таких материалов в природе не существует. Избежать этого недостатка удалось на пути структурного моделирования метаматериалов.

В работе [14] рассматривалась одномерная цепочка, содержащая одинаковые массы$~~{{m}_{1}},$ связанные упругими элементами (пружинами), обладающими одинаковой жесткостью ${{k}_{1}}$, при этом каждая масса внутри себя содержала еще одну массу $~{{m}_{2}}$ и еще один упругий элемент – пружину с жесткостью $~{{k}_{2}}$ (рис. 1). Такая модель, названная цепочкой “масса-в-массе”, не дает упомянутых абсурдных результатов.

Рис. 1.

Механическая модель акустического метаматериала.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И НЕЛИНЕЙНОЕ ЭВОЛЮЦИОННОЕ УРАВНЕНИЕ

Обобщим модель [14] путем учета квадратичной нелинейности внешнего и внутреннего упругих элементов.

Потенциальная энергия элементарной ячейки цепочки “масса-в-массе” запишется в виде:

(1)
$\begin{gathered} {{W}^{{\left( j \right)}}} = \frac{1}{2}\left[ {{{k}_{1}}{{{\left( {u_{1}^{{\left( {j + 1} \right)}} - u_{1}^{{\left( j \right)}}} \right)}}^{2}} + {{k}_{2}}{{{\left( {u_{2}^{{\left( j \right)}} - u_{1}^{{\left( j \right)}}} \right)}}^{2}}} \right. + \\ \left. { + \,\,{{h}_{1}}{{{\left( {u_{1}^{{\left( {j + 1} \right)}} - u_{1}^{{\left( j \right)}}} \right)}}^{3}} + {{h}_{2}}{{{\left( {u_{2}^{{\left( j \right)}} - u_{1}^{{\left( j \right)}}} \right)}}^{3}}} \right], \\ \end{gathered} $
где h1, 2 – коэффициенты, характеризующие нелинейные добавки к жесткостям пружин; а ее кинетическая энергия – в виде:

(2)
${{T}^{{\left( j \right)}}} = \frac{1}{2}\left[ {{{m}_{1}}{{{\left( {\dot {u}_{1}^{{\left( j \right)}}} \right)}}^{2}} + {{m}_{2}}{{{\left( {\dot {u}_{2}^{{\left( j \right)}}} \right)}}^{2}}} \right].$

Позволим ${{u}_{1}}\left( x \right)$ и ${{u}_{2}}\left( x \right)$ быть непрерывными функциями, которые дают смещения всех ${{m}_{1}}$ и ${{m}_{2}}$, соответственно. Используя разложение перемещений в ряд Тэйлора и ограничиваясь при этом двумя слагаемыми, получим

(3)
$u_{1}^{{\left( {j + 1} \right)}} = {{u}_{1}}\left( {x + L} \right) = {{u}_{1}}\left( x \right) + \frac{{\partial {{u}_{1}}}}{{\partial x}}L = u_{1}^{{\left( j \right)}} + \frac{{\partial {{u}_{1}}}}{{\partial x}}L.$

Техника разложения перемещений в (3) эффективно применялась И.А. Куниным [15] при преобразовании многомассовых дискретных систем в квазиконтинуум.

Плотности потенциальной и кинетической энергий для эквивалентного континуума, полученные из (5) и (6), запишутся в виде:

(4)
$\begin{gathered} W = \frac{1}{{2L}}\left[ {{{k}_{1}}{{{\left( {\frac{{\partial {{u}_{1}}}}{{\partial x}}L} \right)}}^{2}} + {{k}_{2}}{{{\left( {{{u}_{2}} - {{u}_{1}}} \right)}}^{2}}} \right. + \\ \left. { + \,\,{{h}_{1}}{{{\left( {\frac{{\partial {{u}_{1}}}}{{\partial x}}L} \right)}}^{3}} + {{h}_{2}}{{{\left( {{{u}_{2}} - {{u}_{1}}} \right)}}^{3}}} \right], \\ \end{gathered} $
(5)
$T = \frac{1}{{2L}}\left[ {{{m}_{1}}{{{\left( {{{{\dot {u}}}_{1}}} \right)}}^{2}} + {{m}_{2}}{{{\left( {{{{\dot {u}}}_{2}}} \right)}}^{2}}} \right].$

Сформируем из (4) и (5) лагранжиан $\mathcal{L} = T - W = \mathcal{L}\left( {{{{\dot {u}}}_{1}},{{{\dot {u}}}_{2}},{{u}_{{1x}}},{{u}_{1}},{{u}_{2}}} \right)$ и воспользуемся уравнениями аналитической механики

$\left\{ \begin{gathered} \frac{\partial }{{\partial t}}\left( {\frac{{d\mathcal{L}}}{{d{{{\dot {u}}}_{1}}}}} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{\partial{ \mathcal{L}}}}{{\partial {{u}_{{1x}}}}}} \right) - \frac{{\partial{ \mathcal{L}}}}{{\partial {{u}_{1}}}} = 0, \hfill \\ \frac{\partial }{{\partial t}}\left( {\frac{{d\mathcal{L}}}{{d{{{\dot {u}}}_{2}}}}} \right) - \frac{{\partial{ \mathcal{L}}}}{{\partial {{u}_{2}}}} = 0 \hfill \\ \end{gathered} \right.$
для получения системы уравнений в перемещениях. В результате получим:

(6)
$\begin{gathered} \frac{{{{m}_{1}}}}{L}{{{\ddot {u}}}_{1}} - {{k}_{1}}L\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{x}^{2}}}} - 3{{h}_{1}}{{L}^{3}}\frac{{\partial {{u}_{1}}}}{{\partial x}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{x}^{2}}}} - \\ - \,\,\frac{{{{k}_{2}}}}{L}({{u}_{2}} - {{u}_{1}}) - \frac{{3{{h}_{2}}}}{{2L}}{{({{u}_{2}} - {{u}_{1}})}^{2}} = 0, \\ \frac{{{{m}_{2}}}}{L}{{{\ddot {u}}}_{2}} - \frac{{{{k}_{2}}}}{L}({{u}_{2}} - {{u}_{1}}) - \frac{{3{{h}_{2}}}}{{2L}}{{({{u}_{2}} - {{u}_{1}})}^{2}} = 0. \\ \end{gathered} $

Перейдем в (6) в движущуюся систему координат ${{\xi }} = x - ct,{\text{\;}}$ 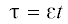, где $c$ – скорость волны, заранее не известная, ${{\varepsilon }}$ – малый параметр, характеризующий отношение максимальной амплитуды перемещения к длине волны. Выбор переменных объясняется тем, что возмущение, распространяясь со скоростью $c$ вдоль оси $x$, медленно эволюционирует во времени из-за нелинейности и дисперсии.

Представим перемещения в виде разложений в ряды по степеням малого параметра

(7)
$\begin{gathered} {{u}_{1}}(\xi ,\tau ) = u_{1}^{{(0)}}(\xi ,\tau ) + \varepsilon u_{1}^{{(1)}}(\xi ,\tau ) + ..., \\ {{u}_{2}}(\xi ,\tau ) = u_{2}^{{(0)}}(\xi ,\tau ) + \varepsilon u_{2}^{{(1)}}(\xi ,\tau ) + ...{\kern 1pt} \,. \\ \end{gathered} $

Подставляя разложения (7) в (6), придем к системе уравнений разного порядка малости по степеням ${{\varepsilon }}$. Нулевое приближение по малому параметру позволяет вычислить значение скорости $c = \sqrt {\frac{{{{k}_{1}}}}{{{{m}_{1}}}}} L$ и определяет связь между перемещениями

(8)
$u_{1}^{{\left( 0 \right)}} = u_{2}^{{\left( 0 \right)}} - \frac{{{{m}_{2}}{{k}_{1}}{{L}^{2}}}}{{{{m}_{1}}{{k}_{2}}}}\frac{{{{\partial }^{2}}u_{2}^{{\left( 0 \right)}}}}{{\partial {{{{\xi }}}^{2}}}}.$

Первое приближение приводит к эволюционному уравнению

(9)
$\begin{gathered} - 2\sqrt {{{m}_{1}}{{k}_{1}}} {{\varepsilon }}\frac{{\partial U}}{{\partial {{\tau }}}} - \frac{{{{m}_{2}}{{k}_{1}}L}}{{{{m}_{1}}}}\frac{{\partial U}}{{\partial {{\xi }}}} + \frac{{2{{m}_{2}}{{k}_{1}}L\sqrt {{{k}_{1}}} }}{{{{k}_{2}}\sqrt {{{m}_{1}}} }}\frac{{{{\partial }^{3}}U}}{{\partial {{{{\xi }}}^{2}}\partial {{\tau }}}} - \\ - \,\,3{{h}_{1}}{{L}^{3}}U\frac{{\partial U}}{{\partial {{\xi }}}} + \frac{{3{{h}_{1}}{{L}^{5}}{{m}_{2}}{{k}_{1}}}}{{{{m}_{1}}{{k}_{2}}}}\frac{{\partial U}}{{\partial {{\xi }}}}\frac{{{{\partial }^{2}}U}}{{\partial {{{{\xi }}}^{2}}}} + \\ + \,\,\frac{{3{{h}_{1}}{{L}^{5}}{{m}_{2}}{{k}_{1}}}}{{{{m}_{1}}{{k}_{2}}}}U\frac{{{{\partial }^{3}}U}}{{\partial {{{{\xi }}}^{3}}}} - 3{{h}_{1}}{{L}^{3}}{{\left( {\frac{{{{m}_{2}}{{k}_{1}}{{L}^{2}}}}{{{{m}_{1}}{{k}_{2}}}}} \right)}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{{{\xi }}}^{2}}}}\frac{{{{\partial }^{3}}U}}{{\partial {{{{\xi }}}^{3}}}} - \\ - \,\,\frac{{3{{h}_{2}}}}{{2L}}{{\left( {\frac{{{{m}_{2}}{{k}_{1}}{{L}^{2}}}}{{{{m}_{1}}{{k}_{2}}}}} \right)}^{2}}{{\left( {\frac{{\partial U}}{{\partial {{\xi }}}}} \right)}^{2}} = 0, \\ \end{gathered} $
где $U = \frac{{{{\partial }^{2}}u_{2}^{{\left( 0 \right)}}}}{{\partial {{{{\xi }}}^{2}}}}.$

Пусть ${{{\xi }} \mathord{\left/ {\vphantom {{{\xi }} {{{{{\xi }}}_{0}}}}} \right. \kern-0em} {{{{{\xi }}}_{0}}}} = X,~$ ${{{\tau }} \mathord{\left/ {\vphantom {{{\tau }} {{{{{\tau }}}_{0}}}}} \right. \kern-0em} {{{{{\tau }}}_{0}}}} = T$, а пространственный и временной масштабы выбраны так, чтобы выполнялось равенство

$\frac{{{{{{\xi }}}_{0}}}}{{{{{{\tau }}}_{0}}}} = \frac{{3{{h}_{1}}{{L}^{3}}}}{{2\sqrt {{{m}_{1}}{{k}_{1}}} {{\varepsilon }}}}.$

В новых переменных уравнение (9) перепишется в виде

(10)
$\begin{gathered} \frac{{\partial U}}{{\partial T}} + {{d}_{1}}\frac{{\partial U}}{{\partial X}} - {{d}_{2}}\frac{{{{\partial }^{3}}U}}{{\partial {{X}^{2}}\partial T}} + U\frac{{\partial U}}{{\partial X}} + \\ + \,\,{{g}_{1}}\frac{{\partial U}}{{\partial X}}\left( {U\frac{{{{\partial }^{2}}U}}{{\partial {{X}^{2}}}}} \right) + {{g}_{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{X}^{2}}}}\frac{{{{\partial }^{3}}U}}{{\partial {{X}^{3}}}} + {{g}_{3}}{{\left( {\frac{{\partial U}}{{\partial X}}} \right)}^{2}} = 0, \\ \end{gathered} $
где

$\begin{gathered} {{d}_{1}} = \frac{{{{m}_{2}}{{k}_{1}}}}{{3{{m}_{1}}{{h}_{1}}{{L}^{2}}}},\,\,\,\,{{d}_{2}} = \frac{{{{m}_{2}}{{k}_{1}}}}{{\varepsilon {{{10}}^{2}}{{m}_{1}}{{k}_{2}}L}},\,\,\,\,{{g}_{1}} = - \frac{{{{{10}}^{{ - 2}}}{{m}_{2}}{{k}_{1}}}}{{{{m}_{1}}{{k}_{2}}}},{\text{\;}} \\ {{g}_{2}} = \frac{{{{{10}}^{{ - 4}}}{{{\left( {{{m}_{2}}{{k}_{1}}} \right)}}^{2}}}}{{{{{\left( {{{m}_{1}}{{k}_{2}}} \right)}}^{2}}}},\,\,\,\,{{g}_{3}} = \frac{{{{h}_{2}}{{{\left( {{{m}_{2}}{{k}_{1}}} \right)}}^{2}}}}{{20{{h}_{1}}{{L}^{3}}{{{\left( {{{m}_{1}}{{k}_{2}}} \right)}}^{2}}}}. \\ \end{gathered} $

Для длинноволновых процессов $\left( {{{{{\xi }}}_{0}}\sim 10L} \right)$, ${{g}_{1}},~{{g}_{2}},~{{g}_{3}} \ll 1$ и (10) переходит в известное в нелинейной волновой динамике уравнение Бенджамина–Бона–Махони:

(11)
$\frac{{\partial U}}{{\partial T}} + {{d}_{1}}\frac{{\partial U}}{{\partial X}} - {{d}_{2}}\frac{{{{\partial }^{3}}U}}{{\partial {{X}^{2}}\partial T}} + U\frac{{\partial U}}{{\partial X}} = 0.$

КВАЗИГАРМОНИЧЕСКИЕ МОДУЛИРОВАННЫЕ ВОЛНЫ

Пусть в цепочке, описываемой уравнением (11), распространяются три волновых пакета (модулированные квазигармонические волны):

(12)
$\begin{gathered} U\left( {X,T} \right) = \sum\limits_{n = 1}^N {{{A}_{n}}\left( {{{\varepsilon }}X,{{\varepsilon }}T} \right)} {\kern 1pt} {{e}^{{i\left( {{{{{\omega }}}_{n}}T - {{q}_{n}}X + \phi _{n}^{{\left( 0 \right)}}} \right)}}} + \\ + \,\,{\text{к}}{\text{.с}}{\text{.}} + {{\varepsilon }}{{Q}_{n}}, \\ \end{gathered} $
где An – комплексные амплитуды, медленно изменяющиеся во времени и в пространстве; $\phi _{n}^{{\left( 0 \right)}}$ – начальные сдвиги фаз; Qn – малые добавки.

Несущие частоты пакетов связаны соотношением

(13)
${{\omega }_{3}} = {{\omega }_{1}} + {{\omega }_{2}}~{\kern 1pt} ,$
а волновые числа – соотношением

(14)
${{q}_{3}} = {{q}_{1}} + {{q}_{2}}.$

Подставляя (12) в уравнение динамики (11) и проводя процедуру усреднения по быстрым переменным [16], приходим к системе

(15)
$\begin{gathered} \frac{{\partial {{A}_{1}}}}{{\partial X}} + \frac{1}{{{{v}_{{{\text{gr}}1}}}}}\frac{{\partial {{A}_{1}}}}{{\partial T}} = - i{{{{\Gamma }}}_{1}}{{A}_{3}}A_{2}^{{\text{*}}},{\text{\;\;}} \\ \frac{{\partial {{A}_{2}}}}{{\partial X}} + \frac{1}{{{{v}_{{{\text{gr}}2}}}}}\frac{{\partial {{A}_{2}}}}{{\partial T}} = - i{{{{\Gamma }}}_{2}}{{A}_{3}}A_{1}^{{\text{*}}},{\text{\;}} \\ \frac{{\partial {{A}_{3}}}}{{\partial X}} + \frac{1}{{{{v}_{{{\text{gr}}3}}}}}\frac{{\partial {{A}_{3}}}}{{\partial T}} = - i{{{{\Gamma }}}_{3}}{{A}_{1}}{{A}_{2}}, \\ \end{gathered} $
где
${{v}_{{{\text{gr}}j}}} = \frac{{{{d}_{1}} - 2{{q}_{j}}{{{{\omega }}}_{j}}{{d}_{2}}}}{{1 + q_{j}^{2}{{{{\omega }}}_{j}}{{d}_{2}}}}$
– групповые скорости;

${{\Gamma }_{j}} = - ~\,\frac{{~{{q}_{j}}}}{{\varepsilon ({{d}_{1}} - 2{{q}_{j}}{{\omega }_{j}}{{d}_{2}})~}}.$

При отсутствии нелинейного взаимодействия (${{{{\Gamma }}}_{j}} = 0$) правые части системы (15) исчезают и каждый волновой пакет распространяется со своей групповой скоростью.

В [17] показано, что в квадратично-нелинейной среде могут сформироваться трехчастотные, параметрически связанные солитоны огибающих. Такие солитоны распространяются с некоторой общей групповой скоростью ${{v}_{{{\text{grс}}}}}$.

Профили солитонов определяются из системы уравнений

(16)
$\begin{gathered} {{v}_{{c1}}}\frac{{d{{B}_{{1c}}}}}{{d{{\theta }_{c}}}} = - {{\Gamma }_{1}}{{B}_{{3c}}}{{B}_{{2c}}},\,\,\,\,~{{v}_{{c2}}}\frac{{d{{B}_{{2c}}}}}{{d{{\theta }_{c}}}} = - {{\Gamma }_{2}}{{B}_{{3c}}}{{B}_{{1c}}}, \\ ~{{v}_{{c3}}}\frac{{d{{B}_{{3c}}}}}{{d{{\theta }_{c}}}} = {{\Gamma }_{3}}{{B}_{{1c}}}{{B}_{{2c}}}, \\ \end{gathered} $
которая получается из системы (15) при нахождении ее квазистационарных решений. Здесь ${{B}_{{nc}}}\left( {{{{{\theta }}}_{c}}} \right)~$ – действительные амплитуды волновых пакетов; ${{{{\theta }}}_{c}} = T - {X \mathord{\left/ {\vphantom {X {{{v}_{{{\text{grc}}}}}}}} \right. \kern-0em} {{{v}_{{{\text{grc}}}}}}}$; ${{v}_{{cj}}} = \frac{1}{{{{v}_{{{\text{gr}}j}}}}} - \frac{1}{{{{v}_{{{\text{grc}}}}}}}.$

Одним из решений системы уравнений (16) является набор из трех квазистационарных профилей амплитуд квазигармонических волн:

(17)
$\begin{gathered} {{B}_{{1c}}} = {{{\rm E}}_{{01}}}{\text{sech}}\left( {{{{{{{\theta }}}_{c}}} \mathord{\left/ {\vphantom {{{{{{\theta }}}_{c}}} {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}}} \right),\,\,\,\,{{B}_{{2c}}} = {{{\rm E}}_{{02}}}{\text{sech}}\left( {{{{{{{\theta }}}_{c}}} \mathord{\left/ {\vphantom {{{{{{\theta }}}_{c}}} {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}}} \right), \\ {{B}_{{3c}}} = {{{\rm E}}_{{03}}}{\text{th}}\left( {{{{{{{\theta }}}_{c}}} \mathord{\left/ {\vphantom {{{{{{\theta }}}_{c}}} {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}}} \right). \\ \end{gathered} $

Амплитуды огибающих ${{E}_{{01}}}$, их длительность ${{T}_{c}}$ и групповая скорость связаны соотношениями

(18)
${{v}_{{nc}}}E_{{0n}}^{2} = {{\Gamma }_{n}}{{T}_{c}}{{E}_{{01}}}{{E}_{{02}}}{{E}_{{03}}}~\left( {n = 1,2,3} \right).$

НЕСИНУСОИДАЛЬНАЯ ЛОКАЛИЗОВАННАЯ ВОЛНА

Кроме решений, описывающих квазигармонические процессы, уравнение (11) имеет точное аналитическое решение в виде уединенной стационарной волны (солитона) [18]:

(19)
$U = 3\left( {V - {{d}_{1}}} \right){\text{sec}}{{{\text{h}}}^{2}}\left[ {\frac{{\sqrt {V - {{d}_{1}}} }}{{2V{{d}_{2}}}}\left( {X - VT} \right)} \right],$
где ${{d}_{2}} > 0,\,\,V > {{d}_{1}}$.

Из (19) следует, что для рассматриваемого метаматериала амплитуда солитона определяется соотношением

(20)
$A = 3\left( {V - \frac{{{{m}_{2}}{{k}_{1}}}}{{3{{m}_{1}}{{h}_{1}}{{L}^{2}}}}} \right),$
а его ширина соотношением

(21)
${{\Delta }} = \frac{{2V{{m}_{2}}{{k}_{1}}}}{{{{\varepsilon }}{{{10}}^{2}}{{m}_{1}}{{k}_{2}}L\sqrt {V - \frac{{{{m}_{2}}{{k}_{1}}}}{{3{{m}_{1}}{{h}_{1}}{{L}^{2}}}}} }}.$

Амплитуда солитона линейно растет с ростом скорости. Для системы с “мягкой” нелинейностью (h1< 0) нарастает стремительнее, чем для систем с “жесткой” нелинейностью (h1> 0). С ростом скорости увеличивается и ширина солитона, что говорит о принципиальном различии свойств солитона (19) и классического солитона Кортевега–де Вриза.

Заметим, что дальнейшие обобщения рассматриваемой модели могут быть получены путем учета соударений внешней и внутренней масс цепочки. Подобные задачи рассматривались в работах [19].

Работа выполнялась при поддержке Российского научного фонда (грант № 21-19-00813).

Список литературы

  1. Буров В.А., Волошинов В.Г., Дмитриев К.В., Поликарпова Н.В. Акустические волны в метаматериалах, кристаллах и структурах с аномальным преломлением // Успехи физ. наук. 2011. Т. 181. № 11. С. 1205−1211.

  2. Norris A.N., Haberman M.R. Introduction to the Special issue on acoustic metamaterials // J. Acoust. Soc. Am. 2012. V. 132. № 4(2). P. 2783–2945.

  3. Acoustic metamaterials and phononic crystals / Ed. Deymier P.A. Berlin: Springer-Verlag, 2013. 378 p.

  4. Acoustic metamaterials: negative refraction, imaging, lensing and cloaking / Eds. Craster R.V., Guenneau S. Dordrecht: Springer, 2013. 323 p.

  5. Бобровницкий Ю.И. Эффективные параметры и энергия акустических матаматериалов и сред // Акуст. журн. 2014. Т. 60. № 2. С. 137–144.

  6. Бобровницкий Ю.И. Модели и общие волновые свойства двумерных акустических метаматериалов и сред // Акуст. журн. 2015. Т. 61. № 3. С. 283–294.

  7. Бобровницкий Ю.И., Томилина Т.М., Лактионова М.М. Дискретная модель акустических метаматериалов с потерями // Акуст. журн. 2016. Т. 62. № 1. С. 3–9.

  8. Федотовский В.С. Поперечные волны в дисперсном метаматериале со сферическими включениями // Акуст. журн. 2015. Т. 61. № 3. С. 311–316.

  9. Li J., Chan C.T. Double-negative acoustic metamaterial // Phys. Rev. 2004. E 70. 055602.

  10. Fang N., Xi D., Xu J., Ambati M., Srituravanich W., Sun C., Zhang X. Ultrasonic metamaterials with negative modulus // Nat. Mater. 2006. V. 5. P. 452–456.

  11. Ding Y., Liu Z., Qiu C., Shi J. Metamaterial with simultaneously negative bulk modulus and mass density // Phys. Rev. Lett. 2007. V. 99. P. 093904.

  12. Cheng Y., Xu J.Y., Liu X.J. One-dimensional structured ultrasonic metamaterials with simultaneously negative dynamic density and modulus // Phys. Rev. B. 2008. V. 77. P. 045134.

  13. Chan C.T., Li J., Fung K.H. On extending the concept of double negativity to acoustic waves // J. Zhejiang Univ. SCIENCE A. 2006. V. 7(1). P. 24–28.

  14. Huang H.H., Sun C.T., Huang G.L. On the negative effective mass density in acoustic metamaterials // Int. J. Eng. Sci. 2009. V. 47. P. 610−617.

  15. Kunin I.A. Elastic Media with Microstructure I & II. Springer-Verlag, Berlin, Heidelberg, New York, 1982–1983.

  16. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука, 1984. 432 с.

  17. Сухоруков А.П. Нелинейные волновые взаимодействия в оптике и радиофизике. М.: Наука, Физматлит, 1988. 232 с.

  18. Селезов И.Т., Корсунский С.В. Нестационарные и нелинейные волны в электропроводящих средах. Киев: Наукова думка, 1991. 200 с.

  19. Крупенин В.Л. Об описании сильно нелинейных вибропроводящих и виброгенерирующих сред // Проблемы машиностроения и надежности машин. 2016. № 4. С. 9−19.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал