Акустический журнал, 2022, T. 68, № 4, стр. 385-390

ВВЕДЕНИЕ

Во многих практических акустических задачах находят применение резонаторы в виде плоскопараллельных слоев волновых размеров. В качестве примеров можно упомянуть задачи, связанные с созданием мощных источников когерентного излучения, локальных областей с высокими интенсивностями ультразвука для реализации технологических процессов и т.д.

Резонаторы, как известно, представляют собой колебательные системы, предназначенные для создания и накопления энергии колебаний за счет резонанса при совпадении частоты вынуждающей силы с одной из собственных частот резонатора. Важнейшей характеристикой резонатора является его добротность

или связанная с ней величина – декремент затухания ${{\delta }} = \frac{{{\pi }}}{Q}$ [1]. В формуле (1) ${{f}_{0}}$ – собственная частота резонатора, ${{\alpha }}$ – временной коэффициент затухания амплитуды колебаний.

Основными факторами, препятствующими достижению больших плотностей энергии в резонаторе, т.е. снижающими добротность, являются внутренние потери акустической энергии в рабочем теле резонатора, а также потери, связанные с переизлучением акустической энергии через границы резонатора.

В твердотельном резонаторе в виде плоскопараллельного слоя, окруженного с обоих сторон жидкой или газообразной средой, амплитудный коэффициент временного затухания находится из дисперсионного уравнения и равен [2]

где ${{\omega }}$ – частота колебаний, $c$ и $с{\kern 1pt} '$ – реальная и мнимая части скорости звуковых волн в материале резонатора, $\left| R \right|$ – модуль коэффициента отражения от границ резонатора, $l$ – толщина резонатора. В (2) первое слагаемое представляет собой часть общего поглощения, связанную с превращением энергии колебаний в тепло в объеме резонатора, а второе – с переизлучением границ резонатора. При этом, как видно из (2), влияние второго фактора усиливается для резонаторов малых физических размеров $l$. Для резонаторов со свободными границами повышение их добротности связано с помещением в разреженные среды, однако при этом практически исключается возможность отвода тепла, выделяющегося за счет объемных потерь в материале резонатора, возникают технические проблемы при реализации крепления и т.д. Создание же твердотельных резонаторов высокой добротности с акустически жесткими границами для реальных материалов выглядит проблематичным. В приложениях важной может также оказаться возможность вывода накопленной в резонаторе колебательной энергии. Для резонаторов с акустически жесткими или мягкими границами это, очевидно, невозможно. Таким образом, задача исследования возможности управления прозрачностью границ резонаторов является актуальной.

1. ПОСТАНОВКА ЗАДАЧИ

Для управления прозрачностью границ резонатора можно использовать физические поля, например, электрическое. В такой постановке задача выглядит естественной для пьезоэлектриков, поскольку и сами колебания в пьезоэлектрических резонаторах возбуждаются электрическим полем. Возможности электрического управления параметрами пьезоизлучателей и волноводов, например, для излучения коротких акустических импульсов, рассматривались ранее в статьях [3–5].

Рассмотрим вначале установившиеся продольные колебания частоты ${{\omega }}$ в плоскослоистой структуре, показанной на рис. 1. Исследуемая электромеханическая система состоит из четырех слоев пьезоэлектрика и ограничена плоскостями $z = 0; \pm {{l}_{1}};~ \pm {{l}_{2}}$. Удельный волновой импеданс слоев равен ${{z}_{p}}$. Направление вектора поляризации P пьезоэлектрика совпадает с осью z для слоев, ограниченных плоскостями $z = 0;\,{{l}_{1}};\,{{l}_{2}}$ и противоположно направлению оси z для слоев, ограниченных плоскостями $z = 0; - {{l}_{1}}; - {{l}_{2}}$. Слева и справа рассматриваемая структура окружена упругой средой с удельным волновым импедансом продольных волн ${{z}_{0}}$. Возбуждение механических колебаний происходит за счет приложения электрических потенциалов ${{{{\varphi }}}_{1}}$ и ${{{{\varphi }}}_{2}}$ к электродам, расположенным на границах $z = 0;\, \pm {{l}_{1}};\,~ \pm {{l}_{2}}$, как показано на рис. 1. Потенциал электрода, расположенного в сечении z = 0, принимается равным нулю.

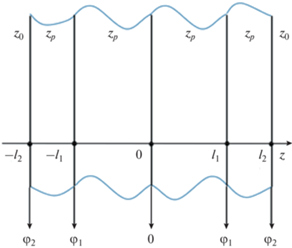
В отсутствие потенциалов звукопрозрачность границ структуры $z = \pm {{l}_{2}}$ определяется только соотношением импедансов ${{z}_{p}}$ и ${{z}_{0}}$. В частном случае ${{z}_{p}} = {{z}_{0}}$ структура вообще не будет проявлять резонансных свойств.

Как указывалось выше, высокие значения добротности рассматриваемого резонатора могут быть достигнуты при акустически непрозрачных границах С. Учитывая, что в плоских бегущих волнах в средах, удовлетворяющих закону Гука, механические напряжения T и колебательная скорость ${{\dot {\xi }}}$ связаны простой функциональной зависимостью $T = \pm {{z}_{p}}{{\dot {\xi }}}$, легко прийти к выводу, что для устранения оттока энергии из резонатора возможны три варианта граничных условий:

– акустически жесткие границы ${{\left. {\dot {\xi }} \right|}_{с}} = 0$;

– свободные границы, где ${{\left. T \right|}_{с}} = 0$;

– границы, на которых одновременно выполнены условия ${{\left. {\dot {\xi }} \right|}_{с}} = 0$ и ${{\left. T \right|}_{с}} = 0$.

Первые два варианта хорошо известны и обсуждались выше. Рассмотрим электромеханическую задачу о колебаниях в системе (рис. 1) с граничными условиями третьего типа. В этом случае решение задачи очевидно не будет зависеть от акустических свойств среды ${{z}_{0}}$, окружающей колебательную систему.

2. РЕШЕНИЕ ДЛЯ СТАЦИОНАРНОГО РЕЖИМА РАБОТЫ РЕЗОНАТОРА

В силу симметрии механических и электрических свойств системы достаточно найти решение электромеханической задачи справа от плоскости $z = 0$, заменив влияние ее левой части условиями на акустически жесткой границе.

Рассматривается краевая задача

где ${{T}^{{\left( {1,2} \right)}}}$, ${{{{\xi }}}^{{\left( {1,2} \right)}}}$ – комплексные амплитуды z-компонент тензора механических напряжений и смещений в первом $(0 < z < {{l}_{1}})$ и втором $({{l}_{1}} < z < {{l}_{2}})$ слоях пьезоэлектрика, соответственно; ${{E}^{{\left( {1,2} \right)}}} = - \frac{{d{{\varphi }}}}{{dz}}$ и ${{D}^{{\left( {1,2} \right)}}}$ – комплексные амплитуды z-компонент векторов напряженности и индукции электрического поля; ${{\rho }}$ – плотность пьезосреды; ${{\omega }}$ – круговая частота. В (3) свойства пьезосреды описываются соответствующими компонентами электроупругой матрицы материала, где ${{h}_{{33}}}$ – пьезоконстанта деформации; ${{\beta }}_{{33}}^{S}$ – диэлектрическая непроницаемость; $c_{{33}}^{D}$ – упругий модуль [6]. В (3) предполагается, что слои пьезоэлектрика имеют тождественные электроупругие матрицы и плотность.

Решение (3) удобно записывать в обезразмеренном виде, введя следующие обозначения: $a = \frac{{{{l}_{2}}}}{{{{l}_{1}}}}$; пространственная переменная ${{z}_{1}} = \frac{z}{{{{l}_{1}}}}$; фазовая переменная ${{{{\varphi }}}_{1}} = k{{l}_{1}}$; волновое число $k = \frac{{{\omega }}}{{v_{3}^{D}}}$; скорость продольных волн в пьезоэлектрике $v_{3}^{D} = \sqrt {\frac{{c_{{33}}^{D}}}{{{\rho }}}} ~$; квадрат коэффициента электромеханической связи пьезоматериала $k_{t}^{2} = \frac{{h_{{33}}^{2}}}{{{{\beta }}_{{33}}^{S}c_{{33}}^{D}}}$; коэффициент электромеханической трансформации $N = \frac{{{{h}_{{33}}}C_{1}^{s}}}{S}$, где S – площадь поперечного сечения структуры, $C_{1}^{s}$ – электрическая емкость между электродами в сечениях $z = 0$ и $z = {{l}_{1}}$.

Собственные частоты рассматриваемой электромеханической системы находятся из уравнения

Решение задачи (3) для полей $T$ и ${{\dot {\xi }}}$ представляет собой кусочно-непрерывные на отрезке $\left[ {0,a} \right]$ функции вида

Найденные решения (5) и (6), с учетом симметрии, могут быть продолжены на весь отрезок $\left[ { - a,a} \right]$, занимаемый резонатором.

В решение задачи также входят выражения для отношений возбуждающих напряжений ${{U}_{1}}$, ${{U}_{2}}$ и токов ${{I}_{1}}$, ${{I}_{2}}$, протекающих через поперечные сечения $z = {{z}_{{1,2}}}$ ($0 < {{z}_{1}} < {{l}_{1}},~{{l}_{1}} < {{z}_{2}} < {{l}_{2}})$ структуры, при условии непроницаемости ее внешних границ

Отношение токов возбуждения ${{I}_{{e1}}}$, ${{I}_{{e2}}}$ электродов $z = \pm {{l}_{1}}$ и $z = \pm {{l}_{2}}$ определяется из выражения

Рассчитанные по формулам (5), (6) нормированные распределения амплитуд механических напряжений и скоростей смещений в рассматриваемой электромеханической системе на трех первых модах колебаний приведены на рис. 2а и 2б, соответственно. Расчеты выполнены для значений параметров системы $a = 1.6$ и пьезоэлектрика $k_{t}^{2} = 0.42$.

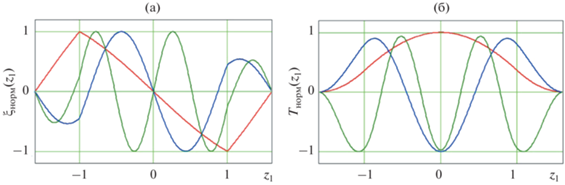
Как видно из рис. 2, на границах исследуемой структуры условие акустической непроницаемости третьего типа левой и правой границ колебательной системы выполняется.

Накопленная в системе энергия может быть высвобождена после отключения электрического поля, обеспечивающего непроницаемость ее границ.

3. ПЕРЕХОДНОЕ ИЗЛУЧЕНИЕ

Полученные результаты для установившихся колебаний рассматриваемой электромеханической системы могут быть использованы для расчета формы волн, переизлучаемых во внешнюю среду после выключения электрического поля. В простейшем случае, когда импедансы пьезоэлектрика структуры и окружающей среды равны (${{z}_{p}} = {{z}_{0}}$), форма профиля прямой ${{T}_{r}}\left( \zeta \right)$ и обратной ${{T}_{l}}\left( {{\eta }} \right)$ волн может быть легко определена по формулам

где $\zeta = t - \frac{z}{{v_{3}^{D}}}$, ${{\eta }} = t + \frac{z}{{v_{3}^{D}}}$, ${{t}_{0}}$ – момент выключения электрического поля.

Как следует из (10) и (11), форма профиля волн, излучаемых из области резонатора после “открытия” его границ, зависит от возбуждаемой моды и момента выключения возбуждающего колебания электрического поля.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Нестационарные режимы работы пьезорезонатора с управляемой прозрачностью границ исследовались методами конечно-элементного анализа в среде Comsol multiphysics в одномерной постановке. Резонатор представлял собой равнотолщинную четырехслойную структуру $\left( {a = 2} \right)$ из пьезокерамики PZT-5A с толщиной слоя 1.95 мм. Ось z нормальна к границам структуры. Левое и правое полупространства заполнялись средой, механические свойства которой совпадают со свойствами пьезокерамики PZT-5A. Таким образом, в отсутствие на электродах структуры электрических напряжений, среда представляет собой однородное упругое пространство. Гармонические колебания возбуждались подачей на электроды ($z = 1.95{\text{\;мм}}$, $z = 2.90{\text{\;мм}}$) импульсного сигнала с гармоническим заполнением частоты ${{f}_{0}} = 372{\text{\;кГц}}$ и плавно нарастающей амплитудой (рис. 3).

Длительность импульса составляла N = 24 полных периода несущей частоты. После достижения амплитуд возбуждающих электрических напряжений на электродах ${{U}_{1}} = 1$ В и ${{U}_{2}} = 4.85$ В, соответственно, электрическое поле выключалось. Точка наблюдения располагалась в правом полупространстве на расстоянии $z = 10~\,\,{\text{мм}}$ от начала координат.

На рис. 4 представлены пространственные распределения z-компоненты механических смещений и тензора напряжений в момент перед выключением электрического поля, когда они достигли наибольшей амплитуды. Видно, что за пределами резонатора амплитуда колебаний существенно меньше, чем внутри структуры.

В момент выключения поля граница резонатора $z = 2.90{\text{\;мм}}$ становится прозрачной, и накопленная колебательная энергия переизлучается в окружающее пространство в виде короткого акустического импульса (рис. 5).

Как указывалось выше (10), (11), форма акустического импульса, переизлучаемого структурой, зависит от фазы колебаний в момент выключения. На рис. 6 представлены формы волны смещений (z-компоненты) в точке наблюдения при различных значениях фазы колебаний ${{\omega }}{{t}_{0}}$ в момент выключения поля.

Как следует из рис. 6, подбирая момент выключения электрического поля, можно управлять формой излучаемого акустического импульса от однополярной обоих знаков до двуполярной, в виде одного периода колебания, близкого к синусоидальному.

ЗАКЛЮЧЕНИЕ

Показана возможность управления акустической прозрачностью границ в пьезоэлектриках с использованием электрического поля. Электромеханические системы, подобные рассмотренной, могут быть использованы для создания источников мощных коротких акустических импульсов, а электрическое поле в них играет роль своеобразной накачки системы колебательной энергией. Рассмотренная задача может рассматриваться как один из подходов к созданию акустических лазеров.

Автор выражает благодарность М.А. Миронову за полезные рекомендации и обсуждение результатов работы.