1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 68, № 2, 2022

Акустический журнал, 2022, T. 68, № 2, стр. 218-232

Фазовые модуляции в речевом сигнале

В. Н. Сорокин a, *, А. С. Леонов b

a Институт проблем передачи информации, Российская академия наук
Москва, Россия

b Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия

* E-mail: vns@iitp.ru

Поступила в редакцию 02.11.2021
После доработки 25.11.2021
Принята к публикации 30.11.2021

Полный текст (PDF)

Аннотация

Исследуются математические модели фазовой функции и ее параметров в задачах анализа речевого сигнала. Фазовый спектр речевого сигнала вычисляется через преобразование Гильберта сигналов на выходе гребенки гамма-тон фильтров. Рассматриваются кратковременные и долговременные модуляции линейной компоненты фазы, производных фазы по частоте, времени и смешанной производной. Описывается метод сегментирования гласных звуков путем агрегирования коэффициентов корреляции фазовых параметров. Выполнены эксперименты по оценке формантных частот, а также частоты основного тона, моментов начала и конца действия голосового источника.

Ключевые слова: речевой сигнал, фазовая функция, частота основного тона, формантные частоты, момент начала голосового источника, момент конца голосового источника

ВВЕДЕНИЕ

Текущий амплитудный спектр речевого сигнала (сонограмма, “видимая речь”) адекватно отображает акустические характеристики процесса речеобразования, по которым можно визуально судить о резонансах речевого тракта, спектре звуков с турбулентным источником возбуждения колебаний и об активности голосового источника. Поэтому анализ такого динамического спектра доминирует в речевых технологиях. Существуют два направления в использовании динамического спектра речевого сигнала. Первое возникло при исследовании методов автоматического распознавания речи и связано с поиском различительных признаков фонетических сегментов. Это оказалось трудной задачей в силу разнообразных видов изменчивости акустического представления таких сегментов. К тому же, для каждого языка необходимо определять свои признаки.

Другое направление состоит в использовании статистики параметров последовательных фрагментов текущего спектра. Это направление технологически более простое, чем поиск признаков речевых элементов. Наиболее успешным здесь оказалось использование в качестве первичных параметров коэффициентов кепстрального преобразования спектра в шкале мел и описание плотности распределения этих параметров смесью нормальных распределений с последующим применением метода скрытых марковских моделей или нейронных сетей. Основанные на этих принципах алгоритмы автоматического распознавания речи оказались достаточно успешными в некоторых областях взаимодействия человека с информационными системами. Тем не менее, устойчивость таких алгоритмов к помехам, искажениям и дикторской изменчивости еще далека от необходимой. Поэтому назрела необходимость в поиске новых способов исследования речевого сигнала, отличных от применения спектра амплитуд. Таким способом является представление параметров речевого сигнала в фазовой области.

В противоположность амплитудно-частотному спектру, фазовый спектр не поддается непосредственной интерпретации в терминах акустики речеобразования. Анализ условий распространения речевого сигнала в пространстве показывает, что фаза компонент речевого сигнала зависит от расстояния и направления на микрофон. Кроме того, фазы претерпевают искажения из-за реверберации помещений, в результате чего вместе с текущим речевым сигналом в микрофон поступают затухающие колебания от предшествующего сегмента речи. Это приводит к неустойчивости фазовых параметров, зависящих от акустических процессов речеобразования. В течение некоторого времени считалось, что фазы не существенны для восприятия фонетических характеристик речи. Поэтому фазовому спектру уделялось мало внимания в задачах идентификации диктора и распознавания речи.

Затем, однако, влияние фазового спектра на восприятие речи выявилось в фазовом вокодере [1, 2]. В этом вокодере отдельно передается огибающая амплитудного спектра и производная от фазы по времени. Обнуление фазовой компоненты или замена ее на случайный сигнал приводят к возникновению паразитного периодического сигнала или шепотному типу речи. Таким образом, фаза сигнала в вокодере оказывается существенной и содержит информацию об источниках возбуждения. Была также обнаружена возможность реконструкции речевого сигнала только по фазе [3]. Это дает основания для поиска параметров речевого сигнала в фазовой области в дополнение к традиционным методам, основанным на анализе амплитудного спектра.

С точки зрения математики, возможность эффективного использования фазового спектра для анализа абстрактного сигнала состоит в ответе на вопрос: содержит ли фазовый спектр этого сигнала информацию, дополняющую информацию от амплитудного спектра. Иначе говоря, могут ли действительная и мнимая части комплексного спектра сигнала быть получены друг из друга. Если это так, то использовать фазовый спектр не имеет смысла. Такая ситуация возникает в некоторых математических моделях сигнала. Например, это реализуется, если сигнал порождается системой дифференциальных уравнений с постоянными коэффициентами или полюса этой системы находятся внутри единичного круга z-преобразования [4].

Однако, независимость действительной и мнимой компонент спектра речевого сигнала была продемонстрирована в экспериментах с восприятием речевого сигнала, синтезированного путем обратного преобразования Фурье от амплитудного или фазового спектра. Так, в [5] было показано, что при определенных параметрах преобразования Фурье восприятие взрывных согласных в сигнале от инвертированного фазового спектра заметно лучше, чем в сигнале от инвертированного спектра амплитуд. Аналогичные эксперименты, выполненные в [6, 7], подтвердили, что разборчивость речи для инвертированного фазового спектра оказалась заметно выше разборчивости сигнала, сформированного путем обратного преобразования Фурье от амплитудного спектра. Было также установлено, что искажение фазы ухудшает восприятие речи [8].

В речевых технологиях вместо фазовой функции используются производные от фазы по частоте и времени. Отрицательное значение производной по частоте, поделенное на 2π, имеет размерность времени и называется групповой задержкой. Производная по времени, поделенная на 2π, имеет размерность частоты и называется мгновенной частотой. И групповая задержка, и мгновенная частота исследуются с целью определения параметров голосового источника и формантных частот.

В работах [7, 9] амплитудный спектр речевого сигнала воспроизводился (с определенными искажениями) функцией, равной обратному значению модуля мгновенной частоты или девиации мгновенной частоты от аргумента при Фурье анализе на интервале в 30–40 мс. B [10] было найдено, что спектр групповой задержки более устойчив к аддитивным шумам при восстановлении формантной структуры, чем спектр амплитуд. В [11] показано, что при определенных условиях формантные частоты речевого сигнала могут определяться по положению экстремумов производной фазы по частоте и смешанной производной фазы по частоте и времени.

Отсюда следует, что фазовый спектр содержит, по крайней мере, не меньше информации об артикуляции, чем амплитудный спектр. Различные модификации способа вычисления групповой задержки используются для определения моментов открытия и закрытия голосовой щели, анализа импульса голосового возбуждения, анализа формантных частот и определения частоты основного тона, распознавания речи и диктора, диагностики заболеваний гортани [12–16].

Непосредственный анализ фазового спектра речевого сигнала затруднителен вследствие разрывности фазовой функции, которая усложняет ее математический анализ, а также препятствует визуальному изучению ее свойств. Тем не менее, в [17] удалось математически изучить распределения максимального значения интервалов между нулями разрывной фазово-частотной функции на вокализованных сегментах речевого сигнала. Численные эксперименты на синтетической и реальной речи показали, что период основного тона, длительность действия голосового источника, моменты открытия и закрытия голосовой щели определяются по экстремумам этого распределения с практически допустимой погрешностью. Отметим, что из разрывной фазовой функции можно получить непрерывную. Простейший и очевидный способ компенсации разрывов состоит в добавлении 2π в каждой точке разрыва, но он обладает определенными недостатками. Обзор методов, использующих Фурье или z-преобразование для трансформации разрывной фазовой функции в непрерывную, представлен в [18].

Цель данной работы состоит в разработке математических моделей и компьютерном моделировании параметров фазовой функции, которые оказались бы информативными для сегментации речевого сигнала на фонетические элементы, для детектирования вокализованных сегментов, а также для оценки параметров голосового источника и формантных частот. Будет также рассмотрена возможность визуализации этих параметров в виде фазограмм как функций от частоты и времени аналогично сонограммам.

1. ПАРАМЕТРЫ ФАЗОВОЙ ФУНКЦИИ

1.1. Кратковременный комплексный спектр сигнала действительной переменной

Существуют различные способы вычисления динамического комплексного спектра абстрактного сигнала, представленного в виде действительной функции $s(t),\,\,0 \leqslant t < \infty $. Наиболее распространено кратковременное преобразование Фурье в скользящем окне w

(1)
$S({{\omega }},t) = \int\limits_0^\infty {w(t - {{\tau }})s({{\tau }}){{e}^{{ - j{{\omega \tau }}}}}d{{\tau }}} {\kern 1pt} .$

Анализ фаз в речевом сигнале также обычно выполняется с помощью комплексного кратковременного преобразования Фурье. Такой подход позволяет использовать соответствующий математический аппарат в задачах подавления шумов, распознавания речи и диктора. При этом большую роль играет эвристический выбор параметров анализа в зависимости от конкретной задачи. Экспериментально установлено, что ширина и вид окна w существенно влияют на вычисленный комплексный спектр и характеристики фазовой функции.

Комплексный кратковременный спектр можно представить как

(2)
$S(\omega ,t) = u(\omega ,t) + jv(\omega ,t) = A(\omega ,t){{e}^{{j\varphi (\omega ,t)}}},$
где$A(\omega ,t)$ – амплитудный спектр, а ${{\varphi }}({{\omega }},t)$ – фазовый спектр. Связи между функциями, входящими в (2), имеют вид
$\begin{gathered} u({{\omega }},t) = A({{\omega }},t)\cos {{\varphi }}({{\omega }},t), \\ v({{\omega }},t) = A({{\omega }},t)\sin {{\varphi }}({{\omega }},t), \\ \end{gathered} $
где

$A({{\omega }},t) = \left| {S({{\omega }},t)} \right| = {{[u_{{}}^{2}({{\omega }},t) + v_{{}}^{2}({{\omega }},t)]}^{{1/2}}},$
$\varphi (\omega ,t) = \left\{ \begin{gathered} {\text{arctg}}\frac{{v(\omega ,t)}}{{u(\omega ,t)}},\,\,\,\,u(\omega ,t) \geqslant 0 \hfill \\ \pi + {\text{arctg}}\frac{{v(\omega ,t)}}{{u(\omega ,t)}},\,\,\,\,u(\omega ,t) < 0 \hfill \\ \end{gathered} \right..$

Вместо $A({{\omega }},t)$ часто используют логарифмический амплитудный спектр ${{S}_{e}}(\omega ,t) = 10\lg {{A}^{2}}(\omega ,t)$. Представленный в виде двумерного изображения, он называется сонограммой или “видимой речью”.

Помимо кратковременного преобразования Фурье (1), существуют и другие способы формирования амплитудных и фазовых характеристик речевого сигнала. В частности, это возможно при использовании аналитического сигнала [4], когда комплексный сигнал x(t) получается из реального сигнала s(t) с помощью преобразования Гильберта:

$x(t) = s(t) + jH\{ s(t)\} .$

Здесь H – преобразование Гильберта, которое формально определяется как

$H\{ s(t)\} = \frac{1}{{{\pi }}}\int\limits_{ - \infty }^\infty {\frac{{s({{\tau }})}}{{t - {{\tau }}}}} d{{\tau }}{\text{.}}$

Функция $x(t)$ может быть записана как

$x(t) = A({{\omega }},t){{e}^{{j{{\varphi }}({{\omega }},t)}}},$
и $A({{\omega }},t)$ интерпретируется как мгновенная амплитуда, а ${{\varphi }}({{\omega }},t) = Im\{ ln(x(t))\} $ – как мгновенная фаза.

Техническое преимущество аналитического сигнала состоит в возможности его дискретизации с вдвое меньшей частотой Найквиста–Котельникова, что ускоряет его обработку. В применении к задачам речевых технологий аналитические сигналы вычисляются гребенкой фильтров, что, в частности, удовлетворяет требованию узкополосности при нахождении мгновенной частоты. Экспериментально показано, что аналитический сигнал на выходе каждого фильтра обладает устойчивостью относительно аддитивных помех и мультипликативного искажения речевого сигнала [19, 20].

Вычисление аналитического сигнала с помощью преобразования Гильберта может оказаться подходящим методом в исследовании свойств фазового спектра сигнала на выходе гребенки фильтров. В речевых исследованиях часто используются фильтры Габора с линейной фазовой характеристикой, что обеспечивает минимальные искажения фаз речевого сигнала. Однако представляется целесообразным уже на этапе первичного анализа применить фильтры, соответствующие какой-либо модели периферического слухового анализа. Одна из таких моделей содержит так называемые гамма-тон фильтры, предложенные в [21, 22].

1.2. Модель кратковременного фазового спектра речевого сигнала

Условия генерирования речевого сигнала, его распространения в пространстве и регистрации приемниками звука определяют состав динамического комплексного спектра речевого сигнала в виде нескольких компонент:

$S({{\omega }},t) = {{S}_{N}}({{\omega }},t) + {{S}_{M}}({{\omega }},t){{S}_{{es}}}({{\omega }},t){{S}_{{vt}}}({{\omega }},t),$
где ${{S}_{N}}({{\omega }},t)$ – спектр аддитивного шума среды и наводки электрических сетей 50 Гц; ${{S}_{M}}({{\omega }},t)$ – искажение речевого сигнала при распространении от диктора до микрофона c передаточной функцией микрофона, ${{S}_{{es}}}({{\omega }},t)$ – спектр источника возбуждения акустических колебаний в речевом тракте; ${{S}_{{vt}}}({{\omega }},t)$ – динамическая передаточная функция речевого тракта.

Допустим, что шум среды пренебрежимо мал или полностью компенсирован средствами шумоподавления, так что ${{S}_{N}}({{\omega }},t) = 0$. Передаточная функция микрофона постоянна во времени, и, если расстояние и направление диктора на микрофон не изменяются в процессе разговора, то передаточная функция среды и микрофона зависит только от частоты ${{S}_{M}}({{\omega }})$, и

$S({{\omega }},t) = {{S}_{M}}({{\omega }}){{S}_{{es}}}({{\omega }},t){{S}_{{vt}}}({{\omega }},t).$

Воспользуемся представлением спектра $S(\omega ,t) = A(\omega ,t){{e}^{{j\varphi (\omega ,t)}}}$. Тогда

$\begin{gathered} \ln S({{\omega }},t) = \ln A({{\omega }}) + j{{\varphi }}({{\omega }}) = \ln {{A}_{M}}({{\omega }}) + \\ + \,\,\ln {{A}_{{es}}}({{\omega }},t) + \ln {{A}_{{vt}}}({{\omega }},t) + \\ + \,\,j[{{{{\varphi }}}_{M}}({{\omega }}) + {{{{\varphi }}}_{{es}}}({{\omega }},t) + {{{{\varphi }}}_{{vt}}}({{\omega }},t)]. \\ \end{gathered} $

В исходном виде динамическая фаза комплексного спектра ${{\varphi }}({{\omega }},t)$ получается при каждом фиксированном $t$ как разрывная (unwrapped) функция, которую обозначим как ${{\hat {\varphi }}}({{\omega }},t)$. Разрывная фазовая функция неудобна для визуального анализа, но все же в ней содержится существенная информация о моментах начала и конца действия голосового источника. Эти параметры можно определить по экстремумам функции ${{\theta }}(t)$, которая представляет собой для каждого момента времени $t$ максимальное значение длины интервала между нулями функции $\hat {\varphi }(\omega ,t)$ [17]. Ниже будет показано, что ${{\theta }}(t)$ также может использоваться в детекторе активности голосового источника.

В отличие от сонограммы, фазограмма, т.е. графическое представление функции фазы, как разрывной $\hat {\varphi }(\omega ,t)$, так и непрерывной $\varphi (\omega ,t)$, практически не поддаются визуальному анализу. На рис. 1 видно, что эти функции, в противоположность сонограмме, не демонстрируют явных отличий на слове /восемь/ от паузы.

Рис. 1.

Сонограмма, разрывная фаза и непрерывная фаза.

Фаза, создаваемая передаточной функцией микрофона ${{{{\varphi }}}_{M}}({{\omega }})$, не зависит от времени; спектр ${{{{\varphi }}}_{{vt}}}({{\omega }},t)$ определяется полосой частот артикуляторных движений <20 Гц; фазовый спектр ${{{{\varphi }}}_{{es}}}({{\omega }},t)$ зависит от частоты колебаний источника голосового возбуждения в диапазоне 60–400 Гц, а турбулентный источник возбуждения содержит частоты выше 1000 Гц. Поэтому частная производная по времени от фазы не содержит характеристик среды и микрофона:

$\frac{{\partial {{\varphi }}({{\omega }},t)}}{{\partial t}} = \frac{{\partial {{{{\varphi }}}_{{es}}}({{\omega }},t)}}{{\partial t}} + \frac{{\partial {{{{\varphi }}}_{{vt}}}({{\omega }},t)}}{{\partial t}},$
а компоненты этой производной, зависящие от источника возбуждения или параметров речевого тракта, можно разделить фильтрацией в частотной или временной областях. В терминах действительной и мнимой частей комплексного спектра производная от фазы по времени есть
$\begin{gathered} \frac{{\partial {{\varphi }}({{\omega }},t)}}{{\partial t}} = \frac{{u({{\omega }},t)\dot {v}({{\omega }},t) - v({{\omega }},t)\dot {u}({{\omega }},t)}}{{{{u}^{2}}({{\omega }},t) + {{v}^{2}}({{\omega }},t)}} = \\ = \frac{{u({{\omega }},t)\dot {v}({{\omega }},t) - v({{\omega }},t)\dot {u}({{\omega }},t)}}{{{{{\left| {S({{\omega }},t)} \right|}}^{2}}}}, \\ \end{gathered} $
где точка сверху обозначает производную по времени. Функция
$Q({{\omega }},t) = \frac{1}{{2{{\pi }}}}\frac{{\partial {{\varphi }}({{\omega }},t)}}{{\partial t}}$
называется мгновенной частотой.

Фильтруя производную фазы по времени в разных частотных полосах или сглаживая ее на интервалах разной длины, мы обнаруживаем разные свойства речевого сигнала. Сглаживание на интервале около 40 мс выявляет неоднородности, коррелированные с артикуляторными движениями и медленными акустическими процессами, тогда как сглаживание на коротких интервалах (порядка 3 мс) позволяет детектировать присутствие голосового источника возбуждения и оценить период основного тона.

Наблюдения за фазовой функцией речевого сигнала показывают, что она содержит значительную линейную составляющую, которая, в отличие от нелинейной компоненты, мало влияет на восприятие речи [6]. Поэтому целесообразно представить фазу как сумму двух функций – линейной по частоте ${{\varphi }_{L}}(\omega ,t) = k(t)\omega $ и нелинейной компонент ${{\varphi }_{A}}(\omega ,t)$:

${{\varphi }_{{}}}(\omega ,t) = {{\varphi }_{L}}(\omega ,t) + {{\varphi }_{A}}(\omega ,t).$

В нашей работе считается, что коэффициент $k(t)$ вычисляется на используемом интервале частот $[{{\omega }_{0}},{{\omega }_{{\max }}}]$ как

${{k}_{\varphi }}(t) = \frac{{\varphi ({{\omega }_{{\max }}},t) - \varphi ({{\omega }_{0}},t)}}{{{{\omega }_{{\max }}} - {{\omega }_{0}}}}.$

Свойства этих компонент заметно отличаются в различных артикуляторных и акустических процессах, протекающих в речевом сигнале.

1.3. Модели параметров фазовой функции

Некоторые элементарные свойства фазовой функции можно установить, анализируя идеализированные модели речевого тракта. Рассмотрим простейшую модель затухающих колебаний гармонического осциллятора с собственной частотой ${{\omega }_{0}}$ и декрементом затухания $\sigma $ (${{\omega }_{0}} > \sigma $). Исследуем ее отклик $s(t) = y(t)$ на δ-импульс, воздействующий на осциллятор в момент ${{t}_{0}}$, решая задачу

(3)
$\left\{ \begin{gathered} \ddot {y} + 2\sigma \dot {y} + \omega _{0}^{2}y = \delta (t - {{t}_{0}}), \hfill \\ y(0) = \dot {y}(0) = 0. \hfill \\ \end{gathered} \right.$

Преобразование Фурье$F[y]$ этого решения есть:

${{( - j\omega )}^{2}}F[y] + 2\sigma ( - j\omega )F[y] + \omega _{0}^{2}F[y] = {{e}^{{ - j\omega {{t}_{0}}}}}.$

Отсюда

$\begin{gathered} F[y] = \frac{{{{e}^{{ - j\omega {{t}_{0}}}}}}}{{(\omega _{0}^{2} - {{\omega }^{2}}) - 2j\sigma \omega }} = \\ = {{e}^{{ - j\omega {{t}_{0}}}}}\frac{{(\omega _{0}^{2} - {{\omega }^{2}}) + 2j\sigma \omega }}{{{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}}}. \\ \end{gathered} $

Комплексную функцию$F[y]$ можно также представить в виде

$F[y] = \frac{{{{e}^{{ - j\omega {{t}_{0}}}}}{{e}^{{j\psi (\omega )}}}}}{{\sqrt {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}} }} = A(\omega ){{e}^{{j(\psi (\omega ) - \omega {{t}_{0}})}}}.$

Здесь функция $A(\omega ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}} }}} \right. \kern-0em} {\sqrt {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}} }}$ представляет амплитудно-частотную характеристику колебаний, а $\Psi (\omega ) = \psi (\omega ) - \omega {{t}_{0}}$ определяет ее фазу, т.е. фазово-частотную характеристику. Разрывная в точке $\omega = {{\omega }_{0}}$ фаза $\psi (\omega )$ удовлетворяет уравнениям

$\begin{gathered} cos\psi (\omega ) = \frac{{\omega _{0}^{2} - {{\omega }^{2}}}}{{\sqrt {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}} }}, \\ \sin \psi (\omega ) = \frac{{2\sigma \omega }}{{\sqrt {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}} }}. \\ \end{gathered} $

Отсюда

(4)
$\psi (\omega ) = \left\{ \begin{gathered} \operatorname{arctg} \frac{{2\sigma \omega }}{{\omega _{0}^{2} - {{\omega }^{2}}}},\,\,\,\,\left| \omega \right| \leqslant {{\omega }_{0}}, \hfill \\ \pi + \operatorname{arctg} \frac{{2\sigma \omega }}{{\omega _{0}^{2} - {{\omega }^{2}}}},\,\,\,\,\left| \omega \right| > {{\omega }_{0}}. \hfill \\ \end{gathered} \right.$

Дифференцируя по частоте в (4), находим производную функции $\Psi (\omega ) = \psi (\omega ) - \omega {{t}_{0}}$:

(5)
$\Psi {\kern 1pt} '(\omega ) = \psi {\kern 1pt} '(\omega ) - {{t}_{0}} = \frac{{2\sigma (\omega _{0}^{2} + {{\omega }^{2}})}}{{{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}}} - {{t}_{0}}.$

Экстремумы этой функции определяются нулями ее производной

$\Psi ''(\omega ) = - \frac{{4\sigma \omega \left( {{{\omega }^{4}} + 2\omega _{0}^{2}{{\omega }^{2}} + 4{{\sigma }^{2}}\omega _{0}^{2} - 3\omega _{0}^{4}} \right)}}{{{{{\left( {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + 4{{\sigma }^{2}}{{\omega }^{2}}} \right)}}^{2}}}}.$

При ${{\omega }_{0}} > \frac{2}{{\sqrt 3 }}\sigma $ (т.е. при “малых” затуханиях) уравнение $\Psi {\kern 1pt} ''(\omega ) = 0$ имеет единственное положительное решение ${{\omega }_{{\max }}} = \sqrt {2{{\omega }_{0}}\sqrt {\omega _{0}^{2} - {{\sigma }^{2}}} - \omega _{0}^{2}} $ и оно соответствует максимуму функции (5). Величина этого максимума определяется формулой

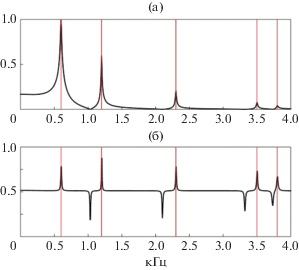
${{\left( {\Psi {\kern 1pt} '} \right)}_{{\max }}} = \frac{{{{\omega }_{0}} + \sqrt {\omega _{0}^{2} - {{\sigma }^{2}}} }}{{2\sigma \sqrt {\omega _{0}^{2} - {{\sigma }^{2}}} }} - {{t}_{0}} = \frac{{1 + {{\omega }_{0}}}}{{2\sigma (\omega _{0}^{2} - {{\sigma }^{2}})}} - {{t}_{0}}.$

Для единственного осциллятора (3) функция $\Psi '(\omega )$ имеет единственный максимум. Если же сигнал порождается системой, содержащей несколько осцилляторов, то у функции $\Psi {\kern 1pt} '(\omega )$ наряду с другими максимумами могут появиться и минимумы. На рис. 2 показаны амплитудно-частотная характеристика и производная от фазы по частоте для суммы 5 колебательных компонент с частотами, характерными для звука /а/. Видно, что максимумы на частотах, равных 600, 1200, 2300, 3500, 3806 и 4742 Гц, сопровождаются отрицательными пиками.

Рис. 2.

(а) – Нормированная АЧХ; (б) – производная фазы.

Аналогично анализу свойств производной от фазы по частоте, рассмотрим свойства производной от фазы по времени, используя кратковременное преобразование Фурье при условии ${{t}_{0}} = 0$. Решение задачи (5) во временной области есть

$y(t) = h(t)\frac{{{{e}^{{ - \sigma t}}}\sin {{\omega }_{0}}t}}{{{{\omega }_{0}}}},$
где $h(t)$ – функция Хевисайда. Комплексный спектр этого сигнала, полученный посредством кратковременного преобразования Фурье с окном $W(t)$, есть

$\begin{gathered} S(\omega ,t) = \int\limits_{ - \infty }^{ + \infty } {W(t - \tau )s(\tau ){{e}^{{ - j\omega \tau }}}d\tau } = \\ = \int\limits_0^{ + \infty } {} W(t - \tau )\frac{{{{e}^{{ - \sigma \tau }}}\sin {{\omega }_{0}}\tau }}{{{{\omega }_{0}}}}{{e}^{{ - j\omega \tau }}}d\tau . \\ \end{gathered} $

В частности, для прямоугольного окна шириной $2\varepsilon $:

$S(\omega ,t) = \frac{1}{{2\varepsilon {{\omega }_{0}}}}\int\limits_{t - \varepsilon }^{t + \varepsilon } {{{e}^{{ - \sigma \tau }}}\sin {{\omega }_{0}}\tau {{e}^{{ - j\omega \tau }}}d\tau } .$

Этот интеграл можно вычислить аналитически, но полученное выражение столь громоздко, что его содержательный анализ не представляется возможным. Поэтому амплитуду $A(\omega ,t)$, фазу $\varphi (\omega ,t)$ и мгновенную частоту этого интеграла лучше находить численно. На рис. 3 показаны зависимости от времени фазы $\Phi (t) = \varphi (\omega ,t)$ для некоторых значений частоты $\omega $ и аналогичные зависимости мгновенной частоты $\Omega (t) = \frac{1}{{2\pi }}\frac{{\partial \varphi (\omega ,t)}}{{\partial t}} = Q(\omega ,t)$. Осциллятор имеет параметры ${{f}_{0}} = 2\pi {{\omega }_{0}} = 0.5$ кГц и $\sigma = $ 0.05. На рисунке видна характерная особенность функции фазы при каждой фиксированной частоте – наличие линейной и колебательной составляющих. Графики функций мгновенной частоты $\Omega (t)$ показывают, что производные этих колебательных составляющих периодичны.

Рис. 3.

(а) – Фаза и (б) – мгновенная частота при различных частотах.

Периодичность фазы в частотной области продемонстрирована на рис. 4, где показаны амплитудные спектры мгновенной частоты этого осциллятора для различных моментов времени $t \in (0,40)$ мс. Видно, что, наряду с частотой осциллятора 0.5 кГц, в спектре мгновенной частоты представлены и гармоники этой частоты.

Рис. 4.

Амплитудные спектры мгновенной частоты для осциллятора с собственной частотой 0.5 кГц. Вычислены для различных времен $t \in (0,40)$ мс.

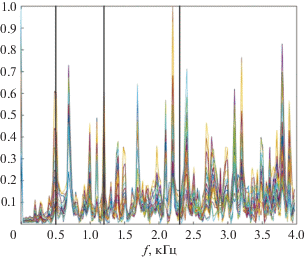
Аналогичные амплитудные спектры мгновенной частоты можно найти для суммарного сигнала нескольких осцилляторов. Соответствующий пример для трех осцилляторов с собственными частотами 0.5, 1.2 и 2.3 кГц для различных времен продемонстрирован на рис. 5.

Рис. 5.

Спектры мгновенной частоты для осцилляторов с собственными частотами 0.5, 1.2 и 2.3 кГц.

Рис. 2 и 5 иллюстрируют важное свойство фазовой функции: фаза суммы сигналов, вообще говоря, не равна сумме фаз этих сигналов. Взаимодействие осцилляторов с разными частотами приводит к потере возможности идентификации этих частот по пикам в спектре мгновенной частоты. Видно, что наряду с пиками, соответствующими частотам осцилляторов 0.5 и 1.2 кГц, присутствует множество “паразитных” пиков, а пик на частоте 2.3 кГц вообще отсутствует.

Кроме мгновенной частоты $Q(\omega ,t) = \frac{1}{{2\pi }}\frac{{\partial \varphi (\omega ,t)}}{{\partial t}}$ в фазовом анализе сигналов часто используется и другая величина, пропорциональная производной фазы по частоте. Выразим ее для произвольного сигнала с кратковременным спектром $S(\omega ,t) = u(\omega ,t) + jv(\omega ,t)$. Представим фазу как

$\begin{gathered} j\varphi (\omega ,t) = \ln \left( {u(\omega ,t) + jv(\omega ,t)} \right) - \\ - \,\,\ln {{\left( {{{u}^{2}}(\omega ,t) + {{v}^{2}}(\omega ,t)} \right)} \mathord{\left/ {\vphantom {{\left( {{{u}^{2}}(\omega ,t) + {{v}^{2}}(\omega ,t)} \right)} 2}} \right. \kern-0em} 2} \\ \end{gathered} $
и найдем ее производную
$\begin{gathered} {{\varphi }_{\omega }} = \frac{{\partial \varphi (\omega ,t)}}{{\partial \omega }} = \frac{{u(\omega ,t)v{\kern 1pt} '(\omega ,t) - v(\omega ,t)u{\kern 1pt} '(\omega ,t)}}{{{{u}^{2}}(\omega ,t) + {{v}^{2}}(\omega ,t)}} = \\ = \frac{{u(\omega ,t)v{\kern 1pt} '(\omega ,t) - v(\omega ,t)u{\kern 1pt} '(\omega ,t)}}{{{{{\left| {S(\omega ,t)} \right|}}^{2}}}}, \\ \end{gathered} $
где штрих обозначает производную по частоте. Функция
${{\tau }}({{\omega }},t) = - \frac{1}{{2{{\pi }}}}\frac{{\partial {{\varphi }}({{\omega }},t)}}{{\partial {{\omega }}}}$
называется групповой задержкой.

Пики функций $Q({{\omega }},t)$ и ${{\tau }}({{\omega }},t)$ на оси частот традиционно пытаются использовать для определения формантных частот речевого тракта аналогично спектру мощности ${{\left| {S(\omega ,t)} \right|}^{2}}$ [9, 23]. Для такого подхода есть определенные основания, продемонстрированные выше на моделях осцилляторов. Но, как было отмечено, даже для простых синтетических сигналов типа суперпозиции колебаний нескольких осцилляторов экстремумы этих функций могут быть и не связаны с собственными частотами осцилляторов. Более детальный анализ показывает еще более сложную структуру этих функций в реальных речевых сигналах.

Из сказанного выше ясно, что для устранения искажений в акустическом и электронном каналах распространения речевого сигнала необходимо использовать производную фазы по времени, тогда как спектральные характеристики речевого сигнала могут проявляться в производной фазы по частоте. Это приводит к необходимости исследования свойств смешанной производной

$\frac{{{{\partial }^{2}}\varphi (\omega ,t)}}{{\partial \omega \partial t}} = \frac{\partial }{{\partial \omega }}\left[ {\frac{{u(\omega ,t)\dot {v}(\omega ,t) - \dot {u}(\omega ,t)v(\omega ,t)}}{{{{u}^{2}}(\omega ,t) + {{v}^{2}}(\omega ,t)}}} \right].$

Опуская аргументы функций, ее можно записать так:

${{\varphi }_{{\omega t}}} = \frac{{\left( {u{\kern 1pt} '\dot {v} + u\dot {v}{\kern 1pt} '\,\, - \dot {u}{\kern 1pt} 'v - \dot {u}v{\kern 1pt} '} \right)\left( {{{u}^{2}} + {{v}^{2}}} \right) - 2\left( {u\dot {v} - \dot {u}v} \right)\left( {uu{\kern 1pt} '\,\, + vv{\kern 1pt} '} \right)}}{{{{{\left| {S(\omega ,t)} \right|}}^{4}}}}.$

В работе [24] в предположении, что сигнал является аналитической функцией переменных $z = (\omega ,t)$, показано, что при каждом фиксированном $t$ формантным частотам могут соответствовать экстремумы (т.е. не только максимумы, но и минимумы) или точки перегиба функции частоты $Q({{\omega }},t)$ при условии, что смешанная производная отрицательна ${{\varphi }_{{\omega t}}} < 0$, а формантные частоты постоянны по времени. Этот результат подтверждается численными экспериментами на синтетических гласных с фиксированными формантами. Однако это гораздо реже встречается для реальных речевых сигналов, где формантные частоты подвержены быстрым (из-за взаимодействия с голосовым источником) и медленным (вследствие артикуляторных движений) изменениям.

Рассмотренные в данном разделе свойства идеализированных моделей параметров фазовой функции, конечно, не исчерпывают свойств реальных речевых сигналов, но, вместе с результатами работ [17, 24], создают основу для разработки алгоритмов анализа речевого сигнала в фазовой области и указывают на направление экспериментальных исследований.

2. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Пользуясь определением модуляции в общем смысле как такое воздействие на некоторую постоянную величину, в результате которого эта величина перестает быть постоянной и начинает изменяться в соответствии с оказываемым на нее воздействием, мы вводим понятие кратковременных и долговременных модуляций фазовых параметров. Кратковременные модуляции формируются путем сглаживания параметров на интервалах времени порядка 2.5 мс. Они используются для оценки параметров голосового источника. Долговременные модуляции формируются путем сглаживания параметров на интервалах времени порядка 25 мс. Они используются для оценки явлений, связанных с артикуляторными движениями.

В [17] была введена функция ${{\theta }}(t) = {{\Delta {{{{\omega }}}_{{\max }}}} \mathord{\left/ {\vphantom {{\Delta {{{{\omega }}}_{{\max }}}} {M(\Delta {{\omega }})}}} \right. \kern-0em} {M(\Delta {{\omega }})}}$, экстремумы которой позволяют оценить моменты начала и конца действия голосового источника с приемлемой погрешностью. Здесь $\Delta {{{{\omega }}}_{{\max }}}$ – максимальный интервал между нулями разрывной фазовой функции ${{\hat {\varphi }}}({{\omega }},t)$,

$M(\Delta \omega ) = \frac{1}{{N - 1}}\left( {\sum\limits_{m = 1}^N {\Delta {{\omega }_{m}}} - \Delta {{\omega }_{{\max }}}} \right),$
а $\Delta {{\omega }_{m}}$ – расстояние между нулями ${{\hat {\varphi }}}({{\omega }},t)$. Модуляции этой функции определяются как ${{{{\theta }}}_{{\bmod }}}(t) = {{d[{{\theta }}(t)]} \mathord{\left/ {\vphantom {{d[{{\theta }}(t)]} {dt}}} \right. \kern-0em} {dt}}$. Модуляции линейной компоненты фазовой функции ${{k}_{{{\varphi }}}}(t)$ определяются как ${{k}_{{\varphi \;\bmod }}}(t) = {{d[{{k}_{\varphi }}(t)]} \mathord{\left/ {\vphantom {{d[{{k}_{\varphi }}(t)]} {dt}}} \right. \kern-0em} {dt}}$. Модуляции мгновенной частоты относительно центральной частоты i-го гамма-тон фильтра ${{Q}_{{\bmod }}}(t)$ вычисляются как среднее значение ${{Q({{\omega }},t)} \mathord{\left/ {\vphantom {{Q({{\omega }},t)} {{\omega }}}} \right. \kern-0em} {{\omega }}}$ в диапазоне частот 1000–3000 Гц. Диапазон 1000–3000 Гц был найден в [25] как оптимальный для анализа параметров голосового источника гласных в спектрально-временной области, и оказался также наилучшим при анализе в фазовой области.

3.1. Голосовой источник в гласных звуках

Гласные звуки являются важным элементом речевого кода. Они характеризуются относительно высокой энергией, явно выраженными пиками (формантами) в амплитудно-частотном спектре и наличием голосового источника возбуждения. Методы детектирования гласных в речевом потоке и определения их признаков обычно реализуются в спектрально-временном пространстве. Рассмотрим возможность разработки аналогичных методов с помощью частотно-временного анализа кратковременной модуляции по формуле фазовой функции речевого сигнала.

Все параметры фазовой функции так или иначе зависят от голосового источника, и можно ожидать, что такая зависимость по-разному проявляется в этих параметрах. Мы исследовали кратковременные модуляции трех параметров: функции ${{{{\theta }}}_{{\bmod }}}(t)$, пропорциональной максимальному интервалу между нулями разрывной фазовой функции, коэффициента наклона линейной компоненты фазы ${{k}_{{{{\varphi }}\;\bmod }}}(t)$ и мгновенной частоты ${{Q}_{{\bmod }}}(t)$.

Обычно степень периодичности речевого сигнала оценивают с помощью коэффициента автокорреляции. При этом часто наблюдаются всплески коэффициента автокорреляции на паузе или глухих фрикативных, которые не имеют отношения к активности голосового источника. Вариации формы сигнала, подвергающегося корреляционному анализу, могут привести к снижению коэффициента автокорреляции внутри последовательности импульсов голосового возбуждения. Такой же эффект появляется и вследствие того, что последовательность импульсов голосового источника, как правило, не строго периодична. Например, после паузы, глухой смычки или глухого фрикативного в начале гласного интервал между первым и вторым импульсами может быть значительно больше, чем между последующими импульсами. Иногда наблюдаются значительные отклонения от среднего значения периодов основного тона на гласном вследствие взаимодействия голосового источника с текущими акустическими процессами в речевом тракте. Эти явления затрудняют обнаружение активности голосового источника на основе его периодичности.

Компенсация подобных явлений может быть достигнута путем параллельного корреляционного анализа параметров другой физической природы, например, параметров фазовой функции. С этой целью окончательная оценка степени периодичности p в нашей работе определялась как максимальное значение коэффициентов автокорреляции среди оценок периодичности функций ${{k}_{{{{\varphi }}\;\bmod }}}(t)$, ${{{{\theta }}}_{{\bmod }}}(t)$ и ${{Q}_{{\bmod }}}(t)$ в каждый момент времени, т.е. $p(t) = max\left\{ {\left| {p({{k}_{{{{\varphi }}\;\bmod }}})} \right|,\left| {p({{{{\theta }}}_{{\bmod }}})} \right|,\left| {p({{Q}_{{\bmod }}})} \right|} \right\}$. Поскольку такая оценка периодичности все же обладает склонностью к кратковременному появлению ложных больших значений коэффициента автокорреляции, выполняется процедура подавления таких оценок, основанная на знании свойств гласных звуков и частоты основного тона.

В алгоритме с жестким принятием решения окончательная оценка степени периодичности приравнивается нулю, если она меньше некоторого порога. Например $p(t) = 0$, если $p(t) < 0.3$. Если длительность сегмента, на котором $p(t) > 0$, меньше 40 мс, то$p(t) = 0$. Это правило вытекает из статистики длительности гласных звуков, а также из требования алгоритма автокорреляции, чтобы на сегменте было не меньше 2.5 периодов основного тона ${{T}_{0}}$, что для нижней оценки частоты основного тона в 60 Гц составляет 41.7 мс. Коэффициент автокорреляции также приравнивается к нулю, если относительное изменение соседних оценок периода основного тона превышает некоторый порог. При этом период основного тона для каждой исследуемой функции определяется как интервал времени между ближайшими максимумами этой функции.

Пример детектирования гласного звука в слове /шесть/ и оценка частоты основного тона приводятся на рис. 6, где показаны коэффициенты автокорреляции кратковременных модуляций наклона фазовой функции ${{k}_{{{{\varphi }}\;\bmod }}}(t)$, интервалов между нулями разрывной фазовой функции ${{{{\theta }}}_{{\bmod }}}(t)$ и мгновенной частоты ${{Q}_{{\bmod }}}(t)$.

Рис. 6.

Слово /шесть/. (а) – Сонограмма; коэффициент автокорреляции кратковременных модуляций: (б) – наклона фазовой функции ${{k}_{{{{\varphi }}\;\bmod }}}(t)$; (в) – интервалов между нулями разрывной фазовой функции ${{{{\theta }}}_{{\bmod }}}(t)$; (г) – модуляции мгновенной частоты ${{Q}_{{\bmod }}}(t)$; (д) – окончательная оценка коэффициента автокорреляции; (е) – оценка частоты основного тона.

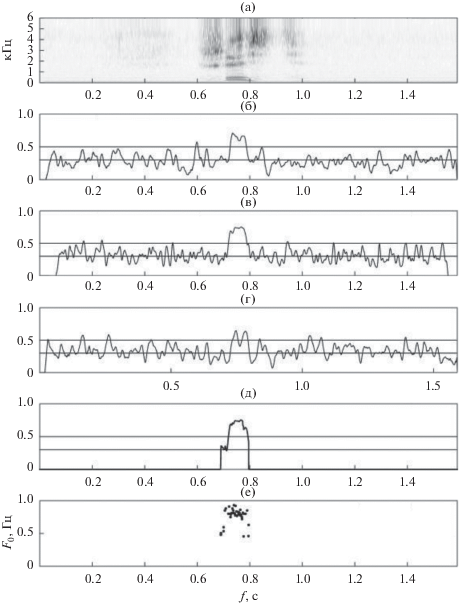
На рис. 6 видно, что коэффициент автокорреляции на каждом из этих параметров может превысить порог, равный 0.5, не только на фрикативных сегментах слова, но и на паузах. Этот порог обычно используется для принятия решения о присутствии голосового возбуждения. С другой стороны, коэффициент автокорреляции на сегменте гласного может оказаться не только ниже величины 0.5, но и величины 0.3, что обычно считается признаком фрикативного или шумового сегмента. Агрегирование коэффициентов автокорреляции разных параметров, т.е. принятие решения по совокупности коэффициентов автокорреляции каждого параметра, позволяет отсеять ложные оценки и определить моменты начала и конца сегмента гласного. Одновременно оценивается и частота основного тона по каждому из параметров.

Выбор частотного диапазона 1000–3000 Гц при вычислении коэффициента автокорреляции позволяет игнорировать звонкие и назальные смычки, как это видно на рис. 7, где представлены сонограмма и оценка максимального коэффициента корреляции для слова /один/.

Рис. 7.

Слово /один/. (а) – Сонограмма и (б) – максимальный коэффициент автокорреляции.

3.2 . Детектирование моментов начала и конца голосового источника

В описанных выше экспериментах было установлено, что кратковременные модуляции параметров фазовой функции связаны с квазипериодическими импульсами источника голосового возбуждения, что позволяет оценить текущий период основного тона ${{T}_{0}}$. В данном разделе описываются эксперименты, выполненные с целью оценки возможности определения не только периода ${{T}_{0}}$, но и моментов начала ${{T}_{{op}}}$ и конца ${{T}_{{cl}}}$ действия голосового источника. Как было показано в [17], функция ${{\theta }}(t)$ позволяет оценить моменты ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ в среднем с весьма малой ошибкой как для синтезированных, так и для реальных речевых сигналов. Однако при этом временами наблюдаются и большие отклонения от непосредственно измеренных параметров. Поэтому мы исследовали возможность коррекции таких отклонений с помощью других параметров фазовой функции. На первом этапе экспериментов использовались синтезированные гласные, для которых эти моменты были известны. Исследовались экстремумы функций ${{{{\theta }}}_{{\bmod }}}(t)$, ${{k}_{{{{\varphi }}\;\bmod }}}(t)$, ${{Q}_{{\bmod }}}(t)$ и кратковременных модуляций групповой задержки ${{{{\bar {\tau }}}}_{{\bmod }}}(t) = {{{{\bar {\tau }}}({{\omega }},t)} \mathord{\left/ {\vphantom {{{{\bar {\tau }}}({{\omega }},t)} {{\omega }}}} \right. \kern-0em} {{\omega }}}$, где ${{\bar {\tau }}}({{\omega }},t)$ есть среднее значение ${{\tau }}({{\omega }},t)$ в диапазоне частот 1000–3000 Гц. Оценки ${{T}_{{op}}}$ приписывались моментам максимального значения этих функций, а оценки ${{T}_{{cl}}}$ – моментам минимального значения этих функций. Было обнаружено, что как для ${{T}_{{op}}}$, так и для ${{T}_{{cl}}}$ эти оценки смещены относительно друг друга, причем величина смещения зависит от гласного. Поэтому для принятия решения на основе агрегирования этих оценок необходимо использовать дополнительную информацию.

Прежде всего, для каждого периода основного тона нужно знать его примерное значение ${{T}_{0}}$. Это значение можно получить любым алгоритмом определения частоты основного тона, включая и алгоритм, описанный выше в разделе 3.1. Среди множества оценок моментов ${{T}_{{op}}}$ или ${{T}_{{cl}}}$ выбираются такие, что сдвиг по времени между ними не превышает 0.6${{T}_{0}}$, и в качестве окончательной оценки принимается оценка с минимальным значением. Отсев оценок с большим сдвигом выполняется по условию$\dot {E}(t) > 0$ для ${{T}_{{op}}}$, и $\dot {E}(t) < 0$ для ${{T}_{{cl}}}$, где $\dot {E}(t)$ – производная по времени от огибающей амплитуды $E(t) = \sum\nolimits_{k = 1}^N {{{A}_{k}}(t)} ,$ $N = 256$ фильтров.

На рис. 8 показаны нормированная объемная скорость воздушного потока голосового источника для сегмента синтетического гласного /а/ и агрегированные оценки моментов начала и конца действия голосового источника.

Рис. 8.

Импульсы объемной скорости синтетического голосового источника и моменты начала и конца его действия ${{T}_{{op}}}$ (—) и ${{T}_{{cl}}}$ (---).

При анализе речевого сигнала обычно отсутствует информация о начале и конце действия голосового источника. Поэтому приходится использовать косвенные сведения об интервалах открытой и закрытой голосовой щели. В экспериментах с синтезированными звуками было найдено, что экстремумы производной $\dot {E}(t)$ находятся вблизи моментов начала и конца всплеска энергии спектральных компонент речевого сигнала на сонограмме, возникающего в результате воздействия голосового источника. При этом для отсева оценок ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ со слишком большим сдвигом достаточно использовать просто знак производной, а не положение ее экстремумов. На рис. 9 показаны сонограмма сегмента гласного /э/ в слове /шесть/, производная суммарной энергии спектра и предположительные моменты ${{T}_{{op}}}$ и${{T}_{{cl}}}$, которые можно сопоставить с сонограммой.

Рис. 9.

(а) – Сонограмма; (б) – производная по времени от огибающей речевого сигнала и разметка на моменты начала и конца голосового источника ${{T}_{{op}}}$ (—) и ${{T}_{{cl}}}$ (---).

Можно ожидать, что агрегирование фазовых параметров приведет к более устойчивой оценке моментов начала и конца голосового источника по сравнению с параметром максимального интервала между нулями разрывной фазовой функции, исследованным в [17].

3.3. Оценка формантных частот

Резонансные частоты речевого тракта определяют фонетическое качество гласных и взрывных согласных. В амплитудно-частотном спектре резонансные частоты тракта проявляются в виде пиков энергии, которые называются формантами. Однако частоты формант не тождественны резонансным частотам, хотя иногда и достаточно близки к ним в высокочастотной области. Амплитудный и фазовый спектры зависят от одних и тех же параметров комплексного спектра $u({{\omega }},t)$ и $v({{\omega }},t)$. Поэтому предпринимаются попытки определения формантных частот в фазовой области. В разделе 2.3 было показано, что спектр производной по частоте от фазы в идеализированной модели для системы осцилляторов содержит различные пики, в том числе и на собственных частотах этих осцилляторов. По аналогии с формантами в амплитудно-частотном спектре, мы будем использовать термин “форманты” и для пиков спектра фазовых параметров. Необходимо выяснить, при каких условиях возможна оценка резонансных частот тракта в фазовой области.

Формантные частоты, найденные по параметрам фазовой функции, будем сравнивать с формантами, найденными в амплитудно-спектральной области следующим простейшим алгоритмом. На сегменте гласного в каждый момент времени определяется частота локальных пиков, среди которых отбираются частоты первых пяти пиков с наибольшей амплитудой. За формантные частоты принимаются частоты пиков в моменты времени, соответствующие оценке ${{T}_{{op}}}$ по алгоритмам из предыдущего раздела. Треки этих пиков и оценки формантных частот для гласного /э/ в слове /шесть/ показаны на рис. 10.

Рис. 10.

(а) – Сонограмма; (б) – треки локальных пиков и оценки формантных частот (⚪).

Исходя из модельного анализа свойств производной от фазы по частоте в разделе 2.1, можно попытаться найти треки формантных частот на долговременных модуляциях групповой задержки ${{{{\tau }}}_{{\bmod }}}({{\omega }},t) = {{{{\tau }}({{\omega }},t)} \mathord{\left/ {\vphantom {{{{\tau }}({{\omega }},t)} {{\omega }}}} \right. \kern-0em} {{\omega }}}$. Представляют также интерес свойства долговременных модуляций смешанной производной. Эти функции представлены на рис. 11 (слово /шесть/).

Рис. 11.

(а) – Сонограмма; (б) – долговременные модуляции производной по частоте; (в) –‑ долговременные модуляции смешанной производной.

Анализ спектральных свойств модуляций групповой задержки ${{{{\tau }}}_{{\bmod }}}({{\omega }},t)$ показал, что высшие форманты обнаруживаются в спектре долговременных модуляций, тогда как в области первой форманты наиболее четко формантные пики проявляются в спектре кратковременных модуляций этой функции (рис. 12). При этом моменты отсчета значений частоты первой форманты также соответствуют моментам начала действия голосового источника ${{T}_{{op}}}$, найденного по алгоритмам из предыдущего раздела.

Рис. 12.

Треки локальных пиков производной от фазы по частоте и оценки формантных частот (*). Гласный /э/ в слове /шесть/.

На рис. 13а сопоставляются оценки формантных частот, выполненные по амплитудно-частотному спектру и спектрам кратковременных и долговременных модуляций групповой задержки на сегменте гласного /э/ в слове /шесть/. Оценки формантных частот, выполненные по спектру долговременных модуляций смешанной производной для этого же гласного, показаны на рис. 13б.

Рис. 13.

Оценки формантных частот по амплитудному спектру (⚪), (а) – модуляциям групповой задержки (*) и (б) – модуляциям смешанной производной (x).

Видно, что оценки формантных частот по всем трем способам анализа совпадают лишь частично, и это может создать основу для разработки алгоритма более точного и устойчивого определения формант.

3. ОБСУЖДЕНИЕ

Исследование модуляций фазовых параметров в речевом сигнале связано с существованием так называемых детекторов амплитудных и частотных модуляций в слуховых системах живых организмов. Моделирование этих детекторов в [26] позволило сегментировать и распознавать с высокой точностью структуры типа “пауза–фрикативный–гласный”. В отличие от амплитудного спектра, фазовая функция располагает гораздо большим числом параметров для оценки таких характеристик речевого сигнала, как частота основного тона, моменты начала и конца действия голосового источника, а также формантные частоты. Кроме того, модуляции некоторых параметров позволяют сегментировать речевой поток на фонетически значимые элементы.

Численное моделирование свойств производных от фазы по частоте и времени, выполненное в разделе 2.2, иллюстрирует важное свойство фазовой функции: фазовая функция суммы сигналов не равна сумме фазовых функций каждого сигнала. Отсюда следует невозможность применения метода вычитания амплитудных спектров, который используется для подавления аддитивных шумов. В этом разделе также показано, что эффекты суммирования настолько маскируют собственные частоты в производной по времени, что для оценки формантных частот предпочтительнее использовать производную по частоте.

В спектрально-временной области создано множество алгоритмов оценки параметров речевого сигнала, таких как частота основного тона, моменты начала и конца действия голосового источника, формантные частоты и др. Но ни один известный алгоритм не обеспечивает абсолютную устойчивость к помехам и искажениям речевого сигнала. Причина этого состоит в разнообразии свойств речевого сигнала и его изменчивости, в результате чего принципиально невозможно создать универсальный алгоритм, использующий лишь какой-то один, пусть и явно выраженный признак искомого параметра. Выход из этой ситуации состоит в совместном использовании алгоритмов, по-разному использующих проявления искомого параметра в речевом сигнале, т.е. в агрегировании алгоритмов.

Неформальная оценка результатов определения моментов начала и конца гласного в различных звукосочетаниях оказалась весьма благоприятной. Несмотря на значительное разнообразие в поведении функций ${{k}_{{{{\varphi }}\;\bmod }}}(t)$, ${{{{\theta }}}_{{\bmod }}}(t)$ и ${{\Omega }_{{\bmod }}}(t)$ для разных дикторов и типов микрофона, гласные в числительных русского языка уверенно детектировались. Это подтверждает перспективность использованного в нашей работе принципа агрегирования для повышения эффективности процессов принятия решений. Представляется целесообразным распространить этот принцип и на совместную оценку параметров, вычисленных в амплитудной и фазовой областях. Например, погрешность определения моментов начала или конца действия голосового источника зависит от типа гласного. Поэтому необходимо принимать во внимание и вид сонограммы, т.е. качественную оценку распределения формант.

При сегментировании гласных с использованием только агрегированного коэффициента автокорреляции, величина этого коэффициента зависит от степени выраженности формантной структуры в спектре фазовых параметров. Поэтому назальные смычки и звуки /в, л/ иногда могут восприниматься как гласно-подобные звуки. Для слитной последовательности гласных звуков сегментатор на основе коэффициента автокорреляции, скорее всего, определит лишь начало и конец такой последовательности.

Рассогласование между оценками формантных частот по амплитудно-частотному спектру и пиками спектров производной по частоте и смешанной производной достаточно мало. Так, наибольшая разница в оценках по амплитудному спектру и по модуляциям производной по частоте наблюдается на 4-й форманте, и она менее 15%. Такое рассогласование соответствует погрешности восприятия в этом диапазоне частот. При этом трек 6-й форманты даже лучше фиксируется по пикам производной по частоте, чем по амплитудно-частотному спектру.

Не все пики на спектрах производной по частоте и, особенно, смешанной производной соответствуют формантам амплитудно-частотного спектра. Однако проблема “лишних формант” существует и при использовании других методов поиска формантных частот. Часть таких пиков может соответствовать резонансам подсвязочной области или резонансам, возникающим при неполном закрытии прохода в носовую полость. В этом случае они полезны при распознавании диктора. До сих пор неясно, какие из этих пиков имеют отношение к процессам речеобразования, а какие являются артефактами принятого метода анализа. В этой ситуации представляется целесообразным совместное использование результатов анализа в фазовой области с другими методами обработки речевого сигнала. Такое агрегирование должно повысить устойчивость и точность определения и других параметров речевого сигнала.

ЗАКЛЮЧЕНИЕ

Динамическая фазовая функция речевого сигнала содержит не меньше информации о речевом сигнале, чем амплитудно-частотный спектр. Предлагаемые в статье методы позволяют извлечь существенную часть этой информации. В частности, агрегирование коэффициентов автокорреляции кратковременных модуляций мгновенной частоты, линейной компоненты фазы и максимальных значений длительностей интервалов между нулями разрывной фазовой функции позволяет оценить частоту основного тона и сегментировать гласные звуки в слитном потоке речи. Кроме того, по экстремумам кратковременных модуляций этих функций можно судить о моментах начала и конца действия голосового источника. Экстремумы спектров долговременных модуляций производной по частоте и смешанной производной от фазы оказываются близкими к формантам, найденным на амплитудно-частотном спектре.

Работа второго автора поддержана Программой повышения конкурентоспособности Национального исследовательского ядерного университета МИФИ (проект 02.a03.21.0005 от 27.08.2013).

Список литературы

  1. Flanagan J., Golden R. Phase vocoder // The Bell System Technical Journal. 1966. P. 388–404.

  2. Laroche J., Dolson M. Improved phase vocoder time-scale modification of audio // IEEE Trans. Speech Audio Processing. 1999. V. 7. № 3. P. 323–32.

  3. Oppenheim A.V., Lim J.S. The importance of phase in signals // Proc. IEEE. 1981. V. 69. N. 5. P. 529–541.

  4. Oppenheim A.V., Schafer R.W., Buck J.R. Discrete-Time Signal Processing. Prentice Hall, 1999.

  5. Liu L., He J., Palm G. Effects of phase on the perception of intervocalic stop consonants // Speech Commun. 1997. V. 22. № 4. P. 403–417.

  6. Paliwal K.K., Alsteris L.D. On the usefulness of stft phase spectrum in human listening tests // Speech Commun. 2005. V. 45. P. 153–170.

  7. Alsteris L.D., Paliwal K.K. Short-time phase spectrum in speech processing: A review and some experimental results // Digital signal processing. 2007. V. 17. P. 578–616.

  8. Aarabi P., Shi G., Shanechi M.M., Rabi S.A. Phase based processing speech. Singapore: World Scientific Publishing Co. Pte. Ltd., 2006.

  9. Stark A.P., Paliwal K.K. Speech analysis using instantaneous frequency deviation // Proc. ISCA Interspeech, 2008. P. 22–26.

  10. Murthy H.A., Yegnanarayna B. Group delay functions and its applications in speech technology // Sadhana. 2011. V. 36. Pt 5. P. 745–782.

  11. Леонов А.С., Сорокин В.Н. Формантный анализ в фазовой области // Информационные процессы. 2021. Т. 21. № 2. С. 125–134. http://www.jip.ru

  12. Yegnanarayana B., Sreekanth J., Rangarajan A. Waveform estimation using group delay processing // IEEE Trans. Audio Speech Lang. Process. 1985. V. 33(4). P. 832–836.

  13. Smits R., Yegnanarayana B. Determination of instants of significant excitation in speech using group delay function // IEEE Trans. Speech Audio Process. 1995. V. 3. № 5. P. 325–333.

  14. Drugman T., Thomas M., Gudnason J., Naylor P., Dutoit T. Detection of glottal closure instants from speech signals: A quantitative review // IEEE Trans. Audio Speech Lang. Process. 2012. V. 20. № 3. P. 994–1006.

  15. Mowlaee P., Saeidi R., StyliaNu Y. Advances in phase-aware signal processing in speech communication // Speech Commun. 2016. V. 81. P. 1–29.

  16. Gurugubelli K., Vuppala A.K. Analytic phase features for dysarthric speech detection and intelligibility assessment // Speech Commun. 2020. V. 121. P. 1–15.

  17. Сорокин В.Н., Леонов А.С. Фазовый анализ активности голосового источника // Акуст. журн. 2021. Т. 67. № 2. С. 185–202.

  18. Drugman T., Stylianou Y. Fast and accurate phase unwrapping // Proceedings of the ISCA Interspeech, 2015. P. 1171–1175.

  19. Sadjadi S.O., Hansen J.H.L. Hilbert envelope based features for robust speaker identification under reverberant mismatched conditions // Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing (ICASSP), 2011. P. 5448–5451.

  20. Sadjadi S.O., Hansen J.H.L. Mean Hilbert envelope coefficients (MHEC) for robust speaker and language identification // Speech Commun. 2015. V. 72. P. 138–148.

  21. Patterson R.D., Robinson K., Holdsworth J., McKeown D., Zhang C., Allerhand M. Complex sounds and auditory images. In: Cazals Y., Demany L., Horner K. (Eds.), Auditory Physiology and Perception. Oxford: Pergamon Press, 1992. P. 429–446.

  22. Patterson R.D., Holdsworth J. A functional model of neural activity patterns and auditory images // Advances in Speech, Hearing and Language Processing. 1996. V. 3. P. 547–563.

  23. Bozkurt B., Couvreur L., Dutoit T. Chirp group delay analysis of speech signals // Speech Commun. 2007. V. 49(3). P. 159–176.

  24. Леонов А.С., Сорокин В.Н. Формантный анализ в фазовой области // Информационные процессы. 2021. Т. 21. № 2. С. 125–134. http://www.jip.ru

  25. Сорокин В.Н. Сегментация периода основного тона голосового источника // Акуст. журн. 2016. Т. 62. № 2. С. 247–258.

  26. Сорокин В.Н. Детекторы артикуляторных событий // Акуст. журн. 2020. Т. 66. № 1. С. 71–85.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал