Акустический журнал, 2022, T. 68, № 1, стр. 83-95
Пространственная коррекция акустической голограммы для восстановления колебаний поверхности аксиально-симметричного ультразвукового излучателя
А. З. Калоев a, Д. А. Николаев a, В. А. Хохлова a, *, С. А. Цысарь a, О. А. Сапожников a
a Московский государственный университет им. М.В. Ломоносова
119991 Москва, ГСП-1, Ленинские горы, Россия
* E-mail: vera@acs366.phys.msu.ru
Поступила в редакцию 18.07.2021
После доработки 18.07.2021
Принята к публикации 22.09.2021
- EDN: LBYGJH
- DOI: 10.31857/S032079192201004X
Аннотация
Предложен метод пространственной коррекции акустической голограммы, зарегистрированной на произвольно ориентированном плоском участке перед аксиально-симметричным ультразвуковым излучателем. Суть метода заключается в определении расположения оси излучателя по измеренной голограмме, переносе данных голограммы на плоскость, перпендикулярную найденной оси, и центрировании относительно нее с использованием алгоритма коррекции в виде соответствующих поворотов и сдвигов. По откорректированной голограмме восстанавливается структура колебаний излучающей поверхности ультразвукового источника. Рассмотрен также упрощенный алгоритм коррекции в случае малых углов наклона исходной голограммы к оси источника с узким угловым спектром. Точность развитых алгоритмов проанализирована численно на примере одиночного фокусирующего излучателя с равномерным распределением колебательной скорости на его поверхности и продемонстрирована экспериментально для кольцевой 12-элементной решетки.
ВВЕДЕНИЕ
Развитие методов ультразвуковой терапии с использованием фокусированного ультразвука большой интенсивности требует разработки уточненных стандартов к применяемым устройствам и создаваемым ими полям. Производители ультразвуковых излучателей обычно предоставляют информацию о геометрических размерах источника, его фокусном расстоянии, рабочей частоте и эффективности преобразования электрической мощности в акустическую. Однако реальная пространственная структура колебаний излучающей поверхности при этом неизвестна. Указанные производителем номинальные геометрические параметры излучателя могут быть использованы для расчета ультразвукового поля, создаваемого излучателем в приближении равномерности распределения амплитуды нормальной компоненты колебательной скорости на его излучающей поверхности. Такое приближение не всегда оправдано и поэтому рассчитанное с его помощью акустическое поле может значительно отличаться от реального, что является существенным недостатком при лабораторном и клиническом использовании ультразвуковых систем.
Для точного предсказания пространственно-временной структуры ультразвукового поля следует исходить из экспериментально восстановленного распределения нормальной компоненты колебательной скорости на поверхности излучателя. Такое распределение может быть получено методом акустической голографии, который позволяет восстановить структуру акустического поля во всем пространстве на основе голограммы – измеренного двумерного поперечного распределения параметров поля на поверхности, расположенной перед излучателем [1–3]. Данный метод недавно был рекомендован как стандарт по характеризации ультразвуковых преобразователей [4].
При регистрации акустической голограммы необходимо контролировать большое число параметров эксперимента, которые могут вносить систематическую ошибку в структуру рассчитанного из измеренной голограммы поля [5]. Голограмма обычно измеряется миниатюрным приемником в большом количестве точек плоского участка, размер которого выбирается несколько большим диаметра ультразвукового пучка, чтобы обеспечить полную регистрацию акустического поля. В случае аксиально-симметричного преобразователя участок, на котором измеряется голограмма, удобно расположить напротив излучателя так, чтобы центр голограммы лежал на оси излучателя, а нормаль к участку была направлена вдоль оси. В реальности обеспечить такое идеальное расположение голограммы не удается, неизбежно появление сдвигов и небольших углов между осью излучателя и нормалью к плоскости голограммы [6].
Следует отметить, что не только при идеальном, но и при наклонном или смещенном положении акустическая голограмма содержит полную информацию о структуре поля. В этом смысле точная ориентация участка записи голограммы непринципиальна, важно лишь, чтобы указанный участок пересекался всем исследуемым пучком. Однако при анализе поля и, особенно, при определении структуры колебаний излучающей поверхности удобнее привести измеренную голограмму к координатам излучателя путем ее пересчета на плоскость, центрированную и перпендикулярную его оси.
В настоящей работе предлагается способ такой пространственной коррекции голограммы. Проводится сравнение результатов точной коррекции c использованием преобразования углового спектра голограммы с результатами приближенной коррекции путем поворота фазового фронта голограммы в лучевом приближении. Точность предлагаемых методов анализируется в численном эксперименте на примере поля одиночного фокусирующего излучателя в виде равномерно колеблющегося сегмента сферической поверхности. Проведена также экспериментальная апробация предложенных подходов при восстановлении структуры колебаний поверхности кольцевой 12-элементной фазированной решетки.
ВЫБОР СИСТЕМ КООРДИНАТ ДЛЯ ЗАПИСИ ГОЛОГРАММЫ
Рассмотрим акустическое поле, создаваемое аксиально-симметричным источником. Как следствие, само поле также является аксиально-симметричным. Ось симметрии будем называть “акустической” осью. Будем называть “идеальной” голограмму, зарегистрированную на плоском участке, центр которого находится на акустической оси, а нормаль ориентирована параллельно указанной оси. Единственным параметром, определяющим взаимное расположение идеальной голограммы и источника, является расстояние между ними, поэтому, зная его, можно рассчитать структуру колебаний излучателя. При произвольном расположении измеренной голограммы соответствующий расчет также возможен, но является более затруднительным, поскольку в этом случае необходимо знать несколько параметров, задающих взаимное расположение излучателя и голограммы. Соответственно, задача расчета колебательной скорости на излучающей поверхности становится громоздкой как в теоретическом, так и в численном плане. Голограмму, которая измеряется в общем случае в эксперименте и отличается от идеальной некоторым сдвигом и поворотом, будем называть “реальной”.
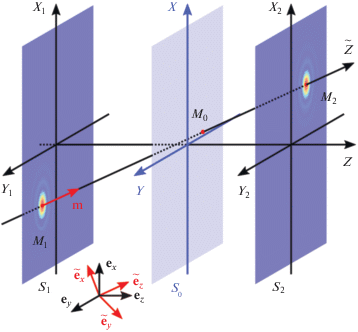
Поскольку и реальная, и идеальная голограммы являются полными записями одного и того же волнового поля, они могут быть пересчитаны друг в друга при их известной взаимной ориентации в пространстве. На практике акустическая голограмма измеряется путем сканирования акустического поля с помощью 3-координатной системы микропозиционирования. В этом случае для задания ориентации реальной и идеальной голограмм естественно использовать декартову систему координат, оси которой расположены вдоль трех направлений перемещения. Будем называть указанные оси X, Y, Z “механическими” осями и считать, что измерение голограммы произведено в результате сканирования поля в плоскости (X, Y) (рис. 1).
Первым этапом в решении задачи построения идеальной голограммы является нахождение акустической оси излучателя в механической системе координат. Пусть ${{S}_{0}}$ – плоский участок, на котором записана исходная голограмма, т.е. двумерное распределение амплитуды и фазы или, что то же самое, комплексной амплитуды волны в плоскости (X, Y). Поскольку исследуемое поле является аксиально-симметричным, распределение амплитуды волны в плоскости измерения голограммы (X, Y) будет также иметь симметрию с выделенным центром даже при наклонном расположении участка записи относительно акустической оси. При измерении голограммы расположим начало механической системы координат (X, Y, Z) = (0, 0, 0) вблизи этого центра. Точность совпадения центра симметрии пучка с началом координат будет определяться шагом сканирования, однако точное совпадение на этом этапе непринципиально. При измерении голограммы, близкой к идеальной, и таком выборе начала координат ось Z будет близка к акустической оси. По данным измеренной голограммы рассчитывается распределение амплитуды волны на оси Z с помощью интеграла Рэлея [7] или метода углового спектра [8–10]. В силу близости оси Z к акустической оси полученное распределение будет примерно совпадать с распределением давления вдоль акустической оси и содержать дифракционные максимумы и минимумы.
Далее рассчитываются вспомогательные поперечные распределения давления на двух плоских участках ${{S}_{1}}$ и ${{S}_{2}}{\kern 1pt} ,$ параллельных плоскости исходной голограммы и расположенных на расстояниях $z = {{z}_{1}}$ и $z = {{z}_{2}}$, в которых амплитуда волны имеет локальные максимумы (рис. 1). Как и при нахождении поля на оси Z, расчет поля на участках ${{S}_{1}}$ и ${{S}_{2}}$ можно провести с помощью интеграла Рэлея или метода углового спектра. Задачей здесь является как можно более точное определение координаты точек пересечения участков ${{S}_{1}}$ и ${{S}_{2}}$ акустической осью. Для ускорения расчетов сначала удобно получить поперечные распределения поля в узлах сетки с большим шагом, затем приближенно найти центр симметрии распределения и в его окрестности заново провести расчеты уже с более мелким шагом сетки. В результате на участках ${{S}_{1}}$ и ${{S}_{2}}$ вспомогательных плоскостей можно определить с высокой точностью координаты ${{{\mathbf{r}}}_{1}} = ({{x}_{1}},{{y}_{1}},{{z}_{1}})$ и ${{{\mathbf{r}}}_{2}} = ({{x}_{2}},{{y}_{2}},{{z}_{2}})$ максимумов поля ${{M}_{1}}$ и ${{M}_{2}}$, через которые проходит акустическая ось.
По найденным координатам точек ${{M}_{1}}$ и ${{M}_{2}}$ далее рассчитываются координаты ${{{\mathbf{r}}}_{0}}$ точки ${{M}_{0}}$ пересечения акустической осью излучателя плоскости исходной голограммы, а также координаты направляющего единичного вектора ${\mathbf{m}}$ акустической оси:
(1)
${{{\mathbf{r}}}_{0}} = {{{\mathbf{r}}}_{1}} - ({{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{1}})\frac{{{{z}_{1}} - {{z}_{0}}}}{{{{z}_{2}} - {{z}_{1}}}},$(2)
${\mathbf{m}} = \frac{{{{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{1}}}}{{\left| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{1}}} \right|}}.$Здесь ${{{\mathbf{r}}}_{0}} = ({{x}_{0}},{{y}_{0}},{{z}_{0}})$ – радиус-вектор точки ${{M}_{0}}$, причем ${{z}_{0}} = 0$ в силу исходного выбора начала координат. Векторы ${{{\mathbf{r}}}_{0}}$ и ${\mathbf{m}}$ полностью задают искомую акустическую ось. Максимальные ошибки $\Delta {{{\mathbf{r}}}_{0}}$ и $\Delta {\mathbf{m}}$ в определения координат векторов ${{{\mathbf{r}}}_{0}}$ и ${\mathbf{m}}$ определяются выбором шагов $\Delta x$ и $\Delta y$ сетки вспомогательных голограмм и расстояния $h$ между ними:
$\Delta {{{\mathbf{r}}}_{0}} = \left( {{{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} 2}} \right. \kern-0em} 2},{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} 2}} \right. \kern-0em} 2},0} \right)$ и
$\Delta {\mathbf{m}} = \frac{1}{h}\left( {\Delta x,\Delta y,\sqrt {(m_{x}^{2}\Delta {{x}^{2}} + {{m_{y}^{2}\Delta {{y}^{2}})} \mathord{\left/ {\vphantom {{m_{y}^{2}\Delta {{y}^{2}})} {m_{z}^{2}}}} \right. \kern-0em} {m_{z}^{2}}}} } \right).$
Приведенное выше описание проводилось в механической декартовой системе координат, соответствующей трем направлениям перемещения в 3-координатной системе микропозиционирования. Для восстановления идеальной голограммы перейдем теперь к новой декартовой системе координат $(\tilde {X},\tilde {Y},\tilde {Z})$, начало которой лежит в точке ${{M}_{0}}$, а ось $\tilde {Z}$ совпадает с акустической осью излучателя. Оси $\tilde {X}$ и $\tilde {Y}$ лежат в плоскости, перпендикулярной оси излучателя, поэтому их направление можно специально не оговаривать в силу аксиальной симметрии задачи; удобно выбрать их близкими к соответствующим осям X и Y. Для удобства описания двух систем введем орты ${{{\mathbf{e}}}_{x}}$,${{{\mathbf{e}}}_{y}}$,${{{\mathbf{e}}}_{z}}$ исходной (механической) системы координат и орты ${{{\mathbf{\tilde {e}}}}_{х}}$,${{{\mathbf{\tilde {e}}}}_{y}}$,${{{\mathbf{\tilde {e}}}}_{z}}$ новой системы, “привязанной” к излучателю (рис. 1). Согласно сказанному выше:
Орты ${{{\mathbf{\tilde {e}}}}_{x}}$ и ${{{\mathbf{\tilde {e}}}}_{y}}$ в старом базисе можно ввести, например, следующим образом:
(4)
${{{\mathbf{\tilde {e}}}}_{y}} = \frac{{{{{{\mathbf{\tilde {e}}}}}_{z}} \times {{{\mathbf{e}}}_{x}}}}{{\left| {{{{{\mathbf{\tilde {e}}}}}_{z}} \times {{{\mathbf{e}}}_{x}}} \right|}} = \left( {0,\frac{{{{m}_{z}}}}{{\sqrt {m_{z}^{2} + m_{y}^{2}} }}, - \frac{{{{m}_{y}}}}{{\sqrt {m_{z}^{2} + m_{y}^{2}} }}} \right),$(5)
$\begin{gathered} {{{{\mathbf{\tilde {e}}}}}_{x}} = {{{{\mathbf{\tilde {e}}}}}_{y}} \times {{{{\mathbf{\tilde {e}}}}}_{z}} = \\ = \left( {\sqrt {m_{z}^{2} + m_{y}^{2}} , - \frac{{{{m}_{x}}{{m}_{y}}}}{{\sqrt {m_{z}^{2} + m_{y}^{2}} }}, - \frac{{{{m}_{x}}{{m}_{z}}}}{{\sqrt {m_{z}^{2} + m_{y}^{2}} }}} \right), \\ \end{gathered} $Заметим, что выбранный таким образом новый базис может быть получен из старого путем двух последовательных поворотов: сначала вокруг оси X на угол $\alpha $, а затем вокруг новой, получившейся после поворота оси $\tilde {Y}$ на угол $\beta $, которые определяются следующими выражениями:
(6)
$\alpha = - \arcsin \left( {{{{{\mathbf{\tilde {e}}}}}_{y}}{{{\mathbf{e}}}_{z}}} \right) = \arcsin \left( {\frac{{{{m}_{y}}}}{{\sqrt {m_{z}^{2} + m_{y}^{2}} }}} \right),$(7)
$\beta = - \arcsin \left( {{{{\mathbf{e}}}_{x}}{{{{\mathbf{\tilde {e}}}}}_{z}}} \right) = - \arcsin \left( {{{m}_{x}}} \right),$РАСЧЕТ ИДЕАЛЬНОЙ ГОЛОГРАММЫ ИЗ РЕАЛЬНОЙ
На втором этапе построения идеальной голограммы используется связь двух описанных выше систем координат. Перевод голограммы из одной системы в другую удобно выполнить в рамках метода углового спектра. Пространственный (угловой) спектр $S({{k}_{x}},{{k}_{y}})$ поля в плоскости измеренной голограммы${{p}_{0}}\left( {x,y} \right)$ имеет вид [8]:
(8)
$S({{k}_{x}},{{k}_{y}}) = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {{{p}_{0}}\left( {x,y} \right)\,{{e}^{{ - i\left( {{{k}_{x}}x + {{k}_{y}}y} \right)}}}} dxdy} .$(9)
$\begin{gathered} p(x,y,z) = \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}} \times \\ \times \,\,\iint\limits_{k_{x}^{2} + k_{y}^{2} \leqslant {{k}^{2}}} {S({{k}_{x}},{{k}_{y}}){{e}^{{i\left( {{{k}_{x}}x + {{k}_{y}}y + \sqrt {{{k}^{2}} - k_{x}^{2} - k_{y}^{2}} z} \right)}}}}d{{k}_{x}}d{{k}_{y}}{\kern 1pt} , \\ \end{gathered} $где $~k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$ – волновое число, $\omega $ – циклическая частота волны, $c$ – скорость звука.
Здесь область интегрирования ограничена кругом радиуса k, что оправдано на расстояниях от излучателя много больших длины волны. Строго говоря,
для записи точного решения (9) область интегрирования следует распространить на всю
плоскость, что позволяет учесть неоднородные (эванесцентные) волны [1]. Однако указанные неоднородные волны быстро затухают при удалении от излучателя
и поэтому для ультразвука мегагерцового диапазона, используемого в медицине и неразрушающем
контроле, их влиянием можно пренебречь. Представление волнового поля (9) имеет вид
суперпозиции плоских волн с комплексной амплитудой, пропорциональной величине  , причем волновой вектор ${\mathbf{k}}$ в системе координат (X, Y, Z) имеет вид:
, причем волновой вектор ${\mathbf{k}}$ в системе координат (X, Y, Z) имеет вид:
(10)
${\mathbf{k}} = \left( {{{k}_{x}},{{k}_{y}},{{k}_{z}} = \sqrt {{{k}^{2}} - k_{x}^{2} - k_{y}^{2}} } \right).$Перейдем в новую систему координат $(\tilde {X},\tilde {Y},\tilde {Z})$ с центром в точке ${{M}_{0}}$. Радиус-вектор точки пространства при этом выражается следующим образом: ${\mathbf{r}} = \tilde {x}\,{{{\mathbf{\tilde {e}}}}_{x}} + \tilde {y}\,{{{\mathbf{\tilde {e}}}}_{y}} + \tilde {z}\,{{{\mathbf{\tilde {e}}}}_{z}} + {{{\mathbf{r}}}_{0}}$. В новой системе координат выражение (9) преобразуется к виду:
(11)
$\begin{gathered} P\left( {\tilde {x},\tilde {y},\tilde {z}} \right) = \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}} \times \\ \times \,\,\iint\limits_{k_{x}^{2} + k_{y}^{2} \leqslant {{k}^{2}}} {S\left( {{{k}_{x}},{{k}_{y}}} \right)}{{e}^{{i\left[ {\tilde {x}\left( {{\mathbf{k}}{{{{\mathbf{\tilde {e}}}}}_{x}}} \right) + \tilde {y}\left( {{\mathbf{k}}{{{{\mathbf{\tilde {e}}}}}_{y}}} \right) + \tilde {z}\left( {{\mathbf{k}}{{{{\mathbf{\tilde {e}}}}}_{z}}} \right) + \left( {{\mathbf{k}}{{{\mathbf{r}}}_{0}}} \right)} \right]}}}d{{k}_{x}}d{{k}_{y}}, \\ \end{gathered} $Выберем в качестве плоскости задания идеальной голограммы ${{P}_{0}}\left( {\tilde {x},\tilde {y}} \right)$ плоскость $\tilde {z} = 0$, проходящую через точку ${{M}_{0}}$. При таком выборе ${{P}_{0}}\left( {\tilde {x},\tilde {y}} \right) = P\left( {\tilde {x},\tilde {y},\tilde {z} = 0} \right)$, и поэтому из выражения (11) следует искомое представление для идеальной голограммы:
(12)
$\begin{gathered} {{P}_{0}}\left( {\tilde {x},\tilde {y}} \right) = \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}} \times \\ \times \,\,\iint\limits_{k_{x}^{2} + k_{y}^{2} \leqslant {{k}^{2}}} {S\left( {{{k}_{x}},{{k}_{y}}} \right)}{{e}^{{i\left[ {\tilde {x}\left( {{\mathbf{k}}{{{{\mathbf{\tilde {e}}}}}_{x}}} \right) + \tilde {y}\left( {{\mathbf{k}}{{{{\mathbf{\tilde {e}}}}}_{y}}} \right) + \left( {{\mathbf{k}}{{{\mathbf{r}}}_{0}}} \right)} \right]}}}d{{k}_{x}}d{{k}_{y}}, \\ \end{gathered} $(13)
${{P}_{0}}\left( {\tilde {x},\tilde {y}} \right) \approx {{e}^{{ - ik\left( {{{m}_{x}}\tilde {x} + {{m}_{y}}\tilde {y}} \right)}}}{{p}_{0}}\left( {\tilde {x} + {{x}_{0}},\tilde {y} + {{y}_{0}}} \right).$Как видно, в указанном приближении переход (13) от измеренной голограммы ${{p}_{0}}\left( {x,y} \right)$ к идеальной голограмме ${{P}_{0}}\left( {\tilde {x},\tilde {y}} \right)$ соответствует перемещению центра координат исходной голограммы в точку ${{M}_{0}}$ и умножению на дополнительный набег фазы, увеличивающийся вдоль поперечных координат, для плоской волны, распространяющейся в направлении вектора ${\mathbf{m}}$. Как отмечалось, первым условием справедливости приближения (13) является требование малости углов поворота, что соответствует условию $\sqrt {m_{x}^{2} + m_{y}^{2}} \ll 1$. На практике его относительно нетрудно выполнить, так как при должной аккуратности излучатели диаметром несколько сантиметров даже вручную могут быть ориентированы относительно осей системы позиционирования с ошибкой, не превышающей одного–двух градусов. Второе условие заключается в локализации углового спектра в узкой области частот $\sqrt {k_{x}^{2} + k_{y}^{2}} \ll k$, что зависит от параметров излучателя. Например, при использовании сильно фокусирующих излучателей ультразвуковой хирургии угловой спектр волны может быть достаточно широким и, следовательно, применение выражения (13) для поворота и центрирования голограммы будет менее точным.
Следует отметить, что для осуществления точного поворота и центрирования измеренной голограммы не удается использовать алгоритм быстрого преобразования Фурье (БПФ), поскольку при сведении интеграла в формуле (12) к форме обратного преобразования Фурье, т.е. при разложении подынтегрального выражения на множители ${{S}_{1}}({{k}_{x}},{{k}_{y}},{\mathbf{r}})\exp (i{\mathbf{kr}})$, эквивалетный спектр ${{S}_{1}}({{k}_{x}},{{k}_{y}},{\mathbf{r}})$ будет зависеть от координат вектора ${\mathbf{r}}$. Таким образом, для точной корректировки голограммы необходимо либо численно рассчитывать интеграл (12), либо реализовывать дискретное преобразование Фурье (ДПФ) со спектром, зависящим от координат. В данной работе в расчетах используется второй способ, а спектр $S({{k}_{x}},{{k}_{y}})$ исходной голограммы вычисляется с помощью БПФ. Ввиду большого числа точек в голограмме, ее точная корректировка может занимать значительное время, особенно для больших голограмм, в то время как приближенный поворот и центрирование по формуле (13) могут быть осуществлены очень быстро умножением голограммы на соответствующую экспоненциальную матрицу. Поэтому представляет интерес изучение обоих методов корректировки, а также анализ ошибки, вносимой при использовании приближенной формулы (13).
ЧИСЛЕННАЯ ВЕРИФИКАЦИЯ МЕТОДА
Численный эксперимент по анализу предложенного алгоритма получения идеальной голограммы и восстановления распределения нормальной компоненты колебательной скорости на излучающей поверхности проводился на примере одноэлементного сферического излучателя с рабочей частотой f0 = 2 МГц, радиусом кривизны $F = 80$ мм и диаметром $D = 100$ мм (рис. 2). Выбранные частота, форма и размеры излучателя соответствовали параметрам описанной в следующем экспериментальном разделе кольцевой фазированной решетки.
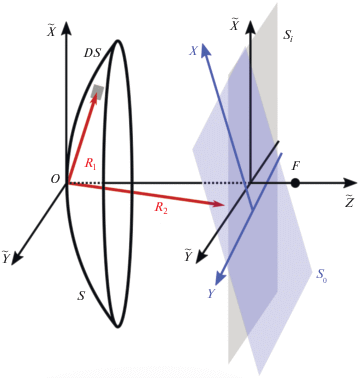
Рис. 2.
Схема расположения одиночного излучателя в виде сферического сегмента относительно плоской поверхности исходной голограммы S0 и поверхности идеальной голограммы Si.
На поверхности $S$ излучателя задавалось равномерное распределение колебательной скорости единичной амплитуды и с помощью интеграла Рэлея рассчитывалось давление на поверхности ${{S}_{0}}$ неидеальной голограммы:
(14)
$P({{{\mathbf{r}}}_{2}}) = - \frac{{ik\rho c}}{{2\pi }}\int\limits_S {{{V}_{n}}({{{\mathbf{r}}}_{1}})} \,\frac{{{{e}^{{ikR}}}}}{R}dS,$Для расчета неидеальной голограммы ${{S}_{0}}$ по формуле (14) необходимо знать уравнение плоскости, в которой лежит данная голограмма. Оно было получено из уравнения плоскости, в которой лежит идеальная голограмма ${{S}_{i}}$, путем ее двух последовательных поворотов: сначала вокруг оси $\tilde {Y}$, а затем вокруг новой, получившейся после первого поворота, оси $X$; а также смещения центра координат в плоскости повернутой голограммы. Таким образом, для однозначного задания положения плоскости реальной голограммы использовалось 5 параметров: расстояние от центра источника O до центра идеальной голограммы ${{S}_{i}}$, углы ее поворотов вокруг осей $\tilde {Y}$ и новой оси $X$, а также смещение центра голограммы по осям X и Y (рис. 2).
После вычисления распределения давления на поверхности ${{S}_{0}}$ (рис. 2) по формуле (14) применялся описанный алгоритм нахождения акустической оси излучателя, затем осуществлялись поворот и центрирование голограммы точным (12) и приближенным (13) методами. Из рассчитанных двух новых голограмм и из исходной неидеальной голограммы с помощью интеграла Рэлея восстанавливались распределения амплитуды и фазы нормальной компоненты колебательной скорости на поверхности в виде сферического сегмента, отсекаемого используемой голограммой от сферы радиуса F = 80 мм с центром на предполагаемой акустической оси и расположенного на некотором расстоянии от голограммы. В случае проведения коррекции предполагалось, что акустическая ось проходила перпендикулярно плоскости скорректированной голограммы через ее центр M0 (1), а в отсутствие коррекции – перпендикулярно плоскости исходной голограммы через ближайший к центру симметрии поля узел сетки. Расстояние от голограмм до сферической поверхности определялось путем совмещения максимумов распределений амплитуды давления на оси, рассчитанных с помощью интеграла Рэлея (14) для номинальных параметров источника и восстановленных из используемых голограмм. Вне поверхности сферического сегмента, отсекаемого голограммой, амплитуда и фаза колебательной скорости полагалась равной нулю.
Плоскость неидеальной голограммы ${{S}_{0}}$ была получена из плоскости идеальной голограммы Si, отстоящей от центра O излучателя на 70 мм (рис. 2). Размер голограммы был выбран равным 301 × 301 точек с шагом $dx = dy = $ 0.35 мм, что соответствовало 0.47 длины волны в воде на рабочей частоте излучателя. Окончательный шаг сетки на вспомогательных плоскостях (рис. 1) составлял 0.01 мм, что соответствовало максимальной ошибке в определении координат центра симметрии полученных неидеальных голограмм 0.014 мм.
Рассматривались три варианта отклонения исходной голограммы от идеальной. В первом случае неидеальная голограмма задавалась путем поворота и смещения идеальной голограммы на относительно большие, по сравнению с характерными экспериментальными значениями, величины: углы поворота вокруг осей $\tilde {Y}$ и X составляли $4^\circ $ и $ - 4^\circ $, соответственно, а центр голограммы смещался в точку $({{x}_{0}},{{y}_{0}}) = (2,4)$ мм. Во втором случае рассматривался случай малых углов поворота и смещения идеальной голограммы: углы поворота вокруг осей $\tilde {Y}$ и X составляли $1^\circ $ и $ - 1^\circ ,$ соответственно, а центр голограммы смещался в точку $({{x}_{0}},{{y}_{0}})$ = (1,1) мм. В третьем случае, для количественной оценки точности восстановления колебательной скорости на поверхности излучателя при использовании точного и приближенного методов корректировки, вычислялись голограммы, не смещенные относительно идеальной, но повернутые вокруг оси $\tilde {X}$ на изменяющийся угол 0° ≤ $\alpha $ ≤ 20°. В этом случае голограмма задавалась на сетке, состоящей из $201 \times 201$ точек.
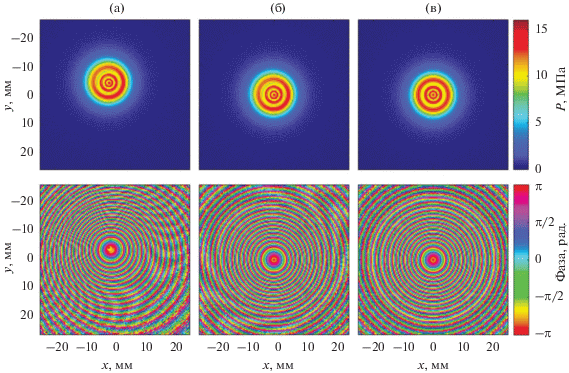
Для первого случая большого поворота и смещения плоскости идеальной голограммы, результаты расчета амплитуды и фазы давления в центральной части полученной неидеальной голограммы, а также после ее приближенной и точной коррекции, представлены на рис. 3. При отсутствии коррекции (рис. 3а) отчетливо видно смещение центра голограммы и нарушение симметрии распределений как для амплитуды, так и для фазы давления. После приближенной коррекции (рис. 3б) распределения и амплитуды, и фазы давления стали центрированы. Угловая асимметрия в распределение фазы по углу вокруг оси пучка существенно уменьшилась, однако сохранилась неизменной в распределении амплитуды, поскольку приближенная коррекция (13) представляет собой перенос центра системы координат и умножение на фазовый множитель. После точной коррекции (рис. 3в) и амплитуда, и фаза стали симметричными относительно центра голограммы. Обратное смещение центра голограммы и углы поворота при корректировке, вычисленные по (1), (6), (7), составили (–2.00, –3.99) мм и (–3.99, 3.97) градуса.
Рис. 3.
Распределение амплитуды (сверху) и фазы (снизу) в плоскости: (а) – исходной голограммы ${{S}_{0}}$ для случая большого поворота и смещения ее плоскости относительно идеальной голограммы, (б) – голограммы, скорректированной приближенным методом, (в) – голограммы, скорректированной точным методом.
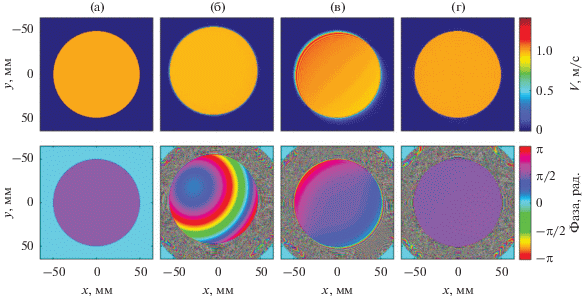
На рис. 4 представлены исходно заданные распределения амплитуды и фазы нормальной компоненты колебательной скорости на поверхности излучателя (рис. 4а) и восстановленные из полученных голограмм (рис. 3). При восстановлении без коррекции голограмма центрировалась путем смещения центра координат в узел сетки с координатами (–2.10, –3.85) мм, наиболее близкий к центру симметрии поля голограммы. Как видно (рис. 4б), бóльшая неточность в нахождении координат центра практически не повлияла на равномерность восстановленного распределения амплитуды давления на поверхности сферы, но произошло ожидаемое смещение поверхности излучателя вдоль сферической поверхности, на которой проводился расчет. В случае приближенной корректировки голограммы (рис. 4в) распределение амплитуды отличается от исходно заданного (рис. 4а) как неравномерностью вдоль поверхности, так и нерезкой границей излучателя. При этом наблюдаемые отличия стали даже сильнее, чем в случае отсутствия корректировки голограммы, что свидетельствует о неточности подхода. Распределение фазы стало более равномерным, однако также отличается от исходного. При точной корректировке голограммы рассчитанная структура колебаний излучателя практически не отличается от исходной (рис. 4г). Заметна лишь небольшая неоднородность в распределении амплитуды на краях излучателя, которая появляется вследствие неучета неоднородных волн при использовании метода углового спектра в решении (9). В реальных измерениях дополнительную ошибку в определение данных величин также могут внести ошибки измерения голограммы [5].
Рис. 4.
Распределение амплитуды (сверху) и фазы (снизу) нормальной компоненты колебательной скорости на излучателе: (а) – изначально заданное; расчитаное из: (б) – исходной голограммы для случая большого поворота и смещения ее плоскости относительно идеальной голограммы, (в) – голограммы, скорректированной приближенным методом, (г) – голограммы, скорректированной точным методом.
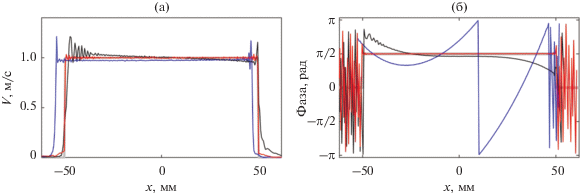
Для большей наглядности на рис. 5 приведено сравнение полученных распределений амплитуды (рис. 5а) и фазы (рис. 5б) на поверхности излучателя вдоль оси $X$ при $y = 0$. Красная кривая соответствует распределению, полученному после точной коррекции голограммы. Видно, что она очень близка к исходно заданному прямоугольному распределению (серая кривая), в то время как результаты, полученные после приближенной коррекции или при ее отсутствии (черная и синяя кривые, соответственно) сильно отличаются от истинных.
Рис. 5.
(а) – Амплитуда и (б) – фаза нормальной компоненты колебательной скорости поверхности вдоль оси Х при $y = 0$. Серая линия соответствует заданному прямоугольному распределению; синяя кривая – восстановленному из исходной голограммы без корректировки для случая большого поворота и смещения ее плоскости относительно идеальной голограммы; красная и черная – востановленным из голограмм, скорректированных точным и приближенным методами, соответственно.
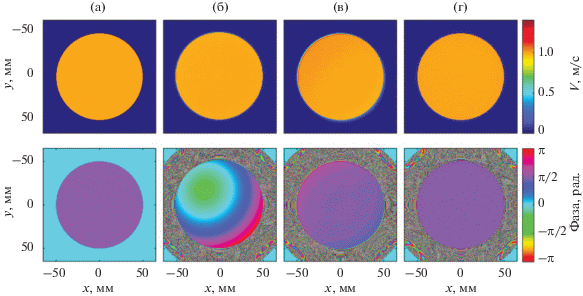
Для второго случая малых углов поворота и смещения исходной голограммы относительно идеальной результаты восстановления амплитуды и фазы колебательной скорости на излучателе представлены на рис. 6. Обратное смещение центра голограммы и углы поворота при корректировке по сравнению с заданными (1.00, 1.00) мм и (1.00, –1.00) градуса составили (–1.01, –1.01) мм и (–1.01, 1.01) градуса; при восстановлении без коррекции центр координат смещался в узел сетки с координатами (–1.05, –1.05) мм. В целом, в восстановленных распределениях хотя и в меньшей степени, но наблюдаются те же отличия, что и в случае больших поворотов и смещений. Интересно отметить, что хотя в данном случае применение приближенного метода является более обоснованным, распределения как амплитуды, так и фазы колебательной скорости на излучателе (рис. 6в), полученные из приближенно скорректированной голограммы, по-прежнему отличаются от исходных (рис. 6а). Связано это с тем, что угловой спектр поля рассматриваемого сильнофокусирующего излучателя является достаточно широким.
Рис. 6.
Распределение амплитуды (сверху) и фазы (снизу) нормальной компоненты колебательной скорости на излучателе: (а) – изначально заданное; расчитаное из: (б) – исходной голограммы для случая малого поворота и смещения ее плоскости относительно идеальной, (в) – приближенно cкорректированной голограммы, (г) – точно cкорректированной голограммы.
Для третьего случая различных углов $\alpha $ поворота голограммы относительно идеальной и использования точного и приближенного методов ее коррекции была проведена количественная оценка величины ошибки определения колебательной скорости на поверхности излучателя. Из полученных голограмм вычислялась колебательная скорость на предполагаемой поверхности излучателя без коррекции и после приближенного и точного поворотов голограммы. Как указывалось выше, вследствие неучета неоднородных волн [8] даже при расчете идеальной голограммы на основе поля с излучателя и обратного перерасчета распределение колебательной скорости на излучателе не будет идентичным исходному. Поэтому возникающая при точном и приближенном поворотах ошибка $\varepsilon \left( \alpha \right)$ в рассчитанном на излучателе распределении колебательной скорости ${{V}_{n}}\left( \alpha \right)$ рассматривалась относительно численно восстановленного распределения ${{V}_{n}}\left( {\alpha = 0} \right)$:
(15)
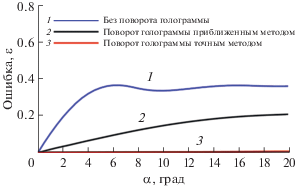
$\varepsilon \left( \alpha \right) = \frac{1}{N}\sum\limits_n^N {\left| {{{V}_{n}}\left( \alpha \right) - {{V}_{n}}\left( {\alpha = 0} \right)} \right|} ,$Сравнение введенной таким образом ошибки для описанных трех случаев представлено на рис. 7. Как и ожидалось, по мере увеличения угла между нормалью к голограмме и осью излучателя, ошибка в определении колебательной скорости на поверхности излучателя, возникающая после приближенной коррекции голограммы, растет значительно быстрее, чем в случае точной коррекции. Появление небольшой ошибки при использовании точного метода корректировки связано как с неточностью определения направления акустической оси и, соответственно, координат векторов ${\mathbf{m}}$ и ${{{\mathbf{r}}}_{0}}$ (1), (2), так и с тем фактом, что при бóльших углах поворота ввиду фиксированного размера голограммы на ее поверхность попадает меньше энергии пучка, поэтому она будет содержать в себе менее полную информацию об акустическом поле.
Рис. 7.
Зависимость ошибки в определении распределения комплексной амплитуды нормальной компоненты колебательной скорости на излучающей поверхности от угла наклона плоскости голограммы к оси излучателя при точной (красная линия 3) и приближенной (черная линия 2) корректировке голограммы, а также при отсутствии корректировки (синяя линия 1).
ЭКСПЕРИМЕНТАЛЬНАЯ ВЕРИФИКАЦИЯ МЕТОДА
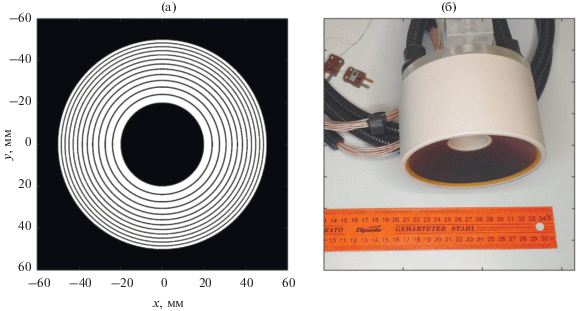
Экспериментальная верификация предложенного метода проводилась для кольцевого фокусирующего пьезокомпозитного преобразователя (Imasonic, Франция) (рис. 8), имеющего форму вогнутой сферической чаши с круглым центральным отверстием. Преобразователь имеет следующие номинальные параметры: внутренний и внешний диаметры ${{D}_{1}} = 40\,\,мм$ и ${{D}_{2}} = 100\,\,мм$, соответственно, фокусное расстояние (радиус кривизны) $F = 80\,\,мм$, резонансная частота ${{f}_{0}} = 2\,\,МГц$. Излучающая поверхность преобразователя разделена на 12 кольцевых сегментов с равной площадью $S = 5.2\,\,{\text{с}}{{{\text{м}}}^{2}}$ и зазором толщиной $dr = 0.5\,мм$, что позволяет использовать его в качестве кольцевой фазированной решетки.
Рис. 8.
(а) – Диаграмма и (б) – фотография исследуемой ультразвуковой фазированной решетки (Imasoniс, France), состоящей из 12 колец равной площади, расположенных на сфере радиуса F = 80 мм.
Излучатель погружался в резервуар с дегазированной водой размером $100 \times 50 \times 50\;$ см и был неподвижно закреплен в процессе измерений. Фильтрация и дегазация воды осуществлялись с помощью системы подготовки воды PA WTS (Water Treatment System, Precision Acoustics, Великобритания). На каждый из элементов фазированной решетки подавалось электрическое напряжение от 12-канального генератора [11]. Напротив решетки был выставлен игольчатый гидрофон HNA-0400 (Onda Corp., США) с диаметром чувствительного участка 0.4 мм. Чувствительность гидрофона с учетом встроенного предусилителя электрического сигнала составляла $1.197\,\,{В \mathord{\left/ {\vphantom {В {МПа}}} \right. \kern-0em} {МПа}}$ на частоте $2\,МГц$. Гидрофон в процессе измерений перемещался автоматическим образом с помощью системы микропозиционирования UMS-3 (Precision Acoustics, Великобритания), расположенной над резервуаром и позволяющей проводить пространственное трехмерное сканирование с гарантируемой точностью позиционирования $6\,\;мкм$. Электрический сигнал гидрофона поступал на осциллограф (TDS5054B, Tektronix Inc., США), подключенный к компьютеру. Управление процессом измерений осуществлялось программой, написанной в среде LabView, входящей в состав системы позиционирования Precision Acoustics. Контроль стабильности температуры воды во время измерений проводился с помощью встроенной в излучатель термопары. Время измерения голограмм составляло приблизительно 10 ч, за это время отклонение температуры от $22^\circ {\text{С}}$ составляло не более $0.3^\circ {\text{С}}$.
Было проведено измерение двух голограмм: первая голограмма записывалась при расположении преобразователя параллельно плоскости измерения голограммы с точностью около $1^\circ $, вторая голограмма – после поворота излучателя на $10^\circ $ вокруг оси Y голограммы. Вращение осуществлялось с помощью поворотного механизма системы позиционирования с номинальной точностью выставления угла до $0.2^\circ $. Голограмма записывалась путем регистрации сигнала гидрофона в узлах плоской квадратной сетки с шагом 0.4 мм, расположенной на расстоянии 15 мм от фокального максимума в сторону излучателя. Соответствующее количество узлов сетки было выбрано равным 221 × 221, размер голограммы в каждом измерении превышал геометрический размер ультразвукового пучка в данной области в 3.6 раза. Центр области сканирования в обоих случаях устанавливался вручную в центре акустического пучка для обеспечения максимально полного попадания акустического пучка в область измерений.
Все кольцевые элементы излучателя возбуждались синфазно электрическим импульсом, состоящим из N = 5 периодов на частоте ${{f}_{0}} = 2\,МГц$, амплитудой $1\,В$, период повторения сигнала составлял T = 4 мс. Сигнал в каждой точке голограммы записывался в пределах временного окна длительностью 100 мкс, что было достаточным для записи регистрируемого гидрофоном импульсного акустического сигнала в каждой точке голограммы. Запись сигнала гидрофона происходила с шагом дискретизации 20 нс, что для выбранного временного окна составляет 5000 временных отсчетов. Для снижения уровня шумов в каждой точке голограммы проводилось усреднение по 48 реализациям периодически повторяющегося сигнала. Результатом измерений являлась нестационарная голограмма, из которой с помощью спектрального разложения выделялась голограмма на резонансной частоте излучателя, которая далее нормировалась на соответствующую составляющую спектра сигнала напряжения на элементах. После учета чувствительности гидрофона было получено распределение комплексной амплитуды давления в паскалях в плоскости измеряемой голограммы, соответствующее режиму работы решетки в монохроматическом режиме на резонансной частоте при напряжении на элементах равном 1 В.
На основе полученных данных с использованием описанных выше методов проводилась реконструкция распределения колебаний поверхности излучателя после предварительной точной и приближенной корректировок измеренных голограмм. Вспомогательные распределения давления на участках ${{S}_{1}}$ и ${{S}_{2}}$ (рис. 1) строились на расстояниях –15.07 и 14.75 мм от исходных голограмм, соответственно, а расчет поля на них проводился с использованием интеграла Рэлея итерационным образом в окне с количеством точек $50 \times 50$ и окончательным шагом сетки 0.01 мм.
В первом случае близкого к идеальному расположения измеряемой голограммы при ее коррекции потребовалось перенести центр координат в точку (0.06, 0.27) мм, совершить поворот вокруг оси X на –0.15° и затем вокруг $\tilde {Y}$ на 0.44°. Расстояние от плоскости скорректированных голограмм до максимума распределения амплитуды на оси излучателя получилось равным 15.01 мм. Распределения амплитуды и фазы колебательной скорости, восстановленные на предполагаемой поверхности излучателя, описанной ранее, как после приближенной (рис. 9а), так и после точной (рис. 9б) корректировок оказались внешне практически неотличимыми.
Рис. 9.
Сравнение распределений амплитуды (сверху) и фазы (снизу) нормальной компоненты колебательной скорости на поверхности фазированной решетки, восстановленные из голограмм, измеренных при (а, б) – малом и (в, г) – большом углах поворота плоскости голограммы относительно акустической оси решетки после коррекции (а, в) – приближенным и (б, г) – точным методами.
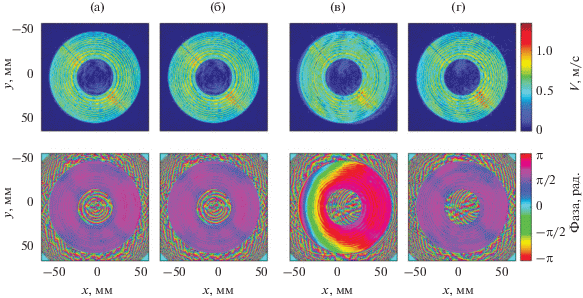
Во втором случае, когда ось излучателя была повернута относительно осей системы позиционирования на достаточно большой угол, для восстановления идеальной голограммы центр координат был перенесен в точку (–0.08, 0.15) мм, а исходная голограмма повернута вокруг оси X на –0.19° и вокруг оси $\tilde {Y}$ на –9.57°. Расстояния от приближенно и точно скорректированных голограмм до фокуса получились равными 13.60 и 15.08 мм, соответственно. В этом случае приближенный способ корректировки голограммы дает неудовлетворительные результаты (рис. 9в). Заметим, что распределение колебательной скорости на излучателе, полученное даже из точно скорректированной голограммы (рис. 9г), несколько отличается от рассчитанного при небольшом угле поворота (рис. 9б). Данное расхождение может быть связано с неучетом диаграммы направленности гидрофона, что вносит дополнительные искажения при измерении голограммы на повернутой плоскости [12].
ЗАКЛЮЧЕНИЕ
В работе предложен метод пространственной коррекции акустических голограмм излучателей, обладающих аксиальной симметрией, для практического использования при характеризации колебаний поверхности самих излучателей и создаваемых ими полей. Метод позволяет построить голограмму на плоскости, перпендикулярной оси излучателя и центрированной относительно нее, что представляется наиболее удобным для последующего задания граничных условий на поверхности излучателя в задачах численного эксперимента, реконструкции поля и сравнения с данными измерений в координатах излучателя. Проанализирована ошибка точного и приближенного методов коррекции голограммы при различных углах между осью излучателя и нормалью к исходной голограмме. Показано, что несмотря на то, что приближенный метод коррекции является гораздо более простым в реализации и быстрым в плане расчета, его использование для источников с широким угловым спектром даже при малых углах наклона плоскости голограммы к оси излучателя может вносить существенные ошибки при реконструкции идеальной голограммы. Таким образом, для практических приложений медицинского ультразвука, требующих высокой точности определения структуры колебаний поверхности излучателя и создаваемого им поля, корректировка акустической голограммы точным методом является предпочтительной.
Работа выполнена при финансовой поддержке грантов РНФ 19-12-00148 и студенческой стипендии от Focused Ultrasound Foundation.
Список литературы
Maynard J.D., Williams E.G., Lee Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH // J. Acoust. Soc. Am. 1985. V. 78. № 4. P. 1395–1413.
Сапожников О.А., Пищальников Ю.А., Морозов А.В. Восстановление распределения нормальной скорости на поверхности ультразвукового излучателя на основе измерения акустического давления вдоль контрольной поверхности // Акуст. журн. 2003. Т. 49. № 3. С. 416–424.
Сапожников О.А., Пономарев А.Е., Смагин М.А. Нестационарная акустическая голография для реконструкции скорости поверхности акустических излучателей // Акуст. журн. 2006. Т. 52. № 3. С. 385–392.
IEC/TS62556. Ultrasonics-field characterization-specification and measurement of field parameters for high intensity therapeutic ultrasound (HITU) transducers and systems // International Electrotechnical Commission, Geneva, Switzerland, 2014, ed. 1.0
Sapozhnikov O.A., Tsysar S.A., Khokhlova V.A., Kreider W. Acoustic holography as a metrological tool for characterizing medical ultrasound sources and fields // J. Acoust. Soc. Am. 2015. V. 138. № 3. P. 1515–1532.
Николаев Д.А., Цысарь С.А., Сапожников О.А. Определение и компенсация перекоса осей трехкоординатных систем позиционирования с помощью метода акустической голографии // Изв. Росс. акад. наук. Сер. физ. 2021. Т. 85. № 6. С. 854–862.
O’Neil N.T. Theory of focusing radiators // J. Acoust. Soc. Am. 1949. V. 21. P. 516–526.
Goodman W. Introduction to Fourier Optics // New York: McGraw-Hill, 1968.
Stepanishen P.R., Benjamin K.C. Forward and backward projection of acoustic fields using FFT methods // J. Acoust. Soc. Am. 1982. V. 71. P. 803–811.
Schafer M.E., Lewin P.A. Transducer characterization using the angular spectrum method // J. Acoust. Soc. Am. 1989. V. 85. № 5. P. 2202–2214.
Maxwell A.D., Yuldashev P.V., Kreider W., Khokhlova T.D., Schade G.R., Hall T.L., Sapozhnikov O.A., Bailey M.R., Khokhlova V.A. A prototype therapy system for transcutaneous application of boiling histotripsy // IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2017. V. 64. № 10. P. 1542–1557.
Ghanem M.A., Maxwell A.D., Kreider W., Cunitz B.W., Khokhlova V.A., Sapozhnikov O.A., Bailey M.R. Field characterization and compensation of vibrational non-uniformity for a 256-element focused ultrasound phased array // IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2018. V. 65. № 9. P. 1618–1630.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал