1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 67, № 4, 2021

Акустический журнал, 2021, T. 67, № 4, стр. 413-430

Применение метода дискретного представления переменных для формирования амплитудно-фазовых распределений поля на вертикальной антенной решетке в волноводе

Д. В. Макаров *

Тихоокеанский океанологический институт им. В.И. Ильичева ДВО РАН
690041 Владивосток, ул. Балтийская 43, Россия

* E-mail: makarov@poi.dvo.ru

Поступила в редакцию 08.07.2020
После доработки 19.04.2021
Принята к публикации 23.04.2021

Полный текст (PDF)

Аннотация

Рассматривается задача о возбуждении акустических полей с заданной пространственной конфигурацией в условиях мелкого моря. Предлагается новый теоретический подход, позволяющий напрямую связать амплитудно-фазовое распределение сигналов для излучателей вертикальной антенны с профилем создаваемого акустического поля. В основе предлагаемой теории лежит математический аппарат функций дискретного представления переменных, известный из квантовой теории. В случае эквидистантных антенн с достаточно высокой плотностью излучателей теория воспроизводит ранее известные результаты. С помощью предлагаемого подхода исследуется влияние плотности расположения излучателей на качество возбуждения требуемого акустического поля.

Ключевые слова: акустическая антенна, акустический волновод, акустический импульс, функции дискретного представления переменных

ВВЕДЕНИЕ

Для решения различных научных и практических задач подводной акустики нередко требуется создание звуковых полей с заданной пространственной конфигурацией. К числу таких задач относится, например, акустическая засветка заданного участка волновода [1–4]. Кроме того, селективное возбуждение отдельных мод или узких лучевых пучков упрощает реконструкцию среды с помощью методов гидроакустической томографии [5–7], а также может быть использовано для создания так называемых слаборасходящихся пучков [8–12], представляющих значительный интерес в контексте подводной связи [13–15].

В этой работе рассматривается задача о возбуждении тональных и импульсных сигналов с помощью вертикальной антенны, представляющей собой цепочку ненаправленных излучателей (монополей). Проблеме расчета амплитудно-фазовых распределений (АФР) для монополей антенны посвящена обширная литература (см., например, [16–24]). В данной работе рассматривается новый подход к этой проблеме, основанный на использовании функций дискретного представления переменных (ДПП). Эти функции являются связующим звеном между точечными значениями акустического поля и его непрерывным профилем. Функции ДПП активно используются в задачах квантовой физики (см., например, [25–29]).

Параллельно в работе рассматривается задача о влиянии числа монополей на эффективность возбуждения требуемого акустического поля. Следует отметить, что сооружение вертикальной антенны с высокой плотностью монополей является технически достаточно сложной задачей даже в условиях мелкого моря. Отсюда возникает потребность в упрощении антенны без существенных потерь в качестве возбуждения. Упрощение предполагает уменьшение числа излучателей и/или длины антенны. Специфической особенностью этой работы также является то, что для оценки эффективности возбуждения используется такая характеристика как воспроизводимость.

Статья построена следующим образом. В следующем параграфе представлена теория расчета амплитудно-фазового распределения антенны с помощью функций дискретного преобразования переменных. Затем вводится модель акустического волновода в мелком море, которая будет впоследствии использована для численного моделирования. В последующих двух разделах рассматривается вопрос о влиянии плотности излучателей на эффективность возбуждения акустических мод с помощью эквидистантной антенны. Предпоследний раздел статьи посвящен применению теории, основанной на функциях ДПП, для случая неэквидистантной антенны. В Заключении подводятся итоги работы и формулируются основные выводы.

ВЫЧИСЛЕНИЕ АМПЛИТУДНО-ФАЗОВОГО РАСПРЕДЕЛЕНИЯ ВЕРТИКАЛЬНОЙ АНТЕННЫ С ПОМОЩЬЮ ФУНКЦИЙ ДИСКРЕТНОГО ПРЕДСТАВЛЕНИЯ ПЕРЕМЕННЫХ

Традиционный подход к синтезу звуковых полей основан на применении антенных решеток с соответствующими АФР [30, 31]. Обозначим АФР решетки с помощью вектора Y, компоненты которого равны комплексным амплитудам поля, создаваемого каждым отдельным монополем (излучателем). Вычисление Y сводится к решению матричных уравнений, связывающих коэффициенты возбуждения отдельных нормальных мод с комплексными амплитудами звукового поля на различных элементах решетки. В простейшем случае эта процедура сводится к приравниванию амплитуды и фазы каждого излучателя к амплитуде и фазе звукового поля в данной точке, т.е.

(1)
${{Y}_{j}}(f) = w{\kern 1pt} \Psi ({{z}_{j}},f),$
где ${{z}_{j}}$ – глубина j-го точечного излучателя (монополя), f – частота сигнала, w – нормировочный коэффициент. Формула (1) легко обобщается на случай импульсного сигнала путем перехода из пространства частот в пространство времен с помощью преобразования Фурье
(2)
${\mathbf{\Phi }}(t) = \int {{\mathbf{Y}}(\Omega )S(\Omega ){{e}^{{ - i\Omega t}}}d\Omega } ,$
где $\Omega = 2\pi f$ – круговая частота, $S(\Omega )$ – спектр Фурье сигнала, а вектор ${\mathbf{\Phi }}$ описывает АФР в импульсном режиме.

Вместе с тем, условия применимости формулы (1) вызывают некоторые вопросы. Во-первых, насколько высокой должна быть плотность монополей, чтобы обеспечивалось эффективное возбуждение требуемого акустического поля? Разумно предположить, что количество монополей должно превышать число распространяющихся мод. Однако в случае широкополосных импульсных сигналов последнее число не является однозначно определенным. Кроме того, влияние профиля скорости звука может предполагать неоднородную плотность монополей. Отсюда возникает другой вопрос, который касается применимости формулы (1) для антенны с неэквидистантным расположением монополей. Очевидно, что в этом случае коэффициент w должен зависеть от номера монополя j. Каким образом вычисляется эта зависимость?

Предлагаемая в данной работе теория позволяет в той или иной степени ответить на поставленные вопросы. В ней АФР вертикальной антенны жестко привязано к непрерывному профилю создаваемого поля, а комплексная амплитуда j-го монополя определяется выражением

(3)
${{\Phi }_{j}}(t) = \int {\Psi (t,z)\chi _{j}^{*}(z)\,dz} ,$
где $\Psi (t,z)$ – акустический импульс, который требуется излучить, ${{\chi }_{j}}(z)$ – функция ДПП, соответствующая j-му монополю. Возможность использования функций ДПП в акустике океана была впервые продемонстрирована в работах [32, 33], где был предложен алгоритм для точной реконструкции профиля звукового поля по данным, полученным с помощью вертикальной приемной антенны. В настоящей работе аналогичный алгоритм используется для синтеза звуковых полей.

Функции ДПП могут быть найдены следующим образом. Рассмотрим в качестве примера подводный акустический волновод, состоящий из двух слоев, водного и осадочного. Снизу осадочный слой граничит со слоем твердых пород, который будем считать непроницаемым для звука. Для простоты будем считать волновод плоскослоистым, тогда граничные условия выглядят следующим образом:

(4)
$\Psi (z = 0) = 0,\,\,\,\frac{{d\Psi }}{{dz}}(z = L) = 0.$

В качестве первого шага для определения функций ДПП необходимо найти набор вспомогательных базисных функций ${{\phi }_{j}}(z)$, которые, во-первых, удовлетворяли бы граничным условиям (4), а во-вторых – обеспечивали бы трехдиагональную форму матрицы ${\mathbf{Z}}$, элементы которой определяются выражением [33]

(5)
${{Z}_{{ij}}} = \int {dz\,\phi _{{_{i}}}^{*}(z)f(z){{\phi }_{j}}(z)} ,$
где f(z) – некоторая обратимая функция. Если такой базис найден, то функции ДПП могут быть определены по формуле [27]
(6)
${{\chi }_{j}}(z) = \sum\limits_{i = 1}^J {{{V}_{{ij}}}} {{\phi }_{i}}(z),$
где ${{V}_{{ij}}}$ – i-ый элемент j-го собственного вектора матрицы ${\mathbf{Z}}$. Число J определяется из требования, что акустическое поле должно полностью описываться первыми J членами разложения по базису функций ${{\phi }_{j}}(z)$, т. е.
(7)
$\Psi (z) = \sum\limits_{j = 1}^J {{{a}_{j}}{{\phi }_{j}}(z)} ,$
где

(8)
${{a}_{j}} = \int\limits_{z = 0}^L {\phi _{j}^{*}(z)} \Psi (z){\mkern 1mu} dz.$

Данное требование можно также переформулировать следующим образом:

(9)
$\sum\limits_{j = 1}^J {{{{\left| {{{a}_{j}}} \right|}}^{2}}} = \int\limits_{z = 0}^L {{{{\left| {\Psi (z)} \right|}}^{2}}} = dz.$

Условия (7) и (9) подразумевают, что матрица ${\mathbf{Z}}$ – квадратная матрица размера J × J.

Трехдиагональность матрицы ${\mathbf{Z}}$ обеспечивает ключевое свойство функций ДПП [25]. Его можно сформулировать следующим образом: при разложении акустического поля по функциям ДПП,

(10)
$\Psi (z) = \sum\limits_{j = 1}^J {{{b}_{j}}} {{\chi }_{j}}(z),$
амплитуды разложения определяются точечными значениями акустического поля по формуле
(11)
${{b}_{j}} \equiv \int {\Psi (z)\chi _{j}^{*}(z)\,dz = \,\,} {{w}_{j}}\Psi ({{z}_{j}}),$
где глубины ${{z}_{j}}$ задаются собственными значениями матрицы ${\mathbf{Z}}$,
(12)
${{z}_{j}} = z({{f}_{j}}).$
Здесь $z(f)$ – это обращенная зависимость $f(z)$ (отсюда становится ясным, почему последняя должна быть обратимой), а весовые коэффициенты ${{w}_{j}}$ определяются по формуле

(13)
${{w}_{j}} = \frac{{V_{{ij}}^{*}}}{{{{\phi }_{i}}({{z}_{j}})}}.$

Таким образом, функции ДПП позволяют установить взаимно однозначную связь между точечными значениями акустического поля и его непрерывным профилем, если акустическое поле удовлетворяет условию (9). Размещая монополи на глубинах (12), мы можем сформировать поле $\Psi (z)$ с помощью АФР следующего вида:

(14)
${{Y}_{j}}(f) = {{w}_{j}}{\kern 1pt} \Psi ({{z}_{j}},f),$
где, в отличие от формулы (1), предполагается, что весовые коэффициенты могут зависеть от номера монополя. Такая ситуация реализуется в случае антенны с неэквидистантным расположением монополей.

Отметим, что базис функций ДПП является ортогональным, т. е.

(15)
$\int\limits_{z = 0}^L {{{\chi }_{i}}} {{\chi }_{j}}dz = {{\delta }_{{ij}}},$
где ${{\delta }_{{ij}}}$ – символ Кронекера.

Весовые коэффициенты ${{w}_{j}}$ в (14) зависят от вида вспомогательного базиса ${{\phi }_{j}}(z)$. Как отмечалось выше, этот базис должен удовлетворять граничным условиям в волноводе, а также обеспечивать трехдиагональность матрицы Z. В работах [32, 33] был предложен вариант такого базиса, удовлетворяющий вышеупомянутым требованиям, в виде пространственных Фурье-гармоник

(16)
${{\phi }_{j}} = \sqrt {\frac{2}{L}} \sin \frac{{(2j - 1)\pi z}}{{2L}},\,\,\,j = 1,2, \ldots ,$
при этом

(17)
$f(z) = \cos \frac{{\pi z}}{L},\,\,\,0 < z \leqslant L.$

В этом случае собственные векторы и собственные значения матрицы ${\mathbf{Z}}$ могут быть найдены аналитически. Собственные векторы описываются формулой

(18)
${{V}_{{ij}}} = \sqrt {\frac{2}{{J + 1}}} \sin \left[ {\frac{{\left( {i - \frac{1}{2}} \right)j\pi }}{{J + 1}}} \right].$

Подставляя (16) и (18) в (6), мы можем найти явный вид функций ДПП. Собственные значения определяются выражением

(19)
${{f}_{i}} = \cos \left( {\frac{{j\pi }}{{J + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \right).$

Учитывая (17) и (19), получаем, что вспомогательный базис (16) отвечает антенне с эквидистантным расположением элементов:

(20)
${{z}_{j}} = z({{f}_{j}}) = j\Delta z,$
где расстояние между соседними монополями

(21)
$\Delta z = \frac{L}{{J + 1}}.$

Весовой коэффициент ${{w}_{j}}$ определяется по формуле

(22)
${{w}_{j}} = \sqrt {\Delta z} $
и не зависит от j. Таким образом, расчет АФР с использованием вспомогательного базиса (16) воспроизводит формулу (1). Из этого следует, что методы расчета АФР, основанные на формулах (1) и (3), эквивалентны друг другу, если выполняется условие (9), а глубины монополей удовлетворяют (20). Разночтения между двумя описанными выше подходами при одном и том же положении монополей могут возникать лишь тогда, когда ограничение на пространственный спектр (9) выполняется недостаточно строго. Сравнительный анализ точности этих подходов приведен ниже, когда будет непосредственно рассматриваться вопрос о возбуждении модовых импульсов.

Функции ДПП являются хорошо локализованными по глубине. Примеры функций ДПП, соответствующих $\Delta z = 10$ м, представлены на рис. 1. Если ввести оператор проекции звукового поля на базис (16)

(23)
${{\hat {P}}_{J}}\Psi = \sum\limits_{j = 1}^J {{{a}_{j}}} {{\phi }_{j}},$
то нетрудно убедиться, что каждая функция ДПП ${{\chi }_{j}}(z)$ удовлетворяет условию
(24)
${{\chi }_{j}}(z) = {{w}_{j}}{{\hat {P}}_{J}}\delta (z - {{z}_{j}}),$
где $\delta (z)$ – дельта-функция. Другими словами, функция ДПП является результатом Фурье-фильтрации дельта-функции, в результате чего отбрасываются гармоники (16) с номерами, превышающими J. Из этого следует, что поле, создаваемое монополем, помещенным на глубину $z = {{z}_{j}}$, эквивалентно j-ой функции ДПП, если звуковое поле полностью описывается суммой гармоник (16) с номерами, не превышающими J. В действительности поле монополя, моделируемое как дельта-функция, характеризуется бесконечным пространственным спектром Фурье. Однако уже на малых расстояниях от источника спектр кардинально трансформируется, обретая верхнюю границу ${{k}_{{\max }}} = {{4\pi } \mathord{\left/ {\vphantom {{4\pi } \lambda }} \right. \kern-0em} \lambda }$. На этом трансформация не заканчивается – спектр вертикальных волновых чисел еще более сужается вследствие затухания волноводных мод с большими номерами, которые активно поглощаются дном. Таким образом, мы приходим к выводу, что наиболее коротковолновая часть спектра излучения монополя является несущественной с точки зрения распространения. Практически это означает, что Фурье-фильтрация, описываемая оператором ${{\hat {P}}_{J}}$ с должным образом заданным значением J, не меняет свойств результирующего поля. Отсюда следует, что функцию ДПП можно рассматривать как эффективный вклад отдельного монополя в акустическое поле при условии расположения остальных монополей на глубинах, описываемых формулой (20). Генерируя каждым из монополей сигнал (3), мы можем сконструировать желаемое акустической поле, используя ортогональность функций ДПП.

Рис. 1.

Профили функций ДПП, соответствующих $\Delta z = 10$ м.

Необходимо подчеркнуть, что вид функции ДПП, связанной с отдельным монополем, не является уникальным. Варьируя расстояние между соседними излучателями $\Delta z$, мы, по сути, меняем степень Фурье-фильтрации. Тем самым мы управляем размером области локализации для соответствующей функции ДПП. Ограничения на степень фильтрации диктуются исключительно требованием быстрого затухания отфильтрованной части спектра.

Можно задаться вопросом: а насколько свободно можно варьировать расстояние между монополями? Сначала рассмотрим случай эквидистантной антенны (неэквидистантные антенны будут рассмотрены позже). Согласно (21), значение $\Delta z$ однозначно определяется положением нижней границы волновода L и числом гармоник J. Последнее может принимать только целые значения, соответственно, расстоянию $\Delta z$ доступно только дискретное множество значений. Это ограничение легко преодолевается, если принять во внимание, что на практике нас интересуют чаще всего только низшие водные моды, способные распространяться на достаточно длинные дистанции. Эти моды практически не чувствительны к положению границы между осадочным слоем и слоем твердых пород. Более того, в натурных экспериментах положение этой границы чаще всего не известно достоверно. Отсюда следует, что для расчета функций ДПП мы можем использовать фиктивную глубину осадочного слоя, значение которой может быть подобрано из условия

(25)
$L{\kern 1pt} ' = (J + 1)\Delta z,$
т.е. расстояние между соседними монополями $\Delta z$ может выбираться согласно нашим пожеланиям. При использовании фиктивной глубины выражение (16) модифицируется следующим образом:

(26)
${{\phi }_{j}} = \sqrt {\frac{2}{{L{\kern 1pt} '}}} \sin \frac{{(2j - 1)\pi z}}{{2L{\kern 1pt} '}},\,\,\,j = 1,2,...,J.$

Естественно предположить, что уменьшение частоты сигнала дает больше свободы для Фурье-фильтрации, позволяя использовать более разреженные антенны. Кроме того, существенно разреженные антенны могут использоваться, если стоит задача создать волновой пакет, распространяющийся почти горизонтально вдоль оси акустического волновода и практически не испытывающий вертикальных осцилляций. Указанные обстоятельства хорошо известны в теории вертикальных акустических антенн [31]. Степень фильтрации, которую мы можем себе позволить, также зависит и от длины трассы. В частности, она зависит от того, насколько быстро затухают высокие моды волновода, дающие основной вклад в коротковолновую часть спектра вертикальных волновых чисел. Таким образом, мы приходим к выводу, что с увеличением расстояния допустимая степень фильтрации может существенно возрастать.

МОДЕЛЬ АКУСТИЧЕСКОГО ВОЛНОВОДА

Рассмотрим мелководный акустический волновод, состоящий из двух слоев: водного, соответствующего интервалу глубин

$0 \leqslant z < h,$
и осадочного, соответствующего

$h \leqslant z < L.$

Звуковое поле в волноводе описывается уравнением Гельмгольца

(27)
$\frac{{{{\partial }^{2}}\Psi }}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial \Psi }}{{\partial r}} + \rho \frac{\partial }{{\partial z}}\left[ {\rho \frac{{\partial \Psi }}{{\partial z}}} \right] + k_{0}^{2}{{n}^{2}}\Psi = 0,$
где z – глубина, r – горизонтальная координата, Ψ(r,z) – звуковое поле, ${{k}_{0}}$ – опорное волновое число, связанное с частотой звука f с помощью формулы ${{k}_{0}} = {{2\pi f} \mathord{\left/ {\vphantom {{2\pi f} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$, n(r,z) – показатель преломления звуковых волн.

Поглощение звука в водном слое является слабым, и мы им в данной работе пренебрегаем. Считая волновод горизонтально-однородным, мы можем представить показатель преломления в следующем виде:

(28)
$n(z) = \frac{{{{c}_{0}}}}{{c(z)}} + 2i\alpha (f)\Theta (z - h),$
где $\Theta (z)$ – функция Хэвисайда. Профиль скорости звука соответствует придонному звуковому каналу и задается выражением
(29)
$c(z) = \left\{ \begin{gathered} {{c}_{{\text{0}}}} - \frac{{{{\Delta }_{{\text{c}}}}}}{2}\left( {1 + {\text{th}}\frac{{z - {{z}_{{\text{c}}}}}}{{{{\Delta }_{{\text{z}}}}}}} \right),\,\,\,\,0 \leqslant z < h, \hfill \\ {{c}_{{\text{b}}}},\,\,\,\,h \leqslant z \leqslant L, \hfill \\ \end{gathered} \right.$
где ${{c}_{0}} = 1500$ м/с, ${{\Delta }_{{\text{с}}}} = 25$ м/с, ${{z}_{{\text{c}}}} = 50$ м, ${{\Delta }_{z}} = 10$ м, ${{c}_{{\text{b}}}} = 1600$ м/c. Водная часть профиля представлена на рис. 2.

Рис. 2.

Профиль скорости звука в водной толще.

Функция $\alpha (f)$ определяет частотную зависимость затухания в осадочном слое. В настоящей работе мы используем акустическую модель осадочного слоя, соответствующую условиям Восточно-Китайского моря, где был получен закон $\alpha (f) \simeq 0.42 \times {{10}^{{ - 6}}}{{f}^{2}}$ [34]. Поскольку, как отмечалось выше, поглощение звука в дне может существенно влиять на скорость фильтрации коротковолновой части спектра акустического поля, также будет рассмотрена модель с ослабленным затуханием, описываемым законом $\alpha (f) \simeq 0.1 \times {{10}^{{ - 3}}}f$.

Профиль плотности в нашей модели описывается формулой

(30)
$\rho (z) = \left\{ \begin{gathered} {\mkern 1mu} {{\rho }_{{{\text{wat}}}}},\,\,\,\,0 \leqslant z < h, \hfill \\ {\mkern 1mu} {{\rho }_{{{\text{sed}}}}},\,\,\,\,h \leqslant z \leqslant L, \hfill \\ \end{gathered} \right.$
где ${{\rho }_{{{\text{wat}}}}} = 1$ г/см3, ${{\rho }_{{{\text{sed}}}}} = 1.7$ г/см3.

Звуковое поле может быть представлено в виде суперпозиции нормальных мод

(31)
$\begin{gathered} \Psi (r,z) = \frac{i}{{4\sqrt {2\pi r} }}{{e}^{{ - i\pi /4}}} \times \\ \times \,\,\sum\limits_{m = 1}^M {\frac{{{{a}_{m}}}}{{\sqrt {{{k}_{{rm}}}} }}{{e}^{{i({{k}_{{rm}}} + i{{\alpha }_{m}})r}}}{{\Psi }_{m}}(z)} + {\text{к}}.~{\text{c}}. \\ \end{gathered} $

Нормальные моды и соответствующие им волновые числа являются решениями задачи Штурма–Лиувилля

(32)
$\rho (z)\frac{d}{{dz}}\left[ {\frac{1}{{\rho (z)}}\frac{{d{{\Psi }_{m}}(z)}}{{dz}}} \right] + \left[ {k_{0}^{2}{{n}^{2}}(z) - k_{{rm}}^{2}} \right]{{\Psi }_{m}}(z) = 0$
с граничными условиями (4) и условием непрерывности на дне

(33)
$\begin{gathered} {{\left. \Psi \right|}_{{z = h - 0}}} = {{\left. \Psi \right|}_{{z = h + 0}}}, \\ \frac{1}{{{{\rho }_{{{\text{wat}}}}}}}{{\left. {\frac{{d\Psi }}{{dz}}} \right|}_{{z = h - 0}}} = \frac{1}{{{{\rho }_{{{\text{sed}}}}}}}{{\left. {\frac{{d\Psi }}{{dz}}} \right|}_{{z = h + 0}}}. \\ \end{gathered} $

Для численного решения задачи Штурма–Лиувилля использовалась программа, написанная П.С. Петровым [35].

Поскольку мы рассматриваем горизонтально-однородный волновод, модовые амплитуды определяются начальным условием,

(34)
${{a}_{m}} = \int\limits_{z = 0}^L {\frac{{\Psi _{m}^{*}(z)\Psi (r = 0,z)}}{{\rho (z)}}} {\mkern 1mu} dz.$

В рассматриваемом нами случае источник представляет собой вертикальную цепочку монополей, расположенных в водной толще, поэтому формула (34) принимает вид

(35)
${{a}_{m}} = \mathop \sum \limits_{j = 1}^{{{J}_{{\text{w}}}}} \frac{{{{\Psi }_{m}}({{z}_{j}})}}{{\rho ({{z}_{j}})}} = \frac{1}{{{{\rho }_{{{\text{wat}}}}}}}\sum\limits_{j = 1}^{{{J}_{{\text{w}}}}} {{{\Psi }_{m}}({{z}_{j}})} ,$
где ${{J}_{{\text{w}}}}$ – число монополей в водной толще, глубины ${{z}_{j}}$ определяются выражением (20).

ВОЗБУЖДЕНИЕ АКУСТИЧЕСКИХ МОД ЭКВИДИСТАНТНОЙ АНТЕННОЙ В ТОНАЛЬНОМ РЕЖИМЕ

Рассмотрим задачу о возбуждении мод с помощью эквидистантной вертикальной антенны в тональном режиме. Это позволит более четко отследить физические механизмы, оказывающие влияние на эффективность антенны. Для оценки качества возбуждения будем использовать воспроизводимость, определяемую по формуле [36]

(36)
$\begin{gathered} F(r,f,m,\Delta z) = \\ = \frac{{{{{\left| {\int\limits_{z = 0}^h {dz{{\Psi }_{m}}(z,f)\Psi {\text{*}}(r,z,f;\Delta z)} } \right|}}^{2}}}}{{\left( {\int\limits_{z = 0}^h {dz{{{\left| {{{\Psi }_{m}}(z,f)} \right|}}^{2}}} } \right)\left( {\int\limits_{z = 0}^h {dz{{{\left| {\Psi (r,z,f;\Delta z)} \right|}}^{2}}} } \right)}}, \\ \end{gathered} $
где ${{\Psi }_{m}}(z,f)$ – акустическая мода, которую мы хотим сформировать на расстоянии $r$ от источника, а $\Psi (r,z,f;\Delta z)$ – звуковое поле, в действительности возбуждаемое вертикальной антенной, у которой расстояние между соседними монополями равно $\Delta z$, и АФР рассчитывается по формуле (3). Для вычисления $\Psi (r,z,f;\Delta z)$ используем формулы (31) и (35). Воспроизводимость можно рассматривать как меру схожести между желаемым и действительным звуковыми полями. Если они совпадают, то воспроизводимость равна своему максимальному значению – единице. По мере нарастания различий между $\Psi (r,z,f;\Delta z)$ и ${{\Psi }_{m}}(z,f)$ воспроизводимость стремится к нулю.

На рис. 3 и 4 представлены зависимости воспроизводимостей первых шести мод волновода от частоты сигнала. Данные, представленные на рис. 3, соответствуют вертикальной антенне с расстоянием между соседними монополями, равным 5 м. Мы видим, что все рассматриваемые моды могут практически точно возбуждаться такой антенной в широком частотном диапазоне, в котором $F \simeq 1$. Впрочем, с ростом номера моды ширина этого диапазона несколько сокращается. Постепенное смещение его верхней границы влево связано с тем, что плотность расположения монополей оказывается недостаточной для разрешения структуры моды при высоких частотах сигнала. Тем не менее, верхняя граница достаточно медленно меняется с ростом номера моды. Существенные отклонения воспроизводимости от единицы наблюдаются в области высоких частот, при $f > 600$ Гц. Именно в этом диапазоне воспроизводимость наиболее чувствительна к тому, насколько быстро поглощается коротковолновая составляющая звукового поля (речь здесь идет о вертикальной длине волны). Одним из следствий этого поглощения является значительный рост воспроизводимости по мере удаления точки наблюдения звукового поля от источника – воспроизводимость при $r = 10$ км существенно выше, чем при $r = 1$ км. Здесь, впрочем, необходимо учитывать, что мы рассматриваем идеализированную модель горизонтально-однородного волновода, которая не учитывает рассеяние звука на неоднородностях. Вследствие рассеяния часть акустической энергии может перекачиваться в более высокие моды, тем самым ухудшая качество возбуждения заданной моды. Вполне предсказуемо, что ослабление затухания в осадочном слое приводит к ухудшению воспроизводимости – это видно по поведению кривой, соответствующей $\alpha (f) \simeq 0.1 \times {{10}^{{ - 3}}}f$.

Рис. 3.

Зависимость воспроизводимости тональных сигналов, соответствующих отдельным модам, от частоты. Случай передающей антенны с расстоянием между монополями 5 м. Номера мод указаны в нижних частях панелей. Жирная сплошная кривая соответствует расстоянию от источника 10 км, тонкая сплошная кривая – расстоянию 1 км. Штриховая соответствует волноводу с ослабленным затуханием звука в дне, описываемым законом $\alpha (f) \simeq 0.1 \times {{10}^{{ - 3}}}f$, расстояние от источника равно 10 км.

Рис. 4.

То же самое, что и на рис. 2, но для более разреженной антенны с расстоянием между монополями 10 м.

Доверительный частотный диапазон антенны, в котором $F \simeq 1$, также сокращается и со стороны низких частот. Начиная со второй моды, в низкочастотной области возникают осцилляции воспроизводимости с ростом частоты. Они связаны с тем, что на низких частотах распространяющиеся моды могут не являться чисто водными, и значительная их часть распространяется в дне. Такие моды не могут эффективно возбуждаться с помощью цепочки монополей, расположенных только в водной толще.

Увеличение расстояния между соседними монополями до 10 м значительно сокращает доверительный частотный диапазон. Результаты моделирования, соответствующие данному случаю, представлены на рис. 3. Антенна обеспечивает относительно надежное возбуждение в диапазоне приблизительно от 100 до 300 Гц, при этом увеличение дистанции существенно улучшает качество возбуждения мод.

Для того чтобы отследить процесс фильтрации коротковолновой компоненты поля, введем погрешность возбуждения моды

(37)
$\varepsilon = 1 - F.$

Рис. 5 демонстрирует зависимость $\varepsilon $ от расстояния до точки наблюдения для частот 150 и 400 Гц. В качестве примеров выбраны третья и шестая моды. Во всех представленных случаях погрешность в среднем спадает с увеличением расстояния, однако скорость и характер этого спадания качественно зависят от частоты сигнала. При частоте 400 Гц происходит резкий спад погрешности уже в течение первого километра дистанции, если плотность расположения монополей является достаточной для практически точного возбуждения моды. Если же присутствует дефицит плотности монополей, то точность нарастает медленно. Такое поведение обусловлено тем, что в первом случае спад погрешности определяется поглощением быстро затухающих паразитных мод, во втором вклад в погрешность также дают и моды со сравнительно медленным затуханием.

Рис. 5.

Зависимость погрешности возбуждения моды в тональном режиме от расстояния. Частота сигнала: (а, б) 150 Гц, (в, г) 400 Гц. Рисунки (а) и (в) соответствуют третьей моде, (б) и (г) – шестой моде. Горизонтальная штриховая линия соответствует уровню $\varepsilon = 0.1$, который можно условно считать границей доверительного интервала антенны.

При частоте 150 Гц во всех случаях спад погрешности является достаточно медленным, поскольку медленным является и затухание паразитных мод – сказывается низкая частота сигнала. Интересной особенностью данных, соответствующих 150 Гц, является то, что более разреженная антенна с $\Delta z = 12$ м демонстрирует на больших расстояниях меньшую погрешность при возбуждении шестой моды, чем антенна с $\Delta z = 8$ м. Это, по всей видимости, связано с тем, что расположение монополей в случае $\Delta z = 12$ м лучше подходит для разрешения экстремумов шестой моды.

Данные, представленные на рис. 5, имеют также значение в контексте возбуждения отдельных мод с использованием механизма обратной связи [18, 23]. Обратная связь реализуется с помощью дополнительной вертикальной приемной антенны, которая устанавливается вдоль направления распространения на небольшом расстоянии от излучающей антенны. Звуковое поле, регистрируемое дополнительной антенной, используется для корректировки АФР излучающей антенны. Приведенные на рис. 5 результаты указывают на то, что эффективное функционирование излучающей системы с обратной связью возможно только тогда, когда дополнительная приемная антенна расположена за пределами области затухания паразитных мод, которая в случае низкочастотных сигналов может быть весьма обширной.

ВОЗБУЖДЕНИЕ МОДОВЫХ ИМПУЛЬСОВ С ПОМОЩЬЮ ЭКВИДИСТАНТНОЙ АНТЕННЫ

В данной работе ключевым объектом исследования является возбуждение модовых импульсов – импульсных сигналов, пространственная структура которых состоит из единственной моды. Интерес к модовым импульсам связан с тем, что их можно отнести к волновым пакетам с повышенной когерентностью: они достаточно слабо расплываются во времени и имеют хорошо определенную геометрию распространения. Они могут не распадаться при прохождении через крупномасштабные неоднородности, испытывая лишь плавную трансформацию. Кроме того, низкочастотные моды слабо подвержены рассеянию на мелкомасштабных неоднородностях, вызывающих лучевой хаос [37]. Так называемые слаборасходящиеся модовые импульсы обладают преимуществами в контексте передачи информации посредством акустических сигналов [13, 14].

В общем случае структура модового импульса определяется формулой

(38)
$\begin{gathered} {{\Phi }_{m}}(t,z;r) = \\ = \int d \Omega {\mkern 1mu} S(\Omega ){{a}_{m}}(r,\Omega ){{\Psi }_{m}}(r,z,\Omega ){{e}^{{ - i({{k}_{{rm}}} - \Omega t) - {{\alpha }_{m}}r}}}, \\ \end{gathered} $
где $S(\Omega )$ – спектр импульсного сигнала. В горизонтально-однородном волноводе модовые амплитуды ${{a}_{m}}$ и сами моды ${{\Psi }_{m}}$ не зависят от r. В данной работе рассматриваются импульсы со спектром следующего вида [38]
(39)
$S(\Omega ) = \frac{1}{{\sqrt {2\pi } {{\Delta }_{\Omega }}}}\exp \left( { - \frac{{{{{(\Omega - {{\Omega }_{{\text{c}}}})}}^{2}}}}{{2\Delta _{\Omega }^{2}}}} \right),$
где ${{\Omega }_{{\text{c}}}}$ – центральная частота. Такой спектр соответствует сигналу, имеющему вид

(40)
$s(t) = \exp \left( { - i{{\Omega }_{{\text{c}}}}t - \frac{{\Delta _{\Omega }^{2}{{t}^{2}}}}{2}} \right).$

Спектральная ширина $\delta \Omega $ и длительность $\tau $ импульса оцениваются как

(41)
$\delta \Omega = \sqrt {2\pi } {{\Delta }_{\Omega }},$
(42)
$\tau = \frac{{2\pi }}{{\delta \Omega }}.$

Мы рассматриваем широкополосные импульсы, для которых $\delta \Omega = {{{{\Omega }_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{\Omega }_{{\text{c}}}}} 2}} \right. \kern-0em} 2}$. Будут рассматриваться импульсы с центральными частотами ${{\Omega }_{{\text{c}}}}$, равными 150 и 400 Гц. Примеры получающихся в этом случае модовых импульсов представлены на рис. 6.

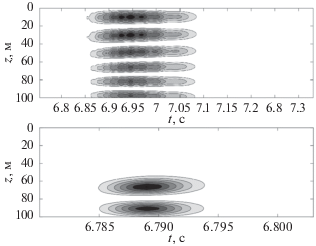
Рис. 6.

Пространственно-временное распределение интенсивности модовых импульсов ${{\left| {{{\Phi }_{m}}(t,z)} \right|}^{2}}$. Верхняя панель – импульс с центральной частотой 150 Гц, шестая мода. Нижняя панель – импульс с центральной частотой 400 Гц, вторая мода. Расстояние от излучающей антенны равно 10 км.

В случае импульсных сигналов можно воспользоваться определением воспроизводимости, аналогичным ранее введенному в работе [39],

(43)
$\begin{gathered} F(r,m,\Delta z) = \\ = \frac{{{{{\left| {\int {dt\int {dz} {\mkern 1mu} } \Phi (t,z;r,\Delta z)\Phi _{m}^{*}(t,z;r)} \right|}}^{2}}}}{{\left( {\int {dt\int {dz} } {{{\left| {\Phi (t,z;r,\Delta z)} \right|}}^{2}}} \right)\left( {\int {dt\int {dz} } {{{\left| {{{\Phi }_{m}}(t,z;r)} \right|}}^{2}}} \right)}}, \\ \end{gathered} $
где ${{\Phi }_{m}}(t,z;r)$ – требуемый модовый импульс, а $\Phi (t,z;r,\Delta z)$ – звуковое поле, собственно создаваемое излучающей антенной на расстоянии r. Зависимость воспроизводимости от расстояния между монополями эквидистантной антенной решетки $\Delta z$ представлена на рис. 7 и 8. Во всех случаях воспроизводимость удерживается вблизи единицы до некоторого значения $\Delta z$. При превышении этого значения начинает сказываться дефицит плотности монополей, и воспроизводимость падает, причем спад, как правило, является немонотонным. Исключение составляет первая мода, которая хорошо возбуждается даже очень разреженными антеннами. Это особенно явно проявляется в случае импульса с ${{\Omega }_{{\text{c}}}} = 150$ Гц. Для более высоких мод воспроизводимость сильно разреженными антеннами главным образом зависит от расположения монополей относительно интерференционных пиков. Именно этим обстоятельством объясняются резкие всплески воспроизводимости при определенных значениях $\Delta z$.

Рис. 7.

Зависимость воспроизводимости импульса с центральной частотой 150 Гц от расстояния между соседними монополями. Сплошная линия соответствует АФР, рассчитанному с помощью функций ДПП, штрихпунктирная линия – расчету с помощью формул (1) и (2). Закрашенные квадратики соответствуют данным, полученным с помощью функций ДПП для волновода с ослабленным затуханием звука в осадочном слое.

Рис. 8.

Зависимость воспроизводимости импульса с центральной частотой 400 Гц от расстояния между соседними монополями. Сплошная линия соответствует АФР, рассчитанному с помощью функций ДПП, штрихпунктирная линия – расчету с помощью формул (1) и (2). Закрашенные квадратики соответствуют данным, полученным с помощью функций ДПП для волновода с ослабленным затуханием звука в осадочном слое.

Напомним, что мы рассматриваем модель придонного звукового канала, поэтому акустическая энергия преимущественно сосредоточена именно в придонной области. Отсюда одним из факторов, влияющих на эффективность антенны при наличии дефицита плотности монополей, является положение самого нижнего монополя – он должен находиться вблизи дна, поскольку именно там располагаются наиболее интенсивные интерференционные пики. Это хорошо прослеживается в случае низкочастотного импульса с центральной частотой 150 Гц (см. рис. 7). Так, антенна с $\Delta z = 16$ м (нижний монополь находится на глубине 96 м) обеспечивает лучшую воспроизводимость импульсов пятой и шестой мод, чем антенна с $\Delta z = 15$ м (нижний монополь располагается на глубине 90 м). В то же время антенна с $\Delta z = 17$ м (нижний монополь расположен на глубине 85 м, т.е. на 15 м выше дна) существенно уступает в эффективности обеим вышеупомянутым антеннам.

Глубина самого нижнего монополя, принадлежащего водной толще, при заданном значении $\Delta z$ определяется формулой (20). Как уже отмечалось, вид этой формулы может меняться в зависимости от граничных условий. В частности, закон (20) отвечает верхнему граничному условию $\Psi (z = 0) = 0$. Если при построении базиса (16) мы воспользуемся не этим граничным условием, а некоторой его модификацией, пускай и не отвечающей реальным условиям, то формула (20) тоже изменит свой вид. Эти изменения, возможно, позволят оптимизировать расположение элементов антенны относительно интерференционных пиков. Ценой, которую мы за это заплатим, будет внесенная погрешность в приповерхностной части АФР, главным образом в самой верхней функции ДПП. Однако в случае преимущественно придонного распространения эта погрешность может оказаться несущественной. В настоящей работе не рассматривается расчет АФР с помощью функций ДПП, соответствующих модифицированному верхнему граничному условию. Тем не менее, при необходимости такая возможность может быть использована.

Если судить по данным, представленным на рис. 7 и 8, ослабление затухания в осадочном слое мало влияет на эффективность возбуждения модовых импульсов, если плотность монополей является достаточно высокой, т.е. критерий (9) выполняется достаточно хорошо. Ослабление модовой фильтрации и, как следствие, усиление паразитных мод начинает сказываться при дефиците монополей. Это приводит к заметному уменьшению воспроизводимости для модовых импульсов с центральной частотой 400 Гц. В случае же модовых импульсов с центральной частотой 150 Гц, эффект от ослабления затухания является незначительным. Более того, в последнем случае ослабление затухания может даже увеличивать воспроизводимость (см. рис. 7в и 7е). Правда, это происходит только при достаточно больших значениях $\Delta z$, когда воспроизводимость далека от единицы, что указывает на некорректность расчета АФР с помощью функций ДПП ввиду значимого нарушения критерия (9).

Надо сказать, что далеко за пределами области своей применимости метод расчета АФР с помощью формулы (3) существенно проигрывает в точности традиционному методу, основанному на уравнении (1). Следует еще раз подчеркнуть, что при выполнении формул (9) и (20) эти методы математически эквивалентны друг другу. В области умеренной погрешности, когда $0.6 < F < 1$, расчет с помощью функций ДПП, как правило, несколько выигрывает по сравнению с традиционным подходом. При большой погрешности более точным оказывается уже традиционный подход. Вообще говоря, расчет АФР с помощью уравнения (1) не ограничен конфигурацией с расположением монополей согласно формуле (20), диктующим расположение монополей при заданном значении $\Delta z$. С другой стороны, математическая эквивалентность этих двух подходов при выполнении критерия (9) указывает, что именно расположение монополей по формуле (20) обеспечивает наилучший результат. В противном случае может возникнуть вышеупомянутая проблема несогласованности с верхним граничным условием в волноводе и, как следствие, связанная с этим погрешность.

РАСЧЕТ АМПЛИТУДНО-ФАЗОВОГО РАСПРЕДЕЛЕНИЯ ДЛЯ АНТЕННОЙ РЕШЕТКИ С НЕЭКВИДИСТАНТНЫМ РАСПОЛОЖЕНИЕМ ИЗЛУЧАТЕЛЕЙ

Выше было показано, что акустическое поле, создаваемое отдельным монополем в эквидистантной антенной решетке, описывается функцией ДПП. Функция ДПП может быть вычислена как результат Фурье-фильтрации дельта-функции по формуле (24). Вид функции ДПП зависит от расстояния между монополями, которое одновременно определяет и число Фурье-гармоник J, и соответствующие весовые коэффициенты ${{w}_{j}}$ (в случае эквидистантной антенны эти коэффициенты равны друг другу). Суперпозиция полей, создаваемая периодической цепочкой монополей, приводит к интерференционному гашению пространственных Фурье-гармоник с номерами $j > J$. С другой стороны, мы знаем, что функции ДПП являются хорошо локализованными по глубине. Это означает, что основной вклад в интерференционное гашение высоких Фурье-гармоник j-го монополя вносят соседние, (j – 1)-ый и (j + 1)-ый, монополи. Другими словами, именно расстояние до соседних монополей играет первостепенную роль в формировании эффективного поля, создаваемого отдельным монополем решетки. Данное обстоятельство подсказывает путь для обобщения теории ДПП на случай антенных решеток с неэквидистантным расположением монополей. Именно этому пути мы и будем следовать ниже.

Рассмотрим в качестве примера антенную решетку, состоящую из двух подрешеток: верхней, перекрывающей интервал глубин $0 \leqslant z \leqslant {{z}_{{\text{c}}}}$, и нижней, перекрывающей интервал глубин ${{z}_{{\text{c}}}} \leqslant z \leqslant h$. Монополи верхней подрешетки расположены на глубинах

(44)
$z_{n}^{{(1)}} = n\Delta {{z}_{1}},\,\,\,\,n = 1,2, \ldots ,{{N}_{1}},\,\,\,\Delta {{z}_{1}} = \frac{{{{z}_{{\text{c}}}}}}{{{{N}_{1}}}}.$

Монополи нижней подрешетки расположены на глубинах

(45)
$z_{n}^{{(2)}} = {{z}_{c}} + n\Delta {{z}_{2}},\,\,\,n = 0,1,2, \ldots ,{{N}_{2}},\,\,\,\,\Delta {{z}_{2}} = \frac{{h - {{z}_{c}}}}{{{{N}_{2}}}}.$

Таким образом, обе подрешетки являются по отдельности эквидистантными, причем монополь на глубине $z = {{z}_{{\text{c}}}}$ принадлежит им обеим, разграничивая их. Нас интересует случай $\Delta {{z}_{1}} \ne \Delta {{z}_{2}}$, когда результирующая решетка является неэквидистантной. Каждая из подрешеток характеризуется своим собственным базисом функций ДПП, который может быть использован для расчета амплитудно-фазового распределения. Однако в случае пограничного монополя, расположенного на глубине $z = {{z}_{{\text{c}}}}$, возникает неоднозначность в определении соответствующей ему функции ДПП, поскольку он одновременно принадлежит двум разным подрешеткам с разными расстояниями $\Delta z$. Перед нами стоит задача найти эффективное поле, создаваемое пограничным монополем. Как отмечалось выше, это поле должно быть результатом интерференционного гашения высоких пространственных Фурье-гармоник. Асимметричность положения соседних монополей предполагает, что это гашение будет тоже асимметричным: выше пограничного монополя оно будет происходить за счет верхней подрешетки, а ниже – за счет нижней подрешетки. Это означает, что составляющие акустического поля, исходящие из пограничного монополя вверх и вниз, будут в разной степени подвержены Фурье-фильтрации. Эти соображения приводят нас к следующему выражению для эффективного поля пограничного монополя:

(46)
${{\chi }_{{\text{c}}}}(z) = \left\{ \begin{gathered} {\mkern 1mu} \chi _{{\text{c}}}^{{(1)}}(z),\,\,\,\,0 < z < {{z}_{{\text{c}}}}, \hfill \\ \frac{{{\mkern 1mu} \chi _{{\text{c}}}^{{(1)}}({{z}_{{\text{c}}}}) + \chi _{{\text{c}}}^{{(2)}}({{z}_{{\text{c}}}})}}{2},\,\,\,\,z = {{z}_{{\text{c}}}}, \hfill \\ {\mkern 1mu} \chi _{{\text{c}}}^{{(2)}}(z),\,\,\,\,{{z}_{{\text{c}}}} < z < h, \hfill \\ \end{gathered} \right.$
где $\chi _{{\text{c}}}^{{(1)}}(z)$ и $\chi _{{\text{c}}}^{{(2)}}(z)$ – функции ДПП пограничного монополя, вычисленные с $\Delta z = \Delta {{z}_{1}}$ и $\Delta z = \Delta {{z}_{2}}$, соответственно. Другими словами, эффективное поле, создаваемое пограничным монополем, описывается симбиозом функций ДПП для верхней и нижней подрешеток. Таким образом, если пронумеровать монополи сверху вниз, то требуемое амплитудно-фазовое распределение описывается формулой

(47)
${{Y}_{j}}(f) = \left\{ \begin{gathered} \int \Psi (z)\chi _{j}^{{(1)*}}(z){\mkern 1mu} dz,\,\,\,\,1 \leqslant j \leqslant {{N}_{1}}, \hfill \\ \int \Psi (z)\chi _{{\text{c}}}^{*}(z){\mkern 1mu} dz,\,\,\,\,j = {{N}_{1}}, \hfill \\ \int \Psi (z)\chi _{{j + {{N}_{1}}}}^{{(2)*}}(z){\mkern 1mu} dz,\,\,\,\,{{N}_{1}} < j \leqslant {{N}_{1}} + {{N}_{2}}. \hfill \\ \end{gathered} \right.$

Если плотность монополей обеих подрешеток является достаточной для полного разрешения требуемого акустического поля, формула (47) принимает вид:

(48)
${{Y}_{j}}(f) = \left\{ \begin{gathered} {\mkern 1mu} \sqrt {\Delta {{z}_{1}}} \Psi ({{z}_{j}}),\,\,\,\,1 \leqslant j \leqslant {{N}_{1}}, \hfill \\ {\mkern 1mu} \int \Psi (z)\chi _{{\text{c}}}^{*}(z){\mkern 1mu} dz,\,\,\,\,j = {{N}_{1}}, \hfill \\ {\mkern 1mu} \sqrt {\Delta {{z}_{2}}} \Psi ({{z}_{j}}),\,\,\,\,{{N}_{1}} < j \leqslant {{N}_{1}} + {{N}_{2}}. \hfill \\ \end{gathered} \right.$
Отметим, что в общем случае
(49)
$\begin{gathered} \int\limits_{z = 0}^L {\chi _{i}^{{(1)}}} \chi _{j}^{{(2)}}dz \ne 0,\,\,\,\,\int\limits_{z = 0}^L {} \int_{}^{} {\chi _{i}^{{(1)}}} {{\chi }_{{\text{c}}}}{\mkern 1mu} dz \ne 0, \\ \int\limits_{z = 0}^L {\chi _{i}^{{(2)}}} {{\chi }_{{\text{c}}}}{\mkern 1mu} dz \ne 0, \\ \end{gathered} $
т.е. условие ортогональности функций ДПП может нарушаться. Следствием этого может являться погрешность в возбуждении заданного поля.

В качестве примера рассмотрим антенную решетку, у которой верхняя подрешетка занимает интервал глубин от поверхности моря до 50 м, а нижняя – от 50 до 100 м, т.е. до дна. Расстояние между монополями в нижней подрешетке равно 5 м. Рассматриваются импульсы первых шести мод с центральной частотой 150 Гц. Как следует из данных, представленных на рис. 7, эквидистантная антенна с $\Delta z = 5$ м, перекрывающая всю водную толщу, обеспечивает точное возбуждение всех рассматриваемых импульсов. Вместе с тем, естественно предположить, что наибольшая часть энергии этих импульсов сосредоточена в придонном звуковом канале. Зададимся вопросом: насколько сильно эффективность такой решетки зависит от расстояния между монополями в верхней подрешетке? Насколько существенными будут потери качества при уменьшении количества излучателей в верхней подрешетке?

На рис. 9 представлена зависимость погрешности возбуждения модового импульса от расстояния между монополями верхней подрешетки. Результаты расчета АФР с помощью формулы (47) сравниваются с результатами, полученными с помощью формулы (1), т.е. в случае ${{w}_{j}} = {\text{const}}$. Согласно представленным данным, оба рассматриваемых алгоритма обеспечивают высокую точность возбуждения в случае импульсов первой моды, при этом формула (47) дает меньшую ошибку. Для более высоких мод удовлетворительная точность обеспечивается только тогда, когда верхняя подрешетка является умеренно разреженной: мы имеем погрешность на уровне 10% и ниже, если расстояние между монополями верхней подрешетки не превышает 10 м. Формула (47) выигрывает в точности по сравнению с (1) практически во всех случаях, кроме случаев чрезмерно разреженной верхней подрешетки с $\Delta {{z}_{1}} \geqslant 25$ м, когда дефицит излучателей сказывается очень сильно.

Рис. 9.

Зависимость погрешности возбуждения модовых импульсов от расстояния между монополями верхней подрешетки. Случай $\Delta {{z}_{1}} = 50$ м означает присутствие только нижней подрешетки. Сплошная линия – расчет по формуле (47), прерывистая линия – расчет по формуле (1).

Проведенное дополнительное исследование показало, что формула (47) предсказывает практически оптимальную амплитуду сигнала, который должен быть подан на монополь, разграничивающий верхнюю и нижнюю подрешетки. Любопытно, что в некоторых случаях значение соответствующего весового коэффициента ${{w}_{{{{N}_{1}}}}}$ (см. формулу (14)) оказывается отрицательным, т.е. сигнал, подаваемый на пограничный монополь, оказывается в противофазе с соответствующим значением акустического поля в данной точке. Это указывает на то, что оптимальное АФР для неэквидистантных антенн в значительной степени определяется поведением акустического поля в областях между монополями – в данном случае недостаточно учета только значений акустического поля в точках расположения монополей.

ЗАКЛЮЧЕНИЕ

Главным результатом данной работы является новый метод расчета амплитудно-фазовых распределений для вертикальных антенн. Метод основан на применении функций дискретного представления переменных. При выполнении условия (9) и эквидистантном расположении монополей этот метод математически эквивалентен традиционному подходу, основанному на уравнении (1). Эквивалентность устанавливается выражением (11). Можно сказать, что в некотором смысле предлагаемый метод расчета обеспечивает дополнительную математическую базу для традиционного подхода. Например, он предсказывает, что при достаточно большом количестве монополей их глубины должны удовлетворять уравнению (20), в противном случае может возникнуть погрешность, обусловленная несогласованностью с верхним граничным условием. При дефиците монополей эта погрешность может оказаться несущественной, тогда на первый план выходит расположение монополей относительно интерференционных пиков. В работе показано, что предлагаемый метод может быть модифицирован для расчета АФР неэквидистантных антенн, в этом случае он обеспечивает более высокую точность, чем формула (1).

Специфической особенностью предлагаемого метода является отсутствие прямой зависимости функций ДПП, на использовании которых он основан, от частоты сигнала и профиля скорости звука. Оба этих фактора учитываются неявно, т.к. от них зависит спектр вертикальных волновых чисел акустического поля и, соответственно, требуемое количество монополей. Отсутствие прямой зависимости от профиля скорости звука — это, скорее, положительное свойство с точки зрения экспериментальной реализации метода, поскольку гидрологические характеристики подвержены изменчивости как в пространстве, так и во времени.

Следует еще раз отметить, что предлагаемый метод может быть использован для возбуждения практически любых волновых пакетов, способных распространяться в волноводе на достаточно большие расстояния. Кроме того, представленный подход, вкупе с ранее предложенным алгоритмом реконструкции профиля акустического поля [32], может быть использован для экспериментального измерения пропагатора акустического поля. Пропагатор – это оператор, который устанавливает непосредственную связь между произвольным начальным и соответствующим ему конечным акустическими полями [9, 40–44]. Знание пропагатора означает наличие практически всей информации об акустических свойствах волновода, которая в принципе может быть получена с помощью двух антенн, одной излучающей и одной приемной. В работе [45] предложена схема для измерения пропагатора в тональном режиме. Данное направление работы является одним из наиболее многообещающих в контексте использования предложенного метода.

В представленной работе рассматривается вопрос о влиянии степени разреженности вертикальных акустических антенн на их способность селективно возбуждать модовые импульсы. Обнаружено, что затухание высоких мод, дающих основной вклад в коротковолновую часть спектра вертикальных волновых чисел, способствует повышению эффективности разреженных антенн. Это особенно актуально для импульсов с центральной частотой порядка нескольких сотен герц.

Проведенные в этой работе расчеты соответствуют модели горизонтально-однородного волновода. Включение горизонтальных неоднородностей приведет к взаимодействию между модами и, тем самым, повлияет на процесс фильтрации коротковолновой компоненты акустического поля. С одной стороны, этот процесс приведет к подкачке высоких мод волновода и, тем самым, ухудшит эффективность возбуждения требуемого волнового пакета. С другой стороны, рассеяние на неоднородностях может увеличить число быстро затухающих мод за счет эффекта раскачки и высвечивания звуковых лучей из волновода [46–49]. Таким образом, вопрос об эффективности разреженных вертикальных антенн в горизонтально-неоднородных волноводах является достаточно нетривиальным и требует отдельного рассмотрения.

Автор признателен П.С. Петрову за предоставленную возможность использовать код [35]. Работа выполнена в рамках госбюджетной тематики ТОИ ДВО РАН “Моделирование разномасштабных динамических процессов в океане” (номер проекта 121021700341-2).

Список литературы

  1. Алексеев Г.В., Комаров Е.Г. Численное моделирование экстремальных задач теории излучения звука в плоском волноводе // Матем. Модел. 1991. Т. 3. № 12. С. 52–64.

  2. Вировлянский А.Л., Нефедова Д.В. Формирование узкого волнового пучка в подводном звуковом канале с помощью вертикальной антенны // Акуст. журн. 2010. Т. 56. № 1. С. 63–69.

  3. Артельный В.В., Артельный П.В., Вировлянский А.Л., Коротин П.И., Наседкин А.В., Потапов О.А., Циберев А.В. Фокусировка звукового пучка в подводном волноводе с помощью вертикальной антенны // Акуст. журн. 2013. Т. 59. № 3. С. 339–346.

  4. Артельный В.В., Артельный П.В., Вировлянский А.Л., Казарова А.Ю., Коротин П.И. Фокусировка поля в гидроакустическом волноводе в заданный интервал глубин // Акуст. журн. 2015. Т. 61. № 4. С. 477–483.

  5. Лучинин А.Г., Хилько А.И. Низкочастотная акустическая томография мелкого моря с использованием маломодовых импульсов // Акуст. журн. 2005. Т. 51. № 2. С. 228–241.

  6. Хилько А.И., Лучинин А.Г., Бурдуковская В.Г., Смирнов И.П. Маломодовая томография неоднородностей мелкого моря // Акуст. журн. 2007. Т. 53. № 3. С. 437–450.

  7. Макаров Д.В., Коньков Л.Е., Петров П.С. Влияние океанических синоптических вихрей на длительность модовых акустических импульсов // Изв. Вузов. Радиофизика. 2016. Т. 59. № 7. С. 638–654.

  8. Бреховских Л.М., Гончаров В.В., Дремучев С.А., Куртепов В.М., Селиванов В.Г., Чепурин Ю.А. Эксперименты по дальнему распространению звука в Канарской котловине Атлантического океана // Акуст. журн. 1990. Т. 36. № 5. С. 824–831.

  9. Makarov D.V., Kon’kov L.E., Uleysky M.Yu., Petrov P.S. Wave chaos in a randomly inhomogeneous waveguide: spectral analysis of the finite-range evolution operator // Phys. Rev. E. 2013. V. 87. № 1. 012911.

  10. Петухов Ю.В., Бурдуковская В.Г. Пространственная расходимость многомодовых акустических пучков, формируемых вертикальной антенной в рефракционном океаническом волноводе // Акуст. журн. 2018. Т. 64. № 2. С. 174–185.

  11. Артельный П.В., Вировлянский А.Л., Казарова А.Ю., Коротин П.И., Любавин Л.Я., Стуленков А.В. Наблюдение устойчивых компонент звуковых полей в Ладожском озере // Акуст. журн. 2018. Т. 64. № 2. С. 174–185.

  12. Петухов Ю.В., Бурдуковская В.Г., Бородина Е.Л. Каустические и слаборасходящиеся пучки в горизонтально неоднородных акустических волноводах // Акуст. журн. 2020. Т. 66. № 2. С. 181–197.

  13. Brown M.G., Udovydchenkov I.A. Underwater communication using weakly dispersive modal pulses // Acoust. Phys. 2013. V. 59. № 5. P. 533–538.

  14. Udovydchenkov I.A. Array design considerations for exploitation of stable weakly dispersive modal pulses in the deep ocean // J. Sound Vibr. 2017. V. 400. P. 402–416.

  15. Волков М.В., Григорьев В.А., Луньков А.А., Петников В.Г. О возможности применения вертикальных приемных антенн для звукоподводной связи на арктическом шельфе // Акуст. журн. 2019. Т. 65. № 3. С. 332–342.

  16. Clay C.S., Huang K. Single mode transmission and acoustic backscattering measurements in a laboratory waveguide // J. Acoust. Soc. Am. 1980. V. 67. № 3. P. 792–794.

  17. Gazanhes C., Garnier J.L. Experiments on signal mode excitation in shallow water propagation // J. Acoust. Soc. Am. 1981. V. 69. № 4. P. 963–969.

  18. Buck J.R., Preisig J.C., Johnson M., Catipovic J. Single-mode excitation in the shallow-water acoustic channel using feedback control // IEEE J. Ocean. Engin. 1997. V. 22. № 4. P. 281–291.

  19. Елисеевнин В.А. Концентрация энергии в одну нормальную волну, излучаемую в водном слое вертикальной линейной антенной // Акуст. журн. 2006. Т. 52. № 2. С. 275–279.

  20. Голубева Е.В., Елисеевнин В.А. Излучение одной нормальной волны вертикальной дискретной линейной антенной в водном слое // Акуст. журн. 2008. Т. 54. № 1. С. 62–68.

  21. Голубева Е.В., Елисеевнин В.А. Мощность, излучаемая вертикальной компенсированной линейной антенной в волноводе Пекериса // Акуст. журн. 2008. Т. 54. № 5. С. 767–773.

  22. Голубева Е.В., Елисеевнин В.А. Излучение одной нормальной волны вертикальной дискретной линейной антенной в волноводе Пекериса // Акуст. журн. 2010. Т. 56. № 1. С. 70–76.

  23. Peng D., Gao T., Zeng J. Study on single-mode excitation in time-variant shallow water environment // J. Comput. Acoust. 2014. № 1. 1440001.

  24. Zeng J., Zhao W.Y., Peng D.Y., Li H.F., Gao T. F., Shang E.C. Measurements of ocean bottom low-angle backscattering by single-mode reverberation // J. Acoust. Soc. Am. 2014. V. 136. № 6. P. 2976–2986.

  25. Beck J., Jäckle A., Worth G., Meyer H.-D. The multiconfiguration time-dependent Hartree (MCTDF) method: a highly efficient algorithm for propagating wavepackets // Physics Reports. 2000. V. 324. P. 1–105.

  26. Pitsevich G.A., Malevich A.E. Comparison of the Fourier and discrete variable representation in optical lattices // J. Appl. Spectroscopy. 2016. V. 82. № 6. P. 893–900.

  27. Yu Hua-Gen. A coherent discrete variable representation method on a sphere // J. Chem. Phys. 2017. V. 147. № 9. 094101.

  28. Shadmehri S., Saeidian S., Melezhik V.S. 2D nondirect product discrete variable representation for Schrӧdinger equation with nonseparable angular variables // J. Phys. B.: At. Mol. Opt. Phys. 2020. V. 53. № 8. 085001.

  29. Piserchia A., Banerjee S., Barone V. General approach to coupled reactive Smoluchovsky equations: integration and application of discrete variable representation and generalized coordinate methods to diffusive problems // J. Chem. Theory Comput. 2017. V. 13. № 12. P. 5900–5910.

  30. Таланов В.И. О синтезе антенн в многомодовых волноводах // Изв. Вузов. Радиофизика. 1986. Т. 28. № 7. С. 872–829.

  31. Городецкая Е.Ю., Малеханов А.И., Таланов В.И., Фикс И.Ш. Синтез и анализ акустических полей в океане / В сборнике “Формирование акустических полей в океане”. Нижний Новгород: ИПФ РАН, 1991. С. 9–31.

  32. Макаров Д.В. Алгоритм реконструкции профиля акустического поля по данным точечных измерений // Подводн. Исслед. Робототех. 2019. № 2. С. 62–67.

  33. Makarov D.V., Petrov P.S. Full reconstruction of acoustic wavefields by means of pointwise measurements // e-print arXiv:2103.06014 [eess.SP].

  34. Zhou J.-X., Zhang X.-Z., Knobles D. Low-frequency geoacoustic model for the effective properties of sandy seabottoms // J. Acoust. Soc. Am. 2009. V. 125. № 5. P. 2847–2866.

  35. Petrov P.S. ac_modes: simple matlab code for the computation of acoustical normal modes in the ocean. 2019. https://github.com/kaustikos/ac_modes (дата обращения 23.04.2021 г.)

  36. Hegewisch K.C., Cerruti N.R., Tomsovic S. Ocean acoustic wave propagation and ray method correspondence: Internal wave fine structure // J. Acoust. Soc. Am. 2005. V. 117. № 2. Pt. 2. P. 1582–1594.

  37. Макаров Д.В., Коньков Л.Е., Улейский М.Ю. Соответствие между лучевой и волновой картинами и подавление хаоса при дальнем распространении звука в океане // Акуст. журн. 2008. Т. 54. № 3. С. 565–573.

  38. Makarov D., Prants S., Virovlyansky A., Zaslavsky G. Ray and wave chaos in ocean acoustics: chaos in waveguides. Singapore: World Scientific, 2010. 388 p.

  39. Макаров Д.В. Об измерении углов прихода акустических импульсов с помощью вертикальной антенны // Акуст. журн. 2017. Т. 63. № 6. С. 637–645.

  40. Вировлянский А.Л., Макаров Д.В., Пранц С.В. Лучевой и волновой хаос в подводных акустических волноводах // Успехи физ. наук. 2012. Т. 182. № 1. С. 19–48.

  41. Hegewisch K.C., Tomsovic S. Random matrix theory for underwater sound propagation // Europhys. Lett. 2012. V. 97. № 3. 34002.

  42. Hegewisch K.C., Tomsovic S. Constructing acoustic timefronts using random matrix theory // J. Acoust. Soc. Am. 2013. V. 134. № 4. P. 3174–3184.

  43. Makarov D.V. Random matrix theory for low-frequency sound propagation in the ocean: a spectral statistics test // J. Theor. Comput. Acoust. 2018. V. 26. № 1. 1850002.

  44. Makarov D.V. Random matrix theory for an adiabatically-varying oceanic acoustic waveguide // Wave Motion. 2019. V. 90. P. 205–217.

  45. Макаров Д.В., Аллилуев А.Д. Об экспериментальном определении пропагатора акустического поля // Подводн. Исслед. Робототех. 2021. № 1. С. 80–83.

  46. Кинбер Б.Е., Комиссарова Н.Н., Кравцов Ю.А. Лучевая теория распространения волн в неоднородных рефракционных волноводах: трансформация мод и раскачка ширины волновых каналов // Изв. ВУЗов. Радиофизика. 1979. Т. 22. № 4. С. 414–424.

  47. Абдуллаев С.С., Заславский Г.М. Нелинейная динамика лучей в неоднородных средах // Журн. эксп. теор. физ. 1981. Т. 80. № 2. С. 524–536.

  48. Makarov D.V., Uleysky M.Yu., Prants S.V. Ray chaos and ray clustering in an ocean waveguide // Chaos. 2004. V. 14. № 1. P. 79–95.

  49. Макаров Д.В., Улейский М.Ю. Высвечивание лучей из горизонтально-неоднородного подводного звукового канала // Акуст. журн. 2007. Т. 53. № 4. С. 565–573.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал