Акустический журнал, 2021, T. 67, № 4, стр. 395-412
Сравнительный анализ помехоустойчивости алгоритмов реконструкции геоакустических параметров морского дна методом когерентного зондирования
В. И. Калинина a, b, *, И. П. Смирнов a, b, А. И. Хилько a, b, А. И. Малеханов a, b
a Институт прикладной физики РАН
603950 Нижний Новгород, ул. Ульянова 46, Россия
b Нижегородский государственный университет им. Н.И. Лобачевского
603950 Нижний Новгород, пр. Гагарина 23, Россия
* E-mail: v.kalinina@ipfran.ru
Поступила в редакцию 09.04.2021
После доработки 16.04.2021
Принята к публикации 23.04.2021
Аннотация
На основе разработанной ранее численной модели проводится сравнительный анализ эффективности алгоритмов реконструкции геоакустических параметров слоистой структуры морского дна при использовании зондирующих сигналов в виде синхронизированной последовательности взаимно-когерентных сложных сигналов. Алгоритмы отличаются способом построения многопараметрической целевой функции, нахождение экстремума которой обеспечивает оценку искомых параметров. В качестве таких функций используются среднеквадратичная норма невязки, функционалы обобщенных методов MUSIC и нейроноподобной свертки. Методом стохастического моделирования исследуется устойчивость полученных оценок (в терминах среднего смещения и дисперсии отклонений от истинного значения) в зависимости от величины отношения сигнал/шум на входе приемников. Показано, что рассмотренные алгоритмы обнаруживают существенно различную помехоустойчивость, которая, в свою очередь, оказывается зависящей от того, какой именно параметр подлежит оценке.
1. ВВЕДЕНИЕ
Типичной схемой выполнения работ по диагностике морского дна и морской сейсморазведке является та, при которой в водной толще исследуемой акватории буксируется приемно-излучающая система, состоящая из гидроакустического излучателя и горизонтальной антенной решетки (АР) приемных гидрофонов (сейсмокосы) или нескольких таких АР. В качестве излучателя используются импульсные источники различного типа и, соответственно, излучаемые ими зондирующие сигналы имеют различные спектральные и временные характеристики. От этих характеристик зависят характеристики самой диагностики – прежде всего, глубина проникновения и разрешающая способность реконструкции вертикального разреза донных пород, т.е. оценивания горизонтов границ раздела донных слоев (сейсмопрофилирования). В работах [1, 2] обсуждались и экспериментально демонстрировались преимущества, связанные с использованием зондирующих сигналов в виде синхронизированной последовательности взаимно-когерентных сложно-модулированных сигналов с большой базой (сложных сигналов). Показано, что использование таких сигналов в качестве “инструментов” зондирования морского дна позволяет реализовать достаточно высокую разрешающую способность и глубину проникновения при относительно низких, в сравнении со стандартным подходом на основе источников ударного типа, уровнях излучения и в более высоком частотном диапазоне.
В общей постановке задача диагностики морского дна не ограничивается профилированием структуры донных слоев, но включает также оценивание ряда геоакустических параметров составляющих их пород (например, [3–10]) и рассматривается еще более широко в контексте обратных задач акустической диагностики океана (см. обзор [11] и цитированную там литературу). К таким параметрам относятся плотность пород, скорости продольных и поперечных волн, декременты их затухания. От совокупности этих параметров зависят амплитудные и фазовые соотношения сигналов, отраженных от границ раздела донных слоев и поступающих на вход приемной АР (полезных сигналов), следовательно, обработка таких сигналов имеет потенциал реконструкции этих параметров наравне с оценкой горизонтов границ раздела. Прием полезных сигналов осуществляется, однако, на фоне помех различного происхождения (шумов моря и буксирующего судна, помех реверберации), которые в совокупности маскируют полезные сигналы и, очевидно, влияют на качество оценки параметров донных слоев. В силу этого актуальной является задача сравнительного анализа эффективности различных алгоритмов оценивания, которые отличаются друг от друга статистической устойчивостью получаемых оценок в таких условиях, особенно при низких значениях отношений сигнал/шум (ОСШ) на входе приемников.
В настоящей работе численно исследуется помехоустойчивость ряда алгоритмов реконструкции геоакустических параметров донных пород в акваториях морского шельфа. В качестве источника зондирующих сигналов предполагается излучатель, работающий в режиме излучения синхронизированной последовательности повторяемых импульсов с линейной частотной модуляцией (ЛЧМ). Численная модель формирования полезных сигналов на входе приемной АР в рамках предположения о слоисто-неоднородной структуре донных пород следует работе [10] и кратко изложена в разделе 2. Здесь же обсуждаются методы обработки сигналов, которые реализуют преимущества такого режима излучения путем когерентного накопления принимаемых импульсов в частотной и пространственной областях и которые “участвуют” затем в моделировании алгоритмов оценивания параметров. В разделе 3 представлены модели помех донной и поверхностной реверберации и результаты расчетов, позволяющие сопоставить их уровень с полезными сигналами в рамках конкретной модели слоистой структуры дна с заданными параметрами. Алгоритмы оценивания параметров (раздел 4) стандартно формулируются нами в терминах решения вариационной задачи поиска экстремума многопараметрической целевой функции, построение которой может быть различным. Мы рассматриваем три подхода к построению таких функций и, соответственно, три алгоритма оценивания. Для количественного сравнения их эффективности проведены расчеты смещения и дисперсии отклонений оценок параметров донных слоев от их истинных (заданных в рамках модели) значений при различных значениях входного ОСШ, результаты которых обсуждаются в разделе 5 и в заключении.
2. МОДЕЛЬ ФОРМИРОВАНИЯ ПОЛЕЗНЫХ СИГНАЛОВ
В качестве модели формирования сигналов, отраженных от границ раздела в морском дне, мы используем достаточно общую физическую модель дна в виде совокупности горизонтальных однородных жидких или упругих слоев с границами раздела, кратные отражения от которых приводят к появлению последовательности полезных сигналов при излучении в водную среду зондирующего импульса. Общий вид такой донной структуры с указанием ее параметров и расположение технических средств (излучателя и приемников) показаны на рис. 1.
Рис. 1.
Модель формирования принимаемой последовательности импульсов, отраженных от границ раздела в рамках модели слоисто-неоднородного дна.

Используемая нами численная модель расчета импульсной последовательности принимаемых
сигналов, в которой учитываются вклады поперечных волн, а также обменные эффекты,
связанные с трансформацией различных типов волн на границах раздела упругих донных
слоев, основана на результатах работы [10]. Каждый из общего числа $N$ слоев, лежащих на подстилающем полупространстве (толщина которого ${{h}_{{N + 1}}}$ считается бесконечной), может быть корректно описан набором шести геоакустических
параметров (рис. 1): толщина (мощность) слоя ${{h}_{n}}$, плотность породы ${{{{\rho }}}_{n}}$, скорости продольных $v_{n}^{P}{\text{\;}}$ и поперечных $v_{n}^{{SV}}$ волн, декременты затухания продольных ${{\delta }}_{n}^{P}$ и поперечных ${{\delta }}_{n}^{{SV}}$ волн ($n = 1,..,N$). Соответственно, полная размерность пространства донных параметров равна $M = 6\left( {N + 1} \right)$, и для каждого слоя совокупность его параметров представляет собой вектор-строку
 .
.
Водный слой, в котором расположена приемно-излучающая система, считается однородным, занимающим интервал глубин $0 < z < H$; его параметры – плотность ${{{{\rho }}}_{0}}$, скорость звука ${{c}_{0}}$ и декремент затухания ${{{{\delta }}}_{0}}$. Система зондирования состоит из ненаправленного излучателя звука $S$, помещенного в точке ${{{\mathbf{r}}}^{S}}$, и приемной АР, состоящей из ${{K}_{R}}{\text{\;}}$ ненаправленных гидрофонов ${{R}_{j}}$, расположенных в точках множества $\left\{ {{\mathbf{r}}_{j}^{{\left( R \right)}},j = 1 \ldots {{K}_{R}}} \right\}$. Излучателем возбуждается импульсный сигнал $g(\omega ) = C(\omega ){{g}_{S}}(\omega )$, где ${{g}_{S}}({{\omega }})$ – спектральная плотность импульса, $C({{\omega }})$ – комплексная амплитуда возбуждения излучателя.
Для расчетов мы используем геометро-акустическое приближение, предполагая, что все неоднородности среды (водной толщи и дна) имеют характерные размеры много больше характерной длины волны зондирующего сигнала. Еще одно предположение касается слабого влияния кратных отражений на границах раздела донных слоев – они входят в модель, но практически не учитываются в последующих численных расчетах (раздел 5).
Спектральная амплитуда импульсной последовательности в точках приема ${{R}_{j}}$, расположенных на горизонтальном расстоянии ${{r}_{{SR}}}$ от источника $S$, представляется суммой волн, отраженных от границ раздела донных слоев: ${{g}_{{{{R}_{j}}}}}({{\omega }}) = \sum\nolimits_{n = 1}^N {{{g}_{n}}} ({{\omega }}),$ где ${{g}_{n}}({{\omega }})$ – сумма волн, отраженных от нижней границы слоя с номером $n = 1, \ldots ,N:$ ${\text{\;}}{{g}_{n}}({{\omega }}) = \sum\nolimits_{k = 0}^{{{2}^{n}} - 1} {g_{n}^{{\left( k \right)}}} ({{\omega }})$ [8–10]. Каждый из приходов $g_{n}^{{\left( k \right)}}({{\omega }})$ дополнительно к номеру слоя отмечается индексом $~k$, который записан в двоичном коде $k = \left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right),$ где ${{s}_{m}},{{z}_{m}} \in $ $\left\{ {0,\,1} \right\}$, m $ = 1, \ldots ,\,n$ – индексы, отвечающие типу волны при ее прохождении через слой $~m$ на пути к слою $n$ и затем обратно: значение $0$ отвечает продольной волне, $1$ – поперечной, при этом первые $n$ индексов $({{s}_{1}}, \ldots {{s}_{{n~}}})$ отвечает волнам, которые распространяются вниз, следующие $n$ индексов $({{z}_{n}}, \ldots {{z}_{1}})$ – волнам, которые распространяются вверх. Лучевая схема формирования совокупности сигналов, принимаемых отдельным элементом АР, поясняется на рис. 2. Вследствие того, что при падении на границу раздела двух упругих сред продольной или поперечной волн образуются отраженные продольная и поперечная волны, а также преломленные продольная и поперечная волны (рис. 2а), на каждом из приемников формируются множественные сигнальные приходы (рис. 2б). В результате на входе каждого гидрофона образуется большой набор монотипных и обменных волновых компонент, полное число которых быстро растет с ростом числа N слоев: $~{{K}_{V}} = \sum\nolimits_{n = 1}^N {{{4}^{n}}} $.
Рис. 2.
Схемы формирования продольных и поперечных волн при отражении и преломлении на границе раздела двух упругих слоев (слева) и множественных сигнальных приходов на каждый из приемников (справа)

Таким образом, формирование волновых приходов $g_{n}^{{\left( k \right)}}({{\omega }})$ для каждого слоя $n$ происходит в результате “накопления” указанных эффектов во всех вышележащих слоях (с номерами $m$). В малоугловом приближении имеем для них выражение [10]:
(1)
$\begin{gathered} g_{n}^{{\left( k \right)}}({{\omega }}) = g_{n}^{{\left( {{{s}_{1}} \ldots {{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}({{\omega }}) = \\ = {{g}_{S}}({{\omega }})\frac{{{{e}^{{ - i{{\varphi }}_{n}^{{\left( {{{s}_{1}} \ldots {{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}} - {{\Delta }}_{n}^{{\left( {{{s}_{1}} \ldots {{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}}}}}}{{R_{n}^{{{{{\left( {{{s}_{1}} \ldots {{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}}}}\prod\limits_{m = 0}^{n - 1} {W_{{m,m + 1}}^{{\left( {{{s}_{m}}{{s}_{{m + 1}}}} \right)}}} \times \\ \times \,\,({{\theta }}_{{mn}}^{{\left( {{{s}_{m}}} \right)}})V_{n}^{{\left( {{{s}_{n}}{{z}_{n}}} \right)}}({{\theta }}_{{nn}}^{{\left( {{{s}_{n}}} \right)}})\prod\limits_{m = n}^1 {W_{{m,m - 1}}^{{\left( {{{z}_{m}}{{z}_{{m - 1}}}} \right)}}} ({{\theta }}_{{mn}}^{{\left( {{{z}_{m}}} \right)}}), \\ \end{gathered} $Для волны типа${\text{\;}}\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)$ начальный угол падения на донную поверхность приближенно равен
Угол падения ${{\theta }}_{{mn}}^{{\left( {{{s}_{m}},\,{{z}_{m}}} \right)}}$ на верхнюю границу слоя $m$ рассчитывается по начальному углу падения ${{{{\theta }}}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}}}$ с помощью закона преломления Снеллиуса, а расстояние, которое волна проходит в этом слое, равно $R_{{mn}}^{{\left( {{{s}_{m}},\,{{z}_{m}}} \right)}} = {{h}_{m}}\sqrt {1 + {{{\left( {\frac{{v_{m}^{{\left( {{{s}_{m}},\,{{z}_{m}}} \right)}}}}{{{{c}_{0}}}}{{\theta }}_{{mn}}^{{\left( {{{s}_{m}},\,{{z}_{m}}} \right)}}} \right)}}^{2}}} $.
Спектральная амплитуда принимаемого сигнала в точке приема ${{R}_{j}}$ получается суммированием волновых компонент (1) для всех слоев и рассчитывается следующим образом:
(2)
$\begin{gathered} {{g}_{{{{R}_{j}}}}}\left( {{\omega }} \right) = \mathop \sum \limits_{n = 1}^N {{g}_{n}}({{\omega }}) = \mathop \sum \limits_{n = 1}^N \mathop \sum \limits_{k = 0}^{{{2}^{n}} - 1} g_{n}^{{\left( k \right)}}({{\omega }}) = \\ = \mathop \sum \limits_{n = 1}^N \mathop \sum \limits_{{{s}_{1}} = 0}^1 \ldots \mathop \sum \limits_{{{s}_{n}} = 0}^1 \mathop \sum \limits_{{{z}_{n}} = 0}^1 \ldots \mathop \sum \limits_{{{z}_{1}} = 0}^1 g_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}({{\omega }}) = \\ = \mathop \sum \limits_{n = 1}^N \mathop \sum \limits_{{{s}_{1}} = 0}^1 \ldots \mathop \sum \limits_{{{z}_{1}} = 0}^1 A_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}{{g}_{S}}({{\omega }}){{e}^{{ - i{{\omega \tau }}_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}}}}. \\ \end{gathered} $При этом принимаемый импульсный сигнал будет определяться выражением:
(3)
$\begin{gathered} {{g}_{{{{R}_{j}}}}}\left( {{\mathbf{\Phi }},t} \right) = \\ = \mathop \sum \limits_{n = 1}^N \mathop \sum \limits_{{{s}_{1}} = 0}^1 \ldots \mathop \sum \limits_{{{z}_{1}} = 0}^1 A_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}{{g}_{S}}(t - {{\tau }}_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}), \\ \end{gathered} $– время распространения волны от источника к приемнику ${{R}_{j}}$ [10], ${\mathbf{\Phi }} = \left\{ {{{{\mathbf{\varphi }}}_{n}}} \right\},~$ $~n = 1 \ldots N$ – полный вектор-строка параметров всех учитываемых донных слоев.
В дальнейшем мы исходим из того, что зондирование дна осуществляется последовательностью сложных импульсных сигналов с ЛЧМ. Сложность сигнала определяется нами стандартно как величина произведения длительности импульса на ширину его спектра (базы сигнала). Согласованная фильтрация сложных сигналов с большой базой, как хорошо известно, дает возможность значительного повышения, в сравнении с простыми сигналами той же длительности, временного разрешения импульсных приходов и достижения более высоких значений выходного ОСШ. Если такие сигналы являются хорошо воспроизводимыми и с высокой точностью синхронизированными, т.е. взаимно когерентными, то дополнительно к этому появляется принципиальная возможность дальнейшего увеличения ОСШ путем когерентного накопления “сжатых” импульсов в пределах интервала их взаимной когерентности. Эти общие соображения мотивировали наши исследования когерентных методов сейсмоакустической диагностики для полевых [12] и затем морских [1, 2] приложений.
Выходной сигнал согласованного фильтра принимаемого сигнала ${{g}_{R}}\left( t \right),{\text{\;\;}}$ имеющего некоторую задержку относительно излученного (опорного) сигнала ${{g}_{{\text{S}}}}\left( t \right)$ на интервал времени ${{\tau }}$, определяется хорошо известным выражением интегральной свертки этих двух сигналов:
(4)
$G\left( {{\tau }} \right) = \mathop \smallint \limits_{ - \infty }^{~\infty } {{g}_{R}}\left( t \right)g_{S}^{*}\left( {t - {{\tau }}} \right)dt.$С учетом введенных выше обозначений, имеем следующее расчетное выражение для сигнала на выходе согласованного фильтра в приемном канале ${{R}_{j}}$:
(5)
$\begin{gathered} {{G}_{{{{R}_{j}}}}}({\mathbf{\Phi }},~{{\tau }}) = \mathop \sum \limits_{n = 1}^N \mathop \sum \limits_{{{s}_{1}} = 0}^1 \cdots \mathop \sum \limits_{{{z}_{1}} = 0}^1 A_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}} \times \\ \times \,\,{{F}_{S}}({{\tau }} - {{\tau }}_{n}^{{\left( {{{s}_{1}}...{{s}_{n}}~{{z}_{n}} \ldots {{z}_{1}}} \right)}}), \\ \end{gathered} $В рамках нашего подхода, основанного на применении взаимно-когерентных сложных сигналов, считаем, что когерентность отраженных от донных границ раздела сигналов сохраняется в пределах определенного временного интервала, что позволяет осуществить их когерентное накопление в приемной системе не только в частотной области (согласованным фильтром), но и по времени. С учетом движения приемно-излучающей системы, временное накопление дает возможность пространственного накопления полезных сигналов вдоль отдельных слоев, “попадающих” в определенные узкие диапазоны времен задержки импульсных приходов относительно излученного сигнала. Такое накопление вдоль слоя, обусловленное движением излучателя и приемников, мы называем когерентным траекторным накоплением (КТН) [1, 2]. В целях увеличения длительности когерентной импульсной последовательности и эффективности такой процедуры, необходимо учитывать возможные (ожидаемые) изменения горизонтов расположения отдельных донных слоев, используя для этого дополнительную процедуру коррекции временных задержек соответствующих принимаемых сигналов, которые используются для “настройки” согласованных фильтров в приемных каналах.
Процедура коррекции горизонтальной неоднородности донных слоев вдоль трассы поясняется на рис. 3 и сводится к следующей последовательности операций. Сначала осуществляется предварительный поиск горизонтов отражающих границ донных слоев по оси временных задержек прихода импульсов путем согласованной фильтрации и затем когерентного накопления серии импульсов. Для каждой границы временная задержка будет определенная и отличная от других; набор таких задержек реализует вертикальное профилирование донных слоев в виде временной развертки (согласованная фильтрация сложно-модулированных сигналов с большой базой обеспечивают возможность высокого временного разрешения отдельных импульсных приходов). Однако, при искривлении границы некоторого слоя, имеющей “свое” время задержки, движение приемников вдоль трассы буксировки системы приводит к постепенной “расстройке” согласованного фильтра и связанной с этим потере эффективности КТН. Простейшей гипотезой относительно горизонтальной изменчивости границы является предположение о линейном ее наклоне на некоторый угол (угол α на рис. 3). С учетом такой гипотезы осуществляется коррекция временных интервалов задержки принимаемых импульсов, которая также линейно растет (или уменьшается, в зависимости от знака угла наклона) вдоль трассы – времена задержки приобретают линейную зависимость от номера импульса, что показано на рис. 3. Такую процедуру можно назвать адаптивным КТН, поскольку заранее угол наклона не известен, он подбирается (оценивается) отдельно для каждого из слоев и становится дополнительным его параметром. Очевидно, что эффективность процедуры, которая выражается в дополнительном росте числа взаимно-когерентных принимаемых импульсов, зависит от соответствия выбранной линейной аппроксимации реальной горизонтальной изменчивости донной структуры. Для увеличения эффективности аналогичным образом должны быть использованы более сложные (криволинейные) аппроксимации.
Рис. 3.
Коррекция времени задержки отраженных сигнальных импульсов с учетом линейного наклона отражающей границы слоя (показана сплошной линией) при когерентном траекторном накоплении сигналов (пояснения в тексте).

Таким образом, при выполнении последующего численного моделирования мы используем приведенные выше расчетные выражения (1)–(5) для полезных сигналов, поступающих на вход приемной АР, в каналах которой осуществляется последовательность процедур когерентной обработки: согласованная фильтрация с использованием опорной реплики излученного сигнала со сканированием по времени задержки (частотное накопление), пространственное накопление по элементам АР и затем КТН в пределах некоторого числа импульсов, которое является дополнительным параметром обработки, имитирующим реальную длину последовательности взаимно-когерентных сигналов на входе АР. Последовательный выигрыш по величине ОСШ в результате применения указанных процедур обработки в зависимости от задаваемых параметров определяется известными выражениями в предположении, что аддитивные шумы не обладают взаимной когерентностью и накапливаются только по мощности (раздел 5).
3. МОДЕЛИ ПОМЕХ РЕВЕРБЕРАЦИИ
Во всем диапазоне частот и временных задержек полезные сигналы маскируются помехами реверберации, которые возникают вследствие рассеяния зондирующих импульсов на граничных и объемных неоднородностях водной среды. Наибольший вклад в такие помехи вносит, как правило, рассеяние зондирующего сигнала на неровной границе дна (донная реверберация) и на взволнованной свободной границе (поверхностная реверберация).
Спектральная плотность мощности помехи может быть найдена интегрированием углового спектра по полному телесному углу ${{{{\Omega }}}_{R}}$ лучей, приходящих на отдельный гидрофон R приемной антенны:
Для углового спектра донной реверберации будем использовать метод касательной плоскости Бреховских–Исаковича [13]:
Суммарную помеху донной реверберации излучаемого импульсного сигнала ${{g}_{{\text{S}}}}\left( t \right)$ моделируем в виде интеграла по всем направлениям, выходящим из точки приема:
Среднее значение $P\left( {{\tau }} \right) = 0$, а интенсивность помехи реверберации равна:
Расчет этой величины зависит от совокупности параметров, которые определяются свойствами донной поверхности. В случае плоской и горизонтальной поверхности имеем:
(6)
$\begin{gathered} {{R}_{{SQ}}}\left( {{{{{\theta }}}_{R}},{{{{\varphi }}}_{R}}} \right) = \sqrt {h_{S}^{2} + {{{({{x}_{Q}} - {{x}_{S}})}}^{2}} + {{{({{y}_{Q}} - {{y}_{S}})}}^{2}}} , \\ {{R}_{{RQ}}}\left( {{{{{\theta }}}_{R}}} \right) = {{{{h}_{R}}} \mathord{\left/ {\vphantom {{{{h}_{R}}} {\cos {{{{\theta }}}_{R}}}}} \right. \kern-0em} {\cos {{{{\theta }}}_{R}}}}, \\ {{h}_{R}} = H - {{z}_{R}},\,\,\,\,{{h}_{S}} = H - {{z}_{S}}, \\ {{q}^{2}} = {{\left( {{{e}_{{1z}}} - {{e}_{{2z}}}} \right)}^{2}} = {{(\cos {{{{\theta }}}_{R}} + {{{{h}_{S}}} \mathord{\left/ {\vphantom {{{{h}_{S}}} {{{R}_{{SQ}}}}}} \right. \kern-0em} {{{R}_{{SQ}}}}})}^{2}}, \\ {{x}_{Q}} = {{x}_{R}} + {{h}_{R}}{\text{tg}}{{{{\theta }}}_{R}}\cos {{{{\varphi }}}_{R}} = \\ = {{x}_{R}} + {{R}_{{RQ}}}\left( {{{{{\theta }}}_{R}}} \right)\sin {{{{\theta }}}_{R}}\cos {{{{\varphi }}}_{R}}, \\ {{y}_{Q}} = {{y}_{R}} + {{h}_{R}}{\text{tg}}{{{{\theta }}}_{R}}\sin {{{{\varphi }}}_{R}} = \\ = {{y}_{R}} + {{R}_{{RQ}}}\left( {{{{{\theta }}}_{R}}} \right)\sin {{{{\theta }}}_{R}}\sin {{{{\varphi }}}_{R}}, \\ {{\kappa }^{2}} = {{\left( {{{e}_{{1x}}} - {{e}_{{2x}}}} \right)}^{2}} + {{\left( {{{e}_{{1y}}} - {{e}_{{2y}}}} \right)}^{2}} = \\ = {{\left( {\sin {{{{\theta }}}_{R}}\cos {{{{\varphi }}}_{R}} - {{\left( {{{x}_{{\text{S}}}} - {{x}_{Q}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{x}_{{\text{S}}}} - {{x}_{Q}}} \right)} {{{R}_{{SQ}}}}}} \right. \kern-0em} {{{R}_{{SQ}}}}}} \right)}^{2}} + \\ + \,\,{{\left( {\sin {{{{\theta }}}_{R}}\sin {{{{\varphi }}}_{R}} - {{\left( {{{y}_{{\text{S}}}} - {{y}_{Q}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{y}_{{\text{S}}}} - {{y}_{Q}}} \right)} {{{R}_{{SQ}}}}}} \right. \kern-0em} {{{R}_{{SQ}}}}}} \right)}^{2}}. \\ \end{gathered} $Для расчета помехи реверберации в случае наклонного дна применим следующий математический прием. Пусть дно есть плоскость, проходящая через точку $\left( {0,0,H} \right)$ и перпендикулярная вектору ${\mathbf{n}} = \left( {\sin {{\alpha }}\cos {{\beta }},\sin {{\alpha }},\cos {{\alpha }}} \right)$ (случай ${{\alpha }} = 0$ соответствует исходному горизонтальному дну). Тогда для расчета можно использовать те же формулы (6), в которых следует сделать замены
На рис. 4 приведены расчеты средней интенсивности донной реверберации на выходе согласованного фильтра отдельного гидрофона как функции задержки ${{\tau }}$ для различных углов наклона ${{\alpha }},{{\beta }}$ и среднеквадратичных наклонов ${{\delta }}$ донной поверхности, величина которых определена здесь через тангенс локального угла наклона (меньшим значениям ${{\delta }}$ отвечает более плоская в среднем поверхность). Параметры расчетов: $H = 200\,\,~{\text{м}}$ – глубина водного слоя, ${{z}_{S}} = 30~\,\,{\text{м}},~$ ${{z}_{R}} = 3~\,\,{\text{м}}$ – глубины расположения источника и приемника, соответственно, ${{x}_{R}} = 60\,\,{\text{\;}}{\kern 1pt} {\text{м}}$ – расстояние между источником и приемником, ${{F}_{{{\text{pulse}}}}} = 200~\,\,{\text{Гц}}$ – нижняя частота излучения, ${{\Delta }}{{F}_{{{\text{pulse}}}}} = 100~\,\,{\text{Гц}}$ – полоса ЛЧМ, ${{T}_{{{\text{pulse}}}}} = 0.125\,\,~{\text{c}}$ – длительность импульса, ${{c}_{0}} = 1475\,\,~{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ – скорость звука в морской воде, ${{{{\rho }}}_{0}} = 1040\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}$ – плотность воды. Видно, что поскольку помеха реверберации формируется импульсами, соответствующими зеркальным направлениям от источника к приемнику. Вклад удаленных участков донной поверхности в суммарный сигнал возможен только при наличии достаточно крутых неровностей, т.е. при больших значениях ${{\delta }},~$ в то время как при малых ${{\delta }}$ реверберация формируется в пределах малого участка донной поверхности, лежащего вблизи середины отрезка, соединяющего источник и приемник (приведенные значения ${{\delta }}$ отвечают изменению среднеквадратичных углов наклона от ~20° до ~60°). Важно, однако, что амплитуды рассеянных импульсов при этом оказываются относительно большими, так как соответствующие диаграммы рассеяния являются более узкими. С увеличением ${{\delta }}$ область формирования помехи реверберации расширяется, пропорционально растут времена задержки отдельных импульсов, но значительно уменьшаются их амплитуды.
Рис. 4.
Модельный расчет интенсивности донной реверберации на выходе согласованного фильтра в отдельном канале АР как функция задержки $\tau $ для различных углов $\alpha ,\beta $ среднего наклона и величины среднеквадратичных наклонов $\delta $ случайного рельефа дна: $\alpha = \beta = 0$ (а); $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},\,\,\beta = 0$ (б); $\alpha = 0,\,\,\beta = {\pi \mathord{\left/ {\vphantom {\pi {~2}}} \right. \kern-0em} {~2}}$ (в).

Минимальное время прихода импульса донной реверберации находится из уравнения:
Уравнение эллипса, от границы которого отражаются импульсы, имеющие времена прихода ${{\tau }}$, имеет вид:
Для расчета помехи реверберации на взволнованной морской поверхности будем использовать формулу Неймана–Пирсона для коэффициента рассеяния звука на ветровом волнении [13]:
На рис. 5 представлены расчеты нормированных интенсивностей ${I \mathord{\left/ {\vphantom {I {{{I}_{1}}}}} \right. \kern-0em} {{{I}_{1}}}}$ полезных сигналов и помех реверберации как функций их временной задержки ${{\tau }}$: для прямого сигнала (d), отраженного от свободной поверхности сигнала (s), отраженного от донной поверхности сигнала (b), совокупности сигналов, отраженных от шести донных слоев (индексы 1–6), сигналов поверхностной реверберации для различных скоростей ветра и тех же значений параметра ${{\delta }}$, соответственно. Для нормировки зависимостей используется величина ${{I}_{1}} = {W \mathord{\left/ {\vphantom {W {4{{\pi }}}}} \right. \kern-0em} {4{{\pi }}}}$ – интенсивность поля, создаваемая источником мощности $W$ на расстоянии $1$ метр. Параметры моделирования приведены в табл. 1.
Рис. 5.
Нормированные интенсивности полезных сигналов (отраженных от донных слоев) и помех реверберации как функции времени их задержки при различных значениях среднеквадратичных наклонов рельефа дна (как на рис. 4) и скоростях ветра 10 и 15 м/с в сравнении с уровнем аддитивного шума (пунктирные линии) при мощности источника 1 и 100 Вт (пояснения в тексте).

Таблица 1.
Параметры моделирования для расчетов рис. 5
| Приемно-излучающая система | |||||
| ${{z}_{S}}~{\kern 1pt} ,\,\,{\text{м}}$ | ${{z}_{R}}~{\kern 1pt} ,\,\,{\text{м}}$ | ${{x}_{R}}{\kern 1pt} ,\,{\text{м}}$ | ${{F}_{{{\text{pulse}}}}},{\kern 1pt} \,\,{\text{Гц}}$ | $\Delta {{F}_{{{\text{pulse}}}}},\,\,{\text{Гц}}$ | ${{T}_{{{\text{imp}}}}}~{\kern 1pt} ,{\text{с}}$ |
| 30 | 3 | 60 | 200 | 50 | 0.125 |
| Водный слой | |||||
| $H,{\text{м}}$ | ${{c}_{{{\text{вода}}}}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ | ${{\rho }_{{{\text{вода}}}}},$${{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ${{{{\delta }}}_{0}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{{{\text{воздух}}}}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{\rho }_{{{\text{вода}}}}},$${{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ |
| 200 | 1475 | 1040 | 0 | 330 | 1.29 |
| Донные слои | |||||
| ${{h}_{1}},{\text{м}}$ | ${{{{\delta }}}_{1}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{1}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{{{\rho }}}_{1}}{\text{\;}}{\kern 1pt} {\text{,}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ||
| 50 | 0.005 | 1490 | 1400 | ||
| ${{h}_{2}},{\text{м}}$ | ${{{{\delta }}}_{2}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{2}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{{{\rho }}}_{2}}{\text{\;}}{\kern 1pt} {\text{,}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ||
| 50 | 0.006 | 1525 | 1440 | ||
| ${{h}_{3}},{\text{м}}$ | ${{{{\delta }}}_{3}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{3}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{{{\rho }}}_{3}}{\text{\;}}{\kern 1pt} {\text{,}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ||
| 50 | 0.005 | 1459 | 900 | ||
| ${{h}_{4}},{\text{м}}$ | ${{{{\delta }}}_{4}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{4}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{{{\rho }}}_{4}}{\text{\;}}{\kern 1pt} {\text{,}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ||
| 50 | 0.007 | 2700 | 2100 | ||
| ${{h}_{5}},{\text{м}}$ | ${{{{\delta }}}_{5}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{5}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{{{\rho }}}_{5}}{\text{\;}}{\kern 1pt} {\text{,}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ||
| 50 | 0.008 | 2250 | 2250 | ||
| ${{h}_{6}},{\text{м}}$ | ${{{{\delta }}}_{6}},\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | ${{c}_{6}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{{{\rho }}}_{6}}{\text{\;}}{\kern 1pt} {\text{,}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | ||
| 50 | 0.009 | 4500 | 2400 | ||
Положение пунктирной прямой ${{\beta }} = {{{{\beta }}}_{a}}$, соответствующей некоторому заданному уровню аддитивных шумов, зависит от мощности источника $W$. Действительно, поскольку здесь приведены относительные величины ${{\beta }} = 10{\kern 1pt} {\text{lg}}\left( {{I \mathord{\left/ {\vphantom {I {{{I}_{1}}}}} \right. \kern-0em} {{{I}_{1}}}}} \right){\text{\;}}$, то для интенсивности и давления в поле зондирующей волны имеем соотношения:
Отсюда, задавая величину давления аддитивного шума ${{p}_{a}}$, несложно рассчитать мощность источника $W$, необходимую для того, чтобы интенсивности отраженных сигналов в своих максимумах были равны интенсивности шума или превосходили ее на определенную величину. Например, если давление шума составляет величину ${{p}_{a}} \approx 15$ мПа, то для уровня шума ${{{{\beta }}}_{a}} = - 90~\,\,{\text{дБ}}$ получаем мощность источника $W \approx 1\,\,{\text{Вт}}$, а для ${{{{\beta }}}_{a}} = - 110\,\,{\text{\;дБ}}$ – мощность $W \approx 100\,\,{\text{Вт}}$ (см. рис. 5). С ростом излучаемой мощности уровни полезных сигналов и помех реверберации на рис. 5 будут оставаться неизменными, а линия уровня аддитивного шума – опускаться. Таким образом, для корректного нанесения на рис. 5 линии уровня шума ${{{{\beta }}}_{a}}$ и сопоставления с ним уровня отраженных сигналов, нужно знать (в эксперименте) или задать (при моделировании) обе величины: интенсивность ${{I}_{a}}$ (давление ${{p}_{a}}$) шумового поля и мощность источника $W$:
Анализ представленных на рис. 5 модельных зависимостей позволяет сделать качественный вывод о том, что максимальная интенсивность отраженных донными слоями сигналов слабее спадает с увеличением номера слоя и соответствующим ростом интервала задержки, чем интенсивность помех реверберации, даже при достаточно больших значениях среднеквадратичных уклонов донной поверхности и скоростях ветра. Это означает, что при оценке параметров отдельного донного слоя реверберация играет тем меньшую роль, чем глубже он расположен.
4. ЦЕЛЕВЫЕ ФУНКЦИИ И АЛГОРИТМЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ
Оценивание геоакустических параметров донных слоев на основе обработки сейсмоакустических данных является характерным примером обратных задач, методы решения которых основаны на теории статистической проверки гипотез (например, [4, 5, 11]). В качестве гипотез ${\mathbf{\tilde {\Phi }}}$ в данной постановке выступают некоторые наперед заданные значения параметров слоистой структуры дна в рамках сформулированной выше модели. Гипотеза ${\mathbf{\hat {\Phi }}}$, при которой достигается экстремум заданной целевой функции, определенным образом зависящей от невязки (расхождения) гипотезы с истинными значениями параметров, “входящих” в принимаемые сигналы, является решением обратной задачи и дает оценку этих параметров. Качество полученных оценок характеризуется, прежде всего, их средним отклонением (смещением) и дисперсией отклонений от истинных значений. Выбор целевой функции (или функционала невязки в широком смысле) и отвечающего ей алгоритма оценивания может быть различным, при этом различным оказывается и качество полученных оценок искомых параметров сигналов, принимаемых на фоне шумов и помех.
В данной работе мы исследуем помехоустойчивость ряда алгоритмов оценивания, которые отличаются способом построения целевой функции и различной степенью использования процедур когерентной обработки принимаемых сигналов. Подобный сравнительный анализ позволяет оптимизировать выбор целевой функции при решении задач морской сейсмоакустики с учетом конкретных условий проведения эксперимента.
Прежде чем перейти непосредственно к рассмотрению целевых функций и алгоритмов на их основе, приведем выражения, которые нам понадобятся для определения тех сигналов, которые “участвуют” в решении обратной задачи оценивания параметров. С учетом представленных выше моделей формирования сигналов на входе АР, необходимо принять во внимание, что полезные сигналы ${{g}_{{{{R}_{j}}}}}\left( {{\mathbf{\Phi }},~t} \right),j = 1, \ldots ,{{K}_{R}}$ (3) принимаются на фоне аддитивных шумов и помех реверберации, сигнал которых в совокупности обозначим как $g_{{{{R}_{j}}}}^{{{\text{Noise}}}}\left( t \right)$. Тогда полная реплика принимаемого сигнала имеет вид:
На выходе согласованного фильтра, используя реплику опорного сигнала, имеем аналогично (4):
(7)
$G_{{{{R}_{j}}}}^{{{\text{Exp}}}}({\mathbf{\Phi }},~{{\tau }}) = \mathop \smallint \limits_{ - \infty }^{~\infty } g_{{{{R}_{j}}}}^{{{\text{Exp}}}}({\mathbf{\Phi }},~t)g_{S}^{*}\left( {t - {{\tau }}} \right)dt.$Модельный принимаемый сигнал, который рассчитывается в предположении гипотезы ${\mathbf{\tilde {\Phi }}}$ относительно значений параметров донных слоев, обозначим как ${{\tilde {g}}_{{{{R}_{j}}}}}({\mathbf{\tilde {\Phi }}},~t)$. Тогда для модельного сигнала на выходе согласованного фильтра имеем:
(8)
${{\tilde {G}}_{{{{R}_{j}}}}}({\mathbf{\tilde {\Phi }}},~{{\tau }}) = \mathop \smallint \limits_{ - \infty }^{~\infty } {{\tilde {g}}_{{{{R}_{j}}}}}({\mathbf{\tilde {\Phi }}},~t)g_{S}^{*}\left( {t - {{\tau }}} \right)dt.$Варьирование параметров модели слоистого дна приводит, очевидно, к варьированию модельного принимаемого сигнала и возможности поиска экстремума целевых функций, связывающих тем или иным образом реплики непосредственно входных сигналов или реплики “сжатых” сигналов (7) и (8). В данной работе мы рассматриваем оба этих варианта в качестве возможных при построении целевой функции.
Lp-норма с когерентным пространственно-частотным накоплением. Наиболее распространенной целевой функцией при решении разного рода обратных задач является степенная Lр-норма функционала невязки принимаемого (реального) и модельного сигналов [14], которая в нашей постановке имеет вид:
(9)
${{W}_{{{{L}_{p}}}}}({\mathbf{\tilde {\Phi }}}) = {{\left( {\mathop \sum \limits_{{{t}_{k}} \in T} \mathop \sum \limits_{{{R}_{{\text{j}}}}} {{{\left| {g_{{{{R}_{j}}}}^{{{\text{Exp}}}}({\mathbf{\Phi }},~{{t}_{k}}) - {{{\tilde {g}}}_{{{{R}_{j}}}}}({\mathbf{\tilde {\Phi }}},~{{t}_{k}})} \right|}}^{p}}} \right)}^{{1/p}}}.$Здесь первое суммирование относится к накоплению сигналов в течение определенного интервала времени $T$, второе суммирование – к накоплению по элементам АР. В случае $p = 2$ выражение (7) определяет стандартную среднеквадратическую невязку, которая используется нами в дальнейшем. Соответствующий метод получения оценок ${\mathbf{\hat {\Phi }}}$ представляет собой не что иное, как метод наименьших квадратов Гаусса, оптимальный при нормальном распределении аддитивных шумов [3].
С учетом описанных выше процедур когерентной обработки, в качестве “когерентного” функционала невязки будем использовать L2-норму следующего вида:
(10)
$\begin{gathered} W_{{{{L}_{2}}}}^{{{\text{Cog}}}}({\mathbf{\tilde {\Phi }}}) = ~ \\ = {{\left( {\mathop \sum \limits_{{{K}_{V}}} \mathop \sum \limits_{{{{{\tau }}}_{{\text{k}}}}} \mathop \sum \limits_{{{R}_{j}}} {{{\left| {G_{{{{R}_{j}}}}^{{{\text{Exp}}}}({\mathbf{\Phi }},~{{{{\tau }}}_{k}}) - {{{\tilde {G}}}_{{{{R}_{j}}}}}({\mathbf{\tilde {\Phi }}},~{{{{\tau }}}_{k}})} \right|}}^{2}}} \right)}^{{1/2}}}. \\ \end{gathered} $Здесь учтено, что в ходе обработки выполняются: корреляционная свертка принятых сигналов с опорными в приемных каналах решетки ${{R}_{j}}$; когерентное пространственное накопление сигналов по элементам АР; когерентное накопление вдоль отдельных траекторий на плоскости $\left( {{{\tau }},{\mathbf{r}}} \right)$ в пределах длины когерентности (процедура КТН); наконец, накопление по всем ${{K}_{V}}$ волновым компонентам, учитываемым в рамках модели формирования сигналов (раздел 2).
Целевая функция адаптивного процессора. Другой подход к построению целевой функции основан на использовании адаптивных методов многоканальной обработки сигналов. Известно большое количество таких методов и их модификаций, одними из наиболее универсальных являются т.н. проекционные методы, которые основаны на анализе спектральных свойств (спектра собственных значений и базиса собственных векторов) матрицы пространственных корреляций сигналов, принимаемых АР.
Рассмотрим векторы спектральных амплитуд принимаемых АР сигналов на некоторой частоте излучаемого импульса. Предполагая отсутствие взаимных корреляций сигнальной и шумовой (в смеси с помехами) компонент, имеем следующее общее выражение для корреляционной матрицы (КМ):
(11)
${{{\mathbf{\hat {K}}}}^{{{\text{Exp}}}}}\left( {{\mathbf{\Phi }},~{{\omega }}} \right) = \frac{1}{L}\mathop \sum \limits_l {{g}^{{{\text{Exp}}}}}\left( {{\mathbf{\Phi }},~{{t}_{l}}} \right){{g}^{{{\text{Exp}}}}}{{\left( {{\mathbf{\Phi }},~{{t}_{l}}} \right)}^{ + }}.$Задача оптимальной обработки состоит в построении такого пространственно-временного фильтра входных сигналов, который позволяет, используя оценку КМ (11), наилучшим (в соответствии с заданным критерием) образом выделить полезный сигнал на фоне аддитивных шумов и помех и затем оценить его неизвестные параметры ${\mathbf{\Phi }}$. Следуя той терминологии, которая принята в обработке сигналов, это означает реализовать максимальную мощность на выходе процессора (блока обработки) в каналах АР и найти такой вектор параметров ${\mathbf{\hat {\Phi }}}$ при варьировании ${\mathbf{\tilde {\Phi }}}$, при котором этот максимум достигается. Мощность на выходе процессора играет при этом роль целевой функции, а обратная к ней величина, которая минимизируется, является аналогом функционала невязки и тоже становится целевой функцией.
Проекционные методы обработки сигналов в антенных решетках применительно к подводной акустике обсуждаются, в частности, в недавних обзорах [15, 16]. Все они основаны на известной процедуре спектрального разложения построенной оценки КМ (11):
где ${{{{\hat {\lambda }}}}_{1}} \geqslant ... \geqslant {{{{\hat {\lambda }}}}_{N}}$ – упорядоченные по убыванию собственные значения КМ, ${\text{\;}}{{{{\hat {\psi }}}}_{j}}$ – ее взаимно ортогональные нормированные собственные векторы (собственный базис КМ). При достаточно большом отношении сигнал/шум (ОСШ) на входе АР основной вклад в эту сумму вносят ее первые (сигнальные) слагаемые (в асимптотике полностью когерентного сигнала и нулевого уровня шума единственное значение ${{{{\hat {\lambda }}}}_{1}} \ne 0$, при этом ${{{{\hat {\psi }}}}_{1}}$ равен нормированному сигнальному вектору). С уменьшением ОСШ растут число и величины “шумовых” собственных значений и размерность подпространства отвечающих им собственных векторов, вследствие чего возникает необходимость классификации “сигнальных” и “шумовых” компонент в базисе КМ.Один из популярных проекционных методов, который изначально был предложен для решения задачи оценки пространственного (углового) спектра входных сигналов, известен как метод MUSIC (от англ. – multiple signal classification) [17]. Мощность реализующего его процессора определяется выражением:
(12)
${{P}_{{{\text{MUSIC}}}}}{\kern 1pt} ({\mathbf{\tilde {\Phi }}}) = {1 \mathord{\left/ {\vphantom {1 {\mathop \sum \limits_{j = J + 1}^N {{{\left| {{{\hat {\psi }}}_{j}^{ + }{{{\mathbf{e}}}_{0}}({\mathbf{\tilde {\Phi }}})} \right|}}^{2}}}}} \right. \kern-0em} {\mathop \sum \limits_{j = J + 1}^N {{{\left| {{{\hat {\psi }}}_{j}^{ + }{{{\mathbf{e}}}_{0}}({\mathbf{\tilde {\Phi }}})} \right|}}^{2}}}},$Подчеркнем, что этот и другие проекционные методы были предложены и достаточно эффективны для условий приема сигналов, когда расчет направляющих векторов не сопровождается какой-либо априорной неопределенностью. Такая ситуация характерна, например, для оценки углового спектра удаленных источников в свободном однородном пространстве, когда сами сигналы и направляющий вектор представляют собой плоские волны (отсюда и термин – направляющий вектор). В нашей задаче направляющий вектор ${{{\mathbf{e}}}_{0}}({\mathbf{\tilde {\Phi }}}) = {{g({\mathbf{\tilde {\Phi }}},{{\omega }}{\mathbf{)}}} \mathord{\left/ {\vphantom {{g({\mathbf{\tilde {\Phi }}},{{\omega }}{\mathbf{)}}} {g({\mathbf{\tilde {\Phi }}},{{\omega }})}}} \right. \kern-0em} {g({\mathbf{\tilde {\Phi }}},{{\omega }})}}$ имеет другой физический смысл, нежели в [17], но его “назначение” остается тем же – обеспечить минимальную величину проекции на подпространство старших собственных векторов КМ. Достижение этого условия означает максимальное приближение пробной КМ ${\mathbf{K}}({\mathbf{\tilde {\Phi }}},~\omega )$ к экспериментальной (наблюдаемой) матрице.
Таким образом, процедура алгоритма MUSIC в нашей постановке сводится к нахождению такого вектора донных параметров, при котором достигается максимум выходной мощности процессора вида (12) или, что эквивалентно, минимум невязки:
В условиях априорной неопределенности относительно модели расчета направляющего вектора в зависимости от оцениваемых параметров, алгоритм MUSIC ожидаемо теряет свою эффективность. Применительно к задаче оценки координат удаленного источника в подводном звуковом канале, расчетная модель которого известна не точно (не полностью согласована с реальной средой распространения), авторами [18] предложен адаптивный вариант данного алгоритма – алгоритм AMUSIC (adaptive MUSIC), который обладает более высокой устойчивостью к “рассогласованию” модели канала. Для этого в алгоритм вводится некоторое контролируемое отклонение направляющего вектора от модельного вектора ${{{\mathbf{e}}}_{0}}({\mathbf{\tilde {\Phi }}})$, т.е. априори учитывается возможная ошибка в построении модели самих сигналов и направляющих векторов. В этом случае оценочный направляющий вектор находится из решения следующей вариационной задачи с дополнительными ограничениями [8, 9, 18]:
(13)
${{W}_{{{\text{AMUSIC}}}}}({\mathbf{\tilde {\Phi }}}) = \mathop \sum \limits_{j = J + 1}^N {{\left| {\hat {\psi }_{j}^{ + }{\mathbf{e}}({\mathbf{\tilde {\Phi }}},{{\varepsilon }})} \right|}^{2}}.$В тех случаях, когда целевая функция (13) зависит от некоторого числа контролируемых параметров $\left\{ {{{p}_{i}}} \right\}_{{i = 1}}^{P}~$, можно использовать эти зависимости для улучшения качества адаптивного процессора. Важно выбрать при этом такие параметры, от которых модельные сигналы зависят существенно, но известным образом. Вычисляя для каждого из них величину “парциальной” невязки $~{{W}_{{{\text{AMUSIC}}}}}\left( {{\mathbf{\tilde {\Phi }}},{{p}_{i}}} \right)$, следует построить обобщенный функционал невязки алгоритма AMUSIC в виде произведения таких целевых функций:
(14)
${{W}_{{{\text{AMUSIC}}P}}}({\mathbf{\tilde {\Phi }}}) = \mathop \prod \limits_{i = 1}^P {{W}_{{{\text{AMUSIC}}}}}{\kern 1pt} ({\mathbf{\tilde {\Phi }}},{{p}_{i}}).$В этом случае искомые параметры оцениваются из условия достижения экстремума более сложного обобщенного функционала, но такое усложнение имеет свои преимущества. В работе [8] было показано, что при этом может быть достигнуто обострение глобального минимума невязки в пространстве оцениваемых параметров, причем эффект такого обострения (фактически, повышения разрешающей способности) растет с ростом числа сомножителей в (14). Одновременно с этим, локальные “паразитные” минимумы (своего рода, боковые лепестки обобщенной целевой функции (14)), напротив, теряют контраст (сглаживаются) в сравнении с расчетом функционала (13), что дополнительно повышает качество функционала. Таким образом, подобное обобщение адаптивного алгоритма указывает полезный способ “накопления” целевых функций с целью улучшения оценки искомых параметров донных слоев.
Например, при использовании широкополосного ЛЧМ-сигнала представляется естественным использование значений целевых функций, отвечающих набору отдельных частот, в результате чего на основе (14) строится обобщенный функционал ${{W}_{{{\text{AMUSIC}}F}}}$. Путем изменения по заданной схеме расстояний между излучателем и АР (при неизменной глубине ее погружения и ориентации), получаем аналогичное обобщение ${{W}_{{{\text{AMUSICR}}}}}$. Оба этих варианта построения обобщенного функционала невязки для алгоритма AMUSIC используются нами при моделировании (раздел 5).
Изложенный здесь подход оперирует непосредственно с оценками входных КМ и не предполагает процедуры согласованной фильтрации принимаемых сигналов в каналах АР. Вследствие этого параметры всех донных слоев “участвуют” в формировании КМ на входе АР одновременно, что приводит к необходимости решать задачу поиска экстремума в пространстве высокой размерности. Можно, однако, и здесь использовать согласованную фильтрацию в качестве предварительной обработки и затем строить оценки модифицированной (в этом смысле) КМ с последующим построением целевой функции. Для этого введем общую для всех приемных каналов задержку ${{\tau \;}}$ и сформируем комплексные векторы, относящиеся к выходным сигналам согласованных фильтров в каналах АР: $G\left( {{\mathbf{\Phi }},~{{\tau }}} \right)$, ${{G}^{{{\text{Noise}}}}}({{\tau }})$ и ${{G}^{{{\text{Exp}}}}}({{\tau }}) = G({\mathbf{\Phi }},~{{\tau }}) + {{G}^{{{\text{Noise}}}}}({{\tau }})$. Предполагая, как и ранее, отсутствие взаимных корреляций сигнальной и шумовой компонент, получаем следующее выражение для модифицированной таким образом КМ:
Поскольку реальная КМ ${\mathbf{K}}_{G}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~\tau } \right)$ так же неизвестна, как и для самих сигналов, то для дальнейшей обработки стандартно используем оценку КМ вида (11):
(15)
${\mathbf{\hat {K}}}_{G}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~{{\tau }}} \right) = \frac{1}{L}\mathop \sum \limits_l G_{l}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~{{\tau }}} \right)G_{l}^{{{\text{Exp}}}}{{\left( {{\mathbf{\Phi }},~{{\tau }}} \right)}^{ + }}.$Конечно, практическая реализация оценки КМ (15) значительно сложнее, чем (11), так как свертка (4) формально требует интегрирования импульсов на бесконечном промежутке времени. Однако вычисление свертки достаточно произвести на конечном интервале в несколько длин импульса, что позволяет практически использовать модифицированные КМ вида (15).
Таким образом, при построении целевых функционалов в рамках проекционного подхода и его обобщений можно использовать состоятельные оценки КМ как для входных сигналов, так и для “сжатых” сигналов на выходе согласованных фильтров, подбирая различные значения задержки ${{\tau }}$.
Целевая функция нейроноподобной свертки сигналов. В работах [19, 20] для оценки параметров сложных сигналов был предложен метод, основанный на анализе работы нейроноподобных сетей. Важно, что выбор целевой функции в виде нейроноподобной свертки (по аналогии с корреляционной сверткой при согласованной фильтрации) дает высокую чувствительность к различию времен прихода сигналов. При этом эффективность данной процедуры слабо зависит от статистического распределения шумов, что выгодно отличает ее от других процедур построения целевой функции [20].
В применении к нашей задаче мы используем, модифицируя ранее полученные выражения [20], следующее выражение для нейроноподобной целевой функции:
(16)
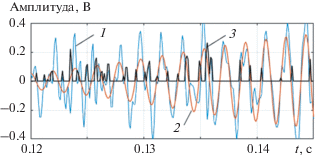
$\begin{gathered} {{W}_{{{\text{NEURO}}}}}\left( {{\mathbf{\tilde {\Phi }}}} \right) = \\ = \mathop \sum \limits_{{{R}_{j}}} 1 - 2\frac{{\left\| {Q\left( {{\text{\;}}G_{{{{R}_{j}}}}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~{{\tau }}} \right),{{{\tilde {G}}}_{{{{R}_{j}}}}}\left( {{\mathbf{\tilde {\Phi }}},~{{\tau }}} \right)} \right)} \right\|}}{{\left\| {G_{{{{R}_{j}}}}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~{{\tau }}} \right)} \right\| + \left\| {{{G}_{{{{R}_{j}}}}}\left( {{\mathbf{\tilde {\Phi }}},~{{\tau }}} \right)} \right\|}}, \\ \end{gathered} $Функция $Q\left( {G_{{{{R}_{j}}}}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~{{\tau }}} \right),{{G}_{{{{R}_{j}}}}}\left( {{\mathbf{\tilde {\Phi }}},~{{\tau }}} \right)} \right)$ указывает правило, в соответствии с которым формируется выходной сигнал в данном алгоритме при сравнении экспериментального сигнала $G_{{{{R}_{j}}}}^{{{\text{Exp}}}}\left( {{\mathbf{\Phi }},~{{\tau }}} \right)$ на выходе согласованного фильтра с аналогичным модельным сигналом ${{G}_{{{{R}_{j}}}}}\left( {{\mathbf{\tilde {\Phi }}},~{{\tau }}} \right)$. Расчет этой функции иллюстрируется на рис. 6, где показаны модельные реализации принятого сигнала в смеси с шумом (метка 1), непосредственного сигнала (метка 2) и сигнала на выходе нейроно-подобного фильтра (метка 3). Как и в других алгоритмах, при переборе параметров гипотезы ${\mathbf{\tilde {\Phi }}}$ находится экстремум (минимум) целевой функции (16), а отвечающий ему вектор параметров ${\mathbf{\hat {\Phi }}}$ становится их оценкой.
5. МОДЕЛИРОВАНИЕ И СРАВНИТЕЛЬНЫЙ АНАЛИЗ АЛГОРИТМОВ
В целях сравнительного анализа обсуждаемых алгоритмов оценивания выполнено их численное моделирование для заданной (достаточно простой) структуры осадочных пород морского дна.
Параметры моделирования приведены в табл. 2. Предполагается, что зондирующие ЛЧМ-импульсы излучаются в широкой полосе 200–1000 Гц, имеют длительность ${{T}_{{{\text{imp}}}}}$=1 с (база сигнала равна 800) и мощность ${{W}_{S}}~$= 0.7515 Вт, источник расположен на глубине 15 м (${{F}_{d}}$ = 5 кГц – частота дискретизации сигнала). Приемная АР предполагается горизонтальной и эквидистантной, расположенной на глубине 10 м и удаленной от излучателя на 10 м (по первому гидрофону), число гидрофонов ${{K}_{R}}{\text{\;}}$ = 15, расстояние между соседними гидрофонами ${{l}_{g}}$ = 2 м. С помощью согласованной фильтрации в каналах решетки осуществляется корреляционное “сжатие” полезных сигналов (в число раз, равное базе) и оценка времени их приходов.
Таблица 2.
Параметры моделирования для расчетов рис. 7
| Модель среды | ||||||||||
| $\rho ,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}~$ | ${{v}^{p}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | ${{v}^{{SV}}},\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}~$ | $h,~\,\,{\text{м}}$ | ${{\delta ,}}\,\,{{{\text{дБ}}} \mathord{\left/ {\vphantom {{{\text{дБ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}~$ | ||||||
| Водный слой | 1040 | 1475 | 0 | 50 | 0 | |||||
| Упругий слой | 1600 ± 120 | 1800 ± 25 | 300 ± 75 | 20 ± 5 | 0.02 | |||||
| Полупространство | 1800 | 2000 | 400 | $\infty $ | 0.03 | |||||
| Приемно-излучающая система | ||||||||||
| $f,~\,\,{\text{Гц}}$ | ${{W}_{S}}~{\kern 1pt} ,{\text{Вт}}$ | ${{x}^{S}},{\text{м}}$ | ${{y}^{S}},{\text{м}}$ | ${{z}^{S}},~{\text{м}}$ | ${{T}_{{{\text{imp}}}}},{\text{с}}$ | ${{F}_{d}}{\kern 1pt} ,{\text{Гц}}$ | ${{l}_{g}}{\kern 1pt} ,{\text{м}}$ | $x_{1}^{{\left( R \right)}},{\text{м}}$ | $y_{1}^{{\left( R \right)}},{\text{м}}$ | $z_{{}}^{{\left( R \right)}},{\text{м}}$ |
| 200–1000 | 0.75 | 15 0 | 0 | 15 | 1 | 5000 | 2 | 10 | 0 | 10 |
Расчеты проводились для модели дна в виде упругого слоя с параметрами, имитирующими водонасыщенную гальку, расположенную на упругом подстилающем полупространстве, параметры которого близки к параметрам влажной глины. Задаваемые как истинные значения геоакустических параметров и интервалы их поиска также приведены в табл. 2. Оценивались следующие параметры слоя: плотность ${{{{\rho }}}_{1}}$, скорости продольных ($v_{1}^{P}$) и поперечных ($v_{1}^{{SV}}$) волн, толщина ${{h}_{1}}$. Затухание δ1 учитывалось в виде некоторого среднего (по частоте) значения, но не оценивалось с учетом того, что при использовании широкополосного сигнала корректная процедура такой оценки требует учета частотной зависимости и дополнительного усложнения расчетов (этот вопрос будет исследован в дальнейшем).
В качестве целевых функций использовались:
a) среднеквадратичная L2-норма невязки (10);
b) функционал невязки обобщенного адаптивного процессора ${{W}_{{{\text{AMUSICR}}}}}$ (14) для двух расстояний между излучателем и АР (10 и 12 м). При этом каждая из двух парциальных функций вида (13) рассчитывается для спектральных амплитуд сигналов (имитирующего принятый и модельного) на центральной частоте ЛЧМ (600 Гц);
c) функционал невязки обобщенного адаптивного процессора ${{W}_{{{\text{AMUSICF}}}}}$ (14) для двух различных частот из полосы ЛЧМ (400 и 800 Гц) и фиксированного расстояния (10 м);
d) функционал нейроноподобной свертки ${{W}_{{{\text{NEURO}}}}}$ (16).
Для сравнительного исследования помехоустойчивости соответствующих алгоритмов реконструкции параметров дна были рассчитаны средние значения отклонений оценок от истинных значений – величины ${{\Delta }}{{{{\rho }}}_{1}}$, ${{\Delta }}v_{1}^{P}$, ${{\Delta }}v_{1}^{{SV}}$, ${{\Delta }}{{h}_{1}}$, и дисперсии этих отклонений – величины ${{\sigma \Delta }}{{{{\rho }}}_{1}}$, ${{\sigma \Delta }}v_{1}^{P}$, ${{\sigma \Delta }}v_{1}^{{SV}}$, ${{\sigma \Delta }}{{h}_{1}}$ в зависимости от величины входного ОСШ. Расчеты проводились путем усреднения по 103 случайным реализациям шума в широком диапазоне значений входного ОСШ, от –15 до 15 дБ, с особым вниманием на области малых значений, которая в наибольшей степени отвечает практически важным ситуациям.
С учетом процедур когерентного накопления полезных сигналов (раздел 2), моделирование алгоритмов включало расчет выигрыша (коэффициента усиления по величине ОСШ) когерентной обработки полезных сигналов в предположении взаимно-некоррелированных реализаций шума. Выигрыш согласованной фильтрации (частотного накопления) сложного сигнала определяется известным соотношением: ${{G}^{f}} = 10\lg \sqrt {\Delta f{{T}_{{{\text{imp}}}}}} $, где $\Delta f$ – полоса сигнала, ${{T}_{{{\text{imp}}}}}$ – его длительность. Выигрыш когерентного накопления по элементам АР (пространственного накопления): ${{G}^{R}} = 10\lg {{K}_{R}}$. Выигрыш процедуры КТН (дополнительного пространственного накопления при движении АР) оценивается аналогично: ${{G}^{T}} = 10\lg {{l}_{{KTN}}}$, где ${{l}_{{KTN}}}$ – количество импульсов, сохраняющих взаимную когерентность при отражениях от разных участков донных слоев (задано величиной ~10, что является сильной оценкой снизу, если ориентироваться на экспериментальные данные [1]).
С учетом значений приведенных в табл. 2 параметров, имеем следующие оценки: ${{G}^{f}}\sim 14$ дБ, ${{G}^{R}}\sim 12$ дБ, ${{G}^{T}}\sim 10$ дБ. Таким образом, для алгоритмов, использующих весь обозначенный “арсенал” когерентной обработки, результирующий выигрыш составляет значительную величину ~36 дБ. В данном случае, это алгоритмы a) и d). Для алгоритмов b) и c) согласованные фильтры в каналах АР не моделировались, поэтому выигрыш составляет ~22 дБ.
Анализ выражений для принимаемых сигналов, а также ранее полученные результаты [9, 10] показывают, что отличия от истинных значений величин плотности слоев ${{\tilde {\rho }}_{n}}$ и поперечных скоростей $\tilde {v}_{n}^{{SV}}$ значительно меньше влияют на реализации принимаемых сигналов и, соответственно, на изменчивость целевых функций, нежели отличия величин продольных скоростей $\tilde {v}_{n}^{P}$ и толщин ${{\tilde {h}}_{n}}$ донных слоев. Поскольку величины поисковых интервалов имеют важное значение с точки зрения общего времени процедуры оценивания параметров, это обстоятельство указывает на возможность избирательной оптимизации таких интервалов.
Результаты моделирования приведены на рис. 7. Видно, что наиболее устойчивые оценки достигаются при использовании алгоритма на основе минимизации L2-нормы невязки с процедурой КТН (кривые 1) – смещение и дисперсия отклонений значений всех искомых параметров от их истинных значений минимальны в сравнении с другими алгоритмами. Это объясняется эффективным использованием совокупности процедур когерентного накопления сигналов и значительным повышением выходного ОСШ. Достаточно устойчивые оценки продольной скорости (рис. 7а, 7б) и толщины слоя (рис. 7ж, 7з) получаются при использовании алгоритма на основе нейроноподобной свертки (кривые 4). Вместе с тем, видно, что при оценке плотности породы (рис. 7д, 7е) и поперечной скорости (рис. 7в, 7г) такой алгоритм практически не работает. Это указывает на высокую чувствительность данной целевой функции к вариациям фазовых набегов принимаемых сигналов (они “откликаются” на продольную скорость и толщину слоя) и, напротив, об очень низкой чувствительности к вариациям амплитуд (зависящих от других двух параметров слоя). Целевая функция ${{W}_{{{\text{AMUSIC}}}}}$ и ее обобщения зависят от свободного параметра ${{\varepsilon }}$, который фиксирует заданное отклонение модельного направляющего вектора от истинного (см. раздел 4). Расчеты показали, что эффективность алгоритмов b) и c) существенно зависит от этой величины, что является ожидаемым результатом – слишком малые значения ${{\varepsilon }}$ понижают устойчивость алгоритмов (повышают дисперсии оценок), в то время как высокие значения “загрубляют” расчетную модель и не дают возможности получить малые смещения оценок, хотя при этом они оказываются более устойчивыми. Приведенные на рис. 7 зависимости (кривые 2 и 3) получены при фиксированном значении ${{\varepsilon }} = {{10}^{{ - 5}}}$.
Рис. 7.
Смещение средних значений (верхний ряд) и дисперсия отклонений (нижний ряд) оценок параметров осадочного слоя (слева направо: продольной и поперечной скорости, плотности, толщины) в зависимости от величины входного ОСШ: 1 – алгоритм на основе L2-нормы невязки; 2 – алгоритм на основе обобщенной целевой функции ${{W}_{{{\text{AMUSICR}}}}}$; 3 – алгоритм на основе обобщенной целевой функции ${{W}_{{{\text{AMUSICF}}}}}$; 4 – алгоритм на основе нейроноподобной свертки.

С точки зрения сравнительной оценки эффективности рассмотренных алгоритмов, интерес представляет и другой аспект – сопоставление алгоритмов по величине требуемых объемов и времени вычислений. В рамках представленного здесь моделирования, такого количественного сопоставления нами не проводилось, поскольку в значительной степени эти характеристики зависят от выбранного метода поиска глобального экстремума целевой функции (заданного вида) в многопараметрическом пространстве, который может быть, в свою очередь, оптимизирован с этой точки зрения. Использованная модель донной структуры является достаточно простой, в силу чего подобная оптимизация нами не проводилась, а поиск глобальных экстремумов осуществлялся наиболее простым способом – перебором значений с определенным шагом в общем цикле расчета всех целевых функционалов. Качественно можно отметить, однако, что нейроноподобный алгоритм представляется относительно более быстрым, поскольку он основан на операции простого сравнения (больше/меньше) двух сигналов (принимаемого в смеси с шумом и “чистого” опорного), в то время как проекционные алгоритмы включают в себя процедуры построения оценки КМ сигналов и ее спектрального разложения (в случае большого числа приемных элементов в АР эти процедуры становятся “затратными”). В более реалистичных условиях, сопряженных с учетом большего количества слоев донной структуры, отмеченный вычислительный аспект сравнительного анализа алгоритмов становится, очевидно, важным и требует дополнительного исследования.
Таким образом, рассмотренные алгоритмы оценивания, различные по способу построения целевой функции, обнаруживают существенно различную помехоустойчивость, которая, в свою очередь, оказывается сильно неравномерной по самим параметрам и зависит от того, какой именно параметр подлежит оценке. Следовательно, для предварительной оценки качества того или иного алгоритма с целью выбора наилучшего в конкретных условиях применения, целесообразно проводить подобное моделирование на основе имеющейся априорной информации относительно структуры донных слоев. Полезной представляется также возможность комбинированного подхода, когда различные геоакустические параметры дна оцениваются с использованием различных целевых функций.
6. ЗАКЛЮЧЕНИЕ
В рамках разработанной модели формирования сигналов и помех реверберации для постановки, отвечающей типичной схеме сейсмоакустического зондирования морского дна с буксируемой приемно-излучаемой системой, проведен сравнительный анализ эффективности алгоритмов реконструкции геоакустических параметров. Наравне со стандартным подходом, основанным на использовании среднеквадратичной нормы невязки в качестве целевой функции, рассмотрены два новых подхода, которые используют целевые функции на основе обобщения известного в обработке сигналов проекционного метода MUSIC и на основе нейроноподобной свертки. Ключевой процедурой предварительной обработки принимаемых сигналов в каналах приемной АР является их когерентное частотное и пространственное накопление, способное обеспечить значительное повышение ОСШ для тех сигналов, которые “участвуют” в построении целевых функций при оценивании параметров дна. Это указывает на реальную возможность получения подобных оценок для относительно глубоких слоев, отраженные сигналы от которых на фоне шумов оказываются слишком слабыми для решения поставленной задачи без использования такой процедуры.
Методом стохастического моделирования исследована устойчивость алгоритмов в терминах среднего смещения оценок и дисперсии их отклонений от истинных значений в зависимости от величины входного ОСШ. Наибольший интерес, очевидно, эти зависимости представляют в области малых (отрицательных) значений ОСШ, при которых оценка параметров практически невозможна без реализации дополнительного выигрыша путем когерентной обработки. Показано, что наилучшую помехоустойчивость в рамках данной постановки задачи моделирования обнаруживает алгоритм на основе стандартного функционала невязки в виде L2-нормы, но при условии выполнения процедуры когерентного накопления “сжатых” импульсов на выходе согласованных фильтров по элементам АР и по траектории ее движения как целого. Целевые функции адаптивного алгоритма AMUSIC также показывают относительно малые смещения оценок, однако, дисперсия отклонений оценки при самых малых ОСШ оказывается относительно большой. Дополнительным ресурсом повышения эффективности таких алгоритмов является использование обобщений вида (14) при достаточно большом наборе парциальных целевых функций (в данном случае мы ограничились только двумя функциями, рассчитанными для двух различных частот и расстояний между источником и АР). При условии использования широкополосного сигнала выбор заметно большего числа частот представляется наиболее практичным подходом к построению обобщенного функционала невязки, который может рассматриваться как альтернатива частотному накоплению в других алгоритмах. Наконец, функционал невязки в виде нейроноподобной свертки демонстрирует неоднозначный результат: он обеспечивает малую дисперсию оценки скорости продольной волны и толщины слоя при низких значениях ОСШ, но при этом оценка такого важного, с точки зрения сейсморазведки, параметра как плотность, имеет относительно низкое качество даже при высоких значениях ОСШ.
В целом, полученные результаты указывают на то, что заранее сделать однозначный вывод относительно эффективности той или иной целевой функции и алгоритма оценивания не представляется возможным. Помимо различного “устройства” самих функционалов невязки, принципиальное влияние оказывает также величина достигаемого выигрыша когерентной обработки принимаемых сигналов, которая может быть разной для разных алгоритмов. С точки зрения приложений, интерес представляет также вывод о целесообразности комбинированного подхода к решению задачи, в рамках которого геоакустические параметры оцениваются с использованием различных целевых функций, корректный выбор которых требует предварительного моделирования. Такое моделирование и сравнительная оценка эффективности алгоритмов могут быть реализованы на основе имеющейся априорной информации относительно структуры донных слоев, которая, как правило, известна с точностью до некоторых интервалов искомых значений, а сами эти интервалы “разумно” ограничивают область формирования гипотез относительно значений тех или иных параметров.
Исследование по разработке алгоритмов оценивания параметров и моделированию их помехоустойчивости (разделы 4, 5) выполнено в рамках базовой части государственного задания ННГУ (тема № 0729-2020-0037); разработка моделей сигналов и помех реверберации (разделы 2, 3) выполнена в рамках государственного задания ИПФ РАН (тема № 0030-2021-0009).
Список литературы
Лазарев В.А., Малеханов А.И., Мерклин Л.Р., Романова В.И., Таланов В.И., Хилько А.И. Когерентное сейсмоакустическое профилирование морского дна с использованием широкополосных сигналов // Океанология. 2013. Т. 53. № 6. С. 843–850.
Калинина В.И., Смирнов И.П., Малеханов А.И., Хилько А.И. Когерентная морская сейсмоакустика: новые подходы к реконструкции структуры донных слоев в шельфовых акваториях // Известия РАН. Сер. физ. 2017. Т. 81. № 8. С. 1020–1027.
Сейсморазведка. Справочник геофизика / Под ред. Гурвича И.И., Номоконова В.П. М.: Недра, 1981. 464 с.
Ампилов Ю.П., Барков А.Ю., Яковлев И.В., Филиппова К.Е., Приезжев И.И. Почти все о сейсмической инверсии. Часть 1 // Технологии сейсморазведки. 2009. № 4. С. 3–16.
Яковлев И.В., Ампилов Ю.П., Филиппова К.Е. Почти все о сейсмической инверсии. Часть 2 // Технологии сейсморазведки. 2011. № 1. С. 5–15.
Jiang Y.-M., Chapman N.R., Gerstof P. Short range travel time geoacoustic inversion with vertical line array // J. Acoust. Soc. Am. 2008. V. 124. № 3. Pt. 2. EL135–140.
Белов А.И., Кузнецов Г.Н. Оценка акустических параметров модели дна в мелком море с использованием априорной геолого-геофизической информации и преобразования Вигнера // Акуст. журн. 2014. Т. 60. № 2. С. 190–195.
Смирнов И.П., Калинина В.И., Хилько А.И. Восстановление параметров морского дна при когерентном сейсмоакустическом зондировании. I. Решающие правила // Акуст. журн. 2018. Т. 64. № 1. С. 46–55.
Смирнов И.П., Калинина В.И., Хилько А.И. Восстановление параметров морского дна при когерентном сейсмоакустическом зондировании. II. Анализ робастности // Акуст. журн. 2018. Т. 64. № 2. С. 207–216.
Калинина В.И., Смирнов И.П., Хилько А.И., Хилько А.А. Восстановление параметров морского дна при когерентном сейсмоакустическом зондировании. III. Накопление сигналов и подавление шумов // Акуст. журн. 2019. Т. 65. № 1. С. 10–21.
Dosso S.E., Dettmer J. Bayesian matched-field geoacoustic inversion // Inverse Problems. 2001. V. 27. P. 055009 (23p).
Лебедев А.В., Малеханов А.И. Когерентная сейсмоакустика // Изв. вузов. Радиофизика. 2003. Т. 66. № 7. С. 579–597.
Бреховских Л.М., Лысанов Ю.П. Теоретические основы акустики океана. М.: Наука, 2007. 370 с.
Rice J.K., White J.S. Norms for smoothing and estimation // SIAM Rev. 1964. № 6. P. 243–256.
Малышкин Г.С., Сидельников Г.Б. Оптимальные и адаптивные методы обработки гидроакустических сигналов (обзор) // Акуст. журн. 2014. Т. 60. № 5. С. 526–545.
Сазонтов А.Г., Малеханов А.И. Согласованная пространственная обработка сигналов в подводных звуковых каналах (обзор) // Акуст. журн. 2015. Т. 61. № 2. С. 233–253.
Schmidt R.O. Multiple emitter location and signal parameter estimation // IEEE Trans. Antennas and Propagation. 1986. V. 34. № 3. P. 276–280.
Сазонтов А.Г., Смирнов И.П. Локализация источника в акустическом волноводе с неточно известными параметрами с использованием согласованной обработки в модовом пространстве // Акуст. журн. 2019. Т. 65. № 4. С. 540–550.
Khobotov A., Khilko A., Yakhno V. Analysis of advantages of neuron-like systems in the procedure of signal comparison-measure calculation // Optical Memory & Neural Networks (Information Optics). 2008. № 5. P. 892–898.
Хоботов А.Г., Хилько А.И., Романова В.И. Использование нейросетевых структур свободной динамики с контекстно-зависимыми параметрами для наблюдения в неоднородных нестационарных средах // Известия вузов. Радиофизика. 2013. Т. LVI. № 2. С. 104–124.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал