Известия РАН. Энергетика, 2019, № 5, стр. 66-79
Поверхностный эффект в коаксиальных кабелях импульсных установок
Б. Э. Фридман 1, *, М. В. Медведев 1
1 Акционерное общество “НИИЭФА им. Д.В. Ефремова”
Санкт-Петербург, Россия
* E-mail: fridman@sintez.niiefa.spb.su
Поступила в редакцию 05.09.2019
После доработки 21.10.2019
Принята к публикации 23.10.2019
Аннотация
В статье представлены результаты изучения поверхностного эффекта в коаксиальных кабелях импульсных установок. Выводятся аналитические выражения для скиновых параметров коаксиальной линии передачи сигналов и даны методы экспериментального измерения этих параметров. Рассматриваются переходные процессы в длинных линиях и описаны методы расчета переходных процессов в электрических цепях с такими линями. Измерения импульсных и высокочастотных сигналов в коаксиальных кабелях подтвердили корректность предложенных математических моделей и методов расчета.
ВВЕДЕНИЕ
Коаксиальные линии передачи применяются в импульсных установках. На основе коаксиальных проводников выполняются коаксиальные длинные линии мощных генераторов импульсных токов. Коаксиальные кабели используются в линях передачи высоковольтных импульсов для запуска элементов мощных импульсных установок и для измерений.
Основной причиной потерь энергии и искажения формы импульсов тока и напряжения в коаксиальных линиях передачи является явление скин-эффекта в проводниках. Явление скин-эффекта в коаксиальных линиях передачи изучалось ранее [1–4]. Цилиндрическая симметрия коаксиальных токопроводов позволяет выразить распределение поля в металле коаксиальных цилиндрических проводников с помощью функций Бесселя (Ханкеля) и использовать это при вычислении распространения волн тока и напряжения вдоль линии [2, 3]. В [2] такой анализ выполнен для проникновения в металл плоской электромагнитной волны, без учета кривизны поверхностей цилиндрических проводников. В [3] использовано асимптотическое представление функций Бесселя (Ханкеля) (первое приближение, соответствующее плоской волне поля) для оценки влияния поверхностного эффекта на искажение фронта импульса напряжения в коаксиальном кабеле.
Ранее в [5, 6] был применен метод пограничного слоя для анализа проникновения электромагнитного поля в массивные проводники произвольной формы. Этот метод определяет асимптотическое разложение падения напряжения на массивных проводниках.
(1)
${{U}_{S}}(t) = {{L}_{e}}\frac{{dI}}{{dt}} + S\frac{d}{{dt}}\int\limits_0^t {\frac{{I(\theta )}}{{\sqrt {t - \theta } }}d\theta } + {{R}_{S}}I(t) + ... = {{L}_{e}}\frac{{dI}}{{dt}} + S\int\limits_0^t {\frac{{I{\kern 1pt} '(\theta )}}{{\sqrt {t - \theta } }}d\theta } + {{R}_{S}}I(t) + ...,$(2)
$S = \sqrt {\frac{{{{\mu }_{0}}}}{{\pi {{\gamma }_{m}}}}} \int\limits_\Lambda {{\mathbf{b}}({\mathbf{r}}) \cdot {\mathbf{dl}}} ,$(3)
${{R}_{S}} = \frac{1}{{{{\gamma }_{m}}}}\int\limits_\Lambda {\frac{{({{k}_{2}} - {{k}_{1}})(b_{1}^{2} - b_{2}^{2})}}{{2b}}dl} ,$Параметры S и RS могут быть рассчитаны и измерены, применение этих параметров для анализа переходных процессов в электрических цепях с массивными проводниками показано в [7, 8].
В настоящей работе рассматривается применение соотношения (1) и скиновых параметров S и RS для анализа переходных процессов в цепях с коаксиальными кабелями. Изучаются методы измерения скиновых параметров, дана оценка влияния скиновых параметров на искажение фронта импульсов напряжения или тока при распространении электромагнитной волны по коаксиальному кабелю.
СКИНОВЫЕ ПАРАМЕТРЫ КОАКСИАЛЬНЫХ ПРОВОДНИКОВ
В коаксиальных сплошных проводниках линии плотности тока параллельны оси кабеля, ток распределен равномерно по цилиндрическим поверхностям внутреннего и наружного проводника, путь интегрирования в (2) и (3) проходит параллельно оси кабеля по наружной поверхности внутреннего проводника и внутренней поверхности внешнего проводника. Для внутреннего проводника ${{k}_{1}} = 0,{{k}_{2}} = r_{1}^{{ - 1}},$ ${{b}_{1}} = \frac{1}{{2\pi {{r}_{1}}}},{{b}_{2}} = 0;$ для наружного проводника ${{k}_{1}} = 0,{{k}_{2}} = - r_{2}^{{ - 1}},$ ${{b}_{1}} = \frac{1}{{2\pi {{r}_{2}}}},{{b}_{2}} = 0,$ где ${{r}_{{{\kern 1pt} 1}}}$ – внешний радиус внутреннего проводника и ${{r}_{2}}$ – внутренний радиус внешнего проводника.
Соотношения (2) и (3) позволяют определить скиновые параметры внутреннего проводника кабеля длиной l
Линейные скиновые параметры коаксиального кабеля (то есть значения скиновых параметров, приходящихся на единицу длины кабеля)
(4)
$S{\kern 1pt} ' = \frac{{{{S}_{{{\text{in}}}}} + {{S}_{{{\text{ext}}}}}}}{l} = \frac{1}{{2\pi }}\sqrt {\frac{{{{\mu }_{0}}}}{{\pi {{\gamma }_{m}}}}} \left( {\frac{1}{{{{r}_{1}}}} + \frac{1}{{{{r}_{2}}}}} \right),$(5)
$R_{S}^{'} = \frac{{{{R}_{{S,{\text{in}}}}} + {{R}_{{S,{\text{ext}}}}}}}{l} = \frac{1}{{4\pi {{\gamma }_{m}}}}\left( {\frac{1}{{r_{1}^{2}}} - \frac{1}{{r_{2}^{2}}}} \right).$В настоящей работе результаты исследования проверялись в экспериментах с образцами трех коаксиальных кабелей, изготавливаемых в России, характеристики которых приведены в табл. 1.
Таблица 1.
Характеристики коаксиальных кабелей
| Тип кабеля | РК50-2-12 | РК50-7-212) | ФКП3) |
|---|---|---|---|
| Внутренняя изоляция | Полиэтилен | Фторопласт | Фторопласт |
| Наружный радиус внутреннего проводника r1, мм | 0.36 | 1.08 | 4.62 |
| Внутренний радиус наружного проводника r2, мм | 1.1 | 3.5 | 6.3 |
| Волновое сопротивление, $\sqrt {{{L{\kern 1pt} '} \mathord{\left/ {\vphantom {{L{\kern 1pt} '} {C{\kern 1pt} '}}} \right. \kern-0em} {C{\kern 1pt} '}}} ,\,\,{\text{Ом}}$ | 50 ± 2 | 50 ± 2 | 12.3 |
| Линейная емкость, $C{\kern 1pt} ',\,\,{{{\text{пФ}}} \mathord{\left/ {\vphantom {{{\text{пФ}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | 100 | 94 | 408.8 |
| Коэффициент укорочения, VF | 1.52 | 1.41 | 1.41 |
| Скиновый параметр первой аппроксимации1) $S{\kern 1pt} ',\,\,{{{\text{Ом}}\sqrt {\text{с}} } \mathord{\left/ {\vphantom {{{\text{Ом}}\sqrt {\text{с}} } {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | 56.03 × 10–6 | 16.19 × 10–6 | $4.953 \times {{10}^{{ - 6}}}$ |
| Скиновый параметр второй аппроксимации1)$R_{S}^{'},\,\,{{{\text{Ом}}} \mathord{\left/ {\vphantom {{{\text{Ом}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | $4.335 \times {{10}^{{ - 4}}}$ | $1.09 \times {{10}^{{ - 3}}}$ | $2.964 \times {{10}^{{ - 5}}}$ |
1) Значения скиновых параметров S ' и $R_{S}^{'}$ рассчитаны по формулам (4) и (5) для цилиндрических сплошных проводников. 2) Медные проволоки кабеля РК50-7-21 покрыты серебром. 3) Внутренний проводник кабеля ФКП выполнен в виде плетенки.
ТЕЛЕГРАФНЫЕ УРАВНЕНИЯ КОАКСИАЛЬНОГО КАБЕЛЯ СО СКИНОВЫМИ ПОТЕРЯМИ
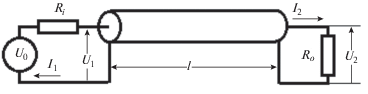
Телеграфные уравнения коаксиального кабеля со скином (рис. 1)
(6)
$\left\{ \begin{gathered} \frac{{\partial I}}{{\partial x}} + C{\kern 1pt} '\frac{{\partial U}}{{\partial t}} = 0, \hfill \\ \frac{{\partial U}}{{\partial x}} + L{\kern 1pt} '\frac{{\partial I}}{{\partial t}} + S{\kern 1pt} '\int\limits_0^t {\frac{{I{\kern 1pt} '(\theta )}}{{\sqrt {t - \theta } }}d\theta } + R_{S}^{'}I + ... = 0, \hfill \\ {{\left. {\left( {U + {{R}_{i}}I} \right)} \right|}_{{x = 0}}} = {{U}_{0}}\left( t \right),\,\,\,{{\left. {\left( {U - {{R}_{o}}I} \right)} \right|}_{{x = l}}} = 0,\,\,\,{{\left. U \right|}_{{t = 0}}} = 0,\,\,\,{{\left. I \right|}_{{t = 0}}} = 0, \hfill \\ \end{gathered} \right.$В частотной области уравнения длинной линии
(7)
$\left\{ \begin{gathered} \frac{{d\dot {I}}}{{dx}} + j\omega C{\kern 1pt} '\dot {U} = 0, \hfill \\ \frac{{d\dot {U}}}{{dx}} + Z{\kern 1pt} '\dot {I} = 0, \hfill \\ {{\left. {\left( {\dot {U} + {{R}_{i}}\dot {I}} \right)} \right|}_{{x = 0}}} = {{{\dot {U}}}_{0}},\,\,\,\,{{\left. {\left( {\dot {U} - {{R}_{o}}\dot {I}} \right)} \right|}_{{x = l}}} = 0, \hfill \\ \end{gathered} \right.$(8)
$Z{\kern 1pt} '\left( \omega \right) = j\omega L{\kern 1pt} '\,\, + \sqrt {j\pi \omega } S{\kern 1pt} '\,\, + R_{S}^{'} + ....$При выводе (7) и (8) учитывалось, что преобразование Фурье интеграла $\int_0^t {\frac{{I{\kern 1pt} '\left( \theta \right)}}{{\sqrt {t - \theta } }}d\theta } $ дает в частотной области функцию $\sqrt {j\pi \omega } \dot {I}\left( \omega \right).$ (Приложение 1).
В (8) доля линейного импеданса, вносимого скин-эффектом, составляет $\sqrt {j\pi \omega } S{\kern 1pt} '\,\, + R_{S}^{'}.$ Следует отметить, что в [4] для анализа переходных процессов была предложена похожая аппроксимация для образа Лапласа сопротивления, вносимого скин эффектом в коаксиальных проводниках, в виде $A + B\sqrt s ,$ где s – оператор Лапласа. При этом коэффициент B определялся с помощью асимптотических разложений функций Бесселя и Ханкеля, описывающих проникновение электромагнитного поля в цилиндрические проводники (в первом приближении плоской электромагнитной волны), а коэффициент A определялся эвристическими соображениями и связывался с сопротивлением постоянному току кабеля. Разработанный в [6, 7] метод дает строгое математическое определение скиновых параметров S и RS, как коэффициентов первого и второго приближения в асимптотическом разложении падения напряжения на массивных проводниках (1) и однозначно определяет соотношения (2), (3) для вычисления этих параметров при произвольной геометрии массивных проводников.
Уравнения (6) и (7) могут быть приведены в безразмерную форму заменой переменных $x = \xi l,$ $t = \frac{l}{{{{{v}}_{P}}}}\tau = l\sqrt {L{\kern 1pt} 'C{\kern 1pt} '} \tau ,$ $U = {{U}_{{0,m}}}u,$ ${{U}_{0}} = {{U}_{{0,m}}}{{u}_{0}},$ $I = \frac{{{{U}_{{0,m}}}\sqrt {C{\kern 1pt} '} }}{{\sqrt {L{\kern 1pt} '} }}i,$ где ${{{v}}_{P}} = \frac{1}{{\sqrt {L{\kern 1pt} 'C{\kern 1pt} '} }}$ – скорость распространения электромагнитной волны в кабеле, U0,m – характерное или максимальное напряжение источника сигнала.
(9)
$\left\{ \begin{gathered} \frac{{\partial i}}{{\partial \xi }} + \frac{{\partial u}}{{\partial \tau }} = 0, \hfill \\ \frac{{\partial u}}{{\partial \xi }} + \frac{{\partial i}}{{\partial \tau }} + s\int\limits_0^t {\frac{{i{\kern 1pt} '(\theta )}}{{\sqrt {\tau - \theta } }}d\theta } + {{r}_{S}}i + ... = 0 \hfill \\ {{\left. {\left( {u + {{r}_{i}}i} \right)} \right|}_{{\xi = 0}}} = {{u}_{0}}\left( \tau \right),\,\,\,\,{{\left. {\left( {u - {{r}_{o}}i} \right)} \right|}_{{\xi = 1}}} = 0,\,\,\,\,{{\left. u \right|}_{{\tau = 0}}} = 0,\,\,\,\,{{\left. i \right|}_{{\tau = 0}}} = 0. \hfill \\ \end{gathered} \right.$(10)
$\left\{ \begin{gathered} \frac{{d\dot {i}}}{{d\xi }} + j\varpi \dot {u} = 0, \hfill \\ \frac{{d\dot {u}}}{{d\xi }} + \zeta \dot {i} = 0, \hfill \\ {{\left. {\left( {\dot {u} + {{r}_{i}}\dot {i}} \right)} \right|}_{{\xi = 0}}} = {{{\dot {u}}}_{0}}\left( \varpi \right),\,\,\,\,{{\left. {\left( {\dot {u} - {{r}_{o}}\dot {i}} \right)} \right|}_{{\xi = 1}}} = 0. \hfill \\ \end{gathered} \right.$ПРИМЕНЕНИЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ ДЛЯ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПЯХ С КОАКСИАЛЬНЫМИ КАБЕЛЯМИ С УЧЕТОМ СКИНОВЫХ ПОТЕРЬ
Уравнения (10) сводятся к краевой задаче для обыкновенного дифференциального уравнения
(11)
$\left\{ \begin{gathered} \frac{{{{d}^{2}}\dot {u}}}{{d{{\xi }^{2}}}} - {{\gamma }^{2}}\dot {u} = 0, \hfill \\ {{\left. {\left( {\dot {u} - \frac{{{{r}_{i}}}}{\zeta }\frac{{d\dot {u}}}{{d\xi }}} \right)} \right|}_{{\xi = 0}}} = {{{\dot {u}}}_{0}},\,\,\,\,{{\left. {\left( {\dot {u} + \frac{{{{r}_{o}}}}{\zeta }\frac{{d\dot {u}}}{{d\xi }}} \right)} \right|}_{{\xi = 1}}} = 0, \hfill \\ \end{gathered} \right.$Решение краевой задачи (11) дает образ Фурье напряжения в длинной линии
(12)
$\dot {u}\left( {\xi ,\varpi } \right) = \frac{{{{{\dot {u}}}_{0}}\zeta \left[ {\left( {\zeta - {{r}_{o}}\gamma } \right)\exp \left[ { - \gamma \left( {1 - \xi } \right)} \right] - \left( {\zeta + {{r}_{o}}\gamma } \right)\exp \left[ {\gamma \left( {1 - \xi } \right)} \right]} \right]}}{{\left( {\zeta - {{r}_{i}}\gamma } \right)\left( {\zeta - {{r}_{o}}\gamma } \right)\exp \left( { - \gamma } \right) - \left( {\zeta + {{r}_{i}}\gamma } \right)\left( {\zeta + {{r}_{o}}\gamma } \right)\exp \left( \gamma \right)}}.$(13)
$\dot {i}\left( {\xi ,\varpi } \right) = - \frac{1}{\zeta }\frac{{d\dot {u}}}{{d\xi }} = - \frac{{{{{\dot {u}}}_{0}}\gamma \left[ {\left( {\zeta - {{r}_{o}}\gamma } \right)\exp \left[ { - \gamma \left( {1 - \xi } \right)} \right] + \left( {\zeta + {{r}_{o}}\gamma } \right)\exp \left[ {\gamma \left( {1 - \xi } \right)} \right]} \right]}}{{\left( {\zeta - {{r}_{i}}\gamma } \right)\left( {\zeta - {{r}_{o}}\gamma } \right)\exp \left( { - \gamma } \right) - \left( {\zeta + {{r}_{i}}\gamma } \right)\left( {\zeta + {{r}_{o}}\gamma } \right)\exp \left( \gamma \right)}}.$Пусть T – длительность изучаемого процесса, $n = {{2}^{m}},$ m – целое число и $\Delta \varpi = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } T}} \right. \kern-0em} T}.$ Тогда прообраз Фурье напряжения $u\left( {\xi ,\tau } \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {\dot {u}\left( {\xi ,\varpi } \right)\exp \left( {\varpi \tau } \right)d\varpi } $ может быть вычислен в моменты времени ${{\tau }_{k}} = k\Delta \tau ,$ $k = 0,1,...,n,$ $\Delta \tau = {T \mathord{\left/ {\vphantom {T n}} \right. \kern-0em} n}$ суммированием
(14)
$\begin{gathered} {{u}_{k}} = u\left( {\xi ,k\Delta \tau } \right) = \frac{{\Delta \varpi }}{{2\pi }}\sum\limits_{p = - n}^{n - 1} {\dot {u}\left( {\xi ,p\Delta \varpi } \right){\kern 1pt} \exp \left( {j\frac{{2\pi }}{n}kp} \right)} = \sqrt {\frac{{\Delta \varpi }}{{2\pi \Delta \tau }}} \left[ {\frac{1}{{\sqrt n }}\sum\limits_{p = - n}^{n - 1} {\dot {u}\left( {\xi ,p\Delta \varpi } \right){\kern 1pt} \exp \left( {j\frac{{2\pi }}{n}kp} \right)} } \right], \\ {{u}_{k}} = u\left( {\xi ,k\Delta \tau } \right) = \frac{{\sqrt n }}{T}\left[ {\frac{1}{{\sqrt n }}\sum\limits_{p = - n}^{n - 1} {\dot {u}\left( {\xi ,p\Delta \varpi } \right)\exp \left( {j\frac{{2\pi }}{n}kp} \right)} } \right]. \\ \end{gathered} $Численные значения выражения в квадратных скобках в (14) вычисляются стандартными алгоритмами Быстрого Преобразования Фурье (БПФ).
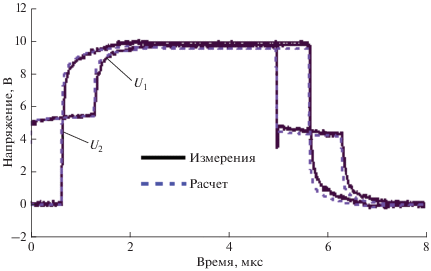
На рисунке 2 представлены результаты измерения и расчета формы импульса напряжения на входе и выходе кабеля в схеме рис. 1. Этот пример показывает удовлетворительное совпадение результатов расчета с реальным переходным процессом в коаксиальном кабеле РК50-2-11.
ИЗМЕРЕНИЕ СКИНОВОГО ПАРАМЕТРА КОАКСИАЛЬНЫХ КАБЕЛЕЙ НА РЕЗОНАНСНЫХ ЧАСТОТАХ
Выражения (4), (5) и (6) основаны на представлении коаксиального кабеля в виде сплошных цилиндрических проводников. Реальные коаксиальные кабели устроены по-другому. Внутренний проводник кабеля представляет собой, как правило, сердечник, изготовленный из набора тонких скрученных металлических проволок, а внешний проводник образован медной плетенкой. Поэтому, практически важной задачей является измерение скиновых параметров реальных коаксиальных кабелей $S{\kern 1pt} '$ and $R_{S}^{'}$.
Скиновые параметры $S{\kern 1pt} '$ and $R_{S}^{'}$ являются коэффициентами асимптотических разложений (1); их доля в падении напряжения на кабеле, как правило, мала по сравнению с долей, вносимой $C{\kern 1pt} '{\text{и}}\,L{\kern 1pt} '.$ Поэтому скиновые параметры возможно измерить в электрических режимах, при которых влияние емкости и индуктивности кабеля незначительно. Такие режимы возникают на резонансных частотах, когда в кабеле возникают стоячие волны напряжения и тока. При ограниченной длине кабеля такие резонансные частоты достаточно велики и доля падения напряжения, вносимая скиновым параметром второго приближения $R_{S}^{'}$ при измерении, мала, что не позволяет измерить $R_{S}^{'}.$ Однако скиновый параметр первого приближения $S{\kern 1pt} '$ может быть надежно измерен на резонансных частотах.
В приложении 2 показано, что для закороченного коаксиального кабеля на частотах, при которых в начале кабеля наблюдается резонанс токов, ${{\varpi }_{k}} = k\pi $ ($k = 1,\,2,\,...$) вещественная и мнимая части импеданса
(15)
$\operatorname{Re} \left[ {z\left( {{{\varpi }_{k}}} \right)} \right] \approx \pi \sqrt {\frac{k}{8}} s + \frac{{{{r}_{S}}}}{2},\,\,\,\,\operatorname{Im} \left[ {z\left( {{{\varpi }_{k}}} \right)} \right] \approx \pi \sqrt {\frac{k}{8}} s.$В этом же приложении показано, что на частотах, при которых в начале кабеля наблюдается резонанс напряжений, ${{\varpi }_{m}} = \frac{{2m - 1}}{2}\pi $ ($m = 1,\,2,\,...$) вещественная и мнимая части адмиттанса
(16)
$\operatorname{Re} \left[ {y\left( {{{\varpi }_{m}}} \right)} \right] \approx \pi \sqrt {\frac{{2m - 1}}{{16}}} s + \frac{{{{r}_{S}}}}{2},\,\,\,\,\operatorname{Im} \left[ {y\left( {{{\varpi }_{m}}} \right)} \right] \approx \pi \sqrt {\frac{{2m - 1}}{{16}}} s.$В физических переменных резонанс токов имеет место при частоте ${{f}_{k}} = k\frac{{{{{v}}_{P}}}}{{2l}},$ $k = 1,\,2,\,...$. С учетом того, что ${{r}_{S}}\,\, \ll \,\,s$ получим из (15)
где ${{R}_{k}} = \operatorname{Re} \left[ {Z\left( {{{f}_{k}}} \right)} \right]$ – сопротивление, вещественная часть импеданса кабеля на частоте резонанса токов ${{f}_{k}}.$Аналогично, из (16) следует, что при резонансе напряжений, при ${{f}_{m}} = \frac{{\left( {2m - 1} \right){{{v}}_{P}}}}{{4l}},$ $m = 1,\,2,\,...$ скиновый параметр
(18)
$S{\kern 1pt} ' \approx \frac{{4{{\rho }^{2}}}}{{\pi \sqrt {\left( {2m - 1} \right)l{{{v}}_{p}}} }}{{G}_{m}},$Частотные характеристики отрезков кабеля могут быть измерены приборами, выпускаемыми промышленностью. На рис. 3 и 4 показаны частотные характеристики вещественной и мнимой части импеданса $Z = R + jX$ и адмиттанса $Y = G + jB$ кабеля РК50-7-21, измеренные прибором Precision Impedance Analyzer WK 6530, изготовленного Wayne Kerr Electronics. Результаты вычисления скинового параметра $S{\kern 1pt} '$ по измеренным значениям $R\left( {{{f}_{k}}} \right)$ и $G\left( {{{f}_{m}}} \right)$ представлены на рис. 5.
Рис. 3.
Активное сопротивление R и реактивное сопротивление X отрезка 50 m закороченного кабеля РК50-7-21.
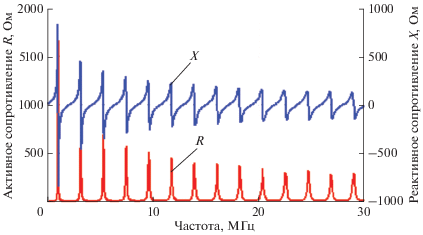
Рис. 4.
Активная проводимость G и реактивная проводимость B отрезка 50 m закороченного кабеля РК50-7-21.
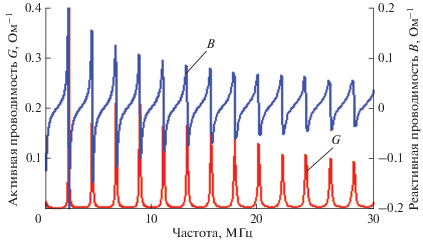
Рис. 5.
Результаты измерений скинового параметра S ', выполненных на отрезке кабеля РК50-7-21 длиной 50 м. Штриховая линия соответствует значению $S{\kern 1pt} ' = 16.19 \times {{10}^{{ - 6}}}\,\,{{{\text{Ом }}{{{\text{с}}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \mathord{\left/ {\vphantom {{{\text{Ом }}{{{\text{с}}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} {{\text{ м}}}}} \right. \kern-0em} {{\text{ м}}}},$ вычисленному по (4) без учета конструктивных особенностей проводников кабеля.
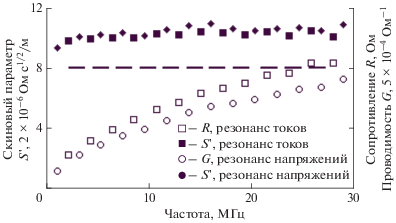
Для измеренного отрезка кабеля РК50-7-21 безразмерные скиновые параметры $s = 0.033,\,\,{{r}_{S}} = 1.09 \times {{10}^{{ - 3}}}$. В соответствии с (15) и (16) доля скинового параметра $R_{S}^{'}$ в измеренных значениях R и G при резонансах на самой низкой частоте ($k = 1,m = 1$) не превышает 2%; при более высоких частотах резонанса это доля уменьшается. Это не позволяет выделить значение скинового параметра второго приближения при таких измерениях.
На рис. 6 и 7 представлены результаты измерения скиновых параметров кабелей РК50-2-12 и ФКП.
Рис. 6.
Результаты измерений скинового параметра S’, выполненных на отрезке кабеля РК50-2-12 длиной 10 м. Штриховая линия соответствует значению $S{\kern 1pt} ' = 5.6 \times {{10}^{{ - 5}}}\,{{{\text{Ом}}\,{{{\text{с}}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \mathord{\left/ {\vphantom {{{\text{Ом}}\,{{{\text{с}}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$, вычисленному по (4) без учета конструктивных особенностей проводников кабеля.
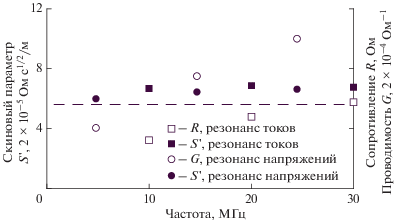
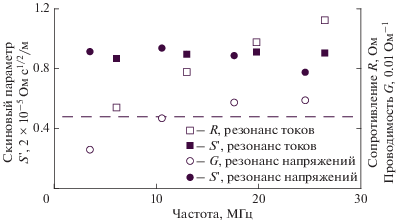
Рис. 7.
Результаты измерений скинового параметра S'’, выполненных на отрезке кабеля ФКП длиной 15.6 м. Штриховая линия соответствует значению $S{\kern 1pt} ' = 0.495 \times {{10}^{{ - 5}}}\,{{\,{\text{Ом}}\,\,{{{\text{с}}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \mathord{\left/ {\vphantom {{\,{\text{Ом}}\,\,{{{\text{с}}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} {\text{м}}}} \right. \kern-0em} {\text{м}}},$ вычисленному по (4) без учета конструктивных особенностей проводников кабеля.
Для исследованных кабелей трех типов измеренные значения S ' превышают расчетные значения S ', вычисленные по (4). Это объясняется тем, что при выводе (4) предполагалось, что коаксиальные проводники образованы сплошными металлическими цилиндрами. В реальных кабелях, выпускаемых промышленностью, внутренний проводник выполнен, как правило, в виде скрутки тонких проводов (РК50-2-12, РК50-7-21); внешний проводник образован плетенкой. Наибольшие отличия между расчетными и измеренными значениями S ' наблюдаются у кабеля ФКП, у которого не только внешний, но и внутренний проводник выполнены в виде плетенки.
Результаты, представленные на рис. 5, 6, 7, свидетельствуют о том, что в пределах точности измерений скиновый параметр S ' практически не зависит от частоты. Это показывает, что, несмотря на сложные и разнообразные конструкции проводников коаксиального кабеля, скиновый параметр S ' является постоянной для каждого кабеля количественной характеристикой, которая не зависит от времени и частоты, и которая позволяет учесть потери в коаксиальном кабеле в широком диапазоне частот и при импульсных переходных процессах. Все это делает целесообразным измерения S ' и применения измеренных значений S ' для исследования переходных процессов в электрических цепях с коаксиальными проводниками.
ВЛИЯНИЕ СКИН-ЭФФЕКТА НА ИСКАЖЕНИЕ ФРОНТА ИМПУЛЬСА НАПРЯЖЕНИЯ
Влияние потерь в кабеле на искажение фронта импульса напряжения, передаваемого по коаксиальному кабелю, изучалось во многих работах, например в [1–4]. Подобная задача рассматривалась для проводов, проходящих над поверхностью земли, с учетом скин-эффекта в проводе и земле [9], [10]. В [2] было построено приближенное линеаризованное решение для образа Лапласа напряжения в кабеле, применение к которому табличных функций обратного преобразования Лапласа позволило выразить во временной области переходную функцию кабельной линии через дополнительную функцию ошибок. Аналогичный метод вычисления может быть применен к (12), (13), описывающих напряжение и ток в частотной области. При этом формула из [2] для переходной функции при согласованной нагрузке $\left( {{{R}_{0}} = \sqrt {\frac{{L{\kern 1pt} '}}{{C{\kern 1pt} '}}} } \right)$ в обозначениях настоящей статьи имеет следующий вид.
(19)
$u\left( {1,\tau } \right) = 1\left( {\tau - 1} \right){\text{erfc}}\left( {\frac{s}{{2\sqrt {\pi \left( {\tau - 1} \right)} }}} \right),$(20)
$u\left( t \right) = 1\left( {t - {{t}_{p}}} \right){\text{erfc}}\left( {\frac{{{{t}_{p}}S{\kern 1pt} '}}{{2L{\kern 1pt} '\sqrt {\pi \left( {t - {{t}_{p}}} \right)} }}} \right),$Формула (20) дает приближенное описание искажений на фронте импульса тока, определяемых скин эффектом в проводниках кабеля.
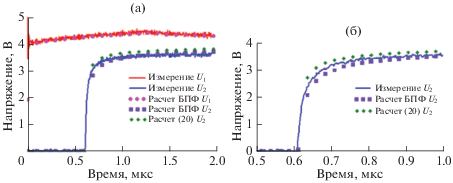
На рис. 8 (a) и (b) показаны измеренные и рассчитанные кривые напряжения на входе и выходе коаксиального кабеля РК50-2-12 длиной 121 м. Расчет выполнялся двумя способами: посредством применения БПФ к (12) и с использованием приближенной формулы (20). Эти графики показывают удовлетворительное совпадение результатов измерений и расчетов.
Рис. 8.
Фронт волны напряжения на входе и выходе кабеля РК50-2-12 длиной 121 м. Амплитуда импульса напряжения, создаваемого источником импульсов 8 В.
В качестве оценки искажения фронта напряжения может быть принят интервал времени, между появлением сигнала на выходе кабеля и достижением уровня этого сигнала, равного половине амплитуды входного сигнала. Учитывая, что обратная функция ${\text{erf}}{{{\text{c}}}^{{ - 1}}}\left( {0.5} \right) = 0.477$ получим, что
(21)
${{\left[ {t - {{t}_{p}}} \right]}_{{u\left( t \right) = 0.5}}} = {{\pi }^{{ - 1}}}{{\left( {\frac{{{{t}_{p}}S{\kern 1pt} '}}{{0.954L{\kern 1pt} '}}} \right)}^{2}},$ЗАКЛЮЧЕНИЕ
Влияние скин-эффекта на переходные процессы в электрических цепях с коаксиальными цилиндрическими проводниками определяется постоянными скиновыми параметрами $S{\kern 1pt} '$ и $R_{S}^{'}$, которые являются коэффициентами асимптотических разложений падения напряжения на проводниках и зависят только от радиусов цилиндрических проводников и проводимости металла.
Переходные процессы в электрических цепях с коаксиальными проводниками могут быть рассчитаны посредством применения БПФ к решению уравнений длинной линии в частотной области со скиновыми параметрами $S{\kern 1pt} '$ и $R_{S}^{'}.$
Скиновый параметр $S{\kern 1pt} '$ коаксиальной линии может быть измерен на частотах резонанса токов или напряжений, при которых влияние емкости и индуктивности на импеданс или адмиттанс длинной линии незначительно. Такие измерения показали, что для выпускаемых промышленностью коаксиальных кабелей измеренное значение $S{\kern 1pt} '$ больше, чем рассчитанное в предположении сплошных цилиндрических проводников. Это объясняется тем, что в реальных коаксиальных кабелях проводники представляют собой набор тонких скрученных металлических проволок или плетенку медных проволок.
Получено удовлетворительное совпадение результатов измерения фронта импульса тока на выходе коаксиального кабеля и расчетов этого фронта с применением измеренных значений $S{\kern 1pt} ',$ выполненных с использованием как БПФ, так и приближенной формулы, учитывающей скин-эффект. Оценка искажения фронта волны напряжения в коаксиальном кабеле пропорциональна квадрату произведения скинового параметра $S{\kern 1pt} '$ на время распространения сигнала ${{t}_{p}}.$
Приложение 1. Преобразование Фурье интеграла $\int_0^t {\frac{{I{\kern 1pt} '(\theta )}}{{\sqrt {t - \theta } }}d\theta .} $
Интеграл $\int_0^t {\frac{{I{\kern 1pt} '(\theta )}}{{\sqrt {t - \theta } }}d\theta } $ представляет собой свертку двух функций $\frac{{dI}}{{dt}}$ и $\frac{1}{{\sqrt t }}.$
(П1.1)
$\int\limits_0^\infty {\left[ {\int\limits_0^t {\frac{{I{\kern 1pt} '(\theta )}}{{\sqrt {t - \theta } }}d\theta } } \right]{{e}^{{ - j\omega t}}}dt} = j\omega \dot {I}\left( \omega \right)\int\limits_0^\infty {\frac{{{{e}^{{ - j\omega t}}}}}{{\sqrt t }}dt.} $Произведем замену переменных $y = j\omega t$ в интеграле
(П1.2)
$\int\limits_0^\infty {\frac{{{{e}^{{ - j\omega t}}}}}{{\sqrt t }}dt} = \frac{1}{{\sqrt {j\omega } }}\int\limits_0^{j\infty } {\frac{{{{e}^{{ - y}}}}}{{\sqrt y }}dy} = \frac{1}{{\sqrt {j\omega } }}\int\limits_0^\infty {\frac{{{{e}^{{ - y}}}}}{{\sqrt y }}dy = \frac{1}{{\sqrt {j\omega } }}\Gamma \left( {\frac{1}{2}} \right) = \sqrt {\frac{\pi }{{j\omega }}} ,} $Подставляя (П1.2) в (П1.1), получим, что преобразование Фурье интеграла $\int_0^t {\frac{{I{\kern 1pt} '\left( \theta \right)}}{{\sqrt {t - \theta } }}d\theta } $ приводит в частотной области к функции $\sqrt {j\pi \omega } \dot {I}\left( \omega \right).$
Приложение 2. Импеданс и адмиттанс коаксиального кабеля на резонансных частотах.
a) Безразмерный импеданс закороченного коаксиального кабеля $z\left( \varpi \right)$ определяется из (12) при ${{r}_{i}} = {{r}_{o}} = 0,\xi = 0.$
(П2.1)
$z\left( \varpi \right) = \frac{{\dot {e}}}{{\dot {i}\left( {0,\varpi } \right)}} = \frac{\zeta }{\gamma }{\text{th}}\left( \gamma \right) = \sqrt {1 + \sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }} + ...} {\text{th}}\left[ {j\varpi \sqrt {1 + \sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }} + ...} } \right],$Учитывая, что s и rs – малые параметры, получим
(П2.2)
$\sqrt {1 + \sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }} + ...} \approx 1 + \frac{1}{2}\left( {\sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }}} \right) = 1 + \varepsilon ,$При частотах ${{\varpi }_{k}} = k\pi ,\,\,\,k = 1,\,2,\,...$ ${\text{th}}\left( {j{{\varpi }_{k}}} \right) = 0$ и импеданс кабеля мал. При этом образуются стоячие волны и имеет место резонанс токов. Используя разложение функции гиперболического тангенса в ряд по степеням малого параметра $j{{\varpi }_{k}}\varepsilon ,$ получим
(П2.3)
$\begin{gathered} z\left( {{{\varpi }_{k}}} \right) = \left( {1 + \varepsilon } \right){\text{th}}\left[ {j{{\varpi }_{k}}\left( {1 + \varepsilon } \right)} \right] = \left( {1 + \varepsilon } \right)\left[ {j{{\varpi }_{k}}\varepsilon - \frac{1}{3}{{{\left( {j{{\varpi }_{k}}\varepsilon } \right)}}^{3}} + ...} \right] \approx j{{\varpi }_{k}}\varepsilon , \\ {\text{или}}\,\,z\left( {{{\varpi }_{k}}} \right) \approx j{{\varpi }_{k}}\varepsilon = \frac{1}{2}\sqrt {j{{\varpi }_{k}}\pi } s + \frac{{{{r}_{S}}}}{2} = \frac{{\pi \sqrt {jk} }}{2}s + \frac{{{{r}_{s}}}}{2} = \pi \sqrt {\frac{k}{8}} s + \frac{{{{r}_{S}}}}{2} + j\pi \sqrt {\frac{k}{8}} s. \\ \end{gathered} $b) В соответствии с (П2.1) безразмерный адмиттанс коаксиального кабеля
(П2.4)
$y\left( \varpi \right) = \frac{1}{{z\left( \varpi \right)}} = \frac{\gamma }{\zeta }{\text{cth}}\left( \gamma \right) = {{\left( {1 + \sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }} + ...} \right)}^{{ - \frac{1}{2}}}}{\text{cth}}\left[ {j\varpi \sqrt {1 + \sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }} + ...} } \right].$Аналогично (П2.2) примем, что $\varepsilon = \frac{1}{2}\left( {\sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }}} \right)$ малый параметр, и получим
(П2.5)
${{\left( {1 + \sqrt {\frac{\pi }{{j\varpi }}} s + \frac{{{{r}_{S}}}}{{j\varpi }} + ...} \right)}^{{ - \frac{1}{2}}}} = {{\left( {1 + 2\varepsilon + ...} \right)}^{{ - \frac{1}{2}}}} \approx \left( {1 - \varepsilon } \right).$При частотах ${{\varpi }_{m}} = \frac{{2m - 1}}{2}\pi ,\,\,m = 1,\,2,\,...,$ ${\text{cth}}\left( {j{{\varpi }_{k}}} \right) = 0$ и адмиттанс кабеля мал. При этом образуются стоячие волны и имеет место резонанс напряжений. Учитывая, что $j{{\varpi }_{m}}\varepsilon $ малый параметр, получим
илиСписок литературы
Kerns Q., Kirsten F., Winningstad C. Pulse Respons of Coaxial Cables. Counting Note // Lawrence Radiation Laboratory, University of Callifornia, Bercley, 1964, File No. CC 2-1A(1).
Wigington R.L., Nahman N.S. Transient Analysis of Coaxial Cables Considering Skin Effect // Proc. IRE 42. 166–174 (Feb. 1957).
Nahman N.S., Holt D.R. Transient Analysis of Coaxial Cables Using the Skin Effect Approximation $A + B\sqrt s $ // IEEE Trans. Circuit Theory, 1972, vol. 19, No. 5, pp. 443–451 (Sept. 1972).
Holt D.R., Nahman N.S. Coaxial-Line Pulse-Response Error Due to a Planar Skin-Effect Approximation // IEEE Trans. on Instrumentation and Measurement, vol. IM-21, No. 4, November 1972, pp. 515–519.
Фридман Б.Э. Скин-эффект в массивных проводниках электроимпульсных установок. I. Электромагнитное поле массивных проводников // ЖТФ. 2002. Т. 72. Вып. 9. С. 44–51.
Фридман Б.Э. Скин-эффект в массивных проводниках электроимпульсных установок. II. Массивные проводники в электрических цепях // ЖТФ. 2002. Т. 72. Вып. 9. С. 52–56.
Fridman B.E. Transients in pulsed electrical circuits with massive conductors // IEEE Trans. Plasma Sci., vol. 34, pp. 1938–1943, May, 2006.
Fridman B. Skin Parameter of Massive Conductors and Transients in Electrical Circuits of Pulsed Power Facilities // IEEE Trans. Plasma Sci., vol. 46, No. 10, 2018, pp. 3273–3278.
Гринберг Г.А., Бонштедт Б.Э. Основы точной теории волнового поля линии передач // ЖТФ. 1954. Т. XXIV. Вып. 1. С. 67–95.
Костенко М.В., Перельман Л.С., Шкарин Ю.Л. Волновые процессы и электрические помехи в многопроводных линиях высокого напряжения. М.: “Энергия”, 1973. 272 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика