Лёд и Снег · 2022 · Т. 62 · № 2
УДК 551.321.84
DOI: 10.31857/S2076673422020133, EDN: EPKDNH
Глобальные гляциологические модели: новый этап в развитии методов прогнозирования
эволюции ледников. Часть 2. Постановка экспериментов и практические приложения
© 2022 г. Т.Н. Постникова1*, О.О. Рыбак2-4
1Московский государственный университет имени М.В. Ломоносова, Москва, Россия; 2Институт водных проблем РАН, Москва,
Россия; 3Субтропический научный центр РАН, Сочи, Россия; 4Филиал Института природно-технических систем, Сочи, Россия
*tasinidze@gmail.com
Global glaciological models: a new stage in the development of methods for predicting glacier evolution.
Part 2. Formulation of experiments and practical applications
T.N. Postnikova1*, O.O. Rybak2-4
1Lomonosov Moscow State University, Moscow, Россия; 2Water Problems Institute of RAS, Moscow, Россия;
3Subtropical Scientific Center of RAS, Sochi, Russia; 4Branch of Institute of Natural and Technical Systems, Sochi, Russia
*tasinidze@gmail.com
Received June 23, 2021 / Revised December 15, 2021 / Accepted April 1, 2022
Keywords: mountain glaciers, glacier modeling, numerical experiments, methods of prediction, climate change.
Summary
Global glacier models provide a new way for studying glaciers on the regional and global scales. They make it possible to
perform predictive experiments - for example, to forecast changes in glaciation and river runoff, and diagnostic ones - to
identify regularities in the behavior of glaciers (a response time to climate change) taking account of their characteristics.
The characteristics and design of global glacier models were described in the first part of the review (see Postnikova T.N.,
Rybak O.O. Global glaciological models: a new stage in the development of methods for predicting glacier evolution.
Part 1. General approach and model architecture. Led i Sneg. Ice and Snow. 2021, 61 (4): 620-636. [In Russian]. doi:
10.31857/S2076673421040111.). In the second part, we present the methods for setting up of numerical experiments
with these models, including model initialization, climate forcing, calibration, and validation procedures. The only way
to provide the climate forcing of a glaciological model on a regional or global scale is to use low-resolution reanalysis
or output of climate modeling on GCMs or RCMs that needs to use a process of scaling to reproduce the local climate
in a complex topography where glaciers are usually located. Calibration of mass balance complements the downscal-
ing of climate forcing for each glacier, and usually it includes parameters responsible for the glacier's response to climate
change. Sampling from the Latin hypercube and Bayesian inversion are some of the methods discussed in this connec-
tion. In this review we present a comparative description of the selected global glaciological models, the results obtained
by both diagnostic and prognostic ones, as well as scale and significance of them. We discuss also ways for further devel-
opment of global glacier models, in particular the inclusion of 3D-modeling and the moraine (debris cover) block. The
difficulties arising in a process of modeling glaciation of a particular mountain region or several regions are noted.
Citation: Postnikova T.N., Rybak O.O. Global glaciological models: a new stage in the development of methods for predicting glacier evolution. Part 2. Formulation
of experiments and practical applications. Led i Sneg. Ice and Snow. 2022, 62 (2): 287-304. [In Russian]. doi: 10.31857/S2076673422020133, edn: epkdnh.
Поступила 23 июня 2021 г. / После доработки 15 декабря 2021 г. / Принята к печати 1 апреля 2022 г.
Ключевые слова: горные ледники, гляциологическое моделирование, численные эксперименты, методы прогнозирования,
изменения климата.
Глобальные гляциологические модели открыли новые возможности для исследования ледников на
региональном и глобальном уровнях. Они позволяют проводить как прогностические эксперименты,
например, предсказывать изменение оледенения и стока рек, так и диагностические - выявлять зако-
номерности поведения ледников (например, время реакции на изменение климата) в зависимости
от их характеристик. Архитектура глобальных гляциологических моделей описана в первой части
обзора. Во второй части представлены методы постановки численных экспериментов на этих моде-
лях, их сравнительная характеристика, основные полученные результаты, их масштаб и значимость.
Обозначены направления развития глобальных гляциологических моделей и сложности, которые воз-
никают при моделировании оледенения в региональном и глобальном масштабах.
Введение
на 0,32 ± 0,08 м [2]. Ожидается, что тающие гор
ные ледники до конца ХХI в. внесут ощутимый
Ледники мира (за исключением ледниковых
вклад в повышение глобального уровня моря [3].
щитов) содержат 158 ± 41 × 103 км³ льда [1], что эк
Горные ледники и современный климат не нахо
вивалентно изменению уровня Мирового океана
дятся в состоянии равновесия, поэтому потеря их
287
Обзоры и хроника
массы в будущем возможна без каких-либо даль
Во второй части статьи рассматриваются: ос
нейших климатических изменений [4, 5]. Ледни
новные приёмы, используемые в тех или иных
ковый сток - важная составляющая речного стока
ГГМ для решения проблемы калибровки ключе
в горных регионах, которая может компенсировать
вых параметров; особенности постановки чис
недостаток пресной воды в тёплые и сухие сезо
ленных экспериментов; методы инициализации,
ны, что важно для населения и экономики, гидро
калибровки и валидации моделей и наиболее зна
энергетики и водных экосистем [6]. Водосборные
чимые результаты их применения, а также слабые
бассейны с ледниковым питанием занимают 26%
места таких моделей и перспективы их развития.
суши за пределами Гренландии и Антарктиды.
На их территории проживает почти 1/3 населения
мира [6]. Эти обстоятельства определяют необходи
Сравнительная характеристика глобальных
мость прогнозов эволюции оледенения и леднико
гляциологических моделей
вого стока на глобальном и региональном уровнях.
Невозможность на современном уровне разви
Рассмотрим основные свойства ГГМ, уча
тия вычислительной техники и численных мето
ствовавших в проекте GlacierMIPI и GlacierMIPII
дов использовать для этой цели сложные трёхмер
(Glacier Model Intercomparison Project) [3]. В про
ные комплексные модели динамики ледников дала
екте GlacierMIPII одиннадцать ГГМ были запу
старт развитию во многом компромиссного подхо
щены при одинаковых начальных условиях (объ
да, реализованного в применении глобальных гля
ёме льда), климатических моделях и сценариях
циологических моделей (ГГМ).
для получения прогнозов изменения оледене
Для постановки прогностических экспери
ния в XXI в., а также оценок неопределённостей.
ментов на ГГМ необходима её настройка: подбор
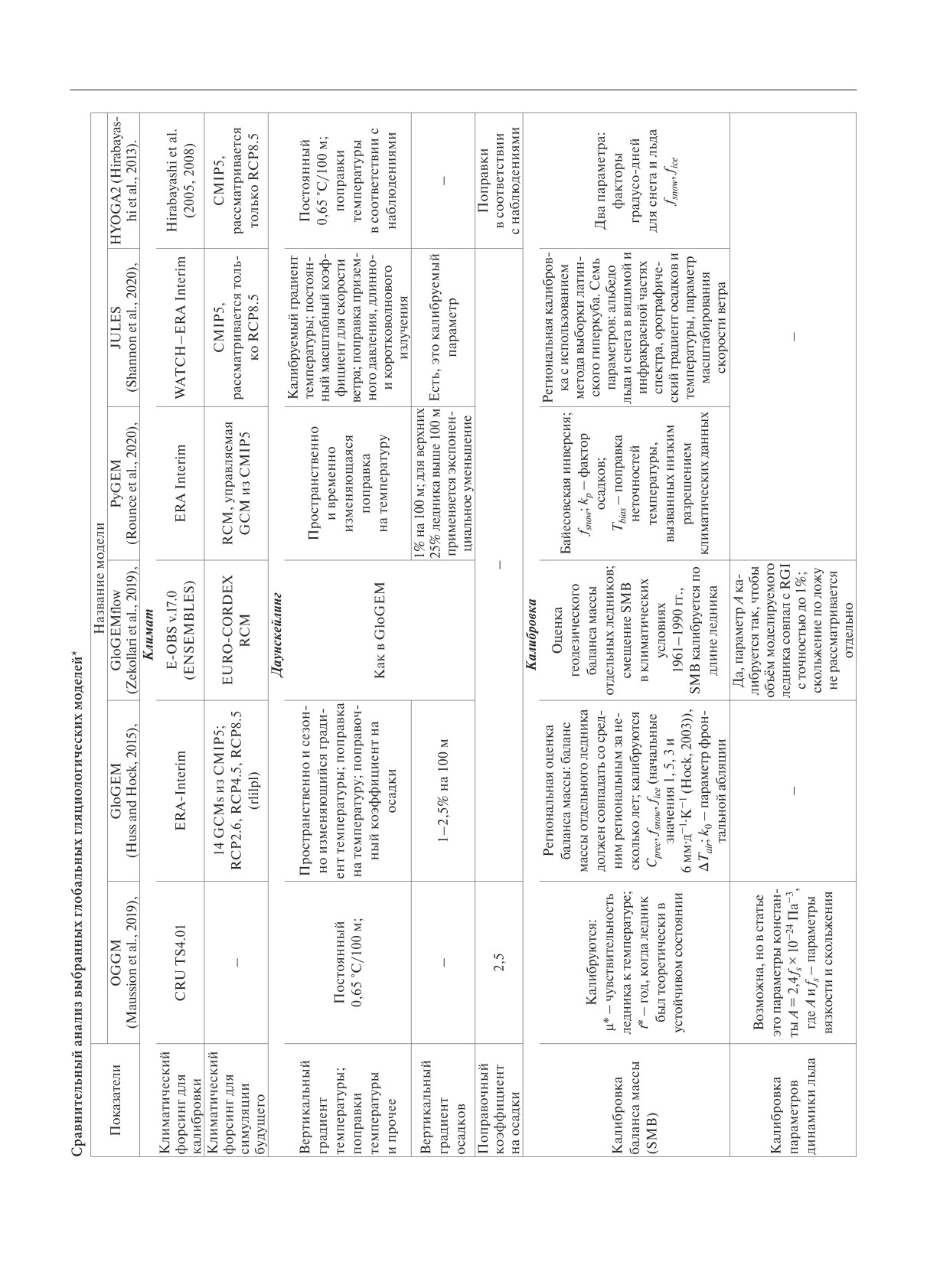
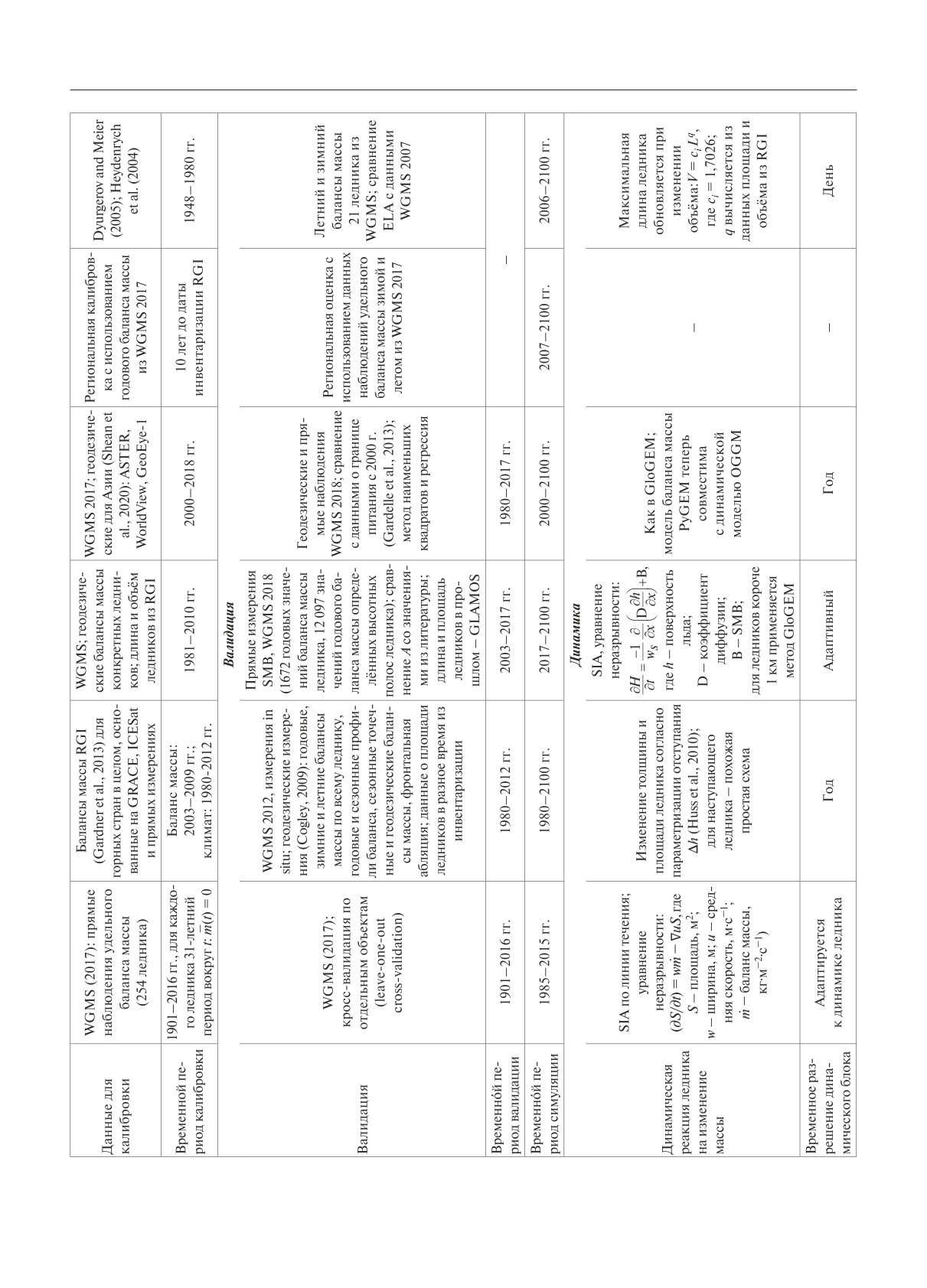
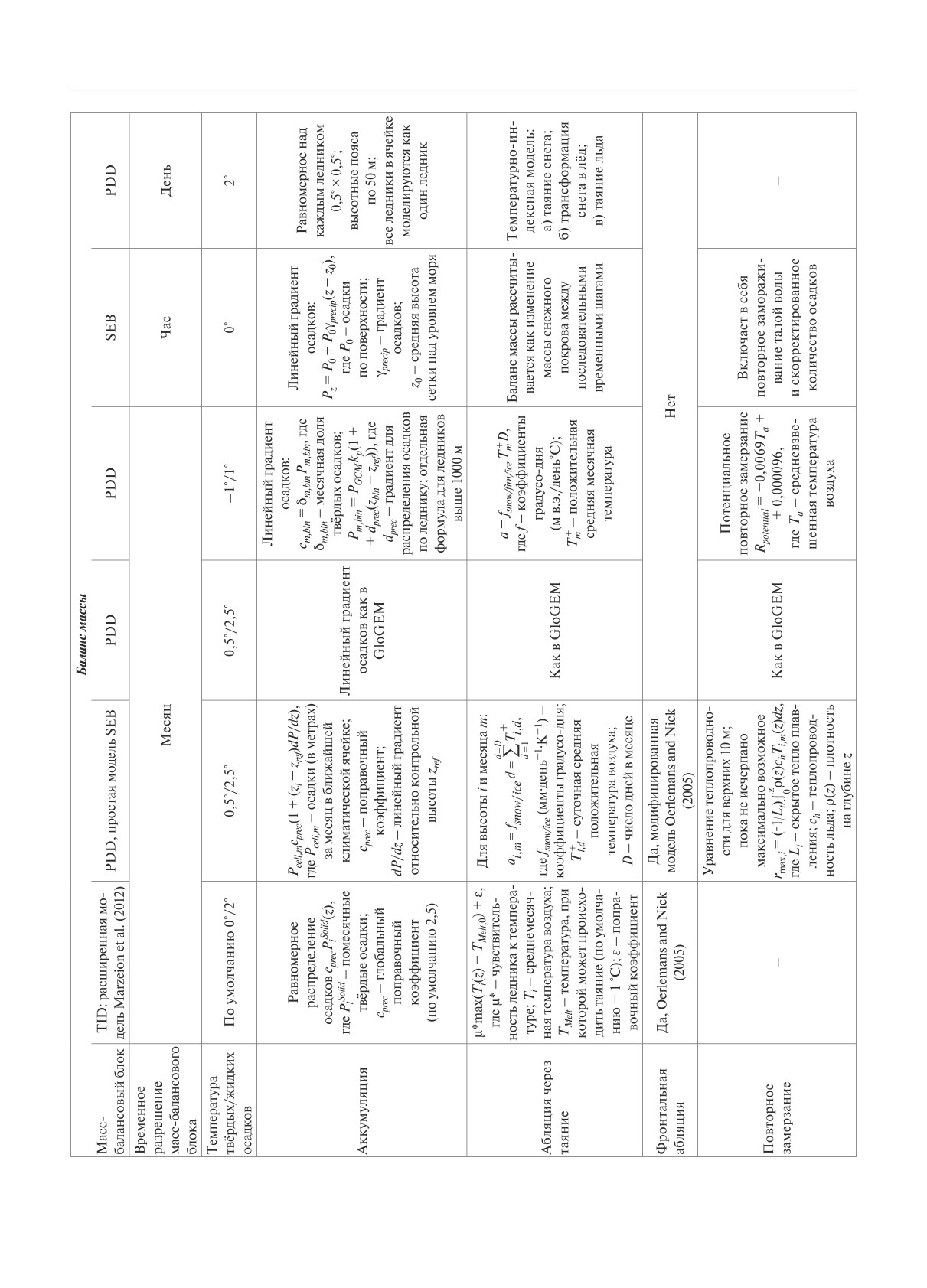
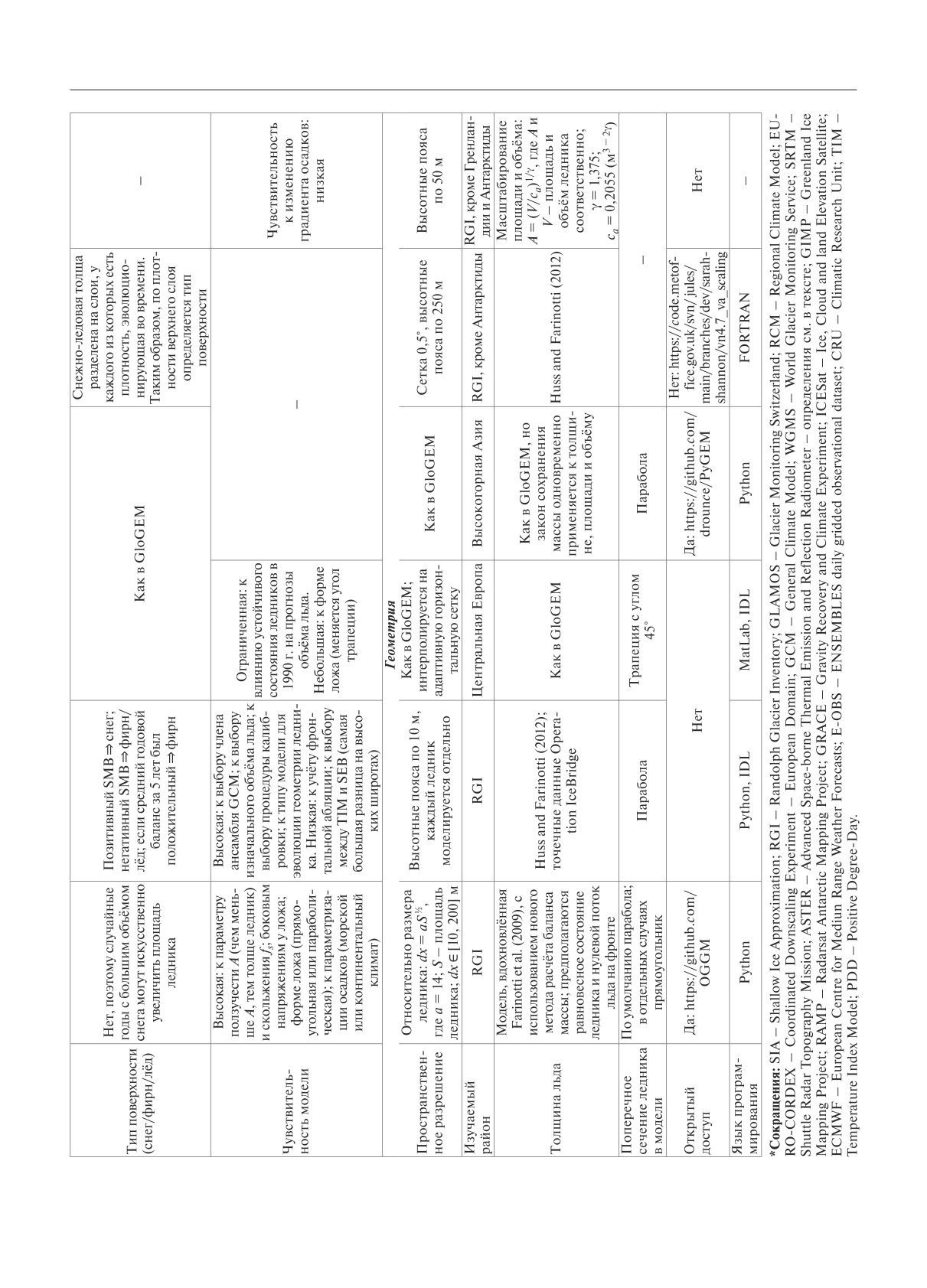
Характеристики шести наиболее значимых, на
начальных условий и калибровка ключевых мо
наш взгляд, моделей (OGGM [8], GloGEM [10],
дельных параметров (см. рис. 1 части 1 обзора). Ва
GloGEMflow [9], PyGEM [7], JULES [12],
лидация инициализированной и откалиброванной
HYOGA2 [13]) представлены в таблице.
модели состоит в том, что результаты расчётов
В настоящее время существуют две ГГМ, в ко
должны максимально соответствовать реальным
торых явным образом описывается течение льда в
наблюдениям в выбранный контрольный период.
приближении мелкого льда и рассчитывается из
Единого подхода к выбору контрольных параме
менение геометрии ледника, исходя из решения
тров не существует. Часто выбирают поверхност
уравнения неразрывности. Это - OGGM [8] и
ный баланс массы, геометрию ледника (длину,
GloGEMflow [9]. В остальных моделях использу
площадь, объём), ледниковый сток, положение
ют различные имитационные схемы, основанные
снеговой линии или границы питания [7]. Из-за не
на эмпирических и полуэмпирических соотноше
достатка наблюдений модели перегружены настра
ниях между площадью, объёмом и длиной ледни
иваемыми параметрами. Данных для окончатель
ка [14-16] или между балансом массы и измене
ной калибровки каждого параметра недостаточно.
нием геометрии [10, 17].
В результате обычно определяют одно наиболее
подходящее решение модели и анализируют её чув
ствительность к выбору настраиваемых параме
Постановка прогностических экспериментов
тров [8-10]. Такой подход приводит к сложно раз
решимой проблеме, поскольку многие комбинации
Климатический форсинг. Для моделирования
наборов параметров могут дать результаты в преде
поверхностного баланса массы (SMB, surface mass
лах условно допустимых ошибок [11]. Кроме того,
balance) данные реанализа и глобального климати
параметры модели, основанной на ограниченном
ческого моделирования в большей мере примени
наборе наблюдений баланса массы, должны при
мы, чем разреженные точечные наблюдения из-за
меняться к ледникам, где наблюдения отсутствуют
того, что метеостанций в высокогорных или по
совсем, т.е. экстраполироваться без достаточных на
лярных регионах мало и они не обеспечивают рав
то оснований, кроме, вероятно, схожести генети
номерного покрытия изучаемого района [18, 19].
ческого типа и внешних условий. Это вносит ещё
Однако пространственное разрешение данных реа
один источник неопределённости [7].
нализа и климатических моделей и их ограниченная
288
Т.Н. Постникова, О.О. Рыбак
возможность воспроизводить поля осадков, темпе
Они определяют дополнительное радиационное
ратуры воздуха и других метеорологических пере
воздействие около 2100 г. относительно доинду
менных в условиях сложного рельефа высокогорья
стриальных значений (2,6, 4,5, 6,0 и 8,5 Вт м-2 со
недостаточно для гляциогидрологических приложе
ответственно). Другое, относительно новое, на
ний [18, 20] и не может быть использовано без соот
правление, формализующее траектории развития
ветствующей корректировки [18, 19]. В прогности
климатической системы с учётом его влияния на
ческих экспериментах на ГГМ недавнего времени
человеческое сообщество, - сценарии SSP (Shared
были использованы результаты расчётов на GCMs
Socioeconomic Pathways - совместные социально-
(Global Circulation Models - Модели общей цир
экономические пути [27]), развиваемые в рамках
куляции), объединённые в проекте CMIP [21, 22],
проекта CMIP 6 [22], до сих пор не использова
и данные реанализа. Например, данные реанали
лось в глобальном гляциологическом моделиро
за ERA-Interim включают в себя среднемесячную
вании [3, 28]. Заметим, что использование SSP в
приповерхностную (2 м) температуру, температуру
экспериментах с ГГМ планируется в третьей фазе
воздуха на разных уровнях (300-1000 гПа) и сумму
эксперимента GlacierMIP [29].
осадков за каждый месяц, начиная с 1979 г., с про
Пространственное разрешение современных
странственным разрешением ~0,7° [23].
RCM не позволяет достаточно точно воспроизве
Для регионализации (даунскейлинга) гля
сти климатические условия для большинства гор
циологических исследований традиционно ис
ных ледников [20]. Чтобы решить эту проблему,
пользуют региональные климатические модели
к выбранным климатическим данным применя
(RCM - Regional Climate Models), имеющие более
ют коррекционные схемы, которые встраиваются
высокое разрешение в ограниченной области (ди
непосредственно в климатический блок ГГМ [3].
намический даунскейлинг [19]). RCM, управляе
Значения температуры воздуха над ледником ин
мая GCM, позволяет обеспечить прогностические
терполируются из ближайших узлов простран
поля с более подробным и более точным пред
ственной сетки климатической модели и приво
ставлением локализованных событий. RCM имеет
дятся к абсолютной высоте ледника с применением
явные преимущества при моделировании осадков
вертикального градиента температуры. В литера
по сравнению с GCM: модельная изменчивость
туре его значения существенно варьируют: от 0,3-
суточных и месячных сумм осадков, будучи ниже
0,4 °C/100 м (Западная Гренландия, Исландия) до
наблюдаемой, тем не менее, оказалась гораздо
0,7-0,8 °C/100 м на Кавказе [30] и в Альпах [19]
более реалистичной, чем генерируемая GCM, так
либо считаются постоянной величиной для всех
как более мелкая сетка уменьшает объём неявного
ледников мира (0,65 °C/100 м в модели OGGM [8]).
пространственного сглаживания [20]. Динамиче
Данные осадков для каждого ледника обыч
ский даунскейлинг требует больших вычислитель
но берут из узла пространственной сетки модель
ных затрат в отличие от статистического даун
ных климатических данных - ближайшей к цент-
скейлинга, основанного на поиске связей между
ральной координате ледника. Изменение суммы
крупномасштабными и локальными особенно
осадков с высотой оценивается с использованием
стями атмосферы с учётом данных наблюдений
вертикального градиента осадков [12, 19, 31] и/
метеостанций [19]. Проект CORDEX (Coordinated
или поправочного коэффициента [8] (см. табли
Regional Downscaling Experiment) [24] объединяет
цу). Последний представляет собой, по сути дела,
региональные климатические модели и эмпири
глобальную поправку на орографические осадки,
ческий статистический даунскейлинг для разных
лавинное питание и метелевый перенос [8]. Ис
регионов мира [25] и успешно применяется для
ключение - модель OGGM, в которой вертикаль
расчётов на ГГМ (например, с разрешением 0,11°
ный градиент осадков не рассчитывается и поле
или около 12 км в работе [9]).
осадков считается однородным. Чтобы различать
Для прогнозирования изменений оледенения
твёрдые и жидкие осадки, используют пороговую
в будущем используют главным образом так назы
температуру воздуха (threshold temperature) от 0
ваемые сценарии RCP (Representative Concentra
до 3 °С (см. таблицу). Возможно, целесообразнее
tion Pathways - пути радиационного воздействия):
использовать разную пороговую температуру для
RCP 2.6, RCP 4.5, RCP 6.0 и RCP 8.5 [26], реали
разного климата (выше для континентального
зуемые в численных экспериментах на GCM.
климата, чем для морского) [32].
289
Т.Н. Постникова, О.О. Рыбак
291
Т.Н. Постникова, О.О. Рыбак
293
Обзоры и хроника
Моделирование энергетического баланса
тим, что инициализация в GloGEMflow проводи
сложнее из-за количества исходных данных. На
лась примерно за десятилетний период (с 1990 г. до
пример, в модели JULES в отличие от исполь
года инвентаризации RGI), что позволило обойти
зуемого в масс-балансовых блоках GloGEM,
проблему неединственности исходного состояния
GloGEMflow и OGGM индексно-температурно
ледника, приводящую к «правильной» геометрии
го метода применяется энергобалансовый, где в
ледника на дату инвентаризации [35].
качестве входных переменных необходимы: ско
Для моделирования прошлых состояний лед
рость ветра, влажность воздуха, баланс длинно- и
ников в ГГМ до настоящего времени использо
коротковолновой радиации, атмосферное давле
валась инициализация, аналогичная для мо
ние [12]. Во многих ГГМ значения некоторых кли
делирования будущих состояний. Например,
матических параметров, необходимых для получе
инициализация модели в работе [14] проведена
ния более точных условий на леднике (например,
таким образом, чтобы при заданной начальной
поправки на температуру и осадки [6, 10]), опреде
площади ледника в прошлом в результате прого
ляют в ходе калибровки масс-балансового блока.
на модели до момента инвентаризации площадь
Инициализация. Ключевой аспект прогнозиро
ледника была близка к измеренным значениям.
вания потери массы ледников на ГГМ с динами
Однако в исследовании [35] показано, что моде
ческим блоком связан с определением начально
лирование прошлого на основании калибровки
го состояния модели. Таким образом, существует
современными данными - некорректная задача.
проблема инициализации модели ледника, которая
Это означает, что существует несколько начальных
решается разными способами. Прежде чем выпол
конфигураций ледника в прошлом, которые в ре
нить эксперимент с требуемыми климатическими
зультате моделирования сходятся к одному и тому
данными, необходимо, как правило, привести мо
же состоянию ледника на момент инвентаризации.
дель в равновесие с заданным климатом. Однако
Альтернативный подход состоит в том, чтобы
ледники практически никогда не находятся в рав
начинать моделирование с года инвентаризации.
новесии с климатом. Поэтому использование рав
Это связано с тем, что ледники находятся далеко от
новесного состояния для инициализации ледника
состояния равновесия. Следовательно, прогности
не позволяет должным образом учитывать моде
ческие изменения площади и объёма, по сути, отра
лям будущую потерю массы, которая «накоплена»
жают реакцию ледника не только на текущие и бу
из-за неравновесия ледника с климатом в послед
дущие, но и на прошлые колебания климата [5, 36].
ние десятилетия [33]. Так, инициализация модели
Такой подход может быть оправдан, например,
GloGEMflow заключается в точном воспроизве
если цель исследования - сравнить эволюцию лед
дении геометрии ледника на дату инвентаризации
ников при различных климатических сценариях,
Randolph Glacier Inventory (RGI) [34]. Сначала мо
каждый из которых имеет очень похожие фоновые
дель запускается для начальной конфигурации, при
климатические условия, и, следовательно, прошлое
которой ледник отсутствует. Под действием кли
изменение геометрии ледника одинаково или похо
матических условий, соответствующих среднему
же для каждого климатического сценария [36].
балансу массы на 1961-1990 гг., происходит на
Калибровка масс-балансового блока. Калиб-
растание льда, и далее ледник эволюционирует до
ровка параметров модели требуется во всех ГГМ
достижения состояния равновесия к 1990 г. Затем
(к ним относятся поправки для температуры воз
ледник эволюционирует с 1990 г. до года инвента
духа и осадков, предназначенные для коррекции
ризации (примерно 2003 г. для большинства ледни
климатических данных для условий конкретного
ков в Альпах в RGI) при соответствующем климате.
ледника, коэффициенты градусо-дней для снега и
Реологический параметр A подбирается таким об
льда fsnow, fice либо настройки в радиационном блоке
разом, чтобы полученная геометрия ледника наибо
и т.д.). Калибровка необходима по двум причинам:
лее близко совпала с данными RGI (объём и длина
во-первых, требуется как можно более аккуратное
модельного ледника должны совпасть с инвентари
описание метеорологических условий на конкрет
зованными с точностью до 1%). Такая процедура
ном леднике; во-вторых, ГГМ не предназначена
инициализации предполагает, что в 1961-1990 гг.
для детального описания сложных процессов энер
ледник был в равновесии с климатом, что, разуме
гообмена каждого из нескольких тысяч ледников.
ется, относится к неочевидному допущению. Отме
Именно поэтому калибровка масс-балансового
294
Т.Н. Постникова, О.О. Рыбак
блока неразрывно связана с даунскейлингом кли
что суммарный модельный баланс массы нахо
матических данных (см. таблицу). Как правило, на
дится в соответствии с измерениями [10].
боры параметров получают путём максимизации
В PyGEM для определения значений набора
соответствия между результатами моделирования
параметров модели θ и соответствующих им нео
и наблюдениями, например, временных рядов еже
пределённостей для каждого ледника применяет
годных и сезонных изменений массы отдельных
ся байесовский подход. Суть его следующая: если
ледников, усреднённых по площади [37] или инте
информация о значении параметра отсутствует, то
грированных во времени многолетних изменений
это значение может быть описано, исходя из зако
массы отдельных ледников или ледников по ре
на распределения, заданного a priori. Наличие на
гионам [38-43]. Однако глобальные базы данных
блюдений приводит к распределению значений не
охватывают горные регионы мира крайне нерав
известного параметра a posteriori. Средние значения
номерно [44] и качество этих данных сильно варьи
и функции распределения вероятности неизвест
рует. Для некоторых горных стран целесообразно с
ных параметров θ~ = [kp, fsnow, Tbias] в модели PyGEM
целью калибровки модели использовать независи
и F(θ) определяются из данных балансов массы c
мые региональные оценки геодезического баланса
помощью теоремы Байеса и метода Монте-Карло
(как, например, для Высокогорной Азии [11]).
по схеме марковской цепи. Этот алгоритм (расчёт
Методы калибровки масс-балансового блока
ная схема) позволяет по исходным наблюдениям
отличаются по уровню сложности. В GloGem и
и априорному распределению получить большую
PyGEM калибруются схожие параметры: попра
выборку из апостериорного распределения.
вочный коэффициент kp, выполняющий функ
Процесс вычислений состоит в следующем. На
цию приспособления климатических данных
вход расчётной схемы подаётся модель F(y|θ), ко
под особенности конкретного ледника (локаль
торая описывает данные y, и априорное мнение о
ные топографические эффекты, дождевая тень
неизвестных параметрах θ, а на её выходе получа
и т.п.); коэффициенты градусо-дней fsnow, fice, ко
ется выборка θ~1, ~2, ~3, …, задающая апостериорное
торые переводят количество дней с положитель
распределение. В PyGEM по методу, схожему с
ной температурой в слой стаявшего снега или
калибровочной процедурой GloGEM, получают
льда; температурная поправка Tbias неточностей,
априорные распределения параметров p(θ), при
вызванных недостаточным пространственным
чём предполагается, что Tbias имеет нормальное,
разрешением климатических данных. При этом
а kp - гамма-распределение. Согласно теореме
в GloGEM используется простая трёхшаговая
Байеса, можно совершить переход от априорных
процедура калибровки: сначала калибруется па
знаний о параметрах модели к апостериорным
раметр kp; потом, если отклонения от данных ба
с учётом наблюдённых данных y: p(θ~) = p(θ|y) =
ланса массы из WGMS остаются большими, ка
= p(y|θ)p(θ)/p(y). На практике определить харак
либруется параметр fsnow; если второй шаг не даёт
теристики апостериорного распределения анали
хорошего результата, то систематически сдвига
тически сложно. Метод Монте-Карло по схеме
ется значение температуры Tbias.
марковской цепи позволяет обойти эту проблему,
Калибровка GloGEM основывается на регио
создавая цепочку наборов параметров модели, ко
нальных оценках. Параметры подбираются так,
торая формируется путём итеративной выборки
чтобы баланс массы каждого отдельного ледни
комбинаций параметров модели из апостериорно
ка соответствовал среднему балансу массы по ре
го распределения [11]. Таким образом, появляет
гиону в течение одного и того же многолетнего
ся возможность постепенно исследовать функции
периода времени, т.е. для каждого ледника под
распределения, где каждое последующее значение
бирается свой набор параметров. В других рабо
определённым способом зависит от предыдущего,
тах [45], где используются региональные оценки
фактически представляя собой марковскую цепь.
баланса массы, применяется иной подход: сумма
Наборы параметров модели, которые хорошо со
модельных балансов массы всех отдельных лед
гласуются с наблюдёнными балансами массы, при
ников должна соответствовать наблюдаемому из
нимаются чаще, чем те, которые плохо согласуются
менению массы в масштабах региона за тот же
(алгоритм Метрополиса-Гастингса [46]).
период. В этом случае балансы массы отдельных
Теория, лежащая в основе методов Монте-Кар
ледников могут быть нереалистичными, при том
ло и марковских цепей, состоит в том, что, если
295
Обзоры и хроника
цепь достаточно длинная, т.е. выполняется доста
объёму стока, в то время как более «сухой» и «хо
точное количество итераций, то она будет сходить
лодный» набор параметров даст значительно мень
ся к уникальному стационарному распределению
ший его объём [11]. В связи с этим будет полезной
и параметры модели в цепочке будут из совмест
калибровка с учётом наблюдений за ледниковым
ного апостериорного распределения [11]. Други
стоком (которые, заметим, весьма редки).
ми словами: если цепочки достаточно длинные, то
Применение методики латинского гиперкуба к
мы можем быть уверены, что полученные наборы
организации численных экспериментов. Отдельно
параметров отражают истинное распределение по
го упоминания заслуживает метод калибровки,
тенциальных наборов параметров модели на осно
представленный в модели JULES, где для органи
ве наблюдений и предшествующей информации.
зации серии численных экспериментов исполь
Описанный подход, на наш взгляд, имеет большие
зуется перспективный метод латинского гиперку
перспективы для калибровки модельных параме
ба [12] - эффективного метода проверки реакции
тров, поскольку он предполагает генерирование
оледенения на множество различных комбинаций
распределения оптимального набора параметров на
параметров, обеспечивающего достаточный охват
основе инструментальных наблюдений за балансом
параметрического пространства без необходимости
массы. В модели PyGEM вместо одного возможно
тестирования всех возможных комбинаций (что
го набора параметров, как в GloGEM, получается,
было бы чрезвычайно затратно в вычислительном
по крайней мере, сто возможных наборов параме
отношении). Путём изменения более одного пара
тров [11]. На основании этих наборов проводится
метра за раз (как и для любого метода многомер
100 симуляций. Это позволяет оценить неопреде
ной выборки) метод латинского гиперкуба позво
лённости, связанные с выбором набора параметров.
ляет также оценить влияние каждого параметра на
Проблема неидентифицируемости параметров
результат моделирования, принимая во внимание
модели. Интерпретация результатов численных
взаимодействие с другими параметрами [48].
экспериментов при использовании любой ГГМ
Гиперкуб - это n-мерный квадрат, содержа
предполагает учёт потенциальной неидентифици
щий позиции выборки, где n - число парамет-
руемости параметров модели: существует беско
ров. Диапазон каждого из параметров делится
нечное число наборов параметров, которые будут
на N равновероятных частей (одинаковых в слу
давать точное совпадение между моделируемым
чае равномерного распределения вероятностей
и наблюдаемым балансом массы. Иными слова
для данного параметра), и выборка выполняется
ми - модель перегружена параметризуемыми пе
по одному разу из каждой части. Тогда гиперкуб
ременными из-за недостатка наблюдений [11, 47].
считается латинским в том и только в том случае,
Рассмотрим пример, как неидентифицируемость
если существует единственная выборка значений
может влиять на прогнозы изменения массы лед
параметров в каждой строке и в каждом столбце.
ников и ледникового стока. Пусть существуют два
Следовательно, выборка латинского гиперкуба -
набора параметров модели Tbias и kp, при которых
это статистический метод генерации почти слу
модельный баланс массы одинаково согласуется
чайной выборки значений параметров из мно
с наблюдением: первый - это более высокие зна
гомерного распределения, при котором каждый
чения Tbias и kp, т.е. более тёплый и влажный кли
из её компонентов представлен полностью стра
мат; второй - более низкие значения Tbias и kp, т.е.
тифицированным образом, независимо от того,
более холодный и сухой климат. Современный ба
какие компоненты могут оказаться важными [49].
ланс массы ледников при этих наборах параме
В модели JULES [12] калибруется семь пара
тров будет одинаковым, и прогнозы также могут
метров масс-балансового блока: четыре параметра
быть одинаковыми, хотя возможны и незначи
для схемы изменения альбедо по мере уплотнения
тельные различия, вызванные влиянием гипсоме
снега (альбедо льда и снега в видимой и инфра
трии ледника на его отступание. При этом разли
красной частях спектра); орографический гради
чия для моделируемого стока ледников, вероятно,
ент осадков и температуры; параметр масштаби
будут значительными. За счёт использования в мо
рования скорости ветра. Случайные комбинации
дели «влажного» и «тёплого» набора параметров
параметров выбирали с использованием описан
будет генерироваться большее количество осадков
ной здесь методики выборки латинского гипер
и больший объём таяния, что приведёт к большему
куба. В модели JULES к каждому из параметров
296
Т.Н. Постникова, О.О. Рыбак
применялись ограничения, которые выбирались
дом, а для калибровки - геодезическим, так как
из разных источников в соответствии с полевы
их больше [6, 8-10]. Например, в Альпах данные
ми наблюдениями [12]. В результате получилось
баланса массы, измеренные геодезическим ме
198 комбинаций параметров, для каждой из кото
тодом, покрывают примерно 1500 ледников, т.е.
рых модель JULES проходила процедуру иници
больше 60% площади оледенения, в то время как
ализации в течение десяти модельных лет. Полу
полевых гляциологических измерений лишь не
ченные значения баланса массы сравнивались с
сколько [9]. Геодезические измерения баланса
данными в WGMS по методу наименьших квадра
массы доступны и для других регионов - Высо
тов, и в результате была выбрана наиболее реали
когорной Азии [43, 51], Южной Америки [52], что
стичная комбинация параметров [12].
позволяет использовать их для калибровки ГГМ в
Калибровка динамического блока. ГГМ с ди
применении к другим регионам. Новая база дан
намическим блоком очень чувствительны к из
ных изменения массы ледников всего мира [53]
менению реологического параметра А [8, 9].
расширяет возможности калибровки ГГМ.
При меньшем значении А лёд характеризуется
меньшей «ползучестью» и моделируемая толщи
на ледника в итоге получается больше. И наобо
Некоторые приложения глобальных
рот, увеличение А приводит к меньшей толщи
гляциологических моделей
не моделируемого ледника. Добавление в модель
скольжения ледника по ложу также уменьшает
Рассмотрим некоторые наиболее интересные
толщину льда, так как и скольжение, и реология
и значимые результаты, полученные в последние
сильно влияют на объёмный расход льда.
годы в численных экспериментах с ГГМ.
Параметры скольжения fs и вязкости А зависят
Построение глобальных и региональных гля-
от множества факторов, поэтому они не могут быть
циологических проекций. В рамках одного из пер
постоянны на глобальном уровне и требуют кали
вых «глобальных» исследований на модели
бровки. В модели OGGM подобная калибровка
GloGEM [10], цель которых - уточнение потен
стала возможна после выпуска (2021 г.) версии 1.4,
циального вклада ледников в повышение среднего
при этом параметры калибруются на региональ
уровня Мирового океана, были построены гляцио-
ном уровне [50]. В модели GloGEMflow параметр
логические проекции всех ледников, включённых
динамики каждого ледника калибруется так, чтобы
в базу RGI [34], в том числе периферийных лед
с точностью до 1% совпадали моделируемый и ре
ников Гренландии и Антарктиды. Установлено,
альный объёмы каждого ледника на дату инвента
что ледники полярных регионов (> 60° с.ш./ю.ш.)
ризации при предположении, что в 1990 г. ледник
доминируют в потенциальном вкладе в увеличе
находился в равновесии с климатом [9]. При этом
ние глобального уровня моря (ледниковые щиты
применяется калибровка температурной поправки
в ГГМ не раcсматриваются). Вклад ледников сред
так, чтобы совпали реальная и моделируемая длина
них и низких широт относительно мал, хотя имен
ледника на дату инвентаризации. Для каждого лед
но в этих регионах прогнозируется потеря боль
ника динамический блок модели калибруется ин
шей части современного объёма льда к 2100 г.
дивидуально в связи с тем, что геометрические дан
(более 90% для некоторых сценариев и регионов).
ные доступны для каждого ледника в отличие от
Например, для Кавказа предсказаны потери льда
данных баланса массы. Недостаток подобного под
от 70±11% при реализации сценария RCP 2.6 и до
хода - параметры модели фактически подбирают
96±3% при RCP 8.5. Это обстоятельство приведёт
ся таким образом, чтобы неравновесный ледник
к изменению гидрологического режима на обшир
был в равновесии с климатом в 1990 г.
ных территориях и, как следствие, снизит доступ
Валидация. Для валидации ГГМ использу
ность воды на региональном уровне [10]. Однако
ют данные, не пересекающиеся с данными для
здесь не принимается во внимание экранирующая
калибровки. Считается, что лучшее покрытие из
роль моренного чехла, учёт которой может суще
учаемого района данными для калибровки важ
ственно скорректировать результаты.
нее, чем для валидации [9]. Поэтому часто для
Результаты различных ГГМ [6, 8-10, 12-
валидации используют данные баланса массы
14, 16, 45, 54-58] в построении глобальных гля
ледников, измеренного гляциологическим мето
циологических проекций (без учёта покров
297
Обзоры и хроника
ных ледников) сравнивались в рамках проекта
сокращения модельных ледников. В связи с этим
GlacierMIP [59]. Большинство прогнозов схо
возникает следующий вопрос: насколько надёжны
дится в том, что к 2100 г. в мире исчезнет менее
прогностические оценки деградации оледенения и
половины современной площади ледников (от
изменения режима ледникового стока на моделях,
18±13% современного оледенения при сценарии
в которых не учитывается динамика ледников [12]
RCP 2.6 и до 36±20% при RCP 8.5). Однако моде
или учитывается слишком упрощённо [6]?
ли GlacierMIPII прогнозируют потерю более 85%
Подобно описанному здесь исследованию эво
льда в некоторых районах (Кавказ, Центральная
люции оледенения Альп были построены гляцио
Европа, Западная Канада и США, низкие широ
логические проекции для Высокогорной Азии на
ты) к 2100 г. при реализации сценария RCP 8.5.
модели PyGEM [7]. Установлено, что в отличие от
Ход дегляциации в разных регионах зависит от на
Альп деградация оледенения Высокой Азии будет
чальной массы льда. В регионах с преобладанием
протекать меньшими темпами: к концу века лед
крупных ледников (Антарктика и Субантарктика,
ники потеряют от 29±12% (RCP 2.6) до 67±10%
Север Арктики и Канады) ожидается рост потерь
(RCP 8.5) своей общей массы по сравнению с
массы в течение XXI в. в рамках сценария RCP 8.5
2015 г. Видимо, это объясняется тем, что ледни
(т.е. максимум дегляциации можно ожидать после
ки расположены на более значительных высотах и
2100 г.), поскольку сохраняются относительно
большая часть льда останется выше поднимающей
большие площади ледников, к которым приме
ся границы питания. В будущем здесь вероятнее
няется отрицательный баланс массы. В регионах
достижение состояния равновесия [7, 10]. Пара
с относительно небольшими ледниками (Запад
доксально, но, несмотря на то, что только в моде
ная Канада и США, Центральная Европа, Кавказ,
ли KRA 2017 [56] учитывается моренный чехол, по
Новая Зеландия) прогнозируется замедление по
лученные на ней результаты эволюции ледников
тери массы в течение текущего столетия, незави
Высокогорной Азии хорошо согласуются с резуль
симо от сценария RCP, поскольку либо площадь
татами моделирования на других ГГМ [59]: напри
льда быстро сокращается (для RCP 8.5), либо лед
мер, с помощью модели PyGEM получены при
ники стабилизируются по мере того, как они от
мерно такие же потери массы льда [7]. Это можно
ступают в более высокий пояс (для RCP 2.6) [3].
объяснить тем, что в массив ледников, выбранных
Среди региональных гляциологических проек
для калибровки данных моделей, попали и ледни
ций отметим работу, посвящённую будущему аль
ки, покрытые мореной. Следовательно, не учиты
пийских ледников, исследованных в экспериментах
ваемые явным образом поверхностные процессы
на GloGEMflow [9]. В 2015-2050 гг. в Альпах около
теплообмена неявно компенсируются в ходе на
50% объёма льда будет потеряно при любом сцена
стройки моделей или требуется иное описание мо
рии RCP: во-первых, до 2050 г. различия в темпера
ренного блока, чем в этой модели.
туре воздуха для разных сценариев незначительны;
Неточности глобальных и региональных гля-
во-вторых, часть потерь обусловлена тем, что лед
циологических прогнозов. В рамках GlacierMIP [3]
ники не находятся в равновесии с климатом и их
был проведён анализ неточностей глобальных
объём сократился бы приблизительно на 40% даже
гляциологических прогнозов, вызванных несо
при стабилизации современных климатических ус
вершенством гляциологической (1) и климатиче
ловий [5]. При реализации самого мягкого сцена
ской (2) суб-моделей, неопределённостью в про
рия RCP 2.6 к 2100 г. ожидается сокращение объёма
гнозируемых климатических характеристиках (3)
оледенения Альп на 2/3 от современного (2017 г.).
и естественными флуктуациями климата, не свя
В случае реализации наиболее экстремального сце
занными с радиационным воздействием (4). В на
нария RCP8.5 большинство альпийских ледников
чале симуляции (условный 2015 г.) наибольший
исчезнет к концу текущего столетия.
вклад в ошибку вносят гляциологические модели
Эксперименты с GloGEMflow, которая пред
(около 50%), и в течение XXI в. эта неопределён
ставляет собой модификацию модели GloGEM,
ность растёт. Однако неопределённости, связан
наглядно показали важность учёта динамики лед
ные с климатическими моделями и сценариями,
ника. Формализация в модели динамического го
растут быстрее, и к концу XXI в. ошибка, связан
ризонтального переноса льда из области аккуму
ная с будущим климатом, становится наиболь
ляции в область абляции привела к замедлению
шей. Таким образом, было показано, что, чем
298
Т.Н. Постникова, О.О. Рыбак
дальше в будущее уходит прогноз, тем меньше
туациях, связанных как с высокой, так и с низ
возможность уменьшить его неопределённость за
кой водностью. Ожидается, что в районах с пре
счёт улучшения гляциологической модели. Тем
обладанием ледникового питания рек изменения
не менее, уменьшение ошибки ГГМ может иметь
средних значений расхода воды в будущем будут
большое значение для улучшения прогнозов в
умеренными и не превысят 30%. Однако будущий
рамках первой половины XXI в. Относительный
максимум и особенно минимум экстремального
вклад разных источников неточностей зависит
стока будут отличаться от современных. Мини
от региона: для одних регионов (Западная Кана
мальный расход воды увеличится за счёт больше
да и Америка, Северная Азия, низкие широты) в
го накопления зимних осадков. Максимальный
течение всего XXI в. преобладает ошибка гляцио
же расход уменьшится из-за сокращения количе
логической модели (1), для других (Исландии) -
ства поступающей талой воды.
ошибка климатической модели (2).
В большинстве речных бассейнов с муссонным
Прогнозирование изменений ледникового стока.
питанием (Ганг, Брахмапутра) ледниковый сток
В горных и предгорных регионах сток рек в значи
достигнет максимума до 2050 г., в то время как в
тельной степени зависит от состояния горных лед
бассейне р. Инд и других речных бассейнах, где
ников. Ледниковый сток, который в пиковые ме
наблюдается увеличение зимней аккумуляции за
сяцы абляции может составлять более половины
счёт западных ветров, пиковый расход воды будет,
общего стока горных рек [60], стабилизирует ги
вероятно, достигнут после 2050 г. [6]. В этой работе
дрологический режим и обеспечивает устойчивое
вводится понятие избыточной талой воды - стока,
водоснабжение в регионе. Долгосрочный прогноз
вызванного чистой потерей массы ледника. При
эволюции параметров горного оледенения акту
сценариях с более высоким радиационным воз
ален для расчётов характеристик речного стока
действием пиковый расход воды задержится из-за
в условиях, когда региональный климат меняет
увеличения избыточного таяния ледников, в то
ся. Например, модель GloGEM была использова
время как сценарии с более низким RCP позволят
на для прогноза изменений стока рек в 56 речных
многим ледникам приблизиться к новому равно
бассейнах. Авторы подтвердили широко известное
весию, в результате чего ледниковый сток в начале
обстоятельство [61, 62]: объём модельного годово
XXI в. (2020 г. при RCP 2.6) сократится.
го ледникового стока продолжает расти до тех пор,
Палеогляциологическое моделирование. Помимо
пока не будет достигнут максимум, после которого
решения прогностических задач, ГГМ используют
неизбежно его снижение. Однако происходит это
для моделирования прошлых состояний оледене
только приблизительно в половине исследован
ния. Наиболее масштабным как по временнóму,
ных бассейнов, в остальных бассейнах этот пере
так и по пространственному охвату было иссле
ломный момент уже пройден. Например, ледни
дование эволюции 412 ледников из 16 регионов
ки в бассейне Кубани, вероятно, уже прошли этот
RGI (кроме Канадской Арктики и Антарктиды),
пик [62]. Достижение максимума стока спрогно
начиная с 850 г. на модели OGGM [64]. Авторы
зировано позднее в бассейнах рек с более круп
применяли «наивный» (терминология авторов)
ными ледниками и более высокой долей оледене
подход для калибровки модели с помощью совре
ния. Как правило, объём ледникового стока будет
менных данных [8]. Для валидации использова
расти в начале лета, но сокращаться в его конце по
ли наблюдения за длиной ледников [65], большая
сравнению с современным. Хотя большая часть из
часть которых берёт начало после 1850 г., а самые
56 исследованных в работе [6] бассейнов покрыта
старые наблюдения датируются 1530 г. Некото
льдом менее чем на 2%. К 2100 г. в одной трети из
рые из шести использованных климатических мо
них может наблюдаться уменьшение стока более
делей позволили получить правдоподобную кар
чем на 10% из-за потери ледниковой массы, как
тину эволюции ледников в течение тысячелетия
минимум, за один месяц сезона таяния, с наиболь
в некоторых регионах (Аляска, Западная Канада
шим сокращением в Центральной Азии и Андах.
и США, периферия Гренландии, Скандинавия,
Детали будущих изменений стока на регио-
Центральная Европа и Центральная Азия). Авто
нальном уровне - в Альпах - исследованы на
ры делают вывод, что OGGM - в используемой
модели GloGEMflow [63]. Акцент сделан на так
ими конфигурации и в тысячелетнем масштабе
называемых экстремальных гидрологических си
времени - не может достаточно точно воспроиз
299
Обзоры и хроника
вести особенности эволюции отдельных ледни
деляется, прежде всего, уклоном ледника, а также
ков в количественном выражении, однако OGGM
диапазоном высот и градиентом баланса массы.
удаётся уловить качественную реакцию на доста
Ледники с большим уклоном способны эффек
точно крупномасштабные климатические тенден
тивно переносить массу и быстро адаптироваться к
ции в региональном масштабе [64].
изменению климата, а значит, имеют более корот
Исследование [14] охватило намного более
кое время релаксации. Ледники с большим гради
короткий промежуток времени, с 1850 г., и было
ентом баланса массы также способны реагировать
сфокусировано главным образом на эволюции
быстрее на климатические изменения.
оледенения в ХХ в. Установлено, что самые боль
шие потери массы льда происходили в 1930-х
годах (до 2,5 мм эквивалента уровня моря в год).
Основные проблемы и перспективы развития
После этого скорость потерь уменьшалась вплоть
до 1970-х годов (до 0,5 мм эквивалента уровня
Ключевая проблема применения ГГМ заклю
моря в год). С тех пор скорость потерь массы уве
чается в труднодоступности или неточности не
личивается (до 1 мм эквивалента уровня моря в
обходимых исходных данных. Почти все ГГМ
год). Точность модельных палеореконструкций
используют базу данных RGI. Однако в RGI ото
на ГГМ ограничивается объективным препят
бражены не все ледники, очертания некоторых из
ствием: многие из ныне разделённых ледниковых
них искажены или ошибочны [59, 67]. В RGI часто
объектов были в прошлом частью крупных ком
попадают данные, относящиеся к разному време
плексов. Поскольку в ГГМ каждый объект рас
ни, они также могут быть устаревшими и неакту
сматривается независимо от других, ледниковые
альными, а некоторые ледники разделены непра
комплексы прошлого не могут быть воспроиз
вильно [8]. Так, многие из ледников Восточного и
ведены как один динамически связный ледник
Западного Кавказа обозначены лишь номинально
ни одной из ГГМ. Вопрос, насколько важен этот
(в виде кругов), для Центрального Кавказа RGI со
фактор для оценки характеристик горного оледе
держит множество неточностей, а 40 ледников не
нения прошлого, остаётся открытым [64].
вошли в базу данных даже номинально [67]. Поэ
Исследование времени реакции ледников на кли-
тому для региональных исследований целесообраз
матические изменения. Очевидно, что геометрия
нее использовать более точные региональные ин
ледников меняется в зависимости от флуктуаций
вентаризации ледников: например, GAMDAM для
климата. Их адаптация к меняющимся климатиче
Высокогорной Азии [58], базу данных Института
ским условиям происходит медленно. В результа
географии РАН для Кавказа [68]. Объём и толщи
те длительного времени релаксации большинство
на льда из RGI содержат большую ошибку [8]. При
ледников продолжали бы терять массу даже без
этом рассчитанные на ГГМ потери льда к 2100 г.
дополнительного потепления [5]. Время релакса
очень чувствительны к его начальному объёму.
ции ледников колеблется от десятилетий до тысяч
В работе [10] чувствительность ГГМ к исходному
лет для ледников в морском (влажном и тёплом)
объёму льда оценивалась путём вариации толщины
и континентальном (сухом и холодном) климате
на ±30% для каждого ледника и высотного пояса.
соответственно. По-видимому, время релаксации
Оказалось, что неточности оценки современного
зависит от климатических условий, а не от разме
объёма льда почти линейно отражаются на резуль
ра ледника: может расти по мере увеличения пло
тирующем вкладе в изменение уровня моря.
щади ледника (например, на островах Канадско
Дискуссии относительно перспектив разви
го Арктического архипелага и на Шпицбергене),
тия ГГМ ведутся главным образом вокруг даль
практически не изменяться (Северная Скандина
нейшего включения в модели физических про
вия, Южная Норвегия и Альпы) или даже умень
цессов: ведёт ли это к улучшению результатов или
шаться (Кавказ и Новая Зеландия) [66].
лишь создаёт «шум» [69]. Неопределённости, свя
Среднее время релаксации альпийских ледни
занные с упрощённым описанием динамики лед
ков, рассчитанное на модели GloGEMflow, состав
ников в ГГМ, трудно определить количественно,
ляет 50 ± 28 лет [6]. Подтверждён вывод работы [66]
поскольку все существующие модели эволюции
о том, что площадь/объём ледников действительно
ледников чрезмерно параметризованы из-за ис
не влияет на время релаксации. Последнее опре
пользования ограниченных калибровочных дан
300
Т.Н. Постникова, О.О. Рыбак
ных. Следовательно, даже если конкретный про
Междекадные изменения (тренд) оказались неза
цесс не включён или плохо представлен в модели,
висимы от межгодовых флуктуаций, т.е. их можно
то параметры модели, вероятно, компенсируют
накладывать друг на друга [74]. Эта модель была
его посредством калибровки.
успешно применена к отдельным ледникам - окан
Одно из направлений совершенствования ГГМ
чивающихся морем [74] или сушей [75]. В перспек
в ближайшее время - включение алгоритмов, опи
тиве будет возможно включение стохастического
сывающих теплообмен моренного чехла с атмо-
уравнения динамики в ГГМ.
сферой и ледником, а также эволюцию моренного
Замечательная черта глобальных гляциологиче
покрытия во времени (например, как в [70, 71], см.
ских моделей - унификация архитектуры, что по
рис. 1 в части 1 статьи). При этом, хотя чувстви
зволяет «собирать» новые конструкции из отдель
тельность к потеплению покрытых мореной лед
ных блоков разных моделей. Например, сейчас уже
ников меньше, чем предполагалось ранее, реакция
можно использовать динамический блок OGGM
этих ледников на потепление может усиливаться
совместно с масс-балансовым блоком PyGEM [76].
за счёт динамического отступания путём откалы
Вместе с тем постепенно унифицируются и согла
вания айсбергов в приледниковые озёра - про
совываются форматы исходных данных.
цесс, который происходит во многих горных стра
нах [57], но в ГГМ освещён слабо [3].
Ледниковые купола и поля в RGI разделены на
Заключение
отдельные динамические объекты. Геометрия ледя
ных шапок часто нетривиальна. Например, OGGM
Во второй части обзора рассмотрены вопро
воспроизводит их динамику не совсем реалистично,
сы, связанные с постановкой численных экспери
особенно в зонах ледоразделов [8]. Таким образом,
ментов на глобальных гляциологических моделях,
следующий шаг в развитии глобальных моделей -
наиболее интересные результаты их применения и
включение 2D- или 3D-моделей (SIA) леднико
перспективы их развития. В последнее десятиле
вых куполов и полей. Уже сейчас идёт разработка
тие сделан большой шаг вперёд в моделировании
трёхмерных ГГМ [72, 73]. Они должны улучшить
оледенения в глобальном масштабе. Значитель
воспроизведение динамики ледниковых куполов,
ный прогресс в технологиях дистанционного зон
фронтальной абляции (откалывание айсбергов) и
дирования способствовал появлению новых баз
эволюции моренного чехла ледников.
данных изменения ледников с беспрецедентным
Отметим, что усложнение ГГМ возможно до
охватом и временным разрешением [42, 44, 51, 52].
какого-то предела, после которого они потеряют
Эти данные предоставляют уникальные возмож
своё основное преимущество - вычислительную
ности для лучшей калибровки параметров, а также
эффективность. Возможно, одним из перспек
валидации глобальных моделей ледников, тем
тивных направлений может стать стохастический
самым дополнительно снижая неопределённости
подход, в основе которого лежит идея о том, что
проекций. Недавние достижения в систематиче
инерционная система (в нашем случае - ледник),
ских наблюдениях за изменением высоты [43, 51]
управляемая быстро флуктуирующими воздействи
и скоростями ледников [77], которые могут быть
ями (в нашем случае - климатические характери
объединены с оценками толщины льда [1], позво
стики), способна находиться в равновесии, которое
ляют точнее оценивать баланс массы [78, 79] и по
основано на балансе медленных изменений и нако
тенциально минимизируют проблему чрезмерной
пленных случайных воздействий [74, 75]. Несмотря
параметризации в ближайшем будущем.
на то, что исходная модель динамики ледника де
Проекты, нацеленные на сравнение моделей,
терминированно основана на физическом законе
среди которых - GlacierMIP [59], могут помочь
сохранения массы льда (см. Приложение 2 в части 1
установить источники неопределённостей и оце
обзора), модель изменения длины ледника может
нить их количественно. Однако пока модели чрез
быть интерпретирована как стохастическая [74, 75].
мерно параметризованы будет по-прежнему слож
С математической точки зрения, температуру или
но оценить относительную важность включения
высоту границы питания можно рассматривать как
в модель конкретного физического процесса, по
белый шум, а изменение длины аналогично броу
скольку схемы калибровки могут компенсировать
новскому движению вокруг положения равновесия.
его отсутствие или упрощённое представление.
301
Обзоры и хроника
Этот вопрос касается динамики ледников, морен
ственными вариациями таяния под моренном чех
ного чехла, лавинного питания и любых других
лом и снижением движущих напряжений [56].
физических процессов, которые могут отсутство
вать или плохо отражаться в моделях. Дальнейшая
Благодарности. Работа поддержана РФФИ, грант
работа может быть направлена на количественную
№ 20-35-90042. О.О. Рыбак получил поддержку в
оценку воздействия моренного чехла ледников на
рамках темы № FMWZ-2022-0001 Государствен
прогнозы изменения массы ледников и стока. Для
ного задания ИП РАН.
этого типа анализа требуются оценки толщины
Acknowledgements. This work was supported by the
морены, позволяющие выделить толстый слой мо
Russian Foundation for Basic Research, RFBR grant
ренного чехла [79], и усовершенствованные ди
№ 20-35-90042. O.O. Rybak was supported by the
намические модули ГГМ [8, 9], которые могут
Governmental Order to Water Problems Institute of
симулировать обратную связь между простран
RAS, subject № FMWZ-2022-0001.
References
12. Shannon S., Smith R., Wiltshire A., Payne T., Huss M.,
Betts R., Caesar J., Koutroulis A., Jones D., Harrison S.
Global glacier volume projections under high-end
1. Farinotti D., Huss M., Fürst J.J., Landmann J., Mach-
climate change scenarios. The Cryosphere. 2019, 13:
guth H., Maussion F., Pandit A. A consensus esti
mate for the ice thickness distribution of all glaciers
13. Hirabayashi Y., Zang Y., Watanabe S., Koirala S.,
on Earth. Nature Geoscience. 2019, 12 (3): 168-173.
Kanae S. Projection of glacier mass changes under a
high-emission climate scenario using the global glacier
2. Cogley J.G. Area of the ocean. Marine Geodesy. 2012,
model HYOGA2. Hydrol. Research Letter. 2013, 7 (1):
35: 379-388. doi: 10 688 .1080/01490419.2012.709476.
3. Marzeion B., Hock R., Anderson B., Bliss A., Champol-
14. Marzeion B., Jarosch A., Hofer M. Past and future sea-
lion N., Fujita K., Huss M., Immerzeel W.W., Kraaijen-
level change from the surface mass balance of glaciers.
brink P., Malles J.-H., Maussion F, Radić V., Rounce D.R.,
Sakai A., Shannon S., van de Wal R., Zekollari H. Par
org/10.5194/tc-6-1295-2012.
titioning the Uncertainty of Ensemble Projections of
15. Bahr D.B., Meier M.F., Peckham S.D. The physical
Global Glacier Mass Change. Earth's Future. 2020, 8 (7):
basis of glacier volume-area scaling. Journ. of Geo
4. Marzeion B., Kaser G., Maussion F., Champollion N.
phys. Reseasrch. 1997, 102 (B9): 20355- 20362.
Limited influence of climate change mitigation on
short-term glacier mass loss. Nature Climate Change.
16. Van de Wal R.S.W., Wild M. Modelling the response
of glaciers to climate change by applying volume-area
2018, 8: 305-308. doi: 10.1038/s41558-018-0093-1.
5. Zekollari H., Huss M., Farinotti D. On the imbalance and
scaling in combination with a high resolution GSM.
response time of glaciers in the European Alps. Geo
Climate Dynamics. 2001, 18 (3-4): 359-366. doi:
10.1007/s003820100184.
phys. Research Letter. 2020, 47 (2): e2019GL085578.
17. Huss M., Jouvet G., Farinotti D., Bauder A. Future high-
6. Huss M., Hock R. Global-scale hydrological response to
mountain hydrology: a new parameterization of glacier
future glacier mass loss. Nature Climate Change. 2018,
retreat. // Hydrology and Earth System Sciences. 2010,
7. Rounce D.R., Hock R., Shean D. Glacier mass change
18. Hofer M., Marzeion B., Mölg T. A statistical downscal
in high mountain Asia through 2100 using the open-
ing method for daily air temperature in data sparse,
source Python Glacier Evolution Model (PyGEM).
glaciated mountain environments. Geosci. Model Dev.
org/10.3389/feart.2019.00331.
2015.
8. Maussion F., Butenko A., Champollion N., Dusch M., Eis J.,
19. Morozova P.A., Rybak O.O. Regionalization of global
Fourteau K., Gregor P., Jarosch A.H., Landmann J., Oes-
climate modeling data for calculating the mass balance
terle F., Recinos B., Rothenpieler T., Vlug A., Wild C.T.,
of mountain glaciers. Led i Sneg. Ice and Snow. 2017,
Marzeion B. The Open Global Glacier Model (OGGM)
v1.1. Geoscientific Model Development. 2019, 12: 909-
2017-4-437-452. [In Russian]
20. Murphy J. An Evaluation of Statistical and Dynamical
9. Zekollari H., Huss M., Farinotti D. Modelling the future
Techniques for Downscaling Local Climate. Journ. of
evolution of glaciers in the European Alps under the EU
Climate. 1999, 12 (8): 2256-2284.
RO-CORDEX RCM ensemble. The Cryosphere. 2019,
21. Taylor K.E., Stouffer R.J., Meehl G.A. An overview of
CMIP5 and the experiment design. Bull. Amer. Me
10. Huss M., Hock R. A new model for global glacier
change and sea-level rise. Frontiers in Earth Science.
BAMS-D-11-00094.1.
22. Eyring V., Bony S., Meehl G.A., Senior C.A., Ste-
11. Rounce D.R., Khurana T., Short M.B., Hock R.,
vens B., Stouffer B., Taylor K.E. Overview of the Cou
Shean D.E., Brinkerhoff D.J. Quantifying parameter un
pled Model Intercomparison Project Phase 6 (CMIP6)
certainty in a large-scale glacier evolution model using
experimental design and organization. Geoscientif
Bayesian inference: application to High Mountain Asia.
ic Model Development. 2016, 9 (5): 1937-1958. doi:
Journ. of Glaciology. 2020, 66 (256):175-187.
10.5194/gmd-9-1937-2016.
302
Т.Н. Постникова, О.О. Рыбак
23. Dee D.P., Uppala S.M., Simmons A.J., Berrisford P.,
Poli P., Kobayashi S., Andrae U., Balmaseda M.A.,
org/10.7265/N5-RGI-60.
Balsamo G., Bauer P., Bechtold P., Beljaars A.C.M.,
35. Eis J., Maussion F., Marzeion B. Initialization of a
van de Berg L., Bidlot J., Bormann N., Delsol C.,
global glacier model based on present-day glacier ge
Dragani R., Fuentes M., Geer A.J., Haimberger L.,
ometry and past climate information: an ensemble ap
Healy S.B., Hersbach H., Hólm E.V., Isaksen L., Kåll-
proach. The Cryosphere. 2019, 13: 3317-3335. doi:
berg P., Köhler M., Matricardi M., McNally A.P.,
10.5194/tc-13-3317-2019.
Monge-Sanz B.M., Morcrette J.-J., Park B.-K., Peu-
36. Shahgedanova M., Afzal M., Hagg W., Kapitsa V.,
bey C., de Rosnay P., Tavolato C., Thépaut J.-N., Vi-
Kasatkin N., Mayr E., Rybak O., Saidaliyeva Z., Sev-
tart F. The ERA-Interim reanalysis: Configuration and
erskiy I., Usmanova Z., Wade A., Yaitskaya N., Zhuma-
performance of the data assimilation system. Quarterly
bayev D. Emptying Water Towers? Impacts of Future
Journ. of the Royal Meteorological Society. 2011, 137
Climate and Glacier Change on River Discharge in the
Northern Tien Shan, Central Asia. Water. 2020, 12:
24. Gutowski Jr.W.J., Giorgi F., Timbal B., Frigon A., Jacob D.,
Kang H.S. Raghavan K., Lee B., Lennard Ch., Nikulin G.,
37. WGMS: Fluctuations of Glaciers Database. World
O’Rourke E., Rixen M., Solman S., Stephenson T., Tan-
Glacier Monitoring Service, Zürich, Switzerland. 2017.
gang F. WCRP coordinated regional downscaling experi
ment (CORDEX): a diagnostic MIP for CMIP6. Geo
38. Cogley J.G. Geodetic and direct mass-balance mea
scientific Model Development. 2016, 9 (11): 4087-4095.
surements: comparison and joint analysis. An
nals of Glaciology. 2009, 50 (50): 96-100. doi:
25. Jacob D., Petersen J., Eggert B., Alias A., Bøssing O.,
10.3189/172756409787769744.
Bouwer L.M., Braun A., Colette A., Georgopoulou E.,
39. Scherler D., Bookhagen B., Strecker M.R. Spatial
Gobiet A., Menut L., Nikulin G., Haensler A., Kriegs-
ly variable response of himalayan glaciers to climate
mann A., Martin E., van Meijgaard E., Moseley C.,
change affected by debris cover. Nature Geoscience.
Pfeifer S., Preuschmann S., Radermacher C., Radtke K.,
2011, 4 (3): 156-159. doi: 10.1038/ngeo1068.
Rechid D., Roundsevell M., Samuelsson P., Somot S.,
40. Gardelle J., Berthier E., Arnaud Y., Kääb A. Region-wide
Soussana J.-F., Teichmann C., Valentini R., Vautard R.,
glacier mass balances over the Pamir-Karakoram-Hi
Weber B., Yiou P. EUROCORDEX: new high-resolu
malaya during 1999-2011. The Cryosphere. 2013, 7 (4):
tion climate change projections for European impact
research. Reg. Environ. Change. 2014, 14: 563-578.
41. Gardner A.S., Moholdt G., Cogley J.G., Wouters B., Ar-
endt A.A., Wahr J., Berthier E., Hock R., Pfeffer W.T.,
26. Van Vuuren D.P., Edmonds J., Kainuma M., Riahi K.,
Kaser G., Ligtenberg S.R.M., Bolch T., Sharp M.J.,
Thomson A., Hibbard K., Hurtt G.C., Kram T., Krey V.,
Hagen J.O., van den Broeke M.R., Paul F. A reconciled esti
Lamarque J.-F., Masui T., Meinshausen M., Naki-
mate of glacier contributions to sea level rise: 2003 to 2009.
cenovic N., Smith S.J., Rose S.K. The representative
Science. 2013, 340: 852-857. doi: 10.1126/science.1234532.
concentration pathways: an overview. Climatic Change.
42. Zemp M., Huss M., Thilbert E., Eckert N., McNabb R.,
2011, 109: 5-31. doi: 10.1007/s10584-011-0148-z.
Huber J., Barandun M., Machguth H., Nussbaum-
27. O’Neill B.C., Kriegler E., Riahi K., Ebi K.L., Hal-
er S.U., Gärtner-Roer I., Thomson L., Paul F., Mauss-
legatte S., Carter T.R., Mathur R., Detlef P., van
ion F., Kutuzov S., Cogley J.G. Global glacier mass
Vuuren D.P. A new scenario framework for climate
changes and their contributions to sea-level rise from
change research: the concept of shared socioeconomic
1961 to 2016. Nature. 2019, 568 (7752): 382-386.
pathways. Climatic Сhange. 2014, 122 (3): 387-400.
43. Shean D.E., Bhushan S., Montesano P., Rounce D.R.,
28. Edwards T. Quantifying uncertainties in the land ice
Arendt A., Osmanoglu B. A systematic, regional assess
contribution to sea level from ISMIP6 and Glacier
ment of High Mountain Asia glacier mass balance.
MIP. EGU General Assembly Conference Abstracts.
2020: 11241.
org/10.3389/feart.2019.00363.
44. Zemp M, Frey H., Gärtner-Roer I., Nussbaumer S., Hoel-
activities-experiments.
zle M., Paul F., Haeberli W., Denzinger F., Ahlstrøm A.P.,
30. Rybak O.O., Rybak E.A., Kutuzov S.S., Lavrentyev I.I.,
Anderson B., Bajracharya S., Baroni C., Braun L.N.,
Morozova P.A. Calibration of the mathematical model
Cáceres B.E., Casassa G., Cobos G., Dávila L.R., Del-
of the dynamics of the Marukh glacier, Western Cau
gado Granados H., Demuth M.N., Espizua L., Fisch-
casus. Led i Sneg. Ice and Snow. 2015, 55 (2): 9-20.
er A., Fujita K., Gadek B., Ghazanfar A., Ove Hagen J.,
Holmlund P., Karimi N., Li Z., Pelto M., Pitte P., Pop-
Russian].
ovnin V.V., Portocarrero C.A., Prinz R., Sangewar C.V.,
31. Radić V., Hock R. Regionally differentiated contribu
Severskiy I., Sigurđsson O., Soruco A., Usubaliev R., Vin-
tion of mountain glaciers and ice caps to future sea-
cent C. Historically unprecedented global glacier decline
level rise. Nature Geoscience. 2011, 4 (2): 91-94.
in the early 21st century. Journ. of Glaciology. 2015, 61
(228): 745-762. doi: 10.3189/2015JoG15J017.
32. Jennings K.S., Winchell T.S., Livneh B., Molotch N.P.
45. Radić V., Bliss A., Beedlow A.C., Hock R., Miles E.,
Spatial variation of the rain-snow temperature threshold
Cogley J.G. Regional and global projections of twen
across the Northern Hemisphere. Nat. Commun. 2018,
ty-first century glacier mass changes in response to
climate scenarios from global climate models. Cli
33. Pattyn F. The paradigm shift in Antarctic ice sheet
org/10.1007/s00382-013-1719-7.
org/10.1038/s41467-018-05003-z.
46. Berg B.A. Introduction to Markov chain Monte Carlo
34. RGI Consortium. Randolph Glacier Inventory (RGI) -
simulations and their statistical analysis. Markov Chain
A dataset of global glacier outlines: Version 6.0. Tech
Monte Carlo Lect Notes Ser Inst Math Sci Natl Univ
nical Report. Global Land Ice Measurements from
Singap. 2005, 7: 1-52.
303
Обзоры и хроника
47. Renard B., Kavetski D., Kuczera G., Thyer M.,
impacting summer river runoff and peak discharges.
Franks S.W. Understanding predictive uncertainty in
hydrologic modeling: the challenge of identifying input
org/10.1007/s10584-020-02931-y
and structural errors. Water Resources Research. 2010,
63. Brunner M.I., Farinotti D., Zekollari H., Huss M.,
46 (5): 1-22. doi: 10.1029/2009WR008328.
Zappa M. Future shifts in extreme flow regimes in Al
48. Stone E.J., Lunt D.J., Rutt I.C., Hanna E. Investigating
pine regions. Hydrology and Earth System Sciences.
the sensitivity of numerical model simulations of the
modern state of the Greenland ice-sheet and its future
hess-23-4471-2019.
response to climate change. The Cryosphere. 2010, 4:
64. Parkes D., Goosse H. Modelling regional glacier length
changes over the last millennium using the Open
49. McKay M.D., Beckman R.J., Conover W.J. Comparison
Global Glacier Model. The Cryosphere. 2020, 14:
of Three Methods for Selecting Values of Input Vari
ables in the Analysis of Output from a Computer Code.
65. Leclercq P.W., Oerlemans J., Basagic H.J., Bushueva I.,
Technometrics. 1979, 21: 239-245.
Cook A.J., Le Bris R. A data set of worldwide glacier
length fluctuations. The Cryosphere. 2014, 8 (2): 659-
51. Brun F., Berthier E., Wagnon P., Kääb A., Treichler D. A
spatially resolved estimate of high mountain Asia glacier
66. Raper S.C.B., Braithwaite R.J. Glacier volume response
mass balances from 2000 to 2016. Nat. Geosci. 2017, 10
time and its links to climate and topography based on a
conceptual model of glacier hypsometry. The Cryosphere.
52. Braun M.H., Malz P., Sommer C., Farías-Baraho-
na D., Sauter T., Casassa G., Soruco A., Skvarca P.,
67. Tielidze L.G., Wheate R.D. The Greater Caucasus Gla
Seehaus T.C. Constraining glacier elevation and mass
cier Inventory (Russia, Georgia and Azerbaijan). The
changes in South America. Nat. Clim. Change. 2019, 9:
tc-12-81-2018.
53. Hugonnet R., McNabb R., Berthier E., Menounos B.,
Nuth Ch., Girod L., Farinotti D., Huss M., Dussaillant I.,
ковые-районы/кавказ.
Brun F., Kääb A. Accelerated global glacier mass loss in
the early twenty-first century. Nature. 2021, 592: 726-
70. Anderson L.S., Anderson R.S. Modeling debris-cov
ered glaciers: response to steady debris deposition.
54. Giesen R.H., Oerlemans J. Climate-model induced
differences in the 21st century global and regional gla
org/10.5194/tc-10-1105-2016.
cier contributions to sea-level rise. Climate Dynamics.
71. Verhaegen Y., Huybrechts P., Rybak O., Popovnin V.V. Mod
elling the evolution of Djankuat Glacier, North Caucasus,
s00382-013-1743-7.
from 1752 until 2100 AD. The Cryosphere Discuss. 2020,
55. Slangen A.B.A., Katsman C.A., van de Wal R.S.W., Ver-
meersen L.L.A., Riva R.E.M. Towards regional projections
72. Zekollari H., Goelzer H., Pattyn F., Wouters B., Lher-
of twenty-first century sea-level change based on IPCC
mitte S. Towards a 3-D model for large-scale gla
SRES scenarios. Climate Dynamics. 2012, 38 (5-6):
cier simulations. EGU General Assembly 2020, On
56. Kraaijenbrink P.D.A., Bierkens M.F.P., Lutz A.F., Im-
org/10.5194/egusphere-egu2020-10947.
merzeel W.W. Impact of a global temperature rise of
1.5 degrees celsius on Asia’s Glaciers. Nature. 2017,
grant-for-glacier-research/
549: 257-260. doi: 10.1038/nature23878.
74. Kislov A.V., Glazovsky A.F. Simulation of the dynamics of the
57. Anderson B., MacKintosh A. Controls on mass balance
Hans tidal glacier (Svalbard) based on a stochastic model.
sensitivity of maritime glaciers in the Southern Alps,
Led i Sneg. Ice and Snow. 2019, 59 (4): 452-459. https://
New Zealand: The role of debris cover // Journ. of
doi.org/10.15356/2076-6734-2019-4-441. [In Russian].
Geophys. Research: Earth Surface. 2012, 117 (1): 1-15.
75. Kislov A.V., Morozova P.A. The Grosser Aletschgletscher
dynamics: from a «Minimal model» to a stochastic equa
58. Sakai A., Fujita K. Contrasting glacier responses to re
tion. Geography. Environment. Sustainability. 2016, 9 (1):
cent climate change in High-Mountain Asia. Scientific
Reports. 2017, 7: 13717. doi: 10.1038/s41598-017-14256-5.
59. Hock R., Bliss A., Marzeion B., Giesen R.H., Hira-
77. Dehecq A., Gourmelen N., Gardner A.S., Brun F.,
bayashi Y., Huss M., Radić V., Slangen A.B. Glacier
Goldberg D., Nienow P.W., Berthier E., Vin-
MIP-A model intercomparison of global-scale gla
cent Ch.,Wagnon P.,Trouvé E. Twenty-first century glacier
cier mass-balance models and projections. Journ.
slowdown driven by mass loss in High Mountain Asia. Nat.
Geosci. 2019, 12: 22-27. doi: 10.1038/s41561-018-0271-9.
org/10.1017/jog.2019.22.
78. Brun F., Wagnon P., Berthier E., Shea J.M., Immer-
60. Barnett T.P., Adam J.C., Lettenmaier D.P. Potential
zeel W.W., Kraaijenbrink P.D.A., Vincent Ch., Rever-
impacts of a warming climate on water availability in
chon C., Shrestha D., Arnaud Y. Ice cliff contribution
snow-dominated regions. Nature. 2005, 438 (7066):
to the tongue-wide ablation of Changri Nup glacier,
Nepal, central Himalaya. Cryosphere. 2018, 12: 3439-
61. Jansson P., Hock R., Schneider T. The concept of glacier
3457. doi: 10.5194/tc-12-3439-2018.
storage. A review. Journ. of Hydrology. 2003, 282: 116-
79. Rounce D.R., King O., McCarthy M., Shean D.E., Saler-
no F. Quantifying debris thickness of debris-covered gla
62. Rets E.P., Durmanov I.N., Kireeva M.B., Smirnov A.M.,
ciers in the Everest region of Nepal through invesion of a
Popovnin V.V. Past ‘peak water’ in the North Cauca
subdebris melt model. Journ. of Geophys. Research Let
sus: deglaciation drives a reduction in glacial runoff
ters. 2018, 123: 1094-1115. doi: 10.1029/2017JF004395.
304