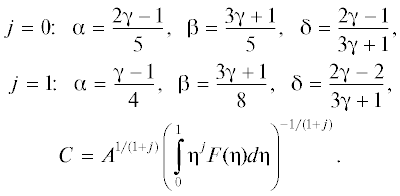Коллоидный журнал, 2022, T. 84, № 4, стр. 380-395

Течение в микроканале с супергидрофобными стенками

Наиболее простым и часто используемым решением уравнений вязкой жидкости с условием проскальзывания является решение задачи о стационарном течении в плоском канале с одной либо двумя супергидрофобными стенками. Такие решения несложно построить аналитическими методами. Например, для напорного течения в бесконечном плоском канале ширины H с нижней супергидрофобной стенкой, на которой задано эффективное условие проскальзывания Навье, решение задачи для скорости u* и расхода жидкости Q* через поперечное сечение канала имеет вид [7]:

Предполагается, что течение происходит вдоль одного из главных направлений тензора скольжения СГП, характеризуемого постоянной длиной скольжения b*. Остальные обозначения здесь: x*, y* – продольная и поперечная координаты, p* – давление, μ* – динамическая вязкость жидкости. Данное решение позволяет по измерению расхода при заданном перепаде давления определить значение длины скольжения супергидрофобной поверхности b*. Видно, что перепад давления в канале с супергидрофобной стенкой, обеспечивающий тот же расход, будет меньше, чем в канале с обычными стенками. Эффект снижения сопротивления канала тем выше, чем больше отношение b*/H. Поскольку для существующих СГП величина проскальзывания не превосходит сотен микрометров, эффект относительного снижения сопротивления должен быть наиболее заметен в микроканалах.

Оседание сферы или диска вблизи супергидрофобной поверхности

Другим известным примером решения уравнений гидродинамики с условием проскальзывания на твердых стенках является задача о вычислении силы сопротивления малой сферы, оседающей с постоянной скоростью U* вблизи супергидрофобной стенки при стоксовом режиме течения [8, 9]. Полученная сила имеет вид:

Здесь h* – зазор между сферой и плоскостью. Аналогичная задача для оседающего тонкого диска радиуса R* решена в [10]. В этом случае решение для силы сопротивления имеет вид:

В последнем случае использовалось условие проскальзывания в тензорном виде для двух компонент скорости жидкости. При этом предполагалось, что длины скольжения, соответствующие главным направлениям на СГП ($b_{1}^{*}$, $b_{2}^{*}$), зависят от высоты зазора h* между диском и СГП. В [11] описаны экспериментальные методики, разработанные на основе указанных аналитических решений, для определения длины скольжения на СГП с периодической текстурой и величины снижения трения, обусловленного макроскопическим проскальзыванием жидкости.

Растекание тонкого слоя жидкости от локализованного источника по горизонтальной СГП

Течения тонких слоев вязкой жидкости возникают на практике в различных физических контекстах и охватывают широкий диапазон характерных масштабов: от микрофлюидики до геофизических приложений. На сегодняшний день опубликовано большое количество теоретических, расчетных и экспериментальных работ, посвященных самым разным аспектам исследования таких течений с учетом различных физико-химических свойств жидкости (реологии, тепломассообмена, зависимости поверхностного натяжения от температуры, расклинивающего давления и пр.) с классическим условием прилипания на твердой стенке [12, 13]. В некоторых публикациях использовалось граничное условие проскальзывания при моделировании окрестности точек разрыва в очень тонких пленках [14, 15] и для устранения неинтегрируемой особенности вблизи динамического угла контакта трех сред.

Имеется класс автомодельных решений, соответствующий задачам растекания тонкого слоя вязкой жидкости по твердой поверхности от локализованного источника массоподвода в поле силы тяжести с условием прилипания [16, 17]. При рассмотрении растекания пленки жидкости по СГП с условием Навье в постановку задачи добавляется параметр с размерностью длины (длина проскальзывания), что ставит под вопрос существование автомодельных решений. Тем не менее, в работе авторов [18] удалось построить несколько типов автомодельных решений для растекания пленки от локализованного источника по однородным и неоднородным СГП. Характерная толщина рассматриваемых пленок жидкости на подстилающей поверхности составляет несколько миллиметров, поэтому проскальзывание на СГП в таких задачах оказывает очень заметное влияние на эволюцию тонкого слоя: скорость распространения переднего фронта, геометрию пятна смачивания и форму поверхности слоя.

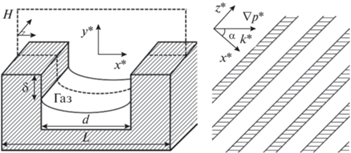
Рассматривается плоское (линейный источник) либо осесимметричное (точечный источник) растекание жидкости вдоль горизонтальной СГП при наличии локализованного источника массоподвода в пленку, расположенного в начале координат (рис. 1) и имеющего заданный объемный расход Q*(t*).

Считается, что растекание происходит вдоль главного направления тензора проскальзывания, в общем случае, неоднородной СГП, поэтому граничное условие (в безразмерном виде) принимает вид $u = b\left( x \right)\left( {{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}} \right)$. При обезразмеривании в качестве характерных масштабов выбраны: продольной координаты – расстояние от источника L, толщины пленки – ${{h_{0}^{*} = Q_{0}^{*}} \mathord{\left/ {\vphantom {{h_{0}^{*} = Q_{0}^{*}} {{{\pi }^{j}}{{L}^{{j + 1}}}}}} \right. \kern-0em} {{{\pi }^{j}}{{L}^{{j + 1}}}}}$, скорости растекания жидкости – ${{Q_{0}^{{*3}}g} \mathord{\left/ {\vphantom {{Q_{0}^{{*3}}g} {{{\pi }^{{3j}}}{{L}^{{3j + 4}}}}}} \right. \kern-0em} {{{\pi }^{{3j}}}{{L}^{{3j + 4}}}}}\nu {\kern 1pt} *$, времени – ${{\pi }^{{3j}}}{{L}^{{3j + 5}}}\nu {\kern 1pt} *{\kern 1pt} {\text{/}}Q_{0}^{{*3}}g$. Здесь $Q_{0}^{*}$ – объем жидкости, подведенный в пленку (в плоском случае – на единицу размаха) за время, когда передний фронт проходит расстояние L, ν* – кинематическая вязкость жидкости, j = 0 соответствует линейному источнику массоподвода, j = 1 – точечному источнику массоподвода. Безразмерная длина скольжения в условии проскальзывания (отнесенная к $h_{0}^{*}$) имеет вид b(x) = Bx^δ, в котором координата x совпадает с направлением растекания жидкости. В частном случае δ = 0 получается класс однородных СГП, для которых b(x) = const. В предположении малости толщины слоя по сравнению с продольным масштабом длины задача об эволюции тонкого слоя на горизонтальной поверхности в поле силы тяжести сводится к решению асимптотических уравнений стоксовой пленки. Интегрирование этих уравнений с учетом граничного условия проскальзывания на СГП, а также динамического и кинематического условий на внешней границе слоя, приводит к уравнению типа нелинейной теплопроводности, описывающему эволюцию формы поверхности слоя (в безразмерном виде) h(x, t) на неоднородной СГП:

Для принудительного режима растекания, вызванного наличием локализованного источника массоподвода в слой, капиллярные эффекты, как правило, малы, поэтому в уравнении поверхностное натяжение не учитывается. Математическая постановка задачи об эволюции тонкого слоя дополняется условиями известного объема жидкости в пленке в каждый момент времени и нулевой толщины на переднем фронте:

Здесь Q(t) – заданный (отнесенный к $Q_{0}^{*}$) закон массоподвода в слой, x_f(t) – закон движения безразмерной координаты переднего фронта смачивания. При B = 0 уравнение принимает известный в литературе вид [16].

В общем случае, когда параметры B и δ не равняются нулю, удается построить два различных типа автомодельных решений, соответствующих двум разным законам массоподвода в слой – степенному и экспоненциальному по времени. Для степенного закона массоподвода Q(t) = (2π)^jAt^γ автомодельное решение ищется в виде h = t^αF(η), η = x/Ct^β, для экспоненциального закона массоподвода Q(t) = (2π)^jAe^γt – в виде h = exp(αt)F(η), η = = x/Cexp(βt). Здесь A и γ – заданные константы; значения параметров C, α и β вычисляются в процессе решения задачи. Существует однозначная функциональная связь между значениями α, β и γ, определяющими конкретный вид автомодельного решения, и параметром δ в выражении для b(x). Например, для степенного закона массоподвода имеем [18]:

Здесь функция F(η) рассчитывается численно из решения обыкновенного дифференциального уравнения, получающегося из уравнения эволюции пленки [18]. Для возможного сравнения с экспериментом важное значение имеет закон движения переднего фронта. В размерных переменных этот закон имеет вид [18]:

Для частного случая однородной СГП (B = = const) автомодельное решение существует лишь для специальных законов массоподвода [18]:

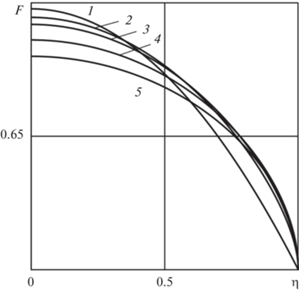
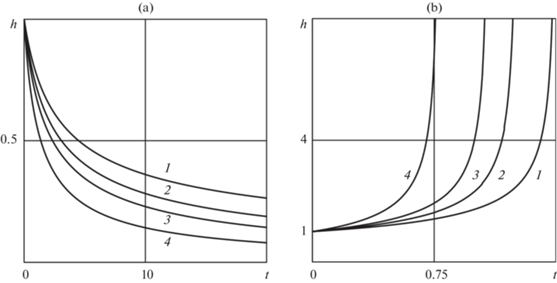
Из полученного решения следует, что при растекании по СГП за то же время передний фронт жидкости преодолевает большее расстояние по сравнению с обычной поверхностью. Отметим, что в отличие от задач капиллярной гидродинамики, в которых капиллярные силы определяют распространение фронта смачивания, для рассматриваемого класса задач динамика пятна смачивания не зависит от деталей течения в малой окрестности динамического угла контакта трех сред, а определяется лишь законами подвода массы и импульса в локализованном источнике. Поэтому, несмотря на то что построенные решения не описывают течение в очень малой окрестности фронта смачивания, они правильно предсказывают закон его распространения [16]. На рис. 2 представлены результаты расчетов автомодельной функции F(η) для степенного закона массоподвода в слой и некоторых значений параметров γ и B.

В [18] было построено и исследовано аналогичное решение для экспоненциального закона массоподвода, а также дано обобщение построенных автомодельных решений на случай неодномерных течений от линейного источника массоподвода.

Аналогичные решения рассматривались и в более поздних работах других авторов. Так, в [19] исследованы автомодельные режимы растекания вулканической лавы по горизонтальной поверхности с частичным условием проскальзывания. В [20] рассмотрено течение тонкого слоя вдоль СГП с длиной скольжения, зависящей от продольной координаты.

Стекание ручейка вязкой жидкости по наклонной неоднородной СГП

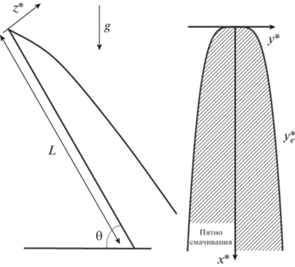
В работе авторов [21] рассмотрена задача о стекании ручейка вязкой жидкости от постоянного локализованного источника по наклонной неоднородной СГП в поле силы тяжести (рис. 3). Условие проскальзывания Навье (в безразмерном виде) задавалось для двух компонент вектора скорости жидкости ${{u}_{i}} = {{b}_{i}}\left( {x,y} \right)\left( {{{\partial {{u}_{i}}} \mathord{\left/ {\vphantom {{\partial {{u}_{i}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)$, при этом предполагалось, что направление стекания совпадает с одним из главных направлений тензора скольжения, а главные значения тензора скольжения в безразмерной форме имеют вид b_1,2(x, y) = B_1,2x^γy^δ. Здесь x и y – декартовы координаты на наклонной поверхности с началом в источнике; координата x совпадает с направлением стекания ручейка и направлена вдоль поверхности.

При обезразмеривании в качестве масштабов выбраны: характерное расстояние от источника L, характерная ширина пятна смачивания ${{\left( {{{\nu {\text{*}}{\kern 1pt} {{L}^{3}}Q_{0}^{*}} \mathord{\left/ {\vphantom {{\nu {\text{*}}{\kern 1pt} {{L}^{3}}Q_{0}^{*}} g}} \right. \kern-0em} g}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}$, толщина слоя ${{\left( {{{{{\nu }^{{*2}}}Q_{0}^{{*2}}} \mathord{\left/ {\vphantom {{{{\nu }^{{*2}}}Q_{0}^{{*2}}} {{{g}^{2}}L}}} \right. \kern-0em} {{{g}^{2}}L}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}$, скорость стекания жидкости ${{\left( {{{Q_{0}^{{*4}}{{g}^{3}}} \mathord{\left/ {\vphantom {{Q_{0}^{{*4}}{{g}^{3}}} {{{\nu }^{{*3}}}{{L}^{2}}}}} \right. \kern-0em} {{{\nu }^{{*3}}}{{L}^{2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}$, где $Q_{0}^{*}$ – заданный постоянный объемный расход источника, ν* – кинематическая вязкость, g – ускорение силы тяжести. Длина проскальзывания отнесена к характерной толщине слоя. Указанные масштабы определяются из асимптотического анализа уравнений тонкого слоя в рассматриваемых условиях. Для ручейка выводятся асимптотические уравнения тонкого слоя в приближении Стокса, интегрирование которых с учетом условий скольжения приводит к уравнению в частных производных для установившейся формы поперечного сечения ручейка h(x, y) на неоднородной СГП:

Здесь θ – угол наклона СГП к горизонту (рис. 3), h – безразмерная толщина слоя жидкости. Постановка задачи об установившемся стекании жидкости завершается заданием условия сохранения объемного расхода жидкости через поперечное сечение ручейка, а также условиями симметрии поперечного сечения и равенства нулю толщины слоя на боковых границах пятна смачивания:

Как и в задачах о нестационарном растекании пленки от локализованного источника по плоской стенке, используемая модель не описывает форму свободной поверхности и детали течения в малой окрестности боковых краев пятна смачивания, поэтому величина угла смачивания не существенна для нахождения решения в основной части пленки.

При B_1,2 = 0 уравнение принимает известный в литературе вид [22]. В общем случае, когда параметры B_1,2, δ и γ отличны от нуля, уравнение допускает автомодельное решение в форме h = = x^αF(η), η = y/Cx^β, аналогичной решениям для наклонной поверхности без проскальзывания [22]. Существует однозначная функциональная связь между параметрами δ и γ, определяющими b_1,2(x, y), и значениями α и β:

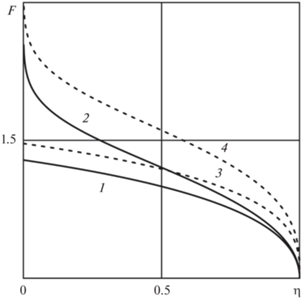
Функция F(η) рассчитывается численно из решения обыкновенного дифференциального уравнения, а затем вычисляется константа C в законе распространения пятна смачивания [21]. Одновременно с нахождением автомодельного решения определяется автомодельная форма пятна смачивания на наклонной СГП. В размерном виде полученное решение и закон распространения пятна смачивания имеют вид [22]:

На рис. 4 представлен график функции F(η) для некоторых значений B₁ и θ = π/3 при δ = 0, γ = = –1/7, что соответствуют аналитическому решению уравнения для автомодельной функции [21].

В [23] граничное условие проскальзывания типа Навье на наклонной СГП с B = const использовано для анализа постоянной в направлении стекания жидкости формы поперечного сечения ручейка с заданным значением контактного угла на границе пятна смачивания.

Стекание тонкого слоя жидкости с горизонтальной цилиндрической супергидрофобной поверхности

В [24] исследована эволюция тонкого слоя жидкости на поверхности горизонтального супергидрофобного кругового цилиндра, ось которого перпендикулярна вектору силы тяжести. Азимутальный угол φ отсчитывается от верхней точки цилиндрической поверхности (рис. 5).

В начальный момент времени жидкость покрывает поверхность цилиндра сплошным слоем толщиной $h_{0}^{*}$ (отсутствуют краевые углы смачивания). Характерная скорость стекания жидкости ${{h_{0}^{{*2}}g} \mathord{\left/ {\vphantom {{h_{0}^{{*2}}g} {\nu {\kern 1pt} * }}} \right. \kern-0em} {\nu {\kern 1pt} * }}$, время утончения слоя ${{\nu {\kern 1pt} *{\kern 1pt} R{\kern 1pt} *} \mathord{\left/ {\vphantom {{\nu {\kern 1pt} *{\kern 1pt} R{\kern 1pt} *} {h_{0}^{{*2}}g}}} \right. \kern-0em} {h_{0}^{{*2}}g}}$. Эти величины используются в качестве масштабов для обезразмеривания величин с соответствующими размерностями. Для азимутальной (безразмерной) компоненты скорости жидкости u на поверхности цилиндра задается условие проскальзывания $u = B{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial r}}} \right. \kern-0em} {\partial r}}$, B = const. В предположении малой толщины слоя по сравнению с радиусом цилиндра $h_{0}^{*} \ll R{\kern 1pt} *$ получены асимптотические уравнения тонкой стоксовской пленки на цилиндрической поверхности. После интегрирования этих уравнений с граничными условиями проскальзывания в пренебрежении силой поверхностного натяжения на свободной поверхности получено уравнение гиперболического типа, описывающее эволюцию безразмерной толщины слоя h(t) на цилиндре:

При B = 0 аналогичное уравнение использовалось ранее для исследования стекания жидкости на цилиндрической поверхности без проскальзывания [25]. Для исследования влияния длины проскальзывания B на эволюцию слоя уравнение удобно переписать в виде системы обыкновенных дифференциальных уравнений вдоль характеристических направлений:

Решение полученной системы уравнений для верхней и нижней точек цилиндра может быть использовано для оценки влияния проскальзывания жидкости на супергидрофобном цилиндре на скорость стекания жидкости, а также для определения параметров скольжения СГП. В этих точках система уравнений сводится к интегрированию одного уравнения:

где φ₀ равняется 0 или π. Соответствующие решения имеют вид:

При B → 0 получается решение h(t) = (3/(3 ± ± 2t))^1/2 [25]. Анализ полученных решений показывает, что время стекания слоя с супергидрофобного цилиндра (время утончения слоя на заданную конечную величину) заметно меньше, чем с обычного цилиндра. В качестве примера влияния параметра B на интенсивность стекания жидкости на рис. 6 представлены результаты расчета толщины слоя в верхней и нижней точках цилиндрической поверхности.

Рассмотренные течения вдоль разных типов СГП и найденные автомодельные решения для формы поверхности тонкого слоя и закона распространения пятна смачивания, а также законы утончения слоя на поверхности супергидрофобного цилиндра могут служить удобным инструментом для экспериментального определения параметров супергидрофобной поверхности.

Постановки задач. Метод граничных интегральных уравнений

Рассматриваются две постановки задач о течении вязкой жидкости вблизи периодической полосчатой СГП, текстура которой образована прямоугольными микрокавернами, содержащими пузырьки газа: напорное течение в микроканале, одна либо обе стенки которого являются супергидрофобными, и сдвиговое течение над полосчатой СГП.

Так как СГП имеет периодическую текстуру, решение задачи удобно проводить для выделенного периодического элемента течения, содержащего каверну с газом (рис. 7). На рис. 7: L – длина периода текстуры поверхности и характерный линейный размер задачи для выделенного элемента течения. Напорное течение в микроканале происходит под действием осредненного градиента давления $\kappa {\kern 1pt} * = \nabla p{\kern 1pt} *$, сдвиговое течение – при наличии заданной скорости сдвига k* вдали от СГП. Так как течение вблизи одиночной каверны стоксово, то в силу линейности уравнений Стокса поле скорости U*, индуцированное заданным перепадом давления или сдвигом скорости, направленным под углом к кавернам СГП (рис. 7), представляется в виде u*(x*, y*) + w*(x*, y*)e_z, где u*(x*, y*) соответствует двумерному течению перпендикулярно каверне с газом, а w*(x*, y*) – течению вдоль каверны; (x*, y*) – декартовы координаты в плоскости перпендикулярной каверне. Если внешнее воздействие, создающее течение над полосчатой СГП, направлено перпендикулярно кавернам, то U* = u*, если вдоль каверн: U* = w*e_z. В общем случае для напорного течения в микроканале и сдвигового течения над каверной можно записать:

Компоненты вектора скорости U*, соответствующие течениям перпендикулярно и вдоль каверны, удовлетворяют уравнениям (в безразмерной форме):

Во втором уравнении A = 1 соответствует уравнению Пуассона для напорного течения в канале, A = 0 – уравнению Лапласа для сдвигового течения над полосчатой СГП. При обезразмеривании в качестве масштабов скорости для течения перпендикулярно каверне выбраны ${{\kappa _{x}^{*}{{L}^{2}}} \mathord{\left/ {\vphantom {{\kappa _{x}^{*}{{L}^{2}}} \mu }} \right. \kern-0em} \mu }{\kern 1pt} *$ и $k_{x}^{*}L{\kern 1pt} *$, для течения вдоль каверны – ${{\kappa _{z}^{*}{{L}^{2}}} \mathord{\left/ {\vphantom {{\kappa _{z}^{*}{{L}^{2}}} \mu }} \right. \kern-0em} \mu }{\kern 1pt} *$ и $k_{z}^{*}L{\kern 1pt} $.

Для медленного течения вблизи малой каверны с газовым пузырьком отношение изменения давления за счет течения жидкости вдоль мениска к скачку давления на межфазной поверхности за счет капиллярных сил определяется капиллярным числом, которое в рассматриваемых случаях очень мало: Ca = μ*U/σ* $ \ll $ 1. Поэтому изменением формы поверхности пузырька, обусловленным течением жидкости, можно пренебречь, а форма поверхности пузырька, как в статике, может быть задана элементом дуги окружности. При этом объем газа в каверне, т.е. положение точек закрепления мениска на стенках каверны при фиксированной температуре, определяется локальным давлением в жидкости над каверной и начальной массой газа в каверне. Легко устанавливается математическая связь между статическим углом смачивания в точке закрепления мениска со стенками каверны и радиусом кривизны мениска [35]. В данном случае статическая форма мениска является следствием условия непрерывности нормального потока импульса на поверхности пузырька.

Математическая задача о течении жидкости в области, соответствующей выделенному элементу периодического течения в направлениях перпендикулярно и вдоль каверны с газом, завершается заданием граничных условий. Для скорости жидкости задаются периодические граничные условия во входном/выходном сечениях расчетной области в случае течения перпендикулярно каверне или на боковых границах для течения вдоль полос [35, 36]. На верхней границе расчетной области задается условие прилипания для скорости в случае течения в канале либо заданное значение скорости, соответствующее сдвиговому потоку. На поверхности пузырька (межфазной границе) задаются кинематическое условие непротекания и динамическое условие отсутствия касательных напряжений; на твердых стенках – прилипание жидкости. В ситуации, когда верхняя граница области течения также содержит каверну с газом, на части границы, соответствующей поверхности пузырька, задаются условия на межфазной границе, а на оставшейся части – прилипание жидкости.

Для решения уравнений Стокса, а также Пуассона/Лапласа в области над каверной, занятой газом, и вычисления скорости жидкости авторами был разработан вариант метода граничных интегральных уравнений, применяемого для решения линейных задач эллиптического типа [46, 47]. Данный метод позволяет заменить линейные дифференциальные уравнения в частных производных в области, содержащей межфазные границы, системой граничных интегральных уравнений, заданных на границе расчетной области. При этом размерность исходной задачи снижается на единицу. Важными преимуществами использованного метода является возможность проводить с контролируемой точностью расчет картины течения жидкости в области над каверной с учетом вкладов окрестностей точек смены типа граничного условия с прилипания на нулевое касательное напряжение. В этих точках производные некоторых переменных, в частности, давления, имеют сингулярности.

Решение сформулированных задач для компонент вектора скорости u и w получается сверткой фундаментальных решений дифференциальных операторов с плотностями, распределенными по границе расчетной области:

В интегральных уравнениях G_ij(x, x₀) и T_ijk(x, x₀) – фундаментальные решения “стокслет” и “стресслет” оператора Стокса [46]; F и ∂F/∂n – потенциалы простого и двойного слоя оператора Лапласа [47]; x и x₀ – радиусы-векторы точек, лежащих на границе или внутри расчетной области, соответственно; Λ равняется 1/2 или 1 для граничных и внутренних точек расчетной области; Γ и Ω – граница и внутренняя часть расчетной области; f = σ_ijn_je_i – вектор напряжений; i, j и k равняются 1 или 2; по повторяющимся индексам производится суммирование. Неизвестные значения плотностей фундаментальных решений определяются из решения граничных интегральных уравнений, записанных для точек на границе расчетной области. Для численного решения системы граничных интегральных уравнений применяется метод коллокаций, согласно которому граница расчетной области заменяется непрерывной ломаной линией, состоящей из конечного числа прямолинейных отрезков (граничных элементов). Интегрирование по границе расчетной области заменяется дискретной суммой интегралов по граничным элементам. Компоненты векторов (u, f) и значения (w, ∂w/∂n) вычисляются в серединах элементов разбиения, поэтому вычисление дискретных интегралов по элементам разбиения сводится к интегрированию фундаментальных решений оператора Стокса или Лапласа вдоль элементов. В результате граничные интегральные уравнения заменяется системой линейных алгебраических уравнений (СЛАУ) высокого порядка относительно неизвестных значений (u, f) и (w, ∂w/∂n) в дискретных точках. К СЛАУ добавляются граничные условия на межфазной поверхности, которые рассматриваются как дополнительные уравнения для граничных точек. В процессе решения СЛАУ вычисляются значения компонент вектора скорости жидкости (u, w) на поверхности пузырька.

Основные особенности численного алгоритма, разработанного для решения интегральных уравнений, соответствующих рассматриваемым задачам, подробно изложены в [35, 36].

После вычисления скорости жидкости на поверхности пузырька и в области над каверной определяются параметры течения жидкости, осредненные по периоду. Для напорного течения в микроканале – это перепад давления, вычисляемый для заданных значений относительной ширины канала H/L, геометрических параметров каверн, формы межфазной границы и безразмерного сдвига мениска внутрь каверн. Величина перепада давления может быть определена из интегрального закона сохранения импульса для конкретной геометрии расчетной области [37]. Для сдвигового течения целевыми параметрами являются осредненная скорость проскальзывания жидкости, осредненное касательное трение и эффективная длина скольжения, которая вычисляется из осредненного по элементу течения условия проскальзывания Навье при заданных значениях остальных параметров подобия (все параметры безразмерные):

Здесь 〈⋅〉 обозначает операцию осреднения по линии, проходящей через угловые точки каверны, b₁ и b₂ – безразмерные длины скольжения, соответствующие течениям перпендикулярно и вдоль каверны.

В последние годы другие авторы также начинают использовать метод граничных интегральных уравнений для анализа течений вблизи периодических полосчатых СГП [48].

Сдвиговое течение вблизи полосчатой СГП

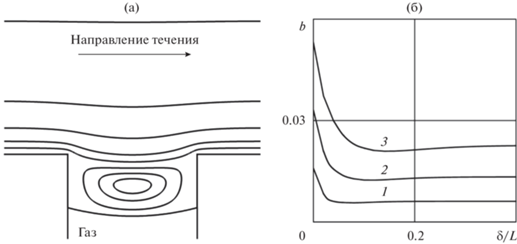
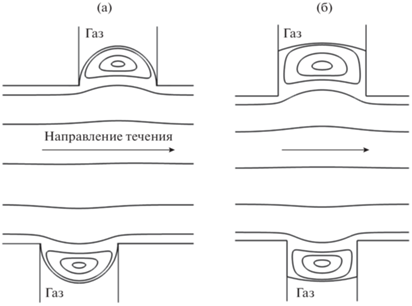
Ниже представлены некоторые результаты расчетов параметров двумерного сдвигового течения перпендикулярно каверне ширины d. В качестве периодических граничных условий до и после каверны для скорости в проведенных расчетах задавался линейный профиль (u, v) = (y, 0). В [35] на основе моделирования обтекания системы каверн было показано, что для достаточно большого расстояния между кавернами (d/L < 0.6) линейный профиль скорости мало отличается от периодического профиля скорости, формирующегося между кавернами. На рис. 8а представлена характерная картина течения жидкости над каверной, частично занятой газом. Для выбранных значений параметров в жидкости над межфазной границей образуется вихревая зона, которая занимает все пространство в каверне. При δ/L → 0 (δ – смещение точек закрепления мениска вглубь каверны), когда точки закрепления мениска приближаются к угловым точкам каверны, вихрь исчезает и жидкость движется вдоль межфазной поверхности. На рис. 8б представлены результаты расчетов осредненной длины скольжения b в сдвиговом потоке при δ/L ≥ 0. Основной результат заключается в том, что смещение точек закрепления мениска на стенках каверны, приводит к почти двукратному уменьшению длины проскальзывания b. Поэтому положение точек закрепления мениска, наряду с другими параметрами текстуры, играет очень важную роль при прогнозировании снижения трения полосчатой СГП. Расчеты параметров течения для других значений d/L, 2R/d (R – радиус кривизны мениска) и δ/L качественно совпадают с результатами, представленными на рис. 8.

Следует упомянуть еще один важный результат: расчеты, проведенные для сдвиговых течений вдоль каверн полосчатой текстуры, показали [36], что в этом случае длина проскальзывания оказывается примерно в два раза больше, чем для течения поперек каверн при тех же остальных параметрах.

Стационарные течения в канале с супергидрофобными стенками

Ниже представлены некоторые результаты расчетов параметров напорного течения в микроканале, обе стенки которого являются супергидрофобными поверхностями, содержащими микрокаверны с газом [37]. В общем случае текстура стенок и положения межфазных поверхностей в кавернах на противоположных стенках могут различаться. При этом предполагается, что можно выделить периодический элемент течения, содержащий по одной каверне на каждой стенке канала (рис. 9).

Данная задача является многопараметрической и может описывать широкий диапазон практических ситуаций. В качестве профиля скорости на входе и выходе из расчетной области использовался профиль Пуазейля, который удовлетворяет условию периодичности для полосчатых СГП с разреженной системой каверн. В общем случае для нахождения периодического профиля скорости необходимо моделировать обтекание системы каверн либо использовать численную процедуру, описанную в [37]. На рис. 10а представлена картина течения в канале с одинаковыми супергидрофобными стенками и смещенными кавернами на периоде течения. Рис. 10б соответствует случаю различных несмещенных каверн на противоположных стенках канала.

Еще один существенный результат был получен в [36], где исследовалось влияние изменения давления при развитии течения в канале с нижней супергидрофобной стенкой. На основании расчетов было показано, что в различных сечениях канала из-за различных значений давления положения пузырьков в кавернах могут различаться, что, в свою очередь, приводит к заметному изменению длины скольжения СГП по длине канала.

Нестационарные течения в канале с супергидрофобной стенкой

Для выяснения возможных механизмов заметного снижения трения в турбулентных течениях над СГП в работах авторов [44, 45] были рассмотрены два модельных примера пульсирующих течений над каверной, содержащей сжимаемый газовый пузырек.

В [45] исследовано возможное влияние одновременных пульсаций давления и скорости во внешнем потоке жидкости на эффективные параметры СГП с полосчатой текстурой. В качестве внешнего решения вблизи выбранной каверны на СГП используется пульсирующий профиль скорости, который вырабатывается в плоском канале при гармоническом законе изменения давления. Предполагается, что толщина канала много больше размера микрокаверн на его стенке. Пульсации давления во внешнем потоке приводят к колебаниям мгновенной формы поверхности и объема пузырька в каверне. При этом пульсации профиля скорости и давления могут приводить к противоположным воздействиям на эффективную скорость проскальзывания и снижение трения. Целью работы являлось параметрическое исследование влияния осцилляций скорости и давления на эффективные параметры супергидрофобной поверхности с полосчатой структурой при различных начальных состояниях газовых пузырьков в кавернах.

Уравнения движения пульсирующего течения вязкой жидкости под действием гармонического изменения градиента давления в плоском канале, записанные для ненулевой компоненты скорости жидкости, в безразмерной форме имеют вид:

Здесь B = Sh ∙ Re, где Sh – число Струхаля, Re – число Рейнольдса; A – безразмерная амплитуда пульсаций давления. При обезразмеривании в качестве масштаба длины выбрана ширина канала H, масштаба скорости –$\kappa {\kern 1pt} * {\kern 1pt} {{H}^{2}}{\text{/}}\mu {\kern 1pt} * $, где κ* – модуль градиента давления при отсутствии пульсаций, μ* – вязкость. Максимальная допустимая амплитуда пульсаций давления определяется из условия удержания газовых пузырьков в кавернах при их выпячивании в основной поток. В качестве граничных условий для u приняты условия прилипания на стенках канала u(t, y = 0) = u(t, y = 1) = 0.

Решение уравнений движения, удовлетворяющее граничным условиям, получается стандартным способом [49]:

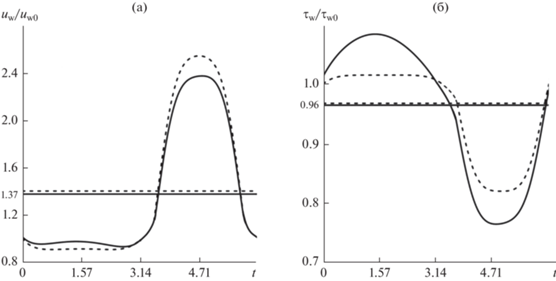
Первые два слагаемые в полученном выражении соответствуют профилю Пуазейля. На рис. 11а и 11б представлены профили пульсационной составляющей скорости, а также характерная зависимость мгновенного значения давления и касательного трения на стенке от времени. Вычисленные мгновенные значения отнесены к значениям, соответствующим течению без пульсаций. Пульсации трения на стенке и давления могут происходить в противофазе, т.е. для некоторых значений безразмерных параметров при сжатии пузырька или сильном искривлении его поверхности может быть лишь незначительное ухудшение средних за период пульсаций давления параметров СГП по сравнению со значениями, соответствующими стационарному течению с заданным профилем Пуазейля.

На масштабе одиночной каверны течение локально стоксово с периодическими по пространству граничными условиями. В постановку задачи о течении жидкости на масштабе каверны время входит как параметр, определяющий состояние газового пузырька в каверне и мгновенный профиль скорости вблизи каверны. Так как внешний профиль скорости пульсирует, мгновенный наклон профиля скорости перед и за каверной также изменяется. Для численного решения уравнений Стокса в области с изменяющейся границей и соответствующими периодическими граничными условиями, как и ранее, используется разработанный авторами численный алгоритм, основанный на методе граничных интегральных уравнений. В расчетах мгновенная форма поверхности пузырька определяется из условий сохранения массы газа в каверне и скачка давлений на поверхности пузырька с использованием уравнения состояния идеального газа. Растворимостью газа пренебрегается. При интенсивном сжатии форма поверхности пузырька, удерживаемого в каверне, не изменяется, мениск смещается вдоль стенок внутрь каверны. При понижении локального давления над каверной точки закрепления мениска доходят до верхних углов каверны, а затем форма поверхности пузырька начинает изменяться, и при достижении некоторого значения давления над каверной мениск может выступать из каверны в основной поток.

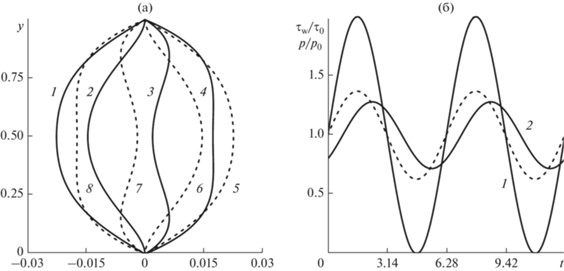
На рис. 12 представлен пример расчетов мгновенных значений осредненных по пространственному периоду скорости проскальзывания u_w (а) и касательного трения τ_w (б) на СГП. Их значения отнесены к u_w0 и τ_w0, вычисленным для стационарного течения с формой поверхности пузырька, соответствующей t = 0 в нестационарном течении. Сплошные линии – расчеты с учетом пульсаций скорости и давления вблизи стенки, пунктирные линии – расчеты с учетом лишь пульсаций давления. Учет лишь пульсаций давления над каверной при фиксированном линейном профиле скорости перед каверной был осуществлен в [44]. Сдвиг фаз между пульсациями давления и скорости приводит к нарушению симметрии кривых относительно четверти периода. Интервал времени 0 < t < 3.14 соответствует сжатию газа, 3.14 < t < 6.28 – расширению пузырька в каверне.

Таким образом показано, что при некоторых начальных положениях пузырьков в кавернах пульсации скорости и давления вблизи стенки могут даже увеличивать осредненное скольжение и снижать осредненное трение на СГП по сравнению с аналогичным стационарным течением. Полученные результаты могут служить основой для объяснения возможного механизма снижения трения на СГП в турбулентном потоке.