Вестник Военного инновационного технополиса «ЭРА», 2023, T. 4, № 1, стр. 51-58
Моделирование кратных отказов в аппаратуре наземных робототехнических комплексов
А. В. Заяра 1, *, А. Р. Абдрахманов 1
1 Военный инновационный технополис “ЭРА”
Анапа, Россия
* E-mail: era_otd3@mil.ru
Поступила в редакцию 10.10.2023
После доработки 10.10.2023
Принята к публикации 10.10.2023
Аннотация
Робототехнические комплексы, которые в ближайшее время поступят на вооружение общевойсковых подразделений, представляют собой совокупность аппаратуры различных принципов действия, подверженной неизбежным отказам. Успешный поиск мест отказов, в том числе кратных, будет определять эффективность системы технического обслуживания и ремонта комплексов. Рассматривается диагностическая модель, описывающая состояние аппаратуры при возникновении в ней кратных отказов. Разработка диагностического обеспечения на основе этой модели позволит успешно выполнять основные задачи технического диагностирования.
ВВЕДЕНИЕ
Сегодня роботизация вооружения сухопутных войск определяется как ведущее направление развития средств вооруженной борьбы. Интеграция боевых наземных робототехнических средств в мотострелковые подразделения для частичной замены солдата-пехотинца на поле боя уже стала очевидной реальностью [1]. В ближайшие годы в состав общевойсковых соединений войдут подразделения робототехнических комплексов (РТК). Одновременно с совершенствованием тактики их применения появится проблема организации их содержания, под которым понимается комплекс мероприятий, направленных на поддержание РТК в готовности к использованию по назначению [2]. Тем более что аппаратура комплексов представляет собой сложную совокупность различных функциональных модулей, каждый из которых, в свою очередь, оснащен аппаратурой различного принципа действия.
Эффективность мероприятий системы технического обслуживания и ремонта (ТО и Р) в соответствии с нормативными документами зависит от пригодности аппаратуры комплексов к проведению технического диагностирования (ТД) – комплекса технологических операций, который проводится с применением штатных контрольно-измерительных приборов, диагностического оборудования и контрольно-проверочных машин [2]. Основными задачами ТД являются контроль технического состояния и поиск места отказа. Для выполнения требований стандартов при проектировании РТК должно разрабатываться диагностическое обеспечение на основе анализа диагностической модели аппаратуры, которая является исходными данными для выбора диагностических параметров и методов их оценки, составления алгоритмов ТД [3].
Общими требованиями к моделям, описывающим отказы в аппаратуре, являются адекватность, универсальность и удобность. В соответствии с этими требованиями модель должна охватывать как можно большее число частных случаев и быть применимой в различных ситуациях [4]. Для выполнения упомянутых требований предлагается рассмотреть применение диагностической модели в форме ориентированного графа причинно-следственных (информационно-энергетических) связей между типовыми элементами замены (ТЭЗ), позволяющих обеспечить методическую достоверность при поиске кратных отказов.
ДИАГНОСТИЧЕСКАЯ МОДЕЛЬ
Анализ эксплуатационной документации на современные образцы вооружения показывает, что при разработке диагностического обеспечения, как правило, строятся аналитические модели – дифференциальные уравнения, логические соотношения, диаграммы прохождения сигналов или передаточные функции, предполагающие применение методов индивидуального контроля [5]. При таком методическом подходе к обеспечению контролепригодности состав диагностических параметров получается избыточным, что влечет за собой дополнительные затраты на средства ТД и увеличивает его продолжительность.
Предлагается диагностическая модель, которая задается представлением совокупности физических свойств объекта и его топологии в виде ориентированного графа с указанием причинно-следственных связей, описывающих взаимоотношения между его элементами и параметрами, и предполагает применение методов совместного контроля [5], что позволит оптимизировать состав диагностических параметров, не снижая методическую достоверность контроля.
Первым этапом построения диагностической модели является ее представление в неявном виде в форме ориентированного графа, который формируется на основе структурно-аналитического метода [5]. Исходными данными служат руководство по эксплуатации и прежде всего функциональная схема объекта диагностирования (ОД) и перечень параметров, используемых при контроле объекта. Такая модель является универсальной для аналоговых и цифровых объектов при условии применения “допусковых” методов контроля параметров, в том числе методов исчерпывающего тестирования (счет переходов и единиц, сигнатурный анализ), и подходит для решения задач диагностирования.
Неявная диагностическая модель (implicit diagnostic model) представляется ориентированным графом
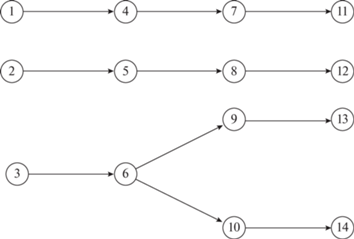
где V – множество вершин, каждая из которых соответствует конкретному контролируемому параметру, F – множество дуг, показывающих аналитические или статистические зависимости и качественные соотношения между параметрами.Размерность модели (1) определяется мощностью множеств видов состояния и параметров. Каждый параметр ${{{v}}_{i}}$ ∈ V (i = 1 … n, n = |P|) сопоставлен определенному ТЭЗ, с глубиной до которого проводится поиск места отказа. Дугам в ориентированном графе соответствуют качественные соотношения между параметрами. Орграф также представляется в виде матрицы смежности размером n × n, в которой каждая строка сопоставлена вершине vi, а столбец – дуге fi. Пример орграфа (1), поясняющий диагностическую модель объекта в неявном виде, приведен на рис. 1.
Как правило, граф-модель всего ОД – составной орграф, состоящий из нескольких связных подграфов. Для решения первой задачи ТД достаточно оценить (проверить) множество концевых параметров Vk, непосредственно характеризующих его техническое состояние. Поскольку электроаппаратура РТК относится к многорежимным объектам, эти параметры проверяются в режимах контроля [6], воспроизводящих штатные режимы работы аппаратуры. Как правило, этим параметрам в орграфе (1) соответствуют вершины с нулевой полустепенью исхода d+(vi) = 0. Обычно это – концевые вершины подграфов (terminal vertex) (подмножество Vtv ⊂ V). Для рассматриваемого примера (рис. 1) ${{V}_{{t{v}}}} = {\text{ }}\{ {{{v}}_{{11}}},\;{{{v}}_{{12}}},\;{{{v}}_{{13}}},\;{{{v}}_{{14}}}\} $. По значениям контролируемых параметров судят об изменении технического состояния.
Представление графа (1) в форме матрицы смежности позволяет выполнить дальнейшие преобразования для получения диагностической модели в явном виде – совокупности формальных описаний неисправных состояний ОД [5].
1. Транзитивное замыкание орграфа (transitive closure) преобразует матрицу смежности орграфа (1) в матрицу смежности транзитивно замкнутого графа |D| → |$D_{{tc}}^{*}$|. Замкнутый орграф $D_{{tc}}^{*}$ наглядно демонстрирует влияние каждой предыдущей вершины на последующие по направлению ориентирования графа. Также процедура замыкания позволяет выявить дополнительные контуры обратной связи в ОД.
2. Исправное состояние каждого ТЭЗ будет проявляться допустимыми значениями диагностических параметров, т.е. каждая вершина в замкнутом графе будет иметь петлю. В матрице достижимости всем диагональным элементам необходимо присвоить значение ${{{v}}_{{ii}}} = {\text{ }}1$.
3. Завершающий этап – инвертирование всех элементов матрицы.
В результате этих преобразований получается матрица, содержащая информацию о состояниях объекта при возможных недопустимых значениях контролируемых параметров. На основе этой матрицы можно построить орграф, поясняющий бинарное отношение между множеством видов состояний (отказов) и множеством альтернативных результатов контроля параметров
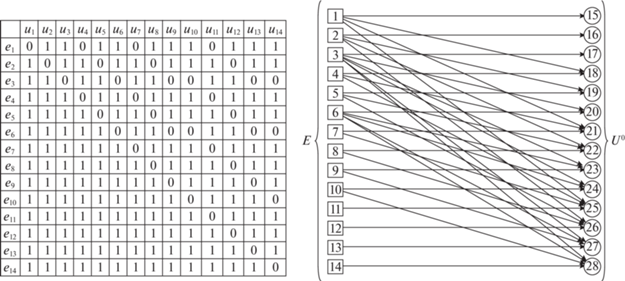
где E – множество вершин, сопоставленных видам состояния вероятных, однократных отказов (строки матрицы), а U – множество вершин, сопоставленных допустимым и недопустимым значениям параметров (столбцы матрицы), которые, в свою очередь, где U1 – подмножество результатов проверок, показавших допустимые значения диагностических параметров, U1 ∈ U, а U0 – подмножество результатов проверок, показавших недопустимые значения диагностических параметров, U0 ∈ U.Бинарное отношение φ представляет собой диагностическую модель в явном виде (explicit diagnostic model), которая может быть визуализирована двудольным орграфом Φexp. Матрица отношения φ и двудольный орграф Φexp представлены на рис. 2. Необходимо обратить внимание на то, что полученная матрица не может быть классифицирована как матрица. Существующие средства визуализации позволяют автоматизировать построение двудольного графа, но применительно к этому случаю необходимо последовательно провести с матрицей φ дополнительные преобразования для получения наглядного рисунка. Тем не менее матрица отношения φ может служить исходными данными для локализации области отказа и оптимизации алгоритмов его поиска, но это – отдельные аспекты решения второй задачи ТД.
Бинарное отношение (2), которое можно записать как
показывает, что отказы элементов определяют значения контролируемых параметров.В матрице отношения (4) каждая i-я строка показывает влияние отказа элемента объекта, следствием которого является недопустимое значение i-го параметра (значение “0” на главной диагонали), на исходы (результаты) проверок остальных диагностических параметров в этом объекте. Каждая i-я строка может классифицироваться как кортеж [7] и является описанием неисправного состояния однократного отказа ТЭЗ.
Вершина ei (отказ элемента объекта, следствием которого является недопустимое значение i-го параметра) соединяется дугами с вершинами, принадлежащими множеству Uj, которое, в свою очередь, представлено объединением двух подмножеств по аналогии с (3), но теперь для конкретного состояния однократного отказа ei:
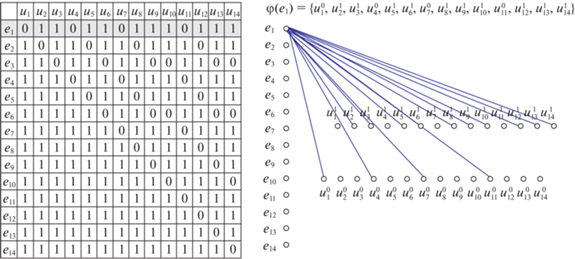
где ${{U}_{j}} \subset U,U_{j}^{0}$ – подмножество результатов проверок j-х параметров, находящихся вне допустимых пределов, которым соответствуют “0” в i‑й строке матрицы |φ|, $U_{j}^{1}$ – подмножество допустимых исходов проверок j-х параметров и имеющим “1” в i-й строке матрицы $\left| \varphi \right|$. Пример матрицы диагностической модели в явном виде для состояния однократного отказа e1 и подграфа φ(e1) поясняется схемой на рис. 3.Каждый однократный отказ ei следствием из (4) имеет свой образ φ(ei), который представлен строкой в матрице графа отношения φ или i-м кортежем длины n, составленным из элементов множества U – различной комбинацией исходов проверок согласно (5):
где $U_{j}^{{0 \vee 1}}$ = {$u_{1}^{{0 \vee 1}},u_{2}^{{0 \vee 1}}, \ldots ,u_{n}^{{0 \vee 1}}$}. Элемент $u_{j}^{{0 \vee 1}}$ называется j-й компонентой кортежа. Каждый кортеж в матрице однократного отказа имеет разное описание (исходы проверок):Другими словами, отказ любого элемента не может проявляться одновременно недопустимым и допустимым значением параметра, т.е. в матрице графа φ нет одинаковых строк [5].
Анализируя матрицу модели в явном виде по столбцам, можно сделать выводы, что граф Φexp обладает следующими свойствами:
(9)
${{\varphi }^{{--1}}}(u_{j}^{0}) \cap {{\varphi }^{{--1}}}(u_{j}^{1}) = \emptyset ,\quad j = 1{\text{ }} \ldots n,$МОДЕЛЬ КРАТНОГО ОТКАЗА
По различным причинам в аппаратуре РТК могут возникнуть одновременно несколько отказов различных ТЭЗ. Универсальность модели в форме матрицы отношения φ заключается как раз в том, что она позволяет получить описание состояния ОД при наличии в нем кратных отказов.
Прежде чем приступить к формированию модели кратного отказа в объекте, следует проанализировать последовательность формирования кортежей (6) на основе причинно-следственных связей орграфа (1).
Формализованное описание однократного отказа в матрице – строка с исходами проверок φ(ei). Значение “0” на j-м порядковом месте в строке показывает, что в матрице транзитивно замкнутого графа есть дуга из i-й вершины графа (1) в j-ю, которая и определяет недопустимый результат проверки j-го диагностического параметра. И, наоборот, значение “1” свидетельствует об отсутствии влияния i-й вершины на исход проверки какого-либо диагностического параметра объекта.
Рассмотрим модель двукратного отказа. Количество строк во вновь сформированной матрице увеличится до значения
(10)
$S = \frac{{\left( {n + 1} \right)!}}{{2~\left( {n - 1} \right)!}}~ \vee S = \frac{{n\left( {n + 1} \right)}}{2},$(11)
$\varphi ({{e}_{i}} \wedge {{e}_{j}}) = \varphi \left( {{{e}_{i}}} \right)^\circ \varphi \left( {{{e}_{j}}} \right),i \ne j.$Для определения появления во вновь формируемой матрице неразличимых состояний проводится анализ связности на основе орграфа диагностической модели (1). Исходными данными служит матрица смежности транзитивно замкнутого орграфа
где Ftc – множество дуг транзитивно замкнутого орграфа, которые удовлетворяют условию(13)
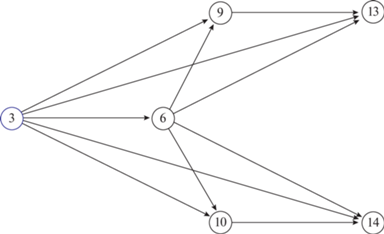
$\exists \forall ({{f}_{k}},{{f}_{l}}) \wedge ({{f}_{l}},{{f}_{m}}) \Rightarrow \exists ({{f}_{k}},{{f}_{m}}),$Рассмотрим в качестве примера независимый подграф модели (1), в частности его транзитивно замкнутую версию с корневой вершиной ${{\delta }^{ - }}({{{v}}_{3}})$ = = 0 (рис. 4). Образ корневой вершины будет включать в себя все остальные вершины $f_{{tc}}^{*}\left( {{{{v}}_{k}}} \right) = \left\{ {{{{v}}_{6}},{{{v}}_{{9,}}}{{{v}}_{{10,}}}{{{v}}_{{13,}}}{{{v}}_{{14~}}}} \right\}$.
При формировании матрицы двукратного отказа внутри каждой такой области будут формироваться неразличимые кортежи. То есть условие (7) для множества двукратных отказов уже не будет работать. Рассмотрим это новое свойство на примере одного отдельного подграфа D3tc (рис. 4) для вершины δ-(f3) = 0.
В матрице, соответствующей модели двукратного отказа (табл. 1), появятся одинаковые строки, соответствующие множествам сочетаний однократных отказов диагностических параметров, входящих в рассматриваемый подграф:
(14)
$\begin{gathered} \varphi \left( {{{e}_{3}}} \right) = \varphi ({{e}_{3}} \wedge {{e}_{6}}) = \varphi ({{e}_{3}} \wedge {{e}_{9}}) = \\ = \varphi ({{e}_{3}} \wedge {{e}_{{10}}}) = \varphi ({{e}_{3}} \wedge {{e}_{{13}}}) = \varphi ({{e}_{3}} \wedge {{e}_{{14}}}), \\ \end{gathered} $(15)
$\begin{gathered} \varphi \left( {{{e}_{6}}} \right) = \varphi ({{e}_{6}} \wedge {{e}_{9}}) = \varphi ({{e}_{6}} \wedge {{e}_{{10}}}) = \\ = \varphi ({{e}_{6}} \wedge {{e}_{{13}}}) = \varphi ({{e}_{6}} \wedge {{e}_{{14}}}), \\ \end{gathered} $(16)
$\varphi \left( {{{e}_{9}}} \right) = \varphi ({{e}_{9}} \wedge {{e}_{{13}}}),\varphi \left( {{{e}_{{10}}}} \right) = \varphi ({{e}_{{10}}} \wedge {{e}_{{14}}}).$Таблица 1.
Матрица двукратных отказов неразличимыми строками
| № | Отказы | Исходы проверок | |||||
|---|---|---|---|---|---|---|---|
| u3 | u6 | u9 | u10 | u13 | u14 | ||
| 1 | e3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | e6 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | e9 | 1 | 1 | 0 | 1 | 0 | 1 |
| 4 | e10 | 1 | 1 | 1 | 0 | 1 | 0 |
| 5 | e13 | 1 | 1 | 1 | 1 | 0 | 1 |
| 6 | e14 | 1 | 1 | 1 | 1 | 1 | 0 |
| 7 | e3 ∧ e6 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | e3 ∧ e9 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | e3 ∧ e10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | e3 ∧ e13 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | e3 ∧ e14 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | e6 ∧ e9 | 1 | 0 | 0 | 0 | 0 | 0 |
| 13 | e6 ∧ e10 | 1 | 0 | 0 | 0 | 0 | 0 |
| 14 | e6 ∧ e13 | 1 | 0 | 0 | 0 | 0 | 0 |
| 15 | e6 ∧ e14 | 1 | 0 | 0 | 0 | 0 | 0 |
| 16 | e9 ∧ e10 | 1 | 1 | 0 | 0 | 0 | 0 |
| 17 | e9 ∧ e13 | 1 | 1 | 0 | 1 | 0 | 1 |
| 18 | e9 ∧ e14 | 1 | 1 | 0 | 1 | 0 | 0 |
| 19 | e10 ∧ e13 | 1 | 1 | 1 | 0 | 0 | 0 |
| 20 | e10 ∧ e14 | 1 | 1 | 1 | 0 | 1 | 0 |
| 21 | e13 ∧ e14 | 1 | 1 | 1 | 1 | 0 | 0 |
По мере удаления от корневой вершины степень влияния последующих снижается и количество одинаковых кортежей уменьшается, что наглядно демонстрируется транзитивно замкнутым орграфом на рис. 4.
Таким образом, при наличии в объекте двукратных отказов свойство (7) нельзя применить для различения состояний (поиска отказавшего ТЭЗ). По этой причине в состав матрицы явной диагностической модели двукратных отказов, построенной на основе ориентированного графа причинно-следственных связей, обязательно будут включены одинаковые строки.
В матрице двукратного отказа появляются четыре группы неразличимых строк в соответствии с (14)–(16). В табл. 1 для наглядности они выделены одинаковыми оттенками серого цвета. После того, как из каждой группы неразличимых строк оставить только по одной уникальной строке, матрица двукратного отказа приобретет вид табл. 2.
Таблица 2.
Матрица различимых состояний двукратных отказов
| № | Состояния | Исходы проверок | |||||
|---|---|---|---|---|---|---|---|
| u3 | u6 | u9 | u10 | u13 | u14 | ||
| 1 | e3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | e6 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | e9 | 1 | 1 | 0 | 1 | 0 | 1 |
| 4 | e10 | 1 | 1 | 1 | 0 | 1 | 0 |
| 5 | e13 | 1 | 1 | 1 | 1 | 0 | 1 |
| 6 | e14 | 1 | 1 | 1 | 1 | 1 | 0 |
| 7 | e9 ∧ e10 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | e9 ∧ e14 | 1 | 1 | 0 | 1 | 0 | 0 |
| 9 | e10 ∧ e13 | 1 | 1 | 1 | 0 | 0 | 0 |
| 10 | e13 ∧ e14 | 1 | 1 | 1 | 1 | 0 | 0 |
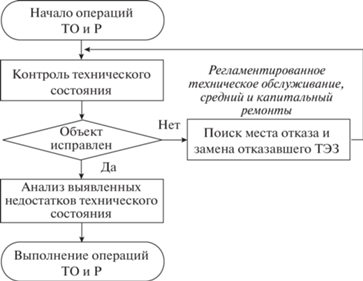
Несмотря на то что условия (8) и (9) в рассматриваемом случае не работают, организация поиска места отказа с использованием рассматриваемой модели обеспечивает требуемую достоверность. Место ТД в технологических операциях ТО и Р, поясняется схемой на рис. 5 [2].
В модели матрицы двукратного отказа (табл. 2) остались только неразличимые состояния, соответствующие сочетаниям определенных отказов, которым в транзитивно замкнутом графе $D_{{tc}}^{*}$ сопоставлены пары вершин, не имеющих отношения связности [9]:
(17)
${{e}_{9}} \wedge {{e}_{{10}}},{{e}_{9}} \wedge {{e}_{{14}}},{{e}_{{10}}} \wedge {{e}_{{13}}},{{e}_{{13}}} \wedge {{e}_{{14}}}.$Все другие неразличимые сочетания состояний будут однозначно содержать в себе отказ элемента, инициирующего отношение связности. Применяя алгоритмы поиска места отказа, разработанные на основе модели однократного отказа, распознается группа сочетаний, которую объединил отказ инициирующего элемента. Также вполне очевидно и то, что используя процедуру диагностирования с восстановлением (рис. 5), алгоритмы поиска приведут к нахождению одного отказавшего элемента из пар (17). Для подтверждения теоретических заключений проведем статистическое моделирование, сущность которого поясняется схемой на рис. 6. В модели двукратного отказа (табл. 2) имитируется поиск отказавшего состояния, которое проявляется определенным размещением исходов проверок: нулей и единиц.
Рис. 6.
Схема, поясняющая процедуру поиска места отказа с использованием безусловного алгоритма в области D3tc.
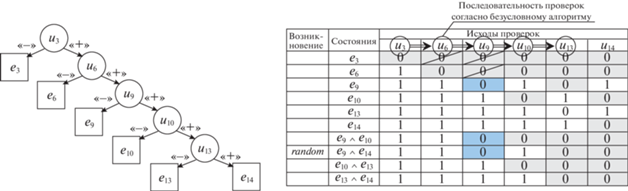
На схеме в левой части рисунка представлен граф безусловного алгоритма поиска места отказа. Окружностями на дихотомическом графе обозначены проверки элементов, входящих в состав подграфа D3tc. Из каждой окружности выходят по две дуги. Одна обозначена знаком “–” и соответствует отрицательному исходу проверки, вторая – “+” и свидетельствует, что значение диагностического параметра находится в пределах допуска.
Моделирование проводится следующим образом. В псевдослучайном порядке выбирается одно из состояний отказов, перечисленных во втором столбце матрицы. Затем с помощью определенной алгоритмом последовательности оцениваются исходы проверок в зависимости от моделируемого состояния объекта. В рассматриваемом примере псевдослучайным образом назначено состояние одновременных отказов e9 ∧ e14. В дереве алгоритма первой проверкой назначена проверка u3. В этом состоянии ее исход определяется в допустимых пределах “+”. Следовательно, назначается вторая проверка в установленной последовательности u6, а состояние e3 вычеркивается из дальнейшего поиска (не рассматривается). Далее, согласно алгоритму, следует проверка u9. В соответствии с матрицей состоянию e9 ∧ e14 сопоставлен недопустимый исход $u_{9}^{0}$. Такой же недопустимый исход определяют состояния e9 и e9 ∧ e10 (выделены синим цветом на схеме). Все три состояния: e9, e9 ∧ e10 и e9 ∧ e14 проверка u9 выделяет своим отрицательным исходом. Истинное состояние объекта диагностирования e9 ∧ e10 ⊂ ⊂ {e9, e9 ∧ e10, e9 ∧ e14} включено в подмножество состояний, которое выделяет $u_{9}^{0}$. Следовательно, поиск с использованием данной модели позволяет различить одно состояние из сочетания отказов. А замена обнаруженного отказавшего ТЭЗ по принципу, поясняемому схемой на рис. 5, гарантирует нахождение второго отказавшего элемента.
Для подтверждения теоретических заключений разработана программа на языке C++, реализующая статистическое моделирование. Проведена 1000 машинных реализаций на основе модели (табл. 2) и безусловного алгоритма поиска места отказа (рис. 6). Во всех случаях состояние отказа было определено.
ЗАКЛЮЧЕНИЕ
Рассмотренная модель позволяет формализовать разработку диагностического обеспечения к сложной аппаратуре, входящей в состав РТК. Помимо этого, еще на этапе разработки модель создает исходные данные для выполнения требований государственного стандарта [10] к номенклатуре диагностических (контролируемых) параметров, к средствам ТД, а также к методам и правилам ТД.
Обоснование с использованием диагностической модели кратного отказа требований к составу встроенных средств технического диагностирования в конструкции изделия позволит автоматизировать процедуру поиска отказавшего ТЭЗ и избежать трудозатратной процедуры ручного поиска, что может обеспечить эффективность системы ТО и Р комплексов РТК, которые в ближайшее время поступят на вооружение общевойсковых подразделений.
Список литературы
Жирнов М.В., Митрофанова С.В., Федорова Е.В. // Воздушно-космические силы. Теория и практика. 2020. № 14. С. 6.
Приказ Министра обороны РФ от 28.12.2013 № 969 “Об утверждении Руководства по содержанию вооружения и военной техники общевойскового назначения, военно-технического имущества в ВС РФ”.
Бородин С.М. // Основы технической диагностики электронных средств: учебное пособие. Ульяновск: УлГТУ, 2019. С. 48.
ГОСТ Р 27.004-2009 Надежность в технике. Модели отказов. М.: Стандартинформ, 2010. С. 14.
Фандеев В.П., Волков В.С. // Изв. вузов. Поволжский регион. Технические науки. 2017. Спецвыпуск № 1. С. 47.
Еремин Е.Л., Пикуль З.Д., Теличенко Д.А. // Вестник ТОГУ. 2015. № 2 (37).
Кривцова И.Е., Лебедев И.С., Настека А.В. Основы дискретной математики. Ч. 1. Учебное пособие. СПб: Университет ИТМО, 2016. С. 92.
Бородин С.М. Основы технической диагностики электронных средств: учебное пособие / Ульяновск: УлГТУ, 2019. С. 48.
Алексеев В.Е., Захарова Д.В. // Теория графов: Учебное пособие. Нижний Новгород: Нижегородский госуниверситет, 2017. С. 119.
ГОСТ 15.016-2016 Система разработки и постановки продукции на производство. Техническое задание. Требования к содержанию и оформлению. М.: Стандартинформ, 2020. С. 20.
Дополнительные материалы отсутствуют.
Инструменты
Вестник Военного инновационного технополиса «ЭРА»