1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 61, № 1, 2023

Теплофизика высоких температур, 2023, T. 61, № 1, стр. 108-117

Тепловой взрыв одиночных частиц в случайном поле температуры среды

И. В. Деревич 1, *, А. К. Клочков 1

1 Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет)
Москва, Россия

* E-mail: DerevichIgor@bmstu.ru

Поступила в редакцию 28.04.2022
После доработки 22.05.2022
Принята к публикации 07.06.2022

Полный текст (PDF)

Аннотация

Предложена модель теплового взрыва одиночной частицы с экзотермической химической реакцией в турбулентном поле температуры среды. Скорость химической реакции представлена модифицированным законом Аррениуса, учитывающим изменение внутренней структуры материала частицы. Флуктуации температуры моделируются случайным процессом Гаусса. Исследование проведено в рамках подходов Лагранжа и Эйлера. В подходе Лагранжа на основе решения системы стохастических обыкновенных дифференциальных уравнений рассчитаны случайные флуктуации температуры среды и ансамбля частиц. На основе результатов численного моделирования ансамбля смоделирована динамика эмпирической функции плотности вероятности распределения случайной температуры частиц. В подходе Эйлера выведено нестационарное замкнутое уравнение для функции плотности вероятности случайных температур частиц, которое численно проинтегрировано с помощью оригинальной консервативной разностной схемы. Результаты расчетов по обоим подходам удовлетворительно согласуются между собой. Показано, что случайное поле температуры среды качественно меняет динамику возникновения теплового взрыва. В случайном поле температуры тепловой взрыв может произойти при условии, когда в детерминированном случае система абсолютно стабильна.

ВВЕДЕНИЕ

Воспламенение облака тепловыделяющих частиц, взвешенных в турбулентном неизотермическом потоке газа, реализуется во многих технических приложениях и может приводить к техногенным катастрофам (см., например, [1‒3]). В связи с актуальностью вопросов пожарной безопасности развиваются теоретические работы по анализу динамики теплового взрыва в запыленной атмосфере [4‒6]. Отмечаются статистический характер процесса воспламенения [7] и роль коллективных эффектов, связанных с кластеризацией частиц [8, 9]. Моделирование коллективных тепловых и гидродинамических эффектов при воспламенении дисперсной примеси в турбулентном неизотермическом потоке газа требует изучения потери тепловой стабильности одиночных тепловыделяющих частиц. В настоящее время сформировалась детерминированная теория теплового взрыва. Литература по данной теории обширна, и здесь отметим только некоторые направления исследований. Они связаны с изучением процесса диффузии тепла в условиях однородного тепловыделения в объеме материала [10‒12], учетом расхода реагентов [13, 14] и выгоранием материала в ходе химического превращения [15]. Привлекаются также перспективные методы вариационного анализа [16].

Практический интерес представляет изучение влияния случайных факторов на поведение систем взрывного типа, когда существует предельный уровень параметров системы, малое превышение которого приводит к потере стабильности. В этой ситуации случайные флуктуации внешних параметров, действующие на динамическую систему, могут принципиально изменить характер ее поведения [17‒20]. Вследствие экспоненциальной зависимости скорости химической реакции от температуры флуктуации температуры оказывают существенное влияние на границу теплового взрыва [21‒23].

Существуют два принципиально различных подхода для изучения влияния флуктуаций температуры среды на динамику температуры частиц. Подход Лагранжа основан на численном решении системы стохастических обыкновенных дифференциальных уравнений (СОДУ), описывающих случайные флуктуации температуры среды и частиц. Популярный метод Монте-Карло для генерации случайных величин не используется, так как его затруднительно встроить в динамические уравнения. Отметим, что подход Лагранжа, использующий СОДУ для моделирования однофазной турбулентности, был впервые предложен в работе [24]. Прямое численное моделирование случайной температуры газа и частиц основано на современных алгоритмах численного решения систем СОДУ. Подход Лагранжа является аналогом прямого численного эксперимента и предоставляет детальную динамику случайной температуры частиц. На основе статистической обработки ансамбля из сотен случайных траекторий температуры частиц методами математической статистики строится эмпирическая функция плотности распределения (ФПР), которая обобщает результаты прямого численного моделирования. Для реализации подхода Лагранжа требуется существенная затрата компьютерных ресурсов.

Значительная экономия процессорного времени достигается в подходе Эйлера, основанного на современных методах теории случайных процессов и прикладного функционального анализа. Адекватным является использование аналитической ФПР, которая содержит всю информацию о случайной системе. В работе получено замкнутое уравнение для ФПР случайной температуры частиц. Для решения уравнения для ФПР разработана оригинальная консервативная численная схема. Сопоставление результатов динамики изменения эмпирической ФПР и численных решений уравнения для функции распределения вероятности иллюстрирует корректность подходов Лагранжа и Эйлера для описания процесса потери тепловой устойчивости в дисперсных системах.

В работе представлены результаты исследования влияния турбулентных флуктуаций температуры газа на тепловой взрыв одиночных частиц с экзотермической химической реакцией. Актуальная температура газа складывается из постоянной осредненной компоненты и флуктуаций. Флуктуации температуры газа являются структурированным случайным процессом (цветной шум) с характерным временем затухания автокорреляционной функции на траектории частиц (интегральный временной масштаб). Использование приближения δ-коррелированного случайного процесса (белый шум), представляющего флуктуации температуры газа [22, 23], является в этом случае некорректным. Частицы обмениваются теплом с окружающей средой в результате теплоотдачи. Степень вовлечения частиц в скоростные и тепловые флуктуации несущей среды определяется как временами их динамической и тепловой релаксации, так и интегральным временным масштабом [25, 26]. Как и во многих моделях горения и термического разложения дисперсных материалов (см., например, [1‒3, 5‒7, 10‒16, 21‒24, 27, 28]), в данной работе ограничимся упрощенной химической кинетикой.

ОСНОВНЫЕ УРАВНЕНИЯ

Рассматривается сферическая частица, в объеме которой равномерно распределен источник тепла, выделяющегося в результате экзотермической химической реакции. Диффузионным сопротивлением газообразных реагентов в объеме частиц пренебрегаем. Уравнение для температуры в объеме частицы в сферически симметричном приближении имеет вид

(1)
$\begin{gathered} {{\rho }_{p}}{{c}_{p}}\frac{{\partial {{\Theta }_{p}}}}{{\partial t}} = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{\lambda }_{p}}{{r}^{2}}\frac{{\partial {{\Theta }_{p}}}}{{\partial r}}} \right) + \\ + \,\,{{\rho }_{p}}QA{{\left[ {1 + {{{\left( {\frac{{R^\circ {{\Theta }_{p}}}}{{E{\kern 1pt} '}}} \right)}}^{n}}} \right]}^{{ - 1}}}\exp \left( { - \frac{E}{{R^\circ {{\Theta }_{p}}}}} \right). \\ \end{gathered} $
Здесь ${{\rho }_{p}},\;{{c}_{p}},\;{{\lambda }_{p}}$ – плотность, теплоемкость и теплопроводность материала частицы; $Q$ – тепловой эффект реакции; $E,\;E{\kern 1pt} '$ – энергии активации химических превращений; $A$ – предэкспоненциальный множитель; $R^\circ $ – универсальная газовая постоянная; ${{\Theta }_{p}}$ – температура частицы; $n$ – показатель степени.

Множитель перед формулой Аррениуса учитывает изменение структуры материала частицы в ходе химического превращения, например выгорание [15, 22, 23].

Граничное условие описывает теплообмен частицы с окружающей средой:

(2)
$ - {{\lambda }_{p}}{{\left. {\frac{{\partial {{\Theta }_{p}}\left( {r,t} \right)}}{{\partial r}}} \right|}_{{r = {{{{d}_{p}}} \mathord{\left/ {\vphantom {{{{d}_{p}}} 2}} \right. \kern-0em} 2}}}} = {{\alpha }_{p}}\left\{ {{{{\left. {{{\Theta }_{p}}\left( {r,t} \right)} \right|}}_{{r = {{{{d}_{p}}} \mathord{\left/ {\vphantom {{{{d}_{p}}} 2}} \right. \kern-0em} 2}}}} - {{\Theta }_{g}}\left( t \right)} \right\}.$
Здесь ${{d}_{p}}$ – диаметр частицы, ${{\alpha }_{p}}$ – коэффициент теплоотдачи, ${{\Theta }_{g}}$ – актуальная температура среды.

Задано начальное распределение температуры внутри частицы ${{\left. {{{\Theta }_{p}}\left( {r,t} \right)} \right|}_{{t = 0}}} = \Theta _{p}^{{\left( 0 \right)}}\left( r \right)$.

Температура среды на траектории частицы является суммой осредненной компоненты и флуктуаций

${{\Theta }_{g}}\left( t \right) = \left\langle {{{\Theta }_{g}}} \right\rangle + {{\theta }_{g}}\left( t \right),\,\,\,\,\left\langle {{{\theta }_{g}}\left( t \right)} \right\rangle = 0,$
где угловыми скобками обозначен результат осреднения по ансамблю случайных реализаций; $\left\langle {{{\Theta }_{g}}} \right\rangle $ – осредненная температура среды; ${{\theta }_{g}}\left( t \right)$ – флуктуации температуры среды, являющиеся стационарным случайным процессом.

Параметры турбулентности на траектории частицы считаются известными. Корреляция флуктуаций температуры среды на траектории частицы определяется как

(3)

В (3) ${{\Psi }_{\Theta }}\left( t \right)$ – автокорреляционная функция; $\left\langle {\theta _{g}^{2}} \right\rangle $ – дисперсия флуктуаций температуры; – два произвольных момента времени.

Интегральный временной масштаб флуктуаций температуры среды равен

${{T}_{\Theta }} = \int\limits_0^\infty {{{\Psi }_{\Theta }}\left( t \right)dt} .$

Представляем уравнение (1) и граничное условие (2) в безразмерном виде. В качестве масштаба температуры используется температура ${{\Theta }_{с}} = {E \mathord{\left/ {\vphantom {E {R^\circ }}} \right. \kern-0em} {R^\circ }}$, тогда безразмерная температура частицы равна

(4)
$\Theta _{p}^{ * } = \frac{{{{\Theta }_{p}} - \left\langle {{{\Theta }_{g}}} \right\rangle }}{{\left\langle {{{\Theta }_{g}}} \right\rangle }}\frac{{{{\Theta }_{c}}}}{{\left\langle {{{\Theta }_{g}}} \right\rangle }} = E{\kern 1pt} *\frac{{{{\Theta }_{p}} - \left\langle {{{\Theta }_{g}}} \right\rangle }}{{\left\langle {{{\Theta }_{g}}} \right\rangle }},$
где $E{\kern 1pt} * = {E \mathord{\left/ {\vphantom {E {\left( {R^\circ \left\langle {{{\Theta }_{g}}} \right\rangle } \right)}}} \right. \kern-0em} {\left( {R^\circ \left\langle {{{\Theta }_{g}}} \right\rangle } \right)}}$ – безразмерная энергия активации.

В качестве масштаба времени используется характерное время адиабатического разогрева частицы. Перепишем уравнение (1) в упрощенном виде

$\frac{{d{{\Theta }_{p}}}}{{dt}} = \frac{{QA}}{{{{c}_{p}}}}{\text{exp}}\left( { - \frac{E}{{R^\circ {{\Theta }_{p}}}}} \right).$

Переходя к безразмерным переменным, получаем масштаб времени адиабатического разогрева

$\frac{{d\Theta _{p}^{ * }}}{{dt{\kern 1pt} *}} = \exp \left( {\frac{{\Theta _{p}^{ * }}}{{1 + {{\Theta _{p}^{ * }} \mathord{\left/ {\vphantom {{\Theta _{p}^{ * }} {E{\kern 1pt} *}}} \right. \kern-0em} {E{\kern 1pt} *}}}}} \right),$
где $t{\kern 1pt} * = {t \mathord{\left/ {\vphantom {t {{{\tau }_{{{\text{ad}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{ad}}}}}}}$ – безразмерное время; τad = $ = \frac{{{{c}_{p}}\left\langle {{{\Theta }_{g}}} \right\rangle }}{{QAE{\kern 1pt} *}}{\text{exp}}\left( {E{\kern 1pt} *} \right)$ – время адиабатического разогрева.

В безразмерных переменных уравнение (1) и граничное условие (2) принимают вид

(5)
$\begin{gathered} \frac{{\partial \Theta _{p}^{ * }}}{{\partial t{\kern 1pt} *}} = \chi _{p}^{ * }\frac{1}{{{{r}^{ * }}^{2}}}\frac{\partial }{{\partial r{\kern 1pt} *}}\left( {{{r}^{ * }}^{2}\frac{{\partial \Theta _{p}^{ * }}}{{\partial r{\kern 1pt} *}}} \right) + \\ + \,\,{{\left\{ {1 + {{{\left[ {\frac{{{{C}_{E}}}}{{E{\kern 1pt} *}}\left( {1 + \frac{{\Theta _{p}^{ * }}}{{E{\kern 1pt} *}}} \right)} \right]}}^{n}}} \right\}}^{{ - 1}}}\exp \left( {\frac{{\Theta _{p}^{ * }}}{{1 + {{\Theta _{p}^{ * }} \mathord{\left/ {\vphantom {{\Theta _{p}^{ * }} {E{\kern 1pt} *}}} \right. \kern-0em} {E{\kern 1pt} *}}}}} \right), \\ \end{gathered} $
(6)
$ - {{\left. {\frac{{\partial \Theta _{p}^{ * }}}{{\partial r{\kern 1pt} *}}} \right|}_{{r{\kern 1pt} * = 1}}} = \alpha _{p}^{ * }\left( {{{{\left. {\Theta _{p}^{ * }} \right|}}_{{r{\kern 1pt} * = 1}}} - \theta _{g}^{ * }} \right).$
Здесь $\chi _{p}^{ * } = {{{{\tau }_{{{\text{ad}}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{{\text{ad}}}}}} {{{\tau }_{\chi }}}}} \right. \kern-0em} {{{\tau }_{\chi }}}}$ – отношение характерного времени адиабатического разогрева к характерному времени диффузии тепла, ${{\tau }_{\chi }} = {{{{{\left( {{{{{d}_{p}}} \mathord{\left/ {\vphantom {{{{d}_{p}}} 2}} \right. \kern-0em} 2}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{{{d}_{p}}} \mathord{\left/ {\vphantom {{{{d}_{p}}} 2}} \right. \kern-0em} 2}} \right)}}^{2}}} {{{\chi }_{p}}}}} \right. \kern-0em} {{{\chi }_{p}}}}$; ${{\chi }_{p}} = {{{{\lambda }_{p}}} \mathord{\left/ {\vphantom {{{{\lambda }_{p}}} {\left( {{{c}_{p}}{{\rho }_{p}}} \right)}}} \right. \kern-0em} {\left( {{{c}_{p}}{{\rho }_{p}}} \right)}}$ – коэффициент температуропроводности; $r{\kern 1pt} * = {{2r} \mathord{\left/ {\vphantom {{2r} {{{d}_{p}}}}} \right. \kern-0em} {{{d}_{p}}}}$ – безразмерная координата; $\alpha _{p}^{ * } = {{{{\alpha }_{p}}{{d}_{p}}} \mathord{\left/ {\vphantom {{{{\alpha }_{p}}{{d}_{p}}} {2{{\lambda }_{p}}}}} \right. \kern-0em} {2{{\lambda }_{p}}}}$ – безразмерный коэффициент теплоотдачи; $\theta _{g}^{ * }\left( {t{\kern 1pt} *} \right) = {{\theta }_{g}}\left( t \right){{E{\kern 1pt} *} \mathord{\left/ {\vphantom {{E{\kern 1pt} *} {\left\langle {{{\Theta }_{g}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{\Theta }_{g}}} \right\rangle }}$ – безразмерные флуктуации температуры среды; ${{C}_{E}} = {E \mathord{\left/ {\vphantom {E {E{\kern 1pt} '}}} \right. \kern-0em} {E{\kern 1pt} '}}$.

В безразмерном виде корреляция флуктуаций температуры среды представляется как

где $\left\langle {\theta _{g}^{{ * 2}}} \right\rangle = {{\left( {{{E{\kern 1pt} *} \mathord{\left/ {\vphantom {{E{\kern 1pt} *} {\left\langle {{{\Theta }_{g}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{\Theta }_{g}}} \right\rangle }}} \right)}^{2}}\left\langle {\theta _{g}^{2}} \right\rangle $ – безразмерная дисперсия флуктуаций температуры.

Интегрируя уравнение для температуры частицы (5) по ее объему с учетом граничного условия (6), запишем уравнение для среднемассовой температуры

(7)
$\begin{gathered} \frac{{d\Theta _{p}^{ * }(t{\kern 1pt} *)}}{{dt{\kern 1pt} *}} = \frac{1}{{\tau _{\Theta }^{ * }}}\left( {\theta _{g}^{ * }\left( {t{\kern 1pt} *} \right) - \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right) + \\ + \,\,{{\left\{ {1 + {{{\left[ {\frac{{{{C}_{E}}}}{{E{\kern 1pt} *}}\left( {1 + \frac{{\Theta _{p}^{ * }}}{{E{\kern 1pt} *}}} \right)} \right]}}^{n}}} \right\}}^{{ - 1}}}\exp \left( {\frac{{\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{1 + {{\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \mathord{\left/ {\vphantom {{\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} {E{\kern 1pt} *}}} \right. \kern-0em} {E{\kern 1pt} *}}}}} \right). \\ \end{gathered} $
Здесь $\tau _{\Theta }^{ * } = {{{{\tau }_{\Theta }}} \mathord{\left/ {\vphantom {{{{\tau }_{\Theta }}} {{{\tau }_{{{\text{ad}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{ad}}}}}}}$ – безразмерное время тепловой релаксации частиц; ${{\tau }_{\Theta }} = {{{{m}_{p}}{{c}_{p}}} \mathord{\left/ {\vphantom {{{{m}_{p}}{{c}_{p}}} {\left( {{{\alpha }_{p}}{{S}_{p}}} \right)}}} \right. \kern-0em} {\left( {{{\alpha }_{p}}{{S}_{p}}} \right)}}$ – время тепловой релаксации частицы; ${{m}_{p}},\;{{S}_{p}}$ – масса и площадь поверхности частицы.

Стохастическое обыкновенное дифференциальное уравнение для флуктуаций температуры среды в безразмерном виде записывается как

(8)
$\frac{{d\theta _{g}^{ * }\left( {t{\kern 1pt} *} \right)}}{{dt{\kern 1pt} *}} = \frac{1}{{T_{\Theta }^{ * }}}\left( {\zeta _{\Theta }^{ * }\left( {t{\kern 1pt} *} \right) - \theta _{g}^{ * }\left( {t{\kern 1pt} *} \right)} \right).$
Здесь $T_{\Theta }^{ * } = {{{{T}_{\Theta }}} \mathord{\left/ {\vphantom {{{{T}_{\Theta }}} {{{\tau }_{{{\text{ad}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{ad}}}}}}}$– безразмерный интегральный временной масштаб флуктуаций температуры среды на траектории частицы; $\zeta _{\Theta }^{ * }\left( {t{\kern 1pt} *} \right)$ – источник флуктуаций температуры среды – δ-коррелированный во времени случайный процесс Гаусса, который генерирует компьютер (белый шум):
где $\left\langle {\zeta _{\Theta }^{{ * 2}}} \right\rangle $ – дисперсия источника флуктуаций, $\tau _{0}^{ * }$ – безразмерный временной микромасштаб ($\tau _{0}^{ * } \ll T_{\Theta }^{ * }$), $\delta \left( t \right)$ – дельта-функция Дирака.

СОДУ для флуктуаций температуры (8) в канонической форме записывается как

$\theta _{g}^{ * }\left( {t{\kern 1pt} * + \,\,\Delta t{\kern 1pt} *} \right) = - \frac{{\Delta t{\kern 1pt} *}}{{T_{\Theta }^{ * }}}\theta _{g}^{ * }\left( {t{\kern 1pt} *} \right) + \frac{1}{{T_{\Theta }^{ * }}}\sqrt {2\left\langle {\zeta _{\Theta }^{{ * 2}}} \right\rangle \tau _{\Theta }^{ * }} \Delta W{\kern 1pt} *.$
Здесь $\Delta W{\kern 1pt} *$ – приращение процесса Винера.

Система уравнений (7) и (8) интегрируется численно на основе современных методов с использованием модернизированных алгоритмов Рунге–Кутты [28, 29]. Автокорреляционная функция флуктуаций температуры среды (8) имеет вид [30]

(9)
${{\Psi }_{\Theta }}\left( {t{\kern 1pt} *} \right) = \exp \left( { - {{t{\kern 1pt} *} \mathord{\left/ {\vphantom {{t{\kern 1pt} *} {T_{\Theta }^{ * }}}} \right. \kern-0em} {T_{\Theta }^{ * }}}} \right).$

Экспоненциальный вид автокорреляционной функции турбулентных флуктуаций температуры газа на траектории инерционных частиц подтверждается данными прямого численного моделирования в двухфазных потоках [31].

ПРИМЕРЫ ЧИСЛЕННЫХ ЭСПЕРИМЕНТОВ

Результаты численных экспериментов приводятся для наиболее интересного случая существования трех стационарных температур уравнения (7) [23, 32]. Стационарные значения температуры частицы находятся из условия равенства мощности, отводимой от частицы в результате теплоотдачи, и мощности, выделяемой в объеме частицы в ходе экзотермической химической реакции:

$ - W_{\alpha }^{ * }\left( {\Theta _{p}^{{ * {\text{st}}}}} \right) + {{W}_{Q}}\left( {\Theta _{p}^{{ * {\text{st}}}}} \right) = 0.$
Здесь мощности теплоотдачи и тепловыделения в результате экзотермической химической реакции равны

(10)
$\begin{gathered} W_{\alpha }^{ * }\left( {\Theta {\kern 1pt} *} \right) = \frac{1}{{\tau _{\Theta }^{ * }}}\Theta {\kern 1pt} *,\,\,\,\,W_{Q}^{ * }\left( {\Theta {\kern 1pt} *} \right) = \\ = {{\left\{ {1 + {{{\left[ {\frac{{{{C}_{E}}}}{{E{\kern 1pt} *}}\left( {1 + \frac{{\Theta _{p}^{ * }}}{{E{\kern 1pt} *}}} \right)} \right]}}^{n}}} \right\}}^{{ - 1}}}\exp \left( {\frac{{\Theta {\kern 1pt} *}}{{1 + {{\Theta {\kern 1pt} *} \mathord{\left/ {\vphantom {{\Theta {\kern 1pt} *} {E{\kern 1pt} *}}} \right. \kern-0em} {E{\kern 1pt} *}}}}} \right). \\ \end{gathered} $

На рис. 1 показаны мощности тепловыделения и теплоотдачи и стационарные температуры $\Theta _{{{\text{cr}}}}^{{ * \left( 1 \right)}},\;\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}},\;\Theta _{{{\text{cr}}}}^{{ * \left( 3 \right)}}$. В качестве примера отметим, что подобная диаграмма соответствует термическому разложению частиц взрывчатого вещества размером ${{d}_{p}} = 100{\text{ мкм}}$ при температуре среды $\left\langle {{{\Theta }_{g}}} \right\rangle = 800{\text{ K}}$ (энергия активации $E \approx 70\,\,{{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}}$, тепловой эффект реакции $Q \approx 50\,\,{{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}}$) [33].

Рис. 1.

Тепловые мощности теплоотдачи (1) и тепловыделения (2) в частице и стационарные температуры $\Theta _{{{\text{cr}}}}^{{ * \left( 1 \right)}},\;\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}},\;\Theta _{{{\text{cr}}}}^{{ * \left( 3 \right)}}$.

В этом случае стационарные температуры составляют $\Theta _{{{\text{cr}}}}^{{ * \left( 1 \right)}} \approx 879{\text{,}}\,\,\,\,\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}} \approx 1160{\text{,}}\,\,\,\,\Theta _{{{\text{cr}}}}^{{ * \left( 3 \right)}} \approx $ 2660 K. Время адиабатического нагрева ${{\tau }_{{{\text{ad}}}}} \approx 2 \times {{10}^{{ - 2}}}\,\,{\text{с}}$. Времена тепловой релаксации частиц и интегральный временной масштаб флуктуаций температуры среды в безразмерных переменных соответственно $\tau _{\Theta }^{ * } = 4$, $T_{\Theta }^{ * } = 4$.

Опишем процедуру исследования корней на устойчивость, в результате которой возникает ряд параметров, использующихся в дальнейшем при выводе замкнутого уравнения для ФПР температуры частиц. Возмущение стационарной температуры задается как

$\Theta _{p}^{ * }(t) = \Theta _{p}^{{ * {\text{st}}}} + \delta \Theta {\kern 1pt} *{\kern 1pt} (t).$

В результате подстановки возмущенной температуры в уравнение баланса тепла (7) и линеаризации получаем уравнение

$\frac{{d\delta \Theta {\kern 1pt} *}}{{dt}} = - \left[ {\frac{1}{{\tau _{\Theta }^{ * }}} - \frac{1}{{\tau _{Q}^{ * }\left( {\Theta _{p}^{{ * {\text{st}}}}} \right)}}} \right]\delta \Theta {\kern 1pt} *{\kern 1pt} ,\,\,\,\,\delta \Theta {\kern 1pt} *\left( 0 \right) = \delta \Theta _{0}^{ * }.$
Здесь характерное время роста температуры час-тиц за счет экзотермической химической реакции равно

$\tau _{Q}^{ * }\left( {\Theta _{p}^{{ * {\text{st}}}}} \right) = {{\left[ {{{{\left. {\frac{{dW_{Q}^{ * }\left( {\Theta {\kern 1pt} *} \right)}}{{d\Theta {\kern 1pt} *}}} \right|}}_{{\Theta * = \Theta _{p}^{{ * {\text{st}}}}}}}} \right]}^{{ - 1}}}.$

Рост начального возмущения стационарной температуры во времени описывается выражением

$\begin{gathered} \delta \Theta {\kern 1pt} *\left( {t{\kern 1pt} *} \right) = \exp \left[ { - \gamma {\kern 1pt} *\left( {\Theta _{p}^{{ * {\text{st}}}}} \right)t{\kern 1pt} *} \right]\delta \Theta _{0}^{ * }, \\ \gamma {\kern 1pt} *\left( {\Theta _{p}^{{ * {\text{st}}}}} \right) = \frac{1}{{\tau _{\Theta }^{ * }}} - \frac{1}{{\tau _{Q}^{ * }\left( {\Theta _{p}^{{ * {\text{st}}}}} \right)}}. \\ \end{gathered} $

Условие теплового взрыва (экспоненциального роста температуры во времени) имеет вид

$\gamma {\kern 1pt} *\left( {\Theta _{p}^{{ * {\text{st}}}}} \right) = \frac{1}{{\tau _{\Theta }^{ * }}} - \frac{1}{{\tau _{Q}^{ * }\left( {\Theta _{p}^{{ * {\text{st}}}}} \right)}} < 0.$

Тепловой взрыв происходит, когда время роста температуры за счет химической реакции становится меньше времени тепловой релаксации частиц $\tau _{Q}^{ * }\left( {\Theta _{p}^{{ * {\text{st}}}}} \right) < \tau _{\Theta }^{ * }$. Анализ показывает, что стационарные значения $\Theta _{{{\text{cr}}}}^{{ * \left( 1 \right)}},\;\Theta _{{{\text{cr}}}}^{{ * \left( 3 \right)}}$ устойчивы. Второй корень $\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}}$ является точкой бифуркации: бесконечно малое превышение корня приводит к росту температуры частицы, в то время как бесконечно малое уменьшение температуры по отношению ко второму корню понижает ее температуру до значения $\Theta _{{{\text{cr}}}}^{{ * \left( 1 \right)}}$. Представленные выводы согласуются с классической диаграммой Н.Н. Семенова [23, 32].

На рис. 2 показаны результаты прямого численного моделирования температуры частиц в турбулентном поле температуры среды ($t_{{{\text{max}}}}^{ * }$ – безразмерное максимальное время моделирования). Расчеты проведены для размеров частиц и теплофизических параметров терморазлагающегося вещества, как для рис. 1. Безразмерная дисперсия флуктуаций температуры газа равна $\left\langle {\theta _{g}^{{ * 2}}} \right\rangle = 2$, что составляет уровень турбулентных флуктуаций температуры среды ${{\sqrt {\left\langle {\theta _{g}^{2}} \right\rangle } } \mathord{\left/ {\vphantom {{\sqrt {\left\langle {\theta _{g}^{2}} \right\rangle } } {\left\langle {{{\Theta }_{g}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{\Theta }_{g}}} \right\rangle }} \approx 0.12$. Такой относительно большой уровень флуктуаций температуры несущего газа выбран с целью сокращения результатов прямого численного моделирования.

Рис. 2.

Примеры траекторий температуры частиц в случайном поле температуры среды без теплового взрыва (а) и с тепловым взрывом (б): 1 – флуктуации температуры среды, 2 – флуктуации температуры частиц, 3 – температура частиц в детерминированном случае.

Видно, что флуктуации температуры среды могут качественно изменить динамику температуры частиц. Даже если начальная температура частиц существенно ниже критического значения $\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}}$, при превышении которого наступает тепловой взрыв, то флуктуации температуры среды обязательно приведут к ситуации, когда взрыв произойдет. Это является следствием двух факторов. Во-первых, случайный процесс с ненулевой вероятностью всегда выйдет за любой назначенный уровень. Во-вторых, вследствие сильной экспоненциальной зависимости скорости химической реакции от температуры наблюдается “дрейф” температуры частиц к критическому уровню. Данный эффект проиллюстрирован ниже на замкнутом уравнении для ФПР случайной температуры частиц.

Для построения эмпирической ФПР рассчитываются случайные траектории ансамбля частиц (здесь 201 частица). В выбранные моменты времени по актуальным значениям температуры методами математической статистики строится эмпирическая ФПР, которая дает представление о динамике изменения осредненных параметров дисперсной фазы.

УРАВНЕНИЕ ДЛЯ ФПР ТЕМПЕРАТУРЫ ЧАСТИЦ

Функция плотности вероятности распределения случайной температуры частиц содержит всю информацию о системе. Для вывода замкнутого уравнения для ФПР используется техника, основанная на аксиоматической теории случайных процессов, развитая в работах академика А.Н. Колмогорова [34]. Аналогично [19] вводится индикаторная функция, “вырезающая” случайную температуру частиц в фазовом пространстве

$\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) = \delta \left( {\Theta {\kern 1pt} * - \,\,\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right).$

В результате дифференцирования индикаторной функции записываем

$\frac{\partial }{{\partial t{\kern 1pt} *}}\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) + \frac{\partial }{{\partial \Theta {\kern 1pt} *}}\left\{ {\frac{{d\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{dt{\kern 1pt} *}}\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right\} = 0.$

Подставляем в последнее равенство уравнение для температуры частиц (7) и учитываем “выкалывающее” свойство δ-функции Дирака

$\begin{gathered} \varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)F\left( {\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right) = \\ = \,\,\delta \left( {\Theta {\kern 1pt} * - \,\,\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)F\left( {\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right) = \\ = \,\,\delta \left( {\Theta {\kern 1pt} * - \,\,\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)F\left( {\Theta {\kern 1pt} *} \right) = \varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)F\left( {\Theta {\kern 1pt} *} \right), \\ \end{gathered} $
где $F\left( {\Theta {\kern 1pt} *} \right)$ – произвольная функция.

В результате получаем замкнутое уравнение Лиувилля

(11)
$\begin{gathered} \frac{{\partial \varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t{\kern 1pt} *}} + \frac{\partial }{{\partial \Theta {\kern 1pt} *}}\left\{ {\left[ {\frac{1}{{\tau _{\Theta }^{ * }}}\left( {\theta _{g}^{ * }\left( {t{\kern 1pt} *} \right) - \Theta {\kern 1pt} *} \right) + _{{_{{_{{_{{_{{_{{}}}}}}^{{}}}}^{{}}}}^{{}}}}^{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{}}}}} \right.} \right. \\ \left. { + \,\,{{{\left\{ {1 + {{{\left[ {\frac{{{{C}_{E}}}}{{E{\kern 1pt} *}}\left( {1 + \frac{{\Theta _{p}^{ * }}}{{E{\kern 1pt} *}}} \right)} \right]}}^{n}}} \right\}}}^{{ - 1}}}\exp \left( {\frac{{\Theta {\kern 1pt} *}}{{1 + {{\Theta {\kern 1pt} *} \mathord{\left/ {\vphantom {{\Theta {\kern 1pt} *} {E{\kern 1pt} *}}} \right. \kern-0em} {E{\kern 1pt} *}}}}} \right)} \right] \times \\ \left. { \times _{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{}}}}^{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{}}}}\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right\} = 0._{{_{{_{{_{{_{{_{{}}}}}}^{{}}}}^{{}}}}^{{}}}}^{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{^{{^{{}}}}}}}} \\ \end{gathered} $

Осреднение индикаторной функции по ансамблю реализаций приводит к ФПР температуры частиц

$\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) = \left\langle {\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right\rangle = \left\langle {\delta \left( {\Theta {\kern 1pt} * - \,\,\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)} \right\rangle .$

Для ФПР выполняется условие нормировки

(12)
$\int\limits_{ - \infty }^\infty {\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)d\Theta {\kern 1pt} * = \int\limits_{ - \infty }^\infty {\left\langle {\delta \left( {\Theta {\kern 1pt} * - \,\,\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)} \right\rangle d\Theta } } = 1.$

Безразмерная температура частиц, как видно из формулы (4), может быть отрицательной. Среднеквадратичное значение флуктуаций температуры существенно ниже, чем осредненное значение температуры, поэтому в интеграле формулы (12) выставлены бесконечные пределы.

Незамкнутое уравнение для ФПР температуры частиц следует из уравнения Лиувилля (11):

$\begin{gathered} \frac{\partial }{{\partial t{\kern 1pt} *}}\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) + \frac{\partial }{{\partial \Theta {\kern 1pt} *}}\left\{ {\left[ { - \frac{1}{{\tau _{\Theta }^{ * }}}\Theta {\kern 1pt} * + _{{_{{}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{_{{_{{}}^{{_{{}}^{{}}}}}}^{{}}}}} \right.} \right. \\ \left. {{{{\left\{ {1 + {{{\left[ {\frac{{{{C}_{E}}}}{{E{\kern 1pt} *}}\left( {1 + \frac{{\Theta _{p}^{ * }}}{{E{\kern 1pt} *}}} \right)} \right]}}^{n}}} \right\}}}^{{ - 1}}}\exp \left( {\frac{{\Theta {\kern 1pt} *}}{{1 + {{\Theta {\kern 1pt} *} \mathord{\left/ {\vphantom {{\Theta {\kern 1pt} *} E}} \right. \kern-0em} E}}}} \right)} \right] \\ \left. { \times _{{_{{}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{_{{_{{}}^{{_{{}}^{{}}}}}}^{{}}}}\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right\} = - \frac{1}{{\tau _{\Theta }^{ * }}}\frac{\partial }{{\partial \Theta {\kern 1pt} *}}\left\langle {{{\theta }_{g}}\left( {t{\kern 1pt} *} \right)\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right\rangle . \\ \end{gathered} $

Корреляция в правой части уравнения раскрывается с помощью формулы Фурутсу–Новикова [19]

(13)
$\begin{gathered} \left\langle {\theta _{g}^{ * }\left( {t{\kern 1pt} *} \right)\varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right\rangle = \\ = \,\,\left\langle {\theta _{g}^{{ * 2}}} \right\rangle \int\limits_0^{t * } {{{\Psi }_{\Theta }}\left( {t{\kern 1pt} * - \,\,t{\kern 1pt} *{\kern 1pt} '} \right)\left\langle {\frac{{\delta \varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}}} \right\rangle dt{\kern 1pt} *{\kern 1pt} '} . \\ \end{gathered} $

Здесь функциональная производная индикаторной функции равна

(14)
$\frac{{\delta \varphi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\delta {{\theta }_{g}}\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}} = - \frac{\partial }{{\partial \Theta {\kern 1pt} *}}\delta \left( {\Theta {\kern 1pt} * - \,\,\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)\frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta {{\theta }_{g}}\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}}.$

Для расчета функциональной производной случайной температуры частиц записывается уравнение (7) с учетом формулы (10) в интегральном виде

$\begin{gathered} \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right) = \frac{1}{{\tau _{\Theta }^{ * }}}\int\limits_0^{t * } {\exp \left( { - \frac{{t{\kern 1pt} * - \,\,s{\kern 1pt} *}}{{\tau _{\Theta }^{ * }}}} \right){{\theta }_{g}}\left( {s{\kern 1pt} *} \right)ds} + \\ + \,\,\int\limits_0^{^{{^{{}}}}t * } {\exp \left( { - \frac{{t{\kern 1pt} * - \,\,s{\kern 1pt} *}}{{\tau _{\Theta }^{ * }}}} \right){{W}_{Q}}\left( {\Theta _{p}^{ * }\left( {s{\kern 1pt} *} \right)} \right)ds{\kern 1pt} *} . \\ \end{gathered} $
Применяя оператор функционального дифференцирования и используя равенство ${{\delta \theta _{g}^{ * }\left( {s{\kern 1pt} *} \right)} \mathord{\left/ {\vphantom {{\delta \theta _{g}^{ * }\left( {s{\kern 1pt} *} \right)} {\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}}} \right. \kern-0em} {\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}} = \delta \left( {s{\kern 1pt} * - \,\,t{\kern 1pt} *{\kern 1pt} '} \right)$, получаем интегральное уравнение для функциональной производной

$\begin{gathered} \frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}} = \frac{1}{{\tau _{\Theta }^{ * }}}\exp \left( { - \frac{{t{\kern 1pt} * - \,\,t{\kern 1pt} *{\kern 1pt} '}}{{\tau _{\Theta }^{ * }}}} \right) + \\ + \,\,\int\limits_{t{\kern 1pt} *{\kern 1pt} '}^{^{{^{{}}}}t{\kern 1pt} *} {\exp \left( { - \frac{{t{\kern 1pt} * - \,\,s}}{{\tau _{\Theta }^{ * }}}} \right){{{\left. {\frac{{d{{W}_{Q}}\left( {\Theta {\kern 1pt} *} \right)}}{{d\Theta {\kern 1pt} *}}} \right|}}_{{\Theta {\kern 1pt} * = \,\,\Theta _{p}^{ * }\left( {s{\kern 1pt} *} \right)}}}\frac{{\delta {{\Theta }_{p}}\left( {s{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}}ds{\kern 1pt} *} . \\ \end{gathered} $

Нижний предел интеграла выставляется из условия физической причинности. Переходим к дифференциальной форме уравнения для функциональной производной

(15)
$\frac{d}{{dt}}\frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}} = - \left( {\frac{1}{{\tau _{\Theta }^{ * }}} - \frac{1}{{\tau _{Q}^{ * }\left( {\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)}}} \right)\frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}}.$

Начальное условие имеет вид

${{\left. {\frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}}} \right|}_{{t{\kern 1pt} * \to t{\kern 1pt} *{\kern 1pt} '}}} = \frac{1}{{\tau _{\Theta }^{ * }}}.$

С учетом данного начального условия для уравнения (15) получаем выражение для функциональной производной

(16)
$\frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}} = \frac{1}{{\tau _{\Theta }^{ * }}}\exp \left\{ { - \int\limits_{t{\kern 1pt} *{\kern 1pt} '}^{t * } {\gamma {\kern 1pt} *\left( {\Theta _{p}^{ * }\left( {s{\kern 1pt} *} \right)} \right)ds{\kern 1pt} *} } \right\}.$

Отметим, что до сих пор при вычислении функциональной производной не было сделано ни одного упрощающего предположения. На основе “теоремы о среднем” записываем оценку интеграла в (16) как

$\frac{{\delta \Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)}}{{\delta \theta _{g}^{ * }\left( {t{\kern 1pt} *{\kern 1pt} '} \right)}} \approx \frac{1}{{\tau _{\Theta }^{ * }}}\exp \left\{ { - \gamma {\kern 1pt} *\left( {\Theta _{p}^{ * }\left( {t{\kern 1pt} *} \right)} \right)\left( {t{\kern 1pt} * - \,\,t{\kern 1pt} *{\kern 1pt} '} \right)} \right\}.$

В выражении для функциональной производной появляются время роста температуры за счет экзотермической химической реакции $\tau _{Q}^{ * }\left( {\Theta {\kern 1pt} *} \right)$ и показатель экспоненты $\gamma {\kern 1pt} *(\Theta {\kern 1pt} *)$, аналогичные соответствующим величинам при исследовании устойчивости стационарных температур.

В результате подстановки выражения для функциональной производной случайной температуры (16) в выражения (13) и (14) приходим к замкнутой форме уравнения для ФПР

(17)
$\begin{gathered} \frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t}} + \frac{\partial }{{\partial \Theta {\kern 1pt} *}}\left[ {\left( { - \frac{1}{{\tau _{\Theta }^{ * }}}\Theta {\kern 1pt} *\,\, + \,\,{{W}_{Q}}\left( {\Theta {\kern 1pt} *} \right)} \right)} \right. \times \\ {{\left. { \times _{{_{{}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{_{{_{{}}^{{}}}}^{{}}}}\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right]}^{{^{{}}}}} = \frac{{\left\langle {\theta _{g}^{{ * 2}}} \right\rangle }}{{{{\tau }_{\Theta }}}}\frac{\partial }{{\partial \Theta {\kern 1pt} *}} \times \\ \times \,\,\left[ {{{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial \Theta {\kern 1pt} *}}} \right]{{.}^{{^{{^{{^{{^{{}}}}}}}}}}} \\ \end{gathered} $
Здесь ${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *} \right)$ – функция отклика температуры частиц на флуктуации температуры среды

${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) = \frac{1}{{\tau _{\Theta }^{ * }}}\int\limits_0^{t{\kern 1pt} *} {{{\Psi }_{\Theta }}\left( {t{\kern 1pt} *{\kern 1pt} '} \right)\exp \left[ { - \gamma {\kern 1pt} *\left( {\Theta {\kern 1pt} *} \right)t{\kern 1pt} *{\kern 1pt} '} \right]dt{\kern 1pt} *{\kern 1pt} '} .$

Начальное ФПР имеет вид

${{\left. {\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)} \right|}_{{t{\kern 1pt} * = 0}}} = {{\Phi }_{0}}\left( {\Theta {\kern 1pt} *} \right).$

В уравнении (17) первое слагаемое в левой части описывает нестационарное изменение ФПР, второе слагаемое представляет дрейф в фазовом пространстве, вызванный теплоотдачей частиц и тепловым эффектом экзотермической реакции. Правая часть уравнения (17) описывает диффузию ФПР в пространстве температур. В результате диффузии в фазовом пространстве к устойчивым стационарным значениям температуры функция распределения пересечет критический уровень температур и произойдет тепловой взрыв.

Для автокорреляционной функции флуктуаций температуры среды в виде (9) получаем функцию отклика

(18)
$\begin{gathered} {{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) = {{\left\{ {1 + \frac{{\tau _{\Theta }^{ * }}}{{T_{\Theta }^{ * }}} - \frac{{\tau _{\Theta }^{ * }}}{{\tau _{Q}^{ * }\left( {\Theta {\kern 1pt} *} \right)}}} \right\}}^{{ - 1}}} \times \\ \times \left\{ {1 - \exp \left[ { - \frac{{t{\kern 1pt} *}}{{\tau _{\Theta }^{ * }}}\left( {1 + \frac{{\tau _{\Theta }^{ * }}}{{T_{\Theta }^{ * }}} - \frac{{\tau _{\Theta }^{{{{ * }^{{^{{}}}}}}}}}{{\tau _{Q}^{ * }\left( {\Theta {\kern 1pt} *} \right)}}} \right)} \right]} \right\}. \\ \end{gathered} $
Функция ${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)$ представляет реакцию температуры частиц на случайные колебания температуры среды. Для медленной химической реакции $\left( {\tau _{\Theta }^{ * } \ll \tau _{Q}^{ * }\left( {\Theta {\kern 1pt} *} \right)} \right)$ функция отклика при $t{\kern 1pt} * \gg \tau _{\Theta }^{ * }$ зависит только от временных масштабов тепловой инерции частиц и интегрального временного масштаба флуктуаций скорости среды

${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) \approx {{\left( {1 + \left( {{{\tau _{\Theta }^{ * }} \mathord{\left/ {\vphantom {{\tau _{\Theta }^{ * }} {T_{\Theta }^{ * }}}} \right. \kern-0em} {T_{\Theta }^{ * }}}} \right)} \right)}^{{ - 1}}}.$

Для интенсивного тепловыделения, когда знаменатель в выражении (18) стремится к нулю, наблюдается монотонный рост коэффициента диффузии вероятности в фазовом пространстве

${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) \approx {{t{\kern 1pt} *} \mathord{\left/ {\vphantom {{t{\kern 1pt} *} {\tau _{\Theta }^{ * }}}} \right. \kern-0em} {\tau _{\Theta }^{ * }}}.$
Для частиц с малой тепловой инерцией $\left( {\tau _{\Theta }^{ * } \ll \left( {T_{\Theta }^{ * },\tau _{Q}^{ * }} \right)} \right)$ функция отклика ${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) \to 1$ и интенсивность флуктуаций температуры частиц и газа совпадают.

Для частиц с большой тепловой инерцией $\left( {\tau _{\Theta }^{ * } \gg \left( {T_{\Theta }^{ * },\tau _{Q}^{ * }} \right)} \right)$ влияние тепловых флуктуаций температуры среды нивелируется ${{f}_{\Theta }}\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) \to 0$.

На рис. 3 представлена функция отклика в различные моменты времени в зависимости от температуры частиц. При низких температурах, когда вклад энерговыделения в частицах мал, функция отклика зависит только от тепловой инерции частиц и всегда меньше единицы. С ростом температуры выше температуры начала теплового взрыва вклад случайных колебаний скорости химической реакции в интенсивность флуктуаций температуры частиц увеличивается, и функция отклика может стать выше единицы.

Рис. 3.

Пример функции отклика для $\tau _{\Theta }^{ * } = 4,\,\,\,\,T_{\Theta }^{ * } = 4$: 1 – $t{\kern 1pt} * = 3$, 2 – 5, 3 – 30.

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ДЛЯ ФПР

Выше на основе анализа случайных температур ансамбля частиц описан метод прямого численного моделирования эмпирической ФПР. В этом разделе представлена оригинальная методика численного интегрирования замкнутого уравнения для ФПР случайной температуры частиц (17).

Уравнение для ФПР (17) переписываем в дивергентном виде

(19)
$\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t{\kern 1pt} *}} + \frac{{\partial J\left( {\Theta {\kern 1pt} *,t{\text{*}}} \right){\kern 1pt} }}{{\partial \Theta {\kern 1pt} *}} = 0.$
Здесь поток в фазовом пространстве равен

$\begin{gathered} J\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) = U\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)\Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) - \\ - \,\,D\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial \Theta {\kern 1pt} *}}. \\ \end{gathered} $

Скорость дрейфа и коэффициент диффузии в пространстве температур определяются как

$\begin{gathered} U\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right) = - \frac{1}{{\tau _{\Theta }^{ * }}}\Theta {\kern 1pt} * + \,\,{{W}_{Q}}\left( {\Theta {\kern 1pt} *} \right), \\ D\left( {\Theta ,t} \right) = \frac{1}{{{{\tau }_{\Theta }}}}{{f}_{\Theta }}\left( {\Theta ,t} \right)\left\langle {\theta _{g}^{2}} \right\rangle . \\ \end{gathered} $

Из условия нормировки ФПР (12) получаем

$\int\limits_{\Theta _{{\min }}^{ * }}^{\Theta _{{\max }}^{ * }} {\left\{ {\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t{\kern 1pt} *}} + \frac{{\partial J\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial \Theta {\kern 1pt} *}}} \right\}d\Theta {\kern 1pt} * = 0} .$
Здесь $\Theta _{{\min }}^{ * },\;\Theta _{{\max }}^{ * }$ – характерные граничные значения температур локализации ФПР. Из условия нормировки следует

$J\left( {\Theta _{{\min }}^{ * },t{\kern 1pt} *} \right) = J\left( {\Theta _{{\max }}^{ * },t{\kern 1pt} *} \right) = 0.$

Координаты узлов сетки равны

$\begin{gathered} \Theta _{i}^{ * },\,\,\,\,i = 1 \ldots N,\,\,\,\,\Theta _{1}^{ * } = \Theta _{{\min }}^{ * }, \\ \Theta _{N}^{ * } = \Theta _{{\max }}^{ * },\,\,\,\,\Theta _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * } = {{\left( {\Theta _{{i + 1}}^{ * } + \Theta _{i}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {\Theta _{{i + 1}}^{ * } + \Theta _{i}^{ * }} \right)} 2}} \right. \kern-0em} 2}. \\ \end{gathered} $
Решение уравнения для ФПР ищем путем численного интегрирования системы ОДУ для значений ФПР в узлах сетки $\Phi _{i}^{ * }\left( {t{\kern 1pt} *} \right) = \Phi \left( {\Theta _{i}^{ * },t{\kern 1pt} *} \right)$. ФПР в промежутке $\Theta _{i}^{ * } \leqslant \Theta {\kern 1pt} * \leqslant \Theta _{{i + 1}}^{ * }$ аппроксимируем линейной функцией
$\Phi {\kern 1pt} * = \Phi _{i}^{ * } + \left( {\Phi _{{i + 1}}^{ * } - \Phi _{i}^{ * }} \right)\frac{{\Theta {\kern 1pt} * - \,\,\Theta _{i}^{ * }}}{{\Theta _{{i + 1}}^{ * } - \Theta _{i}^{ * }}}.$
С целью получения консервативной разностной схемы во внутренних узлах $2 \leqslant i \leqslant N - 1$ уравнение баланса (19) интегрируется в промежутке $\Theta {\kern 1pt} * \in \left[ {\Theta _{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * },\Theta _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }} \right]$:
$\int\limits_{\Theta _{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}^{\Theta _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }} {\left\{ {\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t{\kern 1pt} *}} + \frac{{\partial J\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial \Theta {\kern 1pt} *}}} \right\}d\Theta {\kern 1pt} * = 0} .$
При записи разностной схемы в конечных точках температурного интервала $\Theta _{1}^{ * }$ и $\Theta _{N}^{ * }$ вычисляются следующие интегралы:

$\begin{gathered} \int\limits_{\Theta _{1}^{ * }}^{\Theta _{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}^{ * }} {\left\{ {\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t{\kern 1pt} *}} + \frac{{\partial J\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial \Theta {\kern 1pt} *}}} \right\}d\Theta {\kern 1pt} * = 0} , \\ \int\limits_{\Theta _{{N - 1}}^{ * }}^{\Theta _{N}^{ * }} {\left\{ {\frac{{\partial \Phi \left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial t{\kern 1pt} *}} + \frac{{\partial J\left( {\Theta {\kern 1pt} *,t{\kern 1pt} *} \right)}}{{\partial \Theta {\kern 1pt} *}}} \right\}d\Theta {\kern 1pt} * = 0} . \\ \end{gathered} $

В результате получается система ОДУ для значений ФПР в узлах сетки

(20)
$\begin{gathered} \frac{{d\Phi _{1}^{ * }}}{{dt_{{}}^{ * }}} = - \frac{{U_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}^{ * }\Phi _{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}^{ * }}}{{\Theta _{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}^{ * } - \Theta _{1}^{ * }}} + \frac{1}{{\Theta _{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}^{ * } - \Theta _{1}^{ * }}}D_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}^{ * }\frac{{\Phi _{2}^{ * } - \Phi _{1}^{ * }}}{{\Theta _{2}^{ * } - \Theta _{1}^{ * }}}{{;}_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}^{{}}}}^{{}}}}}}}}} \\ \frac{{d\Phi _{i}^{ * }}}{{dt_{{}}^{ * }}} = - \frac{{U_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }\Phi _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{{{ * }^{{}}}}} - U_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }\Phi _{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}}{{\Theta _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * } - \Theta _{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}} + \frac{1}{{\Theta _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * } - \Theta _{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}} \times \\ \times \,\,\left( {D_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }\frac{{\Phi _{{i + 1}}^{ * } - \Phi _{i}^{{{{ * }^{{^{{}}}}}}}}}{{\Theta _{{i + 1}}^{ * } - \Theta _{i}^{ * }}} - D_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }\frac{{\Phi _{i}^{ * } - \Phi _{{i - 1}}^{ * }}}{{\Theta _{i}^{ * } - \Theta _{{i - 1}}^{ * }}}} \right), \\ 2 \leqslant i \leqslant N - 1; \\ \frac{{d\Phi _{N}^{ * }}}{{dt{\kern 1pt} *}} = \frac{{U_{{N - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }\Phi _{{N - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}}{{\Theta _{N}^{ * } - \Theta _{{N - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}} - \frac{1}{{\Theta _{N}^{ * } - \Theta _{{N - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }}} \times \\ \times \,\,D_{{N - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * }\frac{{\Phi {{{_{N}^{ * }}}^{{^{{^{{}}}}}}} - \Phi _{{N - 1}}^{ * }}}{{\Theta _{N}^{ * } - \Theta _{{N - 1}}^{ * }}}. \\ \end{gathered} $

Значения функций в полуцелых координатах аппроксимируются как

$\begin{gathered} \Phi _{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * } = {{\left( {\Phi _{{i + 1}}^{ * } + \Phi _{i}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {\Phi _{{i + 1}}^{ * } + \Phi _{i}^{ * }} \right)} 2}} \right. \kern-0em} 2},\,\,\,\,U_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * } = {{\left( {U_{{i + 1}}^{ * } + U_{i}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {U_{{i + 1}}^{ * } + U_{i}^{ * }} \right)} 2}} \right. \kern-0em} 2}, \\ D_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{ * } = {{\left( {D_{{i + 1}}^{ * } + D_{i}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {D_{{i + 1}}^{ * } + D_{i}^{ * }} \right)} 2}} \right. \kern-0em} 2}. \\ \end{gathered} $

Система уравнений (20) интегрируется численно с помощью библиотечной программы решения жестких ОДУ в среде MATLAB.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Приведем примеры расчетов динамики изменения эмпирической ФПР и плотности вероятности, полученной в результате решения замкнутого уравнения (17). В расчетах безразмерное время тепловой релаксации частиц $\tau _{\Theta }^{ * } = 4$, интегральный временной масштаб флуктуаций температуры среды $T_{\Theta }^{ * } = 4$.

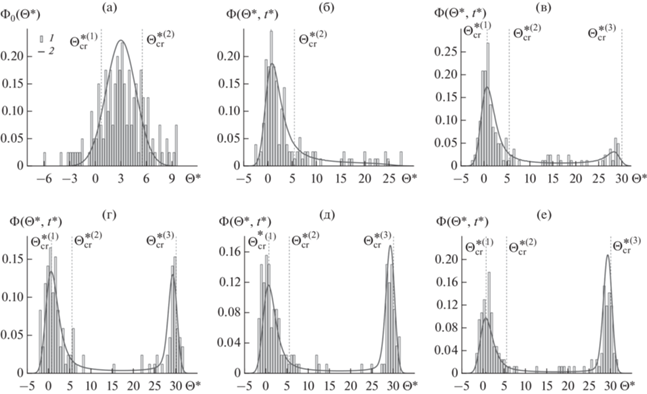
Начальная ФПР выбрана таким образом, чтобы основная масса частиц имела начальную температуру ниже критического значения $\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}}$ (рис. 4а). С течением времени появляется доля частиц, температура которых существенно выше критического значения $\Theta _{{{\text{cr}}}}^{{ * \left( 2 \right)}}$ (рис. 4б, 4в). Следствием флуктуаций температуры среды является тепловой взрыв, приводящий к отчетливой бимодальной структуре ФПР (рис. 4г‒4е). Результаты расчетов ФПР на основе прямого численного моделирования и расчетов плотности вероятности на основе решения замкнутого уравнения для ФПР удовлетворительно согласуются. Случайные значения температуры частиц могут превышать третье стационарное значение $\Theta _{{{\text{cr}}}}^{{ * \left( 3 \right)}}$. Это объясняется положительной обратной связью флуктуаций температуры среды и частиц. Флуктуации температуры среды вызывают флуктуации температуры частиц, которые приводят к случайным колебаниям скорости химической реакции. В свою очередь колебания скорости химической реакции увеличивают дисперсию флуктуаций температуры частиц.

Рис. 4.

Результаты расчета динамики изменения ФПР случайной температуры частиц: 1 – эмпирическая ФПР, 2 – решение замкнутого уравнения для ФПР; (а) ‒ $t{\kern 1pt} * = 0$, (б) ‒ 15, (в) ‒ 37, (г) ‒ 60, (д) ‒ 80, (е) ‒ 100.

ЗАКЛЮЧЕНИЕ

Исследовано влияние флуктуаций температуры среды на границу тепловой стабильности частиц с экзотермической химической реакцией. В рамках подхода Лагранжа на основе решения системы СОДУ представлены примеры случайных траекторий температуры частиц, приводящих к тепловому взрыву. Показано, что флуктуации температуры среды приводят к тепловому взрыву, даже если в детерминированном случае тепловое состояние частиц стабильно. На основе осреднения по ансамблю случайных температур иллюстрируется динамика эмпирической ФПР температуры частиц.

Методом функционального дифференцирования выведено замкнутое уравнение для ФПР случайной температуры частиц. Предложен оригинальный метод интегрирования уравнения для ФПР на основе консервативной разностной схемы.

Представлены результаты численного исследования теплового взрыва для существования трех стационарных температур на диаграмме Н.Н. Семенова. Результаты моделирования динамики эмпирической функции распределения и ФПР, рассчитанной разностным методом на основе решения замкнутого уравнения, удовлетворительно согласуются между собой. Равновесная ФПР имеет бимодальную структуру с максимумами в области низкой стационарной температуры и температуры, соответствующей режиму высокотемпературного реагирования.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 20-08-01061).

Список литературы

  1. Schneider H., Proust Ch. Determination of Turbulent Burning Velocities of Dust Air Mixtures with the Open Tube Method // J. Loss Prevent. Proc. Ind. 2007. V. 20. № 4–6. P. 470.

  2. Hadi K., Ichimura R., Hashimoto N., Fujita O. Spherical Turbulent Flame Propagation of Pulverized Coal Particle Clouds in an O2 /N2 Atmosphere // Proc. Combust. Inst. 2019. V. 37. № 3. P. 2935.

  3. Scheid M., Geißler A., Krause U. Experiments on the Influence of Pre-ignition Turbulence on Vented Gas and Dust Explosions // J. Loss Prevent. Proc. Ind. 2006. V. 19. № 2–3. P. 194.

  4. Smirnov N.N., Nikitin V.F., Legros J.C. Ignition and Combustion of Turbulized Dust–Air Mixtures // Combust. Flame. 2000. V. 123. № 1–2. P. 46.

  5. Eckhoff R.K. Understanding Dust Explosions. The Role of Powder Science and Technology // J. Loss Prevent. Proc. Ind. 2009. V. 22. № 1. P. 105.

  6. El-Sayed S.A. Self-Ignition of Dust Cloud in a Hot Gas // J. Braz. Soc. Mech. Sci. Eng. 2018. V. 40. № 6. 285.

  7. Esclapez L., Collin-Bastiani F., Riber E., Cuenot B. A Statistical Model to Predict Ignition Probability // Combust. Flame. 2021. V. 225. P. 180.

  8. Eaton J.K., Fessler J.R. Preferential Concentration of Particles by Turbulence // Int. J. Multiphase Flow. 1994. V. 20. Suppl. P. 169.

  9. Вараксин А.Ю. Кластеризация частиц в турбулентных и вихревых двухфазных потоках // ТВТ. 2014. Т. 52. № 5. С. 777.

  10. Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.: Наука, 1987.

  11. Зельдович Я.Б., Баренблатт Г.И., Либрович В.Б., Махвиладзе Г.М. Математическая теория горения и взрыва. М.: Наука, 1980. 478 с.

  12. Gray B.F., Sherrington M.E. Explosive Systems with Reactant Consumption. I. Critical Conditions // Combust. Flame. 1972. V. 19. № 3. P. 435.

  13. Gorelov G.N., Sobolev V.A. Mathematical Modeling of Critical Phenomena in Thermal Explosion Theory // Combust. Flame 1991. V. 87. № 2. P. 203.

  14. Shouman A.R., El-Sayed S. Accounting for Reactant Consumption in the Thermal Explosion Problem. Part I: Mathematical Foundation // Combust. Flame. 1992. V. 88. № 3–4. P. 321.

  15. Filimonov V.Yu. Features of Self-Heating for Homogeneous Exothermic Reactions // Combust. Sci. Technol. 2014. V. 186. № 2. P. 173.

  16. Зарубин В.С., Кувыркин Г.Н., Савельева И.Ю. Вариационная форма модели теплового взрыва в твердом теле с зависящей от температуры теплопроводностью // ТВТ. 2018. Т. 56. № 2. С. 235.

  17. Van Kampen N.G. Stochastic Processes in Physics and Chemistry. North-Holland, Amsterdam: Elsevier, 1984. 465 p.

  18. Gardiner C.W. Handbook of Stochastic Methods for Physics, Chemistry, and the Natural Sciences. Berlin‒Heidelberg: Springer, 1985. 443 p.

  19. Klyatskin V.I. Stochastic Equations Through the Eye of the Physicist. Oxford: Elsevier Science, 2005. 556 p.

  20. Хорстхемке В., Лефевр Р. Индуцированные шумом переходы: теория и применение в физике, химии и биологии. М.: Мир, 1987. 400 с.

  21. Warnatz J., Maas U., Dibble R.W. Combustion. Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation. 4th ed. Berlin‒Heidelberg: Springer, 2001. 378 p.

  22. Федотов С.П., Третьяков М.В. Стационарные режимы гетерогенной химической реакции при наличии внешних шумов // Хим. физика. 1988. Т. 7. № 11. С. 1533.

  23. Федотов С.П., Третьяков М.В. О стохастическом воспламенении частицы // Хим. физика. 1991. Т. 10. № 2. С. 238.

  24. Pope S.B. PDF Methods for Turbulent Reactive Flows // Prog. Energy Combust. Sci. 1985. V. 11. № 2. P. 119.

  25. Вараксин А.Ю. К выбору инерционности частиц, используемых для оптической диагностики высокоскоростных газовых потоков // ТВТ. 2021. Т. 59. № 3. С. 411.

  26. Derevich I.V. Influence of Internal Turbulent Structure on Intensity of Velocity and Temperature Fluctuations of Particles // Int. J. Heat Mass Transfer. 2001. V. 44. № 23. P. 4505.

  27. Мержанов А.Г., Руманов Э.Н. Нелинейные аффекты в макроскопической кинетике // УФН. 1987. Т. 151. № 4. С. 553.

  28. Burrage K., Burrage P.M. High Strong Order Explicit Runge–Kutta Methods for Stochastic Ordinary Differential Equations // Appl. Numer. Math. 1996. V. 22. № 1–3. P. 81.

  29. Debrabant K., Rößler A. Classification of Stochastic Runge–Kutta Methods for the Weak Approximation of Stochastic Differential Equations // Math. Comput. Simulation. 2008. V. 77. № 4. P. 408.

  30. Деревич И.В., Клочков А.К. Флуктуации скорости частицы в вязком газе со случайной скоростью в виде суммы двух коррелированных цветных шумов // Матем. и матем. моделирование. 2020. № 1. С. 33.

  31. Wetchagarun S., Riley J.J. Dispersion and Temperature Statistics of Inertial Particles in Isotropic Turbulence // Phys. Fluids. 2010. V. 22. № 6. 063301.

  32. Семёнов Н.Н. О некоторых проблемах химической кинетики и реакционной способности. М.: Изд-во АН, 1954. 350 с.

  33. Князев А.Г., Дюкарев Е.А. О режимах твердофазного разложения одиночных кристаллов инициирующих взрывчатых веществ // Физ. мезомеханика. 2000. Т. 3. № 3. С. 97.

  34. Kolmogoroff A. Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung // Math. Ann. 1931. Bd. 104. S. 415.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал