1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 59, № 3, 2021

Теплофизика высоких температур, 2021, T. 59, № 3, стр. 345-351

Анализ кинематической вязкости и самодиффузии жидких металлов при температуре плавления

Ю. Н. Стародубцев 1, 2, *, В. С. Цепелев 1, **

1 Уральский федеральный университет
Екатеринбург, Россия

2 Научно-производственное предприятие “Гаммамет”
Екатеринбург, Россия

* E-mail: yunstar@mail.ru
** E-mail: v.s.tsepelev@urfu.ru

Поступила в редакцию 23.06.2020
После доработки 29.06.2020
Принята к публикации 14.10.2020

Полный текст (PDF)

Аннотация

В статье приведены результаты исследования влияния размера и массы атомов на кинематическую вязкость и коэффициент самодиффузии металлических жидкостей. Для анализа использовались экспериментальные данные о кинетических свойствах металлов при температуре плавления. Регрессионный анализ показал, что кинематическая вязкость и коэффициент самодиффузии растут с увеличением размера атомов и уменьшением их массы. Причем масса атомов более тесно связана с кинетическими свойствами металлической жидкости, чем размер атомов. Для анализа кинетических свойств жидкости предложено использовать размерно-массовый фактор, который равен отношению размера атома к корню квадратному из его массы. Связь кинетических свойств с размерно-массовым фактором характеризует скорректированный коэффициент детерминации, значение которого больше 0.90. Показано, что с увеличением размера кластеров снижаются кинематическая вязкость жидкости и коэффициент самодиффузии. Из безразмерных кинетических величин определена безразмерная избыточная энтропия при температуре плавления, которая близка к расчетным значениям для точки затвердевания простой жидкости.

ВВЕДЕНИЕ

Диффузия и вязкость относятся к явлениям переноса, которые связаны с тепловым движением атомов или молекул. Кинетические свойства жидкости характеризуют коэффициент самодиффузии D (м2 с–1), который определяет скорость переноса массы, и кинематическая вязкость ν (м2 с–1), определяющая скорость переноса плотности импульса ρv [1], где ρ – плотность, кг м–3, v – скорость, м с–1. Кинематическая вязкость является структурно-чувствительной характеристикой металлической жидкости, поэтому к этой физической величине проявляется наибольший научный и практический интерес [2–4].

Исследование структуры и физических свойств жидкости осуществляется с использованием различных приближений. Первопринципные (ab initio) методы моделирования [5] используют для простой жидкости, состоящей из химически несвязанных друг с другом бездипольных атомов, имеющих сферически симметричные потенциалы взаимодействия [6]. Следующим приближением к реальной жидкости являются физические модели. В решетчатой модели предполагается, что жидкость в среднем имеет структуру решетки, по крайней мере, в первой координационной сфере [7], а колебание атома (молекулы) происходит внутри ограниченного пространства (ячейки). В решетчатой модели используется понятие свободного объема, т.е. пространства, доступного для движения центра тяжести атомов (молекул) [8]. Если количество ячеек больше числа атомов (молекул), то такую модель называют дырочной моделью жидкости.

Линдеман [9] использовал молекулярно-кинетическую теорию для определения частоты колебания атомов при температуре плавления. На основе соотношения между температурой плавления и частотой колебания атомов Андраде [10] получил формулу для динамической вязкости ηm (Па с) при температуре плавления

(1)
${{\eta }_{m}} \propto \frac{{\sqrt {M{{T}_{m}}} }}{{V_{m}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}},$
где M – молярная масса, кг моль–1; Tm – температура плавления, К; Vm – молярный объем, м3 моль–1. Используя соотношение (1) и формулу Стокса–Эйнштейна
$\eta D = \frac{{{{k}_{{\text{B}}}}T}}{{3\pi a}},$
можно найти коэффициент самодиффузии Dm при температуре плавления
(2)
$D \propto a\sqrt {\frac{{R{{T}_{m}}}}{M}} ,$
где a – диаметр атома, м; R = kBNA – универсальная газовая постоянная, Дж К–1 моль–1; kB – постоянная Больцмана, Дж К–1; NA – постоянная Авогадро, моль-1.

Точность предсказания динамической вязкости и коэффициента самодиффузии в соответствии с соотношениями (1) и (2) для чистых металлов достаточно высока [11–13]. Эти формулы связывают вязкость и самодиффузию с размером и массой атомов в жидкости, которая представляет совокупность одинаковых атомов. Однако проверить такую связь экспериментально очень сложно. Для этого необходимо зафиксировать, например, температуру и массу частиц однородной жидкости, а варьировать только их размер. В наножидкости, состоящей из смеси жидкой и твердой нанодисперсных фаз, вязкость тесно связана с объемом твердой фазы, а влияние размера частиц неоднозначно [14].

В настоящей работе исследовано влияние размера и массы атомов на кинематическую вязкость и коэффициент самодиффузии металлических жидкостей с использованием данных, полученных при температуре плавления.

ИСХОДНЫЕ ДАННЫЕ

Для расчета кинематической вязкости и коэффициента самодиффузии можно использовать простые соотношения молекулярно-кинетической теории, которые дают хорошие результаты. Кинетическая энергия колебаний атома ek (Дж) рассчитывается по формуле

(3)
${{e}_{k}} = \frac{1}{2}m{{\omega }^{2}}{{\left( {\alpha a} \right)}^{2}},$
где m – масса атома, кг; ω – частота, с–1; α – относительная амплитуда колебаний атомов, αa – абсолютная амплитуда колебаний, м. Тепловая энергия eT (Дж) при температуре T равна

(4)
${{e}_{T}} = {{k}_{{\text{B}}}}T.$

В качестве частоты колебаний атомов используются результаты различных теорий, чаще всего частота Дебая ωD (c–1) [15–17]

${{\omega }_{D}} = {{\Theta }_{D}}\frac{{2\pi {{k}_{{\text{B}}}}}}{h},$
где ΘD – температура Дебая, К; h – постоянная Планка, Дж с. Сравнивая кинетическую и тепловую энергии, получаем относительную амплитуду колебаний атомов

$\alpha = \frac{h}{{\pi a{{\Theta }_{D}}}}\sqrt {\frac{T}{{2{{k}_{{\text{B}}}}m}}} .$

Из данного соотношения следует, что амплитуда колебаний атомов увеличивается с ростом температуры и с уменьшением размера и массы атомов.

Для молярных величин соотношения (3) и (4) при температуре плавления Tm принимают вид

(5)
${{E}_{k}} = 2{{\pi }^{2}}{{\alpha }^{2}}M{{a}^{2}}\Theta _{D}^{2}{{\left( {\frac{{{{k}_{{\text{B}}}}}}{h}} \right)}^{2}},$
(6)
${{E}_{T}} = R{{T}_{m}}.$

В формулах (5) и (6) M = mNA, кг моль–1.

Оценка приближения полученных формул к линейной зависимости проведена с использованием регрессионного анализа, а степени приближения сравнены с помощью скорректированного коэффициента детерминации $R_{{adj}}^{2}.$ Металлы разбиты на три группы: щелочные и щелочноземельные, расширенная группа тугоплавких металлов и другие металлы, к которым отнесены элементы III, X–XIV групп Периодической таблицы Менделеева. Численные значения молярной массы M, температуры плавления Tm, кинематической вязкости νm и коэффициента самодиффузии Dm при температуре плавления взяты из [18]. Данные по температуре Дебая ΘD получены из [19]. За размер атома a принята величина

$a = \sqrt[3]{{\frac{{{{V}_{m}}}}{{{{N}_{{\text{A}}}}}}}},$
где Vm – молярный объем, м3 моль–1. Сравнение a с удвоенным металлическим радиусом атома [20] дало очень хорошее совпадение значений при скорректированном коэффициенте детерминации $R_{{adj}}^{2}$ = 0.99.

Связь соотношений (5) и (6) для молярной кинетической энергии Ek и молярной тепловой энергии ET при температуре плавления характеризуют коэффициент детерминации $R_{{adj}}^{2}$ = 0.64 и безразмерный коэффициент 2π2α2 = 0.056. Последний соответствует относительной амплитуде колебаний атомов при температуре плавления α = 0.053 и увеличению расстояния между центрами соседних атомов на 0.106a. Эта оценка совпадает с критерием плавления Линдемана [9], который показал, что увеличение расстояния между центрами соседних атомов больше критического значения 0.1 приводит к разрушению кристалла, которое внешне проявляется как плавление.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

С помощью анализа размерностей молярную кинетическую энергию можно записать в виде соотношения, в которое входят кинематическая вязкость или коэффициент самодиффузии

(7)
${{E}_{k}} \propto \frac{1}{2}M{{\left( {\frac{\nu }{{\alpha a}}} \right)}^{2}},$
(8)
${{E}_{k}} \propto \frac{1}{2}M{{\left( {\frac{D}{{\alpha a}}} \right)}^{2}}.$

Величины ν/αa и D/αa имеют размерность скорости и выражают скорость переноса плотности импульса ρv и скорость переноса массы m, обусловленные тепловым колебанием атомов. Сравнивая уравнения (7) и (6), а также (8) и (6), получаем выражения для кинематической вязкости νm и коэффициента самодиффузии Dm при температуре плавления

(9)
${{\nu }_{m}} = {{С}_{1}}a\sqrt {\frac{{R{{T}_{m}}}}{M}} ,$
(10)
${{D}_{m}} = {{С}_{2}}a\sqrt {\frac{{R{{T}_{m}}}}{M}} ,$
где С1 и С2 – безразмерные постоянные. При этом учтено, что при температуре плавления относительная амплитуда колебания атомов для всех металлов является постоянной и равной α = 0.053.

В результате регрессионного анализа соотношения (9) определены постоянная С1 = 5.2 и скорректированный коэффициент детерминации $R_{{adj}}^{2}$ = 0.75. На рис. 1 представлена связь экспериментальных значений кинематической вязкости νm жидких металлов с комплексом в правой части формулы (9).

Рис. 1.

Связь кинематической вязкости νm жидких металлов при температуре плавления с параметром 5.2a(RTmM–1)0.5 – штриховая линия, рассчитанная по (9) с C1 = 5.2 при $R_{{adj}}^{{\text{2}}}$ = 0.75; 1 – щелочные и щелочноземельные металлы, 2 – тугоплавкие металлы, 3 – металлы III, X–XIV групп.

В уравнении (9) можно перейти от кинематической вязкости ν к динамической вязкости η с помощью соотношения

$\eta = \nu \rho = \nu \frac{M}{{{{V}_{m}}}}.$

После преобразований получается известное уравнение Андраде [10]

${{\eta }_{m}} = \frac{{{{С}_{1}}}}{{{{a}^{2}}}}\sqrt {m{{k}_{{\text{B}}}}{{T}_{m}}} = \frac{{{{C}_{1}}\sqrt R }}{{N_{{\text{A}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}\frac{{\sqrt {M{{T}_{m}}} }}{{V_{m}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}.$

Подобное уравнение было получено также в модели твердых сфер [21]

$\begin{gathered} \eta = \frac{{4a}}{{5\sqrt \pi }}\sqrt {m{{k}_{{\text{B}}}}T} \frac{{{{N}_{{\text{A}}}}}}{{{{V}_{m}}}}\left( {\frac{{pV}}{{RT}} - 1} \right) = \\ = \frac{4}{{5\sqrt \pi {{a}^{2}}}}\sqrt {m{{k}_{{\text{B}}}}T} \left( {\frac{{pV}}{{RT}} - 1} \right), \\ \end{gathered} $
гдe pV/(RT) – фактор сжимаемости; p – давление, Па. При температуре плавления фактор сжимаемости принимает значение, близкое к 8 [22].

В результате регрессионного анализа соотношения (10) определяются постоянная С2 = 0.035 и скорректированный коэффициент детерминации $R_{{adj}}^{2}$ = 0.93. На рис. 2 представлена связь экспериментального коэффициента самодиффузии Dm жидких металлов с параметром в правой части формулы (10). В модели твердых сфер для коэффициента самодиффузии получено выражение [21]

$D = \frac{a}{2}\sqrt {\frac{{\pi {{k}_{{\text{B}}}}T}}{m}} {{\left( {\frac{{pV}}{{RT}} - 1} \right)}^{{ - 1}}},$
которое совпадает с (10) при постоянном значении фактора сжимаемости pV/(RT).

Рис. 2.

Связь коэффициента самодиффузии Dm жидких металлов при температуре плавления с параметром 0.035a(RTmM–1)0.5 – штриховая линия, рассчитанная по (10) с C1 = 0.035 при $R_{{adj}}^{{\text{2}}}$ = 0.93; 1 – щелочные и щелочноземельные металлы, 2 – металлы III, X–XIV групп.

После перемножения уравнений (9) и (10) получаем

${{\nu }_{m}}{{D}_{m}} = {{C}_{1}}{{С}_{2}}\frac{{{{a}^{2}}R{{T}_{m}}}}{M}.$

Если в данном соотношении перейти к динамической вязкости η, то оно приобретает вид уравнения Стокса–Эйнштейна

$\eta = {{С}_{1}}{{С}_{2}}\frac{{{{k}_{{\text{B}}}}{{T}_{m}}}}{{aD}}.$

В уравнении Стокса–Эйнштейна безразмерный коэффициент равен (1/3)π = 0.106, и он незначительно отличается от коэффициента С1С2 = = 0.18, полученного в настоящей работе.

Из уравнений (9) и (10) видно, что кинематическая вязкость и коэффициент самодиффузии различаются только постоянными коэффициентами. Тесную связь кинематической вязкости и коэффициента самодиффузии подтверждает высокий скорректированный коэффициент детерминации $R_{{adj}}^{2}$ = 0.87 экспериментальных значений этих физических величин. Из формул можно найти отношение скоростей ν/a и D/a при температуре плавления, которое равно отношению постоянных С1/С2 = 149. Следовательно, при температуре плавления скорость переноса плотности импульса на два порядка выше скорости переноса массы.

Заметим, что постоянные коэффициенты С1·и С2 представляют собой безразмерные величины кинематической вязкости ν* и коэффициента самодиффузии D* при температуре плавления, которые были рассмотрены Розенфельдом [23]. В работе [24] показано, что атомный транспорт связан с избыточной молярной энтропией S (Дж К–1 моль–1), которая равна разности энтропии системы и энтропии эквивалентного идеального газа. В частности, для безразмерного коэффициента диффузии и динамической вязкости получены линейные соотношения [25]

D* ≈ 0.6e–0.8s,

η* ≈ 0.2e0.8s,

где s = S/R – безразмерная избыточная энтропия. Из равенств η* = С1 = 5.2 (постоянный коэффициент для динамической и кинематической вязкости имеет одинаковые значения 5.2) и D* = С2 = = 0.035 получаем значения безразмерной избыточной энтропии при температуре плавления 4.1 и 3.6 соответственно. Эти значения близки к расчетным значениям, которые находятся примерно в интервале от 4 до 5 для точки затвердевания простой жидкости [22].

Из уравнений (9) и (10) также следует, что кинематическая вязкость и коэффициент самодиффузии должны снижаться с увеличением размера колеблющихся частиц и с уменьшением их массы. Однако использовать напрямую численные данные для кинематической вязкости νm и коэффициента самодиффузии Dm нельзя, поскольку каждый металл обладает индивидуальным набором значений физических величин a, m и Tm.

Для того чтобы выделить влияние размера атомов на кинематическую вязкость, с помощью формулы (9) приведем кинематическую вязкость к единице физической величины, в которую входят масса атомов и температура плавления

(11)
$\frac{{{{\nu }_{m}}}}{{5.2}}\sqrt {\frac{M}{{R{{T}_{m}}}}} .$

Нормированная кинематическая вязкость (11) имеет размерность длины и связана с размером атомов линейным соотношением

$\frac{{{{\nu }_{m}}}}{{5.2}}\sqrt {\frac{M}{{R{{T}_{m}}}}} = a.$

На рис. 3 представлена зависимость нормированной кинематической вязкости от размера атомов a. В целом вязкость жидких металлов растет с увеличением размера атомов с коэффициентом детерминации $R_{{adj}}^{2}$ = 0.69, однако эта связь сильно различается для разных групп металлов. Так, вязкость наиболее тесно связана с размером атомов у щелочных и щелочноземельных металлов, для которых скорректированный коэффициент детерминации равен 0.92. У тугоплавких металлов такая связь практически отсутствует и $R_{{adj}}^{2}$ = 0.09, а у металлов III, X–XIV групп она незначительна и $R_{{adj}}^{2}$ = 0.28.

Рис. 3.

Связь нормированной кинематической вязкости νm(5.2)–1M0.5(RTm)–0.5 жидких металлов c размером атомов a – штриховая линия; $R_{{adj}}^{{\text{2}}}$ = 0.69; 1 – щелочные и щелочноземельные металлы, 2 – тугоплавкие металлы, 3 – металлы III, X–XIV групп.

Для оценки влияния массы атомов на кинематическую вязкость она нормируется на физическую величину, в которую входят размер атомов и температура плавления. В этом случае нормированная кинематическая вязкость имеет размерность кг–0.5 моль0.5 и связана с молярной массой соотношением

$\frac{{{{\nu }_{m}}}}{{5.2a\sqrt {R{{T}_{m}}} }} = {{M}^{{ - 0.5}}}.$
На рис. 4 представлена зависимость нормированной кинематической вязкости от молярной массы M–0.5. Вязкость жидких металлов снижается с увеличением массы атомов. Связь нормированной кинематической вязкости νm(5.2a)–1(RTm)–0.5 жидких металлов c молярной массой M–0.5 определяет коэффициент детерминации $R_{{adj}}^{2}$ = 0.88. Высокий коэффициент детерминации свидетельствует о том, что кинематическая вязкость более тесно связана с массой атомов, чем с их размером. Это верно для всех групп атомов. Так, коэффициент детерминации $R_{{adj}}^{2}$ равен 0.97, 0.68 и 0.73 соответственно для щелочных и щелочноземельных металлов, тугоплавких металлов и металлов из III, X–XIV групп Периодической системы Менделеева.

Рис. 4.

Связь нормированной кинематической вязкости νm(5.2a)–1(RTm)–0.5 жидких металлов c молярной массой M–0.5 – штриховая линия; $R_{{adj}}^{{\text{2}}}$ = 0.88; 1–3 – см. рис. 3.

Уравнения (9) и (10) можно записать в виде

${{\nu }_{m}} = {{С}_{1}}\sqrt {\frac{{{{k}_{{\text{B}}}}{{T}_{m}}}}{{{{\rho }_{s}}}}} ,\,\,\,\,{{D}_{m}} = {{С}_{2}}\sqrt {\frac{{{{k}_{{\text{B}}}}{{T}_{m}}}}{{{{\rho }_{s}}}}} ,$
где величина ρs является поверхностной плотностью и определяет массу на единицу поверхности

${{\rho }_{s}} = \frac{m}{{{{a}^{2}}}}.$

На рис. 5 представлена связь нормированной кинематической вязкости νm(5.2)–1(kBTm)–0.5 жидких металлов с размерно-массовым фактором F = = $\rho _{s}^{{ - 0.5}}$ = am–0.5. Эта связь имеет более высокий коэффициент детерминации, а именно $R_{{adj}}^{2}$ = 0.91, чем связь вязкости с атомным размером или массой по отдельности. При фиксированной температуре кинематическая вязкость и коэффициент самодиффузии растут пропорционально размерно-массовому фактору и, следовательно, снижаются с увеличением поверхностной плотности ρs.

Рис. 5.

Связь нормированной кинематической вязкости νm(5.2a)–1(kBTm)–0.5 жидких металлов c размерно-массовым фактором $\rho _{s}^{{ - {\text{0}}{\text{.5}}}}$ = am–0.5 – штриховая линия; $R_{{adj}}^{{\text{2}}}$ = 0.91; 1–3 – см. рис. 3.

На рис. 6 представлена поверхностная плотность ma–2 в зависимости от атомного номера Z металлических элементов. Масса на единицу поверхности растет с увеличением атомного номера. Для щелочных и щелочноземельных металлов линейная связь поверхностной плотности с атомным номером имеет высокий коэффициент детерминации $R_{{adj}}^{2}$ = 0.95. Для остальных металлов вблизи Cu, Ru и Ir наблюдаются локальные пики, и, несмотря на это, коэффициент детерминации остается достаточно высоким $R_{{adj}}^{2}$ = 0.81.

Рис. 6.

Масса на единицу поверхности ma–2 в зависимости от атомного номера Z металлических элементов различных групп: 1–3 – см. рис. 3.

По аналогии с кинематической вязкостью проанализирована связь коэффициента самодиффузии с размером и массой атомов. Для этой связи получены еще более высокие скорректированные коэффициенты детерминации по сравнению с кинематической вязкостью. Например, связь нормированного коэффициента самодиффузии Dm(0.035)–1(kBTm)–0.5 жидких металлов с размерно-массовым фактором am–0.5 определяет коэффициент детерминации $R_{{adj}}^{2}$ = 0.97.

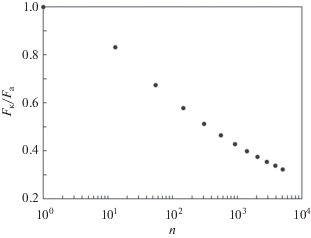
Диаметр и масса кластера зависят от числа атомов [26]. Изменение относительного размерно-массового фактора кластера, т.е. отношение размерно-массового фактора кластера Fк к размерно-массовому фактору атома Fа, в зависимости от числа атомов в кластере n показано на рис. 7. Видно, что с увеличением числа атомов в кластере относительный размерно-массовый фактор снижается. Отсюда можно сделать вывод, что при фиксированной температуре кинематическая вязкость и коэффициент самодиффузии будут снижаться с увеличением размера кластера.

Рис. 7.

Зависимость относительного размерно-массового фактора Fк/Fа от числа атомов в кластере n.

ЗАКЛЮЧЕНИЕ

На основе экспериментальных данных для жидких металлов при температуре плавления показано, что кинематическая вязкость и коэффициент самодиффузии увеличиваются с ростом размера атомов и уменьшением их массы. Для того чтобы выделить влияние размера (массы) атомов, кинематическая вязкость или коэффициент самодиффузии приводятся к единице физической величины, в которую входят масса (размер) атомов и температура плавления. Обнаружено, что масса атомов более тесно связана с кинетическими свойствами металлической жидкости, чем размер атомов.

Для анализа кинетических свойств жидкости предложено использовать поверхностную плотность ρs, которая равна удельной массе атомов (на единицу поверхности), и размерно-массовый фактор $\rho _{s}^{{ - 0.5}},$ равный отношению размера атома к корню квадратному из его массы. Связь кинематической вязкости и коэффициента самодиффузии с размерно-массовым фактором характеризует скорректированный коэффициент детерминации, значение которого больше 0.90. Показано, что с увеличением размера кластеров снижаются кинематическая вязкость и коэффициент самодиффузии жидкости. Из безразмерных кинетических величин определена безразмерная избыточная энтропия при температуре плавления, которая близка к расчетным значениям для точки затвердевания простой жидкости.

Работа выполнена в рамках государственной работы FEUZ-0836-0020.

Список литературы

  1. Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука, 1975. 592 с.

  2. Бельтюков А.Л., Олянина Н.В., Ладьянов В.И. Температурная и концентрационная зависимости вязкости расплавов Co–Si // ТВТ. 2019. Т. 57. № 1. С. 47.

  3. Хуснутдинов Р.М., Мокшин А.В., Бельтюков А.Л., Олянина Н.В. Вязкость расплава кобальта: эксперимент, моделирование и теория // ТВТ. 2018. Т. 56. № 2. С. 211.

  4. Чикова О.А., Цепелев В.С., Московских О.П. Оценка параметров микрогетерогенной структуры металлических расплавов из результатов вискозиметрического эксперимента на основе представлений теории абсолютных скоростей реакций // ЖФХ. 2017. Т. 91. № 6. С. 925.

  5. Гельчинский Б.Р., Мирзоев А.А., Воронцов А.Г. Вычислительные методы микроскопической теории металлических расплавов и нанокластеров. М.: Физматлит, 2011. 200 с.

  6. Физика простых жидкостей / Под ред. Темперли Г., Роулинсона Дж., Рашбрука Дж. Ч. 1, 2. М.: Мир, 1971–1973.

  7. De With G. Liquid-state Physical Chemistry. Fundamentals, Modeling, and Applications. Weinheim: Wiley-VCH, 2013. 526 p.

  8. Глесстон С., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакции. Кинетика химических реакций, вязкость, диффузия и электрохимические явления. М.: ГИИЛ, 1948. 584 с.

  9. Lindemann F.A. Über die Berechnung molekularer Eigenfrequenzen // Phys. Z. 1910. Bd. 11. S. 609.

  10. Andrade E.N. da C. A Theory of the Viscosity of Liquids – Part 1 // Phil. Mag. 1934. V. 17. P. 497.

  11. Iida T., Guthrie R., Isac M., Tripathi N. Accurate Predictions for the Viscosities of Several Liquid Transition Metals, Plus Barium and Strontium // Metall. Mater. Trans. 2006. V. 37B. P. 402.

  12. Iida T., Guthrie R., Tripathi N. A Model for Predictions of Self-diffusivities in Liquid Metals, Semimetals, and Semiconductors // Metall. Mater. Trans. 2006. V. 37B. P. 559.

  13. Kaptay G. A Unified Equation for the Viscosity of Pure Liquid Metals // Metallkd. 2005. V. 96. P. 24.

  14. Mishra P.C., Mukherjee S., Nayak S.K., Panda A. A Brief Rewire on Viscosity of Nanofluids // Int. Nano Lett. 2014. V. 4. P. 109.

  15. Glyde H.R. Relation of Vacancy Formation and Migration Energies to the Debye Temperature in Solids // J. Phys. Chem. Solids. 1967. V. 28. P. 2061.

  16. Grimvall G., Sjödin S. Correlation of Properties of Materials to Debye and Melting Temperatures // Phys. Scripta. 1974. V. 10. P. 340.

  17. Lawson A.C. Physics of the Lindemann Melting Rule // Phil. Mag. 2009. V. 89. P. 1757.

  18. Iida T., Guthrie R.I.L. The Thermophysical Properties of Metallic Liquids. Oxford: University Press, 2015. 586 p.

  19. Stewart G.R. Measurement of Low Temperature Specific Heat // Rev. Sci. Instrum. 1983. V. 54. P. 1.

  20. Greenwood N.N., Earnshow A. Chemistry of the Elements. Oxford: Butterworth-Heinemann, 1998. 1343 p.

  21. Longuet-Higgins H.C., Pople J.A. Transport Properties of a Dense Fluid of Hard Spheres // J. Chem. Phys. 1956. V. 25. P. 884.

  22. Hover W.G., Ree F.H. Melting Transition and Communal Entropy for Hard Spheres // J. Chem. Phys. 1968. V. 49. P. 3609.

  23. Rosenfeld Y. Relation between the Transport Coefficients and the Internal Entropy of Simple Systems // Phys. Rev. A. 1977. V. 15. P. 2545.

  24. Dzugutov M. A Universal Scaling Law for Atomic Diffusion in Condensed Matter // Nature. 1996. V. 381. P. 137.

  25. Rosenfeld Y. A Quasi-universal Scaling Law for Atomic Transport in Simple Fluids // J. Phys.: Condens. Matter. 1999. V. 11. P. 5415.

  26. Poole C.P. Jr., Owens F.J. Introduction to Nanotechnology. New Jersey: John Wiley & Sons, 2003. 388 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал