Теплоэнергетика, 2023, № 9, стр. 45-67
Моделирование процессов смешения однофазных сред в тройниковых соединениях
Ф. В. Тупоносов a, В. И. Артемов a, Г. Г. Яньков a, Н. С. Душин b, О. А. Душина b, А. В. Дедов a, b, *
a Национальный исследовательский университет “Московский энергетический институт”
111250 Москва, Красноказарменная ул., д. 14, Россия
b Федеральный исследовательский центр “Казанский научный центр Российской академии наук”
420111 г. Казань, ул. Лобачевского, д. 2/31, Россия
* E-mail: dedovav@mpei.ru
Поступила в редакцию 31.03.2023
После доработки 07.04.2023
Принята к публикации 27.04.2023
Аннотация
Цель работы – выбор методики численного моделирования и расчет процессов смешения природного газа с так называемыми “отдувками” нефтехимических производств, содержащими метан, водород и азот, в трубах Т-образного соединения (тройнике) для использования полученной смеси в качестве топлива на тепловых электростанциях. Особенностями смешения топливных газов являются высокие числа Рейнольдса моделируемых потоков, достигающие значений Re = (5–10) × 106. Представлен анализ некоторых экспериментальных и современных расчетных исследований процессов смешения потоков в трубах и тройниковых соединениях. Подчеркивается, что при проведении численного моделирования с помощью осредненных по Рейнольдсу уравнений сохранения применение разнообразных популярных моделей для турбулентной вязкости или рейнольдсовых напряжений не позволяет получить удовлетворительного соответствия экспериментальным данным о смешении потоков в Т-образном смесителе без необоснованного уменьшения турбулентного числа Шмидта (Прандтля) до значения 0.1 или увеличения известной константы моделей турбулентности Сμ в 9 раз. Сделан вывод о нецелесообразности выбора вихреразрешающих методов для исследования процессов смешения в соединениях топливных трубопроводов ввиду высоких чисел Рейнольдса и значительных длин основной трубы. Анализ выполненных расчетов позволил обнаружить существенные колебания локального отношения скорости порождения кинетической энергии турбулентных пульсаций к скорости ее диссипации и резкое уменьшение его среднего значения по сечению трубы на расстояниях в несколько диаметров от начала смешения, не свойственное ни течениям в трубах, ни слоям смешения или струям. Предпринята попытка улучшить предсказательные способности стандартной k–ε-модели для развитой турбулентности, оставаясь в рамках обоснованных значений турбулентного числа Шмидта ${\text{S}}{{{\text{c}}}_{t}}$ и константы Сμ. Предложены эмпирическая формула для ${\text{S}}{{{\text{c}}}_{t}}$ и модификация стандартной k–ε-модели, учитывающей переменность Сμ согласно зависимости Роди, тщательно верифицированной на данных о разнообразных свободных течениях. Проведены экспериментальные исследования изотермического смешения в Т-образном смесителе потоков воздуха, один из которых содержал трассеры в виде микрокапель жидкости на основе глицерина. Профили гидродинамических характеристик течения за тройником измерялись планарным оптическим методом SIV на дистанции 5.5D от оси пересечения труб. В целях верификации модифицированной k–ε-модели выполнено численное моделирование процессов смешения газов и жидкостей в Т-образном смесителе и проведено сравнение расчетных и экспериментальных данных. Представлены результаты расчетов процессов смешения природного газа с метановодородной фракцией нефтехимических производств в Т-образном смесителе.
Смешение теплоносителей, имеющих разный состав и/или температуру, в элементах трубопроводов и проточных частях установок – актуальная задача для многих отраслей промышленности, сельского и коммунального хозяйства. Решению этой задачи посвящено значительное число публикаций (например, [1–3]), в которых обсуждаются различные варианты смешения потоков жидкостей и газов (однофазных и двухфазных) с учетом возникающих неоднородностей состава и температуры смеси, гидравлических сопротивлений, возможных нестационарных эффектов, динамических нагрузок на стенки каналов, циклических термонапряжений и т.д. В частности, неизотермическое смешение воды в тройниковых соединениях системы аварийного охлаждения активной зоны ядерных реакторов при авариях с потерей теплоносителя (LOCA) – одна из наиболее важных проблем безопасности, связанных с возможностью теплового удара под давлением (PTS – Pressurized Thermal Shock). Сохраняющаяся актуальность этой проблемы обусловлена и повышенным вниманием к мерам по сокращению эмиссии диоксида углерода в химических технологиях и теплоэнергетике благодаря использованию водородсодержащего топлива. Неоднородная концентрация водорода в потоке смеси и возможный длительный или периодический контакт некоторых фрагментов стенки трубы-коллектора с практически чистым водородом может привести к водородному охрупчиванию материала трубы, что, безусловно, является важным негативным фактором.
Во многих технологических процессах для эффективного смешения потоков различных составов и температуры часто используются смесители-тройники. Они обеспечивают достаточно хорошее перемешивание турбулентных потоков и относительно низкие гидравлические потери. При оптимальном выборе скоростей смешивающихся потоков, диаметров каналов и углов соединения труб такой подход в некоторых случаях обладает технико-экономическими преимуществами перед так называемыми статическими смесителями.
В настоящей работе выполнена верификация модифицированной k–ε-модели с привлечением экспериментальных данных, полученных авторами настоящей статьи, а также данных других авторов по смешению потоков газа и воды. Приведены результаты численного моделирования процесса смешения природного газа и смеси метана, водорода и азота (метановодородной фракции нефтехимических производств) в Т-образном смесителе при высоких числах Рейнольдса газовых потоков.
НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ОПУБЛИКОВАННЫХ ИССЛЕДОВАНИЙ
Далее кратко обсуждаются основные результаты и выводы выполненных исследований по смешению потоков, важных для целей настоящей работы. Эти исследования можно условно разделить на три группы:
первая – экспериментальное изучение характеристик смешения потоков в окрестности тройникового соединения;
вторая – исследование зондовыми и оптическими методами процессов вырождения за счет турбулентной диффузии неоднородностей, созданных тем или иным способом, в протяженных трубах и каналах;
третья – компьютерное моделирование смешения с использованием современных методов вычислительной гидродинамики.
К первой группе относятся работы [4–15], в которых исследовалось смешение газов и/или жидкостей в тройниковых (чаще Т-образных) соединениях трубопроводов. На рис. 1 представлена схема такого смешения. Внутренний диаметр трубы D, среднемассовая аксиальная скорость U основного потока и его плотность ρ обозначены индексом 1, для вторичного потока – индексом 2, за началом смешения (z ≥ 0) – индексом m (y, z – оси координат). Фрагмент основной трубы за началом смешения далее называется коллектором.
На рис. 1 приближенно изображены границы струи вторичного потока при “оптимальных” параметрах. Под ними во многих работах понимаются такие параметры вторичного потока, при которых ось подаваемой струи после ее разворота совпадает с осью основной трубы, что в сечениях основной трубы приводит в дальнейшем к более эффективному вырождению неоднородностей состава среды, температуры, концентрации примеси и других параметров с ростом z (по мере отдаления от начала координат) вследствие турбулентной диффузии. Следует отметить, что понятие оптимальных параметров условно, так как в некоторых случаях вторичный поток подается в виде нескольких взаимодействующих струй, что, в свою очередь, приводит к иным критериям оптимальных условий смешения.
В работах [4, 5] смешивали два изотермических потока воды. Для определения качества смешения в один из них добавляли соль, концентрацию которой измеряли в окрестности тройникового соединения, а также ниже по потоку на достаточно значительных расстояниях (до ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 124, что позволяет отнести эти исследования и ко второй группе). Числа Рейнольдса основного потока ${{\operatorname{Re} }_{1}} = {{{{U}_{1}}{{D}_{1}}} \mathord{\left/ {\vphantom {{{{U}_{1}}{{D}_{1}}} {{{\nu }_{1}}}}} \right. \kern-0em} {{{\nu }_{1}}}}$ достигали значения 105, подмешиваемого (вторичного) потока ${{\operatorname{Re} }_{2}} = {{{{U}_{2}}{{D}_{2}}} \mathord{\left/ {\vphantom {{{{U}_{2}}{{D}_{2}}} {{{\nu }_{2}}}}} \right. \kern-0em} {{{\nu }_{2}}}}$ – примерно 2500 (ν – коэффициент кинематической вязкости, м2/с). Измерения выполнены для двух малых значений параметра ${{d}_{r}} = {{{{D}_{2}}} \mathord{\left/ {\vphantom {{{{D}_{2}}} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}{\text{:}}$ 0.00521 и 0.01042. В качестве характеристики интегральной неоднородности перемешивания использовалось значение второго момента М в виде
Авторы [4, 5] обобщили полученные экспериментальные данные зависимостью, позволяющей рассчитать параметр $R = {{{{U}_{2}}} \mathord{\left/ {\vphantom {{{{U}_{2}}} {{{U}_{1}}}}} \right. \kern-0em} {{{U}_{1}}}}$ для оптимального перемешивания потоков. Анализ полученных данных показал, что при совпадении после поворота оси струи вторичного потока с осью основной трубы длина “полного” перемешивания (например, при М = 0.01) была примерно в 1.5–2.0 раза меньше, чем в случаях, когда струя была прижата к ближней или противоположной части стенки основной трубы. Длина трубы, на которой значение M достигало 0.1, в лучшем случае составляла 50${{D}_{1}}$, а чтобы М = 0.01, требовалась труба протяженностью 70${{D}_{1}}$.
В [6] было исследовано смешение потоков воздуха, имеющих разную температуру (разность температур не превышала 10°С), при умеренных числах Рейнольдса 16 200 ≤ ${{\operatorname{Re} }_{1}}$ ≤ 63 100, ${{\operatorname{Re} }_{2}}$ ≈ 8240 и параметрах 0.097 ≤ ${{d}_{r}}$ ≤ 0.255, 1.5 ≤ R ≤ 10.0. Авторами предложены обобщающие зависимости для оптимального смешения, позволяющие определить значения R при заданных диаметрах труб тройникового соединения и ${{d}_{r}}$ при заданных объемных расходах $\dot {V}$ смешиваемых потоков.
Подробные экспериментальные исследования смешения воздушных потоков при ${{{{z}_{1}}} \mathord{\left/ {\vphantom {{{{z}_{1}}} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ ≤ 10, 104 ≤ ${{\operatorname{Re} }_{1}}$ ≤ 105, ${{\operatorname{Re} }_{2}}$ ≈ 104, 0.00612 ≤ ${{d}_{r}}$ ≤ 0.2 выполнены в работах [7–10]. Подаваемый в Т-образный смеситель вторичный поток воздуха содержал метан в качестве пассивной примеси. Авторами были предложены обобщающие зависимости для определения оптимальных объемных расходов смешиваемых потоков. Показано, что вниз по течению от начала смешения:
максимальная концентрация примеси снижается практически экспоненциально;
оптимальное отношение скоростей R не зависит от чисел Рейнольдса основного и вторичного потоков, если ${{\operatorname{Re} }_{1}}$ ≥ 40 000, ${{\operatorname{Re} }_{2}}$ ≥ 6000;
при числах Фруда Fr ≥ 50 влиянием сил плавучести на процесс смешения можно пренебречь $\left[ {{\text{Fr}}\,\,{\text{ = }}\,\,{{{{U}_{2}}} \mathord{\left/ {\vphantom {{{{U}_{2}}} {{{{\left( {{{g\Delta \rho {{D}_{2}}} \mathord{\left/ {\vphantom {{g\Delta \rho {{D}_{2}}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}} \right)}}^{{\frac{1}{2}}}}}}} \right. \kern-0em} {{{{\left( {{{g\Delta \rho {{D}_{2}}} \mathord{\left/ {\vphantom {{g\Delta \rho {{D}_{2}}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}} \right)}}^{{\frac{1}{2}}}}}}} \right.;$ $\Delta \rho = {{\rho }_{{\,1}}} - {{\rho }_{2}};$ g – модуль вектора ускорения свободного падения, $\left. {^{{^{{^{{}}}}}}{\text{м/}}{{{\text{с}}}^{2}}} \right]$.
В работе [10] экспериментально было изучено смешение газовых потоков при подаче вторичного потока несколько выше по течению поворота на 90° (изгиба) основной трубы. Труба для вторичного потока могла присоединяться в плоскости изгиба со стороны как внутренней, так и внешней образующей основной трубы. Из-за закрутки потока при повороте на 90° возникает сложная структура течения, которая в определенных условиях существенно улучшает качество смешения.
Боковая и встречная соосная подачи вторичного потока в Т-образный смеситель рассматривались в [11]. Исследования были выполнены для различных жидких и газообразных смешиваемых сред в широком диапазоне чисел Рейнольдса и ориентированы на химические технологии, для которых важны скорости и характерные времена реакций непосредственно за началом смешения.
Следует отметить, что в упомянутых ранее работах числа Рейнольдса и диаметры труб для основного потока значительно превышали аналогичные параметры для вторичного потока.
Для верификации моделей турбулентности и CFD-кодов (computational fluid dynamics) наибольший интерес представляют подробные экспериментальные результаты работ [12–15], использованные позднее в качестве эталонных данных (benchmark). В [12] исследовалось смешение потоков водопроводной и деионизированной (опресненной) воды, различающихся электрической проводимостью. Трубы горизонтального Т-образного смесителя были выполнены из оргстекла (${{D}_{1}}$ = ${{D}_{2}}$ = 51 мм), смешение потоков контролировалось с помощью локальной электрической проводимости, измеряемой в различных сечениях трубы 51 ≤ z ≤ 311 мм двумя датчиками с электродной сеткой (WMS – Wire-Mesh Sensor). Позднее на этой же установке были получены новые подробные данные о пульсационных и осредненных полях и спектрах флуктуаций концентрации пассивной примеси в широком диапазоне чисел Рейнольдса, а также отношения скоростей потоков ${{d}_{r}}$ при ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ ≤ 6.1 [13]. В спектрах отчетливо наблюдались четыре характерных режима с наибольшей амплитудой пульсаций при частотах 1–10 Гц.
В [14] представлены результаты экспериментального исследования процессов смешения потоков воды разной температуры в Т-образном соединении, изготовленном из оргстекла (${{D}_{1}}$ = 140 мм, ${{D}_{2}}$ = 100 мм). При этом вторичная труба с “горячей” водой располагалась вертикально. Массовые расходы воды различались вдвое (${{{{Q}_{1}}} \mathord{\left/ {\vphantom {{{{Q}_{1}}} {{{Q}_{2}}}}} \right. \kern-0em} {{{Q}_{2}}}}$ = 2) и соответствовали числам Рейнольдса ${{\operatorname{Re} }_{1}}$ = ${{\operatorname{Re} }_{2}}$ = 1.9 × 105. Важным результатом работы является полученная существенная нестационарность температуры и скорости смешиваемых потоков. “Размах” пульсаций температур с частотой порядка 10 Гц мог превышать 5°С при начальной разности температур потоков ∆t = 15°С. Данные по температурным полям при 2.0 ≤ ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ ≤ 9.46 были получены с помощью зонда с термопарой, а по скоростным полям – методом LDV (laser Doppler velocimetry).
Новые эталонные результаты по неизотермическому смешению потоков воды в Т-образном смесителе были приведены в [15]. В отличие от [14], в этой работе стенки трубы не были адиабатными. Подробные измерения при ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ ≤ 9.46, ∆t = 15°С, ${{Q}_{1}}$ = ${{Q}_{2}},$ ${{D}_{1}}$ = ${{D}_{2}}$ = 54 мм профилей осредненной продольной скорости и ее пульсационной компоненты, температуры жидкости и стенки выполнены для чисел Рейнольдса смеси в основной трубе-коллекторе ${{\operatorname{Re} }_{m}}$ = 40 × 103 и 60 × 103.
Если относительная длина трубы-коллектора ${L \mathord{\left/ {\vphantom {L {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ (L – длина трубы, м) и время перемешивания не являются лимитирующими факторами, то особенности процессов смешения в области тройника оказываются не столь важными. Существует большое количество работ (вторая группа) по определению длины трубы или канала, необходимой для “полного” вырождения неоднородностей, созданных каким-либо способом. Авторы сравнительно недавно вышедшей работы [16] исследовали изменение концентрации пассивной примеси в воздушном потоке в канале прямоугольного сечения. Начальная неоднородность создавалась путем сонаправленного впрыска капель масла диаметром менее 1 мкм при концентрации капель порядка 106 см–3. Число Стокса, характеризующее инерционность частиц, было существенно меньше единицы. Экспериментальные данные представлены для трех значений числа Рейнольдса: 3.5 × 104, 5.0 × 104 и 10.0 × 104. Профиль концентрации частиц в сечении канала нормальном к продольной оси определялся оптическими методами. В качестве измеряемого параметра авторы использовали отношение текущей концентрации примеси к ее гомогенной концентрации при идеальном перемешивании. Представлены данные об эволюции профиля относительной концентрации жидких частиц при ${z \mathord{\left/ {\vphantom {z {{{D}_{h}}}}} \right. \kern-0em} {{{D}_{h}}}}$ ≤ 30, где ${{D}_{h}}$ – гидравлический диаметр канала, м.
Важно подчеркнуть, что увеличение числа Рейнольдса не приводило к улучшению перемешивания, а, напротив, несколько замедляло его на начальном участке. Это согласуется с наблюдениями в ранее выполненных работах [5–7] и связано с тем, что возрастание скорости конвективного переноса неоднородностей вниз по течению с увеличением числа Рейнольдса превосходит скорость роста радиальной турбулентной диффузии, что и влечет за собой увеличение длины перемешивания.
Более ранние работы [4, 5, 17–19] отличаются от [16] применяемой измерительной техникой и способами подачи пассивной примеси в канал, например в виде линейного источника вдоль диаметра трубы, кольцевого по периметру стенки равномерного или неравномерного источника и кольцевого источника, локализованного внутри основной трубы. В [4, 5] авторами предложены обобщающие зависимости, позволяющие рассчитать длину трубы L, необходимую для достижения заданного значения коэффициента σ = ${{M}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ при подаче в трубу центральной или пристеночной струи примеси.
Не останавливаясь на особенностях многих разработанных упрощенных моделей для предсказания характеристик потока после смешения, далее авторы ограничатся лишь обсуждением работ (третья группа), в которых используются современные методы вычислительной гидродинамики.
Вероятно, впервые численное решение дифференциальных уравнений гидродинамики, осредненных по Рейнольдсу (RANS equation – Reynolds-averaged Navier–Stokes equations), для Т-образного смесителя было выполнено в [20] с использованием CFD-кода PHOENIX [21] и стандартной k–ε-модели турбулентности с пристеночными функциями [22]. Сравнение полученных данных в виде зависимости величины M от параметра $R{{d}_{r}}$ при 0.026 ≤ ${{d}_{r}}$ ≤ 0.362 и ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 3 показало их хорошее соответствие эмпирической формуле [10].
В [23] с помощью CFD-кода FLOW3D моделировалось смешение двух потоков бинарных смесей одних и тех же компонентов, различающихся концентрациями. Стандартная k–ε-модель была дополнена уравнением переноса скаляра $\overline {{{{\left( {f{\kern 1pt} '} \right)}}^{2}}} ,$ где $f{\kern 1pt} '$ – пульсационная составляющая безразмерной массовой доли одного из компонентов смеси, а черта над символами означает традиционное осреднение по Рейнольдсу. Результаты моделирования процессов смешения в окрестности тройника (${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ ≤ 3.5) сравнивались с собственными экспериментальными данными авторов [23]. Приемлемое согласование результатов было получено только при задании турбулентного числа Шмидта ${\text{S}}{{{\text{c}}}_{t}}$ = 0.2. Авторы [23] отмечают, что более низкие по сравнению с пристеночными пограничными слоями значения ${\text{S}}{{{\text{c}}}_{t}}$ были ожидаемы, так как для затопленных струй, слоев смешения и других течений, не ограниченных стенками, в литературе (например, [24]) рекомендуются значения ${\text{S}}{{{\text{c}}}_{t}}$ ≈ 0.5. Наиболее однородное смешение по данным [23] было характерно для режима, при котором вторичный поток “проникал” до противоположной поверхности стенки основной трубы Т-образного соединения.
В работе [25] численно исследованы различные устройства смешения. Использовалась стандартная k–ε-модель, турбулентное число Шмидта принималось равным 0.9. Сделан вывод о том, что подача вторичного потока под углом менее 90° (при отсчете угла от оси z против часовой стрелки) более эффективна для выравнивания пространственной неоднородности концентрации пассивной примеси, однако в этом случае формируются вихревые структуры, которые в некоторых случаях являются нежелательными. Лучшие характеристики показывают смесители с несколькими струями, при этом предпочтительнее оказываются устройства с четным количеством струй.
В работе [26] численно моделировались режимы изотермического смешения воды, экспериментально изученные в [13]. В качестве аналога солей, содержавшихся только в основном потоке воды, при численном моделировании применялась пассивная примесь, для которой решалось уравнение переноса. Цель работы состояла в анализе предсказательных способностей трех RANS-моделей турбулентности: стандартной k–ε, k–ω SST и BSL [27], реализованных в CFD-коде ANSYS CFX-10 [28]. Из девяти вариантов расчетов в стационарной постановке, различающихся степенью детализации расчетной сетки и отношениями скоростей смешивающихся потоков (R = 0.4, 1.0, 1.6), для семи вариантов авторам [26] не удалось получить окончательную сходимость. Относительные среднеквадратические невязки уравнений движения осциллировали между значениями 2.2 × 10–5 и 4.7 × 10–5, невязки уравнения сохранения для примеси были на уровне 2.7 × 10–5. Подобное поведение невязок характерно при “слабой” нестационарности течения. В расчетах варьировались значения постоянного турбулентного числа Шмидта в диапазоне ${\text{S}}{{{\text{c}}}_{t}}$ = 0.1–0.9 и известной константы в k–ε-модели турбулентности Сμ = 0.090, 0.405, 0.810 (при ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9). Только увеличение Сμ в 9 раз относительно стандартного значения 0.09 позволило авторам [26] получить удовлетворительное соответствие рассчитанных и экспериментально измеренных профилей продольной компоненты скорости. Выводы авторов состоят в следующем:
ни одна из RANS-моделей не способна предсказать перемешивание в окрестности тройникового соединения с приемлемой точностью;
использование этих моделей при турбулентном числе Шмидта равном 0.9 приводит к близким результатам, значительно отличающимся от экспериментальных данных [13] при ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 3.0 и 5.3;
уменьшение турбулентного числа Шмидта до значения 0.1 существенно улучшает согласование результатов расчетов и экспериментов в части профилей концентрации пассивной примеси в различных сечениях трубы-коллектора, однако не позволяет получить соответствие профилей скорости;
увеличение константы Сμ до 0.81 приводит к разумному соответствию расчетных и экспериментальных полей скорости, хотя некоторые качественные различия в формах профилей концентрации примеси сохраняются.
Любопытно отметить, что одновременно с [26] (в том же номере журнала Nuclear Engineering and Design) была опубликована работа [29], в которой численно моделировались методом URANS (unsteady RANS) с использованием моделей k–ω SST, BSL и SST-SAS (scale-adaptive simulation) режимы изотермического и неизотермического смешения, экспериментально исследованные в [13, 14]. Выводы авторов [30] в отношении предсказательных способностей моделей турбулентности k–ω SST и BSL применительно к изотермическому смешению полностью аналогичны выводам работы [26] – удовлетворительное соответствие экспериментальным данным [13] результатов расчетов, полученных методом URANS, может быть достигнуто лишь при значениях ${\text{S}}{{{\text{c}}}_{t}}$ = 0.1. Что же касается режимов неизотермического смешения [14], то возникающие в окрестности тройника существенные флуктуации скорости и температуры не могут быть предсказаны с использованием моделей указанного класса. В качестве компромисса между традиционным методом URANS и ресурсоемким вихреразрешающим методом LES (large eddy simulation) авторами [29] была выбрана модель SST-SAS на базе URANS. Модель турбулентности SAS, предложенная в [30], обладает способностью разрешать спектр флуктуаций компонент скорости и любой скалярной переменной (температуры, концентрации) в областях нестационарного течения. “LES”-подобные возможности модели SAS достигаются без явной зависимости турбулентной вязкости от размеров ячеек сетки, в отличие от классических методов LES, и оказываются существенно менее затратными. С помощью этой модели, реализованной в кодах ANSYS Fluent [31] и ANSYS CFX, в [29] удалось неплохо воспроизвести осредненные и пульсационные характеристики течения, опытным путем изученные в [14]. Значение турбулентного числа Шмидта при использовании модели SST-SAS в [29] не указано.
В [32] опубликованы некоторые результаты, полученные 29 участниками тестовых CFD-расчетов (benchmark exercise) режима из работы [14]. Мероприятие было организовано под эгидой OECD (Organisation for Economic Cooperation and Development) Nuclear Energy Agency в 2009 г. Исходными данными служили конструктивные характеристики экспериментальной установки и режимные параметры [14]. Полученные опытные данные были скрыты от участников теста (“слепой” тест) до обнародования результатов в [32] (имена участников не сообщались). Расчеты были выполнены следующими методами (далее в скобках указано количество работ): классическим LES (18), гибридным LES/RANS (2), URANS (9). Ранжирование представленных результатов проводилось отдельно по осредненным и мгновенным (с шагом 1 мс) полям скорости и температурам жидкости в точках ее измерения для заданных сечений трубы-коллектора. Наилучшие результаты были достигнуты классическим LES-методом (применялись расчетные сетки, содержащие 13.2–70.5 млн ячеек). При этом общее количество ячеек сетки, как правило, являлось хорошим показателем качества результатов. Неплохие результаты (10-е место в рейтингах) получены с использованием модели k–ω SST на сетке с 11 млн ячеек, что, по мнению организаторов теста, излишне много. Модель SST-SAS оказалась в числе последних позиций в рейтингах. Дополнительную информацию о тесте заинтересованный читатель может почерпнуть в [32].
В работе [33] была исследована эффективность оригинальной конструкции смесителя газов (воздух и биогаз), в состав которого входят две боковые трубы, симметрично примыкающие под углами 135° и 225° к основной трубе в ее узком сечении (угол отсчитывается от оси z против часовой стрелки). Основная труба выполнена в виде трубы Вентури с горловиной диаметром 16 мм и диффузорной частью длиной и диаметром 220 и 34.3 мм соответственно. Характеристики этого смесителя сравниваются с характеристиками тройникового смесителя с углами “врезки” одной боковой трубы 90° и 135°. Расчеты выполнены с использованием низкорейнольдсовой k‒ε‑модели, реализованной в коде ANSYS Fluent (версия модели не указана). Авторы не сообщают о выбранном значении турбулентного числа Шмидта. Представленные данные для изотермического смешения дают основание утверждать, что при подаче биогаза по двум боковым трубам неоднородность его концентрации на выходе из смесителя существенно меньше, чем при односторонней подаче.
В работе [34] методом численного моделирования и в ходе проведения экспериментов было изучено неизотермическое смешение воздушных потоков (температуры ${{t}_{1}}$ = 40°С, ${{t}_{2}}$ = 74.2°С) в тройниковом смесителе, у которого вторичная труба располагалась под углом 135° к основному трубопроводу. Подробные опытные данные по температуре смеси получены в трех сечениях основной трубы ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 1.52, 2.28, 3.04 (шесть точек измерения температуры в каждом сечении) и менее подробные результаты (по две точки измерения) – в сечениях ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 4.57, 6.09, 12.17 при ${{\operatorname{Re} }_{1}}$ = (25–250) × 103, ${{\operatorname{Re} }_{2}}$ = 83 × 103. Численное моделирование выполнено с помощью кода STARCCM+ [35] и реализованных в нем моделей k–ε, RSM (Reynolds Stress Model) и k–ω. О версиях двухпараметрических моделей для турбулентной вязкости, значении турбулентного числа Шмидта, а также о наличии или отсутствии пульсаций температуры в [34] не сообщается. Использование моделей RSM и k–ω приводит к близким результатам, которые, по мнению авторов [34], в большей степени соответствуют экспериментальным данным (хотя различия температур в некоторых точках достигают 15°С) по сравнению с результатами использования k–ε-модели.
Интенсивное развитие вычислительной техники привело к заметному ежегодному росту количества работ, в которых детальный анализ турбулентных течений выполнен методами LES и DNS (direct numerical simulation). Не случайно подавляющее большинство участников теста [32] использовали метод LES. Недавно была опубликована работа [36], в которой изучались не только пульсации температуры в жидкости и стенках тройникового соединения, но и возникающие при этом термонапряжения. Расчеты гидродинамики и теплообмена выполнялись с помощью кода OpenFOAM [37] методом LES для весьма высоких чисел Рейнольдса (27 × 103 ≤ ${{\operatorname{Re} }_{1}}$ ≤ 132 × 103) и разностей температур (92 ≤ $\Delta t$ ≤ 249°C) смешиваемых потоков. Общее число ячеек сетки в зависимости от моделируемого режима изменялось от 16 до 37.5 млн. Для расчета термонапряжений в стенках тройника использовался код Abaqus [38]. Показано, что в самом неблагоприятном из рассчитанных режимов термонапряжения могут достигать 177 МПа.
К сожалению, в публикациях, как правило, не приводятся сведения о временны́х и компьютерных ресурсах, потребовавшихся для расчетов. Некоторые их оценки можно найти в [39]. Так, в [39] тестовый режим [14] моделировался методом LES, причем расчетная сетка содержала всего около 1 млн ячеек, генераторы турбулентного контента на входах в трубы тройника отсутствовали. По информации, предоставленной автором, расчеты нестационарного режима заняли несколько недель. Следует отметить, что числа Рейнольдса в указанном тестовом режиме были весьма высокими (${{\operatorname{Re} }_{1}}$ = ${{\operatorname{Re} }_{2}}$ = 1.9 × 105).
В [40 ] в рамках верификации кода FlowVision [41] выполнены расчетные исследования смешения в тройнике неизотермических потоков натрия. Задача решалась в сопряженной постановке с учетом теплопроводящей стенки для умеренных чисел Рейнольдса (50–70) × 103. Для моделирования использовались методы URANS, LES и квази-DNS. Для метода LES потребовалась сетка с 36 млн ячеек, необходимое время расчетов на 360 ядрах составило 21 сут. В [40 ] показано, что метод URANS позволяет достаточно надежно предсказывать осредненные характеристики процесса смешения и температуры стенки трубы-коллектора, а для получения информации о пульсациях скорости и температуры следует использовать метод LES или DNS. По оценкам авторов [40 ] , необходимые затраты вычислительных и временны́х ресурсов для реализаций методов LES и квази-DNS превысили затраты, необходимые для URANS, в 350 и 1500 раз соответственно.
Необходимость увеличения числа расчетных ячеек по мере роста числа Рейнольдса (сопровождаемого уменьшением шага по времени) для течений, моделируемых классическим методом LES, ограничивает использование этого метода для анализа многих практически важных задач. В последнее время появилось довольно большое число работ, моделирующих смешение потоков в разнообразных тройниках менее затратными методами – VLES (very large eddy simulation), гибридными LES/RANS (например, DES – detached eddy simulation). При этом, как правило, исследуются режимы с небольшими числами Рейнольдса (15–20) × 103 (см., например, [42–44]).
Некоторым исключением из сложившейся практики использования вихреразрешающих методов является работа [45], в которой изучалось смешение водорода с природным газом в трубах Т-образного соединения. Ранее отмечалось, что контакт стенки трубы-коллектора с практически чистым водородом может привести к водородному охрупчиванию материала трубы, поэтому основная цель работы [45] состояла в анализе концентрации водорода около стенки и оптимальном выборе расположения вторичной трубы, по которой подавался водород. Авторы применяли гибридный метод DES с ветвью RANS на базе модели Spalart-Allmaras [46, 47] и CFD-код OpenFOAM [37]. Следует отметить, что для выбранных в [45] параметров газовой магистрали (давление природного газа р = 6.9 МПа, его скорость ${{U}_{1}}$ = 10 м/c, диаметр трубы ${{D}_{1}}$ = 460 мм) число Рейнольдса на входе в тройник оказалось равным 2 × 107, а после смешения с водородом, разумеется, стало еще больше. В работе [45] указано, что количество ячеек сетки изменялось в пределах 2.8–4.8 млн. Сеточная независимость результатов не демонстрируется, верификация выполнена с привлечением данных [15] для значения числа Рейнольдса в трубе-коллекторе равного 40 000, что почти на три десятичных порядка ниже, чем для основного режима, моделируемого авторами. Точность полученных решений для столь высоких чисел Рейнольдса вызывает естественные сомнения.
Анализ некоторых опубликованных работ показывает, что для решения практически важных задач, характеризующихся высокими числами Рейнольдса смешиваемых потоков (Re > 105), с помощью не только классического метода LES, но и гибридных методов LES/RANS требуются чрезвычайно высокие затраты компьютерных ресурсов. В ряде случаев расчетная область должна охватывать более сложные или более протяженные области потока, чем Т-образные соединения. Полезная информация в этих случаях может быть получена при использовании метода URANS, по крайней мере, для выявления проблемных зон в компонентах реальных установок.
Поскольку для рассматриваемой задачи о смешении топливных газов характерны высокие числа Рейнольдса (5–10) × 106, очевидно, что корректное применение вихреразрешающих методов расчета турбулентных течений является чрезмерно ресурсоемким. Далее обсуждаются результаты верификации модифицированной k–ε-модели с привлечением собственных экспериментальных данных (авторов настоящей статьи), а также данных других авторов по смешению потоков газа и жидкости, приводятся результаты численного моделирования смешения природного газа и метановодородной фракции нефтехимических производств в Т-образном смесителе.
ПОСТАНОВКА ЗАДАЧИ
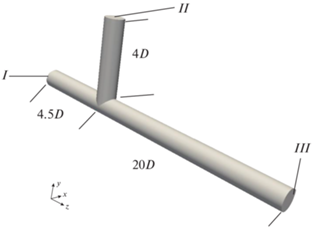
В стандартной постановке задачи смеситель природного газа и метановодородной фракции представляет собой две трубы внутренним диаметром D = 254 мм, соединенные под углом 90°. Входные и выходное сечения тройника и характерные длины труб показаны на рис. 2.
На вход I подается чистый метан (CH4) с массовым расходом ${{Q}_{1}}$ = 10 кг/c и температурой ${{t}_{1}}$ = 60°C, а на вход II – смесь трех газов: метана (CH4), водорода (H2) и азота (N2) – с мольными долями ${{r}_{{C{{H}_{4}}}}}$ = ${{r}_{{{{H}_{2}}}}}$ = 0.4, ${{r}_{{{{N}_{2}}}}}$ = 0.2, расходом смеси Q2 = 10 кг/c и температурой ${{t}_{2}}$ = 90°C. На выходе из смесителя III задается давление pout = 2.75 МПа.
Далее анализируются два параметра, характеризующих состав смеси: массовая (cl) и мольная (rl) доли компонентов смеси (l – индекс, обозначающий один из трех газов – CH4, H2 или N2):
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Основные уравнения. Для моделирования использовалась система уравнений гидродинамики, энергии и диффузии компонентов газовой смеси, осредненных по Рейнольдсу [48] (черта осреднения над символами искомых переменных не используется):
По повторяющимся индексам i, j в выражении для G проводится суммирование i = 1, 2, 3; j = 1, 2, 3. При моделировании использовалась декартова система координат, поэтому обозначения осей координат (${{x}_{1}},$ ${{x}_{2}},$ ${{x}_{3}}$) и (х, у, z) считаются эквивалентными. Центр системы координат совпадает с точкой пересечения осей труб тройника, ось z направлена вдоль основного потока (см. рис. 2).
Свойства газовой смеси. Для расчета свойств смеси газов использовались модель идеального газа и соотношения Уилки, Масона и Саксены [49, 50].
Все свойства чистых компонентов считались постоянными. Их значения приведены в табл. 1. При расчете эффективных коэффициентов диффузии молекулярные числа Шмидта Sc принимались равными единице (Sc = 1) для всех компонентов.
Таблица 1.
Свойства чистых компонентов
| Свойство | Компонент смеси | ||
|---|---|---|---|
| CH4 | H2 | N2 | |
| M, кг/кмоль | 16.043 | 2.016 | 28.016 |
| μ, Па ⋅ с | 1.267 × 10–5 | 9.625 × 10–6 | 1.973 × 10–5 |
| λ, Вт/(м ⋅ К) | 0.04 085 | 0.20 510 | 0.02 927 |
| cp, Дж/(кг ⋅ К) | 2444 | 14 460 | 1075 |
Моделирование турбулентности. Для типичных диаметров топливных трубопроводов и режимных параметров на входе в трубы числа Рейнольдса ($\operatorname{Re} = {{{{U}_{i}}{{D}_{i}}} \mathord{\left/ {\vphantom {{{{U}_{i}}{{D}_{i}}} \nu }} \right. \kern-0em} \nu }$) равны ${{\operatorname{Re} }_{1}}$ = 4.0 × 106 и ${{\operatorname{Re} }_{2}}$ = 5.6 × 106 (${{U}_{i}}$ – среднемассовая скорость на входе в i-ю трубу). Высокие числа Рейнольдса, геометрические особенности тройникового соединения и значительные длины прямолинейного участка трубопровода затрудняют корректное использование вихреразрешающих моделей LES или DES. Поэтому в данной работе использовались стандартная k–ε-модель с пристеночными функциями и модель k–ω SST с универсальными пристеночными функциями [51].
Стандартная k–ε-модель для больших турбулентных чисел Рейнольдса содержит два уравнения переноса и выражение для турбулентной вязкости:
(1)
$\left. \begin{gathered} \frac{{\partial \left( {{{\rho }}k} \right)}}{{\partial {\tau }}}{\text{div}}\left[ {{{\rho }}uk - {{\rho }}\left( {{{\nu }}{ + }\frac{{{{{{\nu }}}_{t}}}}{{{{\sigma }_{k}}}}} \right)\nabla k} \right] = {{\rho }}\left( {{{{{\nu }}}_{t}}G - {{\varepsilon }}} \right); \hfill \\ \frac{{\partial \left( {{{\rho \varepsilon }}} \right)}}{{\partial {{\tau }}}}{\text{div}}\left[ {{{\rho }}u{{\varepsilon }} - {{\rho }}\left( {{{\nu }}{ + }\frac{{{{{{\nu }}}_{t}}}}{{{{\sigma }_{{{\varepsilon }}}}}}} \right)\nabla {{\varepsilon }}} \right] = \hfill \\ = {{\rho }}\frac{{{\varepsilon }}}{k}\left( {{{C}_{{{{{{\varepsilon }}}_{{\text{1}}}}}}}{{{{\nu }}}_{t}}G - {{C}_{{{{{{\varepsilon }}}_{{\text{2}}}}}}}{{\varepsilon }}} \right), \hfill \\ \end{gathered} \right\}$Модель турбулентности (1) справедлива только в зоне развитого турбулентного течения (${{{{{{\nu }}}_{t}}} \mathord{\left/ {\vphantom {{{{{{\nu }}}_{t}}} {{\nu }}}} \right. \kern-0em} {{\nu }}} > > 1$) и не может быть распространена на вязкий подслой и буферную область пристеночного течения. Эффективный метод преодоления указанного недостатка стандартной k–ε-модели предложен Сполдингом и Лаундером [22]. Суть метода заключается в сопряжении k–ε-модели с универсальными эмпирическими законами для скорости и скалярных переменных (температуры, массовой доли компонента смеси) в той области, где справедливы и универсальные законы, и k–ε-модель. Подобное сопряжение выполняется в области универсального логарифмического “закона стенки”, который имеет вид [52]
(2)
$\frac{{{{u}_{{1,{{\tau }}}}}}}{{{{u}_{{{\tau }}}}}} = \frac{1}{\kappa }\ln \left( {Ey_{1}^{ + }} \right);\,\,\,\,{{u}_{{{\tau }}}} = \sqrt {\frac{{{{{{\tau }}}_{w}}}}{{{\rho }}}} ;\,\,\,\,y_{1}^{ + } = \frac{{{{u}_{{{\tau }}}}{{y}_{{1,{{\tau }}}}}}}{{{\nu }}},$Аналогичные эмпирические законы можно использовать для температуры и концентраций компонентов смеси [52].
Описание модели k–ω SST в данной работе не приводится вследствие ее излишней громоздкости. Заинтересованный читатель может познакомиться с деталями этой модели в [51].
Граничные условия. При моделировании тройникового смесителя на входах в трубы (I, II) (см. рис. 2) задавались постоянными плотность массового расхода ${{m}_{{in}}} = \frac{{4{{Q}_{{in}}}}}{{{{\pi }}{{D}^{2}}}}$ (${{Q}_{{in}}}$ – массовый расход на входе в трубу, кг/с; in = 1, 2), температура ${{T}_{{in}}}$ и массовые доли ${{c}_{{l,in}}}$ компонентов смеси
Профиль скорости и турбулентные характеристики (${{k}_{{in}}},$ ${{{{\varepsilon }}}_{{in}}}$) на входах в трубы соответствовали стабилизированному турбулентному течению при соответствующих числах Рейнольдса. На выходе из трубы-коллектора (см. рис. 2) давление принималось постоянным: $p = {{p}_{{out}}}.$ На стенках труб задавались условия прилипания и непроницаемости для компонент вектора скорости и нулевые плотности теплового и диффузионных потоков.
Расчеты были выполнены с помощью CFD-кода ANES [53]. Для описания расчетной области использовались декартовы неструктурные сетки с локальным дроблением. Расчет любого из вариантов, включающий в себя также и тестовые расчеты, проводился в следующей последовательности. На первом этапе моделировалась стационарная постановка задачи для половины смесителя в силу геометрической симметрии конструкции. Если решение сходилось, оно считалось окончательным результатом. При анализе сеточной сходимости и использовании “плотной” сетки в некоторых режимах наблюдались слабо колеблющиеся поля скорости, аналогичные полученным в [26]. В этом случае применялась нестационарная постановка для целой конструкции без учета геометрической симметрии тройникового соединения и с начальными полями искомых переменных, соответствующих не полностью сошедшемуся решению в стационарной постановке. Выявленная нестационарность полей скорости при выходе на квазистационарный режим выражалась в изменяющейся третьей значащей цифре соответствующих искомых переменных (амплитуда колебаний не превышала 2% значений переменных). На каждом шаге по времени решение сходилось при небольшом числе итераций (от пяти до восьми). Следует отметить, что полученные решения с высокой точностью оказывались симметричными относительно диаметральной плоскости у–z тройника (см. рис. 1).
ВЕРИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Изотермическое смешение потоков обычной и опресненной воды
Для верификации моделей использовались данные [12, 13] о смешении в Т-образном смесителе обычной и деионизированной воды. Следует отметить, что для режимных параметров [12, 13] числа Рейнольдса на входах в трубы (${{\operatorname{Re} }_{1}}$ = = ${{\operatorname{Re} }_{2}}$ = 2.5 × 104) были на два десятичных порядка меньше чисел Рейнольдса для рассматриваемого смесителя топлива.
Моделировалось изотермическое смешение потоков воды, концентрация ионов рассматривалась как концентрация пассивной примеси ${{\varphi }} = {c \mathord{\left/ {\vphantom {c {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ (${{c}_{0}}$ – массовая доля условной примеси на входе), для которой решалось стандартное уравнение переноса. На первом этапе анализировалась сеточная независимость решений. С этой целью тестировались три варианта расчетных сеток с числом ячеек приблизительно 0.8, 1.6 и 2.6 млн для половины конструкции. На рис. 3 для наглядности показана численная сетка с количеством ячеек 0.8 млн, а на рис. 4, 5 представлены результаты, полученные для профиля безразмерной аксиальной скорости ${{{{u}_{z}}} \mathord{\left/ {\vphantom {{{{u}_{z}}} {{{U}_{m}}}}} \right. \kern-0em} {{{U}_{m}}}}$ (${{U}_{m}}$ – среднемассовая скорость в трубе-коллекторе, м/с) в разных сечениях при использовании различных сеток и моделей турбулентности. Результаты расчетов по k–ε-модели на сетках с 1.6 и 2.6 млн ячеек оказались практически неразличимыми (см. рис. 4).
Рис. 4.
Профиль безразмерной аксиальной скорости ${{{{u}_{z}}} \mathord{\left/ {\vphantom {{{{u}_{z}}} {{{U}_{m}}}}} \right. \kern-0em} {{{U}_{m}}}}$ в различных сечениях тройника, полученный при использовании k–ε-модели. z/D: а – 1.0; б – 1.8; в – 3.8; г – 6.2 (R = D/2). Число ячеек сетки, млн: 1 – 0.8; 2 – 1.6; 3 – 2.6
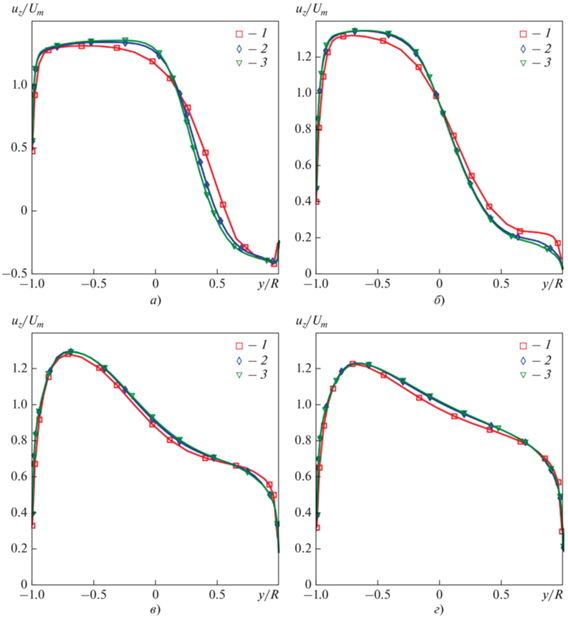
Рис. 5.
Профиль безразмерной аксиальной скорости ${{{{u}_{z}}} \mathord{\left/ {\vphantom {{{{u}_{z}}} {{{U}_{m}}}}} \right. \kern-0em} {{{U}_{m}}}}$ в различных сечениях тройника, полученный при использовании модели k–ω SST. z/D: а – 1.0; б – 1.8; в – 3.8; г – 6.2. Число ячеек сетки, млн: 1 – 0.8; 2 – 1.6; 3 – 2.6
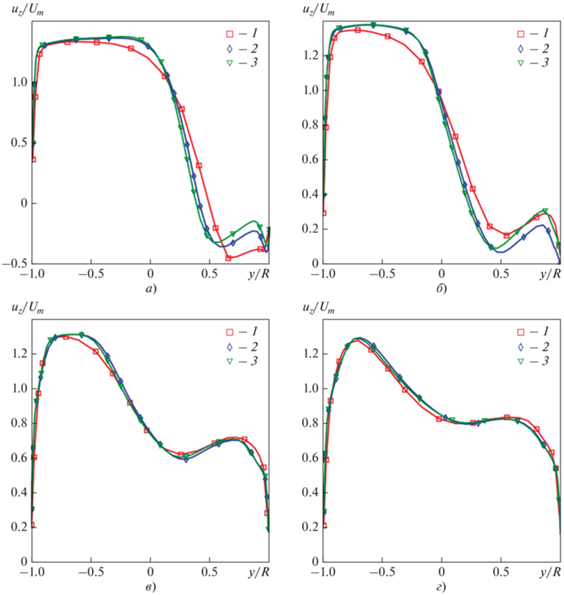
На профилях продольной скорости, рассчитанных по модели k–ω SST на этих же сетках (см. рис. 5), можно заметить небольшие отличия в зоне отрыва и последующего присоединения потока при у/R > 0.5, 0 < z/D < 1.8. Следует отметить, что эта зона весьма “чувствительна” не только к используемым моделям турбулентности, но и к сеткам. Именно в этой зоне наблюдалась слабая нестационарность. В дальнейшем верификационные расчеты выполнялись на сетке с 1.6 млн ячеек для половины конструкции тройника.
Для верификации модели турбулентности k–ω SST кода ANES выполнено сравнение полученных данных с результатами численного моделирования [29] при ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9 и Сμ = 0.09. На рис. 6 представлены расчетные профили безразмерной массовой доли (концентрации) примеси ${{\varphi }} = {c \mathord{\left/ {\vphantom {c {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ а также экспериментальные данные [12].
Рис. 6.
Расчетные профили безразмерной массовой доли примеси ${{\varphi }}{ = }{c \mathord{\left/ {\vphantom {c {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}.$ z/D: а – 1.0; б – 1.8; в – 3.8; г – 6.2. 1, 2 – результаты, полученные в настоящей работе для моделей k–ω SST и k–ε соответственно; 3 – результаты [32] для модели k–ω SST при ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9; 4 – экспериментальные данные [12]
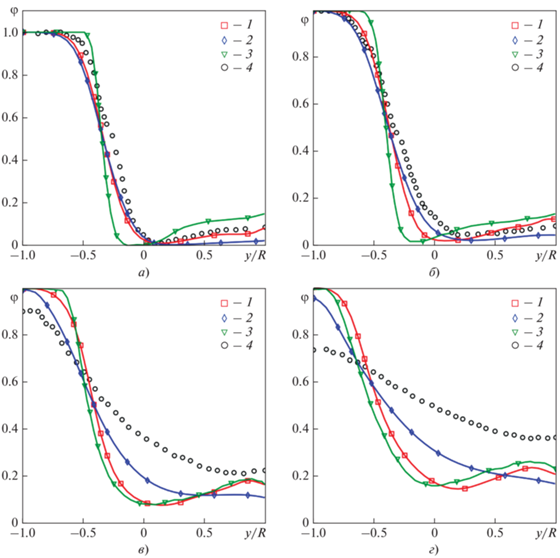
Результаты расчетов, выполненных с использованием кода ANES и модели k–ω SST, неплохо воспроизводят данные [29], полученные с помощью кода ANSYS CFX. Некоторое рассогласование расчетных кривых вызвано применением в кодах ANES и ANSYS CFX принципиально различных численных схем, алгоритмов и неструктурированных сеток. Возможно и некоторое различие реализованных версий модели SST. При z/D = 1.0, 1.8 использование моделей k–ε и k–ω SST приводит к практически идентичным результатам, но при удалении от начала смешения наблюдаются заметные различия рассчитанных профилей концентрации примеси. Наиболее ярко этот эффект проявляется при z/D = 6.2. Для профилей концентрации примеси, полученных с помощью k–ε-модели, характерны большая монотонность и “размазанность”. Этот же эффект можно наблюдать и на профилях продольной компоненты скорости, показанных на рис. 7. В целом, модель SST [51] на этапе верификации не показала заметных преимуществ по сравнению с k–ε-моделью. Поэтому дальнейшие расчеты проводились с помощью k–ε-модели.
Рис. 7.
Профили скорости, рассчитанные с использованием моделей: 1 – k–ω SST; 2 – k–ε (Сμ = 0.09); 3 – k–ε [Сμ вычислено по уравнению (4)]; 4 – экспериментальные данные [13]. Сечение z/D: а – 1.9; б – 4.9
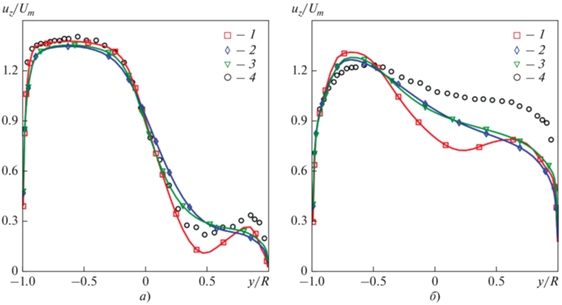
Ранее отмечалось, что аналогичные расхожденияс экспериментальными данными [12] как по концентрации примеси, так и по продольной компоненте скорости с увеличением расстояния от начала смешения были получены в ряде работ при использовании различных моделей для турбулентной вязкости. Очевидно, что попытки “исправить” профили концентраций пассивной примеси только путем “обвала” турбулентного числа Шмидта до значений 0.1 бесплодны, так как профили скорости при этом остаются по-прежнему не соответствующими опытным данным. Лучшего совпадения расчетных и экспериментальных данных можно добиться с помощью увеличения константы Сμ в модели k–ε [26]. Однако для этого потребовалось бы фантастически высокое значение Сμ = 0.81 вместо традиционного значения 0.09. Произвольная манипуляция константами ${\text{S}}{{{\text{c}}}_{t}}$ и Сμ представляется искусственной и лишенной основы в виде имеющихся экспериментальных данных. Авторы настоящей работы попытались “подправить” значения ${\text{S}}{{{\text{c}}}_{t}}$ и Сμ в модели k–ε, опираясь на соотношения, предложенные Гибсоном и Лаундером [54] для течений, удаленных от стенок (струи, слои смешения):
(3)
$\left. \begin{gathered} {{C}_{{{\mu }}}} = \frac{{0.36 + 0.165\left( {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right)}}{{{{{\left( {1.2 + {P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right)}}^{2}}}}; \hfill \\ {\text{S}}{{{\text{c}}}_{t}} = \frac{{0.225\left( {5.4 + {P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right)}}{{1.2 + {P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}}}, \hfill \\ \end{gathered} \right\}$Соотношения (3) не использовались в пристеночных функциях (2) и поэтому не оказывали влияния на динамическую скорость uτ и связанные с ней параметры. Тем самым наличие стенки учитывалось стандартным образом. Анализ полученных профилей величин ${P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}},$ Сμ и ${\text{S}}{{{\text{c}}}_{t}}$ показал их существенное и немонотонное изменение по сечению трубы-коллектора. На участке трубы z/D ≤ 6.2 величины Сμ и ${\text{S}}{{{\text{c}}}_{t}}$ резко изменялись как по длине, так и по сечению трубы, принимая значения 0.03 ≤ Сμ ≤ 0.23, 0.53 ≤ ${\text{S}}{{{\text{c}}}_{t}}$ ≤ 0.95.
В качестве примера на рис. 8 приведены профили ${P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}$ в различных сечениях z/D. Профили концентрации примеси и безразмерной аксиальной скорости, рассчитанные при Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9, 0.5 и согласно выражениям (3), представлены на рис. 9. Влияния переменности параметров Сμ и ${\text{S}}{{{\text{c}}}_{t}}$ на профили скорости и концентрации примеси в целом оказались небольшими. Подобный эффект был ожидаем, так как выражения (3) были получены из уравнений переноса напряжений Рейнольдса (RSM) с учетом ряда упрощений. Как отмечалось в работе [35], использование исходной (без упрощений) модели RSM для рассматриваемой задачи лишь частично улучшает ситуацию и не приводит к приемлемому согласованию профилей скорости и концентрации примеси.
Рис. 8.
Профили Р/ε, рассчитанные по k–ε-модели в различных сечениях трубы z/D: 1 – 1.0; 2 – 1.8; 3 – 3.8; 4 – 6.2
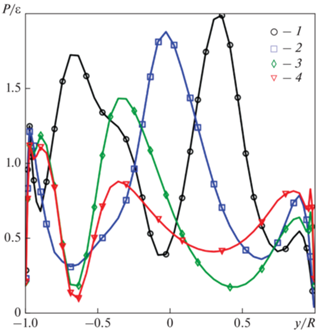
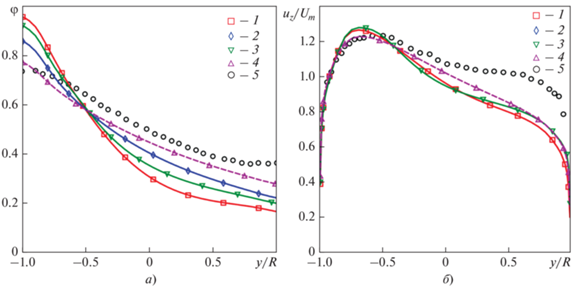
Рис. 9.
Профили безразмерной массовой доли примеси в сечении z/D = 6.2 (а) и безразмерной аксиальной скорости в сечении z/D = 4.9 (б), рассчитанные по k–ε-модели. 1 – Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9; 2 – Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.5; 3 – Сμ и ${\text{S}}{{{\text{c}}}_{t}}$ определяются по уравнениям (3); 4 – Сμ вычисляется по соотношению (4), ${\text{S}}{{{\text{c}}}_{t}}$ – по формуле (5); 5 – экспериментальные данные [12, 13]
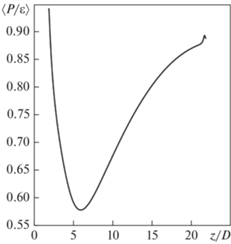
Следует отметить, что течение в трубе-коллекторе при z/D ≤ 10–15 носит исключительно своеобразный характер, непохожий на численно хорошо исследованные течения в каналах и пограничных слоях, струях и слоях смешения. Об этом можно судить по осредненной по сечению канала величине $\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle .$ На рис. 10 наблюдается “кризис” скорости порождения кинетической энергии турбулентных пульсаций Р при 2 ≤ z/D ≤ 10–15, вызванный “перекошенным” и неосесимметричным М-образным профилем продольной скорости, перестраивающимся по длине. Значения $\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle ,$ значительно меньшие единицы, характерны для течений в следах за обтекаемыми телами, но не в трубах, для которых ${P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}$ ≈ 0.87–0.90.
Рис. 10.
График изменения параметра $\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle $ по длине трубы-коллектора, рассчитанного с помощью k–ε-модели и Сμ в соответствии с (3)
Численная оптимизация коэффициента Сμ на основе детального анализа имеющихся экспериментальных данных для различных видов свободных течений была выполнена Роди [55]. В результате автором была предложена эмпирическая формула
(4)
${{С}_{{{\mu }}}} = \frac{2}{3}\frac{{1 - {{\alpha }}}}{{{\omega }}}\frac{{1 - \frac{1}{{{\omega }}}\left( {1 - {{\alpha }}\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle } \right)}}{{{{{\left[ {1 + \frac{1}{{{\omega }}}\left( {\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle - 1} \right)} \right]}}^{2}}}},$Зависимость Сμ/Сμ0 (Сμ0 = 0.09) от $\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle $ изображена на рис. 11. Следует отметить, что в данной работе осреднение по сечению величины ${P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}},$ в отличие от [55], проводилось без введения весового множителя в виде ${{\overline {u_{i}^{'}u_{j}^{'}} } \mathord{\left/ {\vphantom {{\overline {u_{i}^{'}u_{j}^{'}} } {\left\langle {\overline {u_{i}^{'}u_{j}^{'}} } \right\rangle }}} \right. \kern-0em} {\left\langle {\overline {u_{i}^{'}u_{j}^{'}} } \right\rangle }},$ имеющего некоторый смысл только для двумерных течений типа пограничного слоя. Значения Сμ, рассчитанные по (3), превышают значения, полученные по (4), при 4 ≤ ${z \mathord{\left/ {\vphantom {z D}} \right. \kern-0em} D}$ ≤ 12, т.е. в окрестности минимума $\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle .$
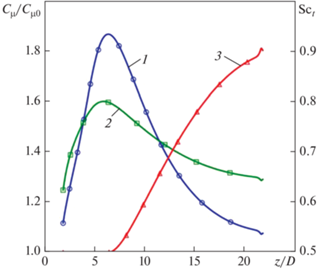
Рис. 11.
Изменение величин Сμ/Сμ0 и Sct по длине трубы. 1 – Сμ/Сμ0 определено по уравнениям (3); 2 – Сμ/Сμ0 вычислено по соотношению (4); 3 – ${\text{S}}{{{\text{c}}}_{t}}$ – по формуле (5)
Что касается величины ${\text{S}}{{{\text{c}}}_{t}}$ (или ее аналога ${\text{P}}{{{\text{r}}}_{t}}$), то универсальная и достоверная модель для ее описания в сложных течениях вряд ли когда-либо будет создана. К настоящему времени известно, что для струйных течений и слоев смешения наиболее подходящими (для расчетов) постоянными значениями ${\text{P}}{{{\text{r}}}_{t}}$ являются 0.5–0.7 (см., например, [4, 24, 56]), а для пристеночных течений – 0.9 [56]. Алгебраические модели для вторых моментов приводят к зависимостям турбулентных чисел Прандтля и Шмидта от значения ${P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}},$ например, как в выражении (3). Но для сложных трехмерных течений, сочетающих в себе признаки и свободных, и пристеночных течений, подобные зависимости отсутствуют. Поэтому в данной работе принята простая формула, в соответствии с которой постоянное по сечению трубы значение ${\text{S}}{{{\text{c}}}_{t}}$ является, как и Сμ, функцией $\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle {\text{:}}$
(5)
${\text{S}}{{{\text{c}}}_{t}} = \left\{ \begin{gathered} 0.5,\,\,\,\,z < {{z}_{{\min }}}; \hfill \\ {\text{S}}{{{\text{c}}}_{{t,\min }}} + 0.4\frac{{\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle - {{{\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle }}_{{\min }}}}}{{{{{\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle }}_{{\max }}} - {{{\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle }}_{{\min }}}}},\,\,\,\,z \geqslant {{z}_{{\min }}}, \hfill \\ \end{gathered} \right.$Хотя выражение (5) и носит сугубо эмпирический характер, оно удовлетворяет предельным переходам, что, по мнению авторов настоящей статьи, выгодно отличается от простого задания ${\text{S}}{{{\text{c}}}_{t}}$ = const во всей расчетной области или скачкообразного изменения в произвольно выбранном сечении трубы-коллектора. Уменьшение значения ${\text{S}}{{{\text{c}}}_{t}}$ ниже 0.5 не имеет какого-либо обоснования ввиду отсутствия данных, указывающих на такую возможность.
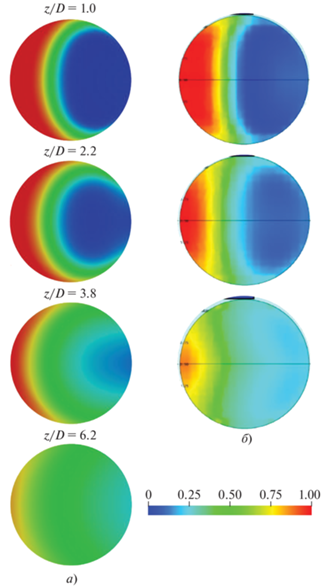
На рис. 9 показаны профили концентрации пассивной примеси и аксиальной скорости, рассчитанные с использованием соотношений (4) и (5) для Сμ и ${\text{S}}{{{\text{c}}}_{t}},$ а на рис. 12 – поля концентрации в различных сечениях трубы. Необходимо признать, что, хотя использование переменных значений Сμ и ${\text{S}}{{{\text{c}}}_{t}}$ заметно приблизило результаты расчетов к экспериментальным данным [12, 13], полного соответствия получить не удалось. По-видимому, следует согласиться с Роди [55] в том, что от инженерных методов расчета сложных турбулентных потоков не следует ожидать точного предсказания характеристик течения, так как последние могут быть получены только в результате решения уравнений Навье – Стокса. Хотя данное замечание автора [55] было сделано на “заре” CFD (1972 г.), для многих важных для практики задач оно остается актуальным и в настоящее время.
Рис. 12.
Поля концентрации примеси в различных сечениях. а – результаты настоящей работы; б – данные [12]
Дальнейшие расчеты тройниковых смесителей выполнены с использованием k–ε-модели при Сμ, определенной по уравнению (4), ${\text{S}}{{{\text{c}}}_{t}}$ – по уравнению (5).
Смешение потоков воздуха
Верификация модели турбулентности была выполнена с привлечением экспериментальных данных работы [7], а также собственных опытных данных авторов. В [7] было изучено смешение двух потоков воздуха в T-образном смесителе, в один из которых был добавлен метан (${{с}_{0}}$ = 0.3%). Длина основной трубы составляла $20{{D}_{1}}$, внутренний диаметр – 65 мм. Отношение диаметра вторичной трубы к диаметру основной трубы ${{{{D}_{2}}} \mathord{\left/ {\vphantom {{{{D}_{2}}} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 0.2. Температура обоих потоков была постоянна и равнялась 15°С, скорость основного потока соответствовала 9.9 м/с, вторичного потока – 24.2 м/с (отношение скоростей – 2.48). Полученные результаты приведены на рис. 13 и 14.
Рис. 13.
Распределение максимальной концентрации метана по длине трубы. 1 – Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9; 2 – Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.5; 3 – Сμ рассчитано по уравнению (4), ${\text{S}}{{{\text{c}}}_{t}}$ – по формуле (5); 4 – экспериментальные данные [7] с отклонением ±15%
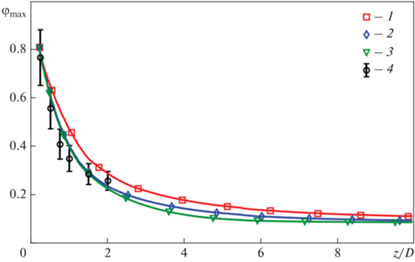
Рис. 14.
Профили распределения пассивной примеси вдоль вертикального диаметра основной трубы на удалении от начала смешения ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 2 (a) и 5 (б). 1 – Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.9; 2 – Сμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = 0.5; 3 – Сμ рассчитано по уравнению (4), ${\text{S}}{{{\text{c}}}_{t}}$ – по формуле (5); 4 – экспериментальные данные работы [7]
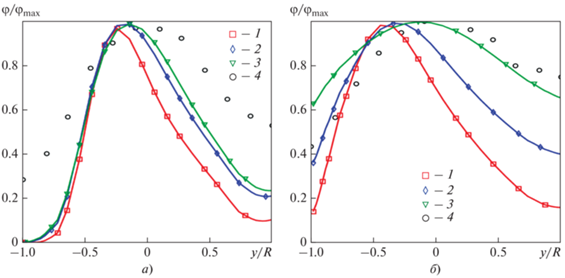
Следует отметить, что опытные данные, представленные на этих рисунках, соответствуют “оптимальной” подаче вторичного потока согласно [7], т.е. после разворота вторичной струи в смесителе ее условная ось практически совпадает с осью основного потока (хотя на рис. 14 видно отсутствие симметрии опытных точек относительно у/R = 1). Минимальное значение величины ${{\left\langle {{P \mathord{\left/ {\vphantom {P {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right\rangle }_{{\min }}}$ = 0.43 достигается в этом режиме при ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 4.9. Можно отметить хорошее соответствие экспериментальных и расчетных данных по величине ${{{{\varphi }}}_{{\max }}}$ (кривая 3 на рис. 13). Что же касается сравнения профилей ${{\varphi } \mathord{\left/ {\vphantom {{\varphi } {{{{\varphi }}_{{\max }}}}}} \right. \kern-0em} {{{{\varphi }}_{{\max }}}}}$, то результаты расчетов свидетельствуют о “недорасширении” струи по сравнению с опытными данными в сечении ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 2 и, напротив, большем расширении при ${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 5 и у/R < 0, что оказалось несколько неожиданным. В целом, соответствие экспериментальных данных расчетным можно признать вполне удовлетворительным.
Далее представлено сопоставление экспериментальных и расчетных данных по распределениям аксиальной компоненты скорости, турбулентным напряжениям, кинетической энергии турбулентных пульсаций, полученных авторами настоящей статьи для Т-образного смесителя из горизонтальных труб диаметром D = 47 мм. Длина труб до соединения – 3 м, длина основной трубы после тройника – до 6 м, рабочая среда – воздух при температуре 24°С. Для регулировки объемного расхода использовались критические сопла. Неопределенность задания расхода соплами составляла ±0.25%. Схема экспериментальной установки показана на рис. 15. Перепад давления, необходимый для создания критического режима течения в соплах, создавался многоступенчатой осевой воздуходувкой, работающей на всасывание, и контролировался по датчику давления, установленному в сопловом блоке. Снятие показаний перепада давления осуществлялось датчиками ПРОМА-ИДМ с верхним пределом измерений 125 Па. Профили гидродинамических характеристик течения за тройником определялись планарным оптическим методом SIV [57] на дистанции 5.5D от оси пересечения бокового отвода с прямолинейной частью канала. Для съемки течения канал в месте измерений разрезался на две части и раздвигался таким образом, чтобы между торцами труб был зазор 0.5D и сохранялась соосность труб. Вокруг разреза устанавливалась герметичная камера с плоскими светопрозрачными стенками (см. рис. 15). Размеры камеры соответствовали 100 × 100 × 300 мм. Описанная конструкция измерительной установки являлась аналогом оптически прозрачной камеры Эйфеля аэродинамической трубы и позволяла устранить оптические искажения и блики от переотражения света внутри канала.
Рис. 15.
Схема экспериментальной установки. 1 – основной канал; 2 – критические сопла с запорной арматурой; 3 – воздуходувка; 4 – камера подготовки тумана; 5 – генератор тумана; 6 – датчики перепада давления; 7 – непрерывный лазер; 8 – скоростная видеокамера; 9 – герметичная камера (увеличенное изображение)
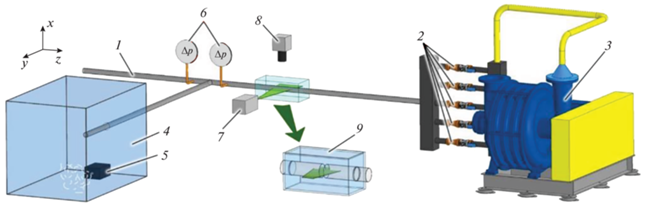
Засев потока трассерами (частицами) осуществлялся через боковую трубу, входное сечение которой помещалось внутрь камеры подготовки тумана, представлявшей собой короб объемом порядка 2 м3 со стенками из продуваемой хлопчатобумажной ткани. Генератор тумана вырабатывал трассеры диаметром до 5 мкм на основе содержащей глицерин жидкости и располагался в нижней части камеры (см. рис. 15), что обеспечило равномерное распределение трассеров по входному сечению канала. Съемка течения осуществлялась скоростной камерой Evercam 2000-4-M со светосильным объективом. Световой нож создавался непрерывным DPSS-лазером с регулируемой мощностью. Толщина светового ножа в области съемки имела порядок 0.5 мм. Измерения выполнялись при расходе через критические сопла 24 м3/ч, что соответствовало среднемассовой скорости в объединенной части трубопровода ${{U}_{m}}$ = 3.845 м/с и числу Рейнольдса, вычисленному по ${{U}_{m}}$ и диаметру канала: ${{\operatorname{Re} }_{m}}$ = 11 700.
Рассчитанные и полученные экспериментально профили аксиальной скорости, турбулентного касательного напряжения и турбулентной энергии в диаметральной плоскости симметрии (у–z) представлены на рис. 16. Для приведения указанных величин к безразмерному виду использовалась динамическая скорость ${{u}_{{{{\tau }},m}}}{\text{:}}$
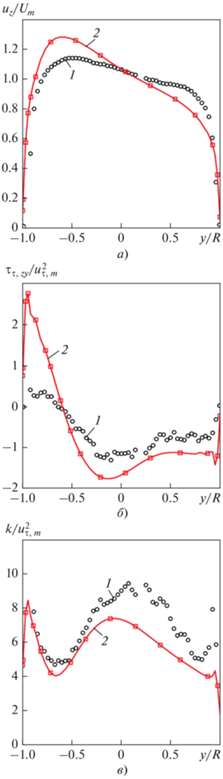
Рис. 16.
Профили безразмерной аксиальной скорости (а), безразмерного касательного турбулентного напряжения (б) и безразмерной турбулентной энергии (в) в плоскости симметрии для сечения z/D = 5.5. 1 – экспериментальные данные; 2 – результаты расчетов
В декартовой системе координат турбулентные касательные напряжения и турбулентная энергия для этой плоскости могут быть записаны в виде
Поскольку в экспериментах пульсационная компонента скорости $u{\kern 1pt} '$ не определялась, приближенно принято
Анализ рис. 15, 16 показывает, что использование предложенной модификации k–ε-модели приводит к завышенному турбулентному переносу импульса по сравнению с экспериментальными данными, хотя что касается профилей скорости и турбулентной энергии, то здесь можно наблюдать обратную тенденцию.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ СМЕШЕНИЯ ТОПЛИВНЫХ ГАЗОВ
Моделирование смешения в тройниковом соединении (см. рис. 2) выполнено с учетом того, что трубы технически гладкие. Турбулентное число Прандтля в уравнении энергии было принято равным турбулентному числу Шмидта. Тестовые расчеты показали, что в исследуемом режиме (${{\operatorname{Re} }_{m}}$ ≈ 107) силы плавучести не оказывают заметного влияния на результаты вычислений. Наибольший интерес представляют поля концентраций компонентов на выходе из смесителя (сечение III на рис. 2). Распределения объемной и массовой долей вдоль вертикальной оси y в плоскости симметрии х = 0 для сечения III показаны на рис. 17. В табл. 2 приведены характеристики массовых долей в выходном сечении, рассчитанные с использованием уравнений (4) и (5), а также при Cμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = ${\text{P}}{{{\text{r}}}_{t}}$ = 0.9. Средняя массовая доля каждого компонента смеси вычислялась по соотношению
Рис. 17.
Распределения по вертикальному диаметру выходного сечения смесителя $({z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}} = 20)$ мольной (а) и массовой (б) долей компонентов. 1 – СН4; 2 – Н2; 3 – N2; сплошные кривые получены при расчете по уравнениям (4), (5), штриховые кривые – при использовании Cμ = 0.09, ${\text{S}}{{{\text{c}}}_{t}}$ = ${\text{P}}{{{\text{r}}}_{t}}$ = 0.9
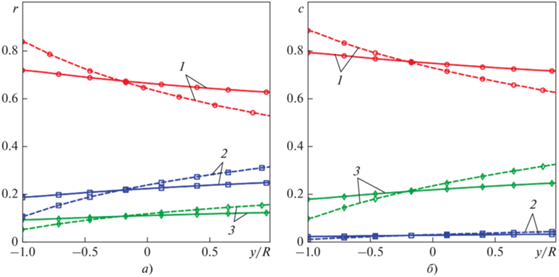
Таблица 2.
Характеристики массовых долей компонентов (${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 20) при использовании соотношений (4) и (5)
| Параметр | CH4 | H2 | N2 |
|---|---|---|---|
| ${{c}_{{l,in}}}$ (I) | 1.0 | 0.0 | 0.0 |
| ${{c}_{{l,in}}}$ (II) | 0.500 | 0.063 | 0.437 |
| ${{c}_{{l,mid}}}$ (III) | 0.750 | 0.0315 | 0.218 |
| ${{c}_{{l,\max }}} - {{c}_{{l,\min }}}$ (III) | 0.077 (0.260)* | 0.01 (0.032) | 0.067 (0.223) |
| ${{H}_{l}} = \left[ {{{\left( {{{c}_{{l,\max \,}}} - {{c}_{{l,\min }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{c}_{{l,\max \,}}} - {{c}_{{l,\min }}}} \right)} {{{c}_{{l,mid}}}}}} \right. \kern-0em} {{{c}_{{l,mid}}}}}} \right]$ × 100% | 10 (34) | 31 (101) | 31 (101) |
параметр ее неоднородности определялся по выражению
Хорошо видно, что при стандартных режимных параметрах и одинаковом диаметре труб на выходе из смесителя наблюдается заметная неоднородность состава смеси. Для поля температуры параметр неоднородности ${{H}_{T}} = \frac{{{{T}_{{{\text{max}}}}} - {{T}_{{{\text{min}}}}}}}{{\Delta T}} \times 100\% $ в сечении (${z \mathord{\left/ {\vphantom {z {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}$ = 20) оказался равным 6%. Следует также отметить, что результаты расчетов с переменными и постоянными значениями Cμ и ${\text{S}}{{{\text{c}}}_{t}}$ существенно различаются (см. рис. 17).
Полученные данные свидетельствуют об актуальности оптимизации тройникового смесителя, анализа вырождения неоднородностей состава смеси в прямолинейном участке трубопровода за тройниковым соединением и целесообразности установки стационарного смесителя. Результаты подобных исследований авторы настоящей статьи планируют отразить в последующих публикациях.
ВЫВОДЫ
1. Анализ литературных источников показал существенное рассогласование имеющихся экспериментальных данных по смешению потоков в Т-образных смесителях и результатов расчетов с использованием различных популярных моделей турбулентности в рамках метода URANS.
2. Предложенные в работе модификация стандартной k–ε-модели, учитывающая переменность величины Сμ, и эмпирическая формула для турбулентного числа Шмидта ${\text{(S}}{{{\text{c}}}_{t}})$ позволили заметно улучшить согласование расчетных и экспериментальных данных по смешению потоков газов и воды без необходимости использования фантастических значений Сμ и ${\text{S}}{{{\text{c}}}_{t}}.$
3. С помощью предложенных моделей выполнено численное моделирование процессов смешения природного газа с метановодородной фракцией в Т-образном смесителе. Результаты расчетов показали заметную неоднородность состава смеси по сечению трубы-коллектора на расстоянии 20D от начала смешения.
4. Полученные данные свидетельствуют о необходимости дальнейших исследований, направленных на оптимизацию конструкции тройникового смесителя и анализ целесообразности установки в трубопроводе стационарного смесителя.
Список литературы
Paul E.L., Atiemo-Obeng V.A., Kresta S.M. Handbook of industrial mixing: science and practice. John Wiley & Sons, 2004.
Static mixers: Mechanisms, applications, and characterization methods – A review / A. Ghanem, T. Lemenand, D.D. Valle, H. Peerhossaini // Chem. Eng. Res. Des. 2014. V. 92. Is. 2. P. 205–228. https://doi.org/10.1016/j.cherd.2013.07.013
Heat and mass transfer mixing enhancements in pipe-line; numerical cfd and experimental chores: A review / Z.H. Khokhar, M.S. Al-Harthi, B.F. Abusharkh, H.H. Al-Ali, R.N. Sharma, H.D. Zughbi, A.A. Shaikh, H.H. Redhwi, A. Abdurraheem, S.U. Rehman, S.J. Zaidi, Z.U. Khan, I.A. Hussain, B.S. Yilbas // Int. J. Eng. Sci. Innovative Technol. (IJESIT). 2013. V. 2. Is. 1. P. 1–11.
Ger A.M., Holley E.R. Turbulent jets in crossing pipe flow. University of Illinois at Urbana-Champaign, 1974.
Ger A.M., Holley E.R. Comparison of single-point injections in pipe flow // J. Hydraulics Division. 1976. V. 102. Is. 6. P. 731–746.
Pipeline mixing between two fluid streams meeting at a T-junction / T. Maruyama et al. // Int. Chem. Eng. 1981. V. 21. Is 2. P. 205–212.
Forney L.J., Kwon T.C. Efficient single-jet mixing in turbulent tube flow // AIChE J. 1979. V. 25. Is. 4. P. 623–630. https://doi.org/10.1002/aic.690250408
Forney L.J., Lee H.C. Optimum dimensions for pipeline mixing at a T-junction // AIChE J. 1982. V. 28. Is. 6. P. 980–987. https://doi.org/10.1002/aic.690280613
O’Leary C.D., Forney L.J. Optimization of in-line mixing at a 90 degree tee // Ind. Eng. Chem. Process Des. Dev. 1985. V. 24. Is. 2. P. 332–338. https://doi.org/10.1021/i200029a019
Sroka L.M., Forney L.J. Fluid mixing in a 90 degree pipeline elbow // Ind. Eng. Chem. Res. 1989. V. 28. Is. 6. P. 850–856.
Tosun G. A study of micromixing in tee mixers // Ind. Eng. Chem. Res. 1987. V. 26. Is. 6. P. 1184–1193. https://doi.org/10.1021/ie00066a021
Investigations on mixing phenomena in single-phase flows in a T-junction geometry / R. Zboray, A. Manera, B. Niceno, H.-M. Prasser // Proc. of the 12th Intern. Topical Meeting on Nuclear Reactor Therm. Hydraulics (NURETH-12). Sheraton Station Square, Pittsburgh, Pennsylvania, USA, 30 Sept.–4 Oct. 2007. No. 71. P. 1–20.
Investigations on mixing phenomena in single-phase flow in a T-junction geometry / C. Walker, M. Simianoa, R. Zboray, H.-M. Prasser // Nucl. Eng. Des. 2009. V. 239. P. 116–126. https://doi.org/10.1016/j.nucengdes.2008.09.003
Experiments and unsteady CFD-calculations of thermal mixing in a T-junction / J. Westin, F. Alavyoon, L. Andersson, P. Veber, M. Henriksson, C. Andersson // OECD/NEA/IAEA Workshop on the Benchmarking of CFD Codes for Application to Nuclear Reactor Safety (CFD4NRS). Munich, Germany, 2006. P. 1–15.
Thermal mixing in a T-junction: novel CFD-grade measurements of the fluctuating temperature in the solid wall / O. Braillard, R. Howard, K. Angele, A. Shams, N. Edh // Nucl. Eng. Des. 2018. V. 330. P. 377–390. https://doi.org/10.1016/j.nucengdes.2018.02.020
Tracer dispersion in a duct: Experimental and numerical approach – application to the well-mixing length determination / T. Gelain, J. Alengry, O. Vauquelin, L. Ricciardi // Nucl. Eng. Des. 2019. V. 353. P. 110229. https://doi.org/10.1016/j.nucengdes.2019.110229
Roley G., Fahien R.W. Gaseous diffusion at moderate flow rates in circular conduits. Ames Laboratory, Iowa State University of Science and Technology, 1960. V. 330.
Evans G.V. A study of diffusion in turbulent pipe flow // J. Basic Eng. 1967. V. 89. Is. 3. P. 624–631. https://doi.org/10.1115/1.3609669
Quarmby A., Anand R.K. Non-axisymmetric turbulent mass transfer in a circular tube // J. Fluid Mech. 1969. V. 38. Is. 3. P. 457–472. https://doi.org/10.1017/S0022112069000279
Monclova L.A., Forney L.J. Numerical simulation of a pipeline tee mixer // Ind. Eng. Chem. Res. 1995. V. 34. Is. 4. P. 1488–1493. https://doi.org/10.1021/ie00043a058
CFD-code PHOENIX. [Электрон. ресурс.] https://www.cham.co.uk/phoenics.php
Launder B.E., Spalding D.B. The numerical computation of turbulent flows // Comput. Methods Appl. Mech. Eng. 1974. V. 3. Is. 2. P. 269–289. https://doi.org/10.1016/0045-7825(74)90029-2
Kok J.B.W., van der Wal S. Mixing in T-junctions // Appl. Math. Model. 1996. V. 20. Is. 3. P. 232–243. https://doi.org/10.1016/0307-904X(95)00151-9
Bird R.B., Stewart W.E., Lightfoot E.N. Transport phenomena. Revised 2nd ed. Wiley India Private Limited, 2006.
Wang X., Feng Z., Forney L.J. Computational simulation of turbulent mixing with mass transfer // Comput. Struct. 1999. V. 70. Is. 4. P. 447–465. https://doi.org/10.1016/S0045-7949(98)00160-6
Steady-state RANS-simulations of the mixing in a T-junction / C. Walker, A. Manera, B. Niceno, M. Simiano, H.-M. Prasser // Nucl. Eng. Des. 2010. V. 240. Is. 9. P. 2107–2115. https://doi.org/10.1016/j.nucengdes.2010.05.056
Menter F.R. Two-equation eddy-viscosity turbulence models for engineering applications // AIAA J. 1994. V. 32. No. 8. P.1598–1605. https://doi.org/10.2514/3.12149
CFD-code ANSYS-CFX. [Электрон. ресурс.] https://www.ansys.com/products/fluids/ansys-cfx
Simulation of turbulent and thermal mixing in T-junctions using URANS and scale-resolving turbulence models in ANSYS CFX / Th. Frank, C. Lifantea, H.-M. Prasser, F. Menter // Nucl. Eng. Des. 2010. V. 240. Is. 9. P. 2313–2328. https://doi.org/10.1016/j.nucengdes.2009.11.008
Menter F., Egorov Y.A. Scale adaptive simulation model using two-equation models // Proc. of the 43rd AIAA Aerospace Sciences Meeting and Exhibition. Reno, Nevada, USA: American Institute of Aeronautics and Astronautics, 10–12 Jan. 2005. Published online: 2012. https://doi.org/10.2514/6.2005-1095
CFD-code ANSYS-Fluent. [Электрон. ресурс.] https://www.ansys.com/products/fluids/ansys-fluent
Smith B.L., Mahaffy J.H., Angele K. A CFD benchmarking exercise based on flow mixing in a T-junction // Nucl. Eng. Des. 2013. V. 264. P. 80–88. https://doi.org/10.1016/j.nucengdes.2013.02.030
Investigation on the flow behaviour of a Venturi type gas mixer designed for dual fuel diesel engines / B.J. Bora, B.K. Debnath, N. Gupta, N. Sahoo, U.K. Saha // Int. J. Energ. Technol. Adv. Eng. 2013. V. 3. Is. 3. P. 202–209.
Study on the coolant mixing phenomenon in a 45° T‑junction based on the thermal-mechanical coupling method / M. Wang, D. Fang, Y. Xiang, Y. Fei, Y. Wang, W. Ren, W. Tian, G.H. Su, S. Qiu // Appl. Therm. Eng. 2018. V. 144. P. 600–613. https://doi.org/10.1016/j.applthermaleng.2018.08.073
CFD-code STAR-CCM+. [Электрон. ресурс.] https://plm.sw.siemens.com/en-US/simcenter/fluids-thermal-simulation/star-ccm/
Flow features and thermal stress evaluation in turbulent mixing flows / C. Evrim, X. Chu, F.E. Silber, A. Isaev, S. Weihe, E. Laurien // Int. J. Heat Mass Transfer. 2021. V. 178. P. 121605.
CFD-code OpenFoam. [Электрон. ресурс.] https:// www.openfoam.com
Abaqus S. V2016 user’s manual and documentation Dassault Systèmes Simulia Corp. USA, 2016.
Höhne T. Scale resolved simulations of the OECD/NEA–Vattenfall T-junction benchmark // Nucl. Eng. Des. 2014. V. 269. P. 149–154. https://doi.org/10.1016/j.nucengdes.2013.08.021
Расчетные исследования процесса перемешивания неизотермических потоков натриевого теплоносителя в тройнике / А.А. Аксёнов, С.В. Жлуктов, В.В. Шмелев, Е.В. Шапоренко, С.Ф. Шепелев, С.А. Рогожкин, А.Н. Крылов // Компьютерные исследования и моделирование. 2017. Т. 9. № 1. С. 95–110. https://doi.org/10.20537/2076-7633-2017-9-95-110
CFD-code FlowVision. [Электрон. ресурс.] https:// flowvision.ru/ru/
Flow and heat transfer in cross-stream type T-junctions: A computational study / B. Krumbein, V. Termini, S. Jakirlić, C. Tropea // Int. J. Heat Fluid Flow. 2018. V. 71. P. 179–188. https://doi.org/10.1016/j.ijheatfluidflow.2018.03.013
Evrim C., Chu X., Laurien E. Analysis of thermal mixing characteristics in different T-junction configurations // Int. J. Heat Mass Transfer. 2020. V. 158. P. 120019. https://doi.org/10.1016/j.ijheatmasstransfer.2020.120019
Thermal mixing characteristics of T-junction incident along central axis based on large-eddy simulations / Z. Lin, L. Yang, J. Tao, X. Li, X. Zheng // Appl. Therm. Eng. 2023. V. 221. P. 119756. https://doi.org/10.1016/j.applthermaleng.2022.119756
Eames I., Austin M., Wojcik A. Injection of gaseous hydrogen into a natural gas pipeline // Int. J. Hydrogen Energy. 2022. V. 47. Is. 61. P. 25745–25754. https://doi.org/10.1016/j.ijhydene.2022.05.300
Spalart P., Allmaras S. A one-equation turbulence model for aerodynamic flows // Proc. of the 30th Aerospace Sciences Meeting and Exhibition. Reno, Nevada, USA: American Institute of Aeronautics and Astronautics, 6–9 Jan. 1992. https://doi.org/10.2514/6.1992-439
Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach / P. Spalart, W.-H. Jou, M. Strelets, S. Allmaras // Advances in DNS/LES. 1997.
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1973.
Wilke C.R. A viscosity equation for gas mixtures // J. Chem. Phys. 1950. V. 18. Is. 4. C. 517–519. https://doi.org/10.1063/1.1747673
Mason E.A., Saxena S.C. Approximate formula for the thermal conductivity of gas mixtures // Phys. Fluids. 1958. V. 1. Is. 5. P. 361–369. https://doi.org/10.1063/1.1724352
The SST turbulence model with improved wall treatment for heat transfer predictions in gas turbines / F. Menter, J.C. Ferreira, T. Esch, B. Konno // Proc. of the Intern. Gas Turbine Congress. Tokyo, Japan, 2–7 Nov. 2003.
Launder B.E. On the computation of convective heat transfer in complex turbulent flows // J. Heat Transfer. 1988. V. 110. Is. 4b. P. 1112–1128. https://doi.org/10.1115/1.3250614
CFD-code ANES. [Электрон. ресурс.] http://anes. ch12655.tmweb.ru
Gibson M.M., Launder B.E. On the calculation of horizontal, turbulent, free shear flows under gravitational influence // J. Heat Transfer. 1976. V. 98. Is. 1. P. 81–87. https://doi.org/10.1115/1.3450474
Rodi W. The prediction of free turbulent boundary layers by use of a two-equation model of turbulence: Thesis … for the degree of Doctor of Philosophy. L.: Engineering University; Imperial College, 1972.
Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974.
Mikheev N.I., Dushin N.S. A method for measuring the dynamics of velocity vector fields in a turbulent flow using smoke image-visualization videos // Instruments Exp. Tech. 2016. V. 59. Is. 6. P. 882–889. https://doi.org/10.1134/S0020441216060063
Дополнительные материалы отсутствуют.
Инструменты
Теплоэнергетика