1. На главную
  2. Электронные версии
  3. Теплоэнергетика
  4. № 9, 2023

Теплоэнергетика, 2023, № 9, стр. 97-105

Прогнозирование тепловой нагрузки для систем централизованного теплоснабжения с помощью моделей TCN и CatBoost

C. Han a, M. Gong a, *, J. Sun a, Y. Zhao a, L. Jing a, C. Dong b, Z. Zhao c

a Tianjin Key Laboratory of Film Electronic and Communication Devices, School of Integrated Circuit Science and Engineering, Tianjin University of Technology
300384 Tianjin, China

b School of Computer Science and Engineering, Tianjin University of Technology
300384 Tianjin, China

c School of Social Sciences, Waseda University
Tokyo, Japan

* E-mail: gmj790@163.com

Поступила в редакцию 10.07.2022
После доработки 08.08.2022
Принята к публикации 30.08.2022

Полный текст (PDF)

Аннотация

Для производства тепла и улучшения управления системами централизованного теплоснабжения (СЦТ) требуется точное прогнозирование тепловой нагрузки. Составить более достоверный прогноз можно с помощью наиболее передовых технологий. В настоящей статье для получения прогнозных данных о тепловой нагрузке СЦТ предложено использовать современные модели машинного обучения: временну́ю сверточную сеть (temporal convolutional network – TCN) и категориальное повышение градиента (categorical boosting – CatBoost). Для проверки и сравнения работы моделей прогнозирования тепловой нагрузки TCN и CatBoost были выбраны две дополнительные показательные модели – дерево решений и множественная линейная регрессия. В качестве обучающего кейса для моделей использовались данные о тепловой нагрузке СЦТ в Тяньцзине (Китай). В качестве входных параметров для моделей выбирались две статистические рабочие характеристики (суточная и часовая тепловые нагрузки) СЦТ и четыре метеорологические (температура и относительная влажность наружного воздуха, скорость ветра и индекс качества воздуха). Представлены и проанализированы результаты прогноза по каждой из обученных моделей. Итоги расчетных экспериментов показали, что прогноз, полученный с помощью TCN и CatBoost, оказался более точным, чем с использованием классических моделей, при том что моделирование с CatBoost является более простым. Следовательно, методы TCN и CatBoost применимы для прогнозирования тепловой нагрузки СЦТ.

Ключевые слова: прогнозирование тепловой нагрузки, система централизованного теплоснабжения, CatBoost, TCN, дерево решений, линейная регрессия, глубокое обучение, машинное обучение, модель прогноза временного ряда

В настоящее время тепловые электростанции, на которых сжигаются ископаемые виды топлива или биомасса, являются основными элементами системы централизованного теплоснабжения Китая. Урбанизация в Китае привела к стремительному росту спроса на централизованное теплоснабжение [1, 2], к основным достоинствам которого можно отнести максимальное удобство использования, а также энергосбережение и снижение выбросов вредных веществ.

Изменение климата – глобальная проблема человечества. Во многих странах мира ведется политика по охране окружающей среды и предпринимаются меры по контролю выбросов парниковых газов. Так, Китай поставил своей целью пройти пик выброса парниковых газов к 2030 г. и достичь углеродной нейтральности к 2060 г. Переход от современных СЦТ к их четвертому поколению (4G СЦТ) – актуальная задача китайской национальной энергетической стратегии [3]. Одой из наиболее отличительных характеристик 4G СЦТ является управление на основе прогнозирующих моделей [4], с помощью которого можно предсказывать возможные потребности тепла и активно регулировать параметры работы СЦТ. Прогнозирование тепловой нагрузки – необходимое требование для реализации этой технологии.

Существующие модели прогнозирования тепловой нагрузки включают в себя, главным образом, модели белого ящика, основанные на физических уравнениях, и модели черного ящика, опирающиеся на ранее полученные данные. Первые прогнозируют теплопотребление зданий с использованием группы физических уравнений для модели частей здания или всего здания [5]. Для разработки модели белого ящика могут применяться несколько общепризнанных программ (EnergyPlus, TRNSYS и др.). Например, для расчета теплопотребления сверхвысотных зданий в работе [6] использовали TRNS-YS. Для разработки модели белого ящика для прогнозирования нагрузки СЦТ требуются особые данные, получить которые очень трудно. В результате, хоть эти модели и являются более точными и однозначными, при составлении прогноза теплопотребления от СЦТ и принятии решений специалисты отдают предпочтение моделям черного ящика.

В моделях черного ящика для прогнозирования тепловой нагрузки используются оперативные данные, полученные при эксплуатации оборудования и систем. В предыдущие годы большинство моделей прогноза тепловой нагрузки СЦТ основывались на статистических моделях и их вариантах, таких как множественная линейная регрессия (multiple linear regression – MLR) [7], авторегрессионная модель скользящего среднего (autoregressive moving average – ARMA) [8] и статистический подход авторегрессионной интегрированной модели скользящего среднего (seasonal autoregressive integrated moving average – SARIMA) [9]. Статистические модели имеют несложные структуры, просты для понимания, но при использовании дают недостаточно точные результаты.

В отличие от статистических, модели машинного обучения более результативны. Многие авторы протестировали и проанализировали эффективность различных технологий машинного обучения при проведении оценки теплопотребления. Наиболее широко используемыми среди них являются метод опорных векторов (support vector machine – SVM) [10–14] и искусственные нейронные сети (artificial neural network – ANN) [15, 16]. Модели прогнозов временных рядов, основанные на стратегии увеличения градиента, также демонстрируют высокое качество и надежность и не требуют особенной подготовки входных данных. Один из методов повышения градиента – его экстремальный рост – был разработан для оценки теплопотребления СЦТ [17, 18]. Кроме того, некоторые авторы полагают, что комбинирование нескольких методов и уточнение параметров одного метода через алгоритм оптимизации являются лучшими способами повысить точность и обобщающую способность моделей [19–25].

Растущий объем измеряемых и собираемых оперативных данных СЦТ способствовал использованию глубокого обучения в проектах прогнозирования тепловой нагрузки. При глубоком обучении могут улавливаться более сложные взаимосвязи между тепловыми нагрузками и входными характеристиками. Обычный алгоритм глубокого обучения (deep neural network – DNN) применялся для прогноза тепловой нагрузки для СЦТ в [26]. В [27, 28] было продемонстрировано, что глубокая нейронная сеть с долговременной краткосрочной памятью (long short term memory – LSTM), специально разработанная для обработки временных рядов, является мощным инструментом для оценки тепловой нагрузки СЦТ.

Фактически у любых алгоритмов имеются ограничения. Всегда целесообразно исследовать, какой из них работает лучше в контексте прогноза тепловой нагрузки СЦТ.

Временная сверточная сеть (TCN) – это новая модель прогнозирования временных рядов, хорошо себя зарекомендовавшая. В работе [29] TCN сравнивалась с рекуррентной нейронной сетью (recurrent neural network – RNN), LSTM и сетью с управляемыми рекуррентными блоками (gate recurrent unit – GRU) в одиннадцати различных вариантах моделирования временны́х последовательностей. TCN быстрее и точнее выполнила более девяти задач. Эта сеть предлагает альтернативное решение проблемы прогнозирования временных рядов, но результаты ее применения для прогнозирования энергопотребления по-прежнему отсутствуют.

Алгоритмы повышения градиента – это тоже прекрасные инструменты прогнозирования. Однако CatBoost, современная модель с повышением градиента, еще не использовалась для расчета тепловой нагрузки.

Чтобы изучить возможности TCN и CatBoost для прогнозирования тепловой нагрузки, в настоящей работе применяются данные о почасовой тепловой нагрузке СЦТ в Тяньцзине (Китай) для создания аналитической структуры. Основные идеи заключаются в следующем:

TCN и CatBoost используются для прогнозирования тепловой нагрузки (в качестве входных параметров выбираются две эксплуатационные характеристики СЦТ и четыре метеорологические характеристики);

для сравнения полученных с помощью TCN и CatBoost результатов выбраны традиционные инструменты прогнозирования – модель дерева решений (decision tree – DT) и модель MLR.

ПРЕДПОСЫЛКИ ПРОГНОЗИРОВАНИЯ ТЕПЛОВОЙ НАГРУЗКИ

На рис. 1 представлена структура исследуемой СЦТ, состоящая из трех основных компонентов: источника тепла, теплораспределительного пункта и тепловых сетей. Источник тепла нагревает воду и передает в тепловой пункт через распределительную сеть. Тепловой пункт принимает тепло из первичных тепловых сетей, непрерывно нагревает воду вторичной тепловой сети и доставляет ее в здания для нужд отопления.

Рис. 1.

Принципиальная схема СЦТ. 1 – источник тепла; 2 – тепловой пункт; 3 – здания; 4, 5 – первичный и вторичный контуры; сплошные линии – прямая сетевая вода; штриховые линии – обратная сетевая вода

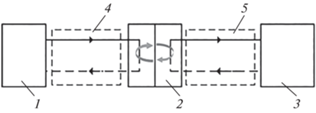
Исследуемая СЦТ используется только для отопления помещений и не обеспечивает жильцов горячей водой для бытовых нужд. На ее базе была выстроена система сбора информации о прогнозируемых погодных изменениях и о работе СЦТ в режиме реального времени. Тепловая нагрузка СЦТ Q, кВт, для зданий рассчитывается по формуле

$Q = \frac{{c\rho q({{t}_{s}} - {{t}_{r}})}}{{3.6 \times {{{10}}^{6}}}},$
где с = 4.2 × 103 Дж/(кг · К) – удельная теплоемкость воды; ρ – плотность воды при температуре 32°С (средней между температурой воды, подаваемой во вторичный контур, ts и температурой возвращаемой воды tr), равная 0.995 × 103 кг/м3; q – объемный расход теплоносителя, м3/ч.

С учетом того что частая регулировка расхода может стать причиной разбалансировки системы, принимается фиксированный расход теплоносителя для управления тепловой нагрузкой СЦТ путем изменения его температуры. Измеренное значение q составляет 400 м3/ч.

Система централизованного теплоснабжения инертна: производителю тепла необходимо заранее так настроить его поставку, чтобы она удовлетворяла требованиям потребителей. Прогнозирование тепловых потерь может быть ориентиром для предварительной корректировки отопления, при том что c, ρ и q – постоянные параметры. Автоматическая система контроля может показывать разницу между температурами воды, подаваемой во вторичный контур и возвращаемой из него согласно прогнозируемой тепловой нагрузке. Температура ts регулируется открытием запорно-регулирующей арматуры на тепловом пункте. Перепад температур подаваемого в сеть и возвращаемого водного теплоносителя поддерживается на заданном уровне. Таким образом осуществляется точная регулировка тепловой нагрузки. В итоге, прогнозирование, направленное на оптимизацию производства тепловой энергии и точное регулирование нагрузки СЦТ, имеет важное для нее значение. Данная статья посвящена прогнозированию потребления зданиями тепла в течение часа, следующего после поступления его в СЦТ.

МЕТОДЫ МОДЕЛИРОВАНИЯ

Временная сверточная сеть (TCN)

Временная сверточная сеть предназначена для прогнозирования временной последовательности. Метод основан на двух принципах:

результат прогноза ${{\hat {y}}_{t}}$ зависит от наблюдаемой последовательности $\{ {{x}_{0}},...,{{x}_{t}}\} ;$

TCN принимает временные ряды любой длины и выводит временные ряды той же длины.

В TCN обработка временных рядов осуществляется с помощью функции отображения

${{\hat {y}}_{0}},...,{{\hat {y}}_{t}} = f({{x}_{0}},...,{{x}_{t}}).$

Целью моделирования последовательности является обучение структуры, которая минимизирует функцию затрат $L\left[ {{{y}_{0}},...,{{y}_{t}},f({{x}_{0}},...,{{x}_{t}})} \right]$ между фактическими и прогнозируемыми результатами. Структура TCN включает в себя случайные свертки, расширенные свертки и остаточные блоки.

Случайные свертки: TCN использует причинно-следственные свертки для удовлетворения первого принципа метода. Элемент ${{i}_{{th}}}$ выходной последовательности может зависеть только от элементов с индексами $\{ 0,...t\} $ во входной последовательности. Кроме того, чтобы выходная последовательность имела ту же длину, что и входная, TCN необходимо выполнить операцию заполнения нулем, а TCN заполняет нулем только с левой стороны входной последовательности.

Расширенные свертки: базовая случайная свертка может просматривать только истории, линейные по размеру в глубине сети, что затрудняет применение вышеуказанных причинно-следственных сверток к задачам моделирования более длительных последовательностей. Для решения этой проблемы вводятся расширенные свертки F для элемента s входной последовательности х, которые выражаются следующим образом:

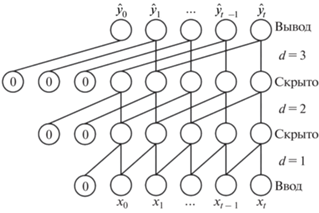
$F(s) = ({{x}_{{*d}}}f)(s) = \sum\limits_{i = 0}^{k - 1} {\left[ {f(i){{x}_{{s - di}}}} \right]} {\kern 1pt} {\kern 1pt} ,$
где d – коэффициент расширения; k – размер фильтра; $s - di$ – предыдущий ориентир.

Установка определенных интервалов между соседними фильтрами потоков входных данных называется расширенной сверткой. Расширенная свертка становится обыкновенной, когда d = 1. Следует отметить, что коэффициент расширения увеличивается по мере углубления сети. Это гарантирует, что некоторые фильтры будут попадать на все входные данные в изучаемой истории (рис. 2).

Рис. 2.

Пример расширенной причинно-следственной свертки (коэффициенты расширения d = 1, 2, 4, размер фильтра k = 3)

Остаточные блоки: если рассмотреть блок нейронной сети, входом которого являтся x, то после серии преобразований будет получено распределение истинных результатов H(x). Разница (невязка) между выходными и входными данными будет определяться набором остатков F(x) = H(x) – x. Следовательно, поиск истинных результатов может быть осуществлен путем изучения остатков по идентификационной связи H(x) = x + F(x):

$o = Activation(x + F(x)),$
где o – вывод остаточного блока; Activation – функция активации.

Это позволяет слоям учитывать изменения результатов преобразования в сравнении с исходными данными, что выгодно отличает глубокие сети от других.

Область восприятия определяется глубиной сети n, коэффициентом расширения d и размером фильтра k. Если результаты прогнозирования зависят от большого объема архивной статистической информации и многомерных входных последовательностей, то может потребоваться очень глубокая сеть. Как следствие, для поддержания стабильности TCN объединяет не сверточные слои в глубокую сеть, а остаточные блоки.

Как показано на рис. 3, один остаточный блок содержит два расширенных случайных сверточных слоя. Выпрямленная линейная функция активации (rectified linear unit – ReLU) применяется для преобразования нелинейности. Нормирование веса выполняется для каждого фильтра. Пространственный отсев используется, чтобы упорядочить расширенный случайный сверточный слой: весь канал обнуляется на каждой итерации обучения.

Рис. 3.

Принципиальная схема остаточного блока. ПО – пространственный отсев; ВЛФА – выпрямленная линейная функция активации; НВ – нормированные веса; РССС – расширенный случайный сверточный слой

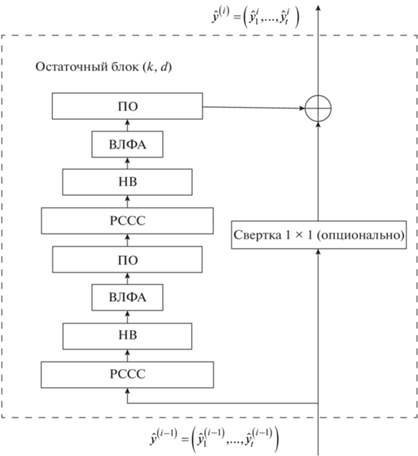
Поскольку вход остаточного блока и выход остаточного соединения могут иметь разную ширину, их нельзя напрямую суммировать. TCN использует свертку 1 × 1, чтобы устранить несоответствие ширины ввода-вывода.

Категориальное повышение (CatBoost)

CatBoost – это новый метод повышения градиента, разработанный в 2018 г. [30]. По сравнению с другими алгоритмами дерева принятия решений с повышением градиента (GBDT), он имеет несколько отличительных характеристик.

Во-первых, CatBoost может обрабатывать не только числовые, но и категориальные признаки на этапе обучения. В CatBoost целевая статистика – эффективный подход к работе с категориальными переменными с наименьшими потерями информации (точная методика описана в [30]).

Во-вторых, CatBoost использует упорядоченное повышение, чтобы предотвратить смещение прогноза, характерное для типичных моделей GBDT (см. алгоритм 1 в [30] для конкретной методики). CatBoost генерирует несколько упорядоченных перестановок обучающего набора. Они применяются для повышения надежности C-atBoost – получения градиентов предсказаний при перестановке значений признака. Обучение различных моделей при разных перестановках позволит избежать переобучения.

Наконец, CatBoost использует забывчивые деревья решений в качестве базовых предсказателей. Такая модель имеет довольно слабое сходство с обычным решающим деревом, хотя и строится по тем же правилам. Забывчивые решающие деревья разрабатывались для задач с большим числом нерелевантных признаков. Этот тип дерева менее уязвим для переобучения.

ЭКСПЕРИМЕНТАЛЬНАЯ СТРУКТУРА

Процесс прогнозирования тепловой нагрузки, как правило, состоит из шести этапов.

Первый этап – интеграция данных: объединяются различные источники данных. Авторы настоящей публикации собрали исторические сводки о тепловой нагрузке СЦТ с 17 февраля по 22 марта 2018 г.

Второй этап – предварительная обработка данных: устраняются аномалии в данных о тепловой нагрузке, а отсутствующие показатели дополняются. Недостающие эксплуатационные характеристики СЦТ и температуру наружного воздуха получают путем линейной интерполяции, в то время как данные о скорости ветра и индексе качества воздуха – с помощью расчетного метода. Наконец, что касается TCN, то входные данные должны быть масштабированы таким образом, чтобы они были приведены в заданный диапазон. В настоящем исследовании выбрана нормализация [min; max] для преобразования данных в диапазон 0–1:

$x{\kern 1pt} ' = \frac{{x - {{x}_{{\min }}}}}{{{{x}_{{\max }}} - {{x}_{{\min }}}}};\,\,\,\,x = x{\kern 1pt} '({{x}_{{\max }}} - {{x}_{{\min }}}) + {{x}_{{\min }}}.$

Третий этап – разделение данных: 72 выборки берутся в качестве тестовых данных, а остальные рассматриваются как обучающие.

На четвертом этапе тренировочный набор используется для обучения моделей прогнозирования.

Оценка модели (пятый этап) происходит после обучения моделей и заключается в использовании набора тестов для проверки их (моделей) производительности. Что касается подходов к анализу ошибок прогнозирования (mean error – ME), то выбираются среднеквадратическая ошибка (mean square error – MSE), средняя абсолютная ошибка (mean absolute error – MAE) и коэффициент вариации среднеквадратической ошибки (coefficient of variation of root mean square error – CVRMSE). Первый показатель отражает надежность алгоритма, второй – реальную ситуацию с ошибкой прогнозирования, а третий представляет собой безразмерную метрику, позволяющую избежать эффекта масштаба. Меньшие значения MSE, MAE и CVRMSE означают более качественный прогноз модели. Данные показатели определяются следующим образом:

$\begin{gathered} \operatorname{MSE} = \frac{1}{n}\sum\limits_{i = 1}^n {{{{({{Q}_{i}} - {{{\hat {Q}}}_{i}})}}^{2}}} ;\,\,\,\,\operatorname{MAE} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{Q}_{i}} - {{{\hat {Q}}}_{i}}} \right|} ; \\ {\text{CVRMSE}} = \frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{{({{Q}_{i}} - {{{\hat {Q}}}_{i}})}}^{2}}} } }}{{\frac{1}{n}\sum\limits_{i = 1}^n {{{Q}_{i}}} }} \times 100\% , \\ \end{gathered} $
где ${{\hat {Q}}_{i}}$ и ${{Q}_{i}}$ – прогнозируемая и фактическая тепловая нагрузка в час $i$, МВт; $n$ – общее число прогнозируемых часов.

Последний, шестой, этап (анализ результатов прогнозирования) основан на их визуализации в тестовом наборе для каждой модели, в результате чего можно наблюдать и оценивать их эффективность.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

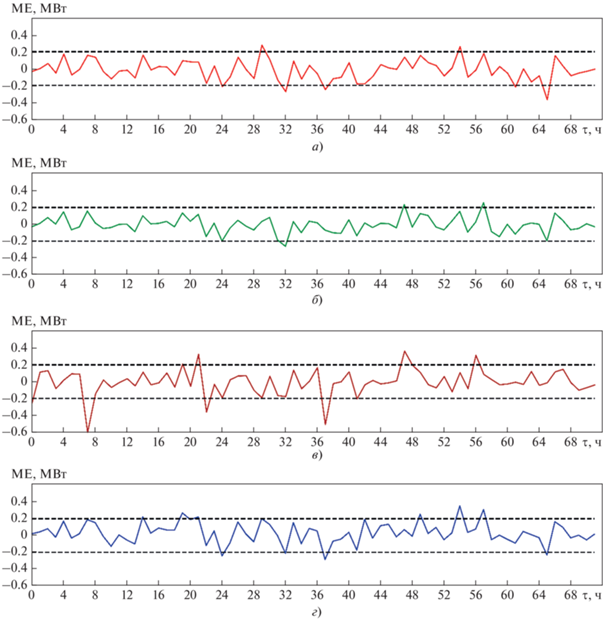
Итак, исходные данные о тепловой нагрузке известны и прерываются случайным образом. 72 выборки выделены в тестовый набор, для которого на рис. 4 представлены прогнозные кривые для всех моделей. На рис. 5 можно наблюдать различия между прогнозируемыми и фактическими значениями в каждый момент времени. В таблице приведены статистические показатели для каждой модели из тестового набора.

Рис. 4.

Результаты прогнозирования тепловой нагрузки Q СЦТ для всех моделей на тестовой выборке. 1 – фактическая; нагрузка, определенная с помощью: 2 – TCN; 3 – CatBoost; 4 – DT; 5 – MLR

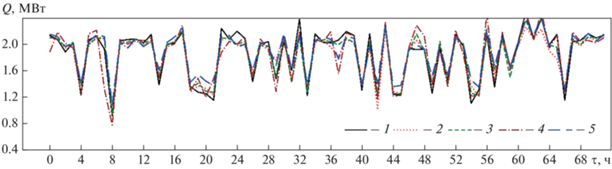
Рис. 5.

Ошибка прогнозирования ME при использовании моделей TCN (а), CatBoost (б), DT (в) и MLR (г) на тестовой выборке в каждый момент времени τ

Статистические показатели моделей в тестовом наборе

Модель MSE, МВт MAE, МВт CVRMSE, %
TCN 0.0153 0.0962 0.0667
CatBoost 0.0091 0.0711 0.0516
DT 0.0244 0.1080 0.0844
MLR 0.0169 0.0989 0.0702

В [17] утверждается, что значение CVRMSE не должно превышать 30% для моделей, используемых в промышленности. Из таблицы следует, что этому критерию удовлетворяют все модели прогнозирования. Что еще более важно, по сравнению с базовыми моделями, TCN и CatBoost дают более точные и надежные результаты прогнозирования (CatBoost показывает наиболее совершенные результаты). Точность предсказания TCN немного ниже, чем у CatBoost, но лучше, чем у MLR и DT. Как видно на рис. 5, а и б, ошибки прогнозирования TCN и CatBoost в определенной степени меняются в зависимости от колебаний фактической тепловой нагрузки, но в большинстве моментов времени находятся в пределах 10%. Прогнозы MLR (см. рис. 5, г) при некоторых минимальных значениях всегда превышают фактическую тепловую нагрузку, что ведет к перерасходу тепловой энергии. Ошибка предсказания DT (см. рис. 5, в) относительно велика: ее прогнозы в момент времени 7 и 37 ч особенно неточны.

ВЫВОДЫ

1. Результаты расчетного эксперимента подтвердили, что все четыре модели черного ящика: TCN, CatBoost, DT, MLR – могут быть применены для прогнозирования тепловой нагрузки СЦТ. Коэффициент вариации среднеквадратической ошибки прогноза тепловой нагрузки не превысил 10% при известном ограничении 30%.

2. При использовании для прогнозирования моделей временных рядов TCN и повышения градиента CatBoost были получены более точные результаты, чем по модели дерева решений DT и статистической модели множественной линейной регрессии MLR. Ошибки прогноза TCN и CatBoost в большинстве моментов времени находились в пределах 10%.

3. Поскольку при реализации модели на основе деревьев решений не требуется нормализация входных данных, процесс моделирования с помощью CatBoost является менее трудозатратным, чем с использованием TCN.

Список литературы

  1. Case study on industrial surplus heat of steel plants for district heating in Northern China / Y.M. Li, J.J. Xia, H. Fang, Y.B. Su, Y. Jiang // Energy. 2016. V. 102. P. 397–405. https://doi.org/10.1016/j.energy.2016.02.105

  2. Heat roadmap China: new heat strategy to reduce energy consumption towards 2030 / W. Xiong, Y. Wang, B.V. Mathiesen, H. Lund, X. Zhang // Energy. 2015. V. 81. P. 274–285. https://doi.org/10.1016/j.energy.2014.12.039

  3. Smart energy systems and 4th generation district heating / H. Lund, N. Duic, P.A. Østergaard, B.V. Mathiesen // Energy. 2016. V. 110. P. 1–4. https://doi.org/10.1016/j.energy.2016.07.105

  4. The status of 4th generation district heating: research and results / H. Lund, P.A. Ostergaard, M. Chang, S. Werner, S. Svendsen, P. Sorknaes, J.E. Thorsen, F. Hvelplund, B.O.G. Mortensen, B.V. Mathiesen, C. Bojesen, N. Duic, X.L. Zhang, B. Moller // Energy. 2018. V. 164. P. 147–159. https://doi.org/10.1016/j.energy.2018.08.206

  5. Li X.W., Wen J. Review of building energy modeling for control and operation // Renewable Sustainable Energy Rev. 2014. V. 37. P. 517–537. https://doi.org/10.1016/j.rser.2014.05.056

  6. Cao J.L., Liu J., Man X.X. A united WRF/TRNSYS method for estimating the heating/cooling load for the thousand-meter scale megatall buildings // Appl. Therm. Eng. 2017. V. 114. P. 196–210. https://doi.org/10.1016/j.applthermaleng.2016.11.195

  7. Applied machine learning: forecasting heat load in district heating system // S. Idowu, S. Saguna, C. Ahlund, O. Schelen // Energy Build. 2016. V. 133. P. 478–488. https://doi.org/10.1016/j.enbuild.2016.09.068

  8. Huang S.J., Shih K.R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations // IEEE Trans. Power Syst. 2003. V. 18. Is. 2. P. 673–679. https://doi.org/10.1109/tpwrs.2003.811010

  9. Fang T.T., Lahdelma R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system // Appl. Energy. 2916. V. 179. P. 544–552. https://doi.org/10.1016/j.apenergy.2016.06.133

  10. Prediction of heat load in district heating systems by support vector machine with firefly searching algorithm / E.T. Al-Shammari, A. Keivani, S. Shamshirband, A. Mostafaeipour, P.L. Yee, D. Petkovic, S. Ch // Energy. 2016. V. 95. P. 266–273. https://doi.org/10.1016/j.energy.2015.11.079

  11. Barman M., Choudhury N.B.D., Sutradhar S. A regional hybrid GOASVM model based on similar day approach for short-term load forecasting in Assam, India // Energy. 2018. V. 145. P. 710–720. https://doi.org/10.1016/j.energy.2017.12.156

  12. Prediction of heat load fluctuation based on fuzzy information granulation and support vector machine / T. Wang, T.Y. Ma, D.S. Yan, J. Song, J.S. Hu, G.Y. Zhang, Y.H. Zhuang // Therm. Sci. 2021. V. 25. Is. 5. P. 3219–3228. https://doi.org/10.2298/tsci200529307w

  13. Appraisal of soft computing methods for short term consumers’ heat load prediction in district heating systems / M. Protic, S. Shamshirband, M.H. Anisi, D. Petkovic, D. Mitic, M. Raos, M. Arif, K.A. Alam // Energy. 2015. V. 82. P. 697–704. https://doi.org/10.1016/j.energy.2015.01.079

  14. Koschwitz D., Frisch J., van Treeck C. Data-driven heating and cooling load predictions for non-residential buildings based on support vector machine regression and NARX recurrent neural network: A comparative study on district scale // Energy. 2018. V. 165. P. 134–142. https://doi.org/10.1016/j.energy.2018.09.068

  15. GMM clustering for heating load patterns in-depth identification and prediction model accuracy improvement of district heating system / Y. Lu, Z. Tian, P. Peng, J. Niu, W. Li, H. Zhang // Energy Build. 2019. V. 190. P. 49–60. https://doi.org/10.1016/j.enbuild.2019.02.014

  16. Heat load prediction of small district heating system using artificial neural networks / M.B. Simonovic, V.D. Nikolic, E.P. Petrovic, I.T. Ciric // Therm. Sci. 2016. V. 20. P. 1355–1365. https://doi.org/10.2298/TSCI16S5355S

  17. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms / P.N. Xue, Y. Jiang, Z.G. Zhou, X. Chen, X.M. Fang, J. Liu // Energy. 2019. V. 188. P. 116085. https://doi.org/10.1016/j.energy.2019.116085

  18. Prediction of residential district heating load based on machine learning: A case study / Z.Q. Wei, T.W. Zhang, B. Yue, Y.X. Ding, R. Xiao, R.Z. Wang, X.Q. Zhai // Energy. 2021. V. 231. P. 120950. https://doi.org/10.1016/j.energy.2021.120950

  19. Heating and cooling loads forecasting for residential buildings based on hybrid machine learning applications: A comprehensive review and comparative analysis / A. Moradzadeh, B. Mohammadi-Ivatloo, M. Abapour, A. Anvari-Moghaddam, S.S. Roy // IEEE Access. 2022. V. 10. P. 2196–2215. https://doi.org/10.1109/access.2021.3136091

  20. Operational thermal load forecasting in district heating networks using machine learning and expert advice // D. Geysen, O. de Somer, C. Johansson, J. Brage, D. Vanhoudt // Energy Build. 20218. V. 162. P. 144–153. https://doi.org/10.1016/j.enbuild.2017.12.042

  21. Dahl M., Brun A., Andresen G.B. Using ensemble weather predictions in district heating operation and load forecasting // Appl. Energy. 2017. V. 193. P. 455–465. https://doi.org/10.1016/j.apenergy.2017.02.066

  22. Heat load prediction of residential buildings based on discrete wavelet transform and tree-based ensemble learning / M.J. Gong, J. Wang, Y. Bai, B. Li, L. Zhang // J. Build. Eng. 2020. V. 32. P. 101455. https://doi.org/10.1016/j.jobe.2020.101455

  23. Eseye A.T., Lehtonen M. Short-term forecasting of heat demand of buildings for efficient and optimal energy management based on integrated machine learning models // IEEE Trans. Ind. Informatics. 2020. V. 16. Is. 12. P. 7743–7755. https://doi.org/10.1109/tii.2020.2970165

  24. Appraisal of the support vector machine to forecast residential heating demand for the district heating system based on the monthly overall natural gas consumption // N. Izadyar, H. Ghadamian, H.C. Ong, Z. Moghadam, C.W. Tong, S. Shamshirband // Energy. 2015. V. 93. P. 1558–1567. https://doi.org/10.1016/j.energy.2015.10.015

  25. Wu D.Z., Foong L.K., Lyu Z.J. Two neural-metaheuristic techniques based on vortex search and backtracking search algorithms for predicting the heating load of residential buildings // Eng. Computers. 2022. V. 38. Is. 1. P. 647–660. https://doi.org/10.1007/s00366-020-01074-z

  26. District heating systems load forecasting: a deep neural networks model based on similar day approach / M. Gong, H. Zhou, Q. Wang, S. Wang, P. Yang // Adv. Build. Energy Res. 2020. V. 14. Is. 3. P. 372–388. https://doi.org/10.1080/17512549.2019.1607777

  27. Heating load forecasting for combined heat and power plants via strand-based LSTM / J.Y. Liu, X. Wang, Y. Zhao, B. Dong, K. Lu, R.R. Wang // IEEE Access. 2020. V. 8. P. 33360–33369. https://doi.org/10.1109/access.2020.2972303

  28. A comprehensive thermal load forecasting analysis based on machine learning algorithms / S. Leiprecht, F. Behrens, T. Faber, M. Finkenrath // Energy Rep. 2021. V. 7. P. 319–326. https://doi.org/10.1016/j.egyr.2021.08.140

  29. Bai S., Kolter J.Z., Koltun V.J. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. 2018. https://doi.org/10.48550/arXiv.1803.01271

  30. CatBoost: unbiased boosting with categorical features / L. Prokhorenkova, G. Gusev, A. Vorobev, A.V. Dorogush, A.J.A. Gulin. 20218. V. 31.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Теплоэнергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал