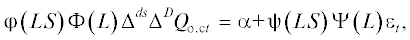Теплоэнергетика, 2021, № 3, стр. 89-98
Выбор модели прогнозирования отпуска тепловой энергии
А. В. Затонский a, Л. Г. Тугашова b, *
a Березниковский филиал Пермского национального исследовательского политехнического университета
618404 г. Березники, ул. Тельмана, д. 7, Россия
b Альметьевский государственный нефтяной институт
423450 г. Альметьевск, ул. Ленина, д. 2, Республика Татарстан, Россия
* E-mail: tugashova@yandex.ru
Поступила в редакцию 06.12.2019
После доработки 26.03.2020
Принята к публикации 20.05.2020
Аннотация
Для решения задач экономии тепловой энергии вместо используемых в настоящее время громоздких методик или сложных математических моделей, например, в виде дифференциальных уравнений в частных производных предложено применять более простые модели временных рядов отпуска и выработки тепловой энергии. В качестве исходных использованы данные конкретной теплоснабжающей организации городского масштаба и сайта Министерства энергетики РФ. Предлагаемый подход основан на сравнении различных математических моделей прогнозирования выработки и отпуска тепловой энергии по критерию адекватности (средняя относительная погрешность и коэффициент детерминации). Представлены результаты исследований, проведенных с помощью программного пакета Matlab. Проведено обоснованное сравнение возможности применения различных моделей. Разработаны модели, отличающиеся учетом сезонной компоненты и более высокой точностью. Исследована возможность применения следующих моделей временных рядов: регрессионных моделей с сезонной составляющей, тройного экспоненциального сглаживания Хольта–Винтерса (Holt’s–Winters’), мультипликативной сезонной авторегрессионной модели проинтегрированного скользящего среднего SARIMA (от англ. seasonal autoregressive integrated moving average), непараметрической модели SSA (от англ. singular spectrum analysis). Сравнивались мультипликативные модели, содержащие тренд в виде линейной или авторегрессионной модели с вычислением индекса сезонности, а также аддитивные модели с трендом в виде линейной или авторегрессионной модели с сезонной составляющей в виде ряда Фурье или суммы синусов. В модели Хольта–Винтерса для определения настроечных параметров применялась fminsearch – функция программного пакета Matlab. В мультипликативной модели SARIMA порядки авторегрессии и скользящего среднего подбирались по автокорреляционной и частной автокорреляционной функции. Непараметрическая модель SSA использовалась для сравнения с перечисленными параметрическими моделями. Получена возможность строить обоснованные прогнозы выработки и отпуска тепловой энергии. Показано, что лучшие результаты (средняя относительная погрешность 6.52%) получены с применением мультипликативной модели SARIMA.
Субъектами теплоснабжения являются потребители тепловой энергии (население, учреждения, бюджетные и прочие организации), теплоснабжающее предприятие, теплосетевая организация. В настоящее время в условиях роста спроса на энергоресурсы и повышения тарифов на тепло- и водоснабжение весьма актуальна проблема экономии тепловой энергии. Поэтому в сфере теплоснабжения особенно важно решение задач реконструкции существующих систем из-за высокой степени износа теплосетей и внедрения систем автоматики для экономии тепловой энергии. Регулирование отпуска тепла потребителям осуществляется качественным, количественным, качественно-количественным и прерывистым способами.
При функционировании системы теплоснабжения необходимо учитывать множество факторов, таких как температура и расход воды, давление в системе, количество тепловой энергии на отопление и водоснабжение, температура в помещении, нормативы потребления, метеоусловия (температура наружного воздуха, ветер, солнечная радиация), характеристики здания и др. При реконструкции и усовершенствовании управления объектами применяются громоздкие методики, сложные математические модели, например в виде системы дифференциальных уравнений в частных производных (ДУЧП) [1], или гибридные методы [2]. Следовательно, к сложности самой модели неизбежно добавляется сложность численных методов, требуемых для ее решения. Большую роль играет также оснащение каждого численного метода, которое не имеет отношения к процессам, происходящим в моделируемом объекте. Даже элементарные методы интегрирования обыкновенных дифференциальных уравнений могут давать совершенно разные решения при изменении шага. С усложнением методов повышается и значимость таких настроек, что также не способствует точности моделирования. Подобная проблема актуальна для любых моделей, в том числе и моделей энергетических объектов. Для решения перечисленных проблем авторы предлагают применять модели временных рядов, являющиеся более простыми, но позволяющие получить результат с приемлемой точностью.
ПОСТАНОВКА ЗАДАЧИ
При реконструкции и усовершенствовании управления существующими системами теплоснабжения, определении оптимальных режимов их работы, построении температурных графиков необходима система прогнозирования временных рядов с разнообразными параметрами. Прогнозы могут быть краткосрочными, среднесрочными, долгосрочными. Они предназначены для решения разных задач. Методы решения также различны. Краткосрочные прогнозы выполняются на несколько часов и могут быть применимы, например, при управлении температурными режимами или при определении температурных графиков. Среднесрочные прогнозы используются, в частности, для контроля нормативов теплопотребления. Долгосрочные прогнозы учитывают ввод новых объектов и зависят также от экономических показателей. Они выполняются на несколько лет.
В настоящее время применяются следующие методы и модели прогнозирования:
параметрические – однофакторные и многофакторные регрессионные [3, 4], авторегрессионные, авторегрессионные скользящего среднего [5] и др.;
непараметрические [6];
методы интеллектуального прогнозирования – искусственные нейронные сети [7], генетические алгоритмы, кластеризация [8], метод опорных векторов SVM (от англ. support vector machine) [9] и др.
При использовании методов интеллектуального прогнозирования требуется большой объем выборки. Для улучшения качества прогноза возможно совмещение классических методов и интеллектуального анализа данных, позволяющего как определять сложные нелинейные взаимосвязи, так и адаптировать решение при поступлении новых данных [2, 10, 11]. Однако при этом сложность гибридных методов возрастает.
Для решения указанных задач различными авторами предлагаются следующие подходы. В работе [12] разработана технико-экономическая модель, позволяющая выполнять экспресс-оценку оптимальной мощности и количества источников тепла в системе теплоснабжения. В представленной методике в пункте “Баланс выработки и потребления тепловой энергии” отпуск тепла потребителям принимается по фактическим значениям предыдущего периода (года), что может вносить погрешность в полученную модель.
В работе [3] описаны методы качественной и количественной оценки эффективности регулирования теплопотребления с использованием регрессионной модели объекта, отражающей зависимость температуры теплоносителя в обратном трубопроводе от расхода и температуры теплоносителя в подающем трубопроводе. Регрессионные модели характеризуются хорошими аппроксимирующими свойствами, но малоэффективны для задач прогнозирования.
В [13] предложена методика долгосрочного прогнозирования спроса на тепловую мощность с учетом функций реализуемости планов строительства.
В настоящей работе поставлены следующие задачи:
выбор методов моделирования и прогнозирования выработки и отпуска тепловой энергии;
сбор статистической информации и выбор структуры моделей с выявлением тренда и сезонной составляющей;
построение и исследование моделей с использованием реальных данных теплосетевой организации, в том числе с применением современных программных средств;
сравнительная оценка качества прогнозирования полученных моделей.
Предполагается рассмотреть следующие типы моделей прогнозирования временных рядов:
мультипликативная модель с выявлением тренда и расчетом индексов сезонности;
аддитивная модель с выявлением тренда и сезонной компонентой в виде ряда Фурье или суммы синусов;
модель экспоненциального сглаживания Хольта–Винтерса;
мультипликативная сезонная авторегрессионная модель проинтегрированного скользящего среднего SARIMA;
непараметрическая модель SSA.
Инструментом для решения поставленных задач выбрана среда Matlab.
ПОСТРОЕНИЕ И СОПОСТАВЛЕНИЕ МОДЕЛЕЙ ПРОГНОЗИРОВАНИЯ
Выработанная тепловая энергия расходуется на отпуск тепла населению, бюджетным организациям, прочим потребителям, на собственные нужды источника тепла (котельных), потери в тепловых сетях, и это может быть представлено следующей формулой:
(1)
${{Q}_{{\text{в}}}} = {{Q}_{{\text{н}}}} + {{Q}_{{{\text{б}}{\text{.п}}}}} + {{Q}_{{{\text{п}}{\text{.п}}}}} + {{Q}_{{{\text{с}}{\text{.н}}}}} + {{Q}_{{\text{п}}}},$Отпуск тепловой энергии в сеть от источника определяется суммой полезного отпуска тепловой энергии потребителям и тепловых потерь. Первые три слагаемых в формуле (1) образуют полезный отпуск тепла потребителям.
В качестве исходных данных для моделирования и прогнозирования отпуска тепловой энергии в сеть приняты данные по балансу производства тепловой энергии АО “Альметьевские тепловые сети” (г. Альметьевск), доступные на сайте [14] за 2013–2017 гг., а также значения среднемесячной температуры воздуха. Фрагмент исходной информации приведен в табл. 1.
Таблица 1.
Баланс производства тепловой энергии
| Период регулирования | Тепловая энергия, ГДж | Среднемесячная температура воздуха, °С | ||||
|---|---|---|---|---|---|---|
| выработка | собственные нужды | потери | полезный отпуск | отпуск в сеть | ||
| 1 | 2 | 3 | 4 | 5 | 6 (4+5) | 7 |
| За год | 3 087 361.69 | 80 386.56 | 397 394.31 | 2 609 580.82 | 3 006 975.13 | – |
| Январь | 527 955.48 | 13 816.44 | 71 175.60 | 442 963.44 | 514 139.04 | –11.64 |
| Февраль | 447 987.60 | 8373.60 | 46 054.80 | 393 559.20 | 439 614.00 | –14.77 |
| Март | 403 816.86 | 11 932.38 | 51 497.64 | 340 386.84 | 391 884.48 | –2.63 |
| Апрель | 271 053.43 | 6447.67 | 17 584.56 | 247 021.20 | 264 605.76 | 2.54 |
| Май | 83 401.06 | 2177.14 | 15 909.84 | 65 314.08 | 81 223.92 | 16.53 |
| Июнь | 52 000.06 | 2344.61 | 14 067.65 | 35 587.80 | 49 655.45 | 17.25 |
| Июль | 43 678.04 | 2093.40 | 11 915.63 | 29 669.00 | 41 584.64 | 16.91 |
| Август | 51 413.90 | 2428.34 | 18 840.60 | 30 144.96 | 48 985.56 | 18.41 |
| Сентябрь | 64 895.40 | 2093.40 | 8373.60 | 54 428.40 | 62 802.00 | 10.32 |
| Октябрь | 291 945.56 | 7661.84 | 51 916.32 | 232 367.40 | 284 283.72 | 1.05 |
| Ноябрь | 387 530.21 | 16 328.52 | 53 004.89 | 318 196.80 | 371 201.69 | –5.48 |
| Декабрь | 461 684.09 | 4689.22 | 37 053.18 | 419 941.69 | 456 994.87 | –7.82 |
Как известно, временной ряд состоит из следующих компонент: тренд, сезонная и случайная компоненты. Соответственно, временной ряд отпуска тепловой энергии содержит сезонную составляющую. Далее проведен анализ одной переменной (отпуска тепловой энергии в сеть Qо.с) по 60 наблюдениям для построения моделей временного ряда.
Мультипликативная модель с выявлением тренда и расчетом индексов сезонности
Сначала можно попробовать представить структуру модели в виде суммы тренда с вычислением индексов сезонности и записать мультипликативную модель временного ряда ${{\hat {Q}}_{{{\text{о}}{\text{.с}}}}}$ в виде произведения тренда и индексов сезонности с учетом остатков (остаточных ошибок) модели ε:
где Ti – тренд; Index – индекс сезонности.Для получения модели этого типа необходимы данные не менее чем за трехлетний период. Для выравнивания уровней ряда динамики можно принять период сглаживания, равный двенадцати месяцам. Далее следует вычислить центрированную скользящую среднюю и найти отношение к ней фактического отпуска тепловой энергии в сеть. По полученным значениям нужно выполнить их группировку по месяцам, а затем рассчитать средний арифметический индекс сезонности и медиану за каждый месяц. Для определения индексов сезонности используются значения медианы, умноженные на поправочный коэффициент. В результате рассчитаны следующие индексы сезонности Index:
| Январь .........................................................1.96 |
| Февраль .......................................................1.85 |
| Март .............................................................1.61 |
| Апрель ..........................................................1.15 |
| Май .............................................................0.33 |
| Июнь ...........................................................0.18 |
| Июль ............................................................0.16 |
| Август ...........................................................0.17 |
| Сентябрь .....................................................0.26 |
| Октябрь .......................................................1.07 |
| Ноябрь .........................................................1.45 |
| Декабрь ........................................................1.78 |
Сумма индексов сезонности равна 11.98, или приближенно 12.
Чтобы получить модель тренда, необходимо исключить из данных сезонную составляющую, в нашем случае данные для модели тренда определяются путем деления фактического отпуска тепловой энергии в сеть на индекс сезонности. Затем тренд можно представить в виде приведенных далее моделей.
1. Простейшей однофакторной моделью является линейный тренд LM, приведенный в [15], коэффициенты которого ${{a}_{0}},$ ${{a}_{1}}$ находятся методом наименьших квадратов:
где T1 – тренд, определенный по этой модели, ГДж; i – номер измерения; τi – время i-го измерения, мес.2. Регрессионная модель без явного времени в формуле – авторегрессионная модель AR (от а-нгл. AutoRegressive), в данном случае выбрана модель второго порядка (AR2) [16]:
(4)
${{T}_{{\text{2}}}}\left( {{{{\tau }}_{i}}} \right) = {{a}_{0}} + {{a}_{1}}{{T}_{{\text{2}}}}\left( {{{{\tau }}_{{i - 1}}}} \right) + {{a}_{2}}{{T}_{{\text{2}}}}\left( {{{{\tau }}_{{i - 2}}}} \right),$3. Авторегрессионная модель с внешним фактором ARX (от англ. AutoRegressive with eXternal input), которая дополнительно учитывает изменение факторов (в данном случае выбрана среднемесячная температура наружного воздуха), влияющих на зависимый параметр:
(5)
${{T}_{{\text{3}}}}\left( {{{{\tau }}_{i}}} \right) = {{a}_{0}} + {{a}_{1}}{{T}_{{\text{3}}}}\left( {{{{\tau }}_{{i - 1}}}} \right) + {{a}_{2}}{{T}_{{\text{3}}}}\left( {{{{\tau }}_{{i - 2}}}} \right) + {{a}_{3}}{{\Theta }_{{{\text{см}}}}}\left( {{{{\tau }}_{i}}} \right),$С помощью функций Matlab выполнена идентификация параметров моделей (3)–(5). Рассчитанные коэффициенты приведены в табл. 2.
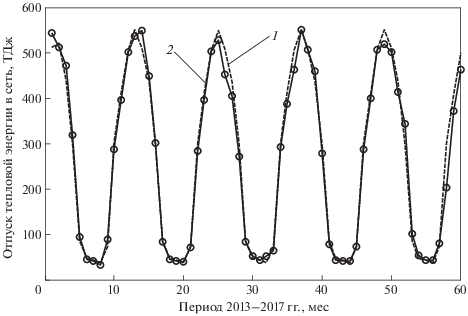
На рис. 1 представлен график для применения в качестве тренда авторегрессионной модели второго порядка AR2.
Рис. 1.
Мультипликативная модель в виде произведения тренда (T2) и индексов сезонности (Index). 1 – модель T2 × Index; 2 – исходные данные
Для анализа качества полученных моделей следует выбрать коэффициент детерминации и среднюю относительную погрешность.
Средняя относительная погрешность ξ рассчитывается по формуле
(6)
$\xi = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{{Q}_{{{\text{о}}{\text{.с}}i}}} - {{{\hat {Q}}}_{{{\text{о}}{\text{.с}}i}}}} \right|}}{{{{Q}_{{{\text{о}}{\text{.с}}i}}}}}} \times 100\% ,$Критерием адекватности моделей служит коэффициент детерминации R2:
(7)
${{R}^{2}} = 1 - \frac{{\sum\limits_{i = 1}^n {{{{\left( {{{Q}_{{{\text{о}}{\text{.с}}i}}} - {{{\hat {Q}}}_{{{\text{о}}{\text{.с}}i}}}} \right)}}^{2}}} }}{{\sum\limits_{i = 1}^n {{{{\left( {{{Q}_{{{\text{о}}{\text{.с}}i}}} - {{{\bar {Q}}}_{{{\text{о}}{\text{.с}}}}}} \right)}}^{2}}} }},$Полученные значения средней относительной погрешности и коэффициента детерминации для каждой модели временного ряда с трендом в виде однофакторной регрессионной модели, авторегрессионной модели и авторегрессионной модели с внешним фактором представлены в табл. 3.
Аддитивная модель с выявлением тренда и сезонной компонентой в виде периодической функции (ряда Фурье или суммы синусов)
Можно представить структуру модели в виде тренда и сезонной компоненты, определенной рядом Фурье или суммой синусов:
(8)
$\begin{gathered} {{F}_{1}}\left( {\tau } \right) = {{b}_{0}} + {{b}_{1}}\cos \left( {\omega {\tau }} \right) + {{c}_{1}}\sin \left( {\omega {\tau }} \right) + \\ + \,\,{{b}_{2}}\cos \left( {{\text{2}}\omega {\tau }} \right) + {{c}_{2}}\sin \left( {{\text{2}}\omega {\tau }} \right) + {{b}_{3}}\cos \left( {{\text{3}}\omega {\tau }} \right) + \\ + \,\,{{c}_{3}}\sin \left( {{\text{3}}\omega {\tau }} \right) + {{b}_{4}}\cos \left( {{\text{4}}\omega {\tau }} \right) + {{c}_{4}}\sin \left( {{\text{4}}\omega {\tau }} \right); \\ \end{gathered} $(9)
$\begin{gathered} {{F}_{2}}\left( {\tau } \right) = {{b}_{1}}\sin \left( {{{\omega }_{1}}{\tau } + {{d}_{1}}} \right) + {{b}_{2}}\sin \left( {{{\omega }_{2}}{\tau } + {{d}_{2}}} \right) + \\ + \,\,{{b}_{3}}\sin \left( {{{\omega }_{3}}{\tau } + {{d}_{3}}} \right) + {{b}_{4}}\sin \left( {{{\omega }_{4}}{\tau } + {{d}_{4}}} \right), \\ \end{gathered} $Результаты расчетов коэффициентов в формулах (8), (9) представлены в табл. 4.
Таблица 4.
Коэффициенты моделей сезонной компоненты по формулам (8) и (9)
| Коэффициент | Ряд Фурье по (8) | Сумма синусов по (9) |
|---|---|---|
| b0 | 9132 | – |
| b1 | 1454 | 289 |
| b2 | 8798 | 6284 |
| b3 | –1116 | 7338 |
| b4 | 2832 | 1446 |
| c1 | –8548 | – |
| c2 | –1732 | – |
| c3 | –2359 | – |
| c4 | 41156 | – |
| ω | 0.13 | – |
| ω1 | – | 0.78 |
| ω2 | – | 0.52 |
| ω3 | – | 1.56 |
| ω4 | – | 0.13 |
| d1 | – | –3.58 |
| d2 | – | –5.24 |
| d3 | – | 3.18 |
| d4 | – | –0.71 |
Аддитивную модель временного ряда можно записать в виде суммы тренда и периодической функции с учетом остатков:
Для определения коэффициентов моделей трендовой и сезонной составляющих применялась функция regress в программной среде Matlab. Остатки ε (случайная составляющая) нормально распределены и неавтокоррелированы. Результаты расчета показателей качества по формулам (6) и (7) полученных моделей вида (2), (10) занесены в табл. 3.
Модель Хольта–Винтерса (Holt’s–Winters’)
Модель Хольта–Винтерса является моделью трехпараметрического экспоненциального сглаживания и, соответственно, характеризуется тремя параметрами: κ, λ, γ. Настроечные параметры необходимо определять перед прогнозированием в диапазоне от 0 до 1.
Мультипликативная модель для прогнозирования имеет следующий вид [17]:
значение тренда Tt оценивается как
коэффициент сезонности для текущего периода St находится по формуле
Для выбора параметров κ, λ, γ по критерию минимума суммы квадратов отклонений применялась функция Matlab fminsearch [18, 19].
Мультипликативная модель SARIMA
Мультипликативная сезонная авторегрессионная модель проинтегрированного скользящего среднего SARIMA является развитием обычной модели ARIMA при условии, что ряды содержат сезонную компоненту. Полная сезонная модель может быть записана следующим образом [20]:
Здесь p – параметр авторегрессии; D – порядок обычной разности; q – параметр скользящего среднего; ps – сезонная авторегрессия; ds – порядок сезонной разности; qs – сезонное скользящее среднее.
Формула мультипликативной модели SARIMA имеет следующий вид:
где ${\varphi }\left( {LS} \right) = 1 - \sum\nolimits_{k = 1}^{ps} {{{{\varphi }}_{k}}L{{S}^{k}}} $ – оператор сезонной авторегрессии; k – порядок модели; LS – сезонный лаг; $\Phi \left( L \right) = 1 - \sum\nolimits_{k = 1}^p {{{\Phi }_{k}}{{L}^{k}}} $ – оператор авторегрессии; L – лаг; ${{\Delta }^{{ds}}} = {{\left( {1 - L} \right)}^{{ds}}};$ ${{\Delta }^{D}} = {{\left( {1 - L} \right)}^{D}};$ Δ – разность; α – константа (в данном случае α = 0);${\psi }\left( {LS} \right) = 1 + \sum\nolimits_{k = 1}^{qs} {{{{\psi }}_{k}}L{{S}^{k}}} $ – оператор сезонного скользящего среднего; $\Psi \left( L \right) = 1 + \sum\nolimits_{k = 1}^q {{{\Psi }_{k}}{{L}^{k}}} $ – оператор скользящего среднего.
К ряду может применяться обычное, сезонное или комбинированное дифференцирование (нахождение разности). При явно выраженной сезонной составляющей сначала определяют сезонную разность первого порядка $Q_{{{\text{о}}{\text{.с}}t}}^{'},$ представляющую собой переход к попарным разностям значений временного ряда в соседних сезонах (в рассматриваемом случае s = 12):
(13)
$Q_{{{\text{о}}{\text{.с}}t}}^{'} = {{Q}_{{{\text{о}}{\text{.с}}t}}} - {{Q}_{{{\text{о}}{\text{.с(}}t - s)}}}.$Инструментами идентификации порядка модели являются автокорреляционная функция (ACF) и частная автокорреляционная функция (PACF).
В общем случае построение модели SARIMA для прогнозирования теплопотребления состоит из следующих шагов:
временной ряд Qо.с сводится к стационарному путем определения сезонной разности по формуле (13) и/или обычной разности;
по виду функций ACF и PACF определяют порядок авторегрессии и скользящего среднего модели вида (11);
вычисляют значения параметров модели и оценивают ее качество;
возвращаются от разности к исходному ряду;
составляют прогноз на определенный период с использованием формулы (12).
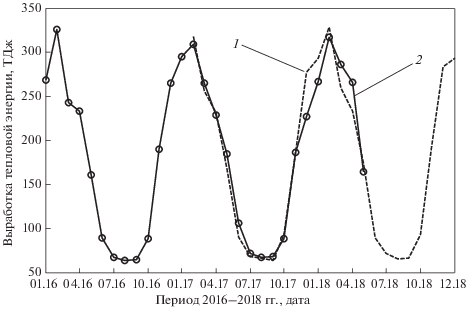
Модель SARIMA строится по 48 наблюдениям за 4 года (см. рис. 1). Остальные 12 значений (за один год) затем используются для проверки качества прогнозирования с помощью полученной модели.
Для идентификации SARIMA следует определить сезонную разность ряда первого порядка и обычную разность первого порядка, затем рассмотреть автокорреляционные и частные автокорреляционные функции.
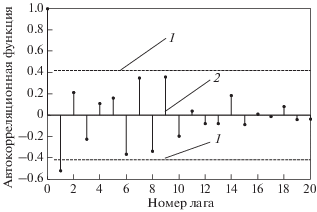
Как видно на рис. 2, коэффициент автокорреляции первого порядка отрицательный и существенно отличается от нуля. После лага 1 значение автокорреляционной функции убывает. По автокоррелограмме ACF можно предположить, что модель содержит один параметр скользящего среднего (q = 1). Коррелограмма PACF имеет резко выделяющееся значение для лага 1, затем убывает. Далее принимается один параметр авторегреcсии (p = 1). Таким образом, была подобрана модель вида (11): SARIMA(1, 1, 1)(1, 1, 2). С помощью функций Matlab вида
Рис. 2.
Автокоррелограмма первых разностей ACF. 1 – граничное значение; 2 – автокорреляционная функция
model1=arima('ARLags', 1, 'MALags', 1, 'D', 1, 'SARLags', 1, 'SMALags', [1, 2], 'Seasonality', 12, 'Constant', 0)
и других определяются параметры мультипликативной модели по формуле (12):
Constant: 0
AR: {–0.798136} at Lags [1]
SAR: {–0.798136} at Lags [1]
MA: {0.830406} at Lags [1]
SMA: {–0.238645 –0.718728} at Lags [1, 2]
Seasonality: 12
Далее рассматривается возможность прогнозирования отпуска тепловой энергии с использованием полученных ранее моделей временного ряда на следующие периоды, а именно на 2017 г. Данные, не включенные в модель (12 значений), можно использовать для проверки точности прогноза. На рис. 3 приведен пример полученного постпрогноза по модели SARIMA.
Качество прогнозирования оценивалось по средней относительной погрешности (6). Полученные результаты занесены в табл. 3.
Модель SSA
Для сравнения с уже рассмотренными параметрическими моделями по тем же исходным данным сайта [14] можно применить непараметрическую модель SSA для прогнозирования отпуска тепловой энергии. В основе этого метода – разложение временнόго ряда на интерпретируемые аддитивные составляющие. При этом не требуются стационарность ряда, знание модели тренда, а также сведения о наличии в ряду периодических составляющих и их периодах [21]. Средняя относительная погрешность прогнозирования по моделям на один год, %:
| SSA ...............................................................9.61 |
| T2 × Index .....................................................8.83 |
| Holt’s–Winters’ ...........................................11.83 |
| SARIMA .......................................................6.52 |
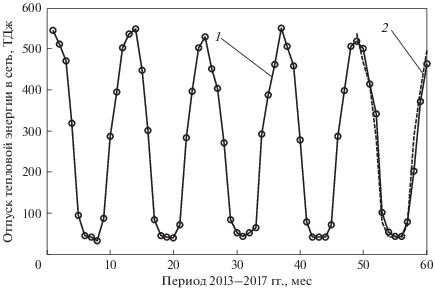
Для проверки возможности построения перечисленных моделей по другим подобным данным и прогнозирования были использованы статистические показатели по выработке тепловой энергии, доступные на официальном сайте Министерства энергетики России [22], за 2013–2018 гг. По значениям выработки за 2013–2016 гг. была получена математическая модель SARIMA. Затем с помощью этой модели выполнен прогноз на 2017–2018 гг. (рис. 4). Сплошной линией показаны экспериментальные данные, пунктирной – прогноз. Период с января 2017 г. по апрель 2018 г. (01.17–04.18) соответствует постпрогнозу, средняя относительная погрешность которого составляет 6.87%.
РЕЗУЛЬТАТЫ РАСЧЕТОВ
Из табл. 3 видно, что наименьшее значение средней относительной погрешности для мультипликативных моделей с расчетом индекса сезонности получено для модели с трендом в виде авторегрессионной модели (T2 × Index). При применении мультипликативной модели с расчетом индексов сезонности для прогнозирования необходимы данные за значительный промежуток времени. Аддитивные модели с сезонной составляющей в виде ряда Фурье и суммой синусов аппроксимируют исходные данные менее точно.
При использовании авторегрессионной модели с внешним фактором в качестве входного параметра учитывается температура наружного воздуха, прогноз которой сложно выполнить. Кроме этого, отпуск тепловой энергии зависит от множества других внутренних и внешних факторов: теплопотребления зданий, определяемого состоянием внутренних инженерных систем и наружных ограждающих конструкций; материала труб, тепловой изоляции, протяженности магистральных сетей, ветровой нагрузки и др.
При применении непараметрической модели SSA отсутствует возможность проверять гипотезы о наличии в ряду той или иной составляющей.
Модель тройного экспоненциального сглаживания Хольта–Винтерса позволяет получать прогноз на несколько периодов. Однако выявлено низкое качество прогнозирования на пиках.
Как видно по результатам расчета средней относительной погрешности прогнозирования по моделям на 1 год и по рис. 4, наиболее подходящей моделью для прогнозирования временных рядов отпуска и выработки тепловой энергии по критерию средней относительной погрешности является мультипликативная сезонная модель SARIMA.
ВЫВОДЫ
1. Исследование, проведенное на математических моделях временнόго ряда выработки и отпуска тепловой энергии за 5 лет, показывает, что лучшими качествами прогнозирования обладает мультипликативная сезонная модель SARIMA.
2. Полученная модель может применяться энергетическими предприятиями, например, при реконструкции и планировании развития систем теплоснабжения. Модель может пригодиться также при составлении существующих и перспективных балансов тепловой энергии (мощности), для получения которых используется архивная информация в Excel.
3. Из-за строительства новых зданий или сноса старых может меняться суммарная площадь помещений, что ведет к изменению объемов отпуска и потребления тепловой энергии. Поэтому в дальнейшем предполагается проводить построение мультипликативной модели с учетом внешних факторов SARIMAX. В качестве таких факторов выступают площадь зданий и перечисленные в работе технологические параметры.
4. Предложенная модель может быть применима также в составе методик по определению оптимальной мощности источников теплоснабжения и распределения тепловой энергии. Например, при строительстве новых зданий можно принять решение, нагрузить ли действующие районные котельные или необходима новая котельная определенной мощности.
Список литературы
Мишин М.А. Тепловой режим жилых зданий // Ползуновский вестник. 2011. № 1. С. 104–115.
Hybrid of ARIMA and SVMs for short-term load forecasting / H. Nie, G. Liu, X. Liu, Y. Wang // Energy Procedia. 2012. V. 16. Part C. P. 1455–1460. https://doi.org/10.1016/j.egypro.2012.01.229
Чипулис В.П., Кузнецов Р.С. Анализ эффективности регулирования теплопотребления с использованием регрессионных моделей объектов теплоэнергетики // XII Всерос. совещание по проблемам управления ВСППУ-2014, 16–19 июня 2014 г. М.: ИПУ РАН, 2014. С. 7529–7539.
Тугашова Л.Г. Моделирование температурного режима системы теплоснабжения зданий: докл. на шестой Всерос. науч.-практ. конф. Березники, 14 октября 2017 г. // Решение. 2017. Т. 1. С. 338–340. [Пермь: ПНИПУ.]
Box George E.P., Jenkins Gwilym M., Reinsel Gregory C. Time series analysis: forecasting and control. 3rd ed. Prentice-Hall, 1994.
Golyandina N., Nekrutkin V., Zhigljavsky A. Analysis of time series structure: SSA and related techniques. N.Y.: Chapman and Hall/CRC, 2001.
Shayeghi H., Shayanfar H.A., Azimi G. STLF based on optimized neural network using PSO // Int. J. Computer and Inform. Eng. 2009. V. 3. № 4 (10). P. 1190–1200. https://doi.org/10.5281/zenodo.1083811
Yufei S., Chuanwen J. Power system short-term load forecasting based on PSO clustering analysis and Elman neural network // Proc. of the 5th WSEAS Intern. Conf. on Simulation, Modelling and Optimization. Corfu, Greece, 17–19 Aug. 2005. P. 268–273.
Sarhani M., El Afia A. Electric load forecasting using hybrid machine learning approach incorporating feature selection // Proc. of the Intern. Conf. on Big Data Cloud and Applications. Tetuan, Morocco, 25–26 May 2015. P. 1–7. Corpus ID: 10991809
ARIMA model, neural networks and SSA in the short term electric load forecast / K. Cassiano, M. Menezes, L.A. Junior, J. Pessanha, Raf. Souza, R. Souza // Economic Forecasting – Past, Present and Future: Intern. Symp. of Forecasting ISF. Rotterdam, 2014. P. 1–23.
An ensemble model based on machine learning methods and data preprocessing for short-term electric load forecasting / Y. Lin, H. Luo, D. Wang, H. Guo, K. Zhu // Energies. 2017. V. 10. Is. 8. P. 1186. https://doi.org/10.3390/en10081186
Методика выбора оптимальной мощности теплоисточников при реконструкции централизованных систем теплоснабжения / Е.А. Бузоверов, О.Н. Махов, М.В. Исаев, И.Д. Чернов // Вестник ИГЭУ. 2017. Вып. 3. С. 20–29. https://doi.org/10.17588/2072-2672.2017.3.020-029
Папушкин В.Н., Григорьев А.С., Полянцев С.О. Прогнозирование спроса на тепловую мощность в схемах теплоснабжения // Новости теплоснабжения. 2014. № 8. С. 8–17. https://www.rosteplo.ru/Tech_stat/ stat_shablon.php?id=2916
http://apts.tatneft.ru
Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование. М.: Финансы и статистика, 2001.
Ефимова М.Р. Статистика. М.: ИНФРА-М, 2006.
Поздняков А.С. Применение метода Хольта–Винтерса при анализе и прогнозировании динамики временных рядов // Проблемы организации и управления на транспорте: сб. науч. тр. (Материалы межвуз. науч.-практ. конф.) Екатеринбуг, 3 ноября 2016 г. Екатеринбург: УрГУПС, 2017. Вып. 11 (230). С. 57–64.
Затонский А.В., Тугашова Л.Г. Моделирование объектов управления в MatLAB: учеб. пособие. СПб.: Лань, 2019.
Тугашова Л.Г. Модели теплообменных процессов в Matlab // Уч. зап. Альметьев. гос. нефтяного ин-та. 2018. Т. 17. С. 191–195.
Hyndman R.J., Athanasopoulos G. Forecasting: principles and practice. Seasonal ARIMA models, 2018. [Электрон. ресурс.] Режим доступа: https://otexts.com/fpp2/
Голяндина Н.Э. Метод “Гусеница” – SSA: анализ временных рядов: учеб. пособие. СПб.: СПбГУ, 2004.
https://minenergo.gov.ru/activity/statistic
Дополнительные материалы отсутствуют.
Инструменты
Теплоэнергетика