Прикладная математика и механика, 2021, T. 85, № 2, стр. 152-171

Введение. Термин “автоколебания” был введен Андроновым в начале XX в. для описания процесса, которому можно в математической модели сопоставить предельный цикл Пуанкаре автономной системы дифференциальных уравнений. Сначала рассматривался случай неконсервативной системы второго порядка. При введении понятия автоколебаний Андронов предложил идею метода отыскания циклов, отвечающих автоколебаниям [1]. Несколько позже эта идея была формализована Понтрягиным [2]. Предложенный подход тесно связан с методом Крылова–Боголюбова, уступая последнему по высоте размерности систем, к которым он применим, но являясь более удобным для систем второго порядка. Так, критерий Андронова–Понтрягина активно развивается и применяется в современных исследованиях динамических систем на плоскости [3–11], в том числе при решении задач, родственных 16-й проблеме Гильберта [12, 13].

Как и метод усреднения Крылова–Боголюбова, критерий Андронова–Понтрягина предполагает наличие в системе малого параметра. Однако для обоих подходов развиты модификации, предполагающие итерационную процедуру и позволяющие снять требование присутствия малого параметра: [14, 15] – для первого, [16–18] – для второго. Скорость сходимости и сам факт сходимости указанных итерационных методов зависят от константы Липшица функции, описывающей негамильтоновы слагаемые в системе.

Понятие автоколебаний естественным образом распространяется на случай механической системы с двумя степенями свободы, описываемой автономной неконсервативной динамической системой четвертого порядка. Но в такой системе автоколебаниям (самоподдерживающимся колебаниям) может соответствовать как предельный цикл, так и аттрактор более сложной структуры, например, квазипериодическая траектория.

По сравнению со случаем одной степени свободы методы исследования автоколебаний для систем с двумя и более обобщенными координатами значительно усложняются. Среди них можно выделить подходы, основанные на прямом интегрировании динамических уравнений, проекционные методы, методы на основе усреднения и др. Краткий обзор алгоритмов поиска периодических решений приведен в [18], для случая квазипериодических решений – в [19], из наиболее новых методов можно отметить [20–24]. Реализация методов, предназначенных для описания квазипериодических решений, требует, как правило, весьма сложных вычислительных алгоритмов.

В данной работе предложен численно-аналитический метод поиска (формирования) автоколебаний, относительно простой в реализации и не требующий дополнительных замен переменных. Подход основан на рассмотрении двух вспомогательных систем второго порядка и применении к каждой из них метода [17], основанного на критерии Андронова–Понтрягина. При этом алгоритм позволяет выявить автоколебания (сформировать, если предполагается наличие управляющего параметра), которым отвечают аттракторы, не являющиеся периодическими траекториями. Однако периодические траектории системы предложенный метод, как правило, не обнаруживает, поскольку не учитывает эффекты, связанные с синхронизацией. Отметим, что известен ряд подходов для формирования периодических автоколебаний определенных классов систем с двумя и более степенями свободы (например, подход [25]).

Ранее [26, 27] предложен метод построения близких к периодическим (но не периодических) траекторий, предназначенный для формирования асинхронных режимов авторотации механической системы с двумя вращательными степенями свободы. При этом был рассмотрен класс систем более узкий, чем в данной работе: в [26, 27] перевязки между подсистемами зависят только от фазовых скоростей, но не от координат, причем в [27] эта зависимость предполагается линейной. В настоящей работе перевязки между подсистемами зависят и от фазовых координат, и от фазовых скоростей (в общем случае нелинейно). Соответственно усложняется метод построения близкого к периодическому решения (метод [26] существенно опирается на отсутствие перевязки по координатам, а подход [27] помимо этого принципиально использует линейный характер перевязок по скоростям). Дополнительное техническое усложнение в настоящей работе связано с тем, что рассматриваются решения, соответствующие не только авторотациям, но и автоколебаниям.

Эффективность алгоритма, предложенного далее, проиллюстрируем на примере задачи о формировании автоколебаний аэродинамического маятника. Определим коэффициенты в законе управления, при которых существует близкая к периодической траектория, отвечающая колебаниям с заданной амплитудой.

1. Постановка задачи. Рассмотрим автономную неконсервативную механическую систему с двумя степенями свободы. Пусть в безразмерных переменных уравнения движения системы имеют следующий вид (точкой обозначена производная по безразмерному времени $\tau $):

Будем рассматривать управление вида

Здесь ${{\varphi }_{i}}$ – обобщенные координаты, ${{\omega }_{i}}$ – соответствующие обобщенные скорости. Здесь и далее $i = 1,2$. Функции ${{F}_{{ik}}}$ определяются на основе выражения для механической энергии системы, а также внешних сил и моментов, в том числе неконсервативных; при этом функции ${{G}_{{ik}}}$ описывают взаимодействие в системе; ${{u}_{i}}$ – компоненты управления; ${{b}_{i}}$ – коэффициенты усиления управляющего воздействия, которые подлежат выбору в соответствии с задачей управления. Функции ${{f}_{i}}$ отвечают за управляющее воздействие, направленное на изменение поведения переменных ${{\varphi }_{i}}$, ${{\omega }_{i}}$. Функция ${{g}_{2}}$ описывает опосредованное влияние управляющего воздействия по ${{\varphi }_{2}}$, ${{\omega }_{2}}$ на изменение переменных ${{\varphi }_{1}}$, ${{\omega }_{1}}$, и аналогичную роль выполняет функция ${{g}_{1}}$.

Функции ${{f}_{i}}$ выбираем так, чтобы было выполнено следующее свойство: ${{\omega }_{i}}{{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}}) > 0$ при ${{\omega }_{i}} \ne 0$ (например, ${{f}_{i}} = {{\omega }_{i}}$). Все функции в (1.1) предполагаются аналитическими.

Пусть требуется посредством управления организовать в механической системе, описываемой уравнениями (1.1), режим асинхронных автоколебаний, таких, что амплитуда колебаний по каждой переменной ${{\varphi }_{i}}$ остается вблизи некоторых заданных значений $\varphi _{i}^{ * }$, и средние по времени (на большом отрезке времени) частоты колебаний по двум переменным несоизмеримы (не происходит синхронизации). Отметим, что асинхронные колебания представляют интерес для ряда прикладных задач [28, 29].

Будем считать, что правые части системы (1.1) зависят от координат ${{\varphi }_{i}}$ $2\pi $-периодически. Наряду с уже поставленной задачей далее рассмотрим две весьма близкие задачи: формирование режима, при котором по обеим координатам происходят ротации с близкими к постоянным угловыми скоростями $\omega _{i}^{ * }$ несоизмеримыми друг с другом; формирование режима, при котором по одной из координат происходят колебания с амплитудой близкой к заданной, а по другой координате – ротация с угловой скоростью близкой к заданной.

2. Частично усредненные системы. Построим две вспомогательные “частично усредненные” системы второго порядка с неопределенными параметрами:

Здесь $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ – неизвестные параметры, которые подлежат определению, их вычисление проводится методом последовательных приближений, верхний индекс j ($j \geqslant 0$) соответствует номеру итерационного шага.

Коэффициент $b_{i}^{j}$ в системе (2.i) отвечает за поворот векторного поля (в силу указанного выше свойства функции ${{f}_{i}}$: ${{\omega }_{i}}{{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}}) > 0$). Этот коэффициент усиления управляющего воздействия требуется выбрать таким образом, чтобы в системе (2.i) существовал предельный цикл, проходящий через точку ($ - \varphi _{i}^{ * }$, $0$). Далее обозначим такой цикл ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$). Предполагаем, что искомое значение $b_{i}^{j}$ существует. Для отыскания величины $b_{i}^{j}$ могут быть применены различные методы формирования/поиска периодических траекторий, обзор приведен, например, в [18]. При необходимости локализацию областей существования предельных циклов можно провести при помощи таких методов, как [30, 31]. В данной работе для определения значений $b_{i}^{j}$ будем использовать метод [16] для случая, если система обладает центральной симметрией, [17] для системы, не обладающей центральной симметрией, либо [18] для случая, если по какой-либо координате происходит авторотация, а не автоколебания. Все перечисленные случаи проиллюстрированы далее на примере задачи об аэродинамическом маятнике.

Параметры $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$ определяются следующим образом:

Здесь $T_{i}^{j}$ – период предельного цикла ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$) системы (2.i), построенного на j-м шаге. Для применения алгоритма удобно использовать при вычислении $\bar {G}_{{ik}}^{j}$ формулы, исключающие зависимость от времени, и то же самое относится к вычислению значений $\bar {g}_{i}^{j}$:

Здесь $\varphi _{i}^{ - } = \varphi _{i}^{ * }$. Точка ($\varphi _{i}^{ + }$, $0$) – самая правая точка периодической траектории ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$) на фазовой плоскости (${{\varphi }_{i}}$, ${{\omega }_{i}}$); $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ – функция, описывающая зависимость ${{\omega }_{i}}$ от ${{\varphi }_{i}}$ вдоль верхней/нижней части предельного цикла ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$), соответственно (т.е. в верхней/нижней полуплоскости); $\omega _{i}^{{j \pm }}(\varphi _{i}^{ + })$ = $\omega _{i}^{{j \pm }}(\varphi _{i}^{ - })$ = 0. Для случая периодической траектории $\omega _{i}^{j}(\varphi )$, отвечающей авторотации по угловой координате, справедливы аналогичные по смыслу формулы; тогда $\omega _{i}^{j}({{\varphi }_{i}})$ – $2\pi $-периодическая функция ${{\varphi }_{i}}$, и, поскольку такая траектория целиком расположена в верхней/нижней части фазового цилиндра, для нее индекс $ \pm $ не требуется:

Предложенный алгоритм позволяет не вычислять явную зависимость переменных от времени на предельном цикле, достаточно определить зависимость ${{\omega }_{i}}$ от координаты ${{\varphi }_{i}}$ вдоль верхней/нижней части цикла. Это радикально снижает объем необходимых вычислений при построении предельных циклов вспомогательных систем. В качестве примера можно сравнить описание предельных циклов возмущенного осциллятора Дуффинга, раскрывающее [32] и не раскрывающее [11] зависимость от времени: во втором случае объем вычислений сокращается многократно.

Итак, на j-м шаге алгоритма с учетом предыдущего шага строится периодическая траектория системы (2.1), проходящая через точку ($ - \varphi _{1}^{ * }$, $0$), как двузначная функция $\omega _{1}^{{j \pm }}({{\varphi }_{1}})$ от координаты. Определяется соответствующее значение $b_{1}^{j}$, обеспечивающее существование такой траектории. Вдоль этой траектории вычисляются средние по времени за период значения $\bar {G}_{{1k}}^{j}$, $\bar {g}_{1}^{j}$ функций $G_{{1k}}^{{}}$, $g_{1}^{{}}$. Эти значения подставляются в правую часть системы (2.2), после чего аналогично выполняется  j-й шаг алгоритма для системы (2.2). Средние значения $\bar {G}_{{2k}}^{{j + 1}}$, $\bar {g}_{2}^{{j + 1}}$ функций ${{G}_{{2k}}}$, ${{g}_{2}}$, полученные на  j-м шаге, используются для $(j + 1)$-го шага в системе (2.1) и т.д., пока для каждого i разница между значениями $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ полученными на j-м и $(j + 1)$-м шагах не станет меньше некоторого заданного порогового значения (критерий практической сходимости алгоритма).

Далее при обсуждении свойств притяжения решений для краткости будем использовать обозначение $db_{i}^{j}{\text{/}}d\varphi _{i}^{ * }$ = ${{\left. {db_{i}^{j}{\text{/}}d\varphi _{i}^{0}} \right|}_{{\varphi _{i}^{0} = \varphi _{i}^{ * }}}}$, где $b_{i}^{j}\left( {\varphi _{i}^{0}} \right)$ – значение $b_{i}^{j}$, обеспечивающее наличие $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ предельного цикла, проходящего через точку ($ - \varphi _{i}^{0}$, $0$). В соответствии со свойствами поворота векторного поля при $db_{i}^{j}{\text{/}}d\varphi _{i}^{ * }$ < 0 предельный цикл $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ орбитально устойчив. Для случая траектории $2\pi $-периодической по ${{\varphi }_{i}}$ справедливо аналогичное утверждение при $db_{i}^{j}{\text{/}}d\omega _{i}^{ * }$ < 0. Соответствующие теоремы подробно обсуждаются в [16–18].

Пусть при численной реализации метода значения $b_{i}^{j}$ на каждом  j-м шаге определены и последовательности $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ сходятся к некоторым предельным значениям при $j \to \infty $. Если при этом, начиная с некоторого j, выполнено $db_{i}^{j}{\text{/}}d\varphi _{i}^{ * }$ < 0, то при достаточно слабых перевязках между подсистемами можно ожидать, что в системе (1.1) при ${{b}_{i}}$ = $b_{i}^{ * }$ = $\mathop {\lim }\limits_{j \to \infty } b_{i}^{j}$ существует притягивающее близкое к периодическому решение, отвечающее автоколебаниям по координатам ${{\varphi }_{i}}$ с амплитудами близкими к $\varphi _{i}^{ * }$. Для случая, когда по какой-либо координате рассматривается ротация и $db_{i}^{j}{\text{/}}d\omega _{i}^{ * }$ < 0, имеет место аналогичное утверждение.

Если указанная гипотеза подтверждается, то проекции близкой к периодической траектории системы (1.1) на плоскости (${{\varphi }_{i}}$, ${{\omega }_{i}}$) приближенно описываются кривыми $\omega _{i}^{ \pm }({{\varphi }_{i}})$, которые представляют собой периодические траектории, существующие в системах (2.i) при предельных значениях $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{ * }$ параметров. В силу непрерывной зависимости траекторий от параметров функции $\omega _{i}^{ \pm }({{\varphi }_{i}})$ определены и являются пределами функциональных последовательностей $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ при $j \to \infty $. Эти функции вычисляются наряду со значениями $b_{i}^{ * }$ в ходе применения алгоритма.

Сформулируем достаточные условия формирования асинхронных колебаний при конечных перевязках между переменными в системе (1.1).

Теорема 1. Пусть для каждого $j \geqslant 0$ определены периодические траектории $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ и соответствующие значения $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ в системах (2.i). Пусть все эти последовательности при $j \to \infty $ сходятся к некоторым пределам $\omega _{i}^{ \pm }({{\varphi }_{i}})$, $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{{\text{*}}}$, причем $\omega _{i}^{ \pm }({{\varphi }_{i}})$ – притягивающий цикл системы (2.i) при $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{{\text{*}}}$. Пусть помимо этого существуют области ${{\Omega }_{i}}$ на плоскостях (${{\varphi }_{i}}$, ${{\omega }_{i}}$), содержащие кривые $\omega _{i}^{ \pm }({{\varphi }_{i}})$, и такие, что при $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ значения правой части 2i-го уравнения системы (1.1) отличаются от значений, которые принимает правая часть второго уравнения системы (2.i) при $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{*}$, на величину ${{\Gamma }_{i}}$, ограниченную по модулю некоторой константой ${{A}_{i}}$. Пусть в областях ${{\Omega }_{i}}$ существуют вспомогательные кривые $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$, определение которых приведено в тексте доказательства. Тогда в системе (1.1) существует аттрактор, проекция которого на плоскость (${{\varphi }_{i}}$, ${{\omega }_{i}}$) расположена внутри полосы, ограниченной кривыми $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ (т.е. проекции аттрактора расположены в окрестности кривых $\omega _{i}^{ \pm }({{\varphi }_{i}})$).

Доказательство. При $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ первые два уравнения системы (1.1) принимают вид:

Формально рассмотрим в пространстве произвольных значений ${{\varphi }_{1}}$, ${{\omega }_{1}}$ неавтономную систему, про которую известно, что $\left| {{{U}_{1}}(t)} \right| \leqslant {{A}_{1}}$:

Для каждой траектории системы (1.1) существует такая функция ${{U}_{1}}$, $\left| {{{U}_{1}}(t)} \right| \leqslant {{A}_{1}}$, что при $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ проекция этой траектории системы (1.1) на плоскость (${{\varphi }_{1}}$, ${{\omega }_{1}}$) совпадает с некоторой траекторией системы (2.3).

Функцию ${{U}_{1}}$ в системе (2.3) можно рассматривать как управление и поставить задачу выбора управления ${{U}_{1}}$, максимально отдаляющего решение от кривой $\omega _{1}^{ \pm }({{\varphi }_{1}})$, т.е. смоделировать “наихудшие” возможные возмущения, вызванные перевязками.

Рассмотрим случай ${{U}_{1}} = {{A}_{1}}{\kern 1pt} {\text{sgn}}{\kern 1pt} {{\omega }_{1}}$. При таком выборе ${{U}_{1}}$ система (2.3) автономна, и функция ${{U}_{1}}$ в этой системе обеспечивает поворот векторного поля системы на положительный угол, при таком повороте векторного поля системы на плоскости/цилиндре притягивающие предельные циклы расширяются, отталкивающие сужаются, и те, и другие могут разрушиться, например, сливаясь друг с другом [33].

При ${{U}_{1}} \equiv 0$ в системе (2.3) существует притягивающая периодическая траектория $\omega _{1}^{ \pm }({{\varphi }_{1}})$. Предположим, что эта периодическая траектория при переходе к системе (2.3) с ${{U}_{1}} = {{A}_{1}}\operatorname{sgn} {{\omega }_{1}}$ не разрушается, а, расширяясь, переходит в некоторый предельный цикл $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$, и что кривая $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ расположена в области ${{\Omega }_{1}}$.

Аналогично рассмотрим ${{U}_{1}} = - {{A}_{1}}\operatorname{sgn} {{\omega }_{1}}$. Такая функция обеспечивает поворот поля на отрицательный угол. Предположим, что периодическая траектория $\omega _{1}^{ \pm }({{\varphi }_{1}})$ при переходе к системе (2.3) с ${{U}_{1}} = - {{A}_{1}}\operatorname{sgn} {{\omega }_{1}}$ не разрушается, а, сужаясь, переходит в некоторую притягивающую траекторию $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$, и кривая $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ расположена в области ${{\Omega }_{1}}$.

Для построения циклов $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ можно использовать, например, метод [17].

Тогда, какой бы ни была функция ${{U}_{1}}$ при условии $\left| {{{U}_{1}}(t)} \right| \leqslant {{A}_{1}}$, траектория системы (2.3), начинающаяся в полосе, ограниченной кривыми $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$, никогда не покидает этой полосы. Если предположим противное, то в точке пересечения траектории системы (2.3) с какой-либо из границ полосы получим противоречие: с одной стороны, функции ${{U}_{1}} = \pm {{A}_{1}}\operatorname{sgn} {{\omega }_{1}}$ обеспечивают в системе (2.3) максимально/минимально возможное значение угла наклона касательной, с другой стороны, в точке пересечения траектории с границей полосы значение угла наклона касательной к траектории больше/меньше, чем угла наклона касательной к границе.

Проведем аналогичные рассуждения для ${{\varphi }_{2}}$, ${{\omega }_{2}}$. Предположим, что соответствующие кривые $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{2}^{ \pm }({{\varphi }_{2}})$ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{2}^{ \pm }({{\varphi }_{2}})$ существуют и расположены в ${{\Omega }_{2}}$.

В предложении существования при $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ кривых $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ получаем, что возмущения, вызванные ограниченными перевязками в системе (1.1), не разрушают близкое к периодическому решение, существующее при формальной замене функций, описывающих взаимовлияние, их средними значениями $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$. Это порождающее решение в полной системе переходит в некоторый аттрактор, проекция которого на плоскость (${{\varphi }_{i}}$, ${{\omega }_{i}}$) расположена внутри полосы, ограниченной кривыми $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$.

Теорема 1 доказана.

Для случая, когда в одной или двух из систем (2.i) периодическая траектория описывает ротации, а не колебания, можно ослабить условия теоремы, рассмотрев случай, когда верхняя и нижняя границы для функций Γ_i, описывающих перевязки, отличаются друг от друга.

Выбор управления ${{U}_{1}}$ максимально расширяющего/сужающего предельный цикл на плоскости, осуществлен по аналогии с подходом, предложенным в [34] и примененным для задачи о раскачивании качелей в [35].

Помимо этого отметим, что систему (2.3) можно рассматривать как систему с нестационарными возмущениями. Современные методы исследования управляемых систем с нестационарными возмущениями обсуждаются и применяются, например, в [36, 37]. В частности, в [36] развит подход, при котором усреднение применяется для построения первого приближения функции Ляпунова.

Проверка условий теоремы 1 нетривиальна, тем не менее, она требует работы только с системами второго порядка, но не четвертого. В случае выполнения достаточных условий локализуется область, внутри которой точно расположен аттрактор полной системы четвертого порядка. Этот аттрактор может иметь небольшую область притяжения, так что обнаружить его перебором начальных условий в четырехмерном пространстве может быть значительно сложнее, чем проверить выполнение условий теоремы 1.

В качестве примера, в котором реализуются условия теоремы 1, рассмотрим один из режимов асинхронной авторотации в системе с двумя степенями свободы, приближение для которого было найдено в статье [26] (методом, представляющим собой частный случай предложенного здесь алгоритма). Это режим авторотации в модели двойной ветротурбины Дарье. Динамические уравнения в форме системы вида (1.1) и значения параметров приведены в указанной работе. Режим характеризуется программными значениями безразмерных угловых скоростей $\omega _{1}^{ * }$ = $\omega _{2}^{ * }$ = 9.4. Для таких $\omega _{i}^{ * }$ определены $2\pi $-периодические по ${{\varphi }_{i}}$ траектории частично усредненных систем вида (2.i), а также определены соответствующие значения $b_{i}^{ * }$ ($b_{i}^{ * } \approx 0.11$). Для данных $\omega _{i}^{ * }$ условия теоремы 1 выполнены, например, при ${{\Omega }_{i}}$ = $\{ {\kern 1pt} |{\kern 1pt} {{\omega }_{i}} - \omega _{i}^{ * }{\kern 1pt} |$ < 0.01}.

В случае если перевязки между подсистемами уравнений (1.1) ограничены малой величиной, условия теоремы 1 можно ослабить. Приведем соответствующий результат.

Теорема 2. Пусть для каждого $j \geqslant 0$ определены периодические траектории $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ и соответствующие значения $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ в системах (2.i). Пусть все эти последовательности при $j \to \infty $ сходятся к некоторым пределам $\omega _{i}^{ \pm }({{\varphi }_{i}})$, $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{ * }$, причем $\omega _{i}^{ \pm }({{\varphi }_{i}})$ – притягивающий цикл системы (2.i) при $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{{\text{*}}}$. Пусть помимо этого существуют конечного размера области ${{\Omega }_{i}}$ на плоскостях (${{\varphi }_{i}}$, ${{\omega }_{i}}$), содержащие кривые $\omega _{i}^{ \pm }({{\varphi }_{i}})$, и такие, что при $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ значения правой части 2i-го уравнения системы (1.1) отличается от значений, которые принимает правая часть второго уравнения системы (2.i) при $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, $b_{i}^{*}$, на величину, ограниченную по модулю некоторым сколь угодно малым значением $\varepsilon $. Иными словами, перевязки в системе (1.1) малы, по крайне мере, если ${{\varphi }_{i}}$, ${{\omega }_{i}}$ принимают значения из конечных окрестностей кривых $\omega _{i}^{ \pm }({{\varphi }_{i}})$. Тогда в системе (1.1) существует некоторый аттрактор, проекция которого на плоскость (${{\varphi }_{i}}$, ${{\omega }_{i}}$) стремится к кривой $\omega _{i}^{ \pm }({{\varphi }_{i}})$ при $\varepsilon \to 0$.

Доказательство. Рассмотрим при $({{\varphi }_{1}},{{\omega }_{1}}) \in {{\Omega }_{1}}$ систему вида (2.3) с ${{U}_{1}} = \varepsilon \operatorname{sgn} {{\omega }_{1}}$. В случае $\varepsilon = 0$ эта система обладает притягивающим грубым циклом $\omega _{1}^{ \pm }({{\varphi }_{1}})$. При достаточно малом $\varepsilon > 0$ такой цикл не разрушится, а перейдет в притягивающий цикл $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$, расположенный вне области, ограниченной кривыми $\omega _{1}^{ \pm }({{\varphi }_{1}})$, (по свойству поворота векторного поля) и стягивающийся к $\omega _{1}^{ \pm }({{\varphi }_{1}})$ при $\varepsilon \to 0$. Аналогично при ${{U}_{1}} = - \varepsilon \operatorname{sgn} {{\omega }_{1}}$ в системе (2.3) существует притягивающий цикл $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$, расположенный внутри области, ограниченной кривыми $\omega _{1}^{ \pm }({{\varphi }_{1}})$, и стягивающийся к $\omega _{1}^{ \pm }({{\varphi }_{1}})$ при $\varepsilon \to 0$. При достаточно малом $\varepsilon $ оба цикла $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ лежат в конечной области ${{\Omega }_{1}}$.

Рассмотрим траекторию системы (1.1) с начальными условиями по (${{\varphi }_{i}}$, ${{\omega }_{i}}$), расположенными на кривой $\omega _{i}^{ \pm }({{\varphi }_{i}})$. Проекция этой траектории на плоскость (${{\varphi }_{1}}$, ${{\omega }_{1}}$) не может выйти из трубки, ограниченной кривыми $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$, пока $({{\varphi }_{2}},{{\omega }_{2}}) \in {{\Omega }_{2}}$, так как в точке пересечения с этой трубкой было бы нарушено условие $\left| {{{U}_{1}}(t)} \right| \leqslant \varepsilon $, что невозможно при $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$. Аналогичное свойство имеет место для проекции этой траектории на плоскость (${{\varphi }_{2}}$, ${{\omega }_{2}}$). Таким образом, рассмотренная траектория стремится к некоторому аттрактору, проекция которого на каждую из плоскостей (${{\varphi }_{i}}$, ${{\omega }_{i}}$) находится внутри трубки, ограниченной кривыми $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{{\varepsilon \pm }}({{\varphi }_{i}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{{\varepsilon \pm }}({{\varphi }_{i}})$, и стремится к кривой $\omega _{i}^{ \pm }({{\varphi }_{i}})$ при $\varepsilon \to 0$.

Теорема 2 доказана.

Для сравнения отметим, что в [38] свойство грубости решения использовано при доказательстве сохранения асинхронных колебаний при малых перевязках в системе четвертого порядка, характерной для моделей нейронных сетей. Возможно, на основании подобных рассуждений можно существенно усилить результат теоремы 2 (например, распространив его на близкие к периодическим траектории системы (1.1), которые не являются притягивающими ни в прямом, ни в обратном времени), но это выходит за рамки данной работы.

3. О численной проверке, вопросах устойчивости и области применимости алгоритма. В случае если условия теоремы 1 не выполнены, наличие в полной системе близкого к периодическому решения, порожденного периодическими траекториями частично усредненных систем, требует дополнительной проверки, например, путем прямого численного интегрирования системы (1.1) с начальными условиями, взятыми на предельных кривых $\omega _{i}^{ \pm }({{\varphi }_{i}})$ или в их окрестности (например, ${{\varphi }_{i}}(0)$ = $\varphi _{i}^{ * }$, ${{\omega }_{i}}(0) = 0$). Отметим, что возможна ситуация, когда в системе (1.1) траектория, близкая к периодической, проекции которой на фазовые плоскости расположены около построенных кривых $\omega _{i}^{ \pm }(\varphi )$, существует, но не является притягивающей ни в прямом, ни в обратном времени. В последнем случае наличие такого решения в результате этапа численной проверки не будет подтверждено. Возможно дальнейшее развитие метода путем построения управления, стабилизирующего такие траектории.

Область применимости метода определяется областью сходимости итерационной процедуры, а также областью, в которой взаимовлияние “подсистем” качественно описывается осредненными значениями функций, отвечающих за перевязки.

Далее приведен пример, который демонстрирует эффективность работы предложенного метода для системы, где перевязки не малы и имеет место дефицит управляющих воздействий.

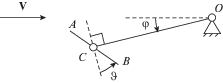
4. Пример применения в задаче об аэродинамическом маятнике. Рассмотрим маятник, который состоит из державки OC, закрепленной в неподвижном шарнире O (ось шарнира вертикальна), и пластины AB, закрепленной в шарнире C (рис. 1). Плоскость пластины вертикальна. Система находится в горизонтальном потоке воздуха скорости V плотности $\rho $. Система имеет две степени свободы, которые будем описывать углом $\varphi $ поворота державки OC, отсчитываемым против часовой стрелки от направления скорости ветра, и углом $\vartheta $ относительной ориентации пластины, отсчитываемым против часовой от направления перпендикулярного державке OC. В шарнире C присутствует спиральная пружина, ненапряженное состояние которой соответствует значению $\vartheta = 0$, а также в этом шарнире действует момент линейного вязкого трения. В шарнире O приложен некоторый управляющий момент ${{M}_{u}}$.

Пусть r – длина державки OC, ${{J}_{1}}$ – момент инерции державки относительно точки O, m – масса пластины, центр масс пластины расположен в точке C, ${{J}_{2}}$ – момент инерции пластины относительно точки C. Кинетическая энергия системы имеет вид (здесь точкой обозначена производная по времени t):

На пластину действуют аэродинамические силы со стороны потока воздуха. Будем считать, что они могут быть представлены в виде силы сопротивления D и подъемной силы L, приложенных в точке C и выражаемых соотношениями

Здесь S – площадь пластины, $\alpha $ – мгновенный угол атаки – угол между воздушной скоростью точки C и плоскостью пластины, ${{C}_{d}}(\alpha )$ и ${{C}_{l}}(\alpha )$ – коэффициенты силы сопротивления и подъемной (боковой) силы соответственно, U – величина воздушной скорости точки C:

Аналогичная модель аэродинамического воздействия рассмотрена [9, 10] для маятника с одной степенью свободы ($\vartheta \equiv 0$), а также для других конструкций однозвенных маятников в потоке [17, 18], подобная модель применена [39] для альтернативной схемы двухзвенного маятника. Этот квазистатический подход к описанию аэродинамики маятника в потоке восходит к работе [40]. Предложены [41, 42] более сложные модификации.

При численных расчетах будем использовать для аэродинамических коэффициентов простейшие аппроксимации, отражающие качественные свойства четности/нечетности этих функций:

Введем следующие обозначения для безразмерных переменных и времени: ω = = ${{V}^{{ - 1}}}rd\varphi {\text{/}}dt$, $w = {{V}^{{ - 1}}}rd\vartheta {\text{/}}dt$, $\tau = {{r}^{{ - 1}}}Vt$.

Обобщенная сила по координате $\varphi $, отвечающая аэродинамическому воздействию, выражается соотношением:

Представим функцию $F(\varphi ,\vartheta ,\omega )$ в следующем виде:

здесь использованы следующие обозначения:

Будем искать автоколебания с относительно небольшой амплитудой по углу $\vartheta $ и при этом ограничимся для функции $F(\varphi ,\vartheta ,\omega )$ членами разложения порядка до $O({{\vartheta }^{2}})$ включительно. Тогда каждое слагаемое в правой части системы уравнений движения будет произведением функций, каждая из которых зависит или только от $\varphi $ и $\omega $ или только от $\vartheta $ и w.

Таким образом, в безразмерных обозначениях уравнения движения системы имеют структуру аналогичную (1.1):

Здесь a – параметр, характеризующий аэродинамическое воздействие, p – коэффициент, характеризующий инерционные параметры, $\kappa $ – безразмерный коэффициент упругости пружины, установленной в шарнире C, $\chi $ – безразмерный коэффициент вязкого трения в шарнире С. Безразмерное управляющее воздействие u выберем в следующем виде:

В обозначениях системы (1.1) получаем: ${{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) = {{\omega }_{1}}$, ${{f}_{2}}({{\varphi }_{2}},{{\omega }_{2}})$ = $\operatorname{sgn} ({{\omega }_{2}})$, ${{g}_{1}}({{\varphi }_{1}},{{\omega }_{1}})$ = = ${{b}_{1}}{{\omega }_{1}}$, ${{g}_{2}}({{\varphi }_{2}},{{\omega }_{2}})$ = ${{b}_{2}}\operatorname{sgn} ({{\omega }_{2}})$.

Требуется подобрать значения параметров ${{b}_{i}}$ так, чтобы в системе (4.1) существовала близкая к периодической траектория, отвечающая автоколебаниям (авторотациям), амплитуда которых по $\varphi $ примерно равна $\varphi {\kern 1pt} *$ (частота которых по $\varphi $ примерно равна $\omega {\kern 1pt} *$), а по $\vartheta $ – примерно $\vartheta {\kern 1pt} *$, и чтобы на этом режиме не происходила синхронизация между углами $\varphi $ и $\vartheta $.

Отметим, что в системе имеет место дефицит управляющих воздействий, сложности, связанные с этим, описаны, например, в [34].

4.1. Асинхронные автоколебания двойного маятника. Рассмотрим задачу формирования асинхронных автоколебаний. Система (4.1) обладает свойством центральной симметрии. Будем искать решения колебательного типа, которые обладают центральной симметрией. С учетом свойств симметрии часть слагаемых при построении вспомогательных частично усредненных систем (2.1), (2.2) зануляется:

Остальные слагаемые не вошли в частично усредненные системы, поскольку в силу свойств центральной симметрии средние значения $\bar {G}_{{ik}}^{j}$ соответствующих функций нулевые на каждом шаге алгоритма.

Квадратными скобками в частично усредненных системах обозначены все слагаемые, кроме консервативной части (отметим, что в консервативные слагаемые не обязательно было из ${{F}_{0}}(\varphi ,\omega )$ включать именно $P(\varphi )$, но это один из наиболее естественных возможных вариантов).

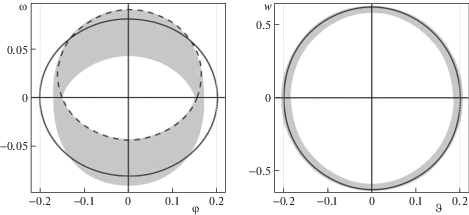
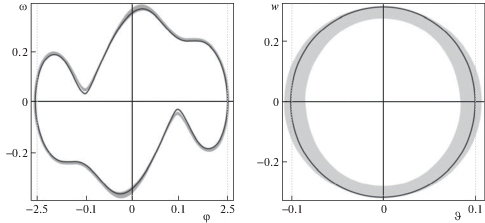
Проиллюстрируем работу предложенного алгоритма. Положим $a = 0.2$, $p = 0.005$ (небольшое значение параметра p существенно, с физическим смыслом оно согласуется), $\kappa = 10$, $\chi = 0.04$. Рассмотрим следующие наборы “программных” значений амплитуд: 1) $\varphi * = 0.2$, $\vartheta * = 0.2$; 2) $\varphi * = 2.5$, $\vartheta * = 0.1$.

На рис. 2, 3 черным цветом изображены кривые ${{\omega }^{ \pm }}(\varphi )$ и ${{w}^{ \pm }}(\vartheta )$, построенные приближенно в ходе применения предложенного алгоритма к вспомогательным системам. Серым цветом показаны приближения для проекций аттрактора системы (4.1) на плоскости ($\varphi $, $\omega $) и ($\vartheta $, $w$), они построены путем прямого численного интегрирования системы (4.1) методом Рунге–Кутты с начальными условиями из окрестностей кривых ${{\omega }^{ \pm }}(\varphi )$, ${{w}^{ \pm }}(\vartheta )$ (проекция траектории закрашивает некоторую область). Система и найденные решения обладают центральной симметрией. Соответствующие значения коэффициентов в законе управления, полученные в результате применения алгоритма составили: 1) $b_{1}^{ * } \approx 0.818$, $b_{2}^{ * } \approx - 0.097$; 2) $b_{1}^{ * } \approx 0.216$, $b_{2}^{ * } \approx - 0.050$.

Пунктирной линией на плоскости ($\varphi $, $\omega $) на рис. 2 показано сечение Пуанкаре для построенной траектории гиперплоскостью $\vartheta = 0$ (в направлении увеличения $\vartheta $). Качественный вид построенного сечения Пуанкаре позволяет предположить, что найденный аттрактор представляет собой двумерный инвариантный тор: характерный вид сечений Пуанкаре, соответствующих различным типам аттракторов приведен, например, в [43].

В рассмотренных примерах при построении периодических траекторий ${{\omega }^{ \pm }}(\varphi )$ и ${{w}^{ \pm }}(\vartheta )$ систем (4.3), (4.4) для каждого шага j было выполнено по 5 итерационных приближений метода [16], и всего было по 3 шага ($j = 0,1,2$).

4.2. Асинхронный режим, при котором авторотация первого звена сопровождается автоколебаниями второго. При жестком закреплении пластины к державке под прямым углом ($\vartheta \equiv 0$) рассматриваемый маятник представляет собой элемент ротора Дарье. Для него характерна авторотация в потоке, и только при относительно большой дополнительной диссипации вместо ротации наблюдаются колебания [10]. Рассмотрим задачу формирования асинхронного режима системы (4.1), характеризующегося ротацией по $\varphi $ и колебаниями по $\vartheta $. Управление будем искать, как и раньше, в форме (4.2). Когда первое звено совершает авторотации, то уже нельзя воспользоваться свойствами центральной симметрии при вычислении средних значений от функций переменных $\varphi $ и $\omega $. В результате в обеих частично усредненных системах появятся дополнительные слагаемые по сравнению с предыдущим случаем.

Параметры, отвечающие за перевязки, вошли и в неконсервативные части вспомогательных систем, и в консервативные. Значения $\bar {g}_{i}^{j}$ в данном случае зависят от $b_{i}^{j}$.

Соответствие между функциями, которые усредняем вдоль периодических траекторий систем (4.5), (4.6), и вспомогательными параметрами следующее: ${{F}_{0}}(\varphi ,\omega ) \to \bar {G}_{{10}}^{j}$, ${{F}_{1}}(\varphi ,\omega ) \to \bar {G}_{{11}}^{j}$, ${{F}_{2}}(\varphi ,\omega ) \to \bar {G}_{{12}}^{j}$, $b_{1}^{j}\omega \to \bar {g}_{1}^{j}$, $w \to \bar {G}_{{20}}^{j}$, $\vartheta \to \bar {G}_{{21}}^{j}$, ${{\vartheta }^{2}} \to \bar {G}_{{22}}^{j}$, $b_{2}^{j}\operatorname{sgn} w \to \bar {g}_{2}^{j}$.

Используем алгоритм, описанный выше. На каждом шаге алгоритма будем применять к системе (4.5) модификацию [18] метода [16], предназначенную для формирования авторотаций в системе второго порядка. При этом для системы (4.6) используем модификацию [17] подхода [16], предназначенную для формирования автоколебаний в системе, не обладающей центральной симметрией.

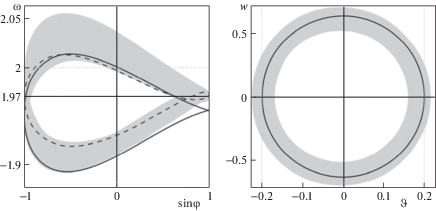
При $\omega * = 2$, $\vartheta * = 0.2$ получаем $b_{1}^{ * } \approx - 0.057$, $b_{2}^{ * } \approx 0.099$.

На рис. 4 черными кривыми представлены порождающие периодические траектории систем (4.5), (4.6), построенные предложенным итерационным методом; серым цветом представлены проекции на фазовые плоскости приближения для аттрактора системы (4.1), построенного методом Рунге–Кутты при ${{b}_{i}} = b_{i}^{ * }$ (траектория закрашивает некоторую область); пунктирной кривой на рис. 4 изображено сечение Пуанкаре гиперплоскостью $\vartheta = 0$ (в направлении увеличения $\vartheta $) для траектории, построенной методом Рунге–Кутты. Качественный вид сечения Пуанкаре, как и в предыдущем примере, косвенно свидетельствует о том, что найденный аттрактор – двумерный инвариантный тор.

Значения вспомогательных параметров $\bar {G}_{{10}}^{j}$, $\bar {G}_{{11}}^{j}$, $\bar {G}_{{12}}^{j}$, $\bar {G}_{{22}}^{j}$, $\bar {g}_{1}^{j}$, $b_{1}^{j}$, $b_{2}^{j}$ за три шага алгоритма ($j = 0,\;1,\;2$) практически перестали меняться. Значения $\bar {G}_{{20}}^{j}$, $\bar {G}_{{21}}^{j}$, $\bar {g}_{2}^{j}$ остаются практически нулевыми на всех итерациях, поскольку периодическая траектория системы (4.6) хотя и не является центрально симметричной, но мало отличается от таковой.

Модификация подхода, предназначенная для формирования асинхронных авторотаций в системе с двумя вращательными координатами, предложена и проиллюстрирована на примерах [26, 27], при этом присутствовали некоторые дополнительные ограничения на форму системы, которые сняты в настоящей работе. В частности, в модификациях [26, 27] перевязки между подсистемами не зависят от координат ${{\varphi }_{i}}$. В результате в [26] параметры аналогичные $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$ не требуется искать итерационно, – они определяются заранее, до построения предельных циклов вспомогательных систем (иными словами, параметры, отвечающие за перевязки, не зависят от j). В силу дополнительных ограничений на вид системы в [27] параметры аналогичные $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$ отсутствуют, а в качестве коэффициентов $b_{i}^{*}$ выступают средние значения фазовых скоростей на траектории, отвечающей авторотации, что значительно упрощает алгоритм поиска такой траектории. В случае авторотаций по обеим координатам на каждом шаге применения алгоритма для вспомогательных систем второго порядка используется метод формирования $2\pi $-периодических траекторий [18].

5. Обсуждение. Отметим некоторые особенности работы алгоритма, обнаруженные при рассмотрении приведенного выше механического примера, а затем опишем возможные направления дальнейшего развития общей задачи.

Относительно большая жесткость $\kappa $ пружины в шарнире C существенна для эффективности работы алгоритма. В предельном случае, если этот коэффициент много больше остальных коэффициентов системы (4.1), система близка к полностью интегрируемой. Для такого случая можно ожидать расширение области применимости алгоритма. Если же жесткость невелика, то значительно расширяется область параметров, при которых происходит синхронизация и система выходит на периодический режим (не описываемый предложенным алгоритмом). Можно предположить, что усиление неконсервативных воздействий по сравнению с консервативными выступает как один из факторов, способствующий синхронизации.

Отметим, что взаимное влияние элементов системы существенно сказывается не только на колебаниях переменных около средних значений (“размывании” аттрактора), но и на форме порождающих периодических решений вспомогательных систем. Чтобы убедиться в этом, можно сравнить решения, полученные в описанных выше примерах, с периодическими решениями в задаче о маятнике с пластиной, жестко закрепленной на первом звене ($\vartheta \equiv 0$). Последние описаны в [10] (но для случая системы с малым параметром).

Предложенный алгоритм позволяет быстро построить приближение для асинхронных колебаний, которое в ряде случаев оказывается достаточно грубым. Например, для рассмотренных значений $\varphi * = 0.2$, $\vartheta * = 0.2$ амплитуда по $\varphi $ у сформированных автоколебаний существенно отличается от $\varphi {\text{*}}$. Однако построенное грубое приближение можно использовать в качестве отправной точки, чтобы путем продолжения по параметрам определить значения коэффициентов управления, обеспечивающие более точное отслеживание программных значений амплитуд.

Среди возможных модификаций предложенного метода необходимо отметить, в первую очередь, алгоритм для поиска асинхронных автоколебаний системы в отсутствие управления. Для обобщения метода на такую задачу требуется искусственное добавление в систему слагаемых вида ${{b}_{i}}{{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}})$, выполнение алгоритма для большого набора пар $(\varphi _{1}^{ * },\varphi _{2}^{ * })$; поиск тех пар $(\varphi _{1}^{ * },\varphi _{2}^{ * })$, при которых $b_{i}^{ * } = 0$; выполнение для таких пар численной проверки наличия в исходной системе близкой к периодической траектории. Такой подход позволяет, по сути, перебирать начальные условия для искомой траектории не в четырехмерном, а в двумерном пространстве, и только в окрестности “подозрительных” пар $(\varphi _{1}^{ * },\varphi _{2}^{ * })$ подбирать начальные условия в пространстве всех четырех переменных.

Помимо этого, отметим, что для управляемой системы целесообразно развитие модификации метода, которая предполагала бы специальный выбор функций ${{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}})$ для обеспечения свойства притяжения траектории, порожденной периодическими решениями вспомогательных систем, или для расширения диапазона значений $(\varphi _{1}^{ * },\varphi _{2}^{ * })$, при котором сходится итерационный процесс.

Дополнительные модификации предложенного алгоритма можно получить, применяя альтернативные методы для построения периодических решений вспомогательных систем (2.i), например методы [14, 15], итерационные методы, основанные на прямом численном интегрировании, или на разложении решения в гармонический ряд, а также методы, основанные на исследовании бифуркаций рождения циклов в окрестности положений равновесия и продолжении по параметру [44, 45]. Применение того или иного подхода в зависимости от специфики конкретной задачи может позволить расширить область сходимости, ускорить сходимость.

Заключение. В работе рассматривается автономная неконсервативная механическая система с двумя степенями свободы. Предполагается, что в системе присутствуют управляющие воздействия в форме обратной связи. Предложен метод формирования асинхронных автоколебаний посредством выбора коэффициентов усиления управляющих воздействий. Близкие подходы для формирования авторотаций предложены ранее [26, 27]. Эффективность работы алгоритма проиллюстрирована на примере задачи о формировании автоколебаний аэродинамического маятника. Обсуждается область применимости предложенного подхода и возможные направления его дальнейшего развития.

Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского университета “Математические методы анализа сложных систем”.