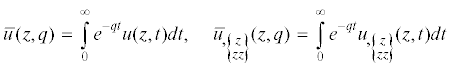Прикладная математика и механика, 2020, T. 84, № 1, стр. 102-121

При изучении контакта деформируемых тел силы межмолекулярного взаимодействия впервые учитывались применительно к герцевскому контакту [1]. В дальнейшем был разработан ряд эффективных подходов к решению контактных задач такого типа, среди которых следует отметить подходы, использующие концепцию поверхностной энергии – модели JKR и DMT [2, 3]. Эти подходы также использовались для расчета адгезионного контакта слоистых [4] и вязкоупругих тел [5–8]. В частности, для такого контакта был выполнен расчет диссипации энергии в зависимости от скорости нагружения [7].

Строгая постановка контактной задачи, учитывающая межмолекулярное взаимодействие, предполагает существование некоторого зазора $r$ между контактирующими телами. Величина этого зазора должна обеспечивать баланс сил, обусловленных контактной деформацией тел и их межмолекулярным взаимодействием (самосогласованный подход по Дерягину [9]). При таком подходе возможны постановки задачи с поверхностным (традиционная постановка [10–12]) и объемным (уточненная постановка [13–15]) приложением сил межмолекулярного взаимодействия.

В данной работе производится расчет напряженно-деформированного состояния (НДС) тонкого вязкоупругого слоя, обусловленного внедрением в него индентора при наличии сил межмолекулярного взаимодействия (самосогласованный подход, традиционная и уточненная постановки задачи). Значительное внимание уделено анализу диссипации энергии и интенсивности касательных напряжений в зависимости от параметров режима нагружения слоя.

1. Постановка задачи и основные уравнения. Рассмотрим контактное взаимодействие абсолютно жесткого тела (индентора) с основанием, состоящим из вязкоупругого слоя толщины $h$, связанного с абсолютно жесткой подложкой (рис. 1). Считается, что индентор и слой разделены контактным зазором $r$, обеспечивающим баланс сил межмолекулярного и вязкоупругого взаимодействия контактирующих тел (самосогласованный подход) [9]. Свяжем с основанием систему координат $Oxyz$, совместив ее плоскость $Oxy$ с границей раздела слоя и подложки. В дальнейшем также будут использоваться обозначения координат с индексом: ${{x}_{1}} = x$, ${{x}_{2}} = y$, ${{x}_{3}} = z$.

Межмолекулярное взаимодействие индентора и основания определяется парными взаимодействиями их молекул [16–18]. Соответствующая сила $F$ зависит от свойств пары молекул и расстояния $l$ между ними. Существуют разные формы такой зависимости, среди которых наиболее известен закон Леннард-Джонса [19]:

где ${{a}_{1}}$, ${{a}_{2}}$, m, n – параметры взаимодействия, причем обычно полагают $m = 7$, $n = 13$. Применительно к рассматриваемой задаче, обозначим через ${{a}_{{1c}}}$, ${{a}_{{2c}}}$ параметры в законе (1.1), отвечающие взаимодействию молекул индентора и слоя, а через ${{a}_{{1b}}}$, ${{a}_{{2b}}}$ – взаимодействию молекул индентора и подложки.

При определенных допущениях [11, 20] суммирование парных взаимодействий молекул позволяет для каждой точки слоя рассчитать объемную силу, обусловленную межмолекулярным взаимодействием. Эта сила направлена вдоль оси $z$ и зависит от расстояния $d = r + s = r + h - z$ между точкой ее приложения и индентором (рис. 1). Таким образом, если обозначить через ${{f}_{i}}$, $i = 1,2,3$ компоненты объемной силы в системе координат $O{\kern 1pt} {{x}_{1}}{\kern 1pt} {{x}_{2}}{\kern 1pt} {{x}_{3}}$, то

Кроме того, суммирование парных взаимодействий молекул позволяет определить силу $p$ воздействия индентора на основание, приходящуюся на единицу площади его поверхности:

которая в рамках самосогласованного подхода интерпретируется как контактное давление [9–11, 15].

В случае закона Леннард–Джонса функции $f$ и $\Phi $ имеют вид [15]

где $k = m - 4$, $l = n - 4$, $H = h + r$, ${{N}_{s}}$, ${{N}_{c}}$ и ${{N}_{b}}$ – концентрации молекул индентора, слоя и подложки, соответственно. Символ # подразумевает индекс $b$ (подложка) или $c$ (слой), причем в формуле (1.4) при $d \in [r,r + h]$ используется индекс $c$, а при $d > r + h$ – индекс $b$. Присутствующая в формулах (1.2), (1.5) толщина слоя $h$ считается постоянной, что допустимо при малых деформациях.

Традиционная постановка контактной задачи при наличии межмолекулярного взаимодействия подразумевает, что определяемое по формуле (1.3) контактное давление прикладывается к границе слоя, в результате чего он деформируется [9–12]. Ниже также рассматривается уточненная постановка, в которой естественным образом предполагается, что деформация слоя порождается объемными силами (1.2), распределенными по его глубине, тогда как граница слоя свободна от нагрузок [13–15]. В качестве параметра нагружения слоя в обеих постановках выступает зазор $r$, однозначно определяющий объемные силы ${{f}_{3}}$ по формуле (1.2) и контактное давление $p$ по формуле (1.3).

Деформационные свойства слоя в каждой точке описываются линейным законом наследственного типа [21–23]

где ${{\delta }_{{ij}}}$ – символ Кронекера, ${{\varepsilon }_{{ij}}}$, ${{\sigma }_{{ij}}}$ – компоненты тензоров деформаций и напряжений, $\theta = {{\varepsilon }_{{kk}}}$, причем здесь и далее применяется правило суммирования по повторяющимся индексам. Величины $\lambda $ и $\mu $ представляют собой мгновенные модули упругости (постоянные Ламе), а функции $\Lambda (t)$, ${\rm M}(t)$ характеризуют вязкие свойства материала слоя и выражаются через ядра сдвиговой ${{R}_{{{\kern 1pt} 1}}}$ и объемной ${{R}_{{{\kern 1pt} 2}}}$ релаксации: причем $K = \lambda + \frac{2}{3}\mu $ – мгновенный модуль объемной упругости. Отметим, что первые два слагаемых в правой части равенства (1.6) отвечают закону Гука с мгновенными модулями упругости $\lambda $ и $\mu $.

Деформации считаются малыми, поэтому [21, 22]

где ${{u}_{i}}$ – компоненты вектора перемещений, $i = 1,2,3$. Здесь и далее для записи частной производной функции по ее аргументу используется общепринятое обозначение с запятой и индексом аргумента (или самим аргументом).

Равенства (1.6) и (1.8) образуют полную систему уравнений НДС слоя, если к ним добавить уравнение равновесия [21, 22]:

Считается, что

т.е. до момента времени $t = 0$ взаимодействие индентора и слоя носит стационарный характер с постоянным во времени зазором ${{r}^{s}}$, после чего зазор начинает меняться некоторым заданным образом. Здесь и далее верхним индексом s обозначается стационарное состояние слоя.

Замечание 1. Вопрос метода реализации заданной зависимости $r(t)$ при $t > 0$ здесь не рассматривается. Отметим только, что зазор $r$ связан равенством (1.3) с контактным давлением $p$, совпадающим с удельной нагрузкой на индентор, поэтому имеется возможность путем изменения этой нагрузки получать требуемую зависимость $r(t)$.

Постоянному значению ${{r}^{s}}$ зазора при $t \leqslant 0$ отвечает некоторое стационарное НДС слоя:

С учетом равенств (1.11) соотношение (1.6) можно записать в следующем виде:

где причем ${{\lambda }^{\infty }}$, ${{\mu }^{\infty }}$ – длительные (равновесные) модули упругости [23].

Согласно формулам (1.2) и (1.3), величина зазора $r$ определяет объемные силы ${{f}_{3}}$ (уточненная постановка) и внешнюю нагрузку на слой – контактное давление $p$ (традиционная постановка). При условии (1.10) эти формулы позволяют установить, что

причем

Наряду с непрерывным режимом нагружения слоя, когда

выражения (1.15) и (1.16) допускают мгновенное нагружение. При таком режиме в момент времени $t = 0$ зазор $r$ принимает значение $r^\circ \ne {{r}^{s}}$, а контактное давление $p$ и объемные силы ${{f}_{3}}$ мгновенно изменяются до значений $p^\circ $ и $f^\circ (z)$, т.е.

Кроме того, взаимодействие индентора и слоя может выходить на асимптотически стационарное состояние:

В соотношениях (1.19) и (1.20), согласно формулам (1.2) и (1.3):

В дальнейшем будет использоваться концепция асимптотически тонкого слоя, согласно которой НДС слоя меняется пренебрежимо мало на расстояниях ~h в его продольном направлении (в плоскости $Oxy$). В точности подобное НДС имеет место в случае бесконечно протяженного плоского индентора (рис. 1), который для определенности будет рассматриваться ниже. Отметим, что в случае контактной задачи теории упругости, концепция асимптотически тонкого слоя приводит к известной модели Винклера [24].

Пренебрегая изменением НДС слоя в продольном направлении, будем считать, что его компоненты ${{u}_{i}}$, ${{\varepsilon }_{{ij}}}$, ${{\sigma }_{{ij}}}$ зависят только от координаты $z$ и времени $t$. В этом случае, как нетрудно убедиться на основе соотношений (1.8) и (1.12), все компоненты НДС равны нулю, кроме

где

Здесь и далее по умолчанию считается, что $t > 0$.

При таком НДС первые два равенства условия равновесия (1.9) выполняются тождественно с учетом первых двух равенств (1.2). Подстановка выражений (1.22) в третье равенство (1.9) приводит к следующим уравнениям относительно перемещения $w$:

причем при традиционной постановке задачи имеет место тождество f ^s(z) = ${{f}_{3}}(z,t) \equiv 0$, а при уточненной постановке эти функции определяются выражениями (1.16), (1.17).

Уравнения (1.25), (1.26) являются основными для рассматриваемой задачи, т.к. определяемое из них перемещение $w$ позволяет с помощью выражений (1.22) найти все отличные от нуля компоненты НДС слоя. Сформулируем для этих уравнений граничные условия.

Ввиду того, что слой сцеплен с абсолютно жестким основанием (рис. 1), всегда имеет место равенство ${{u}_{3}}{{{\text{|}}}_{{z = 0}}} = 0$, т.е.

Как указывалось выше, при традиционной постановке задачи к поверхности слоя прикладывается контактное давление $p = - {{\sigma }_{{33}}}{{{\text{|}}}_{{z = h}}}$, а при уточненной постановке поверхность слоя свободна от нагрузок. С использованием последнего выражения (1.22) данное обстоятельство позволяет записать дополнительные граничные условия

причем при традиционной постановке задачи значения ${{p}^{s}}$ и $p(t)$ определяются выражениями (1.15), (1.17), а при уточненной постановке: ${{p}^{s}} = p(t) \equiv 0$.

Ставится задача: при заданной зависимости контактного зазора $r$ от времени $t > 0$ и соответствующих зависимостях $p(t)$ вида (1.15) (традиционная постановка) и ${{f}_{3}}(z,t)$ вида (1.16) (уточненная постановка) определить вязкоупругое перемещение $w(z,t)$ и соответствующее НДС слоя.

Замечание 2. Вязкоупругие соотношения (1.6) предполагают, что температура слоя в процессе его деформирования не меняется (изотермический процесс), а уравнение равновесия (1.9) записано без учета инерционности материала слоя. Подобные допущения справедливы при условии достаточно медленного протекания процесса деформирования, когда, в частности, выделяемое в слое тепло успевает рассеяться, не вызывая повышение его температуры. Определенный выше режим мгновенного нагружения (1.19) очевидно не удовлетворяет такому условию. Тем не менее, в дальнейшем этот режим будет рассматриваться как предельный случай непрерывного нагружения, допускающий аналитическое описание. В частности, это позволит проводить проверку численных алгоритмов расчета режима непрерывного нагружения.

2. Общее решение задачи. Для решения поставленной в предыдущем разделе задачи потребуется конкретизировать ядра интегральных операторов в соотношении (1.6). Не ограничивая общности рассмотрения, пренебрежем объемной ползучестью материала слоя и положим [23]

причем, из физических соображений ${{R}_{0}} < \alpha $. Подстановка равенств (2.1) в соотношения (1.7) и (1.24) приводит к следующим выражениям

С их помощью можно, в частности, конкретизировать введенные по формулам (1.14) и (1.23) вязкоупругие характеристики материала слоя, получив выражения:

которые будут использоваться при дальнейших выкладках.

Далее также будет использоваться оператор $\mathcal{R}$, который формально определяется как решение краевой задачи

для произвольных функций $u(z) \in {{C}^{2}}[0,h]$, $g(z) \in C[0,h]$, так что [15]

Наконец, для более компактной записи формул будут использоваться обозначения:

в которых верхний/нижний вариант в круглых скобках отвечает традиционной/уточненной постановке задачи. Верхний индекс в последнем равенстве может быть одним из символов: $s$, $ \circ $, $\infty $, введенных в рассмотрение выше, при этом соответствующие величины ${{p}^{{( \bullet )}}}$, ${{f}^{{( \bullet )}}}(z)$ определяются по формулам (1.17), (1.21).

Рассмотрим вначале решение поставленной в предыдущем разделе задачи для стационарного состояния слоя, в котором он находится при $t \leqslant 0$. Соответствующее этому состоянию перемещение ${{w}^{s}}(z)$ удовлетворяет уравнению (1.25) с граничными условиями (1.27) и (1.28). При традиционной постановке задачи (${{f}^{s}}(z) = 0$) функция ${{w}^{s}}(z)$ находится элементарно, тогда как при уточненной постановке (${{p}^{s}} = 0$) она определяется при помощи оператора $\mathcal{R}$ по формуле (2.4). В результате, учитывая обозначения (2.5), можно установить, что

Стационарное НДС слоя при $t \leqslant 0$ определяется по формулам (1.22) с учетом полученного выражения (2.6):

Замечание 3. Полагая в выражении (2.6) $z = h$ и учитывая обозначение (2.5), можно прийти к соотношению ${{w}^{s}}(h) = - {{B}^{\infty }}h{{p}^{s}}$, которое отвечает известной модели Винклера [4, 24].

Получим теперь решение поставленной задачи при $t > 0$. Соответствующее перемещение $w(z,t)$ удовлетворяет уравнению (1.26), которое можно решить известным методом преобразования Лапласа по времени.

Введем в рассмотрение вспомогательную функцию

и допустим, что эта функция, ее первая и вторая производные по $z$ при каждом $z \in [0,h]$ непрерывны по $t \in (0,\infty )$ и ограничены. Кроме того, в силу первого равенства (1.22), имеем: $u(z,t) = 0$, $t \leqslant 0$ . Эти свойства позволяют определить для функции $u(z,t)$ и ее производных преобразование Лапласа (изображение) [25]:

Заменим в уравнении (1.26) функцию $w(z,t)$ на $u(z,t)$ согласно равенству (2.8) и перейдем в полученном уравнении к изображениям. Тогда, применяя формулу преобразования Лапласа свертки [25], получим алгебраическое уравнение относительно изображения :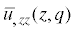

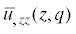в котором $\bar {{\rm N}}(q) = {{{\rm N}}_{0}}{{(q + \alpha )}^{{ - 1}}}$ и $\bar {f}_{3}^{\Delta }(z,q)$ – изображения ядра ${\rm N}(t)$ вида (2.2) и функции $f_{3}^{\Delta }(z,t)$ ≡ ${{f}_{3}}(z,t) - {{f}^{s}}(z)$, соответственно. Если из этого уравнения выразить , в полученном равенстве вернуться к оригиналам, после чего с помощью равенства (2.8) заменить функцию $u(z,t)$ на $w(z,t)$, то после несложных преобразований можно прийти к следующему выражению для второй производной функции $w(z,t)$: где $\beta = \alpha - B{\kern 1pt} {{{\rm N}}_{0}} > 0$, причем последнее неравенство имеет место в силу определения (2.2) величины ${{{\rm N}}_{0}}$ и неравенства ${{R}_{0}} < \alpha $.

Выражение (2.9) позволяет найти саму функцию $w(z,t)$. Действительно, при традиционной постановке задачи ${{f}_{3}}(z,t) \equiv 0$, поэтому из выражения (2.9) следует с учетом (2.6), что ${{w}_{{,zz}}}(z,t) = 0$, т.е. $w(z,t) = {{c}_{1}}(t)z + {{c}_{0}}(t)$. Коэффициенты ${{c}_{0}}$, ${{c}_{1}}$ в последнем равенстве находятся из граничных условий (1.27) и (1.29). При уточненной постановке задачи $p(t) \equiv 0$, поэтому, согласно (1.27) и (1.29), имеют место однородные граничные условия: $w(0,t) = {{w}_{{,z}}}(h,t) = 0$, при которых перемещение $w(z,t)$ может быть найдено из выражения (2.9) с помощью оператора $\mathcal{R}$ по формуле (2.4). Указанные выкладки при учете обозначений (2.5) позволяют получить выражение

в котором функция ${{w}^{s}}(z)$ имеет вид (2.6),

Нетрудно убедиться в том, что выражение (2.10) обеспечивает для функции $u(z,t)$ вида (2.8) и ее производных выполнение сделанных выше допущений о непрерывности и ограниченности.

Отметим, что в случае (1.19) мгновенного нагружения выражение (2.10) допускает мгновенное изменение перемещения $w(z,t)$ в момент $t = 0$. Действительно, с учетом равенств (1.19) и обозначений (2.5), функция $w(z,t)$ при $t = 0$ имеет предел справа

и этот предел не равен пределу слева $w(z,0 - 0) = {{w}^{s}}(z)$. Равенство $w(z,0 + 0)$ = w(z, 0 – 0) имеет место только при $r^\circ = {{r}^{s}}$, т.е. когда контактный зазор изменяется непрерывно.

НДС слоя при $t > 0$ определяется подстановкой выражения (2.10) в формулы (1.22). Таким образом можно установить, что

где

Для вывода выражений (2.13) использовалась формула перестановки

в которой $u(\tau )$ – произвольная ограниченная и непрерывная при $\tau \in (0,t]$ функция.

Замечание 4. Путем предельного перехода $t \to \infty $ равенства (2.12) и (2.13) позволяют определить НДС слоя $\varepsilon _{{ij}}^{\infty }$, $\sigma _{{ij}}^{\infty }$ в асимптотически стационарном состоянии согласно соотношениям (1.20). Как и следовало ожидать, это НДС совпадает со стационарным и описывается выражениями (2.6), (2.7) при формальной замене в них ${{r}^{s}}$ на ${{r}^{\infty }}$.

Пример. Ступенчатое нагружение имеет место, когда после мгновенного изменения в момент $t = 0$ зазор $r$ не изменяется, сохраняя значение $r^\circ $, т.е.

и, следовательно, согласно выражениям (1.15), (1.16): $p(t) = \Phi (r^\circ )$, f(z, t) = $f(r^\circ + h - z)$, $t > 0$. В этом случае формулы (2.10), (2.12) и (2.13) позволяют установить, что тогда как при $t \leqslant 0$ НДС слоя является стационарным и определяется выражениями (2.6) и (2.7). В равенствах (2.15) и (2.16): $\omega ^\circ (z) = - BX^\circ (z)$, причем функция $X^\circ (z)$ имеет вид (2.5).

Полученные выше формулы (2.13) или (2.16) позволяют рассчитывать определенные комбинации компонент ${{\sigma }_{{ij}}}$ тензора напряжений, которые используются в некоторых критериях разрушения [26]. Примером такой комбинации является интенсивность касательных напряжений

В рассматриваемом случае бесконечно протяженного индентора: ${{\sigma }_{{ij}}} = 0$, кроме ${{\sigma }_{{11}}} = {{\sigma }_{{22}}}$ и ${{\sigma }_{{33}}}$, поэтому выражение (2.17) принимает вид

В частности, если взаимодействие индентора и слоя выходит на асимптотически стационарное состояние (1.20), то последняя формула с учетом замечания 4 позволяет рассчитать соответствующую интенсивность касательных напряжений:

причем функция ${{X}^{\infty }}(z){\kern 1pt} {\kern 1pt} $ имеет вид (2.5).

3. Расчет диссипации энергии выполним на основе первого начала термодинамики, согласно которому, если пренебречь кинетической энергией тела, выполняется равенство [22]

где $d{{A}^{e}}$ – работа внешних сил над телом, $dU$ – изменение его внутренней энергии, $dQ$ – количество теплоты, выделенной телом. Внутренняя энергия $U$ является функцией состояния тела и при неизменной температуре определяется эволюцией его НДС, а работу $d{{A}^{e}}$ можно выразить через работу деформации по формуле [22] где $V$ – объем тела.

Диссипация энергии ${{D}_{{{\kern 1pt} [{{t}_{1}},{{t}_{2}}]}}}$ на промежутке времени $[{{t}_{1}},{{t}_{2}}]$ определяется как теплота, выделенная телом за это время, т.е. с учетом (3.1) и (3.2):

где – удельная работа деформации на промежутке $[{{t}_{1}},{{t}_{2}}]$, причем интеграл понимается в смысле Стилтьеса.

В дальнейшем будет использоваться удельная потенциальная энергия упругой деформации [27]

причем последнее выражение отвечает энергии с длительными модулями упругости ${{\lambda }^{\infty }}$ и ${{\mu }^{\infty }}$, $\theta = {{\varepsilon }_{{kk}}}$. В рассматриваемом случае бесконечно протяженного индентора, когда ${{\varepsilon }_{{ij}}} = 0$, кроме ${{\varepsilon }_{{33}}}$, выражения (3.5) упрощаются и принимают вид:

Интеграл Стилтьеса (3.4) допускает разрывы подынтегральных функций при мгновенном нагружении слоя. Выделим соответствующие особенности в интеграле (3.4) и сведем его к интегралу Римана. Не ограничивая общности при этом, будем считать, что функции ${{\varepsilon }_{{ij}}}(t)$ и ${{\sigma }_{{ij}}}(t)$ имеют единственную точку разрыва $\hat {t} \in [{{t}_{1}},{{t}_{2}}]$ первого рода, являясь кусочно-непрерывными на $[{{t}_{1}},{{t}_{2}}]$.

Воспользуемся вторым выражением (1.12) для напряжений ${{\sigma }_{{ij}}}$ и заметим, что для первых двух слагаемых этого выражения справедливо равенство [27]

После подстановки выражения (1.12) в интеграл (3.4) равенство (3.7) позволяет упростить полученный интеграл и прийти к выражению

Присутствующие в последнем равенстве функции $\sigma _{{ij}}^{v}(t)$ определяются по формуле (1.13) и, как нетрудно установить, являются непрерывными даже при наличии разрывов первого рода у функций ${{\varepsilon }_{{ij}}}(t)$. Учитывая это и допуская, что производные ${{\dot {\varepsilon }}_{{ij}}}(t)$ – кусочно-непрерывные на $[{{t}_{1}},{{t}_{2}}]$ (подобно функциям ${{\varepsilon }_{{ij}}}(t)$), сведем в равенстве (3.8) интеграл Стилтьеса к интегралу Римана на основе известной теоремы [28]. Если после этого в полученном интеграле вернуться к напряжениям ${{\sigma }_{{ij}}}$ с помощью второго выражения (1.12) и опять воспользоваться равенством (3.7), то выражению (3.8) можно придать следующий вид

где $\varepsilon _{{ij}}^{ \pm }(\hat {t}) = \mathop {\lim }\limits_{t \to \hat {t} \pm 0} {{\varepsilon }_{{ij}}}(t)$. Здесь и далее точка над символом функции обозначает производную по времени.

В дальнейшем расчет диссипации энергии будет выполняться для перехода тела из одного стационарного состояния в другое. Получим в связи с этим выражение для внутренней энергии тела в стационарном состоянии.

Рассмотрим процесс бесконечно медленного деформирования тела, при котором компоненты НДС ${{\varepsilon }_{{ij}}}$ и ${{\sigma }_{{ij}}}$ связаны законом Гука с длительными модулями упругости ${{\lambda }^{\infty }}$ и ${{\mu }^{\infty }}$ [21]. Наличие такой связи позволяет воспользоваться равенством (3.7) и установить для рассматриваемого процесса соотношение

Кроме того, при бесконечно медленном деформировании диссипация энергии отсутствует – это обусловлено квадратичной зависимостью скорости диссипации от скоростей ${{\dot {\varepsilon }}_{{ij}}}$ деформаций [21]. С учетом данного обстоятельства подстановка в равенство (3.3) выражения (3.4), предварительно преобразованного с помощью соотношения (3.10), приводит к равенству

Представим теперь, что стационарное состояние получается путем бесконечно медленного деформирования тела из недеформированного состояния с нулевой внутренней энергией. Тогда на основе соотношения (3.11) можно заключить, что для такого состояния имеет место выражение

Таким образом, внутренняя энергия вязкоупругого тела в стационарном состоянии определяется как потенциальная энергия упругой деформации с длительными модулями ${{\lambda }^{\infty }}$ и ${{\mu }^{\infty }}$.

В случае деформирования тела с конечной скоростью из стационарного состояния $\varepsilon _{{ij}}^{s}$, $\sigma _{{ij}}^{s}$ в асимптотически стационарное состояние $\varepsilon _{{ij}}^{\infty }$, $\sigma _{{ij}}^{\infty }$, $t \to \infty $ согласно (1.20), формулы (3.3), (3.4) и (3.12) позволяют рассчитать соответствующую диссипацию энергии:

причем и величина ${{W}_{{{\kern 1pt} [0,t]}}}$ определяется по формуле (3.9) или по более общей формуле (3.4).

Применим вышесказанное к рассмотренному в предыдущих разделах вязкоупругому слою, выбрав в качестве тела произвольную его часть, ограниченную прямым цилиндром, основания которого совпадают с границами слоя и имеют площадь $S$. Тогда, учитывая отсутствие зависимости НДС от координат $x$ и $y$, представим выражение (3.13) в следующем виде

где ${{d}^{\infty }} = {{D}^{\infty }}{\text{/}}S$ – диссипация энергии, приходящаяся на единицу площади поверхности слоя.

3.1. Случай ступенчатого нагружения описывается равенствами (2.6), (2.7), (2.15) и (2.16), которые позволяют получить следующие выражения для величин, присутствующих в формуле (3.9) при $\hat {t} = {{t}_{1}} = 0$, ${{t}_{2}} = t$:

причем предел $\varepsilon _{{33}}^{^\circ }(z) \equiv {{\varepsilon }_{{33}}}(z,0 + 0) = {{w}_{{,z}}}(z,0 + 0)$ находится с помощью равенства (2.11).

Подстановка выражений (3.16) в формулу (3.9) с последующим учетом равенств (3.6) и (3.14) приводит к выражению

Используя его и учитывая выражения (2.7), (2.15) и замечание 4, по формуле (3.15) можно определить диссипацию энергии

Присутствующие в выражении (3.17) функции ${{X}^{s}}(z)$ и $X^\circ (z)$ связаны посредством равенств (1.17), (1.21) и (2.5) с функциями $f(d)$ и $\Phi (r)$, которые имеют вид (1.4) и (1.5). Учитывая указанные равенства, можно получить из (3.17) выражение, связывающее диссипацию энергии ${{d}^{\infty }}$ с параметрами межмолекулярного взаимодействия индентора и слоя:

где

Как видно, уточненная постановка задачи приводит к более сложным выражениям для диссипации энергии ${{d}^{\infty }}$ (нижняя часть формулы (3.18)) в сравнении с традиционной постановкой (верхняя часть формулы (3.18)). Это обусловлено сложным характером распределения объемных сил межмолекулярного взаимодействия по глубине слоя, которые учитываются при уточненной постановке задачи.

Обращает на себя внимание также тот факт, что, согласно формуле (3.18), при уточненной постановке задачи диссипация энергии ${{d}^{\infty }}$ зависит только от физико-механических свойств слоя. Однако при традиционной постановке задачи на величину ${{d}^{\infty }}$ оказывают влияние параметры ${{A}_{{1b}}}$, ${{r}_{{eb}}}$ межмолекулярного взаимодействия подложки, что обуславливается влиянием этих параметров на контактное давление в силу равенства (1.3).

3.2. Случай непрерывного нагружения с переходом в асимптотически стационарное состояние. При таком нагружении разрывы во времени у компонент НДС слоя отсутствуют и, поэтому, правая часть равенства (3.9) для удельной работы деформации содержит только последний интеграл. Подстановка в этот интеграл выражений (2.12) и (2.13) для компонент ${{\varepsilon }_{{ij}}}$, ${{\sigma }_{{ij}}}$ и учет равенств (2.6), (2.7), замечания 4 и определения (3.14), приводит к выражению

С учетом этого выражения формула (3.15) позволяет установить, что

причем

Присутствующая в выражении (3.21) функция $X(z,t)$ имеет вид (2.5) и связана посредством равенств (1.15) и (1.16) с функциями $f(d)$ и $\Phi (r)$, которые определяются по формулам (1.4) и (1.5). Учитывая эти равенства, можно получить из (3.21) выражение, связывающее функцию $L(t,\tau )$ с параметрами межмолекулярного взаимодействия индентора и слоя:

где

При записи формул (3.23) используются обозначения (3.19), в которых следует положить $r = {{r}_{{{\kern 1pt} 1}}} = r(t)$, ${{r}_{2}} = r(\tau )$. Подстановка выражения (3.22) в равенство (3.20) позволяет получить связь диссипации энергии ${{d}^{\infty }}$ с параметрами межмолекулярного взаимодействия индентора и слоя.

4. Численный анализ. Главной целью выполненных расчетов был анализ влияния параметров режима нагружения слоя на диссипацию энергии и интенсивность касательных напряжений. Расчеты проводились при $m = 7$, $n = 13$, ${{r}_{{ec}}} = 1$ нм, ${{r}_{{eb}}} = 0.5\,{{r}_{{ec}}}$, $h = 1$ нм, $\lambda = 4.321$ МПа, $\mu = 6.482$ МПа, ${{R}_{0}} = 0.8$ с^–1, $\alpha = 1$ с^–1, причем указанным значениям $\lambda $ и $\mu $ отвечают модуль Юнга $E = {\text{15}}{\text{.56}}$ МПа и коэффициент Пуассона $\nu = 0.2$. Кроме того, полагалось, что ${{A}_{{1c}}} = {{(6\pi )}^{{ - 1}}}{{A}_{H}}$ [9] и ${{A}_{{{\kern 1pt} 1b}}} = 10{{A}_{{{\kern 1pt} 1c}}}$, где ${{A}_{H}}$ – постоянная Гамакера, ${{A}_{H}} = {{10}^{{ - 19}}}$ Дж. Значения остальных параметров указывается отдельно для каждого численного примера.

Режим непрерывного нагружения задавался кусочно-линейной зависимостью

где ${{\dot {r}}_{c}} = ({{r}^{\infty }} - {{r}^{s}}){\text{/}}{{t}_{*}}$, ${{t}_{*}}$ – продолжительность стадии активного нагружения.

На всех представленных ниже рисунках штриховые кривые соответствуют традиционной постановке задачи, а сплошные – уточненной.

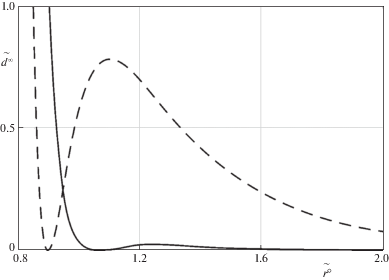
На рис. 2 показана зависимость диссипации энергии ${{d}^{\infty }}$ от величины конечного зазора $r^\circ $ в случае ступенчатого нагружения (2.14). Расчеты проводились на основе формулы (3.18) при начальном зазоре ${{r}^{s}} = 5{\kern 1pt} {\kern 1pt} {{r}_{{ec}}}$. Графики на рис. 2 построены для безразмерных величин: $\tilde {r}^\circ = r^\circ {\text{/}}{{r}_{{ec}}}$ и ${{\tilde {d}}^{{{\kern 1pt} \infty }}} = {{d}^{\infty }}{\text{/}}{{d}_{*}}$, где ${{d}_{*}} = {{({{A}_{{1c}}}{\text{/}}r_{{ec}}^{{m - 4}})}^{2}}\frac{{B{{{\rm N}}_{0}}}}{\alpha }{{B}^{\infty }}h$, причем для выбранных параметров задачи ${{d}_{*}} = 1.086 \times {{10}^{{ - 3}}}$ Дж/м².

На рис. 3 показана зависимость диссипации энергии ${{d}^{\infty }}$ от времени ${{t}_{*}}$ в случае непрерывного нагружения (4.1). Расчеты проводились на основе формулы (3.20) при начальном зазоре ${{r}^{s}} = 5{\kern 1pt} {\kern 1pt} {{r}_{{ec}}}$ и двух значениях конечного зазора: ${{r}^{\infty }} = 0.9{\kern 1pt} {\kern 1pt} {{r}_{{ec}}}$ (a) и ${{r}^{\infty }} = {{r}_{{ec}}}$ (b). При построении графиков использовалась безразмерная величина ${{\tilde {t}}_{*}} = {{t}_{*}}{\text{/}}{{t}_{r}}$, где ${{t}_{r}} = {{\alpha }^{{ - 1}}}$ – время релаксации [21] и величина ${{\tilde {d}}^{{{\kern 1pt} \infty }}}$, определенная выше.

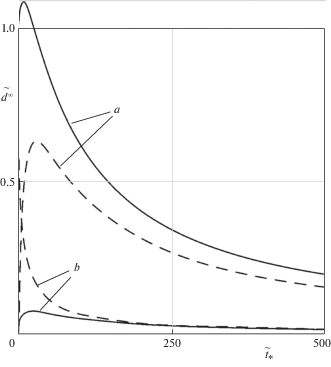
Как и следовало ожидать, результаты расчетов (рис. 2 и 3) свидетельствуют о том, что значения ${{d}^{\infty }}$ при достаточно быстром непрерывном нагружении (${{\tilde {t}}_{*}} \ll 1$) и ступенчатом нагружении отличаются незначительно. Например, если ${{t}_{*}}{\text{/}}{{t}_{r}} = 0.0001$, то при ${{r}^{\infty }} = r^\circ = 0.9{{r}_{{ec}}}$ это расхождение не превышает 0.6%, а при ${{r}^{\infty }} = r^\circ = {{r}_{{ec}}}$ – 0.0015%.

На рис. 4 показана зависимость асимптотически стационарной интенсивности касательных напряжений $\tau _{i}^{\infty }$ от величины соответствующего зазора ${{r}^{\infty }}$ в случае непрерывного нагружения (4.1). Значения $\tau _{i}^{\infty }$ здесь рассчитывались по формуле (2.18) и при построении графиков использовались безразмерные величины ${{\tilde {r}}^{\infty }} = {{r}^{\infty }}{\text{/}}{{r}_{{ec}}}$ и $\tilde {\tau }_{i}^{{{\kern 1pt} \infty }} = \tau _{i}^{\infty }{\text{/}}E$.

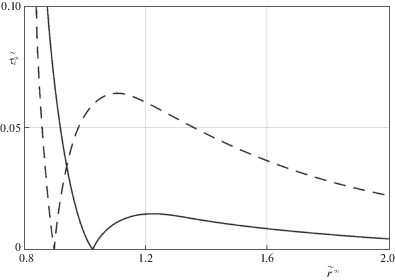
Представленные на рис. 2–4 результаты свидетельствуют о сложном характере зависимостей диссипации энергии и интенсивности касательных напряжений от параметров режима нагружения. В частности, у этих зависимостей могут присутствовать локальные экстремумы, что, по всей видимости, обусловлено наличием немонотонных зависимостей объемных сил (1.4) и контактного давления (1.5) от зазора $r$.

Показанные графики свидетельствуют также о том, что традиционная и уточненная постановки задачи могут приводить к существенно различным результатам расчета контактных характеристик вязкоупругого слоя. Например, на рис. 3 для значения ${{r}^{\infty }} = 0.9{\kern 1pt} {\kern 1pt} {{r}_{{ec}}}$ диссипация энергии ${{d}^{\infty }}$, определенная в рамках уточненной постановки задачи, существенно превосходит величину ${{d}^{\infty }}$, полученную при традиционной постановке. Однако для значения ${{r}^{\infty }} = {{r}_{{ec}}}$ ситуация меняется, и уже традиционная постановка задачи дает более высокие значения ${{d}^{\infty }}$.

5. Выводы. 1. Рассмотрен контакт индентора с вязкоупругим слоем в рамках самосогласованного по Дерягину подхода с поверхностным (традиционная постановка) и объемным (уточненная постановка) приложением сил межмолекулярного взаимодействия. В случае бесконечно протяженного плоского индентора построены аналитические выражения для компонент НДС слоя.

2. Получены формулы для интенсивности касательных напряжений и диссипации энергии в вязкоупругом слое. Выявлены некоторые особенности зависимостей этих величин от параметров режима нагружения.

3. Показано, что традиционная и уточненная постановки задачи могут приводить к существенно различным результатам расчета контактных характеристик вязкоупругого слоя.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (18-58-00014, 18-08-00558).