1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 3, 2019

Прикладная математика и механика, 2019, T. 83, № 3, стр. 478-483

НЕКОТОРЫЕ ОСОБЕННОСТИ ГИДРОДИНАМИЧЕСКОЙ НЕУСТОЙЧИВОСТИ ТЕЧЕНИЯ ТЕРМОВЯЗКОЙ ЖИДКОСТИ В ПЛОСКОМ КАНАЛЕ

В. Н. Киреев 1, А. Д. Низамова 2, С. Ф. Урманчеев 2, *

1 Башкирский государственный университет
Уфа, Россия

2 Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия

* E-mail: said@anrb.ru

Поступила в редакцию 04.03.2019
После доработки 16.03.2019
Принята к публикации 19.03.2019

Полный текст (PDF)

Аннотация

Исследуется влияние экспоненциальной зависимости вязкости несжимаемой жидкости от температуры на критические параметры гидродинамической устойчивости течения в плоском канале при заданных разных значениях температуры стенок. Считается, что возмущения температурного поля отсутствуют. При достаточно больших числах Пекле построены спектры собственных значений для обобщенного уравнения Орра–Зоммерфельда. Показано, что структура спектров, кривые нейтральной устойчивости и критическое число Рейнольдса в значительной степени зависят от свойств жидкости, определяемых показателем экспоненциальной функции вязкости.

Ключевые слова: термовязкая жидкость, критическое число Рейнольдса, гидродинамическая неустойчивость

Введение. В реальных условиях вязкость жидкости как один из параметров, в основном определяющих закономерности течения, весьма чувствителен к изменению температуры. В большинстве моделей зависимость вязкости от температуры имеет вид экспоненциально убывающих функций (модели аррениусовского типа [1]). Был проведен детальный анализ теплообменных процессов и пристеночного трения в трубах при турбулентных течениях жидкостей с физическими параметрами, зависящими от температуры [2]. По всей видимости, наиболее полно современная теория течения вязких жидкостей при наличии теплопроводности и теплообмена изложена Р.Х. Зейтуняном [3, 4].

Был проведен достаточно подробный численный анализ влияния параметров температурной зависимости вязкости на режимы течения в плоских каналах и показано, что профиль скорости может значительно отличаться от пуазейлевского, а относительный расход жидкости в канале теплообменника имеет ярко выраженную зависимость от характера изменения вязкости [5]. Дальнейшие усложнения моделей, включающие немонотонную (аномальную) зависимость вязкости от температуры, привели к установлению целого ряда особенностей течения жидкостей в неоднородном температурном поле [6]. Описаны четыре режима установления потока аномально термовязкой жидкости в зависимости от интенсивности теплообмена, определяемого числом Нуссельта [7].

Хорошо известно, что задача об устойчивости ламинарного течения несжимаемой жидкости с постоянной вязкостью описывается уравнением Орра–Зоммерфельда [8, 9]. В качестве профиля скорости обычно используют профиль течения Пуазейля. Если однако вязкость жидкости зависит от температуры, то профиль скорости необходимо привести в соответствие с законом изменения вязкости, что и было сделано, по-видимому, впервые [10]. При этом многие исследователи придерживались подхода, использующего некоторую модификацию пуазейлевского профиля (например, [11]). Достаточно корректный подход и детальные исследования были предложены Уоллом и Уилсоном [12], получившими “термическое уравнение Орра–Зоммерфельда” и выполнившими большое число расчетов, связанных с сопоставлением с результатами других авторов.

Были получены [13–16] некоторые оценки распределения параметров течения в канале теплообменника и появления неустойчивых режимов течения термовязких жидкостей.

1. Неизотермическая модель ламинарного течения. Исследуется течение несжимаемой ньютоновской термовязкой жидкости в плоском канале при заданных разных температурах его стенок. Поместим начало декартовой системы координат x, y на среднюю линию канала и направим ось x параллельно стенкам. Введем обозначения: ρ – постоянная плотность жидкости, ${\mathbf{v}} = (u,{v})$ – вектор скорости, p – давление, T – температура, μ(T) – динамическая вязкость, $\alpha $ – коэффициент температуропроводности и перейдем к безразмерным переменным следующим образом:

$\hat {x} = \frac{{2x}}{H},\quad \hat {y} = \frac{{2y}}{H},\quad \hat {t} = \frac{{2{{u}_{m}}t}}{H},\quad \hat {p} = \frac{p}{{\rho u_{m}^{2}}}$
$\hat {u} = \frac{u}{{{{u}_{m}}}},\quad {\hat {v}} = \frac{{v}}{{{{u}_{m}}}},\quad \hat {T} = \frac{{T - {{T}_{c}}}}{{{{T}_{h}} - {{T}_{c}}}},\quad \hat {\mu } = \frac{\mu }{{{{\mu }_{m}}}},$
где H – ширина канала, ${{u}_{m}}$ – характерная скорость, ${{{\mu }}_{m}}$ – характерная вязкость.

Исходная система уравнений Навье–Стокса и уравнение сохранения энергии могут быть записаны в виде (крышки над безразмерными величинами далее опущены)

$\nabla \times {\mathbf{v}} = 0,\quad \frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \times \nabla ){\mathbf{v}} = - \nabla p + \frac{1}{{\operatorname{Re} }}\nabla (\mu (T){\mathbf{v}}),\quad \operatorname{Re} = \frac{{\rho {{u}_{m}}H}}{{2{{\mu }_{m}}}}$
$\frac{{\partial T}}{{\partial t}} + ({\mathbf{v}} \times \nabla )T = \frac{1}{{\operatorname{Pe} }}\Delta T,\quad \operatorname{Pe} = \frac{{{{u}_{m}}H}}{{2\alpha }},$
где Re и Pe – числа Рейнольдса и Пекле.

Стационарное невозмущенное течение термовязкой жидкости в плоском канале при разных заданных температурах Th и Tc его стенок определяется следующей системой обыкновенных дифференциальных уравнений:

(1.1)
$ - \frac{{dp}}{{dx}} + \frac{d}{{dy}}\left( {{{\mu }^{0}}\frac{{d{{u}^{0}}}}{{dy}}} \right) = 0,\quad \frac{{{{d}^{2}}{{T}^{0}}}}{{d{{y}^{2}}}} = 0$
с граничными условиями
(1.2)
${{u}^{0}}(1) = 0,\quad {{u}^{0}}( - 1) = 0,\quad {{T}^{0}}(1) = {{T}_{h}},\quad {{T}^{0}}( - 1) = {{T}_{c}},$
где T – температура, u – продольная компонента вектора скорости, $dp{\text{/}}dx$ = const – заданный перепад давления. Верхний индекс “0” относится к невозмущенному потоку.

Для безразмерных уравнений (1.1) с граничными условиями (1.2) получено точное решение.

Используя второе уравнение (1.1) и принимая во внимание граничные условия, легко обнаружить, что невозмущенная температура изменяется линейно по сечению канала. Для аналитического решения первого уравнения (1.1) необходимо указать конкретную форму зависимости вязкости от температуры.

Рассмотрим экспоненциальную зависимость вязкости от температуры в виде

(1.3)
${{\mu }_{e}}(T) = \exp ( - {{\alpha }_{e}}T),\quad {{\alpha }_{e}} = \operatorname{const} $

В этом случае решение первого уравнения (1.1) имеет для профиля скорости вид

(1.4)
$u_{0}^{e} = \frac{{\operatorname{Re} }}{{{{\alpha }_{e}}}}\frac{{dp}}{{dx}}\left[ {\frac{{2\exp ({{\alpha }_{e}}) - (1 + \exp (2{{\alpha }_{e}})\exp ({{\alpha }_{e}}y))}}{{\exp ( - {{\alpha }_{e}}) - \exp ({{\alpha }_{e}})}} - y\exp ({{\alpha }_{e}}(1 + y))} \right]$
и показано в левой части рис. 1.

Рис. 1.

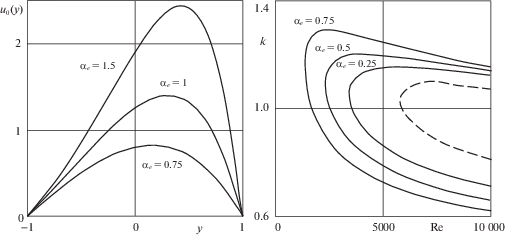
Профили скоростей невозмущенного течения (слева) и нейтральные кривые (справа) при разных значениях параметра αe; штрихами показана нейтральная кривая в случае постоянной вязкости.

2. Результаты анализа устойчивости. Используя стандартный подход к исследованию гидродинамической устойчивости, полагаем

$u = {{u}_{0}}(y) + \tilde {u}(x,y,t),\quad {v} = {\tilde {v}}(x,y,t),\quad p = {{p}_{0}}(x) + \tilde {p}(x,y,t),\quad T = {{T}_{0}}(y),$
где $\tilde {u}(x,y,t)$, ${\tilde {v}}(x,y,t)$ и $\tilde {p}(x,y,t)$ – возмущения продольной и поперечной скоростей и давления; ради простоты полагаем отсутствие возмущений температурного поля (что далеко от реальности и снижает практическую ценность результатов). Используем возмущения в виде бегущей волны
$\tilde {u} = \varphi (y)\exp (ik(x - ct)),\quad \tilde {p} = \psi (y)\exp (ik(x - ct)),$
где $\varphi (y)$ и $\psi (y)$ – амплитуды возмущений скорости и давления.

Таким образом, уравнение для возмущения амплитуды поперечной скорости и граничные условия принимают вид

(2.1)
$\begin{gathered} {{\mu }_{0}}[{{\varphi }^{{{\text{IV}}}}} - 2{{k}^{2}}\varphi {\text{''}} + {{k}^{4}}\varphi ] - ik\operatorname{Re} [({{u}_{0}} - c)(\varphi {\text{''}} - {{k}^{2}}\varphi ) - u_{0}^{{''}}\varphi ] + \\ + \;2\mu _{0}^{'}(\varphi {\text{'''}} - {{k}^{2}}\varphi {\text{'}}) + \mu _{0}^{{''}}(\varphi {\text{''}} + {{k}^{2}}\varphi ) = 0 \\ \end{gathered} $
(2.2)
$\varphi ( - 1) = \varphi (1) = 0,\quad \varphi {\text{'}}( - 1) = \varphi {\text{'}}(1) = 0$

Уравнение (2.1) можно рассматривать как обобщенное уравнение Орра–Зоммерфельда для термовязкой жидкости, которое легко сводится к классическому уравнению Орра–Зоммерфельда при изотермическом течении, а при течении термовязких жидкостей характеризует изменение вязкости по сечению канала. Численное решение задачи получаем с использованием спектрального метода, определяя собственные значения и собственные функции.

Анализ полученных результатов показывает, что при сделанных допущениях спектр собственных значений при малых значениях параметра αe качественно совпадает со спектром, соответствующим классическому уравнению Орра–Зоммерфельда [8]. Собственные значения приближаются к действительной оси, группируются вдоль одной вертикальной ветви, а затем распределяются по двум ветвям справа и слева. При увеличении параметра αe спектр собственных значений существенно изменяется: при достаточно больших αe нижняя вертикальная ветвь начинает распадаться на несколько отдельных ветвей. Кроме того, имеется собственное значение с положительной мнимой частью, которое соответствует неустойчивому режиму термовязкого течения при выбранных значениях числа Рейнольдса и волнового числа.

В правой части рис. 1 показаны кривые нейтральной устойчивости течения жидкости с постоянной вязкостью (штриховая кривая) и течения термовязкой жидкости с профилем скорости (1.4) (сплошные кривые) для разных значений параметра αe. Нейтральные кривые, построенные для термовязких жидкостей с легко определяемой средней вязкостью по поперечному сечению канала, совпадают с нейтральной кривой для классического уравнения Орра–Зоммерфельда и имеют одинаковое критическое число Рейнольдса Rec = 5772.

На рис. 2 представлена зависимость волнового числа k от критического числа Рейнольдса Rec (слева) и зависимость критического числа Рейнольдса от параметра αe (справа) для течения термовязкой жидкости (светлые точки) и течения жидкости с постоянной вязкостью (черная точка).

Рис. 2.

Зависимость волнового числа k от критического числа Рейнольдса Rec (слева) и зависимость критического числа Рейнольдса от параметра αe (справа) для течения термовязкой жидкости (светлые точки) и течения жидкости с постоянной вязкостью (черная точка).

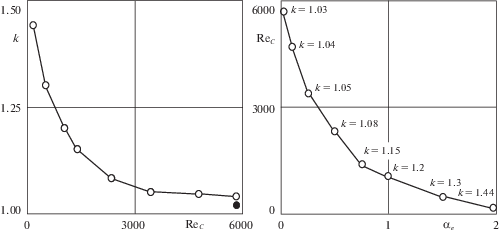
Видно, что при выборе средних значений вязкости волновые числа идентичны и приблизительно равны значению k = 1.03, как и в классической теории, и не зависят от Rec. С другой стороны, при изменении вязкости по сечению канала волновое число – экспоненциально убывающая функция от Rec.

Заключение. Установлено, что использование усредненной вязкости по сечению нагревательного или охлаждающего канала некорректно при определении критического числа Рейнольдса. Учет зависимости вязкости от температуры довольно сильно влияет на выводы относительно гидродинамической устойчивости, что, безусловно, важно при анализе режимов течения в теплообменниках. Вместе с тем предположение об отсутствии возмущений температуры, сделанное вопреки реальности при анализе устойчивости, не дает возможности получить выводы количественного характера.

Исследования С.Ф. Урманчеева и А.Д. Низамовой выполнены за счет средств Государственного задания 2019–2022 гг. (№ 0246-2019-0052). Исследования В.Н. Киреева выполнены при финансовой поддержке Российского фонда фундаментальных исследований (грант 17-41-020999).

Список литературы

  1. Френкель Я.И. Кинетическая теория жидкостей. Ленинград: Наука, 1975. 592 с.

  2. Petukhov B.S. Heat transfer and friction in turbulent pipe flow with variable physical properties // Adv. Heat Transfer. 1970. V. 6. P. 503–564.

  3. Zeytounian R.Kh. Theory and Application of Viscous Fluid Flows. Berlin: Springer, 2004. 491 p.

  4. Zeytounian R.Kh. Navier–Stokes–Fourier Equations, a Rational Asymptotic Modelling Point of View. Berlin: Springer, 2012. 290 p.

  5. Урманчеев С.Ф., Киреев В.Н. О влиянии температурной зависимости вязкости на течение жидкости // Нефтегаз. дело. 2004. № 2. С. 287–295.

  6. Урманчеев С.Ф., Киреев В.Н. Установившееся течение жидкости с температурной аномалией вязкости // Доклады РАН. 2004. Т. 396. № 2. С. 204–207.

  7. Urmancheev S.F., Kireev V.N. The transient flow of liquid with non–monotonous temperature dependent viscosity in a plane channel // AIP Conf. Proc. 1906, 2017. P. 200009-1–4.

  8. Orszag S.A. Accurate solution of the Orr–Sommerfeld equation // J. Fluid Mech. 1971. V. 50. P. 689–703.

  9. Дразин Ф. Введение в теорию гидродинамической устойчивости. Москва: Физматлит, 2005. 288 с.

  10. Yih C.S. Thermal instability of viscous fluids // Quart. Appl. Math. 1959. V. 17. P. 25–42.

  11. Potter M.C., Graber E. Stability of plane Poiseuille flow with heat transfer // Phys. Fluids. 1972. V. 15. P. 387–391.

  12. Wall D.P., Wilson S.K. The linear stability of channel flow of fluid with temperature-dependent viscosity // J. Fluid Mech. 1996. V. 323. P. 107–132.

  13. Низамова А.Д., Киреев В.Н., Урманчеев С.Ф. Об устойчивости ламинарного режима течения термовязких жидкостей // Вестн. ТюмГУ. 2015. Т. 1. № 2. С. 104–111.

  14. Низамова А.Д., Киреев В.Н., Урманчеев С.Ф. Некоторые точные решения стационарной системы уравнений для стратифицированного течения двух термовязких жидкостей // Вестн. УГАТУ. 2016. Т. 20. № 2. С. 90–95.

  15. Kireev V.N., Nizamova A.N., Urmancheev S.F. Instabilities in stratified two thermoviscous liquids flow in a plane channel // Proc. 9th Int. Conf. Multiphase Flow, Florence, Italy CD 4. 2016.

  16. Kulikov Y.M., Son E.E. Stability of thermoviscous fluid flow under high temperature gradients // High Temp. 2017. V. 55. P. 131–138.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал