1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2022

Известия РАН. Механика жидкости и газа, 2022, № 6, стр. 26-33

ЗАДАЧА О БЛОКИРОВАНИИ ТЕХНОГЕННОЙ ТРЕЩИНЫ В ПЛАСТЕ СУСПЕНЗИОННОЙ СМЕСЬЮ

А. Я. Гильманов a, *, К. М. Федоров a, **, А. П. Шевелев a, ***

a Физико-технический институт, Тюменский государственный университет
Тюмень, Россия

* E-mail: a.y.gilmanov@utmn.ru
** E-mail: k.m.fedorov@utmn.ru
*** E-mail: alexandershevelev@mail.ru

Поступила в редакцию 03.05.2022
После доработки 13.06.2022
Принята к публикации 21.06.2022

Полный текст (PDF)

Аннотация

Рассматривается решение задачи о блокировании техногенной трещины в пласте суспензионной смесью. Используется математическая модель, основанная на законах сохранения массы дисперсных частиц и несущей жидкости. Скорость течения дисперсных частиц по трещине рассчитывается из закона Пуазейля, отток несущей жидкости в пласт описывается законом Дарси. Определено наличие контактного разрыва, соответствующего переднему фронту оторочки суспензии. Показано, что при достижении фронтом оторочки суспензии конца трещины начинается движение отраженной волны в виде разрыва объемной доли дисперсных частиц навстречу потоку, трещина начинает блокироваться с этого конца. Установлено, что продвижение обратной волны постепенно замедляется, поэтому заблокировать всю трещину оказывается проблематичным.

Ключевые слова: закон сохранения массы, техногенная трещина, дисперсные частицы, объемное содержание частиц в потоке, распределение давления, контактный разрыв, отраженная волна

В нефтяном пласте могут иметься пропластки суперколлекторов с проницаемостью, в сотни и тысячи раз превышающей проницаемость остальной части пласта, а также высокопроводящие каналы, вызванные региональной трещиноватостью определенного направления. При превышении давлением закачки воды критической величины происходит образование трещины гидроразрыва пласта (ГРП) или автогидроразрыва пласта (автоГРП), что сводит на нет достоинства технологии заводнения. Закачиваемая вода быстро прорывается в добывающие скважины, приводя к значительному обводнению продукции и снижению коэффициента охвата пласта заводнением. Примерами такого развития событий при заводнении являются наличие суперколлектора на Талинской площади [1], развитие трещин автоГРП на Приобском месторождении [2] и ряд других случаев.

Мероприятиями, препятствующими такому развитию событий, являются так называемые потокоотклонящие технологии (ПОТ) [3]. Основой этих технологий является закачка реагентов, в первую очередь, суспензий, проникающих в каналы и трещины с высокой проводимостью, но не способных фильтроваться в основной массе пласта.

В данной работе рассматривается задача о блокировании частично или полностью трещины автоГРП. Определение давления образования автоГРП обычно проводится с использованием двухшагового расходного теста [4]. В ходе этого теста при переходе от одного шага к другому расход закачиваемой воды изменяется и измеряется динамика забойного давления. Отслеживание динамики развития трещины автоГРП и оценка ее параметров осуществляются в ходе регистрации непрерывной кривой изменения давления во времени в процессе смены режимов работы скважины [5]. Контроль за возникновением и развитием трещины автоГРП в промысловых условиях можно проводить методом гидропрослушивания [6]. Более полную информацию по образованию трещин автоГРП дают керновые исследования, например, с помощью бразильского теста [7], в ходе которого керн сжимается в диаметральной плоскости.

Исследования на керне не позволяют детально отследить динамику развития трещины автоГРП на больших масштабах, поэтому актуальным является математическое моделирование этого процесса. В [8] предлагается полуаналитическая модель распространения трещины автоГРП на основе теории напряженного состояния Био [9], которая определяет режим развития трещины. Кроме того, ряд работ [10–12] посвящен применению геомеханического подхода для определения размеров трещины ГРП. Существуют трехмерные модели [13] для описания динамики развития трещины ГРП на основе такого подхода. В [11] отмечается, что скорость закачки реагента в трещину ГРП влияет на ее форму. Геомеханический подход также позволяет оценить взаимодействие трещины ГРП с естественными трещинами в пласте [14]. В целом такой подход позволяет найти параметры трещины ГРП или автоГРП и спрогнозировать ее развитие, но не описывает движения флюида в трещине.

Подходы механики многофазных систем нашли широкое применение к задачам о вытеснении одного флюида другим в пористой среде [15–17]. Развитие этих подходов с учетом эллиптического контура питания позволяет решить задачу о притоке флюида к скважине при наличии трещины ГРП [18]. Кроме того, существуют математические модели, описывающие течение флюида в трещине при воздействии электромагнитным полем [19]. Рассмотренные модели, однако, не описывают блокирования трещины автоГРП, что может быть необходимо для предотвращения притока воды в реагирующие добывающие скважины для снижения обводненности продукции. Решение указанной задачи приводится впервые в настоящей статье.

Для оценки влияния параметров трещины на обводненность окружающих добывающих скважин необходимо рассмотреть секторную модель пласта вблизи трещины. По промысловым данным в результате образования трещин автоГРП эффективность закачки воды может снизиться до 50% из-за более быстрого прорыва воды по трещине [20]. Для оценки влияния трещин автоГРП в работе [21] вводится безразмерный параметр эффективности заводнения. Этот коэффициент показывает отношение объема закачанной воды в идеальном случае, рассчитанном по уравнению материального баланса, к фактическому объему закачки воды.

Модели блокирования трещин рассматривают поток жидкости в трещине с учетом транспорта реагента и оттока воды из боковых стенок трещины в пласт. Как правило, рассматриваются одномерные течения как внутри трещины, так и в пласте. В [22] разработана модель блокирования трещины гелеобразующим составом, в которой координата фронта закачиваемого геля в трещине рассчитывается из уравнения материального баланса. Модель также позволяет определить проницаемость трещины с учетом наличия геля в ней.

Более сложные модели, которые можно применить для описания рассматриваемого процесса, рассматривают размещение, например, проппанта в трещине ГРП как течение суспензии [23–25]. В работе предлагается развитие этого направления для описания процесса блокирования техногенной трещины полимер-дисперсной смесью. Такое описание предлагается впервые. В качестве дисперсных частиц применяются частицы каолинитовой глины, мела или древесной муки [26].

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ БЛОКИРОВАНИЯ ТРЕЩИНЫ СУСПЕНЗИОННЫМ СОСТАВОМ

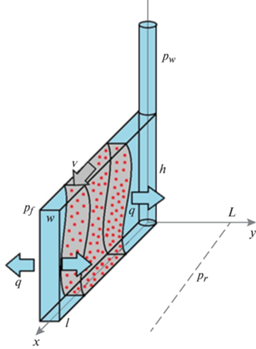
Рассматривается задача о линейном одномерном потоке суспензии по трещине прямоугольной формы с длиной l, шириной w и высотой h, рис. 1. Трещина находится вблизи нагнетательной скважины. На контуре питания трещины L (половине расстояния между боковой границей трещины и ближайшей реагирующей добывающей скважиной) давление равно pr, на конце трещины давление неизвестно и определяется переменной pf. Суспензия закачивается при постоянном давлении на забое скважины pw и движется по трещине со скоростью v. Отток жидкости из трещины через боковые поверхности трещины обозначен переменной q. Вводится декартовая прямоугольная система координат с осью x, направленной вдоль трещины, и осью y, перпендикулярной ей.

Рис. 1.

Схематическое представление задачи о блокировании трещины автоГРП.

Суспензия состоит из недеформируемых частиц, стабилизированных в водной фазе с примесью полимера или мягкого полимерного геля. Объемное содержание частиц в потоке равно α, полный расход суспензии по трещине составляет Q = hw${v}$. Для трещины характерно отсутствие механизмов застревания частиц. Поток рассматривается в гомогенном приближении, когда скорости движения частиц и несущей фазы равны. Несущая жидкость движется по трещине и уходит в пласт за счет разности пластового давления и давления в трещине, отток несущей жидкости q происходит через обе боковые стенки трещины. С учетом этих допущений уравнения сохранения массы частиц и несущей жидкости имеют вид

(1.1)
$\frac{{\partial \left( {hw\alpha } \right)}}{{\partial t}} + \frac{{\partial \left( {hw\alpha {v}} \right)}}{{\partial x}} = 0$
(1.2)
$\frac{{\partial \left( {hw\left( {1 - \alpha } \right)} \right)}}{{\partial t}} + \frac{{\partial \left( {hw\left( {1 - \alpha } \right){v}} \right)}}{{\partial x}} = - q$
где t – время.

Движение суспензии по трещине рассматривается в безынерционном приближении, при котором уравнение сохранения импульса записывается из решения задачи о движении вязкой жидкости при ламинарном течении в параллелепипеде. Это решение имеет вид

(1.3)
${v} = - \frac{{{{w}^{2}}}}{{12\mu }}\frac{{\partial p}}{{\partial x}}$
где μ – вязкость несущей фазы, p – давление в трещине.

Отток несущей жидкости в пласт также полагается линейным, но в перпендикулярном направлении и определяется законом Дарси

(1.4)
$q = \frac{{k{{h}_{e}}}}{{\mu L}}\left( {p - {{p}_{r}}} \right)$
где k – проницаемость пласта, he – эффективная мощность пласта (за вычетом глинистых пропластков).

Рассматриваемая задача расщепляется на две: определение распределения давления в трещине и транспорт частиц в трещине.

2. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ В ТРЕЩИНЕ

Первая задача определяется уравнением для суммарного потока суспензии или суммой уравнений (1.1) и (1.2), в которое подставляются выражения скоростей потока по трещине и отток в пласт

(2.1)
$\frac{{{{d}^{2}}p}}{{d{{x}^{2}}}} = \frac{{12k{{h}_{e}}}}{{{{w}^{3}}Lh}}\left( {p - {{p}_{r}}} \right)$

Для решения полученного уравнения необходимо два граничных условия. Первое определяется постоянством давления закачки суспензии в трещину. В качестве второго условия принимается равенство потока, подаваемого в трещину, и интегральной величины оттока жидкости в пласт

(2.2)
$x = 0:p = {{p}_{w}},\quad - {{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{{x = 0}}} = \frac{{24k{{h}_{e}}}}{{\left( {1 - {{\alpha }_{0}}} \right){{w}^{3}}Lh}}\int\limits_0^l {\left( {p - {{p}_{r}}} \right)} dx$
где α0 – объемная доля дисперсных частиц в закачиваемой суспензии.

Эти граничные условия справедливы до тех пор, пока частицы суспензии не достигнут конца трещины. После этого момента трещина начинает блокироваться с конца, и ее размер сокращается до переменной величины xf. Соответственно верхний предел интеграла в краевом условии (2.2) становится равен xf.

Решение дифференциального уравнения (2.1) с учетом краевых условий (2.2) имеет вид

(2.3)
$p = \frac{{{{p}_{f}} - {{p}_{r}} - a\Delta p}}{{1 - {{a}^{2}}}}{{a}^{{ - \left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} - 1} \right)}}} + \frac{{a\left( {{{p}_{r}} - {{p}_{f}}} \right) + \Delta p}}{{1 - {{a}^{2}}}}{{a}^{{{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}} + {{p}_{r}}$
где введены обозначения $\Delta p = {{p}_{w}} - {{p}_{r}}$, $a = \exp ( - l\sqrt {{{12k{{h}_{e}}} \mathord{\left/ {\vphantom {{12k{{h}_{e}}} {({{w}^{3}}Lh)}}} \right. \kern-0em} {({{w}^{3}}Lh)}}} )$.

Значение давления на конце трещины определяется подстановкой выражения (2.3) во второе краевое условие (2.2):

(2.4)
${{p}_{f}} = \frac{{D\left( {\Delta p + 2{{p}_{r}}a + a\Delta p} \right) + 2{{p}_{r}} - {{p}_{w}}}}{{1 + 2Da}}$

В формуле (2.4) введен безразмерный комплекс $D = \frac{{h\left( {1 - {{\alpha }_{0}}} \right)}}{{2{{h}_{e}}{{{\left( {1 - a} \right)}}^{2}}}},$ характеризующий степень падения давления в трещине в зависимости от соотношения проводимости пласта и трещины.

3. ОСНОВНЫЕ ЭФФЕКТЫ ПРИ ЗАКАЧКЕ ОТОРОЧКИ СУСПЕНЗИИ В ТРЕЩИНУ

Рассмотрим случай закачки суспензии, состоящей из частиц глины и водного раствора полиакриламида, препятствующего гравитационной сегрегации суспензии в скважине и трещине. Расчеты проведены для модельных значений параметров пласта, трещины и суспензии: k = 100 мД, α0 = 0.03, w = 2 мм, l = 200 м, L = 500 м, μ = 1 мПа ∙ с, pw = 35 МПа, pr = 25 МПа, h = 40 м, he = 30 м.

Кроме распределения давления в трещине, интерес представляют отток жидкости из трещины и расход суспензии по трещине. Эти параметры можно получить из решения (2.3), подставляя его в формулы (1.3) и (1.4).

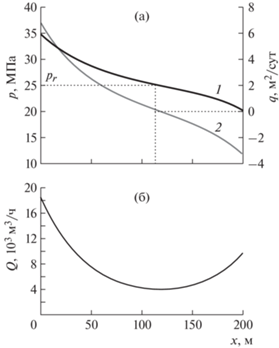
В зависимости от величины введенного безразмерного параметра D возможны следующие сценарии. При D > 1 по мере закачки суспензии несущая жидкость движется по трещине, частично отфильтровываясь в пласт. Давление вдоль трещины, интенсивность оттока несущей жидкости в пласт и скорость движения суспензии монотонно падают с ростом расстояния от скважины. Результаты расчетов давления в трещине и скорости оттока несущей фазы представлены на рис. 2а, а расхода суспензии в трещине – на рис. 2б.

Рис. 2.

(а) Распределение давления в трещине p (1) и оттока несущей жидкости в пласт q (2) при значении D > 1; (б) расход суспензии Q вдоль трещины.

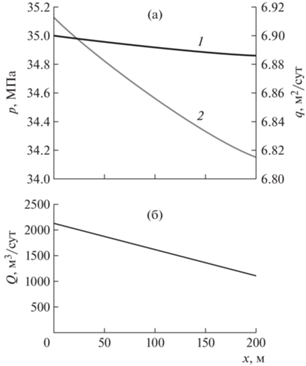
При высокой проницаемости пласта давление и значении параметра D < 1 в трещине может снижаться ниже пластового, тогда на конце трещины наблюдается приток жидкости в пласт. Пример такого расчета приведен на рис. 3, где проницаемость пласта принималась равной 160 Д или 1.6 × 10–10 м2, а параметр D становится меньше единицы. В этом случае расход суспензии в трещине становится немонотонным: его снижение происходит в начале трещины, а в области снижения давления в трещине ниже пластового (рис. 3а), наоборот, начинает расти (рис. 3б).

Рис. 3.

(а) Распределение давления в трещине p (1) и оттока несущей жидкости в пласт q (2) при значении D < 1; (б) расход суспензии Q вдоль трещины.

4. ДВИЖЕНИЕ ОТОРОЧКИ ПО ТРЕЩИНЕ И ЕЕ БЛОКИРОВАНИЕ

Вторая задача состоит в определении эволюции оторочки частиц суспензии. При известном выражении для скорости потока суспензии в трещине (1.3) с учетом (2.3) уравнение переноса частиц суспензии (1.1) можно представить в характеристическом виде

(4.1)
$\begin{array}{*{20}{c}} {\frac{{dx}}{{dt}} = {v}:}&{\frac{{d\alpha }}{{dt}} = - \alpha \frac{{d{v}}}{{dx}}} \end{array}$

Согласно этому решению, передний фронт оторочки суспензии представляет собой контактный разрыв, движущийся с переменной скоростью, траектория которого определяется формулой

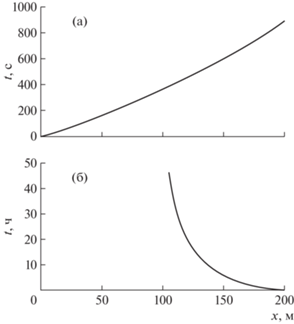
$t = \frac{{wLh\mu \left( {1 - {{a}^{2}}} \right)}}{{k{{h}_{e}}\sqrt { - \gamma \beta } }}\left( {\ln \left| {\frac{{1 + \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} {{a}^{{ - {x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}}}}{{1 - \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} {{a}^{{ - {x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}}}}} \right| - \ln \left| {\frac{{1 + \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} }}{{1 - \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} }}} \right|} \right)$
где введены обозначения $\beta = \left( {{{p}_{r}} - {{p}_{f}}} \right)a + {{a}^{2}}\Delta p$, $\gamma = \Delta p + \left( {{{p}_{r}} - {{p}_{f}}} \right)a$.

Расчетная траектория для приведенных параметров приведена на рис. 4a. Вдоль этой траектории объемное содержание частиц возрастает за счет оттока несущей жидкости в пласт. Решение для эволюции объемной доли частиц на фронте имеет вид:

$\alpha = {{\alpha }_{0}}\exp \left( { - \frac{{k{{h}_{e}}t}}{{wLh\mu (1 - {{a}^{2}})}}(\left( {{{p}_{r}} - {{p}_{f}}} \right)({{a}^{{ - \left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} - 1} \right)}}} - {{a}^{{\left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} + 1} \right)}}}) + \Delta p({{a}^{{ - \left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} - 2} \right)}}} - {{a}^{{{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}}))} \right)$
Рис. 4.

(а) Траектория движения контактного разрыва, соответствующего переднему фронту оторочки; (б) траектория разрыва, разделяющего зону заблокированной трещины и зону притока суспензии.

Для реалистичного случая низкопроницаемого пласта, где в основном и появляются трещины автоГРП, объемная доля частиц на контактном фронте монотонно растет, а скорость фронта падает. Этот случай представлен на рис. 5а.

Рис. 5.

(а) Движение оторочки суспензии по трещине при D > 1; (б) движение оторочки суспензии по трещине при D < 1. На рис. 5 а приведены кривые для следующих моментов времени: 100 с (1), 300 с (2), 500 с (3) и момента времени t0 (4), когда фронт объемной доли дисперсных частиц достигает правой границы трещины. На рис. 5 б приведены кривые для следующих моментов времени: 1.25 с – 1, 2.5 с – 2, 3.75 с – 3, 6 с – 4, 7 с – 5, 8 с – 6 и момента времени t0 – 7, когда фронт объемной доли дисперсных частиц достигает правой границы трещины.

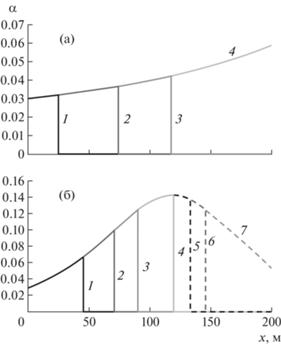
В случае D < 1 продвижение фронта постепенно замедляется, а объемная доля дисперсных частиц на фронте возрастает, пока идет отток несущей фазы в пласт и давление в трещине превосходит пластовое. Как только давление в трещине становится меньше пластового, рис. 3а, начинается приток несущей фазы в трещину, из-за этого объемная доля дисперсных частиц на фронте снижается, рис. 5б, причем, в силу увеличения скорости потока в трещине, движение фронта ускоряется, рис. 5б.

Принципиальной особенностью процесса является установление стационарного распределения объемной доли дисперсных частиц в трещине на момент подхода фронта к ее концу. В дальнейшем эта особенность используется для упрощения процедуры получения полуаналитического решения.

При t = to – в момент подхода контактного разрыва к концу трещины x = l  формируется разрыв объемной доли частиц, в котором перед фронтом разрыва α = α–, а за разрывом α = 1. Значение объемной доли частиц перед разрывом α– определяется решением характеристической системы (4.1). Сформировавшийся разрыв движется как отраженная волна навстречу потоку, условия на разрыве имеют вид

(4.2)
$(1 - {{\alpha }^{ - }})\frac{{d{{x}_{f}}}}{{dt}} + {{{v}}^{ - }}{{\alpha }^{ - }} = 0$
где ${{{v}}^{ - }}$ – значение скорости перед разрывом.

После этого момента давление pf на фронте заблокированной зоны xf становится величиной, зависящей от времени. Неявная зависимость от времени появляется при интегрировании краевого условия (2.2) по интервалу от 0 до xf. После подстановки в (4.2) результата интегрирования по переменному интервалу можно получить уравнение для определения xf от времени. К сожалению, указанная процедура чрезвычайно громоздкая, поэтому решение для α– аппроксимировано квадратичной функцией с квадратом коэффициента корреляции R2 = 0.9992

${{\alpha }^{ - }} = {{F}_{1}}{{x}^{2}} + {{F}_{2}}x + {{\alpha }_{0}}$
где F1, F2 – числовые коэффициенты, для рассматриваемого случая они равны F1 = 4 × 10–7 1/м2 и F2 = 5 × 10–5 1/м.

Решение уравнения (4.2) при условии xf(t0) = l имеет вид

(4.3)
$t = \int\limits_l^{{{x}_{f}}} {\frac{{(1 + 2{{e}^{{ - M{{x}_{f}}}}}\left( {B - 1} \right) + {{e}^{{ - 2M{{x}_{f}}}}})({{F}_{1}}x_{f}^{2} + {{F}_{2}}{{x}_{f}} + {{\alpha }_{0}} - 1)}}{{G(1 - {{e}^{{ - 2M{{x}_{f}}}}})({{F}_{1}}x_{f}^{2} + {{F}_{2}}{{x}_{f}} + {{\alpha }_{0}})}}d{{x}_{f}}} $
где введены обозначения $G = \sqrt {{{kw{{h}_{e}}} \mathord{\left/ {\vphantom {{kw{{h}_{e}}} {\left( {12Lh} \right)}}} \right. \kern-0em} {\left( {12Lh} \right)}}} {{\Delta p\left( {1 - B} \right)} \mathord{\left/ {\vphantom {{\Delta p\left( {1 - B} \right)} \mu }} \right. \kern-0em} \mu }$, $M = \sqrt {{{12k{{h}_{e}}} \mathord{\left/ {\vphantom {{12k{{h}_{e}}} {\left( {{{w}^{3}}Lh} \right)}}} \right. \kern-0em} {\left( {{{w}^{3}}Lh} \right)}}} $, $B = {{h\left( {1 - {{\alpha }_{0}}} \right)} \mathord{\left/ {\vphantom {{h\left( {1 - {{\alpha }_{0}}} \right)} {\left( {2{{h}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{h}_{e}}} \right)}}$.

Интеграл (4.3) определяется численно, например, по методу трапеций. Результаты расчетов динамики разрыва xf(t) представлены на рис. 4б. Как видно из полученного графика, скорость разрыва или расширения области блокирования трещины постепенно замедляется. Замедление разрыва или фронта блокирования трещины нарастает довольно быстро, что указывает на проблематичность полного блокирования трещины.

ЗАКЛЮЧЕНИЕ

Сформулирована задача о блокировании трещины автоГРП суспензией из частиц с размерами, превышающими размеры пор коллектора. Это позволяет продвинуть оторочку суспензии до конца трещины и затем начать ее блокирование.

Установлено, что для высокопроницаемых пластов возможен сценарий, когда несущая фаза отфильтровывается в пласт в начале трещины, в то время как пластовый флюид притекает в трещину ближе к ее концу. Выявлен безразмерный критерий подобия, когда возможна реализация этого сценария.

Выявлена структура решения задачи о блокировании трещины. На первом этапе суспензия движется с замедлением, но довольно быстро по трещине и достигает ее конца. На втором этапе формируется отраженная волна в виде разрыва, на котором и происходит блокирование трещины. Скорость этого разрыва замедляется, что показывает проблематичность полного блокирования трещины.

С использованием метода характеристик и уравнения на разрыве функций получены аналитические решения на всех этапах процесса.

Список литературы

  1. Волков В.П., Бриллиант Л.С. Геологические особенности коллекторов шеркалинской свиты Талинской площади // Нефтяное хозяйство. 2013. № 1. С. 18–22.

  2. Байков В.А., Бураков И.М., Латыпов И.Д., Яковлев А.А., Асмандияров Р.Н. Контроль развития техногенных трещин автоГРП при поддержании пластового далвения на месторождениях ООО “РН-Юганскнефтегаз” // Нефтяное хозяйство. 2012. № 11. С. 30–33.

  3. Ручкин А.А., Ягафаров А.К. Оптимизация применения потокоотклоняющих технологий на Самотлорском месторождении. Тюмень: Изд-во “Вектор Бук”, 2005. 165 с.

  4. Singh P., Agarwal R.G. Two-step rate test: new procedure for determining formation parting pressure // J. Pet. Technol. 1990. V. 42. № 1. P. 84–90. https://doi.org/10.2118/18141-PA

  5. Байков В.А., Давлетбаев А.Я., Усманов Т.С., Степанова З.Ю., Асмандияров Р.Н. Специальные гидродинамические исследования для мониторинга за развитием трещин ГРП в нагнетательных скважинах // Нефтегазовое дело. 2011. № 1. С. 65–77.

  6. Давлетбаев А.Я., Байков В.А., Бикбулатова Г.Р., Асмандияров Р.Н., Назаргалин Э.Р., Слабецкий А.А., Сергейчев А.В., Нуриев Р.И. Промысловые исследования по изучению самопроизвольного развития техногенных трещин в нагнетательных скважинах // Society of Petroleum Engineers. Статья с конференции SPE-171232-RU. 2014. С. 1–9. https://doi.org/10.2118/171232-RU

  7. Cheng C., Milsch H. Hydromechanical investigations on the self-propping potential of fractures in tight sandstones // Rock Mech. Rock Eng. 2021. V. 54. P. 5407–5432. https://doi.org/10.1007/s00603-021-02500-4

  8. Шель Е.В., Кабанова П.К., Ткаченко Д.Р., Базыров И.Ш., Логвинюк А.В. Моделирование инициации и распространения трещины гидроразрыва пласта на нагнетательной скважине для нетрещиноватых терригенных пород на примере Приобского месторождения // PROНЕФТЬ. Профессионально о нефти. 2020. № 2 (16). С. 36–42. https://doi.org/10.7868/S2587739920020056

  9. Николаевский В.Н. Геомеханика и флюидодинамика. М.: Недра, 1996. 447 с.

  10. Смирнов Н.Н., Тагирова В.Р. Автомодельные решения задачи о формировании трещины гидроразрыва в пористой среде // Изв. РАН. МЖГ. 2007. № 1. С. 70–82.

  11. Теодорович Э.В., Трофимов А.А., Шумилин И.Д. Форма плоской трещины гидроразрыва в упругой непроницаемой среде при различных скоростях закачки // Изв. РАН. МЖГ. 2011. № 4. С. 109–118.

  12. Байков В.А., Булгакова Г.Т., Ильясов А.М., Кашапов Д.В. К оценке геометрических параметров трещины гидроразрыва пласта // Изв. РАН. МЖГ. 2018. № 5. С. 64–75.

  13. Киселев А.Б., Ли Кайжуй, Смирнов Н.Н., Пестов Д.А. Моделирование течения жидкости в трещине гидроразрыва неоднородно трещиностойкого пласта в плоско-трехмерной постановке // Изв. РАН. МЖГ. 2021. № 2. С. 15–28.

  14. Акулич А.В., Звягин А.В. Взаимодействие трещины гидроразрыва с естественной трещиной // Изв. РАН. МЖГ. 2008. № 3. С. 104–112.

  15. Смирнов Н.Н., Никитин В.Ф., Коленкина (Скрылева) Е.И., Газизова Д.Р. Эволюция поверхности раздела фаз при вытеснении вязких жидкостей из пористой среды // Изв. РАН. МЖГ. 2021. № 1. С. 80–93.

  16. Голубятников А.Н., Смирнов Н.Н., Тагирова В.Р. Об оптимальной форме полости для сбора вязкой жидкости, насыщающей грунт // Изв. РАН. МЖГ. 2008. № 5. С. 113–119.

  17. Ентов В.М. Микромеханика течений в пористых средах // Изв. РАН. МЖГ. 1992. № 6. С. 90–102.

  18. Каневская Р.Д. О притоке жидкости к скважине с вертикальной трещиной гидроразрыва в кусочно-однородном анизотропном пласте // Изв. РАН. МЖГ. 1999. № 2. С. 64–71.

  19. Давлетбаев А.Я., Ковалева Л.А. Фильтрация высоковязкой нефти в пласте с трещиной гидроразрыва при воздействии высокочастотным электромагнитным полем // Изв. РАН. МЖГ. 2014. № 3. С. 91–97.

  20. Давлетова А.Р., Федоров А.И., Щутский Г.А. Анализ риска самопроизвольного роста трещины гидроразрыва пласта в вертикальном направлении // Нефтяное хозяйство. 2019. № 6. С. 50–53. https://doi.org/10.24887/0028-2448-2019-6-50-53

  21. Feng N., Chang Y., Wang Z., Liang T., Guo X., Zhu Y., Hu L., Wan Y. Comprehensive evaluation of waterflooding performance with induced fractures in tight reservoir: a field case // Geofluids. 2021. V. 2021. P. 1–11. https://doi.org/10.1155/2021/6617211

  22. Seright R. Gel propagation through fractures // Society of Petroleum Engineers. Conference paper SPE 59316. 2000. P. 1–9. https://doi.org/10.2118/59316-MS

  23. Татосов А.В., Шляпкин А.С. Движение проппанта в раскрывающейся трещине гидроразрыва пласта // Изв. Сарат. ун-та. Сер. Математика. Механика. Информатика. 2018. Т. 18. № 2. С. 217–226. https://doi.org/10.18500/1816-9791-2018-18-2-217-226

  24. Mobbs A.T., Hammond P.S. Computer simulations of proppant transport in a hydraulic fracture // SPE Prod. and Fac. 2001. V. 16, № 2. P. 112–121. https://doi.org/10.2118/69212-PA

  25. Dontsov E.V., Peirce A.P. Slurry flow, gravitational settling and a proppant transport model for hydraulic fractures // J. Fluid Mech. 2014. V. 760. P. 567–590. https://doi.org/10.1017/jfm.2014.606

  26. Газизов А.Ш., Низамов Р.Х. Оценка эффективности технологии применения полимер-дисперсной системы по результатам промысловых исследований // Нефтяное хозяйство. 1990. № 7. С. 49–52.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал