1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2022

Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 62-79

ИДЕНТИФИКАЦИЯ ХАРАКТЕРИСТИК СИЛОВОГО АЭРОДИНАМИЧЕСКОГО ВОЗДЕЙСТВИЯ НА КОЛЕБЛЮЩИЕСЯ КОНСОЛЬНО-ЗАКРЕПЛЕННЫЕ БАЛКИ

А. Н. Нуриев a, *, А. М. Камалутдинов b, **

a Казанский (Приволжский) федеральный университет
Казань, Россия

b Казанский национальный исследовательский технический университет им. А.Н. Туполева
Казань, Россия

* E-mail: Artem.Nuriev@kpfu.ru
** E-mail: amkamalutdinov@mail.ru

Поступила в редакцию 08.01.2022
После доработки 05.03.2022
Принята к публикации 05.03.2022

Полный текст (PDF)

Аннотация

Проводится экспериментальное и численное исследование взаимодействия длинных упругих балок с жидкостью в резонансных режимах колебания. Экспериментально изучаются затухающие изгибные колебания консольно-закрепленных тест-образцов в воздухе. С помощью МЭМС гироскопа регистрируются угловые скорости движения свободного конца консоли, с помощью дымовой визуализации проводится наблюдение течений в окрестности балки, индуцированных колебаниями. Строится квазиплоская математическая модель взаимодействия балка–жидкость, позволяющая по измеряемым логарифмическому декременту колебаний и относительному изменению частоты оценить силовое аэрогидродинамическое воздействие на балку. Проводится прямое трехмерное численное моделирование движения жидкости около консоли. По результатам численных и экспериментально-теоретических исследований выполняется анализ структуры течений и аэрогидродинамических сил, индуцированных колебаниями балки при разных параметрах колебаний. Исследуется применимость квазиплоской модели взаимодействия.

Ключевые слова: упругие колебания, нелинейное гидродинамическое воздействие, экспериментальная методика измерения, изгибные колебания, силы сопротивления, силы присоединенных масс

Упругие колебания балки в жидкости – это комплексный процесс, в рамках которого динамически деформируемое тело в каждой своей точке взаимодействует с вязкой средой, индуцируя в ней нелинейные течения (или изменяя их).Индуцированные течения, в свою очередь, влияют на частоту, амплитуду, профиль и другие параметры колебаний, а также могут возбуждать вторичные резонансы. Учет подобного взаимодействия имеет большое значение при проектировании широкого спектра инженерных конструкций, начиная от морских донных трубопроводов и нефтедобывающих платформ [1, 2], крыльев самолетов и топливных баков ракет [3–5], и заканчивая микроустройствами типа головок атомных резонансных микроскопов и “лабораторий на чипе” [6–8]. Настоящая работа посвящена исследованию резонансных изгибных колебаний длинных тонких балок в жидкости в диапазоне малых и умеренных чисел Рейнольдса.

В основе большинства традиционных подходов к изучению колебаний удлиненных балочных конструкций в жидкости лежит квазиплоская модель взаимодействия [9–15], согласно которой аэродинамическое воздействие, оказываемое на каждое сечение балки, можно считать результатом его плоского обтекания. Объединение этой модели с классической теорией колебания балок позволяет установить интегральные связи между параметрами колебания балки и гидродинамическими силами, действующими на нее со стороны жидкости (см., например, [9, 16]). Эта модель широко применяется для предсказания параметров колебания балки по данным двумерных расчетов обтекания колеблющегося цилиндрического тела с аналогичным профилем поперечного сечения [10, 17].

Квазиплоскую модель взаимодействия можно [14, 18] использовать и для получения обратных зависимостей, позволяющих определять характеристики силового аэродинамического воздействия на балку по экспериментально измеренным параметрам колебания. Развитие и апробация такого обратного метода проводятся в настоящем исследовании. Экспериментальная часть метода базируется на измерении перемещений свободного конца дюралюминиевой консоли при колебаниях, вызванных начальным отклонением образца из состояния равновесия. Использования дюраля в качестве материала для изготовления тест-образцов (в силу низких собственных демпфирующих свойств этого материала, практически не зависящих от амплитуды колебаний) позволяет разделять вклады внешнего аэродинамического и внутреннего механического воздействий в демпфирование. В настоящей работе проводится новая серия экспериментов, в рамках которых колебания консоли регистрируются трехосным МЭМС (микроэлектромеханические системы) гироскопом. Конечная точность определения гидродинамических сил, действующих на балку, обратным методом зависит от степени выполнимости квазидвумерной модели взаимодействия. Работы по исследованию границ применимости квазидвумерной гипотезы достаточно немногочисленны. В работе [11] с помощью трехмерного моделирования динамики жидкости около балок авторами установлено, что для консолей c соотношением $L{\text{/}}b \geqslant 3$ (где L и b – длина и ширина консоли) при малых амплитудах колебания $KC = 2\pi A{\text{/}}b < 0.3$ (где A – амплитуда колебания свободного конца консоли) трехмерные эффекты, в том числе сход вихрей со свободного конца балки, оказывают минимальное влияние на распределение аэродинамических сил вдоль балки.

При больших и умеренных амплитудах колебания $1 \leqslant KC \leqslant 6$ трехмерные течения около колеблющихся консолей исследовались в [19]. Показано, что в этом диапазоне амплитуд поперечные течения начинают преобладать над продольными для балок с соотношением сторон $L{\text{/}}b \geqslant 10$. Однако оценки демпфирующих сил, полученные в данной работе для бесконечно тонких пластин, оказывались существенно выше экспериментальных оценок [14]. В действительности это может объясняться различной формой поперечных сечений, так как даже в плоском приближении в зависимости от геометрических характеристик оценки коэффициента сопротивления CD могут отличаться более чем 1.6 раза [20].

Для определения всех характерных особенностей взаимодействия балка–жидкость во второй части работы проводится прямое численное моделирование обтекания консоли с параметрами, идентичными экспериментальным. На базе полученных данных выполняется сравнение моделируемых и экспериментально наблюдаемых (с помощью метода дымовой визуализации) картин течения, анализируется применимость квази-двумерной гипотезы и проводится идентификация ключевых параметров гидродинамического воздействия.

1. ЭКСПЕРИМЕНТАЛЬНЫЕ ИЗМЕРЕНИЯ КОЛЕБАНИЙ БАЛОК В ВОЗДУХЕ

1.1. Регистрация колебаний с помощью МЭМС гироскопа

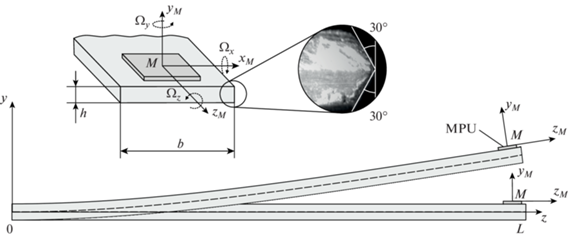
В ходе экспериментов проводились измерения затухающих колебаний, вызванных начальным отклонением свободного конца консоли из состояния равновесия. Схема проведения эксперимента представлена на рис. 1. Для регистрации колебаний балки применялся трехосный датчик МЭМС гироскопа MPU-6500 [21], обеспечивающий регистрацию угловых скоростей в диапазоне $ \pm 2000$ град/сек с частотой обновления до 8 КГц и точностью до 0.05 град/сек. Передача данных с датчика на рабочую станцию осуществлялась с помощью цифрового протокола I2C 400 КГц.

Рис. 1.

Схема установки МЭМС гироскопа (MPU) на балку.

В качестве тест-образцов использовались дюралюминиевые балки толщиной h = 1.7 мм, шириной $b = 20$, 30 мм со стрелой вылета $L$, изменяемой от 150 до 450 мм. Все образцы для эксперимента изготавливались из дюралюминия A1-2024. В ходе обработки с ребер балок снималась фаска, в результате все торцы приобретали характерную треугольную форму (см. рис. 1, фотография торца выполнена с помощью микроскопа).

Датчик МЭМС гироскопа наклеивался непосредственно на тест-образец в окрестности свободного конца вдоль горизонтальной оси симметрии. Показания датчика содержат 3 угловые скорости $({{\Omega }_{x}},{{\Omega }_{y}},{{\Omega }_{z}})$ относительно системы координат xM, yM, zM, жестко связанной с балкой (рис. 1).

Форма тест-образца в условиях рассматриваемой заделки и способа возбуждения колебаний препятствует возникновению ${{\Omega }_{y}}$ составляющей угловой скорости, что имеет подтверждение в настоящих экспериментах. Характерные временные зависимости угловых скоростей ${{\Omega }_{x}}$, ${{\Omega }_{z}}$, соответствующих изгибной и крутильной составляющим колебаний балки, представлены на рис. 2.

Рис. 2.

Изменение угловых скоростей колеблющейся балки шириной 30 мм со стрелой вылета 180 мм: а–г – ${{\Omega }_{x}}$, ${{\Omega }_{y}}$.

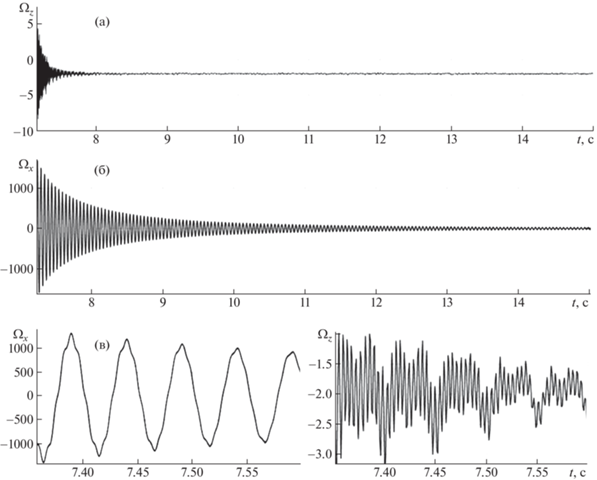
Как видно, наличие ненулевых угловых скоростей фиксируется по $x,z$-осям гироскопа. Регистрируемые сигналы имеют различный частотный спектр, что, в частности, позволяет достаточно точно откалибровать позицию датчика на балке.

1.2. Изгибные колебания

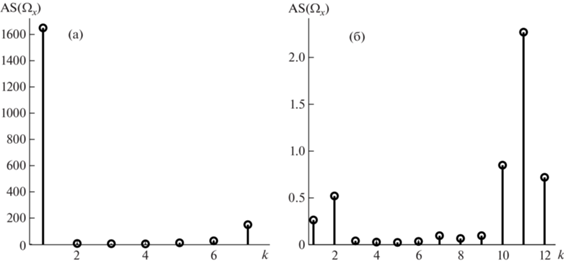
Изгибные колебания являются основным типом движения, вызванным начальным отклонением балки из состояния равновесия. Характерный амплитудный спектр сигнала ${{\Omega }_{x}}$ (соответствующего изгибным колебаниям) представлен на рис. 3а. Абсолютно доминирующей здесь является основная изгибная мода колебаний балки. Помимо нее в сигнале выделяется одна дополнительная гармоника (в рассматриваемом на рис. 2 случае в 7 раз превышающая основную), соответствующая второй собственной частоте изгибных колебаний балки. Ее появление связано с условиями начального отклонения консоли. Профиль балки в начальном деформированном состоянии не полностью совпадает с профилем колебания по первой изгибной моде. Амплитуда дополнительной гармоники в предельном случае (при максимальных амплитудах колебания) не превышает 10% от амплитуды основной гармоники ${{\Omega }_{x}}$, с течением времени это соотношение быстро уменьшается из-за высокой скорости затухания дополнительной составляющей. При переходе к углам поворота и перемещениям вклад дополнительной гармоники уменьшается кратно отношению (основной и дополнительной) частот (см. разд. 2.1), по этой причине он может не учитываться при расчете логарифмического декремента колебаний балки.

Рис. 3.

Амплитудный спектр сигналов ${{\Omega }_{x}}$ (а), ${{\Omega }_{z}}$ (б). k – номер гармоники (k = 1 – соответствует первой собственной частоте колебаний балки).

1.3. Вторичные крутильные колебания

Ненулевые значения другой компоненты угловой скорости ${{\Omega }_{z}}$, регистрируемые в зоне больших амплитуд отклонения консоли от состояния равновесия, свидетельствуют о сопутствующих изгибу крутильных колебаниях балки. Анализ амплитудного спектра ${{\Omega }_{z}}$ указывает на наличие в нем трех основных составляющих (рис. 3б): первой (изгибной) моды, удвоенной изгибной частоты и высокочастотной компоненты.

Регистрируемая первая мода в сигнале ${{\Omega }_{z}}$ не имеет отношения к крутильным колебаниям балки. Как показывают простые оценки, погрешность установки гироскопа, состоящая в повороте датчика относительно оси zM на угол порядка одной десятой градуса, приводит к разложению реальной изгибной угловой скорости $\Omega (t)$ по осям гироскопа в следующих пропорциях $[0.999998\Omega (t),0,0.00175\Omega (t)]$. Именно контроль за величиной этой компоненты в сигнале позволяет калибровать положение датчика гироскопа на балке. Высокочастотная компонента сигнала ${{\Omega }_{z}}$ совпадает с собственной частотой крутильных колебаний балки и вероятнее всего вносится в результате начальных возмущений, связанных с отклонением консоли из состояния равновесия. Возникновение удвоенной изгибной частоты в сигнале ${{\Omega }_{z}}$ может быть вызвано внешним гидродинамическим воздействием или геометрическими нелинейностями закона колебания балки (см., например, [22, 23]). Все крутильные оставляющие более чем на два порядка меньше изгибных и поэтому не могут оказывать существенного воздействия на изгибные колебания.

1.4. Экспериментальная визуализация течений около балки

Для исследования гидродинамических эффектов при относительно больших амплитудах колебания балки проведены вспомогательные эксперименты по визуализации режимов обтекания. Для наблюдения за течением около средней части балки с помощью генератора аэрозолей осуществлялся ввод рассеивающих частиц (дыма). Частицы подсвечивались с помощью лазера, образующего световую завесу в плоскости, ортогональной оси балки. Видеофиксация течения производилась с помощью высокоскоростной камеры с частотой до 960 кадров в секунду. Описание наблюдаемых гидродинамических течений представлено в разд. 4.

2. ИДЕНТИФИКАЦИЯ ОСНОВНЫХ ПАРАМЕТРОВ ИЗГИБНЫХ КОЛЕБАНИЙ И ХАРАКТЕРИСТИК СИЛОВОГО ГИДРОДИНАМИЧЕСКОГО ВОЗДЕЙСТВИЯ

2.1. Алгоритм обработки данных

Рассмотрим более подробно изгибные колебания балки, происходящие по основной моде. Под действием гидродинамических сил и внутреннего демпфирования амплитуда $A(t)$ таких колебаний медленно затухает, а основная частота $\omega $ слабо изменяется со временем t вблизи собственной частоты ${{\omega }_{0}}$.

Для выделения основных параметров таких колебаний из сигнала ${{\Omega }_{x}}(t)$, регистрируемого гироскопом, был разработан следующий алгоритм:

1. Проводится поиск локальных максимумов и минимумов зависимости ${{\Omega }_{x}}(t)$ $\bar {\Omega }_{x}^{1},\bar {\Omega }_{x}^{2},\; \ldots $ (см. рис. 4) и соответствующих им значений времени ${{t}_{1}},{{t}_{2}},\; \ldots $ в окнах, размер которых определяется по теоретической оценке периода колебания балки ($2\pi {\text{/}}{{\omega }_{0}}$).

Рис. 4.

Угловая скорость ${{\Omega }_{x}}(t)$ (круглые маркеры), аппроксимации $\Omega _{x}^{{Appr}}(t)$, построенные на отрезках $\left[ {{{t}_{{k - 1}}},{{t}_{{k + 2}}}} \right]$ (пунктирная линия) и $\left[ {{{t}_{{k - 3}}},{{t}_{k}}} \right]$ (сплошная линия).

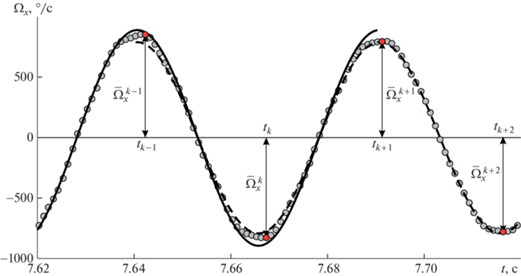
2. На отрезках $\left[ {{{t}_{{k - 1}}},{{t}_{{k + 2}}}} \right]$ выполняется построение гармонической аппроксимации $\Omega _{x}^{{Appr}}(t)$

$\Omega _{x}^{{Appr}}(t) = {{\varepsilon }_{k}} + \Omega _{x}^{k}\sin ({{\omega }_{k}}t + {{t}_{{0k}}})$
где параметры $({{\varepsilon }_{k}},\Omega _{x}^{k},{{\omega }_{k}},{{t}_{{0k}}})$ определяются из условия минимизации среднеквадратичного отклонения $\Omega _{x}^{{Appr}}$ от ${{\Omega }_{x}}$ на рассматриваемых отрезках. В качестве начального приближения для решения $({{\varepsilon }_{k}},\Omega _{x}^{k},{{\omega }_{k}},{{t}_{{0k}}})$ используются следующие значения $(0,0.5(\bar {\Omega }_{x}^{k} - \bar {\Omega }_{x}^{{k + 1}}),$ $2\pi {\text{/}}\left( {{{t}_{{k + 2}}} - {{t}_{k}}} \right),0)$.

3. Полученная аппроксимация используется для расчета амплитуды изгибных колебаний свободного конца консоли

${{A}_{k}} = {{{\text{tg}}({{{\text{|}}\Omega _{x}^{k}{\text{|}}} \mathord{\left/ {\vphantom {{{\text{|}}\Omega _{x}^{k}{\text{|}}} {{{\omega }_{k}}}}} \right. \kern-0em} {{{\omega }_{k}}}})} \mathord{\left/ {\vphantom {{{\text{tg}}({{{\text{|}}\Omega _{x}^{k}{\text{|}}} \mathord{\left/ {\vphantom {{{\text{|}}\Omega _{x}^{k}{\text{|}}} {{{\omega }_{k}}}}} \right. \kern-0em} {{{\omega }_{k}}}})} {\frac{{dW}}{{dz}}(L)}}} \right. \kern-0em} {\frac{{dW}}{{dz}}(L)}}$
где $W$ – профиль изгибных колебаний, который определятся по формуле (2.3).

4. Вычисляются логарифмический декремент колебаний (ЛДК) $\delta (t) = - 2\pi \omega _{0}^{{ - 1}}{{A}^{{ - 1}}}\left( {dA{\text{/}}dt} \right)$ и относительное изменение частоты $\gamma (t) = ({{\omega }_{0}} - \omega ){\text{/}}{{\omega }_{0}}$ балки как функции от времени. На основании этих зависимостей для каждого эксперимента в диапазоне реализующихся в нем амплитуд колебаний строятся зависимости $\delta (A)$, $\gamma (A)$.

Первые два шага алгоритма направлены на выделение основной моды изгибных колебаний. Процедура начального определения периодов колебания (шаг 1) здесь реализована по локальным максимумам и минимумам функции, что позволяет справляться с проблемой “дрейфа нуля” [21], сопутствующей работе гироскопа. Коррекция на движение нуля заложена и в гармонической аппроксимации (шаг 2, коэффициент εk). Детали обработки данных на 4 шаге представлены в разделах 2.2, 2.3.

2.2. Определение логарифмического декремента колебаний

Для определения ЛДК необходимо проводить вычисление производной $d(\ln (A)){\text{/}}dt$. При этом функция амплитуды найдена только как последовательность значений Ak. Для построения гладкой зависимости $\ln (A(t))$ по точкам Ak строится cплайн-аппроксимация. Поскольку искомая функция имеет достаточно простой вид в исследуемом диапазоне, ее можно с высокой точностью аппроксимировать сплайном 4 степени, построенным на 3 отрезках. Коэффициенты такого сплайна определяются с помощью метода наименьших квадратов. Определение узлов сплайна с целью минимизации результирующей погрешности также проводится итерационно.

2.3. Определение относительного изменения частоты

Динамическое изменение частоты колебаний определяется действующими на консоль присоединенными массами воздуха. В проводимых экспериментах плотность материала балок существенно превышала плотность воздуха, что делало влияние присоединенных масс на процесс колебания весьма незначительным. В результате относительное изменение частоты колебаний во всех проводимых экспериментах не превышало 1.5% – рис. 5.

Рис. 5.

Изменение частоты колебаний с течением времени: 1 – экспериментальные данные для случая $L = 180$ мм, $b = 30$ мм; 2 – теоретическая оценка резонансной частоты в вакууме.

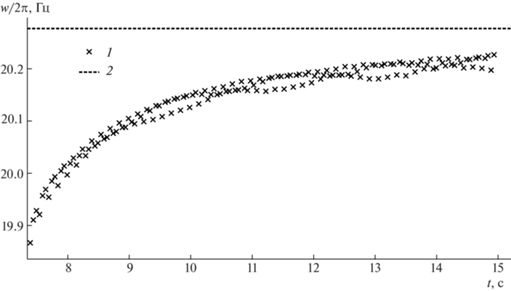
При определении относительного изменения частоты по формуле $\gamma (t) = ({{\omega }_{0}} - \omega ){\text{/}}{{\omega }_{0}}$ погрешность определения собственной частоты балки в вакууме ${{\omega }_{0}}$ должна быть минимальной, иначе действие присоединенных масс становится неразличимым.

Предлагаемый метод определения ${{\omega }_{0}}$ основан на выделении соответствующей составляющей из экспериментально определяемой собственной частоты балки при малых амплитудах колебания. Для этого используются теоретические оценки сил присоединенных масс. Результирующую формулу для вычисления ${{\omega }_{0}}$ можно записать в виде

$A \to 0{\text{:}}\quad {{\omega }_{0}} = \omega {{(1 - \gamma )}^{{ - 1}}},\quad \gamma = \frac{\pi }{8}\frac{{{{\rho }_{a}}}}{\rho }\frac{b}{h}C_{M}^{0}$

Значение $C_{M}^{0}$ для тонкой балки определяется по формуле [11]

$C_{M}^{0} = 1.02 + \sqrt {\frac{2}{\pi }} \left( {3.07} \right){{\left( {\frac{{{{b}^{2}}{{\omega }_{0}}}}{{2\pi \nu }}} \right)}^{{ - 1/2}}}$
где $\nu $ – это кинематическая вязкость жидкости.

2.4. Расчет аэродинамических сил, действующих на балку, по параметрам изгибных колебаний

Структура найденных в эксперименте зависимостей $\gamma (A)$, $\delta (A)$ определяется действующими на консоль внешними аэродинамическими силами (P) и внутренним демпфированием (H). Для установления соответствующих взаимосвязей рассмотрим уравнение колебания консоли. Принимая положения классической теории изгиба балок, колебание консоли в сопротивляющейся среде может быть описано следующим уравнением

(2.1)
$\rho bh\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + \frac{{E{{h}^{3}}b}}{{12}}\frac{{{{\partial }^{4}}w}}{{\partial {{z}^{4}}}} = F(z,t) = H(z,t) + P(z,t)$
с граничными условиями
$\begin{gathered} w(0,t) = 0,\quad \frac{{\partial w}}{{\partial z}}(0,t) = 0, \\ \frac{{{{\partial }^{2}}w}}{{\partial {{z}^{2}}}}(L,t) = 0,\quad \frac{{E{{h}^{3}}b}}{{12}}\frac{{{{\partial }^{3}}w}}{{\partial {{z}^{3}}}}(L,t) - {{M}_{g}}\frac{{{{\partial }^{2}}w}}{{\partial {{z}^{2}}}}(L,t) = 0 \\ \end{gathered} $
отвечающими жесткой заделке при z = 0 и свободному концу z = L с сосредоточенной массой Mg. Здесь $t$ – время, z – продольная координата балки; $w$ – смещение средней линии балки в направлении оси $y$; $\rho $, $E$ – эффективные плотность ($\rho \approx 2700$ кг/м3) и модуль Юнга ($E \approx 70$ ГПа) материала балки, Mg – масса датчика гироскопа.

Поскольку гидродинамические и внутренние демпфирующие силы малы по сравнению с упругой силой, в первом приближении можно положить $H = P = 0$. В этом случае основная мода колебаний примет вид

(2.2)
$w(z,t) = AW(\xi )\cos (\omega t),\quad \xi = z{\text{/}}L$

Постоянные $A$ и $\omega = {{\omega }_{0}}$ представляют амплитуду и собственную частоту основной моды. Профиль $W$ колебаний описывается формулой

(2.3)
$\begin{gathered} W\left( \xi \right) = \frac{1}{2}\left( {\cosh k\xi - \cos k\xi } \right) + {{\zeta }_{r}}\left( {\sinh k\xi - \sin k\xi } \right) \\ {{\zeta }_{r}} = \frac{{\sin k - \sinh k + k\frac{{{{M}_{g}}}}{{\rho bhL}}\left( {\cos k - \cosh k} \right)}}{{\cos k - \cosh k - k\frac{{{{M}_{g}}}}{{\rho bhL}}\left( {\sin k - \sinh k} \right)}} \\ \end{gathered} $
где $k$ – наименьший положительный корень характеристического уравнения
$1 + \cos k\cosh k + k\frac{{{{M}_{g}}}}{{\rho bhL}}\left( {\cos k\sin k - \sin k\cosh k} \right) = 0$
приближенное решение которого для случая $s = {{M}_{g}}{\text{/}}\rho hbL \ll 1$ может быть найдено как

$k \approx {{k}_{0}}(1 - s + \alpha {{s}^{2}}),\quad {{k}_{0}} = 1.875,\quad \alpha = 2.3765$

Частота собственных колебаний балки при этом (без учета воздействия демпфирующих сил) выражается следующим образом [24, 25]

${{\omega }_{0}} = {{k}^{2}}\frac{h}{{{{L}^{2}}}}\sqrt {\frac{E}{{12\rho }}} $

Наличие малых сил в правой части уравнения (2.1) приводит к тому, что амплитуда колебаний $A$ и собственная частота $\omega $ не остаются постоянными, а медленно изменяются со временем. Эти изменения можно описать с помощью следующих зависимостей [14–16, 26]

(2.4)
$\begin{gathered} \delta = \frac{{2\pi }}{{\rho hbA{{\omega }^{2}}}}\left\{ {\sin (\omega t)\left\langle {FW} \right\rangle } \right\}{\text{/}}\langle {{W}^{2}}\rangle \\ \gamma = \frac{1}{{\rho hbA{{\omega }^{2}}}}\left\{ {\cos (\omega t)\left\langle {FW} \right\rangle } \right\}{\text{/}}\langle {{W}^{2}}\rangle \\ \end{gathered} $

Здесь и далее угловыми скобками обозначено усреднение по пространственной координате z, а фигурными скобками – усреднение по времени.

Далее будем полагать, что относительное изменение частоты балки полностью определяется аэродинамическим воздействием, а логарифмический декремент колебаний представляется в виде суммы гидродинамической ${{\delta }_{P}}$ и механической ${{\delta }_{H}}$ составляющих ($\delta = {{\delta }_{P}} + {{\delta }_{H}}$), отвечающих воздействию на колебательный процесс соответствующих компонент силы. При этом механическая составляющая демпфирования для исследуемого случая (дюралюминиевых балок) не зависит от амплитуды колебаний консоли [27–29].

Для проведения оценки аэродинамических сил примем гипотезу о квазидвумерном течении, согласно которой аэродинамические силы в каждом сечении $z = {\text{const}}$ балки можно найти, рассматривая гармонические колебания бесконечно длинной жесткой пластины в вязкой среде с текущей амплитудой $A(z)$. Также используем аппроксимацию Морисона [30] для разделения сил сопротивления и сил присоединенных масс

(2.5)
$P \approx - \frac{\pi }{4}{{\rho }_{a}}{{b}^{2}}{{C}_{M}}\frac{{dU}}{{dt}} - \frac{1}{2}{{\rho }_{a}}b{{C}_{D}}\left| U \right|U$

Здесь $U(z,t) = \partial w{\text{/}}\partial t$ – скорость движения балки в данном сечении, ${{\rho }_{a}}$ – плотность воздуха, CM – локальные коэффициенты присоединенных масс, CD – локальный коэффициент аэродинамического сопротивления.

Подставляя (2.5) в (2.4) и учитывая (2.2), мы получим следующие уравнения

(2.6)
$\delta - {{\delta }_{H}} = {{\delta }_{P}} = \frac{{{{\rho }_{a}}}}{\rho }\frac{b}{h}\frac{4}{3}\frac{A}{b}\frac{{\langle {{C}_{D}}{{W}^{3}}\rangle }}{{\langle {{W}^{2}}\rangle }},\quad \gamma = \frac{\pi }{8}\frac{{{{\rho }_{a}}}}{\rho }\frac{b}{h}\frac{{\langle {{C}_{M}}{{W}^{2}}\rangle }}{{\langle {{W}^{2}}\rangle }}$
связывающие между собой ЛДК и коэффициент аэродинамического сопротивления, а также относительное изменение частоты и коэффициент присоединенных масс колеблющейся балки. Используя подход, предложенный в [14], из (2.6) можно получить следующие приближенные формулы для определения гидродинамических коэффициентов

${{C}_{D}} = \frac{{11.56}}{A}\sqrt {\frac{\nu }{\omega }} + \frac{9}{{32}}\frac{\rho }{{{{\rho }_{a}}}}\frac{h}{b}{{A}^{{ - 8/3}}}b\frac{d}{{dA}}({{A}^{{8/3}}}\left( {\delta (A) - \delta (0)} \right))$
${{C}_{M}} = \frac{3}{\pi }\frac{\rho }{{{{\rho }_{a}}}}\frac{h}{b}{{A}^{{ - 5/3}}}\frac{d}{{dA}}({{A}^{{8/3}}}\gamma (A))$

Они позволяют по экспериментально определенным $\delta $, $\gamma $ найти ${{C}_{D}}$, ${{C}_{M}}$ в каждом сечении (см. подробнее в [14]). Результаты вычисления ${{C}_{D}}$, ${{C}_{M}}$ представлены в разд. 4.

3. ТРЕХМЕРНОЕ ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ БАЛКИ В ЖИДКОСТИ

3.1. Математическая постановка задачи

В качестве второго инструмента для исследования движения балки в жидкости используется прямое численное моделирование. Рассматривается обтекание тонких балок длиной $L$, шириной b и толщиной $h$ с профилем в форме усеченного прямоугольника (аналогично экспериментальным образцам; рис. 1), совершающих вынужденные изгибные колебания в вязкой несжимаемой жидкости по первой моде с фиксированной амплитудой. Задача решается в безразмерных переменных. Нормировка пространственных координат, времени и скорости проводится на b, $b{{U}_{0}}^{{ - 1}}$, $ - {{U}_{0}}$ соответственно. Система уравнений движения жидкости около балки записывается в следующем виде

$\frac{{\partial U}}{{\partial t}} + U \times \nabla U = - \nabla p + \frac{1}{{KC\beta }}{{\nabla }^{2}}U$
$\nabla \times U = 0$

Здесь $U = ({{u}_{x}},{{u}_{y}},{{u}_{z}})$ – безразмерная скорость, p – безразмерное давление, $KC = K{{C}_{{loc}}}(l)$ – безразмерная амплитуда колебания свободного конца балки, $l = L{\text{/}}b$ – безразмерная длина балки. Безразмерная частота $\beta $ и безразмерная амплитуда колебания сечения $K{{C}_{{loc}}}$ определяются как

(3.1)
$K{{C}_{{loc}}}(z) = 2\pi \frac{{{{U}_{{loc}}}(z)}}{{b\omega }} = 2\pi \frac{{{{A}_{{loc}}}(z)}}{b},\quad \beta = \frac{{{{b}^{2}}\omega }}{{2\pi \nu }}$
где ${{A}_{{loc}}}(z),{{U}_{{loc}}}(z) = {{A}_{{loc}}}(z)\omega $ – амплитуда колебаний и амплитуда скорости колебаний поперечного сечения $z = {\text{const}}$.

В декартовой системе координат, начало которой расположено на неподвижном конце балки, ось Oz совмещена с осью балки, находящейся в нейтральном положении, оси Ox, Oy направлены вдоль осей симметрии ее поперечного сечения (см. рис. 1).

Для описания изгибных колебаний консольной балки в жидкости будем использовать классическую теорию Эйлера–Бернулли. Полагая (как и при обработке экспериментальных данных), что гидродинамические силы, действующие на балку, значительно меньше сил упругости, будем задавать профиль колебаний согласно (2.2).

Моделирование движения жидкости около балки будем проводить в ограниченной области, представляющей собой прямоугольный параллелепипед с соотношением сторон $({{l}_{x}},{{l}_{y}},{{l}_{z}})$ = (35, 35, 55). Положение балки в области определим следующим образом: балка будет расположена по центру области в плоскости $xOy$; по оси Oz она будет смещена относительно центра так, что ее зафиксированный конец будет находиться на расстоянии ${{l}_{z}}{\text{/}}5$ от границы области. Внешние границы области будем считать непроницаемыми, на балки зададим условия прилипания.

3.2. Численное моделирование

Для решения задачи использована численная модель, предложенная в работе [19] и реализованная с использованием программных библиотек открытого пакета OpenFOAM. Для дискретизации расчетной области использовались динамически перестраиваемые сетки, узлы которых жестко связаны с точками на поверхности балки (см. рис. 6). Вычисление скоростей движения узлов сетки проводилось на основе решения уравнения Лапласа с переменным в области коэффициентом диффузии. На внешней границе скорости движения узлов считались нулевыми, на балки определялись из (2.2). Коэффициент диффузии выбирался обратно пропорциональным квадрату расстояния от балки для минимизации деформаций сетки в окрестности балки, где их влияние наиболее чувствительно.

Рис. 6.

Характерная структура исходной (а) и деформированной (б) сетки в окрестности свободного конца балки (плоскость $yOz$).

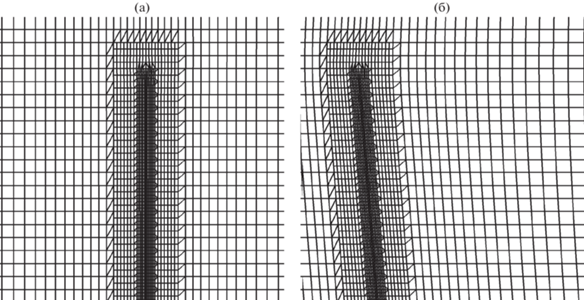
Исходное разбиение области проводилось в нейтральном положении балки. Для всех расчетных случаев оно выполнялось однотипно. Число ячеек расчетных сеток составляло $N \approx 3.3 \times {{10}^{6}}$.

Дискретизация уравнения движения жидкости в области проводилась с помощью метода конечных объемов. Дискретные значения составляющих скорости и дискретные давления локализовались в центрах ячеек расчетных сеток. Для вычисления объемных интегралов по контрольному объему использовалась общая процедура Гаусса. Для аппроксимации градиента давления в расчетах применялась линейная интерполяция. В диффузионных слагаемых при дискретизации оператора Лапласа нормальные градиенты скорости на поверхности ячейки аппроксимировались с помощью симметричной схемы второго порядка с поправкой на неортогональность [31].

Для дискретизации системы уравнений по времени использовалась неявная схема Эйлера. Шаг по времени во всех расчетах выбирался из условия – максимальное число Куранта не превышает единицы. Решение дискредитированной задачи проводилось с помощью метода PIMPLE (который является комбинацией алгоритмов PISO и SIMPLE). Решение системы уравнений для давления выполнялось на основе метода сопряженных градиентов (PCG) с геометро-алгебраическим многосеточным предобуславливателем (GAMG). Системы уравнений для компонент скорости решается методом бисопряженных градиентов (PBiCG) с предиктором на основе неполной LU факторизации. Расчеты выполнялись распределенным образом по технологии MPI с применением метода декомпозиции области решения.

4. РЕЗУЛЬТАТЫ

4.1. Гидродинамика течений около балки

Наиболее полную информацию о структуре течений, индуцированных колебаниями, дает трехмерное численное моделирование. Расчеты проводилось для балок с длиной l = 20 и соотношением сторон $\Delta = h{\text{/}}b = 0,0.1,0.2$, совершающих колебания с безразмерной частотой $\beta = 200,430$ и амплитудой $KC = 1,2,6$.

Для выявления областей преобладания поперечных или продольных потоков исследуем соотношение скоростей соответствующих течений. На рис. 7 изображены графики функции $u_{z}^{{norm}}(z)$, определяющей отношение максимальных осредненных (по периоду) поперечных и продольных скоростей в сечениях вдоль балки

$u_{z}^{{norm}}(z) = {{\mathop {\max }\limits_{x,y} \left\langle {\left| {{{u}_{z}}} \right|} \right\rangle } \mathord{\left/ {\vphantom {{\mathop {\max }\limits_{x,y} \left\langle {\left| {{{u}_{z}}} \right|} \right\rangle } {\mathop {\max }\limits_{x,y} \left\langle {\sqrt {u_{x}^{2} + u_{y}^{2}} } \right\rangle }}} \right. \kern-0em} {\mathop {\max }\limits_{x,y} \left\langle {\sqrt {u_{x}^{2} + u_{y}^{2}} } \right\rangle }},\quad 0 \leqslant z \leqslant l$
Рис. 7.

Отношение максимальных продольных и поперечных скоростей в сечениях: 1–5 – (β, Δ, KC) = = $(200,0,1),(430,0,2),(430,0,6),(430,0.2,6),(200,0.1,6)$.

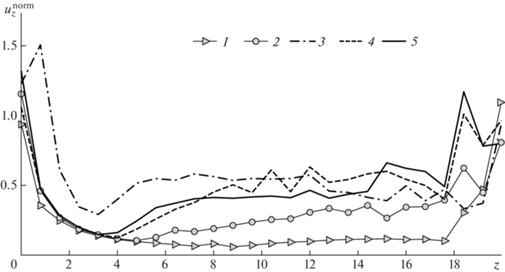
Введенная таким образом функция $u_{z}^{{norm}}(z)$ является индикатором ключевых типов течения: значения $u_{z}^{{norm}} \ll 1$ указывают на доминирующее поперечное течение, $u_{z}^{{norm}} \sim 1$ – на развитое трехмерное течение, $u_{z}^{{norm}} \gg 1$ – на преобладающее продольное течение.

Как можно видеть на рис. 7, продольная составляющая всегда отлична от нуля. Она сильно возрастает на концах консоли (по отношению к поперечным составляющим), где течение фактически становится полностью трехмерным. Вне зоны концевых эффектов среднее по длине значение $u_{z}^{{norm}}$ изменяется от 0.1 для KC = 1, где можно уверенно говорить о квази-двумерном характере течения, до 0.5 для KC = 6, где преобладание поперечных потоков не столь однозначно выражено. Рассмотрим структуру течений около средней части балки для последнего случая.

Трехмерная картина течения и визуализация движения жидкости в поперечных сечениях для случая KC = 6, $\beta = 200$ приведены на рис. 8 а (трехмерная анимация представлена в [32]). Несмотря на наличие достаточно большой продольной скорости, около средней части балки наблюдаются те же ключевые режимы течения, как и при колебаниях абсолютно жестких пластин: симметричный режим (рис. 8б) и циклический диагональный режим обтекания (рис. 8в). Их подробное описание представлено в работе [20]. Отметим, что границы этих режимов в двумерном и трехмерном случаях смещены относительно друг друга в параметрической плоскости. Циклический диагональный режим обтекания при высокоамплитудных колебаниях балки (KC = 6) наблюдается в области $1.5 < K{{C}_{{loc}}} < 5.5$, при колебаниях жестких пластин его нижняя граница находится существенно выше: по данным численных исследований [20], около бесконечно длинных пластин он локализуется при $K{{C}_{{loc}}} \geqslant 4$; по данным экспериментов [33], для конечных пластин он наблюдается при $K{{C}_{{loc}}} > 7$. Формирование диагонального режима около средней части балки в области низких локальных амплитуд подтверждается и экспериментальными наблюдениями, проведенными в настоящей работе.

Рис. 8.

Визуализация трехмерной структуры течения по данным 3D расчетов для $KC = 6$, $\beta = 200$ около средней части балки в момент времени $t{\text{/}}T - {{T}_{0}} = 0$: (a) – изоповерхности z-компоненты завихренности в области $0 \leqslant z \leqslant 15.1$; (б, в) – изолинии z-компоненты завихренности в сечениях $z = 7.4$ (симметричный режим) и 15.1 (диагональный режим).

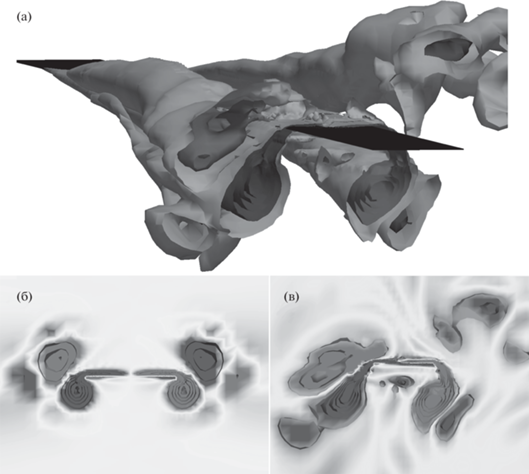
На рис. 9, 10 представлены сопоставления результатов трехмерного моделирования и картин течения, полученных с помощью дымовой визуализации экспериментов. Локальная безразмерная амплитуда колебаний в рассматриваемом сечении равна $K{{C}_{{loc}}} \approx 2.5$. На рис. 9 экспериментальная картина (а) и визуализация расчета (б) выполнены с одинаковой перспективой. В компьютерной визуализации балка изображена сеткой. На рис. 9а балка расположена таким же образом, как и на рис. 9б. По концентрации частиц дыма и положению изоповерхностей завихренности на рисунках можно наблюдать характерный для диагонального режима отрыв вихревых пар с торцов балки, которые формируются каждые полупериода и удаляются в разные стороны от балки под углом 45–60 градусов к оси колебания. Слева и справа на рисунках находятся вихревые пары, оторвавшиеся соответственно в последнем и предпоследнем полупериодах. Заметим, что в эксперименте балка закрывает крупную вихревую структуру, расположенную ниже нее.

Рис. 9.

Сопоставление (а) экспериментально наблюдаемой картины течения (дымовая визуализация) с (б) результатами численного моделирования (изоповерхности завихренности). Безразмерная локальная амплитуда колебаний в сечении $K{{C}_{{loc}}} \approx 2.5$, момент времени $t{\text{/}}T - {{T}_{0}} = 0.16$.

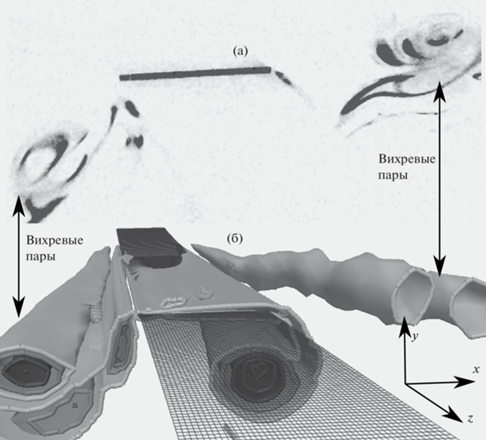
Рис. 10.

Сопоставление экспериментально наблюдаемой картины течения I (дымовая визуализация) с результатами численного моделирования, визуализированными с помощью изолиний z-компоненты поля завихренности II (в той же перспективе, что и на фотографиях) и с помощью невесомых частиц III (в ортогональной проекции). Безразмерная локальная амплитуда колебаний $K{{C}_{{loc}}} \approx 2.5$, моменты времени $t{\text{/}}T - {{T}_{0}} = $ (a) 0.92, (б) 1, (в) 1.08.

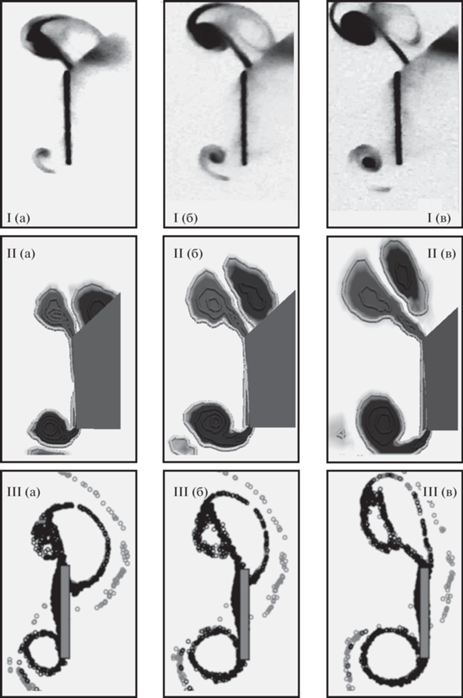
Серия фотографий, полученных в рамках эксперимента, и картины течений, построенных по данным численного моделирования, демонстрирующие момент отрыва вихрей с одного из торцов, представлены на рис. 10. Помимо изолиний завихренности, визуализация численных результатов здесь также проведена с помощью невесомых частиц (картины течения в этом случае представлены в ортогональной проекции), которые выпускались в непосредственной близости к поверхности балки. Этот метод наиболее близок дымовой визуализации, используемой в экспериментах. Сравнивая их результаты, можно отметить, что численное моделирование достаточно хорошо воспроизводит реальную динамику течения.

4.2. Коэффициенты сил сопротивления и сил присоединенных масс

Графики изменения коэффициентов аэродинамических сил (${{C}_{D}}$, ${{C}_{M}}$), действующих на колеблющуюся балку в каждом сечении, в зависимости от локальной амплитуды колебаний $K{{C}_{{loc}}}$ изображены на рис. 11, 12.

Рис. 11.

Кривые зависимостей локального коэффициента сопротивления CD от безразмерной амплитуды колебаний: a – экспериментальные данные, б – численные данные: 1 – экспериментальные результаты [14] для балки при $\beta \approx 250$, $\Delta = 0.1$; 2 – экспериментальные результаты для $\beta = 969$, $\Delta = 0.06$, $l = 8.9$; 3 – экспериментальные результаты для $\beta = 257$, $\Delta = 0.06$, l = 17.6; 4 – экспериментальные данные [34] для жесткой пластины; 5 – экспериментальные результаты [35] для жесткой пластины; 6 – экспериментальные результаты [33] для жесткой пластины при 188 ≤ β ≤ 1685, $\Delta = 0.2$; 7 – данные 3D численного моделирования при KC = 6, $\beta \approx 200$, $\Delta = 0.1$; 8 – результаты [19] 3D моделирования при $\beta = 430$, $\Delta \sim 0$; 9 – данные 3D численного моделирования при KC = 3, $\beta \approx 430$, $\Delta = 0.1$; 10 – результаты [20] 2D моделирования при $\beta \approx 200$, $0.1 \leqslant \Delta \leqslant 0.2$.

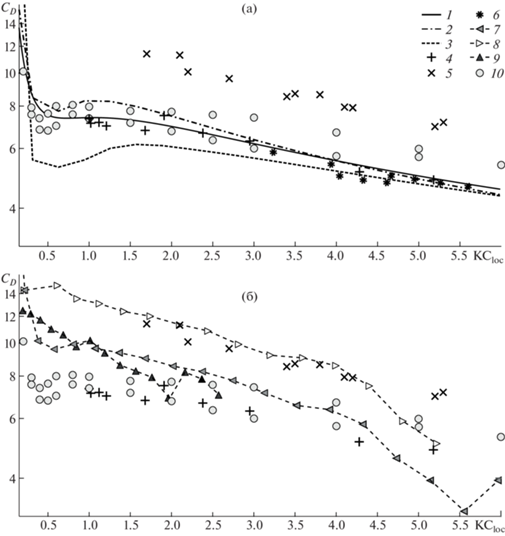
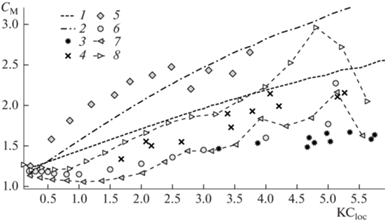
Рис. 12.

Кривые зависимостей коэффициента присоединения масс от безразмерной амплитуды колебаний для разных значений безразмерной частоты: 1 – экспериментальные данные для $\beta = 257$; 2 – экспериментальные данные для $\beta = 704$; 3 – результаты [33] для жесткой пластины при 188 ≤ β ≤ 1685, $\Delta = 0.2$; 4 – результаты [35]; 5 – результаты [13]; 6 – результаты [20] при $\beta = 200$, $\Delta = 0.1$; 7 – результаты численного моделирования при KC = 6, $\beta = 200$, $\Delta = 0.1$; 8 – результаты [19] при $\beta = 430$, $\Delta \sim 0$.

Оценки ${{C}_{D}}$, полученные в разных источниках с использованием различных методов, традиционно имеют большой разброс. Даже для жестких пластин (см., например, [33, 35]), в области двумерных течений, классические экспериментальные оценки отличаются более чем в 1.6 раза. Как отмечено в [20], при одних и тех же параметрах колебания ($K{{C}_{{loc}}}$, $\beta $) у пластин с одинаковой толщиной, но разной формой торцов, значения CD могут отличаться более чем на 10%.

Данные, представленные на рис. 11а, отображают результаты измерений CD балки, полученные в ходе обработки экспериментальных измерений затухающих колебаний тест-образцов, а также численные и экспериментальные результаты измерения CD жестких пластин, полученные в работах [20, 33–35]. Как можно видеть, результаты настоящего исследования при $K{{C}_{{loc}}} > 1.5$ достаточно хорошо согласуются с экспериментальными результатами [33, 34], полученными в том же диапазоне безразмерных частот $100 < \beta < 2000$ для пластин с соотношением толщины и ширины $0.05 < \Delta \leqslant 0.2$. При больших $K{{C}_{{loc}}}$ все полученные зависимости ${{C}_{D}}(K{{C}_{{loc}}})$ имеют приблизительно одно и то же асимптотическое поведение, которое можно описать функцией ${{C}_{D}} \approx 12.86KC_{{loc}}^{{ - 0.58}}$ (т.е. значение коэффициента сопротивления практически не зависит от безразмерной частоты). Заметим также, что значения CD в этом диапазоне достаточно хорошо согласуются и с данными двумерного численного моделирования [20] (полученными для пластин с аналогичными геометрическими характеристиками).

В диапазоне малых амплитуд $K{{C}_{{loc}}} < 1.5$ значение коэффициента сопротивления существенно зависит от параметра $\beta $. При $K{{C}_{{loc}}} < 0.5$ коэффициент сопротивления выходит на малоамплитудную асимптотику [10]: ${{C}_{D}} \approx {{28.97} \mathord{\left/ {\vphantom {{28.97} {(K{{C}_{{loc}}}\sqrt \beta )}}} \right. \kern-0em} {(K{{C}_{{loc}}}\sqrt \beta )}}$. При $0.5 < K{{C}_{{loc}}} < 1.5$ и $\beta < 500$ результаты, полученные при обработке данных с разных тест образцов, имеют некоторый разброс: так, результаты настоящей серии экспериментов лежат в среднем на 20% ниже, чем результаты [14]. Это может объясняться разной длиной и толщиной образцов. При $\beta > 500$ настоящие результаты достаточно хорошо согласуются с данными [14].

На рис. 11б представлены зависимости ${{C}_{D}}(K{{C}_{{loc}}})$, полученные при трехмерном численном моделировании и двумерном расчете [20]. Как можно видеть, данные для бесконечно тонкой балки ожидаемо лежат в среднем на 20% выше (что хорошо согласуется с оценками [20]) данных для балки с относительной толщиной $\Delta = 0.1$. Для случая $\Delta = 0.1$ наибольшие отклонения ${{C}_{D}}$ от плоской теории [20] возникают в зонах концевых эффектов (для $KC = 6$ это $K{{C}_{{loc}}} \leqslant 0.5$ и $K{{C}_{{loc}}} > 4.5$). В средней части балки разница между оценками CD двумерных и трехмерных расчетов составляет в среднем не более 15%.

Значения коэффициента инерциальных сил ${{C}_{M}}$ для квазиплоской и трехмерной моделей также хорошо совпадают (см. рис. 12) в широком диапазоне $K{{C}_{{loc}}}$, влияние концевых эффектов для коэффициента присоединенных масс достаточно сильно выражается только около свободного конца балки. При $K{{C}_{{loc}}} \leqslant 0.5$ зависимость ${{C}_{M}}(K{{C}_{{loc}}})$ выходит на малоамплитудную асимптотику [10]. Экспериментальные оценки ${{C}_{M}}$, полученные при умеренных значениях безразмерной частоты $\beta < 500$, также ложатся достаточно близко с численными данными (они хорошо совпадают с результатами для тонких пластин). При больших значениях $\beta $ значения коэффициента присоединенных масс, полученные по результатам обработки экспериментов, оказываются выше расчетных. Это может быть результатом неточного учета свойств материала. Поскольку аэродинамическое влияние на резонансную частоту дюралевой балки очень мало, для более точной оценки коэффициента присоединенных масс описанным методом необходимо проводить эксперименты в более плотной среде (или с другим материалом образцов).

ЗАКЛЮЧЕНИЕ

Проведено исследование взаимодействия между балкой и жидкостью, когда упругие силы, вызывающие резонансный рост амплитуды колебаний, много больше внешних аэрогидродинамических (случай колебания металлических тонких балок в воздухе). В этих условиях внешние течения не могут изменить мгновенный профиль колебаний балки, но оказывают существенное влияние на амплитуду колебаний и изменяют резонансную частоту в ходе продолжительного воздействия. Изменение амплитуды колебаний и частоты, в свою очередь, приводит к перестроению внешних течений, т.е. изменению силового гидродинамического воздействия на балку.

Экспериментально и численно исследована структура взаимодействия между балкой и жидкостью. Для ее описания была предложена квазиплоская модель, в рамках которой были установлены прямые и обратные зависимости между параметрами колебаний длинных балок и локальными силовыми аэродинамическими характеристиками течений около них. С помощью этой модели проводилась обработка экспериментальных данных, результаты которой сопоставлялись с данными прямого численного моделирования обтекания балок. С помощью трехмерного численного моделирования и визуализации движения жидкости в экспериментах было показано, что течения в сечениях, ортогональных оси балки (за исключением окрестности ее концов), в действительности имеют структуру, аналогичную плоским течениям, наблюдаемым при колебаниях жестких пластин. Оценки локальных коэффициентов гидродинамических сил, полученные в трехмерных расчетах (в области квазиплоских течений) и в экспериментах, в среднем также оказываются достаточно хорошо согласованы с оценками CD, CM для плоских течений.

Работа выполнена при поддержке гранта РФФИ (проект № 19-38-60023) и Программы стратегического академического лидерства Казанского (Приволжского) федерального университета (“ПРИОРИТЕТ-2030”).

Список литературы

  1. Tao L., Thiagarajan K. Low KC flow regimes of oscillating sharp edges.II hydrodynamic forces // Appl. Ocean Res. 2003. V. 25. № 2. P. 53–62.

  2. Tao L., Thiagarajan K. Low KC flow regimes of oscillating sharp edges.I vortex shedding observation // Appl. Ocean Res. 2003. V. 25. № 1. P. 21–35.

  3. Келдыш М.В. Вибрации на самолете. М.: Бюро нов. техн. НКАП, 1942. 56 с.

  4. Бужинский В.А. Колебания тел с острыми кромками в несжимаемой маловязкой жидкости и некоторые задачи гидродинамики космических аппаратов: Дис. … д-ра. физ.-мат. наук: 01.02.05 К., 2003. 178 с.

  5. Бужинский В.А. Вихревое демпфирование колебаний жидкости в резервуарах с перегородками // ПММ. 1998. Т. 62. № 2. С. 235.

  6. Zhu H., Zhang P., Zhong Z., Xia J., Rich J., Mai J., Su X., Tian Z., Bachman H., Rufo J., Gu Y., Kang P., Chakrabarty K., Witelski T.P., Huang T.J. Acoustohydrodynamic tweezers via spatial arrangement of streaming vortices // Science Advances. 2021, V. 7. № 2. P. eabc7885.

  7. Semati A., Amani E., Saffaraval F., Saffar-Avval M. Numerical simulation of oscillating plates at the visco-inertial regime for bio-inspired pumping and mixing applications // Phys. Fluids 2020 V. 32. №. 10. P. 101906.

  8. Sader J.E., Porfiri M. Nonlinear hydrodynamic damping of sharp-edged cantilevers in viscous fluids undergoing multi-harmonic base excitation // J. Appl. Phys. 1998. V. 84. № 1. P. 64.

  9. Aureli M., Porfiri M. Low frequency and large amplitude oscillations of cantilevers in viscous fluids // Appl. Phys. Lett. 2010. V. 96. № 16. P. 164102.

  10. Aureli M., Porfiri M., Basaran M.E. Nonlinear finite amplitude vibrations of sharp-edged beams in viscous fluids // J. Sound Vib. 2012. V. 331. № 7. P. 1624–1654.

  11. Phan C.N., Aureli M., Porfiri M. Basaran M.E. Finite amplitude vibrations of cantilevers of rectangular cross sections in viscous fluids // J. Fluids Struct. 2013. V. 40. P. 52–69.

  12. Facci A.L., Porfiri M. Nonlinear hydrodynamic damping of sharp-edged cantilevers in viscous fluids undergoing multi-harmonic base excitation // J. Appl. Phys. 2012. V. 112. № 12. P. 124908.

  13. Bidkar R.A., Kimber M., Raman A., Bajaj A.K., Garimella S.V. Nonlinear aerodynamic damping of sharp-edged flexible beams oscillating at low Keulegan–Carpenter numbers // J. Fluid Mech. 2009. V. 634. P. 269–289.

  14. Egorov A.G., Kamalutdinov A.M., Nuriev A.N. Evaluation of aerodynamic forces acting on oscillating cantilever beams based on the study of the damped flexural vibration of aluminium test samples // J. Sound Vib. 2018. V. 421. P. 334–347.

  15. Егоров А.Г., Камалутдинов А.М., Нуриев А.Н., Паймушин В.Н. Экспериментальное определение демпфирования колебаний пластины вязкой жидкостью // Доклады РАН. 2017. Т. 474. № 2. С. 172–176.

  16. Egorov A.G., Kamalutdinov A.M., Nuriev A.N., Paimushin V.N. Theoretical-experimental method for determining the parameters of damping based on the study of damped flexural vibrations of test specimens 2. aerodynamic component of damping // Mech. Compos. Mater. 2014. V. 50. № 3. P. 267–278.

  17. Камалутдинов А.М., Нуриев А.Н. Гидродинамическое демпфирование колебаний балок вблизи экрана // Изв. РАН. МЖГ. 2021. №. 5. С. 61–75.

  18. Камалутдинов М.А. Теоретико-экспериментальное исследование аэродинамических свойств колеблющейся пластины: Дис. … канд. физ.-мат. наук: 01.02.04, 01.02.05 К., 2017. 142 с.

  19. Nuriev A.N., Kamalutdinov A.M., Zaitseva O. Hydrodynamics around long vibrating beams // J. Fluids Struct. 2021 V. 101. № 103203.

  20. Nuriev A.N., Kamalutdinov A.M., Egorov A.G. A numerical investigation of fluid flows induced by the oscillations of thin plates and evaluation of the associated hydrodynamic forces // J. Fluid Mech. 2019. V. 874. P. 1057–1095.

  21. MPU-6500 Product Specification Revision 1.3 http://3cfeqx1hf82y3xcoull08ihx-wpengine.netdna-ssl.com/wp-content/uploads/2020/06/PS-MPU-6500A-01-v1.3.pdf

  22. Камалутдинов А.М., Паймушин В.Н. Уточненные геометрически нелинейные уравнения движения удлиненной пластины стержневого типа // Известия вузов. Математика, 2016. № 9. С. 84–89.

  23. Egorov A.G., Affane B. Instability Regions in Flexural-Torsional Vibrations of Plates // Lobachevskii J. Math. 2020. № 41. P. 1167–1174.

  24. Rao S.S. Vibration of continuous systems. NY: John Wiley & Sons, 2007. P. 816.

  25. Erturk A., Inman D.J. Piezoelectric energy harvesting. NY: John Wiley & Sons, 2011. P. 416.

  26. Егоров А.Г., Камалутдинов А.М., Паймушин В.Н., Фирсов В.А. Теоретико-экспериментальный метод определения коэффициента аэродинамического сопротивления гармонически колеблющейся тонкой пластины // ПМТФ. 2016. Т. 57. № 2 (336). С. 96–104.

  27. Guild F.J., Adams R.D. A new technique for the measurement of the specific damping capacity of beams in flexure // J. Phys. E: Sci. Instr. 1981 V. 14. № 3. P. 355.

  28. Adams R.D. The damping characteristics of certain steels, cast Irons and other metals // J. Sound Vib. 1972. V. 23. № 2. P. 199–216.

  29. Zhang J., Perez R.J., Lavernia E.J. Documentation of damping capacity of metallic, ceramic and metal-matrix composite materials // J. Mater. Sci. 1993. V. 28. № 9. P. 2395–2404.

  30. Morison J.R., Johnson J.W., Schaaf S.A. The Force Exerted by Surface Waves on Piles // J. Pet. Technol. 1950. V. 2. P. 149–154.

  31. Jasak H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows: Phd thesis. Department of Mechanical Engineering Imperial College of Science, Technology and Medicine 1996. 394 p.

  32. Hydrodynamics in OpenFOAM (2020) 3D visualization of the fluid flow around a flexurally vibrating beam [Результат 3D моделирования] // YouTube. 23 сентября. (https://www.youtube.com/watch?v=7q7RJFPhpQg ab_channel=HydrodynamicsinOpenFOAM). Просмотрено:18.08.2021

  33. Singh S. Forces on Bodies in Oscillatory Flow: Phd thesis. University of London 1979. 367 p.

  34. Bearman P.W., Downie M.J.,Graham J.M.R., Obasaju E.D. Forces on cylinders in viscous oscillatory flow at low Keulegan-Carpenter numbers // J. Fluid Mech. 1985. V. 154. P. 337–356.

  35. Keulegan G.H., Carpenter L.H. Forces on cylinders and plates in an oscillating fluid // J. Res. Natl. Inst. Stand. Technol. 1958. V. 60. № 5. P. 423–440.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал