Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 25-40

1. ПОСТАНОВКА И МЕТОД РЕШЕНИЯ ЗАДАЧИ

Рассматривается задача об истечении вязкой несжимаемой жидкости в полупространство $\{ x > 0\} $ из круглого отверстия радиусом $R$ (срез сопла) в плоскости {x = 0}. Свойства окружающей среды совпадают со свойствами вытекающей струи. Нестационарное поле скорости $u(t,x)$ ($t$ – время, $x$ – точка пространства) отыскивается путем численного решения уравнений Навье–Стокса

Здесь $p$ – кинематическое давление, $\nu $ – вязкость жидкости.

Задача решается в цилиндрической системе координат $x = (x,r,\theta )$ в цилиндрической расчетной области $\{ 0 < x < {{X}_{m}},\;r < {{R}_{m}}\} $. Радиус расчетной области ${{R}_{m}}$ значительно превышает радиус сопла. На срезе сопла задается нестационарное поле скорости (входные граничные условия): $u(x = 0,r \leqslant R) = {{U}_{0}}(t,r,\theta )$. На остальной площади входного сечения $\{ x = 0,\;r > R\} $ и на цилиндрической границе расчетной области $\{ x > 0,\;r = {{R}_{m}}\} $ ставятся условия непротекания и свободного проскальзывания. На выходной границе $\{ x = {{X}_{m}}\} $ задаются мягкие граничные условия $\partial u{\text{/}}\partial x = 0$. Цель работы состоит в исследовании поведения струи на начальном участке длиной порядка $20R$; для исключения влияния искусственных выходных условий на результаты расчетов в интересующей области длина расчетной области X_m выбирается существенно превышающей этот размер.

Для численного решения задачи применяется универсальный метод решения уравнений Навье–Стокса [9], использующий конечно-разностный метод пространственной дискретизации в направлениях x и r и полунеявную схему интегрирования по времени. В продольном направлении используется равномерная расчетная сетка, а в радиальном – неравномерная, с экспоненциальным ростом шага сетки при $r > R$. Для представления искомых функций по угловой координате используются тригонометрические ряды Фурье. При варьировании сеточных параметров (размеров расчетной области X_m, ${{R}_{m}}$ и числа узлов сетки в соответствующих направлениях Im, Jm) установлено, что набором, достаточным для удовлетворительной точности всех вычислений при рассматриваемом числе Рейнольдса, является ${{X}_{m}} = 40R$, ${{R}_{m}} = 6R$, $Im = 1024$, $Jm = 128$. Большинство представляемых ниже результатов получено при этих значениях параметров.

2. ОСНОВНОЕ ТЕЧЕНИЕ И ЕГО УСТОЙЧИВОСТЬ

В настоящей работе приводятся результаты исследований, соответствующих условиям эксперимента [4, 7, 8] при Re = 2850 (в упомянутых работах число Рейнольдса вычисляется не через радиус, а через диаметр сопла и принимает поэтому вдвое большие значения). Профиль продольной компоненты скорости на срезе сопла ${{U}_{0}}(r)$, реализующийся при этом Re, имеет вид, представленный на рис. 1. Там же изображен профиль завихренности ${{\Omega }_{0}}(r) = - d{{U}_{0}}{\text{/}}dr$. Далее все величины приводятся в безразмерном виде; в качестве масштаба скорости берется средняя скорость ${{U}_{b}}$, а масштаба длины – радиус сопла $R$. Характерной особенностью рассматриваемой струи является наличие трех точек перегиба в профиле скорости ${{U}_{0}}(r)$ (соответствующих трем локальным экстремумам в распределении завихренности ${{\Omega }_{0}}(r)$). Первая точка перегиба расположена в районе $r = 0.5$, а пара других в районе $r = 0.8$. Как будет показано ниже, такой форме профиля скорости отвечают две моды неустойчивых возмущений, развивающихся по существенно различающимся законам.

Рис. 1.

Профиль скорости ${{U}_{0}}(r)$ (а) и завихренности ${{\Omega }_{0}}(r)$ (б) струи на срезе сопла при $\operatorname{Re} = 2850$.

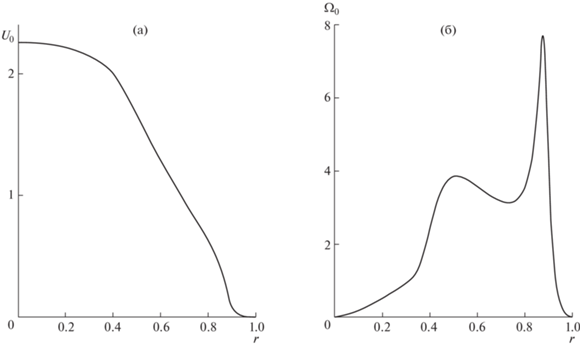
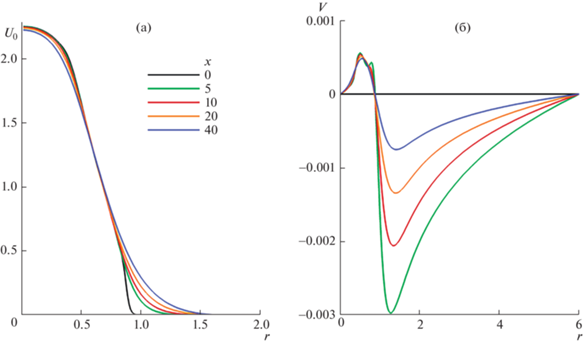
Для расчета основного течения $u = U = (U(x,r),V(x,r),0)$ уравнения (1.1) решаются с осесимметричным стационарным условием на входе $u(x = 0) = ({{U}_{0}}(r),0,0)$ и начальным условием $u(x > 0) = u(x = 0)$. Задача интегрируется по времени до установления стационарного решения. Профили продольной $U(x,r)$ и радиальной $V(x,r)$ компонент скорости основного течения на разных расстояниях $x$ от среза сопла изображены на рис. 2. Скорость на оси струи при рассматриваемом числе Рейнольдса претерпевает лишь незначительные изменения, падение при x = 40 составляет всего около 1%. Основная деформация профиля продольной компоненты наблюдается в периферийной области $r > 0.85$. Внешние точки перегиба, наблюдаюшиеся во входном течении, пропадают уже при $x \approx 7.5$. Соответствующие обобщенные точки перегиба, определяемые из условия $(U{\text{'}}(r){\text{/}}r){\text{'}} = 0$ (штрих обозначает производную) и ответственные за возникновение неустойчивости в осесимметричных течениях [4], пропадают еще раньше, при $x \approx 3.75$. Величина радиальной компоненты скорости на всем протяжении струи остается на три порядка меньше продольной. В каждом сечении $x$ радиальная скорость положительна в области ядра струи, r < 1, что отражает факт расширения струи. Во внешней области радиальная компонента отрицательна, что соответствует увлечению жидкости из окружающего пространства. Этот эффект максимален вблизи входного сечения и ослабевает по мере удаления от него.

Рис. 2.

Профили продольной (а) и радиальной (б) компонент скорости основного течения на разных расстояниях от среза сопла.

При исследовании устойчивости основного течения поле скорости в (1.1) представляется в виде суммы основного течения и возмущения: $u = U + u{\text{'}}$. Возмущения предполагаются малыми, и уравнения линеаризуются относительно $u'$. Решение получающихся таким образом линейных уравнений проводилось в двух постановках. В первой, квазипараллельной постановке, изменение основного течения вдоль направления $x$ учитывается лишь параметрически. Другими словами, уравнения решаются для серии основных течений вида $U = U(r)$, полученных для разных значений координаты $x$, а членами, содержащими производные по x от компонент скорости основного течения, пренебрегается. Обоснованием применения квазипараллельного подхода является малая скорость изменения основного течения вдоль продольной координаты по сравнению с изменениями по радиусу. Во второй, более полной постановке, называемой далее пространственной, линеаризованные уравнения для возмущений решаются без дополнительных упрощений с определенными нестационарными граничными условиями на входе. Факт устойчивости или неустойчивости основного течения устанавливается в этом случае по характеру эволюции разных возмущений вниз по потоку.

Решение задачи устойчивости в рамках квазипараллельного подхода сводится к решению линейных уравнений, коэффициенты которых не зависят от продольной и угловой координат, а также и от времени. Решения таких уравнений можно искать в виде нормальных мод, т.е. с экспоненциальной зависимостью от указанных переменных:

Здесь $n$ – целое азимутальное число, $\alpha $ и $\omega $ – комплексные волновое число и частота. Задача в этом случае сводится к решению задачи на собственные значения $L{\mathbf{v}}{\text{'}} = i\omega {\mathbf{v}}{\text{'}}$ для некоторого линейного дифференциального оператора L, зависящего от параметров $\alpha $ и n. После дискретизации уравнений по r получается задача на собственные значения для комплексной матрицы

Вектор ${\mathbf{v}}{\text{'}}(r)$ представляет в данном случае конечномерный вектор значений компонент скорости возмущения в узлах расчетной сетки по радиальной координате.

По смыслу физической постановки задачи при каждом n требуется отыскание комплексных собственных значений $\alpha $ как функций действительной частоты $\omega $. Однако матрица A в (2.2) зависит от $\alpha $ нелинейно, так что непосредственное определение $\alpha $ при заданном $\omega $ затруднительно. Для этой цели был разработан итерационный алгоритм, основанный на методе Ньютона. На первом этапе алгоритма для некоторого действительного $\alpha $ с помощью QR-алгоритма определяются все (комплексные) собственные значения $\omega $ и собственные векторы ${\mathbf{v}}{\text{'}}(r)$ задачи (2.2). Из них отбирается решение, отвечающее растущему по времени возмущению, т.е. собственное значение $\omega $ с положительной мнимой частью ${{\omega }_{i}}$, и соответствующий ему собственный вектор. Эти значения используются в качестве начального приближения при итерационном продвижении по параметру в сторону уменьшения ${{\omega }_{i}}$ при действительном $\alpha $. Таким образом отыскивается одно решение с действительной частотой $\omega $ и действительным волновым числом $\alpha $, т.е. собственное решение задачи (2.2), обладающее нейтральным поведением как во времени, так и в пространстве. На следующем этапе полученное нейтральное возмущение используется в качестве начального приближения для определения пространственно растущих при $x > 0$ собственных решений, т.е. решений, соответствующих действительным $\omega $ и комплексным $\alpha $, обладающим отрицательной мнимой частью ${{\alpha }_{i}}$.

Среди осесимметричных решений (n = 0) обнаружено две моды растущих возмущений. Одна из них связана с точкой перегиба в профилях скорости, наблюдающейся в районе $r = 0.5$, будем называть ее внутренней модой, в отличие от внешней моды, ассоциированной с точками перегиба в районе внешней границы струи. Коэффициенты нарастания $\sigma = - {{\alpha }_{i}}$ каждой из мод в зависимости от действительной частоты $\omega $ на разных расстояниях от среза сопла приведены на рис. 3. Внутренняя мода остается растущей на всем исследованном отрезке струи. Максимальный рост ее несколько уменьшается с ростом $x$ от $\sigma \approx 0.21$ при x = 0 до $\sigma \approx 0.13$ при x = 20. Соответствующая фазовая скорость остается почти постоянной ${{c}_{r}} = 1.75$, что примерно совпадает со скоростью основного течения во внутренних точках перегиба при разных  x. Частота, соответствующая максимально растущему возмущению, также несколько уменьшается от $\omega \approx 3.0$ при x = 0 до $\omega \approx 2.5$ при x = 20.

Рис. 3.

Коэффициенты нарастания $\sigma $ малых возмущений с азимутальным числом n = 0 как функции частоты $\omega $, полученные в рамках квазипараллельного подхода на разных расстояниях $x$ вниз по потоку. Внутренняя мода (а) и внешняя мода (б).

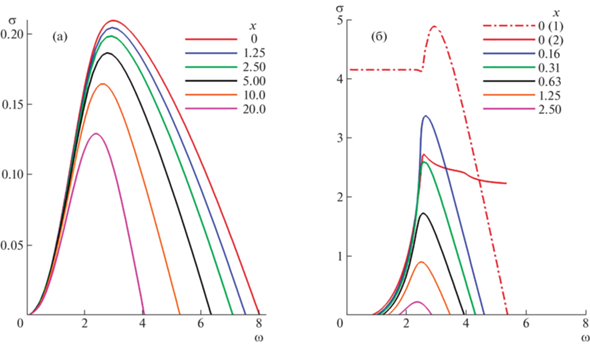
Возмущения внешней моды (рис. 3б) растут существенно быстрее, однако область их нарастания вниз по потоку ограничивается интервалом $x < 3.2$. На бóльших расстояниях от сопла внешние (обобщенные) точки перегиба в профиле скорости пропадают, и связанная с ними неустойчивая мода исчезает. Интересно, что на срезе сопла и в непосредственной близости от него до $x \approx 0.1$ линия $\sigma (\omega )$ не является непрерывной, а состоит из двух ветвей (линии (1) и (2) при x = 0 на рис. 3б). Объяснение такому поведению зависимости $\sigma (\omega )$ дано в [10]. Показано, что разрывное $\sigma (\omega )$ отвечает абсолютному характеру неустойчивости течения. Скорость роста возмущений внешней моды достигает $\sigma \approx 4.9$ при x = 0. С ростом $x$ максимальное значение $\sigma $ быстро уменьшается. Соответствующие частоты также уменьшаются от $\omega \approx 2.9$ при $x = 0$ до $\omega \approx 2.3$ при x = 3.2, а фазовая скорость увеличивается от ${{c}_{r}} \approx 0.44$ до ${{c}_{r}} \approx 0.75$.

На рис. 4 в диапазоне $1.25 < x < 2.5$ и $\omega < 1.25$ можно заметить взаимодействие внутренней и внешней моды, аналогичное обнаруженному в [4] взаимодействию при изменении числа Рейнольдса (см. рис. 26b работы [4]). В отличие от случая n = 0 при малых x, при n = 1 это взаимодействие не приводит к абсолютной неустойчивости, поскольку происходит между двумя движущимися вниз по потоку модами.

Рис. 4.

Коэффициенты нарастания $\sigma $ малых возмущений с азимутальным числом n = 1 как функции частоты $\omega $, полученные в рамках квазипараллельного подхода на разных расстояниях $x$ вниз по потоку. Внутренняя мода (а) и внешняя мода (б).

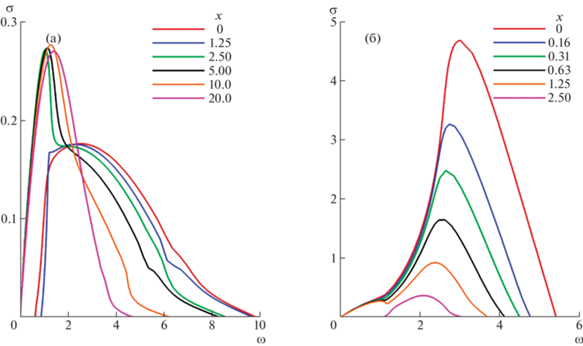
Еще одно заметное различие между растущими возмущениями внутренней и внешней мод касается соответствующих им длин волн. Волновые числа ${{\alpha }_{r}}$ для возмущений с максимальным ростом внутренней моды уменьшаются с ростом $x$ от 1.7 при x = 0 до 1.4 при x = 20. Аналогичные возмущения внешней моды оказываются в 3–4 раза короче, их волновые числа изменяются от 6.7 до 3.1 на отрезке $x$ от 0 до 3.13.

Среди растущих трехмерных возмущений, соответствующих азимутальному числу n = 1, также можно выделить внутреннюю и внешнюю моду (рис. 4). Аналогично случаю осесимметричных возмущений, трехмерные растущие возмущения внешней моды обладают на порядок большими коэффициентами роста по сравнению с возмущениями внутренней моды при малых x, однако растут лишь на ограниченном интервале $x < 3.2$. Растущие возмущения внутренней моды имеются на всей рассмотренной длине струи. Также можно отметить то, что как и в осесимметричном случае, растущие возмущения внешней моды в 3–4 раза короче по длине волны, чем возмущения внутренней моды. В отличие от осесимметричного случая, при n = 1, кроме показанных на рис. 4, имеются еще несколько ветвей растущих возмущений, обладающих незначительными ($\sigma < 0.05$) коэффициентами нарастания.

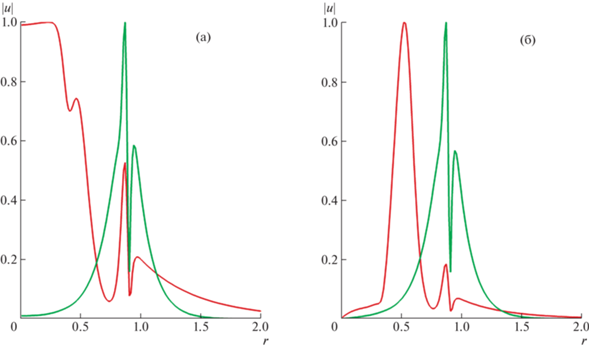
Собственные функции, отвечающие возмущениям внутренней и внешних мод, имеют существенно различающуюся форму. Профили модуля продольной компоненты $\left| {u(r)} \right|$ собственных функций, соответствующих частоте $\omega = 3.0$, близкой к частоте наиболее растущих возмущений при $x = 0$, приведены на рис. 5. Все функции нормированы с условием $\max \left| {u(r)} \right| = 1$. Собственные функции внешней моды при $n = 0$ и $n = 1$ имеют близкую структуру с локализацией возмущений в районе внешних точек перегиба при $r \approx 0.9$, где $\left| {u(r)} \right|$ имеет наибольший градиент и два окружающих резких пика. Схожесть распределений при $n = 0$ и $n = 1$ говорит о том, что изменения собственных функций по углу при $n = 1$ на таком большом расстоянии от оси симметрии струи не имеют большого значения. Внутренние собственные функции при $n = 0$ и $n = 1$, наоборот, имеют сильно различающуюся форму. В осесимметричном возмущении доминируют колебания скорости на оси струи, а в трехмерном – в районе точки перегиба при $r \approx 0.5$. Влияние внутренней точки перегиба на осесимметричное возмущение ограничивается небольшой нерегулярностью в распределении $\left| {u(r)} \right|$ в окрестности этой точки. Интересно, что влияние внешних точек перегиба в виде значительных пиков в профилях $\left| {u(r)} \right|$ для внутренней моды выражено гораздо более отчетливо как для осесимметричных, так и для трехмерных возмущений. Отмеченные пики в профилях собственных функций пропадают при больших $x$ с исчезновением внешних точек перегиба.

Рис. 5.

Профили модуля продольной компоненты |u(r)| собственной функции возмущения при $x = 0$ и $\omega = 3.0$ на отрезке $r \in [0,\;2]$. Красные и зеленые линии отвечают возмущениям внутренней и внешней моды соответственно. Осесимметричные возмущения (а) и трехмерные (n = 1) возмущения (б).

3. ПРОСТРАНСТВЕННОЕ РАЗВИТИЕ МАЛЫХ ВОЗМУЩЕНИЙ

При исследовании пространственного развития малых возмущений поле скорости представляется в виде суммы основного стационарного течения $U = (U(x,r),V(x,r),0)$ и возмущения $u{\text{'}}(t,x,r,\theta )$. Линеаризованные относительно возмущений уравнения Навье–Стокса интегрируются по времени с нулевыми начальными условиями и граничными условиями на входе в виде

Здесь ${\mathbf{v}}{\text{'}}(r)$ – собственный вектор задачи (2.2) при заданных азимутальном числе n и частоте $\omega $; Re{…} обозначает действительную часть комплексной величины. Амплитудный множитель $a(t)$ обеспечивает непрерывное изменение амплитуды входного возмущения от нулевой при $t = 0$ (что согласуется с нулевыми начальными условиями при всех $x$) до единичной при $t = {{t}_{0}} \sim 1$. В качестве нормировки собственного вектора берется условие

С течением времени возмущение распространяется от входного сечения на всю протяженность расчетной области. Расчет продолжается до выхода решения при всех $x$ на периодическое поведение с заданной во входном сечении частотой $\omega $. После этого параллельно с интегрированием по времени вычисляются средние по периоду колебаний величины как функции продольной координаты. На рис. 6 приведены графики изменения вдоль $x$ средней интегральной амплитуды $A(x)$ осесимметричных и трехмерных ($n = 1$) возмущений, полученных с входными условиями, соответствующими внутренней и внешней собственной моде при частоте $\omega = 3.0$. Амплитуда $A(x)$ определяется по формуле

Рис. 6.

Эволюция интегральной амплитуды возмущения (3.3) с частотой $\omega = 3.0$ при n = 0 (а) и при n = 1 (б). Красные и зеленые линии соответствуют возмущениям внутренней и внешней моды соответственно.

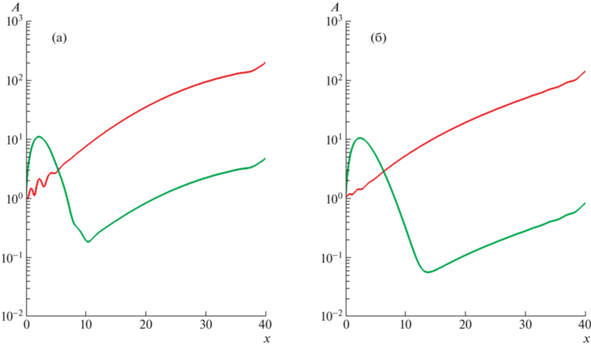
В качестве периода осреднения по времени $T$ берется отрезок, кратный периоду колебаний $2\pi {\text{/}}\omega $. Изменение $A(x)$ для осесимметричных и трехмерных возмущений совершенно идентично. Амплитуда внутренней моды после нескольких небольших колебаний на начальном отрезке выходит на режим монотонного роста, продолжающегося до конца расчетной области. Рост возмущений внутренней моды согласуется с фактом неустойчивости профилей скорости основного течения к таким возмущениям при всех $x \leqslant {{X}_{m}}$, полученным в рамках квазипараллельного подхода.

Развитие возмущений внешней моды происходит совершенно по-другому. Начальный быстрый рост амплитуды заканчивается при $x \approx 2.5$, после чего следует участок затухания, на котором амплитуда падает на два порядка. За пределами этого начального участка развития возмущения снова начинают расти, но уже по закону роста внутренней моды. Начальная эволюция внешней моды также согласуется с предсказанием результатов квазипараллельного подхода. Коэффициент роста таких возмущений на начальном отрезке $x$ существенно превышает аналогичную величину для возмущений внутренней моды, однако уже при $x > 2.5$ возмущения внешней моды при $\omega = 3.0$ затухают, чем и вызвано уменьшение $A(x)$ на рис. 6 при $x > 2.5$. Рост возмущения, аналогичный росту внутренней моды при бóльших $x$ показывает, что на фоне общего затухания в возмущении выделяется составляющая, соответствующая наиболее быстро растущей внутренней моде.

Аппроксимируя линию $A(x)$ в каждой точке $x$ экспонентой, можно оценить локальную скорость роста возмущения как

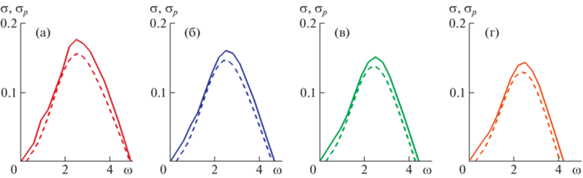
Полученные таким образом оценки скорости роста, рассчитанные для возмущений внутренней моды за пределами начального участка развития при разных значениях частоты $\omega $ для n = 0 и n = 1, даны на рис. 7. Приведенные зависимости для $x \leqslant 20$ качественно и количественно близки к аналогичным графикам $\sigma (\omega )$, полученным в рамках квазипараллельного подхода (рис. 3, 4).

Рис. 7.

Локальные скорости роста σ_p малых возмущений с азимутальным числом n = 0 (а) и n = 1 (б) как функции частоты $\omega $, полученные в рамках пространственного подхода на разных расстояниях $x$ вниз по потоку.

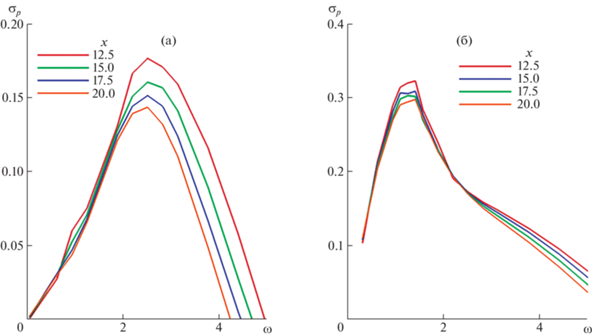
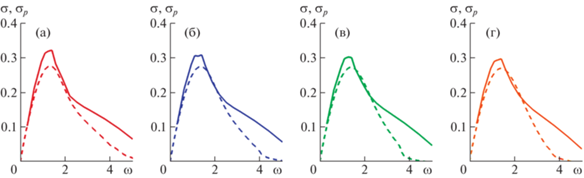
Более подробные сопоставления результатов квазипараллельного и пространственного подходов приведены на рис. 8, где изображены зависимости скорости роста осесимметричных возмущений внутренней моды как функции $\omega $ для разных $x$, полученные в рамках обоих подходов. Аналогичные сопоставления для скорости роста трехмерных возмущений (n = 1) даны на рис. 9. Качественное соответствие результатов двух подходов наблюдается во всех случаях. Частоты, при которых происходит максимальный рост возмущений, совпадают с хорошей точностью. Оценка скорости роста возмущений, полученная в рамках пространственного подхода при всех $\omega $, несколько больше оценки квазипараллельного подхода. При $n = 0$ разница максимальных значений составляет около 10%, при n = 1 – около 15%. Единственное бросающееся в глаза различие касается трехмерных возмущений и состоит в более медленном уменьшении ${{\sigma }_{p}}$ при увеличении $\omega > 2$ по сравнению с $\sigma $. Возможной причиной повышенной скорости роста возмущений ${{\sigma }_{p}}$ при n = 1 и $\omega > 2$ является наличие нескольких ветвей растущих возмущений этого типа, что было обнаружено при использовании квазипараллельного подхода.

Рис. 8.

Скорости роста малых возмущений с азимутальным числом n = 0, полученные в рамках пространственного подхода ${{\sigma }_{p}}$ (сплошные линии) и квазипараллельного подхода $\sigma $ (прерывистые линии): (а) – $x = 12.5$, (б) – $x = 15.0$, (в) – $x = 17.5$, (г) – $x = 20.0$.

Рис. 9.

Скорости роста малых возмущений с азимутальным числом n = 1, полученные в рамках пространственного подхода ${{\sigma }_{p}}$ (сплошные линии) и квазипараллельного подхода $\sigma $ (прерывистые линии): (а) – $x = 12.5$, (б) – $x = 15.0$, (в) – $x = 17.5$, (г) – $x = 20.0$.

4. НЕЛИНЕЙНОЕ ВЗАИМОДЕЙСТВИЕ ВОЗМУЩЕНИЙ И ПЕРЕХОД К ТУРБУЛЕНТНОСТИ

Так же, как и при исследовании пространственного развития малых возмущений, в расчетах нелинейного взаимодействия возмущений поле скорости представляется в виде суммы основного стационарного течения U = (U(x, r), V(x, r), 0) и возмущения u'(t, x, r, θ). Возмущения отыскиваются в виде конечного ряда Фурье по угловой координате:

Нелинейные уравнения Навье–Стокса интегрируются по времени с нулевыми начальными условиями. Граничные условия на входе задаются аналогично (3.1) в виде

Здесь A_n(x) – амплитуда соответствующей гармоники, ${\mathbf{v}}_{n}^{'}$(r) – собственная функция линейной задачи устойчивости для входного течения. Как и в (3.1), a(t) – переходная функция, обеспечивающая непрерывное изменение амплитуды соответствующего входного возмущения от нулевой при t = 0 до A_n(0) при t = t₀ ~ 1. Амплитуда A_n(x) определяется аналогично (3.3) путем интегрирования по r и осреднения по времени величины |${\mathbf{u}}_{n}^{'}$(t, x, r)|².

Расчеты проводились с A_n(0) = 0 при n > 1, т.е. на входе задавались возмущения в виде комбинаций нулевой и первой угловой гармоник с разными амплитудами. Старшие гармоники в этом случае возникают при x > 0 в результате нелинейных взаимодейстий трехмерных возмущений. В случае, если амплитуда A₁(0) входного возмущения задается нулевой, то течение остается осесимметричными при всех x. Число учитываемых гармоник N_m варьировалось в диапазоне от 1 до 32. Обнаружено, что качественное, а в большинстве случаев и количественное поведение течения на отрезке, предшествующем переходу к турбулентному режиму, удовлетворительно воспроизводится уже начиная с N_m = 4. Большинство из представляемых ниже результатов получено при N_m = 8.

В [7] подробно описаны эксперименты, проведенные на установе НИИ механики МГУ, в которых изучалось развитие струи под действием искусственных возмущений осесимметричного вида. Возмущения вносились на расстоянии x = 0.32 от среза сопла с помощью осциллирующих в осевом направлении тонких колец, расположенных соосно со струей. Использовались два кольца разного диаметра, обеспечивающих возбуждение возмущений, близких к внешней и внутренней моде линейной устойчивости. При возбуждении внешней моды длина ламинарного участка струи заметно сокращается в определенном диапазоне частот осцилляции кольца по сравнению со случаем отсутствия возмущений (при покоящемся кольце). Максимальное сокращение ламинарного участка до примерно x = 5 наблюдается при частоте, совпадающей с частотой максимально растущего возмущения, предсказываемой линейной теорией устойчивости. Напомним, что естественный переход в экспериментальных условиях при рассматриваемом числе Рейнольдса Re = 2850 происходит при x ≈ 12. Амплитуда линейной скорости колебаний кольца Δu' поддерживалась постоянной при варьировании частоты; в безразмерных величинах эта скорость составляет ≈0.035. При использующейся в настоящей работе нормировке возмущений (3.2) при n = 1, 2 это соответствует A_n(0) ≈ 10^–2.

Для моделирования нелинейного развития осесимметричных возмущений достаточно ограничиться значением N_m = 0 в (4.1). Расчеты проводились в диапазоне частот 1 ≤ ω ≤ 5, совпадающем с диапазоном максимально растущих линейных возмущений (см. рис. 3). Для воспроизведения экспериментальных условий амплитуда A₀(0) входного возмущения выбиралась равной 10^–2. Обнаружено, что поведение возмущения внешней моды при этой амплитуде на начальном участке качественно повторяет пространственное развитие малого возмущения, приведенного на рис. 6. В силу нелинейности процесса количественные характерные значения несколько меняются. Так, при ω = 3 начальный быстрый рост амплитуды возмущения останавливается уже при x ~ 1: амплитуда за это время вырастает всего в 1.8 раза, тогда как при линейном развитии амплитуда возмущения на начальном участке увеличивается на порядок. После следует этап уменьшения амплитуды и перестройка возмущения в возмущение внутренней моды. Затем происходит близкое к линейному усиление возмущения внутренней моды до достижения A(x) ≈ 0.03 при x = 25, насыщение, и этап некоторой релаксации (медленного уменьшения амплитуды) до A ≈ 0.02 при x = 40. Колебания скорости во всех точках струи вплоть до выходного сечения остаются регулярными, с минимальным отклонением от гармонического закона.

Увеличение начальной амплитуды на порядок A₀(0) = 10^–1 не меняет качественного поведения течения за исключением некоторых деталей. Затухание возмущения начинается сразу при x > 0, минуя отрезок начального роста. После этого так же, как и в случае меньшей начальной амплитуды, возмущение переходит в возмущение внутренней моды, несколько усиливается, в этом случае до A₀ ≈ 0.09 уже при x ≈ 8, и переходит в этап релаксации. Поведение возмущений во времени так же остается близким к гармоническому.

При возбуждении во входном сечении возмущения внутренней моды процесс упрощается за счет отсутствия этапа перестройки возмущения внешней моды во внутреннюю. Остальное качественно сохраняется: при меньшей начальной амплитуде A₀(0) = 10^–2 возмущения нарастают аналогично линейному росту на рис. 6, достигают максимума и релаксируют до A(40) ≈ 0.04; при A₀(0) = 10^–1 после минимального начального роста сразу наступает этап медленного затухания до A(40) ≈ 0.09.

Полученные результаты развития осесимметричных возмущений противоречат эксперименту [7]. В расчетах показано, что развитие осесимметричных возмущений приводит к установлению регулярных колебаний, тогда как в эксперименте установлен не только факт перехода к турбулентности, но и сокращение длины ламинарного участка под действием искусственного осесимметричного возмущения. Такое различие может объясняться тем, что в экспериментальных условиях, кроме искусственного возмущения, имеются трехмерные возмущения неконтролируемой природы, развитие которых на фоне искусственного осесимметричного возмущения и приводит к ускоренному переходу. В пользу этого предположения говорит и тот факт, что и при отсутствии искусственного возмущения в струе происходит переход к турбулентности, а значит, в ней присутствуют неконтролируемые возмущения.

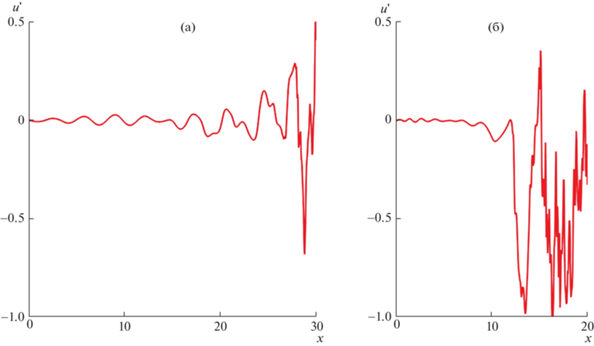
Для изучения возможности возникновения перехода к турбулентности под действием трехмерных возмущений были проведены расчеты нелинейной эволюции исходно достаточно малых возмущений, A_n(0) = 10^–3 при n = 0, 1. Отдельно рассмотрены случаи возмущений, соответствующих внутренней и внешней моде устойчивости. Входные возмущения соответствовали частоте ω = 3, что близко к частоте максимально растущих возмущений на начальном участке струи (см. рис. 3, 4). Возмущения внутренней моды на отрезке 0 < x < 20 растут в этом случае в соответствии с линейным законом развития малых возмущений (рис. 6), практически не взаимодействия друг с другом. Осесимметричное возмущение вырастает примерно в 30 раз, трехмерное – примерно в 20 раз. Начиная с x = 20, рост амплитуды первой угловой гармоники (n = 1) ускоряется, вероятно, под влиянием заметно подросшей к этому моменту нулевой гармоники. Обратное влияние первой гармоники на нулевую квадратичное, поэтому проявляется несколько позже, когда A₁ достигает значения ~10^–1, что происходит примерно при x = 25. Появляющиеся в силу нелинейности возмущения с бóльшими азимутальными номерами быстро нарастают при x > 0, и при x ≈ 25 сравниваются по порядку величины амплитуды с возмущениями, соответствующими n = 0 и n = 1. В этот момент в колебаниях скорости как функции времени и продольной координаты появляются нерегулярные флуктуации большой амплитуды, что можно квалифицировать как переход к турбулентности. Изменение продольной компоненты скорости возмущения u'(x) вдоль продольной координаты при r = 0.5, θ = 0 в некоторый фиксированный момент времени показано на рис. 10а. График ограничен координатой x = 30, при которой уже формируются нерегулярные и значительные по амплитуде колебания.

Рис. 10.

Изменение продольной компоненты скорости возмущения $u{\text{'}}(x)$ вдоль продольной координаты при $r = 0.5$, $\theta = 0$ в некоторый фиксированный момент времени. Входные возмущения внутренней моды (а) и внешней моды (б) при частоте $\omega = 3$ и начальных амплитудах ${{A}_{0}}(0) = {{10}^{{ - 3}}}$, ${{A}_{1}}(0) = {{10}^{{ - 3}}}$.

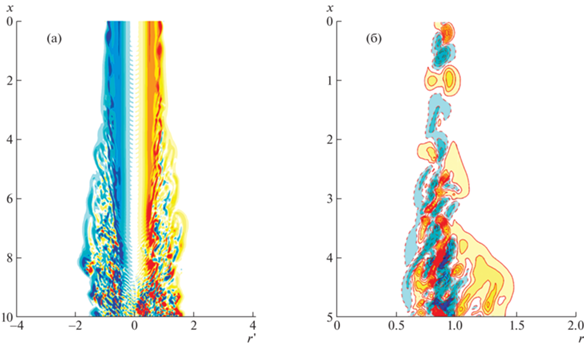
Визуализация течения показана на рис. 11а,б. На первом из них изображено мгновенное поле угловой компоненты завихренности ω_θ = ∂${v}$/∂x – ∂u/∂r (u, ${v}$, w – компоненты вектора скорости u, соответствующие осевой, радиальной и угловой координате цилиндрической системы) в плоскости (x, r' ≥ 0, θ = 0) и поле – ω_θ в плоскости (x, r' < 0, θ = π). Здесь r' = r при r' > 0 и r' = –r при r' < 0. В таком представлении сохраняются непрерывность и гладкость изображаемого поля при пересечении линии r' = 0. Представленная визуализация наглядно демонстрирует начало перехода к турбулентности при x ~ 25, когда в поле завихренности появляется ярко выраженная нерегулярная мелкомасштабная составляющая. При x > 25 используемое пространственное разрешение по угловой координате (4.1) при N_m = 8 становится недостаточным. Проверено, что увеличение числа учитываемых гармоник до N_m = 32 не меняет качественно картину течения на этапе перехода, т.е. при x < 25. Таким образом, можно надеяться, что переходный этап воспроизводится в расчете верно. На рис. 11б изображено поле завихренности возмущения $\omega _{\theta }^{'}$ = ∂${v}$'/∂x – – ∂u'/∂r в плоскости (x, r, θ = 0), дающее некоторое дополнительное представление о характере развития возмущений на переходном этапе. Отметим, что на рис. 11а сохранены геометрические пропорции течения, тогда как на рис. 11б изображение растянуто в горизонтальном направлении. Видно, что возмущения на всем протяжении струи концентрируются вдоль линии r ≈ 0.5, т. е. в области внутренней точки перегиба в профиле скорости основного течения. Длина волны возмущения λ_x ≈ 4 также сохраняется примерно постоянной.

Рис. 11.

Поле угловой компоненты завихренности ${{\omega }_{\theta }}$ (а, в) и возмущения завихренности $\omega _{\theta }^{'}$ (б, г). Входные возмущения внутренней моды (а, б) и внешней моды (в, г) при частоте $\omega = 3$ и начальных амплитудах ${{A}_{0}}(0) = {{10}^{{ - 3}}}$, ${{A}_{1}}(0) = {{10}^{{ - 3}}}$.

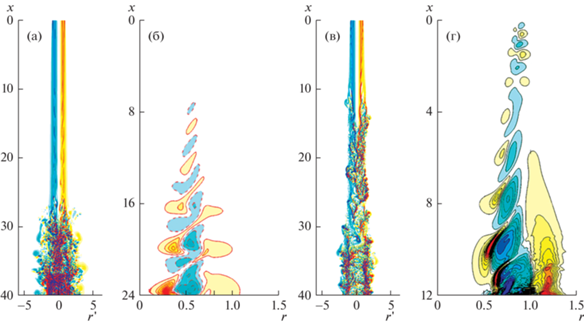
Эволюция возмущений внешней моды устойчивости на начальном этапе также соответствует линейному поведению (рис. 6). Амплитуды обеих гармоник n = 0, 1 вырастают примерно на порядок на отрезке x < 2. Далее изменение A₁(x) происходит иначе, чем в линейном случае. Влияние выросшей осесимметричной составляющей возмущения приводит к более быстрому росту трехмерных компонент. Это относится не только к n = 1, которая продолжает свой рост, но и к возмущениям старших гармоник, начальная амплитуда которых была нулевой. Амплитуда осесимметричного возмущения уменьшается при x > 2, но не на два порядка, как в линейном случае, а менее, чем на порядок. Начиная с x ≈ 5, A₀(x) также начинает расти. Уже при x ≈ 12 в колебаниях скорости (рис. 10б) появляются мощные нерегулярные флуктуации – в течении устанавливается турбулентный режим. После завихренности, изображенное на рис. 11в,г, показывает изменение струи, происходящее на переходном участке. Возмущение, вносимое во внешнюю область струи, r ≈ 0.85, постепенно смещается в сторону r = 0.5 по мере эволюции вниз по потоку. Характерная длина волны возмущения увеличивается от х ≈ 1 на входе до х ≈ 2 уже при x = 10.

Проведенные вычисления показывают, что естественный переход к турбулентности, наблюдаемый в эксперименте при x ≈ 12, может объясняться наличием в потоке неконтролируемых трехмерных возмущений с амплитудой A_n ~ 10^–3. При этом переход вызывается, вероятно, развитием возмущений внешней моды линейной устойчивости. Можно также предположить, что сокращение длины переходной области при внесении искусственных осесимметричных возмущений с амплитудой ~10^–2, наблюдавшееся в эксперименте [6, 7], вызывается не столько развитием самих осесимметричных возмущений, сколько их влиянием на скорость роста фоновых трехмерных возмущений. В пользу этого говорит отмеченный выше факт, что рост трехмерных возмущений малой амплитуды усиливается на фоне осесимметричного возмущения при достижении последней амплитуды порядка 10^–2.

Для проверки высказанной гипотезы была проведена серия численных экспериментов, в которых начальные амплитуды возмущений внешней моды задавались в виде A₀(0) = 10^–2 и A₁(0) = 10^–3. Частота возмущений обеих гармоник при этом совпадала и варьировалась в диапазоне 1 ≤ ω ≤ 5. Такие условия могут примерно соответствовать условиям эксперимента [6, 7] в предположении, что вместе с искусственным осесимметричным возмущением в поток вносится и менее интенсивное трехмерное возмущение той же частоты, например, вследствие неидеальности устройства генерации искусственных возмущений. Визуализация полученных течений при разных частотах вносимых возмущений представлена на рис. 12. На том же рисунке дана фотография дымовой визуализации струй, полученных в эксперименте [6]. И в расчете, и в эксперименте наблюдается зависимость длины переходной области от частоты вносимого возмущения. Быстрее всего турбулентность в обоих случаях возникает при частотах ω ≈ 2.5–3.0. В этом диапазоне наблюдается максимальный рост возмущений по линейной теории.

Рис. 12.

Верхний ряд – визуализация расчетов (поле угловой компоненты завихренности): (а) – $\omega = 1$, (б) – $\omega = 2$, (в) – $\omega = 2.5$, (г) – $\omega = 3$, (д) – $\omega = 3.5$, (е) – $\omega = 4$, (ж) – $\omega = 5$. Нижний ряд – дымовая визуализация эксперимента: (а) – $\omega = 0$, (б) – $\omega = 1.7$, (в) – $\omega = 2.0$, (г) – $\omega = 2.3$, (д) – $\omega = 2.6$, (е) – $\omega = 2.7$, (ж) – $\omega = 2.9$, (з) – $\omega = 3.1$, (и) – $\omega = 3.3$, (к) – $\omega = 3.6$, (л) – $\omega = 3.7$, (м) – $\omega = 6.9$.

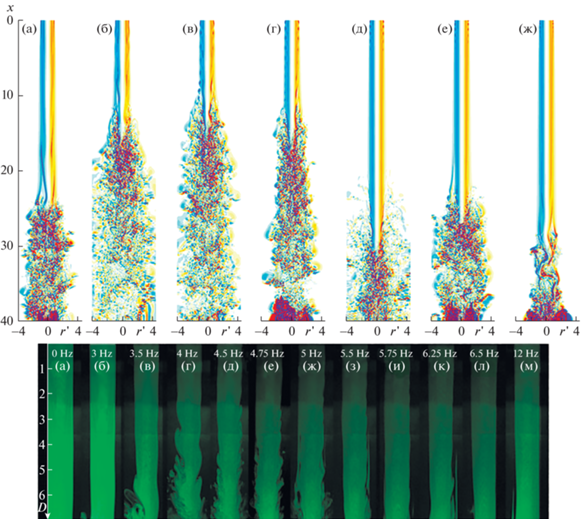
В экспериментах вблизи зоны перехода (рис. 12) очевидно наличие трехмерных возмущений, при том что искусственно вносимые возмущения близки к осесимметричным. Данное обстоятельство согласуется с выводом о необходимости начальных малых трехмерных возмущений, которые, резко вырастая за счет нелинейного взаимодействия, в конечном счете и приводят к турбулизации. Роль осесимметричных возмущений в таком механизме – не в том, чтобы вырасти и самостоятельно турбулизовать струю, а в том, чтобы обеспечить нелинейный рост трехмерных возмущений, которые и приводят к турбулизации.

Обращает на себя внимание, что длина зоны перехода при ω = 3 и амплитудах возмущений A₀(0) = 10^–2, A₁(0) = 10^–3 лишь незначительно сокращается по сравнению с описанным выше вариантом A₀(0) = 10^–3, A₁(0) = 10^–3 (рис. 11в,г). Это может объясняться тем, что величина A₀ = 10^–2 близка к пределу линейного роста осесимметричного возмущения на начальном участке струи. Как было отмечено выше при описании развития осесимметричных возмущений, при A₀(0) = 10^–2 рост нулевой гармоники на начальном участке составляет лишь 1.8 раза, в то время как при A₀(0) = 10^–3 она вырастает почти на порядок. Соответственно и влияние осесимметричного возмущения на рост трехмерных возмущений в этих двух случаях близко. Отметим, что влияние это на эволюцию малых трехмерных возмущений важно. Если отказаться от осесимметричной составляющей во входном возмущении (A₀(0) = 0, A₁(0) = 10^–3), то рост трехмерных возмущений долгое время остается почти линейным, в результате длина области перехода вырастает почти до x = 30.

Следует также отметить, что характер развития течения очень зависит от начальной амплитуды трехмерного возмущения. Во всех описанных выше вариантах рассматривались малые начальные возмущения A₁(0) ≤ 10^–3. Повышение этого уровня даже в отсутствие осесимметричной составляющей приводит к более быстрому включению нелинейных механизмов и, как результат, сокращению длины переходной области. На рис. 13 приведена аналогичная рис. 11 визуализация течения, полученного с чисто трехмерным входным возмущением, но с увеличенной амплитудой: A₀(0) = 0, A₁(0) = 10^–2 (показан начальный участок развития струи). Рост возмущений происходит в этом случае очень быстро, в том числе и благодаря раннему возбуждению старших угловых гармоник. Возникновение турбулентности, сопровождающееся появлением нерегулярных колебаний, происходит уже при x ≈ 4. Этот результат согласуется с экспериментальными данными о быстром переходе в струе под действием искусственных трехмерных возмущений, соответствующих n = 1. Как показано в [8], длина переходной области сокращается в этом случае до 1–2 диаметров струи.

Рис. 13.

Поле угловой компоненты завихренности ${{\omega }_{\theta }}$ (а) и возмущения завихренности $\omega _{\theta }^{'}$ (б). Входные возмущения внешней моды при частоте $\omega = 3$ и начальных амплитудах ${{A}_{0}}(0) = 0$, ${{A}_{1}}(0) = {{10}^{{ - 2}}}$.

5. ЗАКЛЮЧЕНИЕ

В работе приводятся результаты численного исследования устойчивости и нелинейной эволюции возмущений в круглой струе. Воспроизводятся условия лабораторного эсперимента при Re = 2850, проведенного ранее в НИИ механики МГУ им. М.В. Ломоносова [4–8]. Характерная особенность изучаемой струи – наличие трех точек перегиба во входном профиле скорости, что существенно определяет свойства течения. Линейная устойчивость исследуется с использованием двух подходов: квазипараллельного и пространственного. В первом изменение основного течения вдоль потока учитывается параметрически: задача устойчивости решается для серии профилей основного течения, соответствующих разным расстояниям от входа. В пространственном подходе линеаризованные уравнения Навье–Стокса для возмущений интегрируются с учетом изменения основного течения. Получено хорошее количественное согласие результатов двух подходов, а также согласие с результатами невязкой теории [4, 7]. Основное качественное свойство устойчивости течения состоит в существовании двух мод растущих возмущений: внутренней и внешней, отвечающих внутренней ($r \approx 0.5$) и паре внешних ($r \approx 0.85$) точек перегиба. Скорость роста возмущений внешней моды на порядок превышает аналогичную скорость роста возмущений внутренней моды. Однако эта неустойчивость пропадает уже на ранних стадиях развития струи вместе с исчезновением внешних точек перегиба в профиле скорости основного течения. Неустойчивость к внутренним модам сохраняется на всем протяжении развития струи.

Проведены численные расчеты с целью объяснения и интерпретации результатов лабораторного эксперимента [7], в котором обнаружено изменение протяженности зоны перехода к турбулентности в струе под действием периодических во времени осесимметричных возмущений. В расчетах показано, что осесимметричные возмущения даже значительной начальной амплитуды не приводят к переходу к турбулентности. Колебания, вызываемые развитием таких возмущений, сохраняют регулярный, близкий к гармоническому, характер. Наблюдающийся в эксперименте переход к турбулентности может объясняться наличием неконтролируемых трехмерных возмущений, усиливающихся на фоне достаточно интенсивных искусственных возмущений. Проведенные в данной работе исследования подтверждают выдвинутую гипотезу. Входные возмущения в виде комбинации осесимметричного и малого трехмерного возмущения приводят к развитию турбулентности на расстоянии около 5 диаметров струи. Так же, как и в эксперименте, протяженность области перехода сокращается в тех случаях, когда частота входного возмущения близка к частоте наиболее быстро растущих возмущений по линейной теории.

В описанной картине инициатором перехода служат трехмерные возмущения, а осесимметричные возмущения при достаточно большой амплитуде лишь ускоряют их рост. Отсюда следует, что более интенсивные начальные трехмерные возмущения могут быть способными обеспечивать еще более быстрый переход даже при отсутствии осесимметричной составляющей. Последнее предположение подтверждается расчетами с трехмерными начальными возмущениями конечной амплитуды. Длина зоны перехода сокращается в этом случае до 1–2 диаметров струи, что объясняет причину быстрого перехода, полученного в экспериментах [8].

Авторы выражают признательность В.В. Веденееву за плодотворные обсуждения работы и полезные замечания по тексту статьи. Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта № 20-19-00404, с использованием вычислительных ресурсов ОВК НИЦ “Курчатовский институт”, http://computing.nrcki.ru/.