Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 80-93

1. ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Рассмотрим слабо заряженную сферическую каплю равновесного радиуса $R$ идеальной несжимаемой идеально проводящей жидкости с массовой плотностью ${{\rho }_{1}}$, коэффициентом поверхностного натяжения $\sigma $, подвешенную в конвективном облаке в суперпозиции гравитационного g, внутриоблачного коллинеарного g однородного электростатического поля напряженностью ${{{\mathbf{E}}}_{0}}$ и восходящего потока воздуха. Внешнюю среду (воздух) будем считать сжимаемым идеальным диэлектриком с массовой плотностью ${{\rho }_{2}}$ и диэлектрической проницаемостью ${{\varepsilon }_{{ex}}}$. Положим, что в воздухе звук распространяется со скоростью ${v}$. Температуру капли и внешней среды будем считать неизменной, а объём жидкой фазы капли – постоянным. В дальнейших рассуждениях малым зарядом капли будем пренебрегать (он нужен только для того, чтобы обеспечить неподвижность капли).

В соответствии с [13, 14] капля, находящаяся во внешнем электростатическом поле, принимает вытянутую вдоль поля ${{{\mathbf{E}}}_{0}}$ примерно сфероидальную форму с эксцентриситетом e. Примем, что ось z (ось симметрии капли) направлена в сторону, противоположную гравитационному полю g.

Задачу будем решать в сферической системе координат $\left( {r,{{\theta ,\varphi }}} \right)$, начало которой поместим в центре масс капли. Полярный угол ${{\theta }}$ отсчитывается от ${{{\mathbf{E}}}_{0}}$, а азимутальный угол $\varphi $ в дальнейшем не используется ввиду осевой симметрии капли.

Примем, что на поверхности жидкости существует капиллярное волновое движение с амплитудой $\sim {\kern 1pt} \sqrt {\kappa T{\text{/}}\sigma } $, где $\kappa $ – постоянная Больцмана, T – абсолютная температура, порождаемое уже тепловым движением молекул жидкости [15], которое создает малое возмущение ${{\xi (\theta }},t)$ равновесной поверхности капли. Для большинства реальных жидкостей, включая жидкие металлы, тепловая амплитуда капиллярных волн не превышает десятых долей нанометра.

2. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

Уравнение возмущенной поверхности капли представим в виде

где $r({{\theta }})$ – равновесная форма капли. Примем также, что амплитуда капиллярного волнового возмущения ${{\xi (\theta }},t)$ много меньше радиуса невозмущенной капли $\max \left| \xi \right| \ll R$. Отношение $\max \left| \xi \right|{\text{/}}R$ примем в качестве малого параметра $\varepsilon \equiv \left| \xi \right|{\text{/}}R \ll 1$ задачи.

Пусть движение жидкости в капле и движение внешней среды бесконечно малой амплитуды, порождаемое капиллярным волновым движением на границе раздела сред, является потенциальным. Тогда поля скоростей безвихревого движения в капле и среде ${{{\mathbf{V}}}_{j}}(r,\theta ,t)$ определится функциями гидродинамических потенциалов ${{\psi }_{j}}(r,\theta ,t)$ ${{{\mathbf{V}}}_{j}}(r,\theta ,t) = \nabla {{\psi }_{j}}(r,\theta ,t)$ [16], (индексом j = 1 отмечаются величины, относящиеся к капле, j = 2 – к среде). При этом потенциалы скоростей внутри и вне капли, а также возмущение поверхности капли имеют один порядок малости ${{\psi }_{j}}(r,\theta ,t)\sim \xi (\theta ,t)\sim \varepsilon $, поскольку именно зависящая от времени деформация поверхности генерирует капиллярное волновое движение.

Принимая каплю идеальным проводником, для которого характерное время распределения индуцированных внешним электрическим полем зарядов много меньше характерного гидродинамического времени колебаний поверхности капли, электрическое поле вокруг капли будем считать квазистационарным. В этом случае электрическое поле характеризуется электрическим потенциалом $\Phi (r,{{\theta }},t)$, определяемым напряженностью поля E на основе соотношения: ${\mathbf{E}}({\mathbf{r}},t) = - \nabla \Phi (r,{{\theta }},t)$ [17].

Математическая формулировка задачи о расчете спектра капиллярных осцилляций незаряженной капли, во внешнем электростатическом поле, и генерации акустического излучения, состоит из уравнений Лапласа для потенциала поля скоростей движения жидкости в капле ${{\psi }_{1}}(r,\theta ,t)$ и электростатического потенциала $\Phi (r,\theta ,t)$, а также волнового уравнения для потенциала поля скоростей движения внешней среды ${{\psi }_{2}}(r,\theta ,t)$

и граничных условий

Граничное условие для волнового уравнения (2.3) на бесконечности имеет вид $r \to \infty $:

Сформулированную задачу дополним интегральными условиями

В выражениях (2.4)–(2.10) соотношения (2.4) есть граничные условия в центре капли и на бесконечности; (2.5), (2.6) – кинематическое и динамическое условия на ее возмущенной поверхности; (2.7) – условие постоянства электрического потенциала на поверхности идеально электропроводной капли; (2.8) – условие излучения Зоммерфельда [18]; (2.9) – условия постоянства полного объема капли и неподвижности ее центра масс; (2.10) – условие неизменности полного заряда капли.

Так же в (2.4)–(2.10) введены обозначения ${{\Phi }_{s}}(t)$ – постоянное значение электрического потенциала на поверхности капли, $k = {\text{Re}}{{\omega }_{n}}{\text{/}}{v}$ – волновое число, q – малый ($ \sim {\kern 1pt} {\rm O}({{\varepsilon }^{2}})$) заряд капли, o и O – символы порядка малости [19], ${{P}_{j}} = {{P}_{{0j}}} - {{\rho }_{j}}\partial {{\psi }_{j}}\left( {r,\theta ,t} \right){\text{/}}\partial t$ – давления внутренней (j = 1) и внешней (j = 2) среды на поверхность капли, ${{P}_{{0j}}}$ – постоянные давления в капле и среде, ${{P}_{E}} = {{{{\varepsilon }_{{ex}}}{{{\left( {\nabla \Phi } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{ex}}}{{{\left( {\nabla \Phi } \right)}}^{2}}} {8\pi }}} \right. \kern-0em} {8\pi }}$ – давление электрического поля на поверхность капли, ${{P}_{\sigma }} = \sigma \,\left( {{{\nabla }_{s}},{\mathbf{n}}\left( {\theta ,t} \right)} \right)$ – давление капиллярных сил, ${{\nabla }_{s}}$ – поверхностный оператор “набла”, ${\mathbf{n}}\left( {\theta ,t} \right)$ – единичный вектор нормали к возмущенной поверхности капли, вычисляемый как

Сформулированную задачу (2.2)–(2.11) будем решать стандартными методами теории возмущений в линейном приближении по безразмерной амплитуде осцилляций ε [19]. Для этого искомые функции разложим в ряд по степеням малого параметра $\varepsilon $ с точностью до слагаемых первого порядка

где ${{\Phi }^{{\left( 0 \right)}}}(r,\theta )$ – электростатический потенциал у поверхности равновесной капли, ${{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t)$ – добавка к электростатическому потенциалу, связанная с осцилляциями поверхности капли. Верхний индекс в скобках указывает на порядок малости по ε.

Подставляя эти разложения в исходную систему уравнений (2.2)–(2.10) и приравнивая слагаемые одного порядка малости по ε, получим задачи нулевого и первого порядков.

3. РЕШЕНИЕ ЗАДАЧИ НУЛЕВОГО ПОРЯДКА ПО ε

Для отыскания равновесного электрического потенциала ${{\Phi }^{{\left( 0 \right)}}}(r,\theta )$ и равновесной формы поверхности капли $r(\theta )$ решим электрогидродинамическую задачу нулевого порядка по ε, получающуюся из (2.2)–(2.10) группировкой слагаемых $\sim {\kern 1pt} {{\varepsilon }^{0}}$

где ${{{\mathbf{n}}}_{0}}(\theta )$ – от нормали к равновесной поверхности капли $r(\theta )$.

Из приведенной выше задачи несложно найти

где ${{P}_{n}}\left( \mu \right)$ – осесимметричный полином Лежандра n-го порядка [20]; e – эксцентриситет капли; n – целое положительное число; $\mu \equiv \cos \theta $. В (3.1), (3.12) соотношение (3.1) определяет равновесный электростатический потенциал невозмущенной капли, (3.2) – равновесную форму невозмущенной капли.

4. РЕШЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЗАДАЧИ ПЕРВОГО ПОРЯДКА МАЛОСТИ ПО ε

Для определения линейной поправки к потенциалу электрического поля ${{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t)$, связанного с капиллярным волновым движением поверхности капли, сформулируем электрическую задачу в первом порядке малости по $\varepsilon $

Из решения уравнения Лапласа (4.1) при выполнении условия ограниченности (4.2) получим электрический потенциал, представленный в виде ряда по полиномам Лежандра

где ${{P}_{n}}\left( \mu \right)$ – полином Лежандра n-го порядка [20], n – целое число, $\mu \equiv \cos \theta $.

Функцию волнового возмущения $\xi (\theta ,t)$ с гармонической временной зависимостью отдельных слагаемых возьмем в виде $\xi (\theta ,t)$$\sim \exp \left( {i{{\omega }_{n}}t} \right)$ [21]

Здесь минимальное значение индекса суммирования n = 2 определяется исключением радиальных пульсаций и поступательного движения капли в линейном приближении по ε. В выражениях (4.5), (4.6) действительные амплитудные коэффициенты ${{F}_{n}}$, ${{M}_{n}}$ имеют первый порядок малости.

Подставим разложение (4.5) в условие (4.3) постоянства электрического потенциала на поверхности капли и с учетом интегрального условия сохранения заряда капли (4.4) и соотношений (2.1), (4.6) определим амплитудные коэффициенты F_n в (4.5), при помощи которых запишем электрический потенциал ${{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t)$ в виде

5. РЕШЕНИЕ ГИДРОДИНАМИЧЕСКОЙ ЗАДАЧИ ПЕРВОГО ПОРЯДКА МАЛОСТИ ПО $\varepsilon $. ВЫВОД ДИСПЕРСИОННОГО УРАВНЕНИЯ

Математическая формулировка гидродинамической части решаемой задачи первого порядка малости по безразмерной амплитуде осцилляций $\varepsilon $ имеет вид

где n – единичный вектор нормали к возмущенной поверхности капли (2.1), и имеет согласно (2.11) вид

В выписанной задаче первого порядка малости: (5.4) – условие Зоммерфельда, (5.5) – кинематическое граничное условие на поверхности капли; (5.6) – динамическое граничное условие, поправки к давлениям, связанные с возмущением поверхности капли, определяются соотношениями r = R:

Подставим в (5.8) уравнения для волнового возмущения (4.6) и поправки к электрическому потенциалу (4.7) и в результате несложных преобразований получим электрическое давление первого порядка малости по $\varepsilon $

Из формулы (5.9) с учетом функции (4.6) найдем линейную по малому параметру $\varepsilon $ поправку к давлению капиллярных сил

Примем, что гидродинамические потенциалы ${{\psi }_{j}}(r,\theta ,t)$ зависят от времени t гармонически: ${{\psi }_{j}}(r,\theta ,t)$ ~ ${\text{exp}}(i{{\omega }_{n}}t)$. С учетом данных рассуждений волновое уравнение (5.2) приведем к однородному уравнению Гельмгольца

Потенциал поля скоростей течения жидкости в капле ${{\psi }_{1}}(r,\theta ,t)$, являющийся решением уравнения Лапласа (5.1), удовлетворяющий условию ограниченности в центре масс капли (5.3), запишем в виде разложения по осесимметричным полиномам Лежандра

Решение уравнения (5.12) для потенциала скоростей акустического поля при выполнении условия излучения на бесконечности (5.4) представим в виде

где $h_{n}^{{\left( 2 \right)}}\left( z \right)$ – сферическая функция Бесселя третьего рода [22].

Заметим, что в разложениях (5.13), (5.14) коэффициенты A_n, ${{B}_{n}}$ имеют первый порядок малости по безразмерной амплитуде осцилляций.

Подстановка разложений (4.6), (5.13), (5.14) в кинематическое граничное условие при j = 1, 2, позволяет найти коэффициенты A_n, ${{B}_{n}}$ в (5.13), (5.14), выраженные через действительные амплитуды M_n, которые дают решение для потенциалов ${{\psi }_{1}}(r,\theta ,t)$, ${{\psi }_{2}}(r,\theta ,t)$ в виде

где $C_{{mk,lp}}^{{nq\,\,\,\,}}$ – коэффициенты Клебша–Гордана [20], отличные от нуля при условии |m – l| ≤ $n \leqslant m + l$, $m + l + n$ – четное и k + p = q.

Подставляя потенциалы поля скоростей (5.15), (5.16) в (5.7), найдем поправки первого порядка малости к давлениям внутренней и внешней для капли сред

В итоге из условия баланса давлений (5.6) в любой точке на возмущенной поверхности сфероидальной капли с учетом (5.10), (5.11), (5.17), (5.18), пренебрегая взаимодействием различных мод осцилляций, найдем дисперсионное уравнение задачи

Входящую в уравнение (5.19) сферическую функцию Бесселя $h_{n}^{{\left( 2 \right)}}\left( z \right)$ для целого значения индекса представим в виде степенного ряда [22, 23]

Аналогично тому, как это было проделано в [11, 24], при малом значении аргумента z ($z \ll 1$) для функций $T_{0}^{ + }\left( z \right)$, $T_{{12}}^{ - }\left( z \right)$ получим следующие асимптотики

Решение дисперсионного уравнения имеет комплексный вид, поэтому запишем его как ${{\omega }_{n}} = \omega _{n}^{'} + i\omega _{n}^{{''}}$, где мнимая часть $\omega _{n}^{{''}}$ имеет смысл декремента затухания из-за потерь механической энергии осцилляций капли на излучение продольных акустических волн. С учетом малости мнимой части по сравнению с реальной частью $(\omega _{n}^{{''}} \ll \omega _{n}^{'})$ для квадрата частоты осцилляций капли будет справедливо соотношение

Сопоставляя выражения (5.19), (5.23) и учитывая (5.21), (5.22), найдем реальную $\omega _{n}^{'}$ и мнимую $\omega _{n}^{{''}}$ части дисперсионного уравнения для малого аргумента ${{z}_{0}} = kR$ в виде

Подставим в (5.25) решение для реальной части частоты осцилляций и при ${{z}_{0}} = {{\omega }_{n}}R{\text{/}}{v}$ получим декремент затухания n-й моды капиллярных осцилляций капли, связанный с генерацией акустических волн ${{\eta }_{*}}$, в виде

В частности, если плотность внешней среды много меньше плотности внутренней среды (${{\rho }_{2}} \ll {{\rho }_{1}}$), декремент затухания для второй (основной) моды капиллярных осцилляций капли примет вид

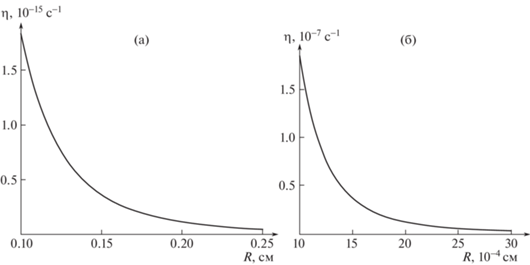
На рис. 1а–б по (26) приведены кривые, иллюстрирующие зависимость декремента затухания η от размера капли $R$. Видно, что с ростом радиуса равновеликой сферической капли величина η весьма быстро снижается: при увеличении размера капли в три раза декремент затухания уменьшается на два порядка. Из (5.26) нетрудно видеть, что декремент затухания линейно зависит от плотности внешней среды, и что возрастание скорости звука в окружающей среде приводит к быстрому уменьшению декремента затухания.

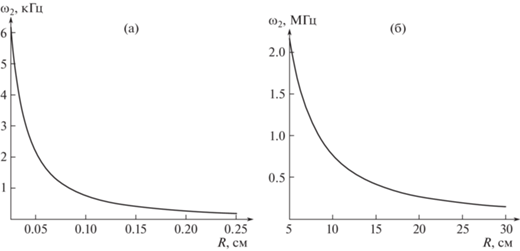
На рис. 2а–б приведены зависимости частот акустических волн по (5.24) с использованием (5.21)–(5.22): а) для крупных капель (капель дождя) и б) для мелких, облачных. Видно, что дождевые капли при осцилляциях излучают акустические волны в диапазоне частот, воспринимаемых человеческим ухом, а облачные капли – в ультразвуковой области.

6. ИНТЕНСИВНОСТЬ АКУСТИЧЕСКОГО ИЗЛУЧЕНИЯ

Интенсивность полного звукового излучения осциллирующей капли, когда длина излучаемой акустической волны велика по сравнению с радиусом капли $\lambda \gg R$, определяется известным выражением [18]

где $\overline {V_{2}^{2}} $ – среднее значение квадрата скорости движения частиц внешней среды в звуковой волне, а интегрирование производится по возмущенной поверхности капли, определяемой выражением (2.1).

Скорость движения внешней среды ${{{\mathbf{V}}}_{2}}(r,\theta ,t) = \operatorname{Re} \left( {\nabla {{\psi }_{2}}(r,\theta ,t)} \right)$ задается нормальной составляющей к поверхности осциллирующей капли и содержит лишь радиальную компоненту

Для нахождения потенциала ${{\psi }_{2}}(r,\theta ,t)$ в дальней области акустического поля (для расстояний, больших длины звуковой волны $r \gg \lambda $) сферическая функция Бесселя $h_{n}^{{\left( 2 \right)}}\left( z \right)$ в (5.20) при больших значениях аргумента $z \gg 1$ имеет асимптотическое представление:

В уравнении (5.16) найдем асимптотическое поведение функции ${{\partial }_{z}}(h_{n}^{{\left( 2 \right)}}\left( z \right))$ для малого аргумента $z \ll 1$

Используя полученные асимптотики (6.3), (6.4), при условии $R \ll r$ потенциал скорости в окружающей каплю среде приобретет вид

Заметим, что на больших расстояниях r от осциллирующей капли в волновой зоне акустического излучения потенциал поля скоростей ${{\psi }_{2}}(r,\theta ,t)$ представлен суперпозицией расходящихся сферических волн с амплитудами, убывающими с расстоянием r по закону $\sim {\kern 1pt} 1{\text{/}}r$.

В итоге, подставляя потенциал (6.5) в (6.2), при $R \ll r$ для скорости движения частиц внешней среды имеем

В общей формуле для интенсивности звукового излучения (6.1) среднее значение квадрата скорости движения внешней для капли среды вычислим в виде $\overline {{{{\left| {{{V}_{2}}} \right|}}^{2}}} = {{{{{\left| {{{V}_{2}}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{{V}_{2}}} \right|}}^{2}}} 2}} \right. \kern-0em} 2}$. Скалярно умножая выражение (6.6) на комплексно сопряженное ему, получим

Подставляя (6.7) в (6.1) и учитывая свойство ортогональности полиномов Лежандра [22], в формуле (6.1) рассчитаем интеграл по поверхности возмущенной капли S = [r = r(θ, t), $0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$. В итоге интенсивность акустического излучения незаряженной осциллирующей сфероидальной капли примет вид

С учетом выражения для волнового числа: $k = \omega _{n}^{'}{\text{/}}{v}$, аналитическое выражение (6.8) преобразуется к виду

где частота n-й колебательной моды капли $\omega _{n}^{'}$ определяется (5.24).

Используя выражение (6.9), оценим величину интенсивности акустического излучения жидко-капельных систем естественного и искусственного происхождения.

Источником акустического излучения в конвективных облаках являются в основном мелкие осциллирующие капли с радиусами от 3 до 30 мкм и концентрацией в облаке ∼10³ см^–3, на долю которых приходится большая часть воды, содержащейся в облаке [25, 26]. Максимальную концентрацию имеют капли радиусом 3–7 мкм [25]. Осцилляции внутриоблачных капель большой амплитуды объясняются микрофизическими внутриоблачными процессами: разрушением крупных капель в результате аэродинамического сопротивления, столкновения с более мелкими каплями, а также капиллярной электростатической неустойчивости и электрического взаимодействия с соседними частицами. Натурные измерения колебаний дождевых капель показали, что капли могут осциллировать с амплитудами, достигающими десятков процентов их радиусов [27, 28]. Для характерных значений напряженности внутриоблачного электрического поля величина параметра Тейлора $w = 16\pi {{e}^{2}}{\text{/}}9$, определяющего электрогидродинамическую устойчивость капли по отношению к индуцированному внешним электрическим полем заряду, много меньше критического значения ${{w}_{{кр}}}$, при котором капля распадается [13, 14].

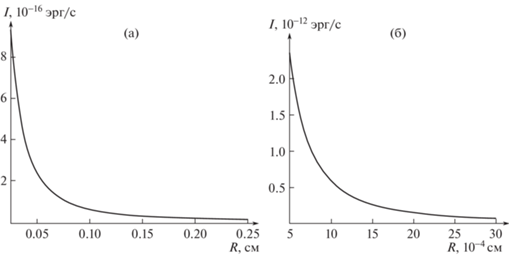
На рис. 3а–б приведем результаты оценки интенсивности акустического излучения единичной капли, осциллирующей на основной моде n = 2 во внешнем электростатическом поле напряженностью ${{E}_{0}} = 0.17$ СГСЭ ($\sim {\kern 1pt} 2 \times {{10}^{{ - 4}}}{{E}_{{0кр}}}$, где ${{E}_{{0кр}}}$ – критическое для электростатического распада капли на более мелкие значение напряженности поля, при R = 3 мкм и $\sim {\kern 1pt} 7 \times {{10}^{{ - 4}}}{{E}_{{0кр}}}$ при R = 30 мкм). Амплитуду осцилляций капли примем ${{M}_{n}} = 0.1R$. Характеристики капли и внешней среды: ${{\varepsilon }_{{ex}}} = 1$, σ = 73 дин/см, ${{\rho }_{1}} = 1$ г/м³, ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м³, ${v} = 3.3 \times {{10}^{4}}$ см/с. По формуле (6.9) найдено, что при радиусе капли R = 3 мкм интенсивность звукового излучения составила $I\,\sim \,7\, \times \,{{10}^{{ - 12}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 5$ МГц. Для радиуса R = 8 мкм получено $I\sim 9 \times {{10}^{{ - 13}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 1$ МГц, а при R = 30 мкм величина интенсивности излучения составила $I\sim 7 \times {{10}^{{ - 14}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 147$ кГц.

Интегральная мощность акустического излучения ансамбля мелких осциллирующих капель в облаке диаметром 10 км будет уже в 5 × 10²⁰ раз больше излучения от одной капли. Принимая для оценки по порядку величины, что все облачные капли имеют одинаковый размер R = 30, получим излучение ${{I}_{{in}}}\sim 3 \times {{10}^{7}}$ эрг/с на ультразвуковой частоте от 147 кГц.

Согласно [29], с. 427, радиусы капель осадков изменяются от R = 0.01 см до R = 0.35 см. При радиусах капель в диапазоне: $0.01 \leqslant R \leqslant 0.025$ см, осадки называются “моросью”, при $0.025 \leqslant R \leqslant 0.35$ см – “дождем”. Капли более крупных размеров разрушаются из-за лобового сопротивления воздуха.

По формуле (6.9) рассчитаем интенсивность акустического излучения дождевых капель при тех же характеристиках, что и выше. Получено, что для дождевой капли с размером R = 0.025 см интенсивность излучения равна $I\sim 1 \times {{10}^{{ - 15}}}$ эрг/с при ${{\omega }_{2}} \approx 6$ кГц. Для более крупной капли R = = 0.25 см звуковое излучение $I\sim 1 \times {{10}^{{ - 17}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 0.2$ кГц, а для самой большой капли с R = 0.35 см интенсивность излучения порядка $I\sim 5 \times {{10}^{{ - 18}}}$ эрг/с при частоте осцилляций второй моды ${{\omega }_{2}} \approx 0.1$ гГц.

Примем, что в дожде концентрация капель с радиусом $R = 0.025$ см, равна 0.3 см^–3, и тогда несложно получить, что интегральное акустическое излучение на границе пространства объемом 1 км³, занятого ливневым дождем, будет иметь интенсивность $I\sim 3 \times {{10}^{{ - 1}}}$ эрг/с на частоте $ \approx {\kern 1pt} 6$ кГц, а для капель радиусом R = 0.25 см при той же концентрации интегральное излучение идет с интенсивностью $I\sim 3 \times {{10}^{{ - 3}}}$ эрг/с на частоте ≈0.2 гГц волн. Полагая для простоты, что дождь идет в кубическом пространстве с характерным линейным размером, в 1 км получим, что через любую грань куба в единицу времени выходит излучение, интенсивностью в шесть раз меньшее. Тогда плотность потока энергии ${{J}_{{in}}} \sim {{10}^{{ - 11}}}$ эрг/с ⋅ см² (R = 0.025 см) и ${{J}_{{in}}} \sim {{10}^{{ - 13}}}$ эрг/с ⋅ см² (R = 0.25 см). Излучение такой интенсивности на несколько порядков величины меньше, чем может зарегистрировать ухо человека. Чтобы увеличить интенсивность излучения в проведенных оценках, можно взять большую амплитуду осцилляций и больший объем пространства, занятого дождем; можно увеличить величину заряда на капле и величину внутриоблачного (или приземного для дождевых капель) электрического поля, все это можно проделать, не выходя за рамки данных натурных метеорологических измерений [26].

Собственно говоря, при принятых выше условиях граница между ультразвуковыми и звуковыми волнами по размеру капель приходится примерно на $R = 0.01135$ см с интенсивностью излучения порядка $I\sim 5 \times {{10}^{{ - 15}}}$ эрг/с с частотой осцилляций второй моды $\omega = 20$ кГц. По классификации [25] такие капли можно отнести к крупным облачным каплям, концентрация которых в грозовом облаке не превосходит 1 см^–3.

С увеличением номера моды осцилляций капли n на единицу интенсивность звукового излучения снижается примерно на два порядка.

Интересно, что если сравнить мощности акустического и электромагнитного излучений от единичной незаряженной капли, осциллирующей в электростатическом поле в грозовом облаке, можно сделать заключение, что интенсивность звукового излучения на 17–18 порядков величины выше полной интенсивности электромагнитного излучения при тех же характеристиках электропроводной капли [24].

ЗАКЛЮЧЕНИЕ

В линейном приближении по безразмерной амплитуде осцилляций и равновесной деформации капли слабом внешнем электрическом поле найдена интенсивность акустического излучения от жидко-капельных объектов естественного происхождения: капель туманов, облаков, дождя. Выяснилось, что туманы и облака излучают акустические волны достаточно большой интенсивности в ультразвуковом диапазоне частот, а вот даже мелкие дождевые капли генерируют при своих осцилляциях акустические волны из звукового диапазона частот с интенсивностью на два-три порядка величины более слабые, чем может зафиксировать ухо человека. Граница между ультразвуковым излучением капель и звуковым проходит в области размеров, чуть больших чем R = 100 мкм. При определении такой границы принималось, что капли несут весьма малый заряд, влияние которого на частоты акустического излучения весьма мало, а амплитуда осцилляций равна одной десятой радиуса капли. Если в оценках взять амплитуды осцилляций в пять-шесть раз больше (как это фиксируется в натурных наблюдениях) и учесть наличие на каплях существенного электрического заряда, то граница между ультразвуковыми и звуковыми акустическими волнами может быть сдвинута в область меньших размеров. При этом интенсивность излучения будет повышена до различаемого человеческим ухом в силу того, что концентрация капель в облаке увеличивается с уменьшением их размера.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-19-00598 “Гидродинамика и энергетика капли и капельных струй: формирование, движение, распад, взаимодействие с контактной поверхностью”, https://rscf.ru/project/19-19-00598/).