1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2022

Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 41-50

УСТОЙЧИВОСТЬ ПОГРАНИЧНОГО СЛОЯ ПРИ ВНУТРЕННЕМ ВЫДЕЛЕНИИ ТЕПЛА И ПОДАЧЕ ГАЗА ЧЕРЕЗ ПОРИСТУЮ СТЕНКУ

С. А. Гапонов a, *

a Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Новосибирск, Россия

* E-mail: gaponov@itam.nsc.ru

Поступила в редакцию 05.03.2022
После доработки 20.05.2022
Принята к публикации 20.05.2022

Полный текст (PDF)

Аннотация

Решена задача устойчивости дозвукового пограничного слоя в условиях подвода тепла внутрь пограничного слоя с инжекцией однородного газа через пористую пластину, частично модулирующая устойчивость пограничного слоя с диффузионным горением. Во всем диапазоне исследованных параметров наиболее растущими являются двумерные волны. Установлено, что при фиксированной норме подвода тепла с увеличением числа Рейнольдса, т.е. при удалении от передней кромки пластины, максимальная температура в пограничном слое увеличивается, что согласуется с известными экспериментами и расчетами параметров пограничного слоя с диффузионным горением. При этом зависимость максимальных по частоте степеней усиления от числа Рейнольдса немонотонна. Показано, что инжекция газа с подводом тепла дестабилизирует пограничный слой, как и в его отсутствие. С другой стороны, показана стабилизирующая роль подвода тепла и в условиях вдува газа через пористую стенку. С увеличением частоты нарастающей волны фазовая скорость стремится к скорости в обобщенной точке перегиба. Несмотря на достаточно большие величины степеней нарастания, справедливо соотношение Гастера, согласно которому пространственная степень усиления равна временной степени усиления, поделенной на групповую скорость.

Ключевые слова: пограничный слой, подвод тепла, пористая пластина, неустойчивость, возмущения

Стимулирующей задачей настоящей работы была проблема устойчивости пограничного слоя с диффузионным горением. Впервые задача диффузионного пламени в пограничном слое была сформулирована Эммонсомом [1]. Исследования пограничного слоя с диффузионным горением проводились неоднократно, что отражено, например, в обзоре [2].

Менее изучена проблема устойчивости пограничного слоя с химическими реакциями. Обзор соответствующих работ, выполненных до конца 70-х гг., имеется в монографии [3]. Однако почти все работы, упомянутые в обзоре, относятся к задаче о гравитационной конвекции. Наибольшее отношение к настоящей теме имеют работы [4–6]. В [4] анализ ограничен невязким приближением, т.е. в уравнениях устойчивости пренебрегается членами, содержащими коэффициенты молекулярного переноса вещества, импульса и энергии. В [3, 5, 6] исследования проведены как в невязком приближении, так и с учетом коэффициентов переноса вещества, импульса и энергии в приближении Дана-Линя [7]. В них изучалась устойчивость в условиях диссоциации и рекомбинации кислорода и азота. Аналогичные исследования в более полной постановке проводились для гиперзвукового пограничного слоя, подробную информацию о которых можно найти в [8, 9]. Однако они касались только устойчивости течения по отношению к двумерным 2D-возмущениям, направление волнового вектора которых совпадает с направлением основного течения.

Первоначальные исследования устойчивости ламинарных течений в присутствии диффузионного пламени проводились для слоев смешения топлива и окислителя или при подаче струи топлива в окислитель, и задача решалась в пренебрежении вязкостью в уравнениях устойчивости. Подробную информацию о таких работах можно найти в обзоре [10]. В связи с этим заслуживает внимания работа [11]. В ней, по-видимому, впервые рассмотрена устойчивость струи в присутствии пламени с учетом вязкости и теплопроводности в уравнениях устойчивости. До настоящего времени отсутствуют исследования по устойчивости пограничного слоя при сгорании топлива, подаваемого через проницаемую поверхность и сгорающего в потоке окислителя.

Наличие диффузионного пламени приводит к внутреннему выделению тепла и изменению состава смеси, а плотность зависит как от температуры, так и состава смеси (ее молекулярной массы). Поэтому устойчивость пограничного слоя с горением зависит от числа Маха, температурных граничных условий, смешения инородных газов и условий теплоподвода внутрь пограничного слоя. Однако во многих случаях, например, при сгорании углеводородных топлив в потоке воздуха плотность газа зависит, в основном, от температуры. Молекулярная масса смеси меняется по пограничному слою незначительно [12], ее изменением можно пренебречь. При подаче топлива через пористую стенку, обтекаемую окислителем, важный фактор, влияющий на устойчивость пограничного слоя, связан с вдуванием газа.

Важный результат работ [3, 5] состоит в том, что члены уравнений устойчивости, связанные с возмущениями источников тепла и концентраций веществ, обратно пропорциональны числу Рейнольдса, и они одного порядка с членами, учитывающими непараллельность течения. Там же показано, что в приближении локальной параллельности потока устойчивость пограничного слоя зависит только от распределения скорости и плотности основного течения. Из этого следует, что влияние возмущений источника концентраций и температуры на устойчивости пограничных слоев сравнимо с влиянием непараллельности основного течения. Слабое влияние возмущений источника тепла на устойчивость пограничного слоя без вдува было подтверждено в [13]. Поэтому при исследовании устойчивости пограничных слоев в приближении параллельного течения этими возмущениями можно пренебречь, что согласуется, кроме того, с теорией устойчивости диффузионного пламени при больших числах Дамкёлера Da (зона пламени много меньше толщины пограничного слоя) [14] и результатами [15] при конечных значениях Da. Таким образом, устойчивость диффузионного пламени в пограничном слое удовлетворительно может описываться устойчивостью течения однородного газа с подводом энергии внутрь слоя и инжекцией газа через пористую стенку.

Поэтому в данной работе распределение температуры в условиях диффузионного пламени моделируется с помощью источника тепла, а плотность обратной пропорциональностью температуре. Исследования проведены при дозвуковом обтекании пластины, число Маха M $ \ll $ 1.

1. ОСНОВНОЕ ТЕЧЕНИЕ В ПОГРАНИЧНОМ СЛОЕ

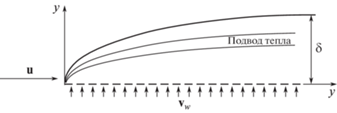
На рис. 1 показан пограничный слой с полосой ввода тепла и вдувом газа через пористую стенку.

Рис. 1.

Схема пограничного слоя с подводом тепла и вдувом газа через пористую стенку.

Ламинарное течение однородного газа в пограничном слое описывается в безразмерных переменных системой уравнений [16]

(1.1)
$\begin{gathered} \frac{{\partial (u\rho )}}{{\partial x}} + \frac{{\partial ({v}\rho )}}{{\partial y}} = 0,\quad \rho \left( {u\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial y}}} \right) = \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) \\ \rho \left( {u\frac{{\partial I}}{{\partial x}} + {v}\frac{{\partial I}}{{\partial y}}} \right) = \frac{\partial }{{\partial y}}\left[ {\frac{\mu }{{\Pr }}\frac{{\partial I}}{{\partial y}} + \mu \left( {1 - \frac{1}{{\Pr }}} \right)u\frac{{\partial u}}{{\partial y}}} \right] + \rho Q \\ \end{gathered} $
$\rho = \frac{{pm}}{{RT}},\quad I = h + \frac{{{{u}^{2}}}}{2},\quad \mu = {{T}^{{3/2}}}\left( {1 + \frac{{{{T}_{s}}}}{{{{T}_{e}}}}} \right){{\left( {T + \frac{{{{T}_{s}}}}{{{{T}_{e}}}}} \right)}^{{ - 1}}}$

Здесь u и ${v}$ – проекции вектора скорости на ортогональные координаты x (параллельная поверхности пластины) и y (нормальная к поверхности) соответственно, ρ – плотность, p – давление, T – температура, h = cpT – энтальпия, Q – количество тепла введенного в единицу времени на единицу массы, m – молекулярный вес газа, R – универсальная газовая постоянная, μ – динамический коэффициент вязкости, cp – удельная теплоемкость при постоянном давлении, Pr – число Прандтля. Предполагается, что cp и Pr постоянны, Ts = 110 K. Система (1.1) нормализована с помощью следующих масштабов: ${{{v}}_{e}}$/ue – длина, μe – вязкость, ue – скорость, Te – температура, ρe – плотность, $u_{e}^{2}$ – энтальпия, $u_{e}^{4}{{\rho }_{e}}{\text{/}}{{\mu }_{e}}$ – подвод тепла, $u_{e}^{2}{\text{/}}{{T}_{e}}$ – удельная теплоемкость и универсальная газовая постоянная, ${{\rho }_{e}}u_{e}^{2}$ – давление. Индексом e помечены параметры на внешней границе пограничного слоя.

На поверхности пластины (y = 0)u = 0, ${v}$ = j/ρw (j – поток массы газа через стенку), T = Tw, а на внешней границе пограничного слоя u = T = 1.

В локальном автомодельном приближении система приводится к виду

(1.2)
$\begin{gathered} \frac{d}{{dY}}\left( {C\frac{{{{d}^{2}}f}}{{d{{Y}^{2}}}}} \right) + \frac{f}{2}\frac{{{{d}^{2}}f}}{{d{{Y}^{2}}}} = 0 \\ \frac{d}{{dY}}\left( {\frac{C}{{\Pr }}\frac{{dg}}{{dY}}} \right) + \frac{f}{2}\frac{{dg}}{{dY}} = \frac{{u_{e}^{2}}}{{{{I}_{e}}}}\frac{d}{{dY}}\left[ {\left( {\frac{1}{{\Pr }} - 1} \right)C\frac{{df}}{{dY}}\frac{{{{d}^{2}}f}}{{d{{Y}^{2}}}}} \right] - Q\frac{{u_{e}^{2}}}{{{{I}_{e}}}}\operatorname{Re} _{b}^{2}{{\left( {\frac{{\operatorname{Re} }}{{{{{\operatorname{Re} }}_{b}}}}} \right)}^{2}} \\ \end{gathered} $
$\frac{{df}}{{dY}} = u,\quad {\text{g}} = \frac{{u_{e}^{2}I}}{{{{I}_{e}}}},\quad dY = \rho \frac{{dy}}{{\operatorname{Re} }}{\text{,}}\quad C = \rho \mu ,\quad {\text{ Re}} = \sqrt x $

Здесь Reb – постоянное число Рейнольдса конкретной задачи. Решение системы (1.2) зависит от x (через Re) параметрически и должно удовлетворять граничным условиям

$f = j\operatorname{Re} ,\quad \frac{{df}}{{dY}} = u = 0,\quad T = {{T}_{w}}(Y = {\text{ }}0);\quad u = g = 1\,\,(Y = \infty )$

Зависимость подвода тепла от нормальной координаты принимается в виде

$Q\frac{{u_{e}^{2}}}{{{{I}_{e}}}}\operatorname{Re} _{b}^{2} = Au(1 - u)\exp \left( { - {{{\left( {\frac{{y - {{y}_{f}}}}{{{{\Delta }_{f}}}}} \right)}}^{2}}} \right)$

Здесь величина Δf пропорциональна ширине полосы подвода тепла, которая много меньше толщины пограничного слоя; yf – параметр задачи, характеризующий положение полосы подвода тепла. В силу того, что основной вклад в подвод тепла осуществляется в узкой полосе, т.е. при $y - {{y}_{f}} \ll 1$, можно ограничиться первым членом разложения скорости по координате вблизи yf, т.е. принять$\left( {u - {{u}_{f}}} \right) \approx {{\left( {du{\text{/}}dy} \right)}_{f}}(y - {{y}_{f}})$, где индексом f помечены значения параметров течения при $y = {{y}_{f}}$. Тогда

$y - {{y}_{f}} \approx \left( {u - {{u}_{f}}} \right)\left( {\frac{{du}}{{dy}}} \right)_{f}^{{ - 1}} = \left( {u - {{u}_{f}}} \right)\frac{{\operatorname{Re} }}{{{{\rho }_{f}}}}{{\left. {{{{\left( {\frac{{du}}{{dY}}} \right)}}^{{ - 1}}}} \right|}_{{Y = {{Y}_{f}}}}}$
$y - {{y}_{f}} \approx \left( {u - {{u}_{f}}} \right){{T}_{f}}({{\operatorname{Re} }_{b}})\frac{{{{T}_{f}}(\operatorname{Re} )}}{{{{T}_{f}}({{{\operatorname{Re} }}_{b}})}}{{\operatorname{Re} }_{b}}\frac{{\operatorname{Re} }}{{{{{\operatorname{Re} }}_{b}}}}{{\left. {{{{\left( {\frac{{du}}{{dY}}} \right)}}^{{ - 1}}}} \right|}_{{Y = {{Y}_{f}}}}}$

Известно, и настоящие предварительные расчеты показывают, что $du{\text{/}}dY$ слабо зависит от Re. Таким образом, можно взять

(1.3)
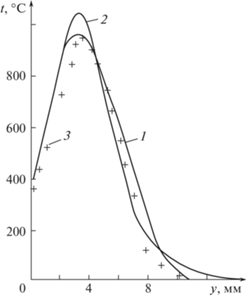
$Q\frac{{u_{e}^{2}}}{{{{I}_{e}}}}\operatorname{Re} _{b}^{2} = Au(1 - u)\exp \left( { - {{{\left( {\frac{{u - {{u}_{f}}}}{\Delta }\frac{{{{T}_{f}}(\operatorname{Re} )}}{{{{T}_{f}}({{{\operatorname{Re} }}_{b}})}}\frac{{\operatorname{Re} }}{{{{{\operatorname{Re} }}_{b}}}}} \right)}}^{2}}} \right)$

Параметры A, Δ и uf были выбраны таким образом, чтобы распределение температуры соответствовало профилю температуры, рассчитанному в [17] для пламени при следующих условиях. Плоская пористая пластина обтекается воздухом, а через ее поры вдувается смесь азота и водорода, массовая концентрация которого составляла 0.4%. Скорость на границе пограничного слоя составляет 5 м/с, а максимум температуры находился на высоте 3.5 мм на расстоянии 0.1 м от переднего края пластины. Расчеты в [17] были проведены при Te = 293 K, Reb = 180 и числе Маха M $ \ll $ 1. Наилучшее соответствие температурных профилей, полученных в [17] и в настоящих расчетах, было достигнуто при A = 15.25, uf = 0.15, $\Delta = 0.158$ (рис. 2).

Рис. 2.

Сравнение распределения температуры настоящих расчетов (1) с расчетными (2) и экспериментальными (3) данными [17].

На рис. 3 представлены профили скорости (рис. 3а) и температуры (рис. 3б) при числе Рейнольдса Re = 180 и разных значениях параметра вдува j. Как и следовало ожидать, при вдуве в профиле скорости появляется точка перегиба, которая удаляется от поверхности пластины с увеличением j. Температура внутри пограничного слоя при этом увеличивается. Расчеты показывают, что при j = 0.004 увеличение числа Рейнольдса с Re = 70 до Re = 180, что равносильно смещению вниз по потоку примерно два раза, повышает максимальную температуру внутри слоя примерно на 35%, что качественно согласуется с данными по диффузионному пламени в пограничном слое, например, с экспериментами [17] и расчетами [18].

Рис. 3.

Распределение скорости (а) и температуры (б) и произведения плотности на завихренность (в) в пограничном слое при Re = 180 и разных величинах вдува газа.

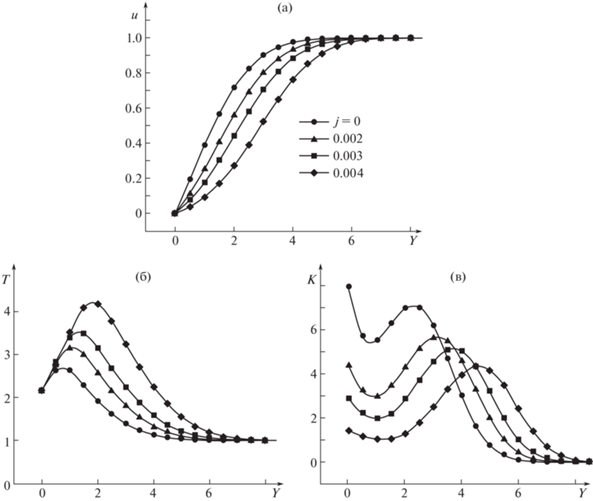
В теории “невязкой” неустойчивости особую роль играет обобщенная точка перегиба, наличие максимума или минимума в произведении плотности и завихренности K = ρ(du/dy) = = ${{\rho }^{2}}(du{\text{/}}dY)$, наличие которых является необходимым условием неустойчивости. Изменение K по пограничному слою показано на рис. 3в. Из него видно, что с увеличением интенсивности вдува положение максимума смещается к внешней границе пограничного слоя, в то время как положение минимума остается неизменным. Сильное влияние вдува на положение максимума, обобщенной точки перегиба, может повлиять на устойчивость течения в пограничном слое.

2. УСТОЙЧИВОСТЬ ПОГРАНИЧНОГО СЛОЯ

Полные динамические уравнения в безразмерном представлении имеют вид

(2.1)
$\rho \frac{{d{\mathbf{v}}}}{{dt}} = - {\mathbf{grad}}\Pi ,\quad \frac{{d\rho }}{{dt}} + \rho {\text{div}}({\mathbf{v}}) = 0,\quad \rho \frac{{dh.}}{{dt}} = \frac{{dp}}{{dt}} - {\text{div}}({\mathbf{q}}) + 2\mu {{\dot {S}}^{2}} + \rho Q$
$\frac{d}{{dt}} = \frac{\partial }{{\partial t}} + u\frac{\partial }{{\partial x}} + {v}\frac{\partial }{{\partial y}}w\frac{\partial }{{\partial z}},\quad {{\dot {S}}_{j}} = \frac{1}{2}\left( {\frac{{\partial {{{v}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{v}}_{j}}}}{{\partial {{x}_{i}}}}} \right),\quad {{\dot {S}}^{2}} = \sum\limits_{i,j = 1}^3 {\dot {S}_{{ij}}^{2}} $
$\Pi = \left( {p + \frac{2}{3}\mu {\text{div}}{\mathbf{v}}} \right)E - 2\mu \dot {S},\quad p = \rho RT,\quad {\mathbf{q}} = - \frac{{{{c}_{p}}\mu }}{{\Pr }}{\mathbf{grad}}T$

Здесь тепловой поток нормирован на ${{\rho }_{e}}u_{e}^{3}$, а время на ${{{v}}_{e}}{\text{/}}u_{e}^{2}$. Нормировка других величин такая же, как и в (1.1). Любую величину ${{\Phi }_{j}}$ можно представить в виде суммы основной стационарной величины и нестационарного возмущения, ${{\Phi }_{i}}(t,x,y,z) = {{\phi }_{i}}(x,y,z) + \varepsilon {{\phi }_{{1i}}}(t,x,y,z)$. Линеаризация (2.1) относительно возмущений ${{\phi }_{{1i}}} = \phi _{i}^{d}(y)\exp [i(ax + bz - Ft)$ приводит к линейной системе дифференциальных уравнений [19, 20], которая в приближении параллельного течения имеет вид

$\frac{{d\phi _{1}^{d}}}{{dY}} = - {{i}_{c}}\phi _{2}^{d} + {{i}_{x}}\phi _{5}^{d} + {{i}_{z}}\phi _{6}^{d} - 2{{\mu }_{r}}\frac{{du_{w}^{d}}}{{dY}},\quad \frac{{d\phi _{2}^{d}}}{{dY}} = \rho \frac{{dT}}{{dY}}\phi _{2}^{d} - u_{w}^{d} - {{i}_{c}}T{{r}^{d}}$
$\frac{{d\phi _{3}^{d}}}{{dY}} = - {{i}_{x}}\phi _{2}^{d} - \frac{{du}}{{dY}}{{\mu }_{t}}{{T}^{d}} + \frac{{\phi _{5}^{d}}}{{{{\mu }_{r}}}},\quad {\text{ }}\frac{{d\phi _{4}^{d}}}{{dY}} = - {{i}_{z}}\phi _{2}^{d} + \frac{{\phi _{6}^{d}}}{{{{\mu }_{r}}}}$
(2.2)
$\frac{{d\phi _{5}^{d}}}{{dY}} = {{i}_{x}}\phi _{1}^{d} + {{i}_{c}}\phi _{3}^{d} - i_{T}^{d} + \rho \frac{{du}}{{dY}}\phi _{2}^{d},\quad \frac{{d\phi _{6}^{d}}}{{dY}} = {{i}_{z}}\phi _{1}^{d} + \left( {{{i}_{c}} - {{\mu }_{a}}} \right)\phi _{4}^{d} - {{i}_{z}}{{\mu }_{r}}u_{w}^{d}$
$\frac{{d\phi _{7}^{d}}}{{dY}} = i\omega RT\phi _{1}^{d} + \rho \frac{{dI}}{{dY}}\phi _{2}^{d} - ui_{t}^{d} + {{i}_{c}}u\phi _{3}^{d} + \left( {{{i}_{c}} - \frac{{{{\mu }_{a}}}}{{\Pr }}} \right)\phi _{8}^{d}$
$\frac{{d\phi _{8}^{d}}}{{dY}} = - \Pr \frac{{du}}{{dY}}\phi _{3}^{d} - \frac{{dh}}{{dY}}{{\mu }_{t}}{{T}^{d}} + \frac{{\Pr \left( {\phi _{7}^{d} - u\phi _{5}^{d}} \right)}}{{{{\mu }_{R}}}}$

Здесь $\phi _{1}^{d}$, $\phi _{2}^{d}$, $\phi _{3}^{d}$, $\phi _{4}^{d}$, $\phi _{5}^{d}$, $\phi _{6}^{d}$, $\phi _{7}^{d}$, $\phi _{8}^{d}$ – амплитуды возмущений давления; нормальной, продольной и боковой скорости; сдвиговых напряжений τ12, τ23; теплового потока и энтальпии. Дополнительными членами системы являются

$u_{w}^{d} = {{i}_{x}}\phi _{3}^{d} + {{i}_{z}}\phi _{5}^{d},\quad i_{t}^{d} = {{i}_{x}}{{\mu }_{r}}u_{w}^{d} + {{\mu }_{a}}\phi _{3}^{d}$
${{\mu }_{a}} = (i_{x}^{2} + i_{z}^{2}){{\mu }_{r}},\quad \tilde {r} = {{\rho }^{d}}{\text{/}}\rho = {{g}_{m}}\phi _{1}^{d} - \rho {{T}^{d}}$
${{T}^{d}} = {{g}_{{m1}}}\phi _{8}^{d},\quad {{i}_{x}} = ia\operatorname{Re} T,\quad {{i}_{z}} = ib\operatorname{Re} T$
${{i}_{c}} = \operatorname{Re} {{u}_{c}} = i\operatorname{Re} (ua - F),\quad {{\mu }_{r}} = \frac{{\mu \rho }}{{\operatorname{Re} }},\quad {{\mu }_{T}} = \frac{1}{\mu }\frac{{d\mu }}{{dT}}$
${{g}_{m}} = \gamma {{M}^{2}},\quad {\text{ }}{{g}_{{m1}}} = (\gamma - 1){{M}^{2}},\quad \gamma = {{c}_{p}}{\text{/}}{{c}_{v}}$
где γ – показатель адиабаты.

Система (2.2) решается с граничными условиями

(2.3)
$\phi _{3}^{d},\phi _{2}^{d},\phi _{4}^{d},\phi _{8}^{d} = 0\quad (Y = 0\,\,{\text{ и}}\,\,Y = \infty )~~$

При заданных значениях M, Re, F и параметрах основного течения решение системы (2.2) с условиями (2.3) существует при собственном значении a=ar + iai. Течение неустойчиво при отрицательном значении ai.

На рис. 4 показаны зависимости степеней пространственного усиления возмущений от частотного параметра при Re = 180, j = 0.004 и различных углах скольжения волны χ = arctg(b/ar).

Рис. 4.

Зависимость степени пространственного усиления от частотного параметра при разных углах скольжения: Re = 180, j = 0.004.

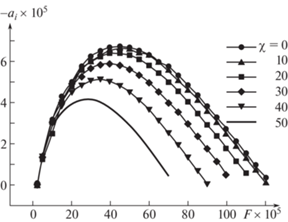
Из представленных данных видно, что практически во всем диапазоне частот нарастающих возмущений наиболее интенсивно растут двумерные волны, χ = 0. Поэтому ниже будут приведены результаты по устойчивости только по отношению к двумерным возмущениям.

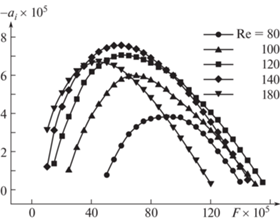
На рис. 5 приведены значения степеней усиления в зависимости от частоты для ряда чисел Рейнольдса. Из этих данных видно, что максимальная степень усиления нарастает с ростом числа Рейнольдса при Re < 150, дальнейшее его увеличение приводит к уменьшению скорости роста возмущений. Частота наиболее растущих волн уменьшается с увеличением числа Рейнольдса, по-видимому, из-за нарастания толщины пограничного слоя с ростом Re = x1/2.

Рис. 5.

Зависимость степени пространственного усиления от частотного параметра при разных числах Рейнольдса: j = 0.004, χ = 0.

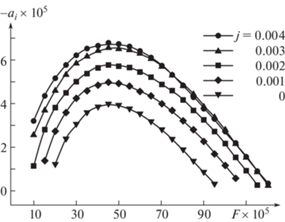
На рис. 6 показана зависимость степени пространственного усиления от частотного параметра при разной подаче газа через пористую стенку при Re = 180. Как и в отсутствие подогрева [21], при подводе тепла увеличение скорости потока массы через стенку приводит к дестабилизации течения. Расчетами установлено, что критическое число Рейнольдса при j = 0.004 уменьшается почти на 70% в сравнении со случаем j = 0.

Рис. 6.

Зависимость степени пространственного усиления от частотного параметра при разной подаче газа через пористую стенку: Re = 180, χ = 0.

Расчеты фазовой и групповой скорости от частотного параметра в неустойчивой области при Re = 180, j = 0.004 показали, прежде всего, что групповая скорость существенно превышает фазовую скорость. С увеличением частоты фазовая скорость стремится к значению скорости основного течения в положении максимума функции K. Она находится в промежутке скоростей в положении минимума и максимума K (рис. 3в, Re = 180, j = 0.004), где выполняется второе необходимое условие “невязкой” неустойчивости [15], $(u - Us)(dK{\text{/}}dY) < 0$, которое является обобщением критерия Фьёртофта [22]. Здесь Us − скорость, соответствующая максимуму K.

Известно [23], что при слабом усилении возмущений их пространственные и временные степени усиления связаны соотношением ai ≈ –Fi/Cgr, где временная степень усиления Fi – мнимая часть собственного значения F задачи (2.2), (2.3) при фиксированном реальном значении a. Специальные расчеты показали, что точное значение степени пространственного усиления практически совпадет с ее приближенной величиной даже при достаточно интенсивном росте амплитуды возмущения.

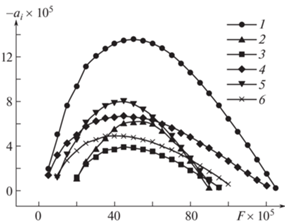
В [13, 24], при исследовании влияния подвода тепла в отсутствие подачи газа через поверхность пластины, была установлена стабилизирующая роль подогрева узкой полосы пограничного слоя. Поэтому в настоящих исследованиях также обращалось внимание на влияние подогрева на устойчивость пограничного слоя в условиях инжекции газа через пористую пластину. На рис. 7 показаны зависимости степеней усиления от частоты при разных соотношениях количества инжектируемого газа (j = 0.0, 0.001, 0.004), как в отсутствие подвода тепла (Q = 0), так и при подводе тепла в соответствии с соотношением (1.3). При этом все зависимости получены при одинаковой температуре стенки Tw = 2.16 (640°K) и числе Рейнольдса Re = 180. Сопоставление максимумов приведенных зависимостей показывает следующее. В отсутствие подвода тепла (зависимости: 1 (j = 0.004), 2 (j = 0.001), 5 (j = 0.0)) вдув газа дестабилизирует течение. Подвод тепла, наоборот, стабилизирует его при нагретой пластине (Tw = 2.16). Сопоставление зависимости 1 и 4 показывает, что в случае большого количества вдуваемого газа (j = 0.004) подвод тепла уменьшает максимальную степень усиления более чем в два раза. Однако она все еще выше, чем в случае без подогрева и вдува газа (зависимость 2). При меньших количествах вдуваемого газа (j = 0.001)в результате подвода тепла (зависимость 6) устойчивость пограничного слоя повышается не только в отношении случая без подвода тепла (зависимость 5), но становится более устойчивым по сравнению со случаем без инжекции и подвода тепла (зависимость 2).

Рис. 7.

Зависимости степеней пространственного усиления от частотного параметра при разных соотношениях подачи газа через стенку и подводе тепла (Re = 180, Tw = 2.16, χ = 0): 1 – j = 0.004, Q = 0.0; 2 – j= 0.0, Q = 0; 3 – j = 0.0, Q ≠ 0; 4 – j = 0.004, Q ≠ 0; 5 – j = 0.001, Q = 0; 6 – j = 0.001, Q ≠ 0.

ЗАКЛЮЧЕНИЕ

В рамках локального автомодельного приближения смоделирован профиль температуры диффузионного пламени работы [17] при массовом вдуве газа через пористую пластину j = = (ρ${v}$)w/(ρu)∞ = 0.004, числе Рейнольдса Re = 180 и числе Маха M $ \ll $ 1. При этом потребовался подвод тепла в соответствии с (1.3). С использованием (1.3) были рассчитаны стационарные параметры пограничного слоя и рассмотрена его устойчивость при разных значениях числа Рейнольдса и расхода вдуваемого через пористую стенку газа. Установлено, что увеличение вдуваемой массы газа через пористую стенку приводит к образованию перегибных профелей скорости. При фиксированной норме вдува увеличение числа Рейнольдса повышает максимальную температуру внутри слоя. Из этого следует рост максимальной температуры вниз по потоку, так как ${\text{Re}} = {{x}^{{1/2}}}$, что наблюдается при диффузионном горении, например, в экспериментах [17] и расчетах [18]. Важная функция в теории “невязкой” неустойчивости, произведении плотности и завихренности K, имеет две обобщенные точки перегиба. Одна из них соответствует минимуму, вторая максимуму K(Y). Минимальное значение K находится на меньшем расстоянии от стенки в сравнении с положением максимума K. Положение максимума с увеличением вдува смещается к внешней границе пограничного слоя, в то время как минимум продолжает оставаться при Y ≈ 1.

Впервые исследована устойчивость пограничного слоя с подводом тепла и вдувом газа при дозвуковом обтекании пластины. В результате исследований установлено, что в условиях вдува газа и внутреннего подвода тепла наиболее опасными (растущими) являются двумерные возмущения, как и в отсутствие подогрева. Существует число Рейнольдса, при котором степень усиления максимальна. С увеличением числа Рейнольдса частота наиболее растущих волн понижается из-за увеличения толщины пограничного слоя. Инжекция газа дестабилизирует пограничный слой. При параметре вдува j = 0.004 критическое число Рейнольдса снижается примерно на 40% в сравнении со случаем j = 0.

Критический слой, где скорость в пограничном слое равна фазовой скорости волны (u = C), располагается в области, соответствующей второму необходимому условию “невязкой” неустойчивости, $(u - Us)(dK{\text{/}}dY) < 0$. С увеличением частоты растущих волн фазовая скорость стремится к скорости течения в максимуме произведения плотности и завихренности, соответствующего обобщенной точки перегиба. Несмотря на довольно большие степени пространственного роста, их приближенные значения, определяемые как отношение степени временного усиления к групповой скорости, практически совпадают с точными величинами.

При нагретой пластине подвод тепла внутри пограничного слоя понижает максимальную степень роста возмущений в пограничном слое с инжекцией газа, как и в случае ее отсутствия.

Исследование выполнено при финансовой поддержке Российского научного фонда (грант № 22-21-00017, https://rscf.ru/project/22-21-00017/).

Список литературы

  1. Emmons H.W. The film combustion of liquid fuel // Z. Math. und Mech. 1956. V. 36. 1/2. P. 60–71.

  2. Волчков Э.П., Терехов В.И., Терехов В.В. Структура течения, тепло- и массоперенос в пограничных слоях со вдувом химически реагирующих веществ (обзор) // Физика горения и взрыва. 2004. № 1. С. 3–20.

  3. Гапонов С.А., Петров Г.В. Устойчивость пограничного слоя неравновеснодиссоциирующего газа. Новосибирск: Наука, 2013. 95 с.

  4. Shen S.F. Effect of chemical reaction on the inviscid criterion for laminar stability of parallel flows // Fifth Midwestern Conference on Fluid Mechanics, Ann Arbor, Michigan, University of Michigan. 1957. P. 11–20.

  5. Петров Г.В. Устойчивость пограничного слоя газа с химическими реакциями на каталитической поверхности // Физика горения и взрыва. 1974. Т. 10. № 6. С. 797–801.

  6. Петров Г.В. Устойчивость пограничного слоя каталитически рекомбинирующего газа // ПМТФ. 1978. № 1. С. 40–45.

  7. Lin C.C. The theory of hydrodynamic stability. Cambridge university press. 1955. 155 p. Линь Ц.Ц. Теория гидродинамической устойчивости. М.: ИЛ, 1958. 195 с.

  8. Han Y., Cao W. Flat-plate hypersonic boundary-layer flow instability and transition prediction considering air dissociation // Appl. Math. Mech. 2019. V. 40. № 5. P. 719–736. doi.org/.https://doi.org/10.1007/s10483-019-2480-6

  9. Marxen O. Hydrodynamic Stability of Hypersonic Chemically Reacting Boundary Layers I.EN-AVT-289-02%20(23).pdf

  10. Jackson T.L. Stability of Laminar Diffusion Flames in Compressible Mixing Layers // In: Hussaini M.Y., Kumar A., Voigt R.G. / Major Research Topics in Combustion. ICASE/NASA LaRC Ser. Springer, New York. NY. 1992 https://doi.org/10.1007/978-1-4612-2884-4_8

  11. See Y.C., Ihme M. Effects of finite-rate chemistry and detailed transport on the instability of jet diffusion flames // J. Fluid Mech. 2014. V. 745. P. 647–681. https://doi.org/10.1017/jfm.2014.95

  12. Лукашов В.В., Терехов В.В., Терехов В.И. Пристенные течения химически реагирующих веществ. Обзор современного состояния проблемы // Физика горения и взрыва. 2015. Т. 51. № 2. С. 23–36.

  13. Гапонов С.А. Устойчивость сверхзвукового пограничного слоя при подводе тепла в его узкую полосу // Теплофизика и аэромеханика. 2021. Т. 28. № 3. С. 351–360.

  14. Jackson T.L., Grosch C.E. Inviscid spatial stability of a compressible mixing layer. Part 2. The flame sheet model // Journal of Fluid Mechanics. 1990. V. 217. P. 391–420. https://doi.org/10.1017/S0022112090000775

  15. Shin D.S., Ferziger J.H. Linear stability of the reacting mixing layer // AIAA Journal. 1991. V. 29 (10). P. 1634–1642. https://doi.org/10.2514/3.10785

  16. Dorrance W.H. Viscous Hypersonic Flow: Theory of Reacting and Hypersonic Boundary Layers. McGraw-Hill Book Co. Inс. 1962. 334 p. Дорренс У.X. Гиперзвуковые течения вязкого газа. М.: Изд-во Мир. 1966. 439 с.

  17. Volchkov E.P., Lukashov V.V., Terekhov V.V., Hanjalic K. Characterization of the flame blow-off conditions in a laminar boundary layer with hydrogen injection // Combustion and Flame. 2013. V. 160. P. 1999–2008. https://doi.org/10.1016/j.combustflame.2013.04.004

  18. Peters N. Analysis of a laminar flat plateboundary-layer diffusion flame // International Journal of Heat and Mass Transfer. 1976. V. 19. P. 385–393. https://doi.org/10.1016/0017-9310(76)90094-6

  19. Петров Г.В. Реакция сверхзвукового пограничного слоя на акустическое воздействие // Теплофизика и аэромеханика. 2001. № 1. С. 77–86.

  20. Гапонов С.А., Юдин А.В. Взаимодействие гидродинамических внешних возмущений с пограничным слоем // Прикладная механика и техническая физика. 2002. Т. 43. № 1. С. 100–107.

  21. Chen T.S., Sparrow E.M., Tsou F.K. The effect of mainflow transverse velocities in linear stability theory // Journal of Fluid Mechanics. 1971. V. 50 (04). P. 741. https://doi.org/10.1017/s0022112071002866

  22. Fjortoft R. Application of integral theorems in deriving criteria of stability for laminar flows and for the baroclinic circular vortex // Geophys. 1950. V. 17. P. 1–52.

  23. Gaster M.A. A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability // J. Fluid Mech. 1962. V. 14. Part 2. P. 222–224. https://doi.org/10.1017/S0022112062001184

  24. Гапонов С.А. Влияние подвода тепла в узкую полосу пограничного слоя на его устойчивость // Прикладная механика и техническая физика. 2020. Т. 61. № 5. С. 5–13. https://doi.org/10.15372/PMTF20200501

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал