Известия РАН. Механика жидкости и газа, 2022, № 4, стр. 11-25
НЕУСТОЙЧИВОСТИ, БИФУРКАЦИИ И НЕЛИНЕЙНАЯ ДИНАМИКА В ДВУМЕРНЫХ ОБОБЩЕНИЯХ ТЕЧЕНИЯ КОЛМОГОРОВА
И. И. Вертгейм a, *, М. А. Закс b, Р. В. Сагитов c, А. Н. Шарифулин d
a Институт механики сплошных сред УрО РАН
Пермь, Россия
b Университет им. Гумбольдтов
Берлин, Германия
c Пермский государственный национальный исследовательский университет
Пермь, Россия
d Пермский национальный исследовательский политехнический университет
Пермь, Россия
* E-mail: wertg@icmm.ru
Поступила в редакцию 08.02.2022
После доработки 12.03.2022
Принята к публикации 15.03.2022
- EDN: MVHPEL
- DOI: 10.31857/S0568528122040119
Аннотация
Рассматривается семейство двумерных течений вязкой несжимаемой жидкости в плоской прямоугольной области с периодическими граничными условиями (двумерный тор). Течения вызваны силой, периодической по двум пространственным координатам и постоянной по времени. В частном случае гармонической зависимости силы от одной координаты и отсутствия осредненного течения реализуется известное течение Колмогорова. В общем двумерном случае численно изучены структурные перестройки стационарных решений уравнений Навье–Стокса, определены области устойчивости в пространстве определяющих физических и геометрических параметров – чисел Рейнольдса, амплитуд силы, пространственных размеров ячейки периодичности. Выяснено, что в квадратной области, сторона которой равна пространственному периоду внешней силы, основное стационарное течение сохраняет устойчивость при изменении амплитуды силы и чисел Рейнольдса. Напротив, в ячейках, в стороны которых укладывается несколько периодов силы, изменение параметров дестабилизирует стационарное течение. Исследованы стационарные и автоколебательные нелинейные вторичные режимы течения. Обсуждается влияние нестационарности на лагранжеву динамику: механизмы перехода к хаотической адвекции пассивных частиц зависят от соизмеримости чисел Рейнольдса, характеризующих осредненное течение во взаимно перпендикулярных направлениях.
Двумерные течения вязкой несжимаемой жидкости, вызванные постоянной по времени пространственно-периодической силой при наличии постоянной прокачки вдоль взаимно перпендикулярных направлений, являются двумерными обобщениями известного пространственно-периодического течения Колмогорова [1], предложенного как модель каскадного переноса энергии в турбулентном потоке. В [2–4] определены границы монотонной устойчивости течения Колмогорова, установлен ее длинноволновый характер и исследованы вторичные пространственно-периодические течения вблизи порога. В дальнейших теоретических и численных исследованиях было показано, что введение боковых границ существенно снижает длину волны опасных возмущений [5], а при высоких числах Рейнольдса ведет к возникновению крупномасштабного когерентного вихря [6]; найдены различные нестационарные режимы течения, включая квазипериодические и перемежаемость [7].
Похожие структуры реализованы и в экспериментах [8–11] с магнитогидродинамическими течениями в тонких слоях слабопроводящей жидкости, где были подтверждены неустойчивость основного течения и переход к вторичным режимам с периодичностью по двум координатам.
Для некоторых конфигураций силы известны стационарные решения уравнений Навье–Стокса, в которых поле скорости двоякопериодично, и периоды по каждой из координат кратны пространственному периоду силы: в частности, двухвихревое с прокачкой в двух направлениях [12] и одновихревое типа “кошачьи глаза” [13]. Лагранжева динамика частиц пассивной примеси в определенной области параметров таких течений необычна, ее свойства являются промежуточными между ламинарными и турбулентными: фрактальный спектр скорости переносимых частиц, аномальные характеристики транспорта и т.п. Известными частными случаями таких течений являются течение Колмогорова (далее К59) [1] и течение с двухкомпонентной двоякопериодической вынуждающей силой (далее ZPK96) [12]. В обоих случаях основное решение с функцией тока, периодичной по одной или двум координатам, устойчиво для возмущений с длиной волны, не превышающей периода вынуждающей силы, и проявляет длинноволновую неустойчивость, монотонную для К59 [2], и, в зависимости от характеристик прокачки, монотонную либо колебательную для его двумерных обобщений [14].
Описанные исследования показали необходимость более глубокого изучения устойчивости известных стационарных течений, развития вторичных режимов и соответствующей им лагранжевой динамики. Ниже, для течения ZPK96 с учетом параметризованного через числа Рейнольдса Rex и Rey ненулевого расхода жидкости в x- и y-направлениях, исследована устойчивость основных и вторичных семейств течений, рассмотрено нелинейное развитие вторичных режимов после потери устойчивости и проведен анализ качественных изменений в лагранжевой динамике переносимых частиц.
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается двумерное течение вязкой несжимаемой жидкости в прямоугольной ячейке бесконечного слоя с условиями периодичности по координатам х и у (двумерный тор), вызванное постоянной по времени двоякопериодической по пространству силой ${\mathbf{F}}(x,y)\, = \,({{f}_{1}}\sin {\kern 1pt} ({y \mathord{\left/ {\vphantom {y {L)}}} \right. \kern-0em} {L)}}$, f2sin(x/L)). В размерных переменных уравнения Навье–Стокса для скорости ${\mathbf{v}} = \left\{ {{{{v}}_{x}},{{{v}}_{y}}} \right\}$ имеют вид:
(1.1)
$\begin{gathered} \frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}}\nabla ){\mathbf{v}} = - \frac{{\nabla p}}{{{{\rho }_{f}}}} + \nu \Delta {\mathbf{v}} + {\mathbf{F}} \\ \operatorname{div} {\mathbf{v}} = 0 \\ \end{gathered} $Здесь ν – коэффициент кинематической вязкости; ρf – плотность жидкости, Lx, Ly – размерные длина и ширина ячейки периодичности; L/(2π), f1, f2– размерные пространственный период и амплитуды внешней силы, α и β – размерные расходы течения по направлениям x и y соответственно.
В безразмерном виде, записанные в терминах функции тока $\Psi (x,y)$, для которой ${{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial y = }}} \right. \kern-0em} {\partial y = }}{{{v}}_{x}},$ ${{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial x = }}} \right. \kern-0em} {\partial x = }} - {{{v}}_{y}},$ уравнения (1.1) принимают вид:
(1.2)
$ - \frac{{\partial \Delta \Psi }}{{\partial t}} - \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \Delta \Psi }}{{\partial x}} + \frac{{\partial \Psi }}{{\partial x}}\frac{{\partial \Delta \Psi }}{{\partial y}} + \Delta \Delta \Psi = - {{\lambda }_{1}}\cos y + {{\lambda }_{2}}\cos x$(1.3)
$\frac{1}{{{{l}_{x}}}}\int\limits_0^{{{l}_{x}}} {dx} \cdot \left( {\Psi (x,{{l}_{y}}) - \Psi (x,0)} \right) = {{\operatorname{Re} }_{x}};\quad - \frac{1}{{{{l}_{y}}}}\int\limits_0^{{{l}_{y}}} {dy} \cdot \left( {\Psi ({{l}_{x}},y) - \Psi (0,y)} \right) = {{\operatorname{Re} }_{y}}.$Задачу (1.2)–(1.3) характеризуют следующие безразмерные параметры:
числа Рейнольдса Rex = α/ν, Rey = β/ν;
внешняя сила с компонентами λ1= f1L3/ν2; λ2= f2L3/ν2;
размеры ячейки: lx = Lx/L; ly = Ly/L.
Удобно разбить функцию тока на линейные по х и у слагаемые, обеспечивающие прокачку, и часть, периодическую по обеим координатам: $\Psi (x,y) = {{\operatorname{Re} }_{х}}y - {{\operatorname{Re} }_{y}}x + \Psi {\kern 1pt} '(x,y)$. Тогда условия периодичности поля скорости записываются как $\Psi {\kern 1pt} '(x + {{l}_{x}},y) = \Psi {\kern 1pt} '(x,y + {{l}_{y}}) = \Psi {\kern 1pt} '(x,y)$.
2. ИЗВЕСТНЫЕ СТАЦИОНАРНЫЕ РЕШЕНИЯ И ИХ УСТОЙЧИВОСТЬ
Частными решениями задачи (1.2) являются течение Колмогорова K59 [1] (λ2 = Rex = Rey = 0) и течение ZPK96 в квадратной области с периодическими граничными условиями, эквивалентное потоку по поверхности двумерного тора [12] (λ1 = λ2 = λ). В обоих случаях известны стационарные решения задачи (1.2). В первом случае это ${{\Psi }_{0}}(x,y)\, = \,\lambda {{{\kern 1pt} }_{1}}\cos (y)$, которое, как показано в [2–4], устойчиво при lx < 2π. Длинноволновая неустойчивость (lx → ∞) получена при ${{\lambda }_{{1cr}}} = \sqrt 2 $, для ячеек конечной длины lx > 2π колебательная неустойчивость найдена в [15], а также для более общего случая при ненулевом расходе Rex в [14]. Стационарное решение ZPK96 [12] при lx = ly = 2π имеет вид:
(2.1)
$\begin{gathered} {{\Psi }_{0}}(x,y) = {{\operatorname{Re} }_{x}}y - {{\operatorname{Re} }_{y}}x + \lambda \frac{{\sin (x + {{\phi }_{x}})}}{{\sqrt {\operatorname{Re} _{x}^{2}\; + 1} }} - \lambda \frac{{\sin (y + {{\phi }_{y}})}}{{\sqrt {\operatorname{Re} _{y}^{2}\; + 1} }} \\ {{\phi }_{x}} = {\text{arctg}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{x}}}}} \right);\quad {{\phi }_{y}} = {\text{arctg}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{y}}}}} \right) \\ \end{gathered} $В отсутствие внешней силы (λ = 0) реализуется тривиальное течение на двумерном торе c числом вращения ρ = Rex/Rey, с прямыми линиями тока и однородной скоростью. Течение “глобально”: частица жидкости, находящаяся первоначально в любой точке области, обходит тор снова и снова, и при иррациональном числе вращения проходит как угодно близко от любого заданного места. Как показано в [12], с ростом амплитуды силы λ линии тока искривляются, а при $\lambda = {{\lambda }_{{{\text{cr}}}}} = \sqrt {\operatorname{Re} _{x}^{2} \cdot \operatorname{Re} _{y}^{2} + \max (\operatorname{Re} _{x}^{2},\operatorname{Re} _{y}^{2})} $ происходит топологическая перестройка: на двух линиях тока возникает по точке сборки – точке стагнации течения, в которых обе компоненты скорости одновременно обращаются в нуль. При дальнейшем росте λ вырожденные точки стагнации распадаются на седловые и эллиптические точки застоя, и на поверхности тора, помимо “глобальной”, формируется “локальная” структура течения; ее образуют два заполненных замкнутыми линиями тока вихря вокруг эллиптических точек. Вихри, отделенные от глобальной компоненты течения сепаратрисами седловых точек, малы непосредственно после своего рождения, но с ростом λ они увеличиваются, постепенно занимая все большую долю площади ячейки периодичности. При λ > λcr и иррациональных числах вращения в глобальной компоненте течения существует нетривиальная лагранжева динамика: поскольку любая линия тока в глобальной компоненте снова и снова проходит как угодно близко к седловой неподвижной точке, в траектории частицы, транспортируемой вдоль этой линии, эпохи относительно быстрого дрейфа чередуются с замедлениями вплоть до полной остановки. Это приводит к ослаблению временных корреляций и вызывает аномальный транспорт частиц-трассеров в субдиффузионном режиме. Заметим, что перестройка топологии течения при λ = λcr, несмотря на глубинные изменения, вносимые ею в динамику, не является бифуркацией: новые решения не ответвляются, а устойчивость существующего не меняется.
Мы провели численное исследование задачи (1.2). Для нахождения стационарных решений системы (кроме решения (2.1)) использован многомерный метод Ньютона, примененный для системы алгебраических уравнений дискретного аналога (2.1) [16].
Разложим пространственно-периодическую часть функции тока $\Psi {\kern 1pt} '(x,y)$ в ряд Фурье
(2.2)
$\Psi {\kern 1pt} '(x,y,t) = \sum\limits_{m = - M}^M {\sum\limits_{n = - N}^N {{{\psi }_{{m,n}}}(t) \cdot {{e}^{{\frac{{imx}}{{l_{x}^{'}}} + \frac{{iny}}{{l_{y}^{'}}}}}}} } ;\quad l_{x}^{'} = \frac{{{{l}_{x}}}}{{2\pi }};\quad l_{y}^{'} = \frac{{{{l}_{y}}}}{{2\pi }}.$Подставляя (2.2) в (1.2) и применяя к полученной системе уравнений стандартную процедуру умножения на комплексную экспоненту с последующим интегрированием по поверхности тора получим (2M + 1) × (2N + 1) – 1 обыкновенных дифференциальных уравнений, задающих эволюцию во времени коэффициентов рядов Фурье
(2.3)
$\begin{gathered} \left( {\frac{{{{m}^{2}}}}{{l_{x}^{{'2}}}} + \frac{{{{n}^{2}}}}{{l_{y}^{{'2}}}}} \right)\left( {\frac{d}{{dt}} + \frac{{{{m}^{2}}}}{{l_{x}^{{'2}}}} + \frac{{{{n}^{2}}}}{{l_{y}^{{'2}}}} + \frac{{im}}{{l_{x}^{'}}}{{{\operatorname{Re} }}_{x}} + \frac{{in}}{{l_{y}^{'}}}{{{\operatorname{Re} }}_{y}}} \right){{\psi }_{{m,n}}} - \\ \, - \sum\limits_{{{m}_{1}} = \max \left( { - M,m - M} \right)}^{\min \left( {M,m + M} \right)} {\sum\limits_{{{n}_{1}} = \max \left( { - N,n - N} \right)}^{\min \left( {N,n + N} \right)} {\frac{{{{n}_{1}}m - {{m}_{1}}n}}{{l_{x}^{'}l_{y}^{'}}}\left( {\frac{{{{{\left( {m - {{m}_{1}}} \right)}}^{2}}}}{{l_{x}^{{'2}}}} + \frac{{{{{\left( {n - {{n}_{1}}} \right)}}^{2}}}}{{l_{y}^{{'2}}}}} \right){{\psi }_{{{{m}_{1}},{{n}_{1}}}}}{{\psi }_{{m - {{m}_{1}},n - {{n}_{1}}}}}} } + {{F}_{{m,n}}} = 0. \\ \end{gathered} $Здесь ${{F}_{{m,n}}}$ = 0, для всех m, n, кроме ${{F}_{{l_{x}^{'},0}}} = {{F}_{{ - l_{x}^{'},0}}} = - \frac{{{{\lambda }_{2}}}}{2}$ и ${{F}_{{0,l_{y}^{'}}}} = {{F}_{{0, - l_{y}^{'}}}} = \frac{{{{\lambda }_{1}}}}{2}$. Штрихованные индексы являются целочисленными в силу выбора сторон ячейки периодичности (длины lx и ширины ly) и определяют, сколько периодов силы (2π) в них содержится.
Для количества мод M и N в разложении Ψ′ в ряд Фурье, критерием служит точность определения критических значений амплитуды силы, соответствующих различным вариантам дестабилизации течения (2.1). При M = N = 5 верно определяются 8 десятичных знаков в критическом значении λ, а использование величин M и N, превышающих 15, смещает пороговые значения на величину, сравнимую с ошибкой округления. Чтобы создать “запас прочности” для аккуратного нахождения нестационарных решений, мы пользовались в расчетах значениями M = N = 20.
Линеаризация (2.3) около стационарного течения (2.1) характеризует устойчивость (2.1) в рамках уравнений Навье–Стокса. Мы определили в пространстве параметров Rex, Rey, λ области устойчивости. В частности, в расчетах установлен несколько неожиданный факт: в квадратной ячейке с длинами сторон, равными периоду вынуждающей силы (${{l}_{x}} = {{l}_{y}} = 2\pi $), стационарное течение (2.1) устойчиво даже при достаточно больших значениях амплитуды силы 0 ≤ λ ≤ 100 и в широком интервале значений расходов –10 ≤ (Rex, Rey) ≤ 10. Увеличение размеров полости до нескольких периодов вынуждающей силы создает возможности для длинноволновых возмущений; расчеты показали, в частности, что в прямоугольных ячейках периодичности (${{l}_{x}} = 2\pi m,$ ${{l}_{y}} = 2\pi n;$ $\max (m,n) > 1;$ $m,n \in \mathbb{N}$) возможна дестабилизация течения (2.1), причем, в зависимости от параметров задачи, вторичные течения могут носить как стационарный, так и автоколебательный характер (рис. 1).
Рис. 1.
Пороги неустойчивости течений K59 и ZPK96 в зависимости от длины ячейки периодичности lx (a); вид основного течения ZPK96 (б) и его критических возмущений при lx/2π = 2 (в) и lx/2π = 3 (г), при ly = 2π.
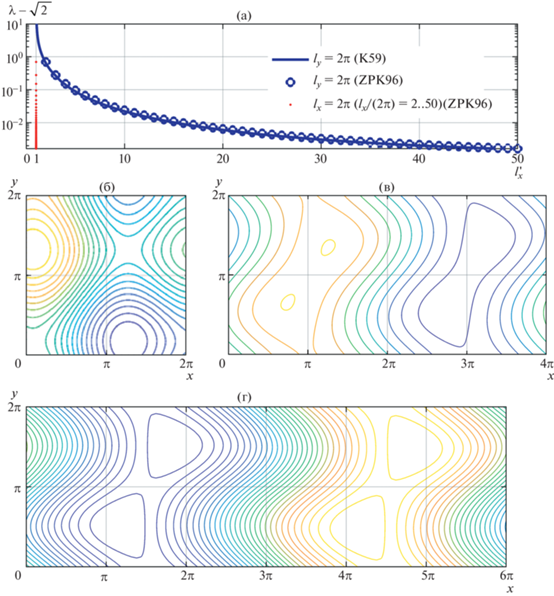
При изменении длины ячейки периодичности lx от 2π до lx → ∞ и фиксированной ширине ly = 2π порог неустойчивости монотонно убывает от ${{\lambda }_{{inst}}}\, \to \;\infty $ для квадратной ячейки до значения ${{\lambda }_{{inst}}} = \sqrt 2 $, соответствующего порогу для течения Колмогорова K59.
На рис. 2 для случая ячейки с lx = 4π, ly = 2π проиллюстрированы зависимости критических значений амплитуды силы λ и частоты нейтральных возмущений ω от параметров прокачки Rex, Rey. Для сравнения здесь же приведены значения λcr, соответствующие возникновению стационарных вихрей в структуре течения (2.1).
Рис. 2.
Нейтральные кривые на плоскостях (Rex, λ), (Rey, λ), (Rex, Rey), (верхний ряд слева направо) и зависимость частоты критических возмущений от Rex, Rey. Кривые из точек соответствуют λcr.
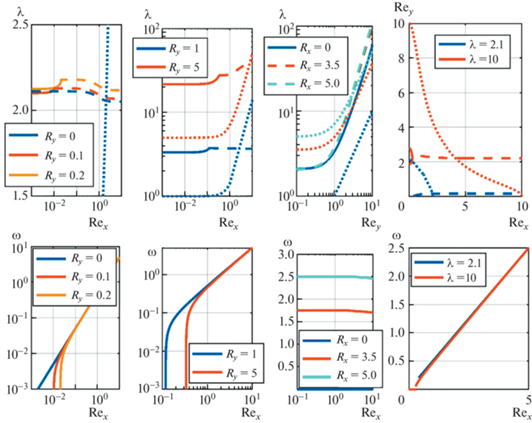
Видно, что возможны как колебательная, так и монотонная неустойчивости решения (2.1), c порогами неустойчивости, соответственно λo и λm. Возможны различные соотношения этих пороговых значений между собой, а также со значением λcr, при котором в структуре течения (2.1) на фоне глобальной компоненты образуются локализованные стационарные вихри. Из результатов линейного анализа можно сделать вывод, что неустойчивость этого течения для рассмотренной геометрии (при lx = 4π, ly = 2π) определяется в основном параметром прокачки вдоль оси х (Rex), рост Rey приводит к существенной стабилизации течения. При отсутствии прокачки всегда реализуется монотонная неустойчивость, при росте Rex появляются колебательные моды неустойчивости (2.1). Ниже мы рассмотрим различные варианты развития неустойчивости и исследуем соответствующие им типы вторичных нелинейных режимов течения на основе численного анализа полных нелинейных уравнений (2.3). В расчетах использовались многомерный метод Ньютона [14, 16] для нахождения стационарных решений и собственных значений λ, метод Рунге–Кутта–Фельберга с адаптивным шагом по времени для численного интегрирования (2.3) в случае нестационарных (в частности колебательных) решений, в сочетании с методом продолжения (отслеживания) по параметру, и идентификации бифуркаций по спектру собственных значений якобиана.
3. БИФУРКАЦИИ И ВТОРИЧНЫЕ ТЕЧЕНИЯ
Для иллюстрации перестроек режимов течения мы выбираем ячейку с соотношением сторон 2:1, так что по ее длине (вдоль координаты x) укладывается два периода стационарной внешней силы, а по ширине (вдоль координаты y), соответственно, один период. По отношению к удвоенной ячейке с периодическими граничными условиями по x, стационарное течение (2.1) обладает симметрией: оно инвариантно относительно сдвига на половину длины ячейки. Соответственно, уравнения (2.3), записанные в терминах фурье-коэффициентов ${{\psi }_{{m,n}}}$, инвариантны относительно смены знака всех коэффициентов с нечетными значениями m, а спонтанное нарушение этой симметрии при монотонном росте возмущений приводит к вилочной бифуркации состояния равновесия.
Рисунок 3 содержит карту основных режимов течения для такой ячейки при фиксированной интенсивности прокачки вдоль координаты y: Rey = 1. Область устойчивости решения (2.1) выделена серым фоном.
Рис. 3.
Карта режимов в плоскости параметров (Rex, λ) течения в ячейке периодичности lx = 4π, ly = 2π при фиксированном среднем расходе Rey = 1. Cтационарное течение (2.1) устойчиво в области с серым фоном. Бифуркационные кривые: B1,2 – вилочные бифуркации стационарных течений, AX1,2 – возникновение автоколебаний (бифуркация Андронова−Хопфа), СУ1,2,3 – седлоузловые бифуркации конечноамплитудного рождения стационарных течений. Темные кружки BT1,2 – точки бифуркаций Богданова−Такенса. Штриховая линия (а) соответствует значению λcr, когда образуется пара вихрей в течении (2.1). Панель (а): общий план в логарифмических координатах. Панель (б): область вокруг точки BT1. Панель (в): область вблизи точки сборки, образованной линиями СУ1 и СУ2.
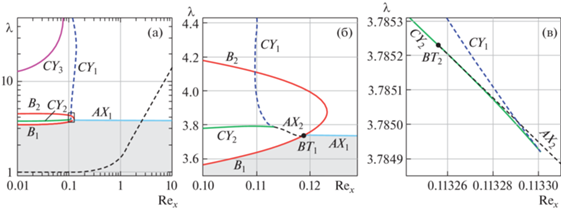
Как показано на левой (а) и центральной (б) панелях рисунка, при малых значениях Rex неустойчивость течения (2.1) носит монотонный характер и сопровождается вилочными бифуркациями B1, B2, порождающими симметричные пары стационарных течений (элементы пары переходят друг в друга при сдвиге на 2π вдоль оси x). При этом бифуркация B1 является надкритической, а бифуркация B2 – подкритическая, так что ветви стационарных решений, рождающиеся из (2.1) на линии B1, заканчиваются на B2. При Rex = 0.1233 линии B1 и B2 сливаются; выше этого значения Rex вилочных бифуркаций течения (2.1) нет. Но еще несколько ранее, при Rex = 0.1189 на линии B1 происходит другое определяющее событие: в точке BT1 одновременно обращаются в 0 два собственных значения линеаризованной задачи. В результате этого явления коразмерности 2, известного как бифуркация Богданова–Такенса [17], бифуркационный сценарий меняется: при более высоких значениях Rex неустойчивость течения (2.1) носит колебательный характер, так что на линии AX1 бифуркация Андронова-Хопфа порождает из равновесия, соответствующего течению (2.1), устойчивый предельный цикл, и структура течения периодически осциллирует.
Из-за упомянутой симметрии течения (2.1) бифуркация Богданова–Такенса в точке BT1 имеет особенный характер [17]. Поскольку первичное решение не исчезает на B1, а лишь теряет устойчивость, то, как видно на средней панели рис. 3б, выходящая направо из точки BT1 линия AX1 имеет продолжение и при меньших значениях Rex: это линия AX2, на которой бифуркация Андронова-Хопфа происходит со вторичными стационарными режимами, ответвившимися от (2.1) на линии B1.
Помимо бифуркаций, непосредственно затрагивающих основное течение (2.1), при малых значениях Rex имеет место и конечноамплитудное рождение/исчезновение вторичных стационарных течений: оно происходит в результате седлоузловых бифуркаций на линиях СУ1 и СУ2. Линии СУ1 и СУ2 заканчиваются в точке “сборки” при Rex = 0.1133; в клине, образованном этими линиями, имеет место мультистабильность: сосуществование при фиксированном значении параметров нескольких устойчивых стационарных течений. Как видно на правой панели рис. 3, в, в этот клин заходит справа и линия AX2 бифуркации Андронова–Хопфа; эта линия заканчивается на СУ2 в точке BT2 другой бифуркации Богданова–Такенса, происходящей со вторичными стационарными течениями. Таким образом, обе концевые точки линии AX2 на плоскости параметров – это точки Богданова–Такенса. Поскольку вторичные стационарные течения не обладают симметрией по отношению к пространственному сдвигу, бифуркация BT2 (в отличие от BT1) носит общий характер.
Движение вверх вдоль линии СУ1 приводит к изменению характера происходящей на ней седлоузловой бифуркации: в фазовом пространстве из локальной (затрагивающей два равновесия) она становится глобальной, и включает гомоклиническую траекторию к седлоузловой точке. Разрушение этой траектории, в современной литературе нередко именуемое бифуркацией SNIC (Saddle-Node on Invariant Circle), порождает устойчивое периодическое движение, период которого неограниченно нарастает по мере приближения к бифуркационному значению параметра. При Rex = 0 (отсутствие среднего расхода жидкости вдоль оси x) основное течение обладает еще одной симметрией: инвариантностью к зеркальному отражению относительно прямой, параллельной оси y. Эту симметрию наследуют и вторичные стационарные течения, возникающие при седло-узловых бифуркациях. Поэтому монотонная неустойчивость таких течений приводит к новой вилочной бифуркации и возникновению пар зеркально симметричных третичных стационарных течений. При как угодно малых ненулевых значениях прокачки вдоль оси x симметрия отсутствует, и вилочная бифуркация разрушается, заменяясь еще одной седлоузловой бифуркацией (линия СУ3 на рис. 3). На рис. 3a указана и линия, на которой происходит описанное выше изменение топологической структуры основного течения (2.1): рождение точек застоя и стационарных вихрей. На рисунке видно, что при достаточно больших значениях Rex колебательная неустойчивость основного стационарного течения может предшествовать этой перестройке.
На рис. 4 мы приводим несколько типичных бифуркационных диаграмм, соответствующих движению вдоль вертикальных линий на рис. 3: увеличению амплитуды силы λ при фиксации параметра Rex. В качестве количественной характеристики течения использована величина $\delta = {{v}_{y}}(0,0) - {{v}_{{y0}}}(0,0)$ (здесь и ниже индекс “0” указывает на характеристики основного течения (2.1)). Для стационарного решения δ соответствует отклонению y-компоненты скорости течения от значения для основного стационарного решения (2.1), колебательное решение характеризуется максимальным δmax и минимальным δmin значениями этого отклонения по периоду, а также величиной периода T. Кроме этого, для построения фазовых траекторий использованы эйлеровы переменные $(\Delta {{v}_{x}},\Delta {{v}_{y}},\Delta {{\Psi }_{с}})$, где:
Рис. 4.
Бифуркационные диаграммы δ (λ) течения в ячейке периодичности lx = 4π, ly = 2π при фиксированном среднем расходе Rey = 1 и характерных значениях среднего расхода Rex. Сплошные линии: устойчивые стационарные течения. Точечные линии: неустойчивые стационарные течения. Штриховые линии: устойчивые автоколебательные решения. Бифуркации B1,2,3 – вилочные бифуркации стационарных течений, СУ1,2,3 – седлоузловые бифуркации конечноамплитудного рождения стационарных течений, AX1,2 – бифуркации Андронова−Хопфа (возникновение автоколебаний). (а): Rex = 0; (б): Rex = 0.01; (в, г): Rex = 0.115 (д): Rex = 0.125; (e): ${\text{R}}{{{\text{e}}}_{x}}\; = {{(\sqrt 5 \; - 1)} \mathord{\left/ {\vphantom {{(\sqrt 5 \; - 1)} 2}} \right. \kern-0em} 2}~$. Панели (ж, з, и): Зависимость периода колебаний от амплитуды силы λ: Rex = 0.115 (ж, з) и Rex = 0.125 (и).
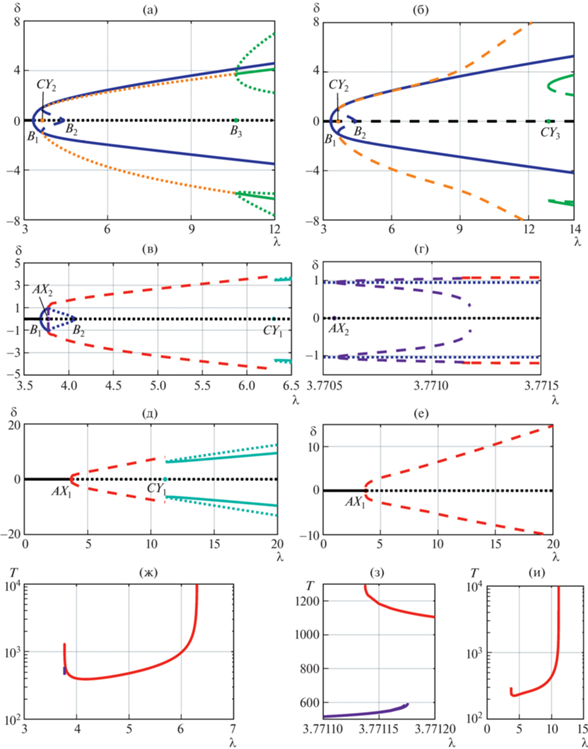
Здесь же показаны соответствующие зависимости T(λ) в случае колебательных решений. Cплошные и точечные линии характеризуют, соответственно, устойчивые и неустойчивые стационарные течения, а штриховые линии – устойчивые автоколебательные режимы. Вилочные бифуркации отмечены на бифуркационных диаграммах рис. 4 индексами B1 и B2, бифуркации Андронова–Хопфа – индексами AX1 и AX2. Оба эти типа бифуркаций могут быть надкритическими (B1) либо подкритическими (B2, AX1, AX2). Cедлоузловые бифуркации указаны индексами СУ1, СУ2, …, сюда относится и ранее упомянутая бифуркация SNIC появления седлоузла на инвариантном цикле (рис. 4 в, г при λ ≈ 6.3; рис. 4ж при λ ≈ 11).
Наиболее сложная картина бифуркационных переходов получена при малых, но конечных значениях прокачки Rex вдоль координаты x. При отсутствии прокачки (Rex = 0, рис. 4а), или при слабой прокачке (Rex =0.01, рис 4б) все моды неустойчивости монотонны, первая из колебательных мод возникает правее точки BT2 при Rex ~ 0.113, затем при Rex ~ 0.117 эта мода переходит в колебательную моду неустойчивости решения (2.1) AX1, которая при дальнейшем росте Rex остается наиболее опасной.
Таким образом, общая картина и разнообразие бифуркаций основного решения определяются в основном величиной прокачки по направлению x, соответствующему максимальной стороне ячейки периодичности (lx = 4π). При слабой прокачке чередуются вторичные стационарные течения, при более сильной устанавливаются автоколебания, которые могут появляться либо как результат бифуркации Андронова–Хопфа основного решения (2.1) при достаточно больших значениях Rex и амплитуды силы λ, либо в области их промежуточных значений как результат разрушения седлоузловой гомоклинической траектории (бифуркация SNIC). Перечисленные варианты динамики системы можно видеть на рис. 5. Насколько общими являются эти закономерности, покажут дальнейшие расчеты для других ячеек периодичности.
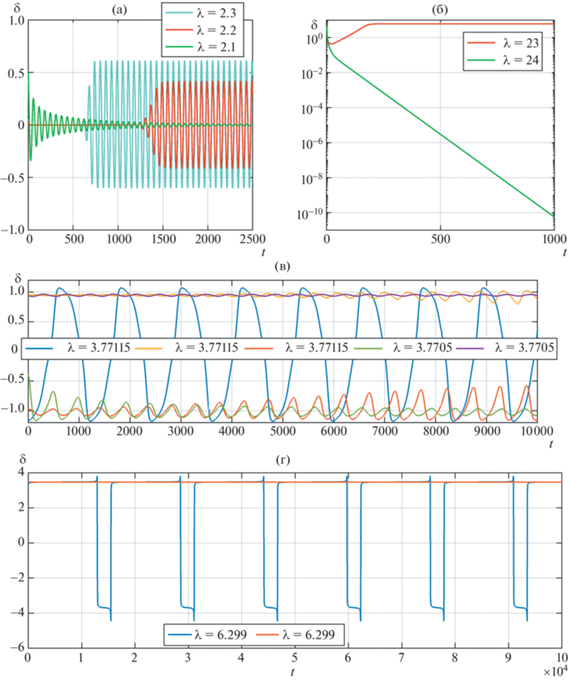
Рис. 5.
Характерные зависимости отклонения от стационарного течения (2.1) δ от времени: (a) – поведение возмущений вблизи порога колебательной неустойчивости АХ1: Rex = 0.2, Rey = 0 (λcr ≅ 0.2, λo1 = 2.1), λ = 2.1 – затухание колебаний, λ = 2.2, 2.3 – установление колебательного вторичного режима; (б) – поведение возмущений вблизи порога монотонной вилочной неустойчивости В1: Rex = 0.2, Rey = 5 (λcr ≅ 7.074, λm1 = 23.5), λ = 23 – затухание возмущений, λ = 24 – установление стационарного вторичного режима (логарифмический масштаб по оси ординат);(в) – сосуществование трех устойчивых колебательных режимов вблизи бифуркации БТ: Rex = 0.115, Rey =1 (λcr ≅ 1.006, ${{\lambda }_{{o2}}}$ = 3.7705); (г) – колебательные и стационарный режимы при бифуркации SNIC. Rex = 0.115, Rey = 1 (λcr ≅ 1.006, ${{\lambda }_{{s1}}} = 6.3$).
4. ДИНАМИКА ЧАСТИЦ ЖИДКОСТИ В ЭЙЛЕРОВОМ И ЛАГРАНЖЕВОМ ПРЕДСТАВЛЕНИИ
Система уравнений (2.3) записана в лабораторной системе отсчета: в эйлеровых переменных, привязанных к конкретным точкам физического пространства. Для наблюдаемых, выраженных в терминах таких переменных, обсуждавшиеся выше динамические режимы либо не зависят от времени (основное и вторичные стационарные течения), либо являются его периодическими функциями (течения, возникшие в ходе развития колебательных неустойчивостей). Гораздо более богатую динамику демонстрируют выражаемые через лагранжевы переменные наблюдаемые, соответствующие пассивным частицам, переносимым вдоль линий тока.
Транспортные уравнения таких частиц
Они решались для поля скорости $({{v}_{x}},{\kern 1pt} \,{{v}_{y}})$, полученного численным интегрированием уравнений (2.3). Для визуализации лагранжевой динамики строились фазовые портреты в координатах $\left( {{{v}_{x}},{{v}_{y}},\Psi {\kern 1pt} '} \right)$.
Приводимые ниже результаты относятся к случаю ${{l}_{x}} = 4\pi ,$ ${{l}_{y}} = 2\pi $, $M = 20,$ $N = 20$.
Начнем с поля скорости, не зависящего от времени. Уравнения лагранжевой динамики для любого двумерного стационарного течения несжимаемой жидкости задаются консервативной динамической системой с одной степенью свободы, в которой функция тока играет роль гамильтониана. Траектории лагранжевых частиц совпадают с линиями тока, и в случае отсутствия точек стагнации у течения (что для течения ZPK96 (2.1) соответствует λ < λcr) лагранжева динамика может быть только периодической или квазипериодической, в зависимости от числа вращения ρ = Rex/Rey .
Спектр мощности скорости частиц в обоих случаях дискретен [18]. При рациональных числах вращения поверхность тора расслаивается на континуум неоднократно обходящих его замкнутых линий тока: каждая частица жидкости движется периодически, причем период этого движения зависит от линии тока. При иррациональных ρ имеет место эргодичность, и каждая траектория плотна на торе.
При λ > λcr в структуре линий тока появляются особые точки и траектории. Для ячейки периодичности размером 2πm × 2πn это 2mn седловых точек и их сепаратрисы, ограничивающие 2mn вихрей: зон локализованного течения, внутри каждой из которых находится стационарная эллиптическая точка, окруженная континуумом замкнутых линий тока. Траектории частиц из “глобальной компоненты” не могут проникнуть внутрь вихрей, а на границах вихрей около седловых точeк происходит существенное замедление скорости частиц (время обтекания вихря имеет особенность логарифмического типа). Вследствие этого динамика лагранжевых частиц в глобальной компоненте существенно меняется. Поскольку при иррациональных числах вращения траектории глобальной компоненты всюду плотны в ней, они снова и снова возвращаются в окрестности седловых точек и снова покидают их: эффект многократных ускорений и замедлений аккумулируется, приводя к качественным переменам. Хотя из-за двумерности фазового пространства траектории лагранжевых частиц по-прежнему не могут быть хаотическими, они проявляют ряд необычных свойств, промежуточных между ламинарным и турбулентным течением: сингулярно-фрактальный характер спектра мощности, степенное убывание корреляций скорости и аномалии характеристик транспорта [12, 13].
Монотонные неустойчивости основного течения (2.1) не вносят качественных изменений в эту картину: они (так же как и бифуркация SNIC) порождают новые устойчивые стационарные поля скорости, причем любое стационарное течение, вне зависимости от деталей его структуры, по-прежнему характеризуется тем же числом вращения ρ, разбивается на глобальную и локализованные компоненты, а лагранжевы наблюдаемые в случае иррационального ρ демонстрируют декорреляцию и слабую неупорядоченность во времени.
Совершенно иной характер носят перемены, вызываемые колебательной неустойчивостью основного течения. Как отмечалось выше, такая неустойчивость наблюдается в широком диапазоне параметров, что приводит к появлению зависящего от времени вторичного течения (периодического в эйлеровых переменных). Периодическими по времени являются и режимы, рождающиеся с конечной амплитудой в результате бифуркации SNIC. Фазовое пространство системы, описывающей динамику лагранжевой частицы в периодически зависящем от времени плоском поле скорости, трехмерно. Поскольку система сохраняет фазовый объем, ее типичные траектории экспоненциально неустойчивы [19]. Это явление – хаотическая динамика частиц жидкости в полях скорости с простыми эйлеровыми свойствами – известно как “лагранжев хаос” или “хаотическая адвекция” [20].
Ниже мы ограничимся влиянием автоколебательного характера течения на общий вид лагранжевой траектории; влияние на спектральные и корреляционные характеристики скорости лагранжевой частицы будет рассмотрено в других публикациях.
Присутствие хаотических линий тока приводит к перемешиванию фазовых траекторий, которые могут проникать (при λ > λcr) и в ранее недоступные области с вихрями. Как и прежде, детали процесса зависят от того, является ли число вращения ρ рациональным. До возникновения неустойчивости фазовое пространство двумерно и при рациональном ρ представляет из себя континуум замкнутых линий тока: “однооборотных” в компоненте течения, локализованной внутри вихрей, и многооборотных в глобальной компоненте. Появление нового масштаба времени, соответствующего периоду автоколебаний в эйлеровых переменных, делает фазовое пространство трехмерным, а континуумы периодических орбит превращаются в семейства двумерных так называемых КАМ-торов (торов Колмогорова-Арнольда-Мозера [21]). Новорожденные двумерные торы вложены друг в друга и образуют в трехмерном фазовом пространстве непроницаемую структуру: каждая частица жидкости квазипериодически движется вдоль поверхности соответствующего тора, не смещаясь поперек структуры. По мере интенсификации эйлеровских автоколебаний КАМ-торы начинают разрушаться, что ведет к постепенному исчезновению барьеров и расширению доли пространства, доступной каждой частице. По-видимому, первыми распадаются торы, лежащие вблизи седловых точек стагнации; это порождает (первоначально слабое) перемешивание между локализованной и глобальной компонентами течения. Разрушение торов приводит к хаотизации движения. Поначалу лагранжев хаос не глобален: существует множество хаотических компонент, между которыми нет обмена, поскольку каждая из них “зажата” между еще неразрушенными КАМ-торами. Некоторые из компонент соответствуют многократным (в соответствии со знаменателем числа вращения) проходам через всю ячейку периодичности, в то время как другие ограничиваются слабо хаотизированными вращениями внутри бывших вихрей. Постепенно хаотические компоненты сливаются, и после разрушения последнего КАМ-тора все фазовое пространстве делается доступным всем хаотическим траекториям.
В ситуации иррационального числа вращения картина несколько иная: здесь после перехода к автоколебаниям эйлеровских переменных континуум КАМ-торов возникает только в локализованной компоненте течения. Хаотизация глобального движения происходит около седловых неподвижных точек: их инвариантные многообразия ответственны за геометрию перемешивания в фазовом пространстве [22]. В результате по мере роста λ глобальные хаотические траектории все глубже проникают в бывшие внутренние области вихрей, где, тем временем, идет процесс разрушения КАМ-торов, и, в конечном счете, развитой лагранжев хаос занимает все фазовое пространство.
В рассматриваемой задаче это общее описание эволюции лагранжева хаоса при росте параметра справедливо для относительно высоких значений параметра Rex: к примеру, при Reу = 1, в области Rex > 0.15. При более низких Rex бифуркация SNIC резко прерывает механизм постепенного расширения области хаотической адвекции: автоколебания эйлеровых переменных прекращаются, и система возвращается к стационарным полям скорости, подобным вышеописанным.
Рисунки 6 и 7 иллюстрируют эти переходы: при рациональном значении ρ переход к лагранжеву хаосу происходит от периодического решения (замкнутая орбита на торе) при λ < λcr, через квазипериодический режим, и затем к новому стационарному режиму после бифуркации SNIC (рис. 6), а при иррациональном – от квазипериодического режима при λ < λcr, через режим с сингулярно-фрактальным спектром (рис. 7).
Рис. 6.
Варианты лагранжевой динамики при рациональном числе вращения ρ = 1/8: ${{l}_{x}} = 4\pi ;$ ${{l}_{y}} = 2\pi $, ${{\operatorname{Re} }_{x}}~$ = = 0.125, ${{\operatorname{Re} }_{y}} = 1;$ ${{\lambda }_{{cr}}} = 1.008,$ ${{\lambda }_{{o1}}} = {\text{ }}3.737,$ ${{\lambda }_{{s1}}} = {\text{ }}11.20$, вар. рис. 4 д.
По горизонтали сверху – глобальные траектории лагранжевых частиц, начинающиеся в точке (1,1); второй ряд – фазовые портреты для глобальных траекторий, третий ряд – траектории частиц, начинающиеся вблизи центра вихря, снизу – фазовые портреты для этих траекторий. Для рядов по вертикали амплитуды силы равны: (a) – λ = 3.7, (б) – λ = 3.8, (в) – λ = 20.
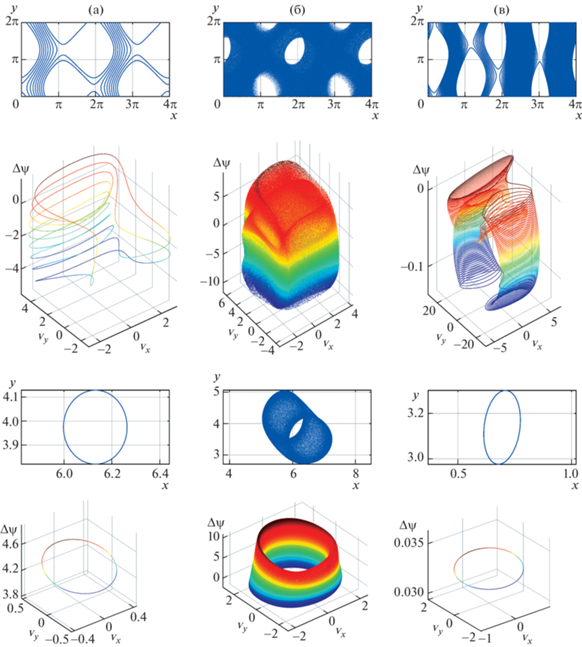
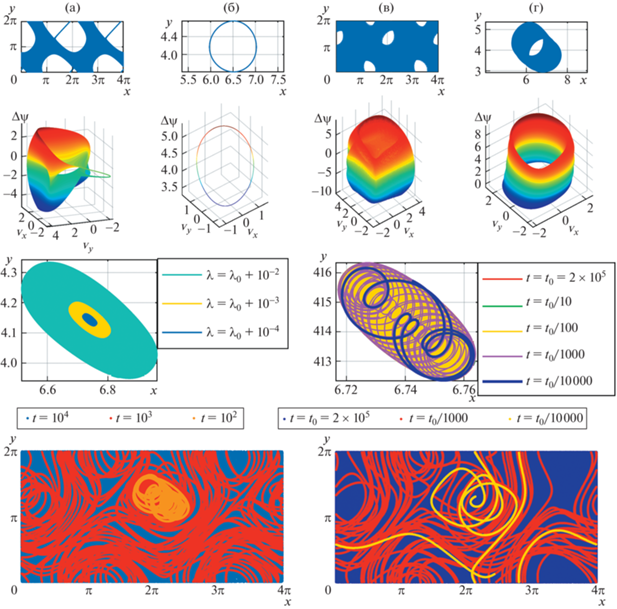
Рис. 7.
Варианты лагранжевой динамики при иррациональных числах вращения: (${{l}_{x}} = 4\pi ;$ ${{l}_{y}} = 2\pi $). По горизонтали сверху – глобальные траектории лагранжевых частиц, второй ряд – фазовые портреты для этих траекторий, для следующих амплитуд силы и начальных точек: a) $~\lambda = 3.7$ (1, 1), б) $\lambda = 3.7$ (6, 4), в) $~\lambda = 3.728$ (1, 1), г) $\lambda = 3.728$ (6, 3.75); ${{\operatorname{Re} }_{x}} = {{(\sqrt 5 - 1)} \mathord{\left/ {\vphantom {{(\sqrt 5 - 1)} 2}} \right. \kern-0em} 2},~$ ${{\operatorname{Re} }_{y}} = 1;$ ${{\lambda }_{{cr}}} = 1.175,$ ${{\lambda }_{{m1}}} = {\text{ }}3.727$.
Третий и четвертый ряды (д, е, ж, з) – изменение фазовых портретов для траекторий, начинающихся вблизи центра вихря, при росте амплитуды колебаний после колебательной потери устойчивости основного решения при λ = λo: ${{R}_{x}} = 1,$ ${{\operatorname{R} }_{y}} = (\sqrt 5 - 1){\text{/}}2,$ ${{\lambda }_{{{\text{cr}}}}} = {\text{1}}{\text{.272}},$ ${{\lambda }_{o}} = {\text{2}}{\text{.712561}}$; д) $\lambda = {{\lambda }_{o}} + {{10}^{{ - 4}}};$ ${{\lambda }_{o}} + {{10}^{{ - 3}}};$ ${{\lambda }_{o}} + {{10}^{{ - 2}}};$ е) $\lambda = {{\lambda }_{o}} + {{10}^{{ - 4}}};$ ж) $\lambda = {{\lambda }_{o}} + 3 \times {{10}^{{ - 1}}};$ з) $\lambda = {{\lambda }_{o}} + 4 \times {{10}^{{ - 1}}}.$
Видно, что по мере роста амплитуды колебаний с увеличением λ площадь “запретной области” для лагранжевой траектории в окрестностях вихрей постепенно уменьшается и затем эта область исчезает. Ранее неявно предполагалось, что неустойчивость наступает при наличии вихрей. Возникновение лагранжевого хаоса при отсутствии вихрей, что, как отмечено выше, реализуется для некоторой области параметров (Rex, Rey), имеет другой характер, соответствующий переходу от периодического или квазипериодического режима к хаотическому.
ЗАКЛЮЧЕНИЕ
Анализ устойчивости рассматриваемого семейства стационарных по времени пространственно-периодических плоских течений показал, что возникновение гидродинамической неустойчивости требует, чтобы длина хотя бы одной из сторон полости вмещала несколько периодов вынуждающей пространственной силы. В квадратной полости с длиной стороны, равной периоду силы, основное течение остается устойчивым в широком диапазоне амплитуд внешней силы и интенсивностей прокачки. В вытянутых полостях неустойчивость, возникающая при достаточно большой вынуждающей силе, может, в зависимости от величин среднего расхода жидкости в двух перпендикулярных направлениях, быть монотонной либо колебательной. В пространстве параметров задачи диаграмма состояний организована вокруг бифуркации Богданова-Такенса, в которой два собственных числа линеаризации около основного течения одновременно обращаются в нуль. Лагранжева динамика пассивных частиц, переносимых нелинейными вторичными течениями, определяется отсутствием или наличием зависимости эйлеровского поля скорости от времени. Так, вторичные стационарные течения в результате повторяющихся медленных проходов частиц около точек застоя обладают теми же свойствами, что и основное течение: дальние временные корреляции, сингулярно-непрерывный Фурье-спектр скорости, аномальный перенос. Если же вторичные течения в эйлеровом представлении периодичны по времени, то достаточно высокие амплитуды внешней силы приводят к разрушению в фазовом пространстве задачи вложенных друг в друга КАМ-торов, и к установлению хаотической адвекции (“лагранжева хаоса”) пассивных частиц.
Общность обсуждаемых результатов не ограничена применявшимися соотношением сторон ячейки периодичности и простой геометрией вынуждающей силы. В рамках нашего подхода возможен расчет аналогичных бифуркационных диаграмм и для ячеек, у которых отношение длин сторон нецелочисленно; длины могут быть и несоизмеримы. Для возникновения вторичных течений, длина хотя бы одной из сторон ячейки должна превосходить пространственные периоды силы (которые могут и не совпадать друг с другом). Если сила явно зависит от более высоких Фурье-гармоник пространственных координат, структура основного стационарного течения делается более сложной, содержащей вихри разного размера. С точки зрения лагранжевых характеристик – спектра мощности и корреляционных функций скорости частиц-трассеров – важна не геометрия силы, а отношение интенсивностей прокачки в перпендикулярных направлениях: при рациональных значениях этого отношения спектр у всех (!) стационарных течений дискретен, а корреляции не затухают. Напротив, иррациональность отношения интенсивностей прокачки влечет за собой наличие (сингулярно) непрерывной спектральной компоненты и алгебраическое затухание корреляций. В этой связи нужно отметить, что транспортные аномалии при переносе частиц таким стационарным течением усиливаются, если в его структуре вихри, вращающиеся по часовой стрелке и против часовой стрелки, несбалансированы. Для нестационарных течений, развившихся в ходе колебательных неустойчивостей, количественные характеристики, разумеется, зависят от геометрии вынуждающей силы, однако общая картина перехода к лагранжеву хаосу остается неизменной.
Список литературы
Обухов А.М. Течение Колмогорова и его лабораторное моделирование // Успехи математических наук. 1983. Т. 38. Вып. 4 (232). С. 101–111.
Мешалкин Л.Д., Синай Я.Г. Исследование устойчивости стационарного решения одной системы уравнений плоского движения вязкой жидкости // Прикладная математика и механика. 1961. Т. 25. № 6. С. 1700–1705.
Юдович В.И. Численные методы решения задач математической физики. М.: Наука, 1966. С. 242–249.
Непомнящий A.A. Об устойчивости вторичных течений вязкой жидкости в неограниченном пространстве // Прикладная математика и механика. 1976. Т. 40. С. 836–841.
Thess A. Instabilities in two-dimensional spatially periodic flows. Part I: Kolmogorov flow // Physics of Fluids. 1992. A4. P. 1385–1395.
Doludenko A.N., Fortova S.V., Kolokolov I.V., Lebedev V.V. Coherent vortex in a spatially restricted two-dimensional turbulent flow in absence of bottom friction // Physics of Fluids. 2021. V. 33. 011704.
Armbruster D., Heiland R., Kostelich E.J., Nicolaenko B. Phase-space analysis of bursting behavior in Kolmogorov flow // Physica D. 1992. V. 58 (1). P. 392–401.
Бондаренко Н.Ф., Гак М.З., Должанский Ф.В. Лабораторная и теоретические модели плоского периодического течения // Изв. АН СССР. Физ. атмосф. и океана. 1979. Т. 15. № 10. С. 1017–1026.
Sommeria J. Experimental study of the two-dimensional inverse energy cascade in a square box // J. Fluid Mech. 1986. V. 170. P. 139–168.
Cardoso O., Marteau D., and Tabeling P. Quantitative experimental study of the free decay of quasi-two-dimensional turbulence // Physical Review E. 1994. V. 49. P. 454–461.
Tithof J., Suri B., Pallantla R.K., Grigoriev R.O., Schatz M.F. Bifurcations in a quasi-two-dimensional Kolmogorov-like flow // J. Fluid Mech. 2017. V. 828. P. 837–866.
Zaks M.A., Pikovsky A.S., Kurths J. Steady viscous flow with fractal power spectrum // Physical Review Letters. 1996. V. 77. P. 4338–4341.
Pöschke P., Sokolov I.M., Zaks M.A., Nepomnyashchy A.A. Transport on intermediate time scales in flows with cat’s eye patterns // Physical Review E. 2017. V. 96 (6). 062128.
Wertgeim I.I., Zaks M.A., Sagitov R.V., Sharifulin A.N. Stability and nonlinear secondary modes of double-periodic flows with pumping // J. Phys.: Conf. Ser. IOP Publishing, 2020. V. 1675. № 1. P. 012002.
Мелехов А.П., Ревина С.В. Возникновение автоколебаний при потере устойчивости пространственно-периодических двумерных течений вязкой жидкости относительно длинноволновых возмущений // Изв. РАН. Механика жидкости и газа. 2008. № 2. С. 41–56.
Сагитов Р.В., Шарифулин А.Н. Бифуркации и устойчивость стационарных режимов конвективных течений в наклоненной прямоугольной полости // Вычислительная механика сплошных сред. 2018. Т. 11. № 2. С. 185–201.
Гукенхеймер Дж., Холмс Ф. Нелинейные колебания, динамические системы и бифуркации векторных полей. М.-Ижевск: Ин-т комп. исслед., 2002. 561 с.
Колмогоров А.Н. О динамических системах с интегральным инвариантом на торе // Докл. Акад. Наук СССР. Сер. мат. 1953. Т. 93. С. 763–766.
Arnold V.I. Sur la Géométrie Différentielle des Groupes de Lie de Dimension Infinie et ses Applications a l’Hydrodynamique des Fluides Parfaits // Annales de l’Institut Fourier. 1966. V. XVI. P. 319–361.
Aref H. Stirring by Chaotic Advection. J. Fluid Mech. 1984. V. 143. P. 1–21.
Арнольд В.И. Математические методы классической механики. М.: Наука, 1974. 432 с.
Rom-Kedar V. Homoclinic tangles – classification and applications // Nonlinearity. 1994. V. 7. P. 441–473.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


