1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2022

Известия РАН. Механика жидкости и газа, 2022, № 4, стр. 86-95

ПЛОСКИЕ И ОСЕСИММЕТРИЧНЫЕ ТЕЛА, ОБТЕКАЕМЫЕ С НАИБОЛЬШИМИ “КРИТИЧЕСКИМИ” ЧИСЛАМИ МАХА

А. Н. Крайко a, *, В. А. Шаповалов a

a Центральный институт авиационного моторостроения им. П.И. Баранова
Москва, Россия

* E-mail: akraiko@ciam.ru

Поступила в редакцию 10.03.2022
После доработки 15.03.2022
Принята к публикации 15.03.2022

Полный текст (PDF)

Аннотация

Строятся двумерные (плоские и осесимметричные) тела, которые при ряде дополнительных ограничений обтекаются идеальным (невязким и нетеплопроводным) газом с наибольшими “критическими” числами Маха М*. Если число Маха набегающего потока М0 < М*, то во всем потоке, включая обтекаемые поверхности, М < 1, отсутствуют ударные волны и, как следствие, равно нулю волновое сопротивление. При М0 = М* равенство М = 1 выполняется хотя бы в одной точке потока, а при М0 > М* появляются сверхзвуковые зоны, в общем случае с образованием ударных волн и волновым сопротивлением, растущим с ростом М0. Как известно, максимальные М* реализуют двумерные конфигурации, при обтекании которых потоком с М0 = М* часть их контуров – отрезки звуковых линий тока. Тривиальными примерами таких конфигураций служат не возмущающие течение пластина под нулевым углом атаки и отрезок прямой (“осесимметричная игла”) в равномерном потоке с М ≡ М0 ≡ М* ≡ 1. Отнесенная к квадрату фиксированной хорды площадь их продольного сечения S = 0. Если в дополнение к длине хорды задать площадь S > 0, то критические контуры таких тел составят передний и задний торцы и соединяющие их без изломов верхняя и симметричная нижняя звуковые линии тока. При S → 0 высота торцов стремится к нулю, М0 и М* стремятся к единице и получаются тривиальные решения. Чтобы при S > 0 избавиться от практически неизбежных отрывов за телами, построенными в предположении безотрывного обтекания, вводится ограничение на величину угла наклона контуров их кормовых частей. В результате вместо задних торцов появляются наклонные прямолинейные отрезки, и плоская критическая конфигурация становится симметричным профилем крыла. При принципиальной простоте структуры двумерных критических конфигураций известные методы их построения весьма сложны. Численные “инструменты”, примененные в данном исследовании, оказались более простыми. В их основе лежат генетический алгоритм “прямой” оптимизации с представлением искомых отрезков звуковых линий тока кривыми Бернштейна–Безье и процедура установления с интегрированием уравнений течения идеального газа модифицированной схемой Годунова повышенного (на гладких решениях) порядка аппроксимации. Ранее эти инструменты развивались и применялись авторами и их коллегами при построении широкого круга оптимальных аэродинамических форм.

Ключевые слова: плоские и осесимметричные тела, обтекаемые с наибольшими критическими числами Маха, отрезки звуковых линий тока, кривые Бернштейна–Безье, прямые методы оптимизации, генетический алгоритм

Наличие отрезков звуковых линий тока в контурах симметричных профилей и тел вращения, обтекаемых под нулевым углом атаки равномерным безграничным набегающим потоком идеального газа с наибольшими критическими числами Маха набегающего потока М0 = М* < 1, установлено в [1]. Последующие обобщения [2] на тела в цилиндрических каналах и в решетках, на контуры с отрезками горизонталей и даже с конечными областями поступательного звукового потока не столь принципиальны. Поскольку при числах Маха набегающего потока М0 ≤ М* эти тела не имеют волнового сопротивления, то их естественно называть и “критическими”, и “оптимальными”. Анализ обтекания таких тел [1, 2] включал доказательство и применение “свойства прямолинейности” звуковых линий (“линий перехода”), отличных от звуковых линий тока, “теорем сравнения” и “принципа максимума” для дозвуковых течений. Как и в [1, 2], под “дозвуковыми” здесь и далее понимаются течения, в которых М ≤ 1.

Построенные в [3–10] примеры оптимальных тел в безграничном равномерном дозвуковом набегающем потоке включают симметричные профили и замкнутые тела вращения, обтекаемые под нулевым углом атаки, а также головные или кормовые части полубесконечных пластины и кругового цилиндра. Для их построения в [3–10] созданы численно-аналитические инструменты с неизменно весьма сложными аналитическими составляющими. В этом отношении подход, возможности которого иллюстрируют приводимые ниже примеры, намного проще. В его основе прямой метод оптимального профилирования с численным решением “установлением” уравнений Эйлера, описывающих дозвуковое обтекание идеальным газом искомых плоских и осесимметричных тел, представление выпуклых звуковых участков их контуров кривыми Бернштейна–Безье (КББ) и нахождение оптимальных КББ с помощью генетического алгоритма. При этом в задачах оптимального профилирования минимизируется интеграл по выпуклому участку контура от (р – ${{p}_{*}}$)2 – квадрата разности давления р и его известной (см. ниже) “критической” величины ${{p}_{*}}$, отвечающей М = 1. У оптимальных тел выпуклые участки – отрезки звуковых линий тока и этот интеграл или сумма интегралов, если таких участков несколько, равен нулю.

1. ПОСТАНОВКА ЗАДАЧИ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПО М* ДВУМЕРНЫХ КОНФИГУРАЦИЙ И ИХ ОСОБЕННОСТИ

Несколько плоских и осесимметричных оптимальных тел, обтекаемых равномерным набегающим потоком идеального газа с наибольшими критическими числами Маха М*, изображены на рис. 1. Это – обтекаемые под нулевым углом атаки симметричный профиль или тело вращения (а) и головная (б) и кормовая (в) части полубесконечных пластины или кругового цилиндра (далее – “головные или кормовые части”). Во всех примерах ось х декартовых или цилиндрических координат ху направлена по скорости V0 набегающего потока и совмещена с осью или плоскостью симметрии оптимальных тел. Начало координат и линейный масштаб выбраны так, что, если не оговорено особо, то 0 ≤ х ≤ 1.

Рис. 1.

Структура оптимальных по М* контуров: симметричного профиля или тела вращения (а), головной (б) и кормовой (в) частей; ab – отрезки звуковых (при М0 = М*) линий тока.

При построении оптимальных по М* конфигураций наряду с заданием длины, принятой за линейный масштаб, ставятся дополнительные условия. Для головных и кормовых частей естественно задаются ординаты точек гладкой стыковки искомого контура у = у(х), 0 ≤ х ≤ 1 с горизонтальной образующей пластины или кругового цилиндра (yf и yi на рис. 1б и 1в, индексы i, f, … метят переменные в точках i, f, …). Возможны и иные ограничения, например,

(1.1)
$\frac{{dy}}{{dx}} \equiv tg\theta \geqslant tg{{\theta }_{m}},\quad S \equiv \int\limits_i^f {ydx} \geqslant {{S}_{m}},\quad y \leqslant {{y}^{m}}$
с заданными константами θm < 0, Sm > 0 и ym.

Как уже отмечалось, первое ограничение (1.1), вводимое, в первую очередь, для профилей, тел вращения (рис. 1а) и кормовых частей (рис. 1в), приводит к появлению у них наклонных прямолинейных участков dy/dx = tgθm, заканчивающихся в точке x = 1, y = 0. Ограничение на площадь “продольного” сечения S, введенное еще в [1], привело к появлению в искомом контуре выпуклого участка – отрезка звуковой линии тока, на котором М = 1 и р = ${{p}_{*}}$. У оптимальных головных и кормовых частей выпуклые отрезки звуковых линий тока появляются без этого условия. Получающаяся при этом площадь продольного сечения S = S0(l, θm) – функция удлинения l, равного отношению длины к yf или yi, и θm. Ограничение площади S влияет на форму оптимальной головной или кормовой части и на величину М* при Sm, превышающих S  0(l, θm). Для таких Sm у оптимальной головной части также появляется наклонный концевой участок bf, на котором (рис. 2а) dy/dx = tgθm, а у оптимальной кормовой части – торец ia (рис. 2б). Из-за увеличения их длины здесь за линейный масштаб взята ордината полубесконечной гоизонтальной образующей.

Рис. 2.

Возможные оптимальные по М* при ограничениях (1.1) контуры: головной (а) и кормовой (б) частей и профиля или тела вращения (в); ab и a'b' – отрезки звуковых (при М0 = М*) линий тока.

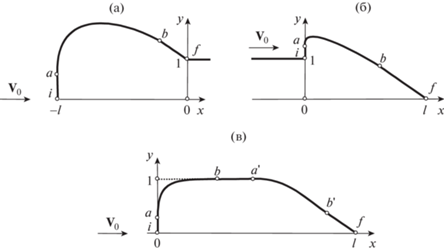
Ограничение на максимально допустимую ординату – третье условие (1.1), вводимое в дополнение к двум первым, также начинает работать не сразу, а лишь тогда, когда растущая с увеличением Sm максимальная ордината оптимального контура на рис. 1а, 2а или 2б превзойдет ym. При таких Sm один звуковой отрезок (ab на рис. 1а) оптимального контура заменят два выпуклых звуковых отрезка (ab и a'b' на рис. 2в) и горизонтальный дозвуковой у = уm между ними (ba' на рис.  2в). При появлении горизонтального участка у профиля или тела вращения за линейный масштаб берется его ордината (рис. 2в). Если при построении оптимальной головной части (рис. 1б) заданное уm = yf, то при Sm > S  0 наряду с единственным звуковым участком ab появляется дозвуковой (М < 1) горизонтальный участок bf с у = уm. Если уm = yi, то аналогичная ситуация возникает при построении оптимальной кормовой части.

При гладкой стыковке всех участков оптимальных образующих (непрерывности угла наклона касательной к ним θ) кривизна звуковых участков в их концевых точках обращается в бесконечность [7–11]. При приближении к этим точкам по отрезкам θ = const бесконечны производные p и V, а при приближении по нормали к контуру – производные всех параметров [11].

Сказанное выше о структуре изображенных на рис. 1 и на рис. 2 оптимальных конфигураций либо установлено в [1, 2], либо получается с привлечением сформулированных и доказанных в этих работах утверждений, справедливых для названных дозвуковыми течений, в которых М ≤ 1. Не вдаваясь в подробности, перечислим указанные утверждения. Первое из них – свойство прямолинейности звуковых линий, отличных от звуковых линий тока, отрезки которых при безграничном набегающем потоке с М0 = М* < 1 формируют оптимальные контуры. Второе утверждение – принцип максимума. Согласно ему в таких течениях число Маха может достигать своего максимального значения М = 1 только на обтекаемых контурах. Свойство прямолинейности звуковых линий тока и принцип максимума справедливы и при дозвуковом (с М ≤ 1) обтекании несимметричных профилей. Однако для них доказать ключевые (при выяснении структуры оптимальных тел рис. 1 и 2) утверждения, названные в [1] “теоремой сравнения” и “леммой граничной точки”, не удалось.

2. ПРЯМОЙ МЕТОД ПОСТРОЕНИЯ ДВУМЕРНЫХ КОНФИГУРАЦИЙ, ОБТЕКАЕМЫХ ДОЗВУКОВЫМ ПОТОКОМ С НАИБОЛЬШИМИ КРИТИЧЕСКИМИ ЧИСЛАМИ МАХА

Как уже отмечалось, в применяемом далее прямом методе минимизируется интеграл по звуковому для оптимального тела выпуклому участку контура

(2.1)
$I = \int\limits_a^b {{{{(p - {{p}_{*}})}}^{2}}d\xi } .$

Здесь ξ – расстояние, отсчитываемое вдоль контура, ${{p}_{*}}$ – отвечающее М = 1 критическое давление. Далее за масштабы плотности и скорости взяты их размерные (с индексом “градус”) критические величины $\rho _{*}^{{^{ \circ }}}$ и $a_{*}^{{^{ \circ }}}$, а давление отнесено к $\rho _{*}^{{^{ \circ }}}a_{*}^{{^{ \circ }2}}$. При этом для совершенного газа с постоянными теплоемкостями и их отношением (показателем адиабаты) γ безразмерное ${{p}_{*}}$ = 1/γ.

Наряду с равным нулю для оптимальных контуров функционалом I ниже вычисляются коэффициент волнового сопротивления cx и площадь или объем

(2.2)
${{c}_{x}} = \frac{2}{{{{\rho }_{0}}V_{0}^{2}}}\int\limits_i^f {(p - {{p}_{0}})d{{y}^{\nu }}} ,\quad S = \int\limits_i^f {{{y}^{\nu }}dx} $
с ν = 1 и 2 для плоских и осесимметричных конфигураций. Для совершенного газа входящие в формулу для cx в (2.2) ${{\rho }_{0}}V_{0}^{2}$ и давление газа в набегающем потоке р0 – функции его числа Маха

$V_{0}^{2} = \frac{{(\gamma + 1)M_{0}^{2}}}{{2 + (\gamma - 1)M_{0}^{2}}},\quad {{p}_{0}} = \frac{1}{\gamma }{{\left( {\frac{{\gamma + 1}}{2} - \frac{{\gamma - 1}}{2}V_{0}^{2}} \right)}^{{\gamma /(\gamma - 1)}}},\quad {{\rho }_{0}}V_{0}^{2} = \gamma {{p}_{0}}M_{0}^{2}.$

Выпуклые участки искомых оптимальных контуров аппроксимировались кривыми Бернштейна–Безье (КББ). КББ задается параметрически [12]

(2.3)
$P(t) = \sum\limits_{k = 0}^K {B_{k}^{K}(t){{P}_{k}}} ,\quad B_{k}^{K}(t) = \frac{{K!}}{{k!(K - k)!}}{{t}^{k}}{{(1 - t)}^{{K - k}}},\quad t \in [0,1].$

Здесь P – координаты КББ x и y, t – параметр, $B_{k}^{K}(t)$ – полиномы Бернштейна, а Pk – координаты концов (контрольных точек) отрезков ломаной (“полигона”). В общем случае КББ проходит лишь через крайние контрольные точки, касаясь в них соответствующего отрезка полигона. Важное достоинство КББ – линейная зависимость ее координат от координат Pk контрольных точек.

Как КББ представляет выпуклый звуковой (при М0 = М*) отрезок образующей симметричного профиля, демонстрирует рис. 3 с тремя первыми контрольными точками (0–2) на оси у и тремя последними (6–8) на продолжении прямого отрезка bf  и с многократно увеличенной (для наглядности) ординатой. Такое расположение точек 0–2 и 6–8 обеспечивает гладкую стыковку искомого звукового участка контура с передним торцом и с приходящим в точку f прямым концевым отрезком dy/dx = tgθm.

Рис. 3.

К построению полигона КББ, задающего выпуклый участок оптимального контура; 0–7 – контрольные точки полигона.

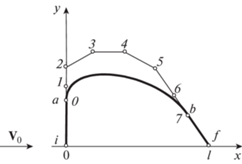
В рассчитанных далее примерах абсциссы K контрольных точек кроме предпоследней (xK – 1), фиксировались. При построении оптимальных профилей у первых трех точек они, как на рис. 3, были нулевыми, а у точек с k от 3 до (K – 2) задавались формулой xk = 0.85(k – 2)/(K – 3). Это обеспечивало равномерное разбиение ими отрезка оси х от ха = 0 до xK = xb = 0.85 – абсциссы точки b, заданной вместо θm и Sm, которые находились в процессе оптимизации. Предпоследняя контрольная точка с изменяющейся координатой xK – 1 лежит на наклонной прямой с dy/dx = = tgθm между (K – 2)-й и K-й точками. Поэтому в процессе счета справедливы неравенства: 0.85(K – 4)/(K – 3) < xK – 1 < 0.85.

При построении оптимальных головных частей первые три контрольные точки также были на оси у; у последней точки (b) xK = 1; ординаты трех последних контрольных точек yk = yb = 1/l при k = K – 2, K – 1, K, реализуя плавную стыковку с полубесконечной горизонтальной образующей, а абсциссы точек с k от 3 до K – 1 находились в процессе оптимизации (были “свободными”).

Все оптимальные профили и головные части строились прямым методом, который ранее развивался и применялся при профилировании оптимальных форм в до-, транс- и сверхзвуковых потоках в [12–17]. При этом оптимальные параметры КББ – оставшиеся не заданными (“свободными”) координаты контрольных точек, обеспечивающие близкие к нулю значения введенных в (2.1) и (2.2) функционалов I и сх, находил двухкритериальный “генетический алгоритм (ГА)”. В нем наряду с I при заданном М0 у профиля минимизировался сх, а у головной части – удлинение l = 1/yf.

В ГА “начальную популяцию” контуров создает случайный выбор свободных параметров. Из них отбираются “решения-родители”, такие, что среди всех оставшихся нет лучших по обоим критериям. Решения-родители образуют “Парето-оптимальный фронт” – совокупность лучших из всех построенных по этим критериям решений. Новые контуры генерирует вариация (“мутация”) параметров случайно выбранного родителя. Для более близкого приближения решения к оптимальному в процессе оптимизации амплитуда мутаций постепенно уменьшается.

Величины I и сх при стационарном обтекании каждого сгенерированного ГА профиля и головной части находились установлением по времени при численном решении уравнений течения идеального газа (“уравнений Эйлера”). Записанные в дивергентной форме нестационарные уравнения Эйлера интегрировались схемой Годунова [18] повышенного согласно [19, 20] порядка аппроксимации (на гладких решениях). В плоскости ху расчет велся в области, ограниченной окружностью: для профилей r ≡ (x2 + y2)1/2 = 15, а для головных частей r = 100yf с параметрами невозмущенного потока в примыкающем к окружности слое “вспомогательных” ячеек [21]. Ячейки разностной сетки, адаптированной к обтекаемым телам, увеличивались линейно по r. Чтобы избежать связанного с этим роста времени установления, интегрирование уравнений велось по неявной схеме [22] с числом Куранта cu = 10–20. Расчеты, выполненные с увеличением r и числа ячеек разностной сетки N, показали, что в представляемых ниже примерах r = 15 и N = 6.2 × 103 для профилей и r = 100yf  и N = 6.4 × 103 для головных частей обеспечивали необходимую точность результатов. При таких r и N для профиля время 2780 прямых расчетов составило 85 ядрочасов, а для головной части время 103 прямых расчетов – около 70 ядрочасов.

3. ПРИМЕРЫ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПО М* ПРОФИЛЕЙ И ОСЕСИММЕТРИЧНЫХ ГОЛОВНЫХ ЧАСТЕЙ

Все расчеты выполнены для γ = 7/5 = 1.4 с заданием выпуклых звуковых участков симметричных профилей кривыми Бернштейна−Безье 11-го порядка (K = 11), а головных частей – КББ 5‑го порядка (K = 5). При представлении полей параметров координаты х и у будем относить к хорде профиля, а для головных частей – к радиусу цилиндра.

В табл. 1 собраны координаты контрольных точек полигона КББ, которая определила форму оптимального звукового участка симметричного профиля, реализовавшего наибольшее число Маха набегающего потока М0 = М* = 0.8 при tgθm = –0.22 и Sm = 0.04212. Максимальное число Маха, получившееся в расчете на этом участке Mm = 1.005, а коэффициент волнового сопротивления cx = 6 × 10–5. Столь малая величина cx – свидетельство высокой точности счета. Обратим внимание на близость точки с k = 1 к точке с k = 0 и точки с k = K – 1 к точке с k = K. Отмеченная близость отражает стремление ГА с КББ увеличить кривизну звукового контура при приближении к его начальной и конечной точкам. Из-за того, что в параметрическое представление КББ (2.3) входят только положительные целочисленные степени t и (1 – t), кривизна найденных звуковых участков не может стать бесконечной, как требуется согласно [7–11]. Тем не менее она при фиксированном порядке КББ возрастает максимально возможно.

Таблица 1.

Координаты контрольных точек полигона КББ профиля

k 0 1 2 3 4 5 6 7 8 9 10 11
xk 0 0 0 0.106 0.212 0.318 0.421 0.53 0.636 0.744 0.842 0.85
yk × 104 137 142 367 485 521 526 618 548 519 463 349 332

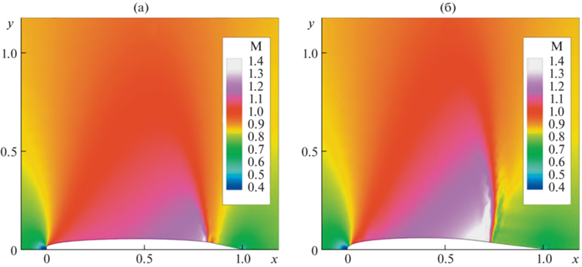
На рис. 4а показано поле чисел Маха вблизи оптимального профиля, а на рис. 4б – вблизи симметричного профиля NACA0012 практически той же площади S = 0.04208 при набегающем потоке с М0 = 0.8. При на порядок большем cx = 5.9 × 10–4 в таком набегающем потоке его сопротивление с ростом М0 растет намного быстрее, чем у оптимального профиля (верхняя и нижняя кривые на рис. 5 с cx = 0.0132 и 0.00138 при М0 = 0.84). Здесь и ниже значки – результаты расчета, соединенные гладкими кривыми. Поля чисел Маха вблизи этих профилей при М0 = 0.84 представлены на рис. 6.

Рис. 4.

Поля чисел Маха над профилями: оптимальным по М* = 0.8 при tgθm = –0.22 и Sm = 0.04212 (а) и NACA0012 с S = 0.04208 (б) в набегающем потоке с М0 = 0.8.

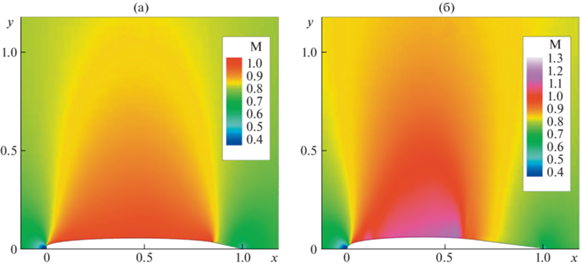
Рис. 5.

Рост сх с увеличением М0 профилей: оптимального по М* = 0.8 (нижняя кривая) и NACA0012 (верхняя кривая).

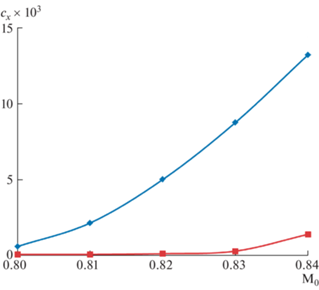
Рис. 6.

Поля чисел Маха над профилями: оптимальным по М* = 0.8 (а) и NACA0012 (б) в набегающем потоке с М0 = 0.84.

В табл. 2 приведены координаты контрольных точек полигонов КББ, которые определили форму оптимальных звуковых участков осесимметричных головных частей, реализующих наибольшие числа Маха набегающего потока М0 = М* = 0.8, 0.9 и 0.96 при удлинениях l = xb/yb = x5/y5 = x5. Как и у оптимального профиля, близость координат точек с k = 0 и 1 и с k = 4 и 5 при K = 5 и с k = 5 и 6 при K = 6 демонстрирует стремление метода максимально возможно увеличить кривизну построенных контуров в начальной и конечной точках их звуковых участков. Величины сх и I у оптимальных головных частей получились в 20–40 раз больше, чем у оптимального профиля. Тем не менее во всех примерах они не превышают 5 × 10–3. Почти не изменив сх, повышение порядка КББ при М* = 0.96 заметно повлияло лишь на отличие от звуковой скорости газа на выпуклом участке контура (см. ниже).

Таблица 2.

Координаты контрольных точек полигонов КББ головных частей

M0 = M* k 0 1 2 3 4 5 6 cx × 103 I × 103
0.8 xk 0 0 0 0.640 1.565 1.567   2.33 4.71
yk 0.5613 0.5618 0.764 1 1 1  
0.9 xk 0 0 0 1.678 3.38 3.57   1.41 4.29
yk 0.3982 0.4020 0.747 1 1 1  
0.96 xk 0 0 0 0.265 7.52 7.89   1.10 3.77
yk 0.2606 0.2645 0.374 1 1 1  
0.96 xk 0 0 0 3.625 7.25 7.82 8.02 1.09 2.85
yk 0.2548 0.2637 0.777 0.992 1 1 1

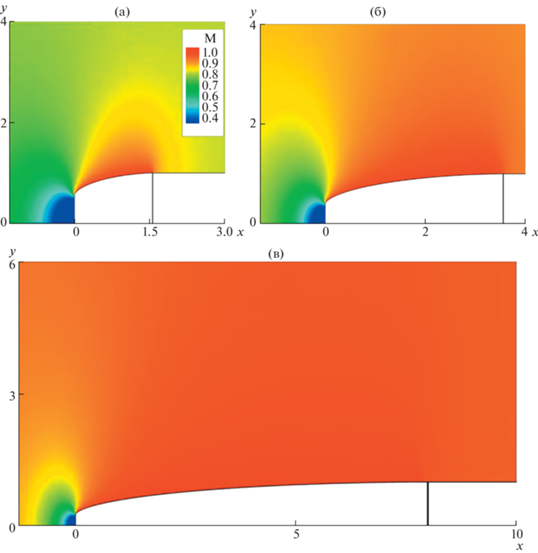
Поля чисел Маха вблизи оптимальных по М* осесимметричных головных частей в набегающих потоках с М0 = М* представлены на рис. 7. Сечения стыковки их контуров и горизонтальных образующих цилиндров даны вертикальными отрезками. Максимальные значения числа Маха Mm, которые во всех рассчитанных примерах получались на выпуклых участках контура, указаны в подписи к рис. 7.

Рис. 7.

Поля чисел Маха при М0 = М* вблизи оптимальных головных частей трех удлинений: l = 1.567, М* = 0.8, Mm = 1.002 (а); l = 3.57, М* = 0.9, Mm = 1.0001 (б) и l = 7.89, М* = 0.96, Mm = 1.027 при K = 5 и 1.002 при K = 6 (в).

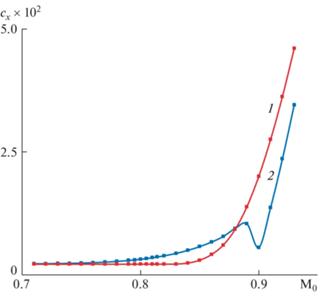
С ростом М0 > М* волновое сопротивление оптимальных по М* головных частей растет. Монотонное увеличение сх оптимальной головной части с М* = 0.8 демонстрирует на рис. 8 кривая 1. Кривая 2 дает сх = сх(М0) головной части [23], реализующей минимум полного сопротивления при том же удлинении l = 1.567 в потоке с М0 = 0.9. В нем сх головной части [23] естественно меньше сх головной части, оптимальной по М* = 0.8. Намного лучше, однако, она только в малой окрестности М0 = 0.9, которая начинается с М0 > 0.88. При М0 = 0.9 волновое сопротивление головной части [23] меньше в 3.6 раза, а уже при М0 = 0.93 – лишь в 1.3 раза.

Рис. 8.

Зависимость сх от М0 головных частей удлинения l = 1.567: 1 – оптимальной по М* = 0.8 и 2 – минимального полного сопротивления при М0 = 0.9, построенной в [23].

ЗАКЛЮЧЕНИЕ

При существенном упрощении по сравнению с [3–10] процедуры построения оптимальных по М* конфигураций авторам не удалось расширить их круг в направлении построения пусть не оптимальных, но хотя бы близких к оптимальным несущих профилей. В итоге ставшие легко доступными оптимальные по М* конфигурации по-прежнему ограничены симметричными профилями, телами вращения и головными и кормовыми частями при том, что все они обтекаются только под нулевым углом атаки. Тем не менее хочется верить, что легкость проб поможет найти структуру принципиально иных оптимальных по М* двумерных конфигураций.

Авторы благодарны К.С. Пьянкову за предоставленные программы, консультации и обсуждения и С.А. Таковицкому – за информацию о головных частях минимального сопротивления.

Работа выполнена при поддержке РФФИ (коды проектов № 19-01-00671 и 20-01-00100).

Список литературы

  1. Gilbarg D., Shiffman M. On Bodies Achieving Extreme Values of the Critical Mach Number. I // J. Ration. Mech. and Analysis. 1954. V. 3. № 2. P. 209–230.

  2. Крайко А.Н. Плоские и осесимметричные конфигурации, обтекаемые с максимальным критическим числом Маха // ПММ. 1987. Т. 51. Вып. 6. С. 941–950.

  3. Fisher D.D. Calculation of Subsonic Cavities with Sonic Free Streamlines // J. Math. Phys. 1963. V. 42. № 1. P. 14–26.

  4. Брутян М.А., Ляпунов С.В. Оптимизация формы симметричных плоских тел с целью увеличения критического числа Маха // Учен. зап. ЦАГИ. 1981. Т. 12. № 5. С. 10–22.

  5. Щербаков С.А. Расчет головной или кормовой части плоского тела, обтекаемого дозвуковым потоком с максимально возможным критическим числом Маха // Учен. зап. ЦАГИ. 1988. Т. 19. № 4. С. 10–18.

  6. Schwendeman D.W., Kropinski M.C.A., Cole J.D. On the Construction and Calculation of Optimal Nonlifting Critical Airfoils // ZAMP. 1993. Bd 44. P. 556–571.

  7. Зигангареева Л.М., Киселев О.М. О расчете кавитационного обтекания кругового конуса дозвуковым потоком сжимаемой жидкости // ПММ. 1994. Т. 58. Вып. 4. С. 93–107.

  8. Зигангареева Л.М., Киселев О.М. Отрывное обтекание диска идеальным газом и тела с наибольшими критическими числами Маха // Изв. РАН. МЖГ. 1996. № 3. С. 166–172.

  9. Зигангареева Л.М., Киселев О.М. О полубесконечных телах вращения, обтекаемых с максимальным критическим числом Маха // ПММ. 1997. Т. 61. Вып. 1. С. 97–107.

  10. Зигангареева Л.М., Киселев О.М. О плоских конфигурациях, обтекаемых потоком идеального газа с максимальным критическим числом Маха // ПМТФ. 1998. № 5. С. 106–115.

  11. Крайко А.Н., Тилляева Н.И. О кривизне граничных линий тока течений идеального газа в точках схода и присоединения // ПММ. 2022. Т. 96. Вып. 3.

  12. Крайко А.Н. Теоретическая газовая динамика: классика и современность. М.: Торус пресс, 2010. 440 с.

  13. Пьянков К.С., Тилляева Н.И. Многокритериальная многодисциплинарная оптимизация лопатки рабочего колеса вентилятора на основе генетического алгоритма // ТВФ. 2010. № 3. С. 58–67.

  14. Крайко А.А., Пьянков К.С., Тилляева Н.И. и др. Оптимизация биротативного вентилятора с учетом напряженно-деформированного состояния на основе генетического алгоритма // ТВФ. 2014. № 1. С. 22–34.

  15. Крайко А.А., Пьянков К.С., Тилляева Н.И. Профилирование двусторонних несимметричных плоских сопел максимальной тяги // Изв. РАН МЖГ. 2016. № 1. С. 115–120.

  16. Тилляева Н.И. Сравнение эффективности штыревых и комбинированных кольцевых сопел // Изв. РАН. МЖГ. 2017. № 4. С. 140–152.

  17. Крайко А.Н., Пьянков К.С., Тилляева Н.И., Шаповалов В.А. Внутренние скачки уплотнения при сверхзвуковом обтекании контуров оптимальных тел и сопел // Изв. РАН. МЖГ. 2020. № 6. С. 121–138.

  18. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. 400 с.

  19. Колган В.П. Применение принципа минимальных значений производной к построению конечноразностных схем для расчета разрывных решений газовой динамики // Учен. зап. ЦАГИ. 1972. Т. 3. № 6. С. 68–77.

  20. Тилляева Н.И. Обобщение модифицированной схемы С.К. Годунова на произвольные нерегулярные сетки // Учен. зап. ЦАГИ. 1986. Т. 17. № 2. С. 18–26 = Газовая динамика. Избр. В 2-х Т. Изд. 2-е, исправ. Т. 2 / Ред.-составители А.Н. Крайко, А.Б. Ватажин и А.Н. Секундов. М.: Физматлит, 2005. С. 201–210.

  21. Гринь В.Т., Крайко А.Н., Славянов Н.Н. Решение задачи о запуске сопла, вмонтированного в торец ударной трубы // Изв. АН СССР. МЖГ. 1981. № 6. С. 117–123.

  22. Браилко И.А., Попов Е.Н. Расчеты стационарных двух- и трехмерных вязких течений в межлопаточных каналах турбин // Тр. НПО Энергомаш им. акад. В.П. Глушко. 2002. № 20. 448 с. С. 4–22.

  23. Мазуров А.П., Таковицкий С.А. Носовая часть тела вращения с минимальным аэродинамическим сопротивлением в диапазоне больших дозвуковых скоростей // Изв. РАН. МЖГ. 2022. № 1. С. 90–100.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал