1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2022

Известия РАН. Механика жидкости и газа, 2022, № 4, стр. 41-51

АКУСТИКА ЖИДКОСТИ С ПОКРЫТЫМИ ОБОЛОЧКОЙ КАПЛЯМИ ПРИ НАЛИЧИИ ФАЗОВЫХ ПЕРЕХОДОВ

Д. А. Губайдуллин a, *, К. А. Панин a, **, Ю. В. Федоров a, ***

a Казанский научный центр РАН, Институт механики и машиностроения
Казань, Россия

* E-mail: gubaidullin@imm.knc.ru
** E-mail: paninkirill590@gmail.com
*** E-mail: kopperfildd@yandex.ru

Поступила в редакцию 28.01.2022
После доработки 09.03.2022
Принята к публикации 15.03.2022

Полный текст (PDF)

Аннотация

Выведено модифицированное уравнение Релея–Ламба, учитывающее радиальные колебания покрытой вязкоупругой оболочкой капли жидкости, в центре которой находится пузырек пара, и находящейся в вязкоупругой среде. Для малых колебаний включения решена задача тепломассообмена между паром, жидкой фазой, оболочкой и несущей жидкостью. Найдено уравнение энергии. На основе полученных уравнений радиальных колебаний включения, энергии и известного волнового уравнения для пузырьковой жидкости определено дисперсионное соотношение. Для смеси жидкости с покрытыми оболочкой каплями додекафторпентана C5F12 и октафторпропана C3F8 с пузырьками пара в центре построены зависимости фазовой скорости и коэффициента затухания от частоты возмущений. Проиллюстрировано влияние фазовых переходов, оболочки включений и упругой несущей фазы на динамику акустических волн. В частном случае проведено сравнение теории с известными экспериментальными данными.

Ключевые слова: акустические волны, капля жидкости, пузырек пара, вязкоупругая оболочка, массообмен

В последнее время большой интерес представляет изучение эмульсий с фазовыми переходами, обладающих следующей особенностью. Под действием ультразвука внутри капель жидкости образуются пузырьки пара. Этот процесс известен как акустическое испарение капель [1]. Использование данных эмульсий имеет огромный потенциал в биомедицине [2, 3], поскольку, в отличие от обычных газовых микропузырьков капли жидкости могут быть достаточно маленькими и могут спокойно протекать через тонкие капилляры. К примеру, при использовании эхографической визуализации капли жидкости, протекающие через сосудистую систему опухолей, могут испаряться и использоваться в качестве контрастных веществ для получения изображения внутренней структуры опухоли [4]. В качестве капель жидкости обычно используют капли перфтор-углерода, такие как декафторбутан C4F10, октафторпропан C3F8 и додекафторпентан C5F12 [5–7]. Выбор данных веществ связан с тем, что они остаются метастабильными при физиологической температуре и не могут самопроизвольно испаряться. Для их испарения требуется акустическая энергия. Чтобы предотвратить быстрое растворение капель в несущей жидкости их обычно покрывают полимерной оболочкой [8].

Аналитическое решение задачи об испарении капли впервые получено в работе [9]. Здесь выведено уравнение Релея–Плессета, описывающее эволюцию пузырька внутри перегретой капли перфторуглерода, расположенной в центре жесткой трубы. Однако данная модель была получена при сильном упрощении. Считалось, что скорость испарения капли постоянна на протяжении всего процесса парообразования. Описание теплообмена и скорости испарения в зависимости от температуры представлено в [10, 11] на основе подхода, который используется при моделировании пузырька пара в обычной жидкости [12]. Дано сравнение численных расчетов со сверхбыстрыми оптическими измерениями роста парогазового пузырька. Подчеркнута важная роль диффузии газа в росте включения. Однако обе модели получены в предположении, что пузырек пара находится в бесконечной жидкой среде перфторуглерода. В работе [13] предложена математическая модель динамики роста парового пузырька, находящегося в капле жидкости конечного размера. Найдено хорошее сопоставление теоретических расчетов изменения радиуса парового пузырька в каплях C5F12, C3F8, C4F10, находящихся в воде, с экспериментальными данными. Учет вязкоупругой оболочки капли проведен в работах [14, 15]. Показано существенное влияние наличия упругой оболочки на процесс испарения капли. Влияние реологических свойств несущей жидкости на динамику пузырька исследовано в [16, 17]. В настоящей работе впервые рассмотрена динамика акустических волн в вязкоупругой среде с покрытыми упругой оболочкой каплями жидкости, внутри которых находятся пузырьки пара.

1. УРАВНЕНИЕ РАДИАЛЬНЫХ КОЛЕБАНИЙ

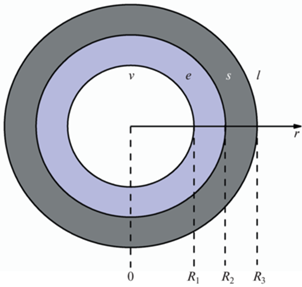
Рассмотрим покрытую вязкоупругой оболочкой каплю жидкости с пузырьком пара в центре, и находящейся во внешней вязкоупругой жидкости (рис. 1). Уравнения неразрывности и импульса в сферической системе координат при наличии центральной симметрии записываются следующим образом

(1.1)
$\frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}({{r}^{2}}{{u}_{{v}}}{{\rho }_{{v}}}) = - \frac{{\partial {{\rho }_{{v}}}}}{{\partial t}},\quad r < {{R}_{1}}$
(1.2)
$\frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}({{r}^{2}}{{u}_{k}}) = 0,\quad r > {{R}_{1}},\quad k = e,s,l$
(1.3)
${{\rho }_{k}}\left( {\frac{{\partial {{u}_{k}}}}{{\partial t}} + {{u}_{k}}\frac{{\partial {{u}_{k}}}}{{\partial r}}} \right) = - \frac{{\partial {{p}_{k}}}}{{\partial r}},\quad r > {{R}_{1}},\quad k = e,s,l$
Рис. 1.

Схема включения: $v$ – пар, e – жидкая фаза, s – оболочка, l – несущая жидкость.

Здесь ρ – плотность, r – радиальная координата, t – время, u – радиальная скорость, p – давление. Решения уравнений (1.1) и (1.2) имеют вид

(1.4)
${{u}_{{v}}} = \frac{r}{{{{R}_{1}}}}{{U}_{{v}}},\quad {{u}_{k}} = \frac{{R_{1}^{2}}}{{{{r}^{2}}}}{{U}_{k}},\quad k = e,s,l$
где ${{U}_{{v}}}$ и Uk – соответственно скорости пара, жидкости и оболочки на границах включения. Следует заметить, что рассматривается только однородная деформация пара.

Записываются граничные условия на границе R1 с учетом фазовых переходов, R2 и R3 без фазовых переходов

(1.5)
$\begin{gathered} {{p}_{e}}({{R}_{1}}) - {{p}_{{v}}}({{R}_{1}}) + \frac{{2{{\sigma }_{1}}}}{{{{R}_{1}}}} = {{\tau }_{e}}({{R}_{1}}) - {{\tau }_{{v}}}({{R}_{1}}) + J\left( {{{u}_{e}}({{R}_{1}}) - {{u}_{{v}}}({{R}_{1}})} \right) \\ J = {{\rho }_{{v}}}({{{\dot {R}}}_{1}} - {{U}_{{v}}}) = {{\rho }_{e}}({{{\dot {R}}}_{1}} - {{U}_{e}}) \\ \end{gathered} $
(1.6)
${{p}_{s}}({{R}_{2}}) - {{p}_{e}}({{R}_{2}}) + \frac{{2{{\sigma }_{2}}}}{{{{R}_{2}}}} = {{\tau }_{s}}({{R}_{2}}) - {{\tau }_{e}}({{R}_{2}}),\quad {{u}_{e}}({{R}_{2}}) = {{u}_{s}}({{R}_{2}}) = {{\dot {R}}_{2}}$
(1.7)
${{p}_{l}}({{R}_{3}}) - {{p}_{s}}({{R}_{3}}) + \frac{{2{{\sigma }_{3}}}}{{{{R}_{3}}}} = {{\tau }_{l}}({{R}_{3}}) - {{\tau }_{s}}({{R}_{3}}),\quad {{u}_{s}}({{R}_{3}}) = {{u}_{l}}({{R}_{3}}) = {{\dot {R}}_{3}}$

Здесь σ – коэффициент поверхностного натяжения, τ – нормальные напряжения, J – интенсивность фазовых переходов. Нормальные напряжения для пара, капли жидкости, вязкоупругой оболочки и несущей жидкости задаются в виде [18, 19]

(1.8)
$\begin{gathered} {{\tau }_{{v}}} = 2{{\mu }_{{v}}}\frac{{\partial {{u}_{{v}}}}}{{\partial r}},\quad {{\tau }_{e}} = 2{{\mu }_{e}}\frac{{\partial {{u}_{e}}}}{{\partial r}} \\ {{\tau }_{s}} = - \frac{{4R_{2}^{2}}}{{{{r}^{3}}}}\left( {\frac{{{{G}_{s}}{{R}_{2}}}}{3}\left( {1 - \frac{{R_{{20}}^{3}}}{{R_{2}^{3}}}} \right) + {{\mu }_{s}}{{u}_{s}}} \right),\quad {{\tau }_{l}} = - \frac{{4R_{3}^{2}}}{{{{r}^{3}}}}\left( {\frac{{{{G}_{l}}{{R}_{3}}}}{3}\left( {1 - \frac{{R_{{30}}^{3}}}{{R_{3}^{3}}}} \right) + {{\mu }_{l}}{{u}_{l}}} \right) \\ \end{gathered} $
где μ – динамическая вязкость, G – модуль сдвига, индекс 0 относится к начальному радиусу в состоянии покоя. Следует заметить, что вязкоупругость оболочки и несущей жидкости учитывается по реологической модели Кельвина–Фойгта. Поскольку вязкость пара меньше, чем вязкость жидкости, поэтому ${{\tau }_{{v}}} \ll {{\tau }_{e}}$ и, следовательно, в дальнейшем величиной ${{\tau }_{{v}}}$ можно пренебречь. Уравнение импульса (1.3) интегрируется от R1 до бесконечности. В этом случае интервал от R1 до R2 будет соответствовать параметрам капли жидкости, от R2 до R3 – параметрам вязкоупругой оболочки капли, от R3 до бесконечности – параметрам несущей жидкости. Тогда, приняв во внимание (1.4)–(1.8), можно получить уравнение радиальных колебаний рассматриваемого включения

${{\rho }_{d}}{{R}_{1}}{{\dot {U}}_{e}} - 0.5{{\rho }_{{d2}}}U_{e}^{2} + 2{{\rho }_{d}}{{\dot {R}}_{1}}{{U}_{e}} = {{p}_{{v}}} - {{p}_{\infty }} - \frac{{2{{\sigma }_{1}}}}{{{{R}_{1}}}} - \frac{{2{{\sigma }_{2}}}}{{{{R}_{2}}}} - \frac{{2{{\sigma }_{3}}}}{{{{R}_{3}}}} + \left( {\frac{1}{{{{\rho }_{{v}}}}} - \frac{1}{{{{\rho }_{e}}}}} \right){{J}^{2}} - $
(1.9)
$\begin{gathered} \, - \frac{4}{{{{R}_{1}}}}{{\mu }_{d}}{{U}_{e}} - \frac{{4{{G}_{s}}}}{3}\left( {1 - \frac{{R_{2}^{3}}}{{R_{3}^{3}}}} \right)\left( {1 - \frac{{R_{{20}}^{3}}}{{R_{2}^{3}}}} \right) - \frac{{4{{G}_{l}}}}{3}\left( {1 - \frac{{R_{{30}}^{3}}}{{R_{3}^{3}}}} \right),\quad {{U}_{e}} = {{{\dot {R}}}_{1}} - \frac{J}{{{{\rho }_{e}}}} \\ {{\rho }_{d}} = {{\rho }_{e}} + ({{\rho }_{s}} - {{\rho }_{e}})\frac{{{{R}_{1}}}}{{{{R}_{2}}}} + ({{\rho }_{l}} - {{\rho }_{s}})\frac{{{{R}_{1}}}}{{{{R}_{3}}}},\quad {{\rho }_{{d2}}} = {{\rho }_{e}} + ({{\rho }_{s}} - {{\rho }_{e}})\frac{{R_{1}^{4}}}{{R_{2}^{4}}} + ({{\rho }_{l}} - {{\rho }_{s}})\frac{{R_{1}^{4}}}{{R_{3}^{4}}} \\ \end{gathered} $
${{\mu }_{d}} = {{\mu }_{e}}\left( {1 - \frac{{R_{1}^{3}}}{{R_{2}^{3}}}} \right) + {{\mu }_{s}}\left( {\frac{{R_{1}^{3}}}{{R_{2}^{3}}} - \frac{{R_{1}^{3}}}{{R_{3}^{3}}}} \right) + {{\mu }_{l}}\frac{{R_{1}^{3}}}{{R_{3}^{3}}}$

Линеаризуем уравнение (1.9): $\psi = {{\psi }_{0}} + \psi {\kern 1pt} '$, $\psi {\kern 1pt} ' \ll {{\psi }_{0}}$, $\psi = {{R}_{1}}$, ${{R}_{2}}$, ${{R}_{3}}$, p, J, получим

(1.10)
$\begin{gathered} {{\rho }_{{d0}}}{{R}_{{10}}}\ddot {R}_{1}^{'} - \frac{{{{\rho }_{{d0}}}{{R}_{{10}}}}}{{{{\rho }_{e}}}}\dot {J}{\kern 1pt} ' + \frac{{4{{\mu }_{{d0}}}}}{{{{R}_{{10}}}}}\dot {R}_{1}^{'} - \frac{{4{{\mu }_{{d0}}}}}{{{{\rho }_{e}}{{R}_{{10}}}}}J{\kern 1pt} ' = p_{v}^{'} - p_{\infty }^{'} + \frac{{2{{\sigma }_{1}}}}{{R_{{10}}^{2}}}R_{1}^{'} + \frac{{2{{\sigma }_{2}}}}{{R_{{20}}^{2}}}R_{2}^{'} + \frac{{2{{\sigma }_{3}}}}{{R_{{30}}^{2}}}R_{3}^{'} - \\ \, - \frac{{4{{G}_{s}}}}{{{{R}_{{20}}}}}\left( {1 - \frac{{R_{{20}}^{3}}}{{R_{{30}}^{3}}}} \right)R_{2}^{'} - \frac{{4{{G}_{l}}}}{{{{R}_{{30}}}}}R_{3}^{'},\quad R_{{30}}^{2}\dot {R}_{3}^{'} = R_{{20}}^{2}\dot {R}_{2}^{'} = R_{{10}}^{2}\left( {\dot {R}_{1}^{'} - \frac{{J{\kern 1pt} '}}{{{{\rho }_{e}}}}} \right) \\ \end{gathered} $

Здесь индекс “0” относится к параметрам равновесного состояния. В случае, когда отсутствуют фазовые переходы $J = J{\kern 1pt} ' = 0$ уравнения (1.9) и (1.10) принимают вид [20].

2. МЕЖФАЗНЫЙ ТЕПЛОМАССООБМЕН

Для учета межфазного тепломассообмена записываются уравнения теплопроводности для пара, жидкой фазы и оболочки [18, 19]

(2.1)
${{\rho }_{{v}}}{{c}_{{p{v}}}}\frac{{\partial {{T}_{{v}}}}}{{\partial t}} = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{\lambda }_{{v}}}{{r}^{2}}\frac{{\partial {{T}_{{v}}}}}{{\partial r}}} \right) + \frac{{\partial {{p}_{{v}}}}}{{\partial t}},\quad 0 < r < {{R}_{1}}$
(2.2)
${{\rho }_{e}}{{c}_{{pe}}}\frac{{\partial {{T}_{e}}}}{{\partial t}} = {{\lambda }_{e}}\frac{{{{\partial }^{2}}{{T}_{e}}}}{{\partial {{r}^{2}}}},\quad {{R}_{1}} < r < {{R}_{2}}$
(2.3)
${{\rho }_{s}}{{c}_{{ps}}}\frac{{\partial {{T}_{s}}}}{{\partial t}} = {{\lambda }_{s}}\frac{{{{\partial }^{2}}{{T}_{s}}}}{{\partial {{r}^{2}}}},\quad {{R}_{2}} < r < {{R}_{3}}$
где T – температура, cp – удельная теплоемкость, λ – коэффициент теплопроводности. Здесь и далее предполагается, что толщина внутреннего слоя жидкой фазы и оболочки капли много меньше, чем размер пузырька пара, поэтому уравнения теплопроводности (2.2) и (2.3) для них записаны в плоско-одномерном приближении. При отсутствии внешнего подвода тепла среднемассовую температуру несущей жидкости будем считать постоянной ${{T}_{l}} = {{T}_{0}} = {\text{const}}$. В уравнении (2.1) давление ${{p}_{{v}}}$ считается только функцией времени ${{p}_{{v}}}(t)$, тем самым выполняется условие гомобаричности [18]. Это предположение позволит избежать решения уравнения движения пара внутри пузырька и тем самым упростить систему уравнений. При постановке задачи необходимо задать граничные условия, которые для температур имеют вид

(2.4)
$r = 0{\text{:}}\;\;\frac{{\partial {{T}_{{v}}}}}{{\partial r}} = 0,\quad r = {{R}_{1}}{\text{:}}\;\;{{T}_{{v}}} = {{T}_{e}} = {{T}_{a}},\quad J = \frac{1}{L}\left( {{{\lambda }_{e}}\frac{{\partial {{T}_{e}}}}{{\partial r}} - {{\lambda }_{{v}}}\frac{{\partial {{T}_{{v}}}}}{{\partial r}}} \right)$
(2.5)
$r = {{R}_{2}}{\text{:}}\;\;{{T}_{e}} = {{T}_{s}},\quad {{\lambda }_{e}}\frac{{\partial {{T}_{e}}}}{{\partial r}} = {{\lambda }_{s}}\frac{{\partial {{T}_{s}}}}{{\partial r}},\quad r = {{R}_{3}}{\text{:}}\;\;{{T}_{s}} = {{T}_{l}} = {{T}_{0}} = {\text{const}}$

Следует отметить, что здесь принята квазиравновесная схема фазового перехода, о чем свидетельствует условие равенства температуры на поверхности пузырька пара температуре насыщения Ta. Таким образом, интенсивность фазовых переходов J определяется по последнему соотношению (2.4) из решения уравнения теплопроводности для жидкости (2.2) и пара (2.1). Температура насыщения Ta определяется из уравнения Клапейрона–Клаузиуса

(2.6)
${{T}_{a}} = {{\left( {\frac{1}{{{{T}_{{a0}}}}} - \frac{{{{B}_{{v}}}}}{L}\ln \left( {\frac{{{{p}_{{v}}}}}{{{{p}_{\infty }}}}} \right)} \right)}^{{ - 1}}}$

Здесь ${{T}_{{a0}}}$ – температура на линии насыщения, зависящая от вида жидкости, ${{B}_{{v}}}$ – приведенная паровая постоянная, L – удельная теплота парообразования жидкости. Решение выше поставленной задачи (2.1)–(2.6) для случая малых колебаний включения с малой амплитудой определяется в виде действительных частей комплексных функций [21]

(2.7)
${{T}_{j}} = {{T}_{0}} + T_{j}^{'}\exp (i\omega t),\quad j = {v},e,s,\quad {{p}_{{v}}} = {{p}_{\infty }} + p_{v}^{'}\exp (i\omega t)$
где ω – частота возмущений. Уравнение (2.1) с учетом решения вида (2.7) запишется следующим образом

(2.8)
$\frac{{{{\partial }^{2}}T_{v}^{'}}}{{\partial {{r}^{2}}}} + \frac{2}{r}\frac{{\partial T_{v}^{'}}}{{\partial r}} - \frac{{i\omega }}{{{{\kappa }_{{v}}}}}T_{v}^{'} = - \frac{{i\omega }}{{{{\lambda }_{{v}}}}}p_{v}^{'},\quad {{\kappa }_{{v}}} = \frac{{{{\lambda }_{{v}}}}}{{{{\rho }_{{v}}}{{c}_{{p{v}}}}}}$

Общее решение дифференциального уравнения второго порядка (2.8) находится в виде суммы частного решения $T_{v}^{'} = {{\kappa }_{{v}}}p_{v}^{'}{\text{/}}{{\lambda }_{{v}}}$ и линейной комбинации двух независимых решений однородного уравнения

$T_{v}^{'} = \frac{{{{\kappa }_{{v}}}}}{{{{\lambda }_{{v}}}}}\left( {1 + {{V}_{1}}\frac{{{\text{sh}}(r{{Y}_{{v}}})}}{r} + {{V}_{2}}\frac{{{\text{ch}}(r{{Y}_{{v}}})}}{r}} \right),\quad {{Y}_{{v}}} = \sqrt {\frac{{i\omega }}{{{{\kappa }_{{v}}}}}} $
где V1 и V2 – неизвестные переменные. Аналогично выписываются решения уравнений (2.2) и (2.3)

$T_{e}^{'} = {{E}_{1}}{\text{sh}}\left[ {(r - {{R}_{{10}}}){{Y}_{e}}} \right] + {{E}_{2}}{\text{ch}}\left[ {(r - {{R}_{{10}}}){{Y}_{e}}} \right],\quad {{Y}_{e}} = \sqrt {i\omega {\text{/}}{{\kappa }_{e}}} $
$T_{s}^{'} = {{S}_{1}}{\text{sh}}\left[ {(r - {{R}_{{20}}}){{Y}_{s}}} \right] + {{S}_{2}}{\text{ch}}\left[ {(r - {{R}_{{20}}}){{Y}_{s}}} \right],\quad {{Y}_{s}} = \sqrt {i\omega {\text{/}}{{\kappa }_{s}}} $

Неизвестные переменные ${{V}_{1}}$, ${{V}_{2}}$, ${{E}_{1}}$, ${{E}_{2}}$, ${{S}_{1}}$ и ${{S}_{2}}$ определяются из граничных условий (2.4)–(2.6). Таким образом, определяются аналитические выражения для распределения температур пара ${{T}_{{v}}}$, капли жидкости Te, оболочки Ts и интенсивности фазовых переходов J. На следующем этапе выводится уравнение энергии для пузырька пара. В качестве уравнения состояния пара используется уравнение Клапейрона–Менделеева

(2.9)
${{p}_{{v}}} = {{\rho }_{{v}}}{{B}_{{v}}}{{T}_{{v}}} = \frac{{\gamma - 1}}{\gamma }{{c}_{{p{v}}}}{{\rho }_{{v}}}{{T}_{{v}}}$
где γ – показатель адиабаты. Уравнение (2.9) дифференцируется по времени t и с учетом (1.1) примет вид

(2.10)
$\frac{{d{{p}_{{v}}}}}{{dt}} = \frac{{\gamma - 1}}{\gamma }{{\rho }_{{v}}}{{c}_{{p{v}}}}\frac{{d{{T}_{{v}}}}}{{dt}} - \frac{2}{r}{{p}_{{v}}}{{u}_{{v}}}$

Уравнение притока тепла для паровой фазы (2.1) интегрируется по радиальной координате от нуля до R10, линеаризуется и, приняв во внимание (2.10), записывается следующим образом

$\frac{{dp_{v}^{'}}}{{dt}} = - \frac{{3\gamma {{p}_{{{v}0}}}}}{{{{R}_{{10}}}}}U_{v}^{'} + 3(\gamma - 1)\frac{{{{\lambda }_{{v}}}}}{{{{R}_{{10}}}}}{{\left( {\frac{{\partial T_{v}^{'}}}{{\partial r}}} \right)}_{{r = {{R}_{{10}}}}}},\quad U_{v}^{'} = \dot {R}_{1}^{'} - J{\kern 1pt} '{\text{/}}{{\rho }_{{v}}}$,

С учетом найденных выражений для $T_{v}^{'}$ и $J{\kern 1pt} '$ данное уравнение окончательно примет вид

$\frac{{dp_{v}^{'}}}{{dt}} = - \frac{{3\gamma {{p}_{{{v}0}}}}}{{{{R}_{{10}}}}}\frac{{dR_{1}^{'}}}{{dt}} - 3i\omega \Psi p_{v}^{'}$
(2.11)
$\begin{gathered} \Psi = 3(\gamma - 1)\frac{{{{y}_{{v}}}{\text{cth}}{{y}_{{v}}} - 1}}{{y_{{v}}^{2}}}\left( {1 - \frac{{{{\lambda }_{{v}}}{{\tau }_{{v}}}}}{{{{\kappa }_{{v}}}}}} \right)\left( {1 - \frac{\gamma }{{\gamma - 1}}\frac{{{{p}_{{{v}0}}}}}{{{{\rho }_{{v}}}L}}} \right) - 3i\frac{{\gamma {{p}_{{{v}0}}}}}{{{{\rho }_{{v}}}{{R}_{{10}}}}}\frac{{{{\lambda }_{e}}{{y}_{e}}}}{{L{{r}_{e}}}}\frac{{W{{\tau }_{{v}}}}}{\omega } \\ {{\tau }_{{v}}} = \frac{{{{B}_{{v}}}}}{{{{p}_{{{v}0}}}L}}{{\left( {\frac{1}{{{{T}_{{a0}}}}} - \frac{{{{B}_{{v}}}}}{L}\ln \left( {\frac{{{{p}_{{{v}0}}}}}{{{{p}_{\infty }}}}} \right)} \right)}^{{ - 2}}},\quad W = \frac{{1 + \chi {\text{cth}}{{y}_{s}}{\text{cth}}{{y}_{e}}}}{{{\text{cth}}{{y}_{e}} + \chi {\text{cth}}{{y}_{s}}}},\quad \chi = \frac{{{{\lambda }_{s}}{{y}_{s}}{{r}_{e}}}}{{{{\lambda }_{e}}{{y}_{e}}{{r}_{s}}}} \\ \end{gathered} $
${{y}_{{v}}} = \sqrt {\frac{{i\omega R_{{10}}^{2}}}{{{{\kappa }_{{v}}}}}} ,\quad {{y}_{e}} = \sqrt {\frac{{i\omega r_{e}^{2}}}{{{{\kappa }_{e}}}}} ,\quad {{y}_{s}} = \sqrt {\frac{{i\omega r_{s}^{2}}}{{{{\kappa }_{s}}}}} ,\quad {{r}_{e}} = {{R}_{{20}}} - {{R}_{{10}}},\quad {{r}_{s}} = {{R}_{{30}}} - {{R}_{{20}}}$

Здесь re – толщина внутреннего слоя жидкой фазы, rs – толщина оболочки.

3. ДИСПЕРСИОННОЕ УРАВНЕНИЕ

Представим решения уравнений (1.10) и (2.11) в виде бегущих волн $R_{j}^{'} = \Delta {{R}_{j}}\,\exp (i\omega t)$, j = 1, 2, 3, $p_{v}^{'} = \Delta {{p}_{v}}\exp (i\omega t)$, $J{\kern 1pt} ' = \Delta J\exp (i\omega t)$, где $\Delta {{R}_{j}}$, $\Delta J$ и $\Delta {{p}_{{v}}}$ – амплитуды волн. Определим из полученной системы уравнений $\Delta {{R}_{1}}$

(3.1)
$\Delta {{R}_{1}} = - \frac{{\Delta {{p}_{\infty }}}}{{{{\rho }_{{d0}}}{{R}_{{10}}}(\omega _{0}^{2} + i\omega \delta - {{\omega }^{2}})}}$
$\omega _{0}^{2} = X + \frac{{{{p}_{{v0}}}}}{{{{\rho }_{{d0}}}R_{{10}}^{2}}}\operatorname{Re} \Phi + \frac{{\omega \operatorname{Im} {{J}_{0}}}}{{{{\rho }_{e}}}} - \frac{{4{{\mu }_{{d0}}}}}{{{{\rho }_{{d0}}}{{\rho }_{e}}}}\frac{{\operatorname{Re} {{J}_{0}}}}{{R_{{10}}^{2}}} - \frac{{\operatorname{Im} {{J}_{0}}}}{{\omega {{\rho }_{e}}}}\left( {X + \frac{{2{{\sigma }_{1}}}}{{{{\rho }_{{d0}}}R_{{10}}^{3}}}} \right)$
$\delta = \frac{{4{{\mu }_{{d0}}}}}{{{{\rho }_{{d0}}}R_{{10}}^{2}}} + \frac{{{{p}_{{{v}0}}}}}{{{{\rho }_{{d0}}}R_{{10}}^{2}}}\frac{{\operatorname{Im} \Phi }}{\omega } - \frac{{\operatorname{Re} {{J}_{0}}}}{{{{\rho }_{e}}}} - \frac{{4{{\mu }_{{d0}}}}}{{{{\rho }_{{d0}}}{{\rho }_{e}}}}\frac{{\operatorname{Im} {{J}_{0}}}}{{\omega R_{{10}}^{2}}} + \frac{{\operatorname{Re} {{J}_{0}}}}{{{{\rho }_{e}}{{\omega }^{2}}}}\left( {X + \frac{{2{{\sigma }_{1}}}}{{{{\rho }_{{d0}}}R_{{10}}^{3}}}} \right)$
(3.2)
${{J}_{0}} = \frac{{{{p}_{{{v}0}}}\Phi }}{{L{{R}_{{10}}}}}\left( {\frac{{{{\lambda }_{e}}{{y}_{e}}}}{{{{r}_{e}}}}W{{\tau }_{{v}}} - i\omega {{R}_{{10}}}\frac{{{{y}_{{v}}}{\text{cth}}{{y}_{{v}}} - 1}}{{y_{{v}}^{2}}}\left( {1 - \frac{{{{\lambda }_{{v}}}{{\tau }_{{v}}}}}{{{{\kappa }_{{v}}}}}} \right)} \right),\quad \Phi = \frac{{3\gamma }}{{1 + \Psi }}$
$X = \frac{1}{{{{\rho }_{{d0}}}R_{{10}}^{2}}}\left( {\frac{{4{{G}_{s}}R_{{10}}^{3}}}{{R_{{20}}^{3}}}\left( {1 - \frac{{R_{{20}}^{3}}}{{R_{{30}}^{3}}}} \right) + \frac{{4{{G}_{l}}R_{{10}}^{3}}}{{R_{{30}}^{3}}} - \frac{{2{{\sigma }_{1}}}}{{{{R}_{{10}}}}} - \frac{{2{{\sigma }_{2}}R_{{10}}^{3}}}{{R_{{20}}^{4}}} - \frac{{2{{\sigma }_{3}}R_{{10}}^{3}}}{{R_{{30}}^{4}}}} \right)$
${{p}_{{{v}0}}} = {{p}_{\infty }} + \frac{{2{{\sigma }_{1}}}}{{{{R}_{{10}}}}} + \frac{{2{{\sigma }_{2}}}}{{{{R}_{{20}}}}} + \frac{{2{{\sigma }_{3}}}}{{{{R}_{{30}}}}}$

Следует заметить, что если не учитываются фазовые переходы ${{J}_{0}} = 0$, то выражения для затухания радиальных колебаний δ и резонансной частоты включения ${{\omega }_{0}}$ по виду совпадают с соответствующими выражениями, полученными в работах [20, 22]. В случае, когда имеется только паровой пузырек в жидкости, выражения для δ и ${{\omega }_{0}}$ приобретают вид [23]. Рассмотрим распространение акустической волны в вязкоупругой среде, когда в ней имеется множество расположенных хаотически на длине волны покрытых капель жидкости, внутри которых имеются пузырьки пара. Будем считать, что расстояние между включениями много больше их размера. Как было отмечено выше, размеры внутреннего жидкого слоя и оболочки капли удовлетворяют условиям ${{r}_{e}} \ll {{R}_{{10}}}$, ${{r}_{s}} \ll {{R}_{{10}}}$. В этом случае учет многократного рассеяния волны может производиться обычным для пузырьковой среды способом на основе известного волнового уравнения типа Фолди в длинноволновом приближении [24]

(3.3)
$\frac{1}{{C_{l}^{2}}}\frac{{{{\partial }^{2}}{{p}_{\infty }}}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}{{p}_{\infty }}}}{{\partial {{x}^{2}}}} = 4\pi {{\rho }_{l}}\int\limits_0^\infty {R_{{10}}^{2}{{{\ddot {R}}}_{1}}} fd{{R}_{{10}}}$

Здесь f – функция распределения включений по размерам, Cl – скорость звука в несущей жидкости. С учетом того, что ${{\ddot {R}}_{1}} = - {{\omega }^{2}}\Delta {{R}_{1}}$, ${{\partial }^{2}}{{p}_{\infty }}{\text{/}}\partial {{t}^{2}} = - {{\omega }^{2}}\Delta {{p}_{\infty }}$ и выражения (3.1), волновое уравнение (3.3) перепишется в виде

(3.4)
$\frac{{{{\partial }^{2}}\Delta {{p}_{\infty }}}}{{\partial {{x}^{2}}}} + K_{*}^{2}\Delta {{p}_{\infty }} = 0,\quad \frac{{K_{*}^{2}}}{{{{\omega }^{2}}}} = \frac{1}{{C_{l}^{2}}} + 4\pi {{\rho }_{l}}\int\limits_0^\infty {\frac{{{{R}_{{10}}}f}}{{{{\rho }_{{d0}}}(\omega _{0}^{2} + i\omega \delta - {{\omega }^{2}})}}d{{R}_{{10}}}} $
где ${{K}_{*}}$ – комплексное волновое число, а второе уравнение (3.4) является дисперсионным уравнением. Если выбрать $f = n\delta (R - {{R}_{{10}}})$, где δ – функция Дирака, $n = 3\alpha {\text{/}}4\pi R_{{10}}^{3}$ – количество включений в единице объема жидкости, то интеграл в (3.4) можно опустить и включения считать монодисперсными.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

На рис. 2 представлены результаты сравнения зависимостей фазовой скорости ${{C}_{p}} = \omega {\text{/}}\operatorname{Re} {{K}_{*}}$ (а) и коэффициента затухания ${{K}_{{**}}} = {\text{Im}}{{K}_{*}}$ (б) для смеси воды с каплями додекафторпентана C5F12 (DDFP) и пузырьками пара в центре (кривая 1), каплями октафторпропана C3F8 (OFP) и пузырьками пара в центре (кривая 2). Следует заметить, что для двух различных веществ DDFP и OFP без учета фазовых переходов дисперсионные кривые практически одинаковы, поэтому на рис. 2 приведена единственная кривая 3. Температура смеси ${{T}_{0}} = 310$ К, ${{p}_{\infty }} = {{10}^{5}}$ Па, объемное содержание включений α = 0.001, радиус пузырьков пара ${{R}_{{10}}} = 7 \times {{10}^{{ - 6}}}$ м, толщина капель жидкости ${{r}_{e}} = {{10}^{{ - 6}}}$ м. На данном этапе упругая оболочка капель не учитывается, поэтому ${{r}_{s}} = 0$. Расчеты проведены с помощью дисперсионного уравнения (3.4). Теплофизические параметры веществ DDFP и OFP взяты из работ [13, 25] и приведены в табл. 1. Как видно из рис. 2, наличие фазовых переходов приводит к существенному уменьшению фазовой скорости (а) и увеличению коэффициента затухания (б) на частотах, меньших резонансной частоты включений. При этом сама резонансная частота включений тоже зависит от интенсивности фазовых переходов, что следует также из формулы (3.2). Для капель DDFP интенсивность массообмена выше, чем для капель OFP, о чем свидетельствуют низкая скорость звука и высокий коэффициент затухания. Данный результат согласуется с выводами [5–7]: для испарения капли DDFP нужно затратить больше акустической энергии по сравнению с каплей OFP. Отметим, что в частном случае для смеси воды с паровыми пузырьками наблюдается похожая картина [23, 26]. Учет процессов массобмена приводит к уменьшению резонансной частоты пузырьков и фазовой скорости, а также к увеличению коэффициента затухания на дорезонансных частотах.

Рис. 2.

Зависимости фазовой скорости (а) и коэффициента затухания (б) от частоты возмущений для смеси воды с каплями жидкости и пузырьками пара в центре: 1 – DDFP, 2 – OFP, 3 – без учета массообмена.

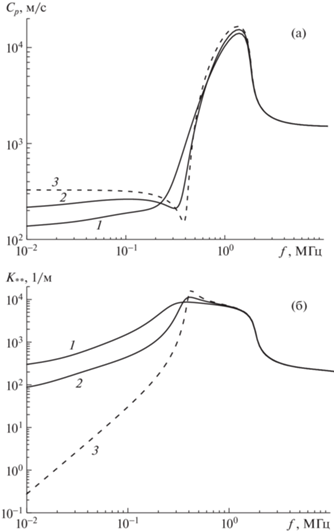
Таблица 1.

Теплофизические параметры

  ${{c}_{{p{v}}}}$ Дж/кг · К ${{\mu }_{{v}}} \times {{10}^{{ - 6}}}$ Па · с ${{B}_{{v}}}$ $\gamma $ ${{\lambda }_{{v}}} \times {{10}^{{ - 2}}}$ кг ∙ м/с3 ∙ К $L \times {{10}^{5}}$ м2/с2 ${{T}_{{a0}}}$ К ${{\rho }_{e}}$ кг/м3 ${{\mu }_{e}} \times {{10}^{{ - 4}}}$ Па · с ${{c}_{{pe}}}$ Дж/кг · К ${{\lambda }_{e}} \times {{10}^{{ - 2}}}$ кг ∙ м/с3 ∙ К
DDFP 842 2.37 28.8 1.05 2 1.16 302 1590 6.52 1090 5.6
OFP 1110 2.3 44.2 1.04 1.38 2.43 236.4 1600 1.08 1270 3.85

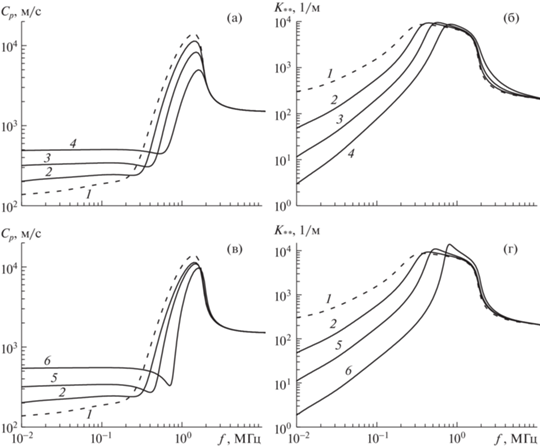
На рис. 3 приведены зависимости фазовой скорости (а), (в) и коэффициента затухания (б), (г) для смеси воды с покрытыми полимерной оболочкой каплями DDFP и пузырьками пара в центре при различных размерах оболочки rs и модулях сдвига Gs. Параметры оболочки: ${{\rho }_{s}} = 1475$ кг/м3, ${{\mu }_{s}} = 0.99$ Па · с. Остальные параметры те же, что и на рис. 2. В случае, когда упругая оболочка капли отсутствует ${{r}_{s}} = 0$, а также не учитываются поверхностные натяжения и упругость несущей фазы ${{G}_{l}} = 0$, то для резонансной частоты включения из формулы (3.2) можно получить

${{f}_{r}} = \frac{{{{\omega }_{0}}}}{{2\pi }} = \frac{1}{{2\pi }}{{\left( {\frac{{{{p}_{\infty }}}}{{{{\rho }_{{d0}}}R_{{10}}^{2}}}\operatorname{Re} \Phi + \frac{{\omega \operatorname{Im} {{J}_{0}}}}{{{{\rho }_{e}}}} - \frac{{4{{\mu }_{{d0}}}}}{{{{\rho }_{{d0}}}{{\rho }_{e}}}}\frac{{\operatorname{Re} {{J}_{0}}}}{{R_{{10}}^{2}}}} \right)}^{{\frac{1}{2}}}}$
Рис. 3.

Фазовая скорость (а), (в) и коэффициент затухания (б), (г) при различных толщинах оболочки ${{r}_{s}}$ (а), (б) и модулях сдвига ${{G}_{s}}$ (в), (г): 1–4 – ${{r}_{s}} = 0$, ${{10}^{{ - 8}}}$, $3 \times {{10}^{{ - 8}}}$, $8 \times {{10}^{{ - 8}}}$ при ${{G}_{s}} = {{10}^{7}}$ Па; 5–6 – ${{G}_{s}} = 3 \times {{10}^{7}}$, ${{10}^{8}}$ Па при ${{r}_{s}} = {{10}^{{ - 8}}}$ м.

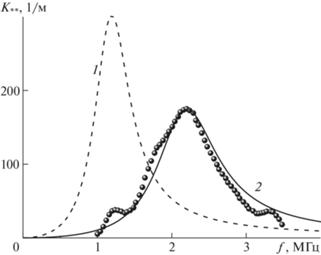
Таким образом, из рис. 3 следует, что увеличение толщины и модуля сдвига упругой оболочки капли приводит к уменьшению коэффициента затухания акустической волны и увеличению фазовой скорости на частотах $f < {{f}_{r}}$. При этом сама резонансная частота включений увеличивается, а диапазон изменения фазовой скорости уменьшается. Расчеты также показали, что при увеличении модуля сдвига Gl несущей среды полученные дисперсионные кривые качественно совпадают с кривыми на рис. 3 в, г, поэтому здесь они не приводятся. Вышеприведенные утверждения хорошо согласуются с экспериментами [27, 28] для упругой среды с пузырьками газа и для воды с пузырьками газа, покрытыми резиновой оболочкой. Сравнение теории с этими экспериментальными данными проведено в работах авторов [29, 30]. Отметим, что размеры пузырьков в этих экспериментах были порядка 1 мм и 1 см. Более близкие к медицинским приложениям экспериментальные измерения коэффициента затухания в смеси жидкости с инкапсулированными пузырьками типа Sonazoid представлены в работах [31, 32]. Пузырьки покрыты полимерным материалом и заполнены фторуглеродным газом. Средний размер пузырьков ${{R}_{{10}}} = 2.6 \times {{10}^{{ - 6}}}$ м, количество пузырьков в единице объема жидкости $n = 2.5 \times {{10}^{{10}}}$, толщина оболочки ${{r}_{s}} = 4 \times {{10}^{{ - 9}}}$ м, вязкость ${{\mu }_{s}} = 0.9$ Па · с, модуль сдвига ${{G}_{s}} = 50 \times {{10}^{6}}$ Па. На рис. 4 приведено сопоставление теории с данными результатами измерений. Расчет выполнен по формуле (3.4) в предположении отсутствия фазовых переходов ${{J}_{0}} = 0$ и жидкой прослойки ${{r}_{e}} = 0$. Как показано на рис. 4, наличие достаточно тонкой упругой оболочки пузырьков (толщина оболочки в 650 раз меньше радиуса пузырька газа) приводит к более высокому значению резонансной частоты, а также к заметному уменьшению пикового значения коэффициента затухания, что и подтверждается экспериментальными данными. Физически это объясняется следующим образом. Оболочка пузырька или упругая несущая фаза сдерживает его радиальные колебания. Чем больше толщина оболочки или модуль сдвига, тем радиальные колебания проходят менее интенсивно и вследствие этого акустическая волна рассеивается менее существенно по сравнению с обычными пузырьковыми средами.

Рис. 4.

Сравнение зависимостей коэффициента затухания от частоты возмущений с экспериментальными данными [31], 1–2 – ${{r}_{s}} = 0$, $4 \times {{10}^{{ - 9}}}$ м.

ЗАКЛЮЧЕНИЕ

Впервые рассмотрена динамика акустических волн в вязкоупругой среде с покрытыми упругой оболочкой каплями жидкости, внутри которых находятся пузырьки пара.

Установлено, что при распространении акустической волны в смеси жидкости с каплями перфторуглерода и пузырьками пара в центре фазовые переходы приводят к существенному уменьшению фазовой скорости и увеличению коэффициента затухания на частотах, меньших резонансной частоты включения, которая также зависит от интенсивности фазовых переходов. Поскольку при рассмотрении капель додекафторпентана C5F12 фазовая скорость меньше, а коэффициент затухания волны больше, чем для капель октафторпропана C3F8, поэтому интенсивность фазовых переходов для C5F12 выше, чем для C3F8.

Получено, что увеличение толщины и модуля сдвига упругой оболочки капли, модуля сдвига упругой несущей среды приводит к сдвигу дисперсионных кривых в сторону увеличения частоты возмущений. В частном случае для смеси жидкости с инкапсулированными пузырьками газа найдено хорошее согласие теоретической зависимости коэффициента затухания волны с известными экспериментальными данными. Показано, что наличие достаточно тонкой упругой оболочки пузырьков приводит к заметному уменьшению пикового значения коэффициента затухания и к более высокому значению резонансной частоты пузырьков.

Исследование выполнено за счет гранта Российского научного фонда (проект № 21-71-00025).

Список литературы

  1. Kripfgans O.D., Fowlkes J.B., Miller D.L., Eldevik O.P., Carson P.L. Acoustic droplet vaporization for therapeutic and diagnostic applications // Ultrasound Med. Biol. 2000. V. 26. P. 1177–1189.

  2. Sheeran P.S., Dayton P.A. Phase-change contrast agents for imaging and therapy // Curr. Pharm. Des. 2012. V. 18. P. 2152–2165.

  3. Kee A.L.J., Teo B.M. Biomedical applications of acoustically responsive phase shift nanodroplets: current status and future directions // Ultrason. Sonochem. 2019. V. 56. P. 37–45.

  4. Rapoport N., Gao Z., Kennedy A. Multifunctional nanoparticles for combining ultrasonic tumor imaging and targeted chemotherapy // J. Natl Cancer Inst. 2007. V. 99. № 14. P. 1095–1106.

  5. Sheeran P.S., Wong V.P., Luois S., McFarland R.J., Ross W.D., Feingold S., Matsunaga T.O., Dayton P.A. Decafluorobutane as a phase-change contrast agent for low-energy extravascular ultrasonic imaging // Ultrasound Med. Biol. 2011. V. 37. P. 1518–1530.

  6. Sheeran P.S., Luois S., Dayton P.A., Matsunaga T.O. Formulation and acoustic studies of a new phase-shift agent for diagnostic and therapeutic ultrasound // Langmuir. 2011. V. 27. P. 10412–10420.

  7. Sheeran P.S., Luois S., Mullin L.B., Matsunaga T.O., Dayton P.A. Design of ultrasonically-activatable nanoparticles using low boiling point perfluorocarbons // Biomaterials. 2012. V. 33. P. 3262–3269.

  8. Rapoport N. Phase-shift, stimuli-responsive perfluorocarbon nanodroplets for drug delivery to cancer // Wiley Interdiscip Rev Nanomed Nanobiotecnol. 2012. V. 4. № 5. P. 492–510.

  9. Qamar A., Wong Z.Z., Fowlkes J.B., Bull J.L. Dynamics of acoustic droplet vaporization in gas embolotherapy // Appl. Phys. Lett. 2010. V. 96. P. 143702.

  10. Shpak O., Kokhuis T.A., Luan J., Lohse D., Jong D., Fowlkes B., Fabiilli M., Versluis M. Ultrafast dynamics of the acoustic vaporization of phase-change microdroplets // J. Acoust. Soc. Am. 2013. V. 134. P. 1610–1621.

  11. Shpak O., Stricker L., Versluis M., Lohse D. The role of gas in ultrasonically driven vapor bubble growth // Phys. Med. Biol. 2013. V. 58. P. 2523–2535.

  12. Hao Y., Prosperetti A. The dynamics of vapor bubbles in acoustic pressure fields // Phys. Fluids. 1999. V. 11. P. 2008–2019.

  13. Doinikov A.A., Sheeran P.S., Bouakaz A., Dayton P.A. Vaporization dynamics of volatile perfluorocarbon droplets: A theoretical model and in vitro validation // Med. Phys. 2014. V. 41. P. 102901.

  14. Lacour T., Guedra M., Brasier T., Coulouvrat F. A model for acoustic vaporization dynamics of a bubble/droplet system encapsulated within a hyperelastic shell // J. Acoust. Soc. Am. 2018. V. 143. P. 23–37.

  15. Lacour T., Brasier T., Coulouvrat F. Ultimate fate of a dynamical bubble/droplet system following acoustic vaporization // Phys. Fluids. 2020. V. 32. P. 051702.

  16. Голубятников А.Н., Украинский Д.В. О динамике сферического пузырька в неньютоновских жидкостях // Изв. РАН. МЖГ. 2021. № 4. С. 52–62.

  17. Чжан Ц., Ци Н., Цзян Ц. Влияние вязкости гидравлической жидкости на кавитационную люминесценцию // Изв. РАН. МЖГ. 2021. № 3. С. 67–79.

  18. Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987.

  19. Ландау Л.Д. Теоретическая физика: В 10 т. Т. 7. Теория упругости. М.: Наука, 1986.

  20. Губайдуллин Д.А., Федоров Ю.В. Волновая динамика покрытых оболочкой включений в вязкоупругой среде // ПМТФ. 2020. Т. 61. № 4. С. 22–30.

  21. Петров А.Г. Аналитическая гидродинамика. М.: Физматлит, 2010. 520 с.

  22. Губайдуллин Д.А., Федоров Ю.В. Акустические волны в жидкости с газовыми включениями, имеющими жидкую прослойку и вязкоупругую оболочку // ТВТ. 2021. Т. 59. № 4. С. 533–540.

  23. Fuster D., Montel F. Mass transfer effects on linear wave propagation in diluted bubbly liquids // J. Fluid Mech. 2015. V. 779. P. 598–621.

  24. Commander K.W., Prosperetti A. Linear pressure waves in bubbly liquids: Comparison between theory and experiments // J. Acoust. Soc. Am. 1989. V. 85. № 2. P. 732–746.

  25. Park S., Son G. Numerical investigation of acoustic vaporization threshold of microdroplets // Ultrason. Sonochem. 2021. V. 71. P. 105361.

  26. Шагапов В.Ш., Галимзянов М.Н., Вдовенко И.И. Особенности отражения и прохождения акустических волн на границе “чистой” и пузырьковой жидкостей при прямом их падении // ТВТ. 2019. Т. 57. № 2. С. 284–290.

  27. Lee K.M., Wilson P.S., Wochner M.S. Attenuation of low-frequency underwater sound using an array of air-filled balloons and comparison to effective medium theory // J. Acoust. Soc. Am. 2017. V. 142. № 6. P. 3443–3449.

  28. Leroy V., Strybulevich A., Page J.H., Scanlon M.G. Influence of positional correlations on the propagation of waves in a complex medium with polydisperse resonant scatterers // Phys. Rev. E. 2011. V. 83. P. 046605.

  29. Губайдуллин Д.А., Федоров Ю.В. Акустические волны в жидкости с пузырьками газа, покрытыми вязкоупругой оболочкой // Изв. РАН. МЖГ. 2019. № 2. С. 126–133.

  30. Gubaidullin D.A., Fedorov Yu.V. Acoustics of a viscoelastic medium with encapsulated bubbles // J. Hydrodyn. 2021. V. 33. № 1. P. 55–62.

  31. Xia L., Porter T.M., Sarkar K. Interpreting attenuation at different excitation amplitudes to estimate strain-dependent interfacial rheological properties of lipid-coated monodisperse microbubbles // J. Acoust. Soc. Am. 2015. V. 138. № 6. P. 3994–4003.

  32. Sarkar K., Shi W.T., Chatterjee D., Forsberg F. Characterization of ultrasound contrast microbubbles using in vitro experiments and viscous and viscoelastic interface models for encapsulation // J. Acoust. Soc. Am. 2005. V. 118. № 1. P. 539–550.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал