Известия РАН. Механика жидкости и газа, 2022, № 4, стр. 77-85

ОДНО ТОЧНОЕ РЕШЕНИЕ ОБ ОБЖАТИИ ПОЛОСТИ В ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ СЖИМАЕМОЙ СРЕДЕ

А. Н. Голубятников^a, Д. В. Украинский^a, *

^a Московский государственный университет им. М.В. Ломоносова
Москва, Россия

Поступила в редакцию 14.03.2022
После доработки 15.03.2022
Принята к публикации 15.03.2022

EDN: MDIAYU
DOI: 10.31857/S0568528122040028

Аннотация

Представлено частично сферически-симметричное точное решение уравнений динамики теплопроводной среды с термодинамическими уравнениями состояния совершенного газа, для которой тензор вязких напряжений произвольным образом зависит от тензора скоростей деформаций. Предполагается однородность скоростей деформаций и давления, а также отсутствие ускорения, тогда уравнения движения тождественно удовлетворяются. В результате разделения переменных в уравнении притока тепла для зависимости плотности от лагранжевых координат получено трехмерное уравнение Пуассона. Его решение моделирует обжатие в данной среде области существенно переменной плотности, например, в случае полной сферической симметрии пузырька или капли. Возможны и не сферические поверхности уровня плотности. Течение может происходить из состояния покоя с конечной массой среды за счет движения сжимающего сферического поршня. Исследованы степенные неньютоновские жидкости. Вычислена энергия среды и представлено ее поведение в окрестности момента сжатия в точку.

Ключевые слова: сжатие пузырька, сжимаемая среда, вязкость, теплопроводность, точное решение, концентрация энергии

Для решения проблемы о концентрации энергии в сжимаемой среде в адиабатическом случае в работе [1] был применен подход к построению решений уравнений газовой динамики, двойственных [2] к решению задачи о точечном взрыве [3]. Под двойственностью понимается переход к новому решению путем взаимного аналитического продолжения состояний газа относительно разрыва с последующим изменением знака времени. Однако данные исследования показывают, что из-за автомодельности решения с образованием ударной волны для концентрации конечной энергии газа необходимо приложить бесконечную работу сжимающего поршня. Кроме того, вопрос о концентрации энергии был подробно исследован для несжимаемых идеальных [4] и ньютоновских [5] жидкостей, а также реологических сред со степенной зависимостью вязкости от скорости деформации [6]. В работе [5, с. 110] также указано, что “может играть роль нагревание внутренних слоев из-за вязкости”. В настоящей работе дано точное решение задачи динамики вязкого теплопроводного совершенного газа при однородном давлении и скорости, пропорциональной расстоянию до центра симметрии [7, 3 ], но с переменной плотностью, которая входит в коэффициент теплопроводности, а ее логарифм в результате разделения переменных удовлетворяет пространственному уравнению Пуассона. При этом допускается произвольная зависимость тензора напряжений от однородного тензора скоростей деформаций, в результате чего полностью удовлетворяются уравнения движения. Данные исследования могут быть обобщены на вязкоупругие среды [8] и действие однородных сил, зависящих от времени, типа сил инерции, а также на зависимость коэффициентов вязкости и температуропроводности от давления. Существенным моментом в работе [8] была минимизация полной диссипации кинетической энергии при заданном импульсе, которая достигается на однородных деформациях. Исследование захлопывания кавитационного пузырька около стенки с образованием кумулятивной струйки в рамках идеальной несжимаемой жидкости дано в работе [9]. Современным вопросам физических процессов в кавитирующих пузырьках посвящена статья [10].

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается задача о сжатии нелинейно-вязкого теплопроводного совершенного газа с однородной деформацией, вызванное движением сферического поршня с постоянной скоростью ${{v}_{p}} < 0$.

Уравнения неразрывности и движения сплошной среды при отсутствии массовых сил имеют вид [11]

(1.1)

$\frac{{d\rho }}{{dt}} + \rho {\kern 1pt} {\text{div}}{\kern 1pt} {\mathbf{v}} = 0,\quad \rho \frac{{d{\mathbf{v}}}}{{dt}} + \nabla p = {{\nabla }_{j}}({{\tau }^{{ij}}}{{{\mathbf{e}}}_{i}})$

где $\rho $ – плотность, ${\mathbf{v}}$ – скорость, p – давление, ${{\tau }^{{ij}}}$ – компоненты тензора вязких напряжений и ${{{\mathbf{e}}}_{i}}$ – базисные векторы.

К системе (1.1) нужно добавить уравнения состояния. Предполагается, что тензор вязких напряжений зависит только от тензора скоростей деформаций изотропным образом. Общий вид такой зависимости указан в добавлении 1 к книге [11]. Он представляет собой формулу Гамильтона–Кэли, которая состоит из трех тензорных членов – шарового тензора, линейной части и квадратичной с коэффициентами, зависящими от трех инвариантов тензора скоростей деформаций $e_{j}^{i}$

$\tau _{j}^{i} = \tau _{j}^{i}(e_{j}^{i}),\quad e_{j}^{i} = \frac{1}{2}({{\nabla }_{i}}{{v}^{j}} + {{\nabla }_{j}}{{v}^{i}})$

Также считается, что справедливы термодинамические соотношения для совершенного газа

$p = {{c}_{{\text{V}}}}(\gamma - 1)\rho T,\quad u = {{c}_{{\text{V}}}}T,\quad f: = A\exp (s{\text{/}}{{c}_{{\text{V}}}}) = p{\text{/}}{{\rho }^{\gamma }}$

при постоянных удельной теплоемкости ${{c}_{{\text{V}}}}$ и показателе адиабаты $\gamma $. Здесь u и s – удельные внутренняя энергия и энтропия соответственно, f – так называемая энтропийная функция.

Для определения температуры T добавляется уравнение притока тепла

$\rho T\frac{{\partial s}}{{\partial t}} = {{\tau }^{{ij}}}{{e}_{{ij}}} + {{\nabla }_{i}}({{c}_{{\text{V}}}}\rho k{{\nabla }^{i}}T)$

где коэффициент температуропроводности k также рассматривается постоянным.

Кинематические и динамические условия на поршне имеют вид

(1.2)

${{v}_{n}} = {{v}_{p}},\quad {{{\mathbf{v}}}_{\tau }} = 0$

(1.3)

$ - p{\kern 1pt} {\mathbf{n}} + {{\tau }^{{ij}}}{{{\mathbf{e}}}_{j}}{{n}_{i}} = {{{\mathbf{p}}}_{p}}$

Таким образом, предполагается, что поршень за счет ${{{\mathbf{p}}}_{p}}$ уравновешивает любую поверхностную силу, создаваемую средой. Здесь n – внешняя к среде нормаль, ${{v}_{n}}$ – нормальная компонента скорости и ${{{\mathbf{v}}}_{\tau }}$ – вектор касательной скорости.

Температура поршня считается равной температуре среды. Кроме этого, выставляется условие равенства для потоков тепла и работ поверхностых сил, что с учетом (1.2) и (1.3) дает

(1.4)

$T = {{T}_{p}},\quad {{q}_{n}} = {{q}_{p}}$

Ищется решение уравнений (1.1), которое удовлетворяет кинематическим условиям на поршне (1.2). Рассматривается сферически-симметричное движение с однородной деформацией, для которого скорость в декартовых координатах и давление имеют вид

${{v}_{i}} = {{x}_{i}}{\text{/}}t,\quad p = p(t)$

Тогда компоненты ${{{v}}_{i}}$ вектора v представляют собой три лагранжевы переменные. Таким образом, ускорение равно нулю, а компоненты тензоров скоростей деформаций и вязких напряжений представляются в виде

(1.5)

$e_{j}^{i} = \delta _{j}^{i}{\text{/}}t,\quad {\text{|}}e{{{\text{|}}}^{2}} = {{e}^{{ij}}}{{e}_{{ij}}} = 3{\text{/}}{{t}^{2}},\quad \tau _{j}^{i} = \sigma (t)\delta _{j}^{i},\quad {{\tau }^{{ij}}}{{e}_{{ij}}} = 3\sigma (t){\text{/}}t$

где $\delta _{j}^{i}$ – символы Кронекера. Вид $\sigma (t)$ зависит от вида реологического состояния среды. Уравнения движения в (1.1) удовлетворяются.

При сжатии t < 0. Состояние покоя ${\mathbf{v}} = 0$ в начальных условиях соответствует начальной точке $t = - \infty $.

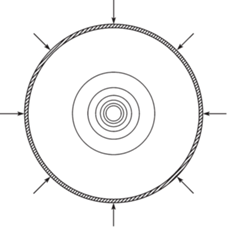
Схематически задача изображена на рис. 1, где указаны линии уровня плотности, чередующиеся через 0.1 от ее максимального значения. На уровне 0.9 расположен поршень. Сгущение этих линий отражает большой градиент уменьшения плотности.

Рис. 1.

Пузырек в сжимаемой поршнем среде.

2. РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ

Уравнение неразрывности приводит к разделению переменных для плотности

$\rho = {{\rho }_{1}}(t){{\rho }_{2}}({{{v}}_{i}}),\quad {{\rho }_{1}}(t) = {\text{|}}t{{{\text{|}}}^{{ - 3}}}$

что вместе с однородностью давления дает разделение переменных и для энтропийной функции

$f = {{f}_{1}}(t){{f}_{2}}({{{v}}_{i}}),\quad {{f}_{1}}(t) = p(t){\text{|}}t{{{\text{|}}}^{{3\gamma }}}$

Переменные $t$ и ${{v}_{i}}$ в уравнении притока тепла также разделяются

(2.1)

$ - {{\Delta }_{{\mathbf{v}}}}(\ln {{\rho }_{2}}({{{v}}_{i}})) \equiv \lambda \equiv \frac{{{{t}^{2}}}}{{k{{f}_{1}}(t)}}\left( {\frac{{d{{f}_{1}}(t)}}{{dt}} - (\gamma - 1){{\tau }^{{ij}}}{{e}_{{ij}}}{\text{|}}t{{{\text{|}}}^{{3\gamma }}}} \right)$

где ${{\Delta }_{{\mathbf{v}}}}$ – оператор Лапласа в переменных ${{{v}}_{i}}$.

Следовательно, для $\ln {{\rho }_{2}}({{{v}}_{i}})$ получается уравнение Пуассона. Его решение приводит к формуле

(2.2)

${{\rho }_{2}}({{{v}}_{i}}) = {{\rho }_{0}}\exp \left( { - \frac{{\lambda {\text{|}}{\mathbf{v}}{{{\text{|}}}^{2}}}}{6} + \varphi ({{{v}}_{i}})} \right)$

где $\varphi ({{{v}}_{i}})$ – произвольное решение уравнения Лапласа ${{\Delta }_{{\mathbf{v}}}}\varphi ({{{v}}_{i}}) = 0$.

Итак, имеется сферически-симметричное движение газа с однородным давлением и плотностью, допускающей разделение переменных t и ${{{v}}_{i}}$.

Формальное решение уравнения (2.1) для функции ${{f}_{1}}(t)$ имеет вид

(2.3)

${{f}_{1}}(t) = \left( {C + (\gamma - 1)\int \,{{\tau }^{{ij}}}{{e}_{{ij}}}{\text{|}}t{{{\text{|}}}^{{3\gamma }}}\exp \left( { - \frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right)dt} \right)\exp \left( {\frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right)$

Вычисление полной энергии между центром и поршнем дает

$E = K + U = \int\limits_{{{V}_{0}}} \left( {\frac{{{\text{|}}{\mathbf{v}}{{{\text{|}}}^{2}}}}{2} + \frac{p}{{(\gamma - 1)\rho }}} \right){{\rho }_{2}}dV = \int\limits_{{{V}_{0}}} \frac{{{\text{|}}{\mathbf{v}}{{{\text{|}}}^{2}}}}{2}{{\rho }_{2}}dV + \frac{{4\pi {{f}_{1}}(t){\text{|}}{{{v}}_{p}}{{{\text{|}}}^{3}}}}{{3(\gamma - 1){\text{|}}t{{{\text{|}}}^{{3(\gamma - 1)}}}}}$

где ${{V}_{0}}$ – объем шара радиуса ${\text{|}}{{{v}}_{p}}{\text{|}}$.

Исходя из уравнения (2.1) для величины U выгодны значения $\lambda \geqslant 0$, связанные с увеличением роста ${{f}_{1}}(t)$. В дальнейшем рассматриваются только неотрицательные $\lambda $.

Таким образом, кинетическая энергия при сжатии сохраняется и конечна, в то время как внутренняя энергия растет до бесконечности при $t \to - 0$, если порядок функции ${{f}_{1}}(t)$ ниже, чем $O({\text{|}}t{{{\text{|}}}^{{3(\gamma - 1)}}})$. Если порядок ${{f}_{1}}(t)$ равен $O({\text{|}}t{{{\text{|}}}^{{3(\gamma - 1)}}})$, то получается постоянная. Если выше, то ноль.

Данный метод построения решений применим и для случаев цилиндрической и плоской симметрий, когда $e_{1}^{1} = e_{2}^{2} = 1{\text{/}}t$, $e_{3}^{3} = 0$ или $e_{1}^{1} = 1{\text{/}}t$, $e_{2}^{2} = e_{3}^{3} = 0$ соответственно.

3. СФЕРИЧЕСКАЯ СИММЕТРИЯ

В случае сферической симметрии для описания движения лучше использовать массовую лагранжеву переменную m, отсчитываемую от центра.

Тогда радиальная координата равна

$r(m,t) = {v}(m)t$

где ${v}(m) < 0$ – радиальная скорость, являющаяся однозначной функцией переменной m, для которой предполагается ${v}(0) = 0$. В начальный момент времени $t = - \infty $ газ покоится, а при t = 0 – сжимается в точку.

Плотность газа имеет вид

$\rho = {{(4\pi {{r}^{2}}{{r}_{m}})}^{{ - 1}}} = {{\rho }_{1}}(t){{\rho }_{2}}(m)$

${{\rho }_{1}}(t) = {\text{|}}t{{{\text{|}}}^{{ - 3}}},\quad {{\rho }_{2}}(m) = {{(4\pi {{{v}}^{2}}(m){\text{|}}{v}{\kern 1pt} '(m){\text{|}})}^{{ - 1}}}$

Общее решение уравнения (2.1) для функции ${{\rho }_{2}}({v})$ представляется в виде

(3.1)

${{\rho }_{2}}({v}) = {{\rho }_{0}}\exp \left( { - \frac{{\lambda {{{v}}^{2}}}}{6} + \frac{\alpha }{{v}}} \right)$

откуда

$m({v}) = 4\pi {{\rho }_{0}}\int\limits_{v}^0 \,{{\xi }^{2}}\exp \left( { - \frac{{\lambda {{\xi }^{2}}}}{6} + \frac{\alpha }{\xi }} \right)d\xi $

Для обезразмеривания соотношения (3.1) можно использовать модуль скорости поршня ${\text{|}}{{{v}}_{p}}{\text{|}}$.

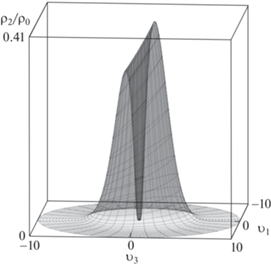
При $\alpha > 0$ вблизи центра имеется полость, характерные графики решения приведены на рис. 2. Если $\lambda = 0$ функция ${{\rho }_{2}}({v})$ монотонно выходит на значение ${{\rho }_{0}}$ при стремлении ${\text{|}}{v}{\text{|}}$ к бесконечности, при $\lambda > 0$ – стремится к 0. Кроме того, в последней ситуации существует максимум плотности в точке

(3.2)

${{v}_{*}} = - {{(3\alpha {\text{/}}\lambda )}^{{1/3}}}$

Рис. 2.

Качественный график функции ${{\rho }_{2}}{\text{/}}{{\rho }_{0}}$ для случаев ($\lambda = 0$, $\alpha = 1$) – кривая 1 и ($\lambda = 1$, $\alpha = 1$) – кривая 2.

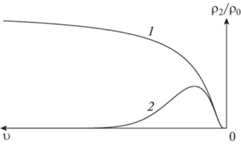
Допускается следующая физическая интерпретация: в первом случае вблизи центра имеется пузырек, во втором – капля с пузырьком. При $\alpha = 0$ и $\lambda > 0$ имеется капля без пузырька. Следует отметить, что движение поршня может быть медленным, но термодинамическое состояние газа, например, плотность, с течением времени существенно растет.

Поскольку давление однородно, то при возрастании плотности с ростом ${\text{|}}{v}{\text{|}}$ температура убывает и, следовательно, в пузырьке поток тепла направлен от центра. При убывании плотности с ростом ${\text{|}}{v}{\text{|}}$ поток тепла направлен к центру. Если движение среды совершается под действием “вмороженного” в нее поршня, то его лучше расположить в точке максимума (3.2) функции ${{\rho }_{2}}({v})$, т.е. принять ${{{v}}_{p}} = {{{v}}_{*}}$. При этом нет ухода тепла через поршень, q_p = 0. Потоки тепла создаются за счет действия сил вязкости, которые разогревают среду.

Решение имеет достаточно глубокую и широкую полость вблизи центра, ее границу можно отсчитывать от ближайшей точки перегиба. Например, при $\lambda = 0$ она расположена в точке ${{v}_{{**}}} = - \alpha {\text{/}}2$ со значением ${{\rho }_{2}}({{v}_{{**}}}){\text{/}}{{\rho }_{0}} = \exp ( - 2)$.

Полная энергия газа в случае сферической симметрии имеет вид

$E(m,t) = \int\limits_0^m \left( {\frac{{{{{v}}^{2}}(\xi )}}{2} + u(\xi ,t)} \right)d\xi = \int\limits_0^m \frac{{{{{v}}^{2}}(\xi )}}{2}d\xi + \frac{{4\pi {{f}_{1}}(t){\text{|}}{v}(m){{{\text{|}}}^{3}}}}{{3(\gamma - 1){\text{|}}t{{{\text{|}}}^{{3(\gamma - 1)}}}}}$

4. РЕОЛОГИЧЕСКИЕ СЖИМАЕМЫЕ ЖИДКОСТИ

В решении (2.3) можно явно задать пределы интегрирования

(4.1)

${{f}_{1}}(t) = \left( {{{f}_{1}}( - \infty ) + (\gamma - 1)\int\limits_{ - \infty }^t {{\tau }^{{ij}}}{{e}_{{ij}}}{\text{|}}\theta {{{\text{|}}}^{{3{\mathbf{\gamma }}}}}\exp ( - \lambda k{\text{/|}}\theta {\text{|}})d\theta } \right)\exp \left( {\frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right)$

За счет положительности интеграла внутри (4.1) функция ${{f}_{1}}(t)$ в случае $\lambda > 0$ стремится к бесконечности при $t \to - 0$, так же ведут себя давление, плотность и энергия.

Для исследования сходимости интеграла делается замена переменной $\theta = - 1{\text{/}}\eta $

$\int\limits_{ - \infty }^t \,{{\tau }^{{ij}}}{{e}_{{ij}}}{\text{|}}\theta {{{\text{|}}}^{{3\gamma }}}\exp ( - \lambda k{\text{/|}}\theta {\text{|}})d\theta = \int\limits_0^{1/|t|} \,{{\tau }^{{ij}}}{{e}_{{ij}}}{{\eta }^{{ - (3\gamma + 2)}}}\exp ( - \lambda k\eta )d\eta $

Поскольку

$\exp ( - \lambda k{\text{/|}}t{\text{|}}) \leqslant \exp ( - \lambda k\eta ) \leqslant 1,\quad {{\tau }^{{ij}}}{{e}_{{ij}}}{{\eta }^{{ - (3\gamma + 2)}}} \geqslant 0$

справедлива оценка

(4.2)

$\exp ( - \lambda k{\text{/|}}t{\text{|}})\int\limits_\varepsilon ^{1/|t|} \,{{\tau }^{{ij}}}{{e}_{{ij}}}{{\eta }^{{ - (3\gamma + 2)}}}d\eta \leqslant \int\limits_\varepsilon ^{1/|t|} \,{{\tau }^{{ij}}}{{e}_{{ij}}}{{\eta }^{{ - (3\gamma + 2)}}}\exp ( - \lambda k\eta )d\eta \leqslant \int\limits_\varepsilon ^{1/|t|} \,{{\tau }^{{ij}}}{{e}_{{ij}}}{{\eta }^{{ - (3\gamma + 2)}}}d\eta $

где $\varepsilon \to + 0$, что отражает рассуждения классической теоремы о среднем значении интеграла. Исходя из (4.2) видно, что экспонента под интегралом не влияет на его сходимость при $\varepsilon \to + 0$.

Сходимость зависит от выбора реологического закона $\tau _{j}^{i}(e_{j}^{i})$. Например, если

$\tau _{j}^{i} = 2\mu {\text{|}}e{{{\text{|}}}^{{2\beta - 1}}}e_{j}^{i},\quad {{\tau }^{{ij}}}{{e}_{{ij}}} = 2\sqrt 3 \mu {{3}^{\beta }}{\text{|}}t{{{\text{|}}}^{{ - (2\beta + 1)}}}$

что соответствует модели степенной неньютоновской жидкости, которая использовалась в работе [6], сходимость интеграла для фиксированного момента t < 0 будет достигаться при условии $\beta > (3{\text{/}}2)\gamma $, т.е. в случае твердеющих дилатантных жидкостей. Расходимости интеграла также можно избежать, если начальный момент времени взять равным $t = {{t}_{0}} > - \infty $, однако в этом случае необходимо обеспечить задание начальной скорости газа, что усложняет физическую реализацию решения.

Вычисление радиальной составляющей $p_{p}^{r}$ вектора p_p, необходимой для поддержания процесса сжатия, с учетом (1.3) и (1.5) дает

$p_{p}^{r} = - p(t) + \sigma (t) = - \left( {\frac{{{{f}_{1}}(t)}}{{{\text{|}}t{{{\text{|}}}^{{3\gamma }}}}} + \frac{{2\mu {{3}^{\beta }}}}{{\sqrt 3 {\text{|}}t{{{\text{|}}}^{{2(\beta + 1)}}}}}} \right)$

Интеграл в (4.1) легко вычисляется в случаях $\lambda = 0$, $\beta > (3{\text{/}}2)\gamma $ или $\lambda > 0$, $\beta = (3\gamma + 1){\text{/}}2$.

При $\lambda = 0$ и $\beta > (3{\text{/}}2)\gamma $ имеется

(4.3)

$\begin{gathered} {{f}_{1}}(t) = {{f}_{1}}( - \infty ) + \frac{{2\sqrt 3 \mu {{3}^{\beta }}(\gamma - 1)}}{{(2\beta - 3\gamma ){\text{|}}t{{{\text{|}}}^{{2\beta - 3\gamma }}}}} \\ - p_{p}^{r} = \frac{{{{f}_{1}}( - \infty )}}{{{\text{|}}t{{{\text{|}}}^{{3\gamma }}}}} + \frac{{2\sqrt 3 \mu {{3}^{\beta }}(\gamma - 1)}}{{(2\beta - 3\gamma ){\text{|}}t{{{\text{|}}}^{{2\beta }}}}} + \frac{{2\mu {{3}^{\beta }}}}{{\sqrt 3 {\text{|}}t{{{\text{|}}}^{{2(\beta + 1)}}}}} \\ \end{gathered} $

Главным членом в (4.3) при ${\text{|}}t{\text{|}} \to 0$ является третье слагаемое.

Если $\lambda > 0$ и $\beta = (3\gamma + 1){\text{/}}2$, то получается

(4.4)

$\begin{gathered} {{f}_{1}}(t) = \left( {{{f}_{1}}( - \infty ) + \frac{{2\sqrt 3 \mu {{3}^{\beta }}(\gamma - 1)}}{{\lambda k}}\left[ {1 - \exp \left( { - \frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right)} \right]} \right)\exp \left( {\frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right) \\ - p_{p}^{r} = \left( {{{f}_{1}}( - \infty ) + \frac{{2\sqrt 3 \mu {{3}^{\beta }}(\gamma - 1)}}{{\lambda k}}\left[ {1 - \exp \left( { - \frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right)} \right]} \right)\exp \left( {\frac{{\lambda k}}{{{\text{|}}t{\text{|}}}}} \right)\frac{1}{{{\text{|}}t{{{\text{|}}}^{{3\gamma }}}}} + \frac{{2\mu {{3}^{\beta }}}}{{\sqrt 3 {\text{|}}t{{{\text{|}}}^{{3(\gamma + 1)}}}}} \\ \end{gathered} $

При ${\text{|}}t{\text{|}} \to 0$ главным членом роста в (4.4) является $\exp (\lambda k{\text{/|}}t{\text{|}}){\kern 1pt} {\text{|}}t{{{\text{|}}}^{{ - 3\gamma }}}$ с коэффициентом порядка единицы.

В случае сферической симметрии при $\lambda = 0$ нельзя считать ${{q}_{n}} = 0$ на поршне, вычисления при $\beta > (3{\text{/}}2)\gamma $ показывают, что должен быть отток тепла

(4.5)

${{q}_{p}} = - {{c}_{{\text{V}}}}k{{\left. {\left( {\rho \frac{{\partial T}}{{\partial r}}} \right)} \right|}_{{{v} = {{{v}}_{p}}}}} = \left( {{{f}_{1}}( - \infty ) + \frac{{2\sqrt 3 \mu {{3}^{\beta }}(\gamma - 1)}}{{(2\beta - 3\gamma ){\text{|}}t{{{\text{|}}}^{{2\beta - 3\gamma }}}}}} \right)\frac{{k\alpha }}{{(\gamma - 1){\text{|}}t{{{\text{|}}}^{{3\gamma + 1}}}{v}_{p}^{2}}}$

где ${{{v}}_{p}} < 0$ – задаваемая скорость поршня. Главным членом в (4.5) является второе слагаемое в скобках.

Как отмечено в предыдущем пункте, в случае $\lambda > 0$ всегда можно выбрать скорость поршня в виде (3.2), тогда ${{q}_{p}} = 0$.

Во всех приведенных примерах вязкость играет существенную роль.

5. СЛУЧАЙ ОТЛИЧИЯ ОТ СФЕРИЧЕСКОЙ СИММЕТРИИ

Анализ решения (2.2) при различных функциях ${{\rho }_{2}}({{{v}}_{i}})$ может быть проведен, например, в случае осевой симметрии, где $O{{{v}}_{3}}$ – ось симметрии. Здесь рассмотрены две ситуации: аргумент экспоненты возмущается решениями уравнения Лапласа первой и второй степени по ${\text{|}}{\mathbf{v}}{\text{|}}$, не изменяющими поведения плотности в центре и на бесконечности. Графики изображаются на плоскости $({{{v}}_{1}},{{{v}}_{3}})$, т.е. при ${{{v}}_{2}} = 0$.

Случай 1.

(5.1)

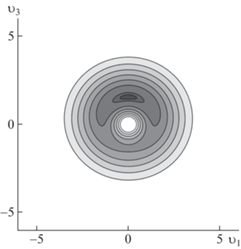
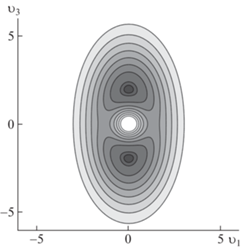
${{\rho }_{2}}({{{v}}_{i}}) = {{\rho }_{0}}\exp \left( { - \frac{{\lambda {\text{|}}{\mathbf{v}}{{{\text{|}}}^{2}}}}{6} - \frac{\alpha }{{{\text{|}}{\mathbf{v}}{\text{|}}}} + {{\delta }_{1}}{{{v}}_{3}}} \right)$

На рис. 3 приведена форма распределения плотности, как функции $({{{v}}_{1}},{{{v}}_{3}})$, при $\lambda = 1$, $\alpha = 1$ и ${{\delta }_{1}} = 0.1$. На рис. 4 указаны линии уровня объемной фигуры, приведенной на рис. 3. В результате сжатия при $t \to - 0$ значение функции $\rho = {\text{|}}t{{{\text{|}}}^{{ - 3}}}{{\rho }_{2}}({{{v}}_{i}})$ будет увеличиваться, что можно интерпретировать как движение неоднородности плотности к центру, своего вида осесимметричная струйка.

Рис. 3.

Форма распределения плотности ${{\rho }_{2}}$ для решения (5.1).

Рис. 4.

Контурный график плотности ${{\rho }_{2}}$ для решения (5.1).

Случай 2.

(5.2)

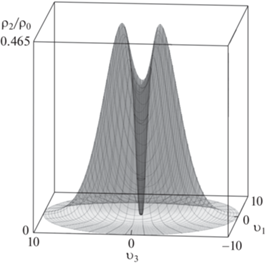
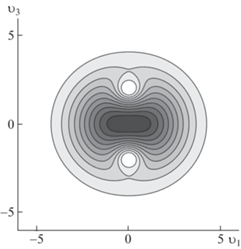
На рис. 5 приведена форма распределения плотности при $\lambda = 1$, $\alpha = 1$ и ${{\delta }_{2}} = 0.05$. На рис. 6 указаны линии уровня данной фигуры. Здесь будут две симметричные струйки, направленные к центру.

Рис. 5.

Форма распределения плотности ${{\rho }_{2}}$ для решения (5.2).

Рис. 6.

Контурный график плотности ${{\rho }_{2}}$ для решения (5.2).

Графики пространственных фигур – полупрозрачные, соответственно, внутренность затемнена. На контурных графиках более светлые области соответствуют меньшим значениям плотности.

В принципе, можно рассмотреть любые гармонические функции $\varphi ({{{v}}_{i}})$, например, представляющие произвольное количество пузырьков с центрами в особых точках типа источника $\sum\nolimits_k ( - {{\alpha }_{k}}){\text{/|}}{\mathbf{v}} - {{{\mathbf{v}}}_{k}}{\text{|}}$. На рис. 7 указана система двух пузырьков для значений параметров $\lambda = 1$, ${{\alpha }_{1}} = 1$, ${{\alpha }_{2}} = 1$, ${{{\mathbf{v}}}_{1}} = (0,0,2)$, ${{{\mathbf{v}}}_{2}} = (0,0, - 2)$.

Рис. 7.

Контурный график системы двух пузырьков.

Стоит заметить, что температура перед поршнем распределена не сферически-симметричным образом, но в условии (1.4) будут присутствовать только радиальные компоненты вектора потока тепла. Рационально выбирать скорость поршня так, чтобы средний по сфере поток тепла равнялся нулю.

ЗАКЛЮЧЕНИЕ

Таким образом, дано точное частично сферически-симметричное решение вида ${\mathbf{v}} = {\mathbf{r}}{\text{/}}t$ уравнений динамики вязкой теплопроводной сжимаемой жидкости, формулы термодинамического состояния которой соответствуют совершенному газу. Решение представлено в элементарных функциях. Предполагается однородность давления и зависимость тензора вязких напряжений только от тензора скоростей деформации, в данном случае однородной. Также отсутствует ускорение, что позволяет полностью удовлетворить уравнениям движения. В результате разделения переменных для зависимости плотности от лагранжевых координат ${\mathbf{v}}$ получено трехмерное уравнение Пуассона, которое эффективно решается. Решение моделирует обжатие в данной среде области существенно переменной плотности, например, в случае полной сферической симметрии пузырька или капли. Рассматриваются также случаи и осесимметрического распределения плотности, моделирующие сжатие при наличии струек, приведены графики. Течение может происходить из состояния покоя с конечной массой газа за счет движения сжимающего поршня сферической формы. Вычислена полная энергия среды, как функция времени, представлено ее поведение в момент окончательного сжатия. При этом кинетическая энергия сохраняется и ограничена, а внутренняя энергия при определенных значениях параметров задачи стремится к бесконечности, при этом существенную роль играет вязкость, повышающая энтропию. Показано, что на участках, где плотность массы возрастает, температура убывает и, таким образом, происходит отток тепла.

Список литературы

Голубятников А.Н. Об ускорении ударных волн и концентрации энергии // Труды МИАН имени В.А. Стеклова. 2013. Т. 281. С. 162–169.
Богоявленский О.И. Методы качественной теории динамических систем в астрофизике и газовой динамике. М.: Наука, 1980. 320 с.
Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1981. 448 с.
Lord Rayleigh (Strutt J. W.) On the pressure developed in a liquid during the collapse of a spherical cavity // Philosophical Magazine. Series 6. 1917. V. 34. Issue 200. P. 94–98.
Забабахин Е.И., Забабахин И.Е. Явления неограниченной кумуляции. М.: Наука, 1988. 173 с.
Голубятников А.Н., Украинский Д.В. О динамике сферического пузырька в неньютоновских жидкостях // Известия РАН. Механика жидкости и газа. 2021. № 4. С. 52–62.
Овсянников Л.В. Новое решение уравнений гидродинамики // ДАН СССР. 1956. Т. 111. № 1. С. 47–49.
Голубятников А.Н. Оптимизация ускорения вязкоупругого тела // Тез. докл. междунар. конф. “Современные проблемы механики сплошной среды”, посв. 110-летию акад. Л.И. Седова. 2017. С. 79–80.
Воинов В.В., Воинов О.В. О схеме захлопывания кавитационного пузырька около стенки и образования кумулятивной струйки // ДАН СССР. 1976. Т. 227. № 1. С. 63–66.
Нигматулин Р.И., Лэхи (мл.) Р.Т., Талейархан Р.П., Вест К.Д., Блок Р.С. О термоядерных процессах в кавитирующих пузырьках // Успехи физических наук. 2014. Т. 184. № 9. С. 947–960.
Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1994. 528 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал