Известия РАН. Механика жидкости и газа, 2022, № 4, стр. 60-68
ВНУТРЕННИЕ ГРАВИТАЦИОННЫЕ ВОЛНЫ ОТ ОСЦИЛЛИРУЮЩЕГО ИСТОЧНИКА ВОЗМУЩЕНИЙ В СТРАТИФИЦИРОВАННОЙ СРЕДЕ С ДВУХМЕРНЫМИ СДВИГОВЫМИ ТЕЧЕНИЯМИ
В. В. Булатов a, *, И. Ю. Владимиров b, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b Институт океанологии им. П.П. Ширшова РАН
Москва, Россия
* E-mail: internalwave@mail.ru
** E-mail: iyuvladimirov@rambler.ru
Поступила в редакцию 31.01.2022
После доработки 15.03.2022
Принята к публикации 15.03.2022
- EDN: HVSDBS
- DOI: 10.31857/S0568528122040016
Аннотация
Рассмотрена задача о генерации внутренних гравитационных волн локализованным гармоническим источником возмущений в стратифицированной среде с двухмерными линейными сдвиговыми течениями. В предположении постоянства частоты плавучести получены интегральные представления решений при выполнении условия устойчивости Майлса–Ховарда. Исследованы свойства спектральной задачи при малых волновых числах. Для различных линейных распределений сдвиговых течений приведены результаты численных расчетов дисперсионных кривых и фазовых картин возбуждаемых волновых полей. Показано, что учет двухмерности сдвиговых течений является причиной заметной асимметрии как дисперсионных кривых, так и линий равной фазы. Численно изучена трансформация фазовых картин полей внутренних гравитационных волн в зависимости от параметров генерации.
В реальных природных стратифицированных средах (океан, атмосфера) генерация и распространение внутренних гравитационных волн (ВГВ) в значительной степени связаны с вертикальной и горизонтальной динамикой фоновых сдвиговых течений [1–3]. В океане такие течения могут проявляться, например, в области сезонного термоклина и оказывать заметное влияние на эволюцию ВГВ [4, 5]. Обычно предполагается, что фоновые течения с вертикальным сдвигом скорости слабо зависят от времени и горизонтальных координат. В общей постановке описание динамики ВГВ в стратифицированной среде с фоновыми полями сдвиговых течений является весьма сложной задачей уже в линейном приближении [1, 2, 6, 7]. В этом случае задача сводится к анализу системы уравнений в частных производных, и при одновременном учете вертикальной и горизонтальной неоднородности эта система уравнений не допускает разделение переменных [1, 4, 5, 8–13].
Для исследования механизма взаимовлияния течений и ВГВ можно рассматривать различные модельные представления частоты плавучести и сдвиговых течений [1, 6, 7, 14–17]. Синтез численных, аналитических и асимптотических результатов может дать первоначальное качественное и количественное представление о волновых процессах с учетом сдвиговых течений. Одним из основных методов решения задач волновой динамики стратифицированных сред со сдвиговыми течениями является метод Фурье. Полученные с помощью этого метода интегральные представления решений требуют численного и асимптотического анализа. Методы прямого численного моделирования не всегда эффективны для исследования генерации ВГВ, особенно с учетом изменчивости основных гидрологических параметров, и требуют верификации и сравнения с асимптотическими решениями модельных задач [4, 5, 12]. Поэтому для исследования ВГВ в реальных природных средах необходимо сочетание, как точных численных методов исследования волновых полей, так и различных асимптотических подходов, позволяющих изучать основные качественные особенности возбуждаемых волн.
В [7, 14–17] были рассмотрены задачи о генерации полей ВГВ в стратифицированных средах с модельными и реальными распределениями одномерного сдвигового течения. Целью настоящей работы является построение решений, описывающих фазовую структуру полей ВГВ, возбуждаемых осциллирующим источников возмущений в слое стратифицированной среды с двухмерными модельными сдвиговыми течениями. В качестве такого механизма возбуждения ВГВ в океане можно рассматривать, например, генерацию волн периодическим течением на склонах поперечных хребтов в морских проливах [3, 4, 18–20].
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается вертикально стратифицированная среда конечной глубины H. Исходной является линеаризованная система уравнений гидродинамики относительно невозмущенного состояния, которая имеет вид [1, 2, 7]
(1.1)
$\begin{gathered} \frac{{\mathop D\nolimits^2 }}{{Dt{}^{2}}}\left( {\Delta + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)W - \frac{D}{{Dt}}\left( {\frac{{{{d}^{2}}U}}{{dz{}^{2}}}\frac{\partial }{{\partial x}} + \frac{{{{d}^{2}}V}}{{dz{}^{2}}}\frac{\partial }{{\partial y}}} \right)W + {{N}^{2}}(z)\Delta W = \frac{D}{{Dt}}\left( {\frac{\partial }{{\partial z}}\left( {\frac{{DQ}}{{Dt}}} \right)} \right) \\ \Delta = \frac{{{{\partial }^{2}}}}{{\partial x{}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}},\quad {{N}^{2}}(z) = - \frac{g}{{{{\rho }_{0}}(z)}}\frac{{d{{\rho }_{0}}(z)}}{{dz}} \\ \end{gathered} $Далее используются следующие предположения. Рассматривается гармонический источник возмущений интенсивности q, расположенный на горизонте ${{z}_{0}}$: $Q(x,y,z,{{z}_{0}},t)$ = $q{\text{exp}}(i\omega t)\delta (x)\delta (z)$(z – z0). Частота плавучести предполагается постоянной: $N(z) = N = \operatorname{const} $. Предполагается также, что выполнено условие устойчивости Майлса–Ховарда для числа Ричардсона [1, 2, 21]: $Ri = {{N}^{2}}{\text{/}}\left( {{{{\left( {\frac{{dU}}{{dz}}} \right)}}^{2}} + {{{\left( {\frac{{dV}}{{dz}}} \right)}}^{2}}} \right)$ > 1/4. Так как при наличии фоновых сдвиговых течений ВГВ взаимодействуют с этими течениями и обмениваются с ними энергией, то собственные волновые колебания могут быть экспоненциально нарастающими [1, 12, 22, 23]. Поэтому необходимо, чтобы вертикальный градиент фоновых сдвиговых течений был невелик по сравнению с частотой плавучести. Если выполнено условие Майлса–Ховарда, то соответствующая спектральная задача не имеет комплексных собственных значений [1, 13, 24, 25]. Характерные значения чисел Ричардсона в реальных океанических условиях при отсутствии динамической неустойчивости фоновых сдвиговых течений могут находиться в интервалах от 2 до 20 [3, 4, 18–20]. Функции $U(z),$ $V(z)$ – линейные: $U(z) = {{U}_{0}} + ({{U}_{0}} - {{U}_{H}})z{\text{/}}H$, $V(z) = {{V}_{0}} + ({{V}_{0}} - {{V}_{H}})z{\text{/}}H$, ${{U}_{0}} = U(0),$ ${{U}_{H}} = U( - H)$, ${{V}_{0}} = V(0),$ ${{V}_{H}} = V( - H)$. В безразмерных переменных $x{\kern 1pt} * = \pi x{\text{/}}H,$ $y{\kern 1pt} * = \pi y{\text{/}}H,$ $z{\kern 1pt} * = \pi z{\text{/}}H,$ $W{\kern 1pt} * = W{{H}^{2}}{\text{/}}{{\pi }^{2}}q$, $\omega {\kern 1pt} * = \omega {\text{/}}N,$ t* = tN, ${{M}_{x}}(z{\kern 1pt} *)$ = $\pi U(z{\kern 1pt} *){\text{/}}NH = {{a}_{x}} + {{b}_{x}}z{\kern 1pt} *,$ ${{a}_{x}} = \pi {{U}_{0}}{\text{/}}NH,$ ${{b}_{x}} = ({{U}_{0}} - {{U}_{H}}){\text{/}}NH$, My(z*) = = $\pi V(z{\kern 1pt} *){\text{/}}NH = {{a}_{y}} + {{b}_{y}}z{\kern 1pt} *,$ ${{a}_{y}} = \pi {{V}_{0}}{\text{/}}NH,$ ${{b}_{y}} = ({{V}_{0}} - {{V}_{Н}}){\text{/}}NH$ (индекс “*” далее опускается) уравнение (1.1) имеет вид
(1.2)
$\begin{gathered} \frac{{{{D}^{2}}}}{{Dt{}^{2}}}\left( {\Delta + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)W + {{N}^{2}}(z)\Delta W = \frac{D}{{Dt}}\left( {\frac{\partial }{{\partial z}}\left( {\frac{D}{{Dt}}(\exp (i\omega t)\delta (x)\delta (z)\delta (z - {{z}_{0}}))} \right)} \right) \\ \frac{D}{{Dt}} = \frac{\partial }{{\partial t}} + {{M}_{x}}\frac{\partial }{{\partial x}} + {{M}_{y}}\frac{\partial }{{\partial y}} \\ W = 0\quad {\text{при}}\quad z = 0, - \pi \\ \end{gathered} $Параметр $b = \sqrt {b_{x}^{2} + b_{y}^{2}} $ есть величина, обратная квадратному корню из числа Ричардсона: $b = 1{\text{/}}\sqrt {Ri} $. Условие устойчивости Майлса–Ховарда означает, что $\left| b \right| < 2$. Параметр $a = \sqrt {a_{x}^{2} + a_{y}^{2}} $ определяет отношение модуля скорости течения на поверхности $\sqrt {U_{0}^{2} + V_{0}^{2}} $ к максимальной групповой скорости распространения ВГВ в стратифицированной среде конечной глубины, равной $NH{\text{/}}\pi $ [2, 6].
Решение (1.2) ищется в виде [7, 14, 15]
(1.3)
$\begin{gathered} {{(\omega - f(z))}^{2}}\frac{{\mathop \partial \nolimits^2 \varphi }}{{\partial \mathop z\nolimits^2 }} + k_{2}^{{}}(1 - \mathop {(\omega - f(z))}\nolimits^2 )\varphi = \Pi \\ \Pi = {{(\omega - f(z))}^{2}}\delta {\kern 1pt} '(z - {{z}_{0}}) - f{\kern 1pt} '(z)(\omega - f(z))\delta (z - {{z}_{0}}) \\ \varphi (\omega ,\mu ,\nu , - \pi ) = \varphi (\omega ,\mu ,\nu ,0) = 0,\quad {{k}^{2}} = {{\mu }^{2}} + {{\nu }^{2}},\quad f(z) = \mu {{M}_{x}}(z) + \nu {{M}_{y}}(z) \\ \end{gathered} $Решения для источников более общего вида определяются соответствующей сверткой [2, 6, 7].
2. СВОЙСТВА РЕШЕНИЙ КРАЕВОЙ ЗАДАЧИ
В общем случае аналитическое исследование краевой задачи (1.3) представляет значительную математическую трудность, и для произвольных распределений $N(z),\;V(z),\;U(z)$ возможно только ее численное решение [1, 5–7, 9, 25]. При изучении одномерного модельного сдвигового течения ($V(z) = 0$, ${{M}_{y}}(z) = 0$) аналитическое решение краевой задачи (1.3) с нулевой правой частью выражается через модифицированные функции Бесселя мнимого индекса [7, 16, 17]:
Фазовая структура дальних полей ВГВ, генерируемых точечным источником возмущений в стратифицированной среде со сдвиговыми течениями, зависит от поведения стационарных точек фазовой функции $S = t(\mu \mathop V\nolimits_x + \nu \mathop V\nolimits_y - \mathop \omega \nolimits_n (\mu ,\nu ))$, которые определяются из решения системы уравнений [6, 7]: ${{V}_{x}} = x{\text{/}}t = \frac{{\partial \mathop \omega \nolimits_n (\mu ,\nu )}}{{\partial \mu }},$ ${{V}_{y}} = y{\text{/}}t = \frac{{\partial \mathop \omega \nolimits_n (\mu ,\nu )}}{{\partial \nu }}$. Множество точек на горизонтальной плоскости $(x,y)$, для которых существуют решения этой системы уравнений, определяет для каждой отдельной моды ВГВ пространственную зону, внутри которой волновое поле осциллирует, вне этой зоны при больших временах волновое поле экспоненциально мало. Поведение волнового поля на границах волновой зоны определяется аналитическими свойствами дисперсионных соотношений.
Для реальных распределений частоты плавучести и фоновых сдвиговых течений волновая зона может быть ограничена двумя замкнутыми кривыми: передним и задним фронтом. Передний волновой фронт определяется асимптотикой поведения дисперсионных соотношений при малых волновых числах. Задний волновой фронт зависит от характера асимптотик дисперсионных соотношений при больших волновых числах. При отсутствии течений передний фронт – окружность с радиусом Ct, где C – максимальная групповая скорость отдельной волновой моды, а задний фронт стягивается в начало координат. Максимальная групповая скорость ВГВ в стратифицированной среде без учета наличия сдвиговых течений и вращения достигается при $k = 0$ [2, 6, 7].
Для данного модельного линейного двухмерного распределения сдвигового течения возможно построить асимптотики собственных функций ${{\varphi }_{n}}(\mu ,\nu ,z)$ и собственных значений $\mathop \omega \nolimits_n (\mu ,\nu )$спектральной задачи (1.3) с нулевой правой частью при малых волновых числах. Введем полярные координаты: $\mu = k\cos \psi ,$ $\nu = k\sin \psi $. В результате из (1.3) можно получить
(2.1)
$\begin{gathered} {{(\mathop \xi \nolimits_n - (a + bz))}^{2}}\frac{{{{\partial }^{2}}{{\varphi }_{n}}}}{{\partial {{z}^{2}}}} + (1 - {{k}^{2}}{{(\mathop \xi \nolimits_n - (a + bz))}^{2}}){{\varphi }_{n}} = 0 \\ {{\varphi }_{n}} = 0\quad {\text{при}}\quad z = 0, - \pi \\ \end{gathered} $Тогда для определения функций $\varphi _{n}^{0}(\psi ,z)$, $\xi _{n}^{0}(\psi )$ можно получить
(2.2)
$\begin{gathered} {{(\xi _{n}^{0} - (a + bz))}^{2}}\frac{{{{\partial }^{2}}\varphi _{n}^{0}}}{{\partial {{z}^{2}}}} + \varphi _{n}^{0} = 0 \\ \varphi _{n}^{0}(\psi ,0) = \varphi _{n}^{0}(\psi , - \pi ) = 0 \\ \end{gathered} $Общее решение (2.2) имеет вид: $\varphi _{n}^{0} = \sqrt \xi ({{C}_{1}}{\text{cos}}(B{\text{ln}}\left| \xi \right|) + {{C}_{2}}{\text{sin}}(B{\text{ln}}\left| \xi \right|))$, где $\xi = \xi _{n}^{0} - (a + bz)$, $B = \sqrt {1{\text{/}}{{b}^{2}} - 1{\text{/}}4} $ (в силу условия Майлса–Ховарда $\left| b \right| < 2$). Значения C1, 2 определяются из граничных условий. В результате можно получить: $\xi _{n}^{0}(\psi ) = a + \pi b{\text{/}}D$, $D = \exp (sign(b)\pi n{\text{/}}B) - 1$, $n = \pm 1, \pm 2$, ... . Таким образом, при малых волновых числах собственные значения спектральной задачи (1.3) в первом приближении имеют вид: ${{\omega }_{n}}(k) = (a + \pi b{\text{/}}D)k + O({{k}^{3}})$.
3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ
Собственные значения краевой задачи (1.3) можно представить в виде ${{\omega }_{n}}(\mu ,\nu )$ или ${{\mu }_{n}}(\nu ,\omega )$. Далее рассматриваются дисперсионные зависимости ${{\mu }_{n}}(\nu )$($\omega $ – фиксированный параметр). В использованных моделях линейных двухмерных сдвиговых течений параметр a < 1, это означает, что амплитуды скорости сдвиговых течений на поверхности не превышают (по порядку величины) максимальной групповой скорости распространения ВГВ, что наблюдаемо в условиях Мирового океана [3, 4, 18–20]. Параметр $\omega $ определяет отношение частоты свободной волны к значению частоты плавучести, и в численных расчетах использовались типичные значения этого параметра, наблюдаемые при измерении ВГВ в реальных океанических условиях [3, 4, 18–20].
В настоящей работе используется гидрологическая модель двумерного линейного сдвигового течения, в том числе с возможностью изменения течением своего направления с увеличением глубины. Это означает, в частности, что выбрав соответствующую систему координат можно, без ограничения общности, рассматривать постоянную и линейную зависимости компонент сдвигового течения от глубины. Действительно, пусть $(U{\kern 1pt} '(z),V{\kern 1pt} '(z))$ – компоненты вектора скорости сдвигового течения в системе координат $Ox{\kern 1pt} 'y{\kern 1pt} '$, которая получается из исходной системы координат $Oxy$ поворотом на некоторый угол $\alpha $ относительно начала координат. Тогда в новой системе координат компоненты вектора сдвигового течения можно представить в виде
Выбирая угол поворота $\alpha $ таким образом, что $tg\alpha = - {{b}_{x}}{\text{/}}{{b}_{y}}$, можно получить: $bx{\kern 1pt} ' = 0$, и, соответственно, если $tg\alpha = {{b}_{y}}{\text{/}}{{b}_{x}}$, то $by{\kern 1pt} ' = 0$.
На рис. 1 представлены результаты расчетов дисперсионных кривых $\mu (\nu )$ для различных значений частоты $\omega $ и параметров течения: линии 1–6 – $\omega = $ 0.125, 0.25, 0.5, 0.75, 1.0, 1.25. Здесь и далее все расчеты приведены для первой волновой моды, индекс n опущен. Исходя из многочисленных результатов океанологических наблюдений фоновых сдвиговых течений в различных акваториях Мирового океана [3, 4, 18–20], для численных расчетов использовались следующие модельные распределения двухмерного сдвигового течения по глубине – функций $U(z),\;V(z)$: $U(z) = 2\pi {\text{/}}15$ (рис. 1а, б, 2–4), $U(z) = 6\pi {\text{/}}15$ (рис. 1в, г, 5–6), $V(z) = 2\pi {\text{/}}15 + 0.2z$ (рис. 1–6).
Рис. 1.
Нижние (а, в) и верхние (б, г) ветви дисперсионной кривой: 1–6 – $\omega = $ 0.125, 0.25, 0.5, 0.75, 1.0, 1.25; $U(z) = 2\pi {\text{/}}15$ (а, б), $U(z) = 6\pi {\text{/}}15$ (в, г), $V(z) = 2\pi {\text{/}}15 + 0.2z$ (а, б, в, г).
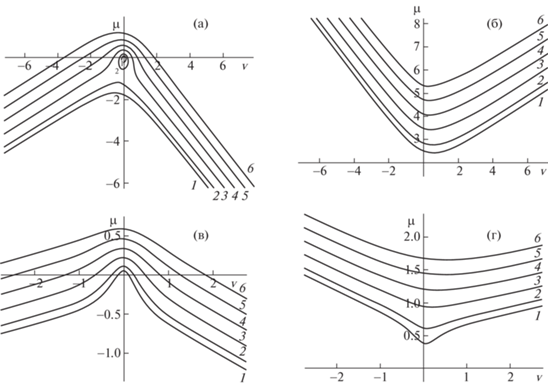
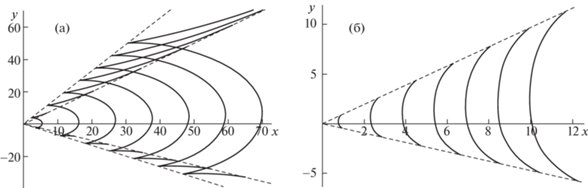
Рис. 2.
Линии равной фазы $S = 2\pi k$ для нижней (а) и верхней (б) ветвей: $k = - 3, - 2,..,5$ (а), $k = - 2, - 1,..,2$ (б).
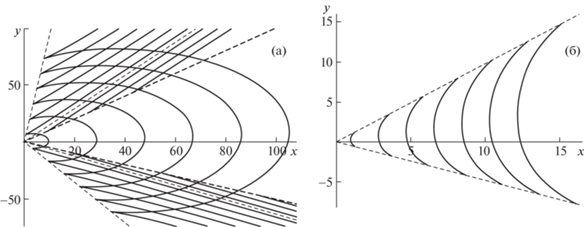
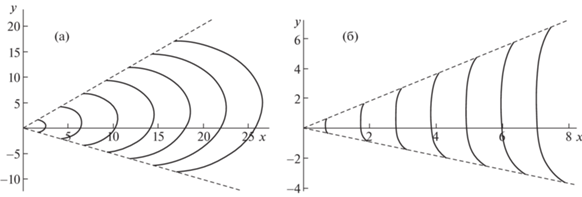
Рис. 5.
Линии равной фазы $S = 2\pi k$ для нижней (а) и верхней (б) ветвей: $k = 0,1,..,7$ (а), $k = - 2, - 1,..,2$ (б).
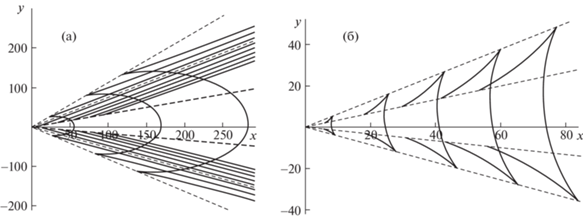
На рис. 2–6 изображены результаты расчетов линий равной фазы, которые имеют вид параметрического (с параметром $\nu $) семейства кривых
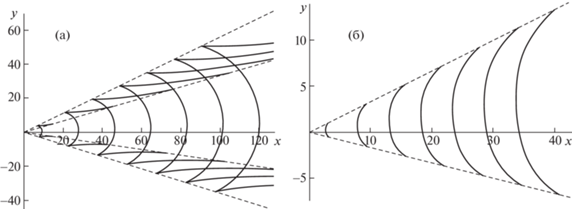
Значения параметров для численных расчетов были следующие: $\omega = 0.45,$ $t = 35$ (рис. 2), $\omega = 0.75,$ $t = 21$ (рис. 3, 6), $\omega = 1.5,$ $t = 11$ (рис. 4), $\omega = 0.125,$ $t = 125$ (рис. 5). Сплошные линии на рис. 2–6 – линии равной фазы, штриховые линии – волновые фронты.
Численные расчеты показывают, что двухмерность сдвиговых течений является причиной заметной асимметрии дисперсионных зависимостей $\mu (\nu )$ относительно оси $O\mu $. Различный характер поведения функций $\mu (\nu )$ при $\nu \to \pm \infty $ может приводить к появлению дополнительных волновых фронтов. Каждая дисперсионная кривая при фиксированных значениях параметра $\omega $ состоит из нескольких ветвей: нижней и верхней. Значения $\mu (\nu )$ на верхней ветви всегда больше нуля, и эта ветвь представляет собой одну разомкнутую линию с одним минимумом, причем значение этого минимума уменьшается при уменьшении параметра $\omega $. Значения $\mu (\nu )$ на нижней ветви могут быть как положительные, так и отрицательные, и эта ветвь может состоять как из одной, так и двух линий. При относительно небольших значениях параметра $\omega $ нижняя ветвь может состоять из одной замкнутой и одной разомкнутой кривой. Далее, по мере увеличения частоты $\omega $ происходит качественная перестройка этих двух кривых, и при некотором значении $\omega $ ветви могут сливаться, образуя одну омега-образную линию, отвечающую многозначности функции $\mu (\nu )$для определенных интервалов значений $\nu $. По мере увеличении параметра $\omega $ происходит размыкание замкнутых кривых, и нижние ветви дисперсионных кривых становятся однозначными функциями переменной $\nu $.
Двухмерность сдвиговых течений является причиной заметной пространственной (относительно оси Ox) асимметрии линий равной фазы. Генерируемая волновая система состоит из волн двух типов: кольцевых (поперечных) и клиновидных (продольных). Кольцевые (поперечные) волны занимают все пространственную область внутри волнового клина с углом раствора $\gamma $ (γ = = ${\text{|}}arctg(\mu {\kern 1pt} '(\nu _{1}^{*})) - arctg(\mu {\kern 1pt} '(\nu _{2}^{*})){\text{|}}$, где $\nu _{{1,2}}^{*}$ – корни уравнения $\mu {\kern 1pt} '{\kern 1pt} '(\nu ) = 0$ для рис. 2а, 3а, 5а, б, 6а, и $\nu _{{1,2}}^{*} = \pm \infty $ для рис. 2б, 3б, 4а, б, 6б и могут иметь форму вогнутых (рис. 3а, 4а, 5а, б, 6а) или выпуклых (рис. 2б, 3б, 4б, 6б) дуг. Клиновидные (продольные) волны каждой моды ограничены как волновым фронтом с углом раствора $\gamma $, так и одной (рис. 3а, 5б, 6а) или двумя (рис. 2а, 5а) парами внутренних волновых фронтов. Внутренние фронты на рис. 3а, 5б, 6а, а также внутренняя пара из двух пар внутренних фронтов на рис. 2а, 5а задаются уравнениями $y = - \mu {\kern 1pt} '( \pm \infty )x$. Внешняя пара из двух пар волновых фронтов на рис. 2а, 5а (т.е. средняя пара из трех пар фронтов) определяется уравнениями $y = - \mu {\kern 1pt} '({{\nu }_{{1,2}}})x$), где ν1, 2 – корни уравнения $\mu {\kern 1pt} '(\nu ) = \mu (\nu ){\text{/}}\nu $.
ЗАКЛЮЧЕНИЕ
Решена задача о генерации полей внутренних гравитационных волн, возбуждаемых осциллирующим источником возмущений в конечном слое стратифицированной среды с двумерными модельными линейными сдвиговыми течениями в предположении постоянства частоты плавучести. Построены асимптотики дисперсионных зависимостей при малых волновых числах. Численно исследованы дисперсионные соотношения и фазовые картины возбуждаемых волновых полей для различных режимов волновой генерации, характерных для реальных условий Мирового океана. Показано, что учет двухмерности сдвиговых течений является причиной заметной асимметрии как дисперсионных кривых, так и линий равной фазы. Аналитические оценки и численные результаты показывают, что асимптотические конструкции, использующие модельные представления частоты плавучести и сдвиговых скоростей качественно верно могут описывать фазовую структуру ВГВ.
Асимптотики дисперсионных соотношений позволяют в дальнейшем исследовать более реалистичную задачу изучения динамики ВГВ в океане медленноменяющимися и нестационарными параметрами. В этом случае решение можно представить в виде суммы волновых пакетов, фазовая структура которых определяется аналитическими свойствами соответствующих дисперсионных зависимостей. Конкретный выбор фазовой функции (модельных интегралов) определяется аналитическими свойствами дисперсионных соотношений, зависящих от реальной гидрологии океана. Аналитические выражения дисперсионных кривых также могут использоваться, в частности, для качественной интерпретации наблюдаемых волновых явлений в океане и для разработки дистанционных методов обнаружения ВГВ методами радиолокации.
Полученные результаты дают возможность эффективно рассчитывать фазовую структуру волновых полей, а также исследовать различные режимы волновой генерации для модельных представлений частоты плавучести и сдвиговых течений.
Работа выполнена по темам государственного задания: В.В. Булатов (№ АААА-А20-120011690131-7), И.Ю. Владимиров (№ FMWE-2021-0002) и частичной финансовой поддержке РФФИ проект № 20-01-00111А.
Список литературы
Fabrikant A.L., Stepanyants Yu.A. Propagation of waves in shear flows. World Scientific Publishing, 1998. 304 p.
Miropol’skii Yu.Z., Shishkina O.V. Dynamics of internal gravity waves in the ocean. Kluwer Academic Publishers, Boston, 2001. 406 p.
Morozov E.G. Oceanic internal tides. Observations, analysis and modeling. Berlin: Springer, 2018. 317 p.
Velarde M.G., Tarakanov R.Yu., Marchenko A.V. (Eds.). The ocean in motion. Springer Oceanography. Springer International Publishing AG, 2018. 625 p.
Vlasenko V., Stashchuk N., Hutter K. Baroclinic tides. N.Y.: Cambridge University Press, 2005. 372 p.
Булатов В.В., Владимиров Ю.В. Волны в стратифицированных средах. М.: Наука, 2015. 735 с.
Булатов В.В. Новые задачи математического моделирования волновой динамики стратифицированных сред. М.: Изд-во “ОнтоПринт”, 2021. 277 с.
Young W.R., Phines P., Garret C.J.R. Shear flows dispersion, internal waves and horizontal mixing // J. Phys. Oceanography, 1982. V. 2(6). P. 515–527.
Bouruet-Aubertot P.I., Thorpe S.A. Numerical experiments of internal gravity waves an accelerating shear flow // Dyn. Atm. Oceans. 1999. V. 29. P. 41–63.
Meunier P., Dizиs S., Redekopp L., Spedding G. Internal waves generated by a stratified wake: experiment and theory // J. Fluid Mech. 2018. V. 846. P. 752–788.
Fraternale F., Domenicale L., Staffilan G.,Tordella D. Internal waves in sheared flows: lower bound of the vorticity growth and propagation discontinuities in the parameter space // Phys. Rev. 2018. V. 97. № 6. P. 063102.
Slepyshev A.A., Vorotnikov D.I. Generation of vertical fine structure by internal waves in a shear flows // Open J. Fluid Mechanics, 2019. V. 9. P. 140–157.
Howland C.J., Taylor J.R., Caulfield C.P. Shear-induces breaking of internal gravity waves // J. Fluid Mechanics. 2021. V. 921. A24.
Булатов В.В., Владимиров Ю.В., Владимиров И.Ю. Внутренние гравитационные волны от осциллирующего источника возмущений в океане // Изв. РАН. ФАО. 2021. Т. 57. № 3. С. 362–373.
Булатов В.В., Владимиров Ю.В., Владимиров И.Ю. Фазовые характеристики полей внутренних гравитационных волн в океане со сдвигом скорости течений // Морск. гидрофиз. журн. 2021. Т. 37. № 4. С. 473–489.
Bulatov V.V., Vladimirov Yu.V. Dynamics of internal gravity waves in the ocean with shear flows // Russ. J. Earth Sciences. 2020. V. 20. ES4004
Булатов В.В., Владимиров Ю.В. Внутренние гравитационные волны в стратифицированной среде с модельными распределениями сдвиговых течений // Изв. РАН. МЖГ. 2020. № 5. С. 56–60.
Morozov E.G., Tarakanov R.Yu., Frey D.I., Demidova T.A., Makarenko N.I. Bottom water flows in the tropical fractures of the Northern Mid-Atlantic Ridge // J. Oceanography. 2018. V. 74 (2). P. 147–167.
Frey D.I., Novigatsky A.N., Kravchishina M.D., Morozov E.G. Water structure and currents in the Bear Island Trough in July-August 2017 // Russ. J. Earth Sciences. 2017. V. 17. ES3003.
Khimchenko E.E., Frey D.I., Morozov E.G. Tidal internal waves in the Bransfield Strait, Antarctica // Russ. J. Earth. Science. 2020. V. 20. ES2006.
Miles J.W. On the stability of heterogeneous shear flow // J. Fluid Mech. 1961. V. 10 (4). P. 495–509.
Hirota M., Morrison P.J. Stability boundaries and sufficient stability conditions for stably stratified, monotonic shear flows // Phys. Letters A. 2016. 380 (21). P. 1856–1860.
Churilov S. On the stability analysis of sharply stratified shear flows // Ocean Dynamics. 2018. 68. P. 867–884.
Carpenter J.R., Balmforth N.J., Lawrence G.A. Identifying unstable modes in stratified shear layers. // Phys. Fluids. 2010. 22. P. 054104.
Gavrileva A.A., Gubarev Yu.G., Lebedev M.P. The Miles theorem and the first boundary value problem for the Taylor–Goldstein equation // J. Appl. Industrial Math. 2019. 13 (3). P. 460–471.
Найфэ А. Введение в методы возмущений. М: Мир, 1984. 536 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа