Известия РАН. Механика жидкости и газа, 2022, № 3, стр. 56-64

ЛИНЕЙНАЯ УСТОЙЧИВОСТЬ ФИЛЬТРАЦИОННОГО ТЕЧЕНИЯ С ПОВЕРХНОСТЬЮ РАЗДЕЛА ГАЗ–НЕФТЬ В РАМКАХ ПОДХОДА БРИНКМАНА

Г. Г. Цыпкин^a, *, В. А. Шаргатов^a, **

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^* E-mail: tsypkin@ipmnet.ru
^** E-mail: shargatov@mail.ru

Поступила в редакцию 28.11.2021
После доработки 21.12.2021
Принята к публикации 21.12.2021

EDN: LNTVIJ
DOI: 10.31857/S056852812203015X

Аннотация

Рассматривается задача об устойчивости вертикального течения в нефтяном коллекторе с газовой шапкой, когда движение нефти подчиняется уравнению Бринкмана. Выведены граничные условия на подвижной границе газонефтяного контакта и получено базовое решение. Методом нормальных мод исследована устойчивость поверхности раздела газ–нефть. Проведено исследование полученного дисперсионного соотношения. Найдены условия устойчивости течения при всех значениях параметров и показано, что в линейном приближении скорость роста коротковолновых возмущений стремится к нулю при возрастании волнового числа.

Ключевые слова: поверхность раздела газ–нефть, вертикальное течение, уравнение Бринкмана, устойчивость, метод нормальных мод

На нефтяные коллекторы с газовой шапкой приходится значительная доля газовых и нефтяных месторождений [1]. Добыча нефти из таких месторождений обладает определенными особенностями и отличается от разработки чисто нефтяных коллекторов. Так, снижение давления в области, насыщенной нефтью, вызывает движение границы газонефтяного контакта. Движение этой поверхности раздела может быть неустойчивым, что приводит к газовому пробою к добывающей скважине и формированию в пласте и призабойной области неподвижной нефти [2]. В других случаях разрушение в результате неустойчивости поверхности газонефтяного контакта может вызвать дробление потока и формирование остаточной неподвижной нефти в месторождении [3]. На основании этого можно сделать вывод, что определяющим фактором многих процессов является неустойчивость фильтрационных течений.

В последние годы были проведены аналитические и численные исследования неустойчивости поверхностей раздела при фильтрации в геотермальных системах, грунтах и горных породах [4–7]. В этих работах в основе математического описания процесса фильтрации в пористых средах был положен закон Дарси. Найдено, что во многих важных для приложений случаях переход к неустойчивости реализуется для всех значений волнового числа одновременно или при бесконечно больших волновых числах. При этом наиболее быстрорастущей модой неустойчивого течения является мода, соответствующая бесконечно малому линейному размеру. В этом случае можно сделать вывод о неприменимости математической модели, основанной на законе Дарси, для описания как самого перехода к неустойчивости, так и последующего развития течения с разрушением поверхности раздела, приводящим к образованию “пальцев”.

В [8] в рамках теории фильтрации Дарси исследовалась устойчивость поверхности раздела газ–нефть при падении давления в области, насыщенной нефтью. Был найден критерий устойчивости поверхности и показано, что при изменении параметров переход в неустойчивый режим осуществляется одновременно при всех волновых числах. Естественно предположить, что закон Дарси, хорошо описывающий течения с большим характерным масштабом длины, может не всегда давать адекватное математическое описание мелкомасштабных явлений. В этих случаях при исследовании фильтрационных течений вместо закона Дарси предлагается использовать уравнение Бринкмана [9].

Интерес к уравнению Бринкмана, как обобщенной форме уравнения фильтрации Дарси, возник во многом вследствие попыток сформулировать корректные граничные условия на поверхности контакта течения свободной жидкости и течения в пористой среде [10–12]. Свойства уравнения Бринкмана и граничных условий на поверхности контакта свободной жидкости и пористой среды исследовались в работах [13, 14]. Анализ влияния инерционных членов на течение контактирующих свободной жидкости и жидкости в пористой среде в рамках уравнения Бринкмана представлен в [15]. В работе [16] приведены данные экспериментов по устойчивости поверхности раздела между двух смешивающихся жидкостей, проведенных для вертикальной ячейки Хеле-Шоу. Проведено сравнение с результатами исследований линейной устойчивости для течения, подчиняющего уравнению Бринкмана. Устойчивость плоскопараллельного течения свободной жидкости над насыщенной пористой средой рассматривалась в [17]. Дан сравнительный анализ результатов с использованием двух подходов. В одном случае использовалась модель Бринкмана с граничными условиями Очоа-Тапиа–Уитекера, а в другом – уравнения Дарси-Форхгеймера с граничными условиями Биверса-Джозефа.

Эволюция бесконечно малых и конечных локализованных возмущений для движущегося фронта фазового перехода изучалась в [18, 19] в приближении Дарси. Развитие гравитационной неустойчивости в двухслойной жидкости постоянной и переменной вязкости в пористой среде численно исследовалось в [20, 21] также с использованием закона Дарси. Уравнение Бринкмана использовалось в [22] для моделирования течения микрополярной жидкости в пористой среде.

В настоящей работе в рамках обобщенного уравнения фильтрации Бринкмана проведено исследование устойчивости контактной поверхности газ–нефть при понижении давления в области, насыщенной нефтью.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим движение нефти в пористой среде для случая, когда горизонтальный пласт, насыщенный нефтью, сверху граничит с газовой шапкой, а снизу – с высокопроницаемым пропластком или трещиной. Предполагается, что движение нефти описывается обобщенным уравнением фильтрации Бринкмана. Пусть нижняя граница пласта имеет вертикальную декартову координату z = 0, а верхняя – z = L. Бесконечный в горизонтальном измерении пласт включает в себя область Ω_f, содержащую нефть при 0 < z < S(x, t) и область Ω_g с координатами S(x, t) < z < L, насыщенную газом. Считаем, что объем газа достаточно большой и можно пренебречь его движением и считать давление в нем постоянным. Тогда на контактной поверхности газ–нефть z < S(x, t) давление постоянно и равно P_G. Растворением газа в нефти и дегазацией нефти пренебрегаем. При откачке нефти из высокопроницаемого пропластка, соответствующего границе z = 0, можно считать, что давление в нем изменяется мгновенно на всем протяжении и равно постоянной величине P_F.

Нефть предполагается несжимаемой и ее движение описывается уравнением Бринкмана с учетом силы тяжести

(1.1)

$div\overrightarrow V = 0$

(1.2)

$ - \nabla \left( {P + \rho gz} \right) + {{\mu }_{e}}\Delta \overrightarrow V - \frac{\mu }{k}\overrightarrow V = 0$

Здесь P – давление, ρ – плотность, g – ускорения свободного падения, μ – вязкость, μ_e – эффективная вязкость, k – проницаемость, ${\kern 1pt} \overrightarrow V $ – вектор скорости фильтрации.

Найдем базовое решение, которое предполагается исследовать на устойчивость. Используем условие несжимаемости жидкости (1.1) и применим операцию дивергенции к уравнению (1.2). В результате получаем уравнение Лапласа для давления

(1.3)

$\Delta {\kern 1pt} P = 0$

Если контактная поверхность нефть–газ является плоской и в момент времени t имеет z-координату H(t) > 0, то уравнению (1.3), а также граничным условиям

(1.4)

$P(x,0,t) = {{P}_{F}},$

(1.5)

$P(x,H(t),t) = {{P}_{G}}$

удовлетворяет решение

(1.6)

${{P}_{b}}(x,z,t) = \frac{{\left( {{{P}_{G}} - {{P}_{F}}} \right)z}}{{H(t)}} + {{P}_{F}}$

Из уравнения (1.2) находим, что

(1.7)

${{V}_{{z,b}}}(x,z,t) = - \frac{k}{\mu }\left( {\frac{{{{P}_{G}} - {{P}_{F}}}}{{H(t)}} + \rho g} \right),$

(1.8)

${{V}_{{x,b}}}(x,z,t) = 0,$

где V_x,b и V_z,b – x - и z-компоненты скорости ${\kern 1pt} \vec {V}$ для базового решения.

Если процессы растворения газа в нефти и дегазации нефти не учитываются, то скорость перемещения контактной поверхности в направлении внешней нормали совпадает с нормальной компонентой скорости фильтрации $\vec {V}(H(t))$, поэтому для базового решения справедливо уравнение

(1.9)

$\frac{{dH(t)}}{{dt}} = - \frac{k}{\mu }\left( {\frac{{{{P}_{G}} - {{P}_{F}}}}{{H(t)}} + \rho g} \right),$

из которого получаем

(1.10)

$t = \frac{\mu }{k}\left( {\frac{{{{P}_{G}} - {{P}_{F}}}}{{{{\rho }^{2}}{{g}^{2}}}}\ln \left( {\frac{{\rho g{{H}_{0}} + {{P}_{F}} - {{P}_{G}}}}{{\rho gH(t) + {{P}_{F}} - {{P}_{G}}}}} \right) - \frac{{H(t) - {{H}_{0}}}}{{\rho g}}} \right),$

где H₀ – z-координата контактной поверхности при t = 0. Соотношение (1.10) определяет неявную функцию H(t).

На поверхности раздела выполняется условие равенства нормальных составляющих напряжений, которое имеет вид

(1.11)

$P(x,s(x,t),t) - 2{{\mu }_{e}}\left( {\frac{\partial }{{\partial n}}{{V}_{n}}(x,z,t)} \right) = {{P}_{G}}$

Здесь V_n – нормальная к поверхности S(x, t) компонента скорости ${\kern 1pt} \overrightarrow V $, $\left( {\frac{{\partial {{V}_{n}}}}{{\partial n}}} \right)$ – производная этой компоненты по направлению нормали к поверхности S(x, t).

Условие для касательного напряжения, которое равно нулю (см., например, [23]), может быть записано в виде

(1.12)

$\frac{\partial }{{\partial n}}{{V}_{\tau }}(x,z,t) + \frac{\partial }{{\partial \tau }}{{V}_{n}}(x,z,t) = 0,$

где V_τ – касательная к поверхности S(x, t) компонента скорости $\overrightarrow V $, $\left( {\frac{\partial }{{\partial n}}{{V}_{\tau }}} \right)$ – производная этой компоненты по направлению нормали, $\left( {\frac{\partial }{{\partial \tau }}{{V}_{n}}} \right)$ – производная нормальной компоненты скорости в направлении касательной.

2. ВЫВОД ДИСПЕРСИОННОГО УРАВНЕНИЯ

Будем искать решение задачи о линейной устойчивости в виде

(2.1)

$S(x,t) = H(t) + s(x,t)$

(2.2)

$P(x,z,t) = {{P}_{b}}(x,z,t) + p(x,z,t)$

(2.3)

${{V}_{x}}(x,z,t) = u(x,z,t),$

(2.4)

${{V}_{z}}(x,z,t) = {{V}_{{z,b}}}(x,z,t) + {v}(x,z,t),$

где p(x, z, t), u(x, z, t), ${v}$(x, z, t), s(x, t) – малые возмущения давления, горизонтальной и вертикальной компонент скорости, а также положения границы раздела нефть–газ соответственно.

В силу линейности уравнения (1.3) для p(x, z, t) справедливо уравнение

(2.6)

$\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}p(x,z,t) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}p(x,z,t) = 0$

Будем искать решение для p(x, z, t) в виде

$p(x,z,t) = \Pi (z)f(t)\exp (iKx),$

тогда из уравнения (2.6) получаем

(2.7)

$ - {{K}^{2}}\Pi (z) + \frac{{{{d}^{2}}}}{{d{{z}^{2}}}}\Pi (z) = 0$

Общее решение уравнения (2.7) запишем как

(2.8)

$\Pi (z) = {{C}_{1}}\exp (Kz) + {{C}_{2}}\exp ( - Kz)$

С учетом того, что возмущения возникают на свободной поверхности и затухают на нижней границе низкопроницаемого слоя, вторым слагаемым в правой части выражения (2.8) можно пренебречь, тогда

(2.9)

$\Pi (z) = {{C}_{1}}\exp (Kz)$

Решение для u(x, z, t) и ${v}$(x, z, t) будем искать в виде

(2.10)

$u(x,z,t) = U(z)f(t)\exp (iKx)$,

(2.11)

${v}(x,z,t) = V(z)f(t)\exp (iKx)$

Подставляя (2.2), (2.3) и (2.4) в уравнение (1.2), с учетом (2.9), (2.10) и (2.11) получаем

(2.12)

$U(z) = - ic{{C}_{1}}K{{e}^{{Kz}}} - {{K}^{2}}U(z){{m}_{e}} + \left( {\frac{{{{d}^{2}}}}{{d{{z}^{2}}}}U(z)} \right){{m}_{e}}$

(2.13)

$V(z) = - c{{C}_{1}}K{{e}^{{Kz}}} - {{K}^{2}}V(z){{m}_{e}} + \left( {\frac{{{{d}^{2}}}}{{d{{z}^{2}}}}V(z)} \right){{m}_{e}}$

где $c = k{\text{/}}\mu $, ${{m}_{e}} = с{{\mu }_{e}}$.

Для общего решения уравнения (2.12)

$U(z) = - ic{{C}_{1}}K\exp (Kz) + {{C}_{3}}\exp ( - \sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z) + {{C}_{4}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z)$

также при достаточно большой толщине нефтесодержащего пласта можно пренебречь членом в правой части, который убывает при увеличении z и записать решение в виде

(2.14)

$U(z) = - ic{{C}_{1}}K\exp (Kz) + {{C}_{u}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z)$

Аналогично из уравнения (2.13) получаем:

(2.15)

$V(z) = - c{{C}_{1}}K\exp (Kz) + {{C}_{{v}}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z)$

Из условия несжимаемости жидкой фазы (1.1) следует, что

(2.16)

$\frac{\partial }{{\partial x}}u(x,z,t) + \frac{\partial }{{\partial z}}{v}(x,z,t) = 0$

Воспользовавшись соотношениями (2.10) и (2.11), из уравнения (2.16) получаем, что

(2.17)

$iKU(z) + \frac{d}{{dz}}V(z) = 0$

Подставляя (2.14) и (2.15) в уравнение (2.17), находим уравнение, связывающее коэффициенты C_u и ${{C}_{{v}}}$:

(2.18)

$i{{C}_{u}}K\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z) + {{C}_{{v}}}\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} \exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z) = 0$

Из (2.18) получаем

(2.19)

${{C}_{u}} = i\frac{{\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} }}{K}{{C}_{{v}}}$

Линеаризованное уравнение получено из (1.11) в предположении того, что

(2.20)

$s(x,t) = {{C}_{\eta }}f(t){{e}^{{iKx}}}$

и выполняется условие ∂s/∂x $ \ll $ 1, имеет вид

(2.21)

$\begin{gathered} {{C}_{1}}(2{{K}^{2}} + 1{\text{/}}{{m}_{e}})\exp (KH(t)) + {{C}_{\eta }}\frac{{{{P}_{G}} - {{P}_{F}}}}{H} - \\ - \;{{C}_{{v}}}\frac{{2\sqrt {{{m}_{e}}} }}{c}\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} \exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t)) = 0 \\ \end{gathered} $

В линейном приближении нормальная скорость контактной поверхности может быть найдена из уравнения

(2.22)

${{C}_{{v}}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t)) - c{{C}_{1}}K\exp (KH(t)) - {{C}_{\eta }}\frac{{f{\kern 1pt} {\text{'}}(t)}}{{f(t)}} = 0$

Из уравнения (1.12) в линейном приближении получаем

(2.23)

$\frac{\partial }{{\partial z}}u(x,z,t) + \frac{\partial }{{\partial x}}{v}(x,z,t) = 0$

Используя соотношения (2.14), (2.15) и (2.19), преобразуем уравнение (2.23) к виду

(2.24)

$\left( {\frac{i}{K}({{K}^{2}} + 1{\text{/}}{{m}_{e}}) + iK} \right)\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t)){{C}_{{v}}} - 2ic{{C}_{1}}{{K}^{2}}\exp (KH(t)) = 0$

и получаем однородную систему уравнений (2.21), (2.22) и (2.24) относительно неизвестных C₁, ${{C}_{{v}}}$, C_η. Система имеет нетривиальное решение, если детерминант матрицы коэффициентов равен нулю

(2.25)

$Det \equiv \left| {\begin{array}{*{20}{c}} {(2{{K}^{2}} + 1){{e}_{k}}}&{ - \frac{2}{c}2\sqrt {{{m}_{e}}} {{f}_{k}}{{e}_{H}}}&{\frac{{{{P}_{G}} - {{P}_{F}}}}{{H(t)}}} \\ { - cK{{e}_{k}}}&{{{e}_{H}}}&{ - \frac{{f{\text{'}}(t)}}{{f(t)}}} \\ { - 2ic{{e}_{k}}{{K}^{2}}}&{\frac{{if_{k}^{2}{{e}_{H}}}}{{{{m}_{e}}K}} + iK{{e}_{H}}}&0 \end{array}} \right| = 0$

Здесь ${{e}_{H}} = \exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t))$, ${{e}_{K}} = \exp \left( {KH(t)} \right)$, ${{f}_{k}} = \sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} $.

Из (2.25) находим

$\frac{{f{\kern 1pt} {\text{'}}(t)}}{{f(t)}} = - \frac{{Kc({{P}_{G}} - {{P}_{F}})({{K}^{2}}{{m}_{e}} - {{f}_{k}})}}{{H(t)(2{{K}^{4}}m_{e}^{2} - 4{{k}^{3}}m_{e}^{{3/2}}{{f}_{k}} + 2{{K}^{2}}f_{k}^{2}{{m}_{e}} + {{K}^{2}}{{m}_{e}} + f_{k}^{2})}}$

или

(2.26)

$\frac{{f{\kern 1pt} {\text{'}}(t)}}{{f(t)}} = \frac{{Kc({{P}_{G}} - {{P}_{F}})}}{{H(t)(2{{K}^{4}}m_{e}^{2} - 4{{k}^{3}}m_{e}^{{3/2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} + 2{{K}^{2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} {{m}_{e}} + 2{{K}^{2}}{{m}_{e}} + 1)}}$

3. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ТЕЧЕНИЯ

Если эффективная вязкость μ_e равна нулю, соответственно m_e = 0, то из дисперсионного соотношения (2.26) следует, что в приближении Дарси это соотношение приводится к виду

(3.1)

$\frac{{f{\kern 1pt} {\text{'}}(t)}}{{f(t)}} = \frac{{Kc\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{{H(t)}}$

Условие затухания возмущений на контактной границе, следующее из соотношения (3.1), совпадает с условием, которое получается при использовании закона Дарси [6, 7]. В случае неустойчивости, когда P_G > P_F, скорость роста амплитуды возмущений неограниченно увеличивается с ростом волнового числа K → ∞.

Рассмотрим поведение$f{\kern 1pt} {\text{'}}(t)$ при неограниченном росте волнового числа K → ∞, когда m_e ≠ 0. Из формулы (2.26) получаем

(3.2)

$\frac{{f{\kern 1pt} {\text{'}}(t)}}{{f(t)}} \approx \frac{{c\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{{2{{m}_{e}}H(t)K}}$

Следовательно, в приближении Бринкмана скорость затухания или роста коротковолновых возмущений стремится к нулю при K → ∞, как в устойчивом (P_F > P_G), так и в неустойчивом случае (P_F < P_G).

Если воспользоваться условием квазистационарности процесса, которое следует из того, что характерное время движения границы газонефтяного контакта много больше характерного времени перераспределения давления, то можно пренебречь зависимостью H от t в правой части уравнения (2.26) и полагать, что поверхность раздела неподвижна. Аналогичные условия квазистационарности справедливы для многих задач теории фильтрации с поверхностями разрывов [3, 24]. Тогда

$f(t) = \exp (\sigma t)$

и соотношения (2.26), (3.1) и (3.2) принимают вид

(3.3)

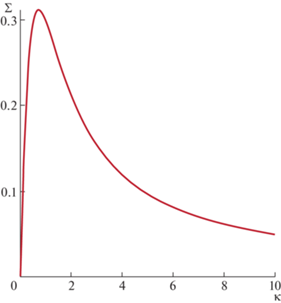
$\sigma = \frac{{Kc({{P}_{G}} - {{P}_{F}})}}{{H(2{{K}^{4}}m_{e}^{2} - 4{{k}^{3}}m_{e}^{{3/2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} + 2{{K}^{2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} {\kern 1pt} {{m}_{e}} + 2{{K}^{2}}{{m}_{e}} + 1)}}$

(3.4)

$\sigma = \frac{{Kc\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{H}$

$\sigma \approx \frac{{c\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{{2{{m}_{e}}HK}}$

соответственно.

На рис. 1 для соотношения (3.3) представлен график зависимости безразмерного параметра $\Sigma = \frac{{\sigma H\sqrt {{{m}_{e}}} }}{{c{{P}_{k}}}}$ от безразмерного волнового числа $\kappa = K\sqrt {{{m}_{e}}} $, где P_k = P_G – P_F. Видно, что скорость роста возмущений имеет максимум, который достигается при $K\sqrt {{{m}_{e}}} \approx 0.72$ и стремится к нулю с ростом волнового числа K → ∞.

Рис. 1.

График зависимости безразмерного параметра Σ от безразмерного волнового числа κ, где P_k = P_G – P_F.

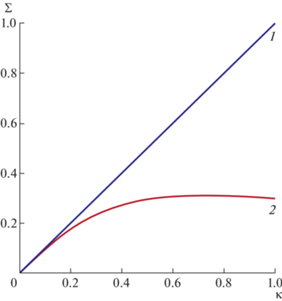
На рис. 2 представлено сравнение безразмерной скорости роста возмущений при малых безразмерных волновых числах для уравнений фильтрации Дарси (кривая 1) и Бринкмана (кривая 2). Видно, что при K$\sqrt {{{m}_{e}}} $ $ \ll $ 1 уравнение Дарси хорошо описывает поведение физической системы, а при больших волновых числах ошибка от использования закона Дарси становится существенной.

Рис. 2.

График зависимости безразмерного параметра Σ от безразмерного волнового числа κ: 1 – закон Дарси; 2 – приближение Бринкмана.

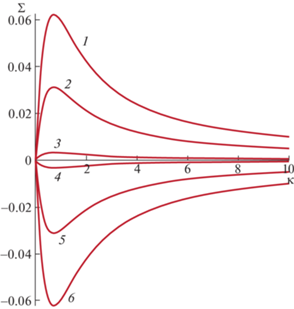
Из формулы (3.3) следует, что поскольку выражение, стоящее в знаменателе, всегда положительно, то переход к неустойчивости происходит при смене знака разницы между давлением в газовой шапке P_G и давлением в высокопроницаемом пропластке P_F. На рис. 3 показана зависимость безразмерной скорости роста или затухания возмущений $\frac{{\sigma H\sqrt {{{m}_{e}}} }}{{c{{P}_{k}}}}$ от безразмерного волнового числа $K\sqrt {{{m}_{e}}} $ при фиксированном P_G и различных значениях P_F. Видно, что переход к неустойчивости происходит при P_G = P_F одновременно при всех значениях волнового числа.

Рис. 3.

График зависимости безразмерного параметра Σ от волнового числа κ: 1–6 – P_F = (0.8, 0.9, 0.99, 1.01, 1.1, 1.2) P_G.

ЗАКЛЮЧЕНИЕ

Исследованы динамика и устойчивость вертикального течения, возникающего в нефтяном коллекторе с газовой шапкой. Течение нефти описывалось с помощью обобщенного уравнения фильтрации Бринкмана. Представлен закон движения плоской горизонтальной границы раздела нефть–газ. Методом нормальных мод исследована устойчивость течения по отношению к бесконечно малым возмущениям плоской границы. Показано, что такие возмущения растут, если давление в газовой шапке больше, чем давление в высокопроницаемом пропластке, из которого происходит отбор нефти. Если плоская граница раздела покоится, то давление в газовой шапке меньше, чем в высокопроницаемом пропластке, которое равно гидростатическому давлению. На первой стадии уменьшения давления в пропластке контактная поверхность начнет двигаться вниз, но останется устойчивой до тех пор, пока давление в пропластке не упадет ниже давления в газовой шапке. После этого движение границы раздела нефть–газ станет неустойчивым. В этом случае нелинейная неустойчивость имеет место для любой длины волны, но зависит от волнового числа K таким образом, что при K → ∞ и K → 0 эта скорость стремится к нулю. Существует некоторое значение волнового числа, при котором скорость роста имеет максимум.

При использовании закона Дарси неустойчивость также возникает, если давление в газовой шапке больше, чем давление в пропластке. Однако в этом случае скорость роста возмущений неограниченно возрастает с уменьшением длины волны возмущения. В этом случае коротковолновые возмущения растут сколь угодно быстро, что не позволяет получить достоверную картину течения и свидетельствует о неприменимости математической модели, основанной на законе Дарси, для описания как самого перехода к неустойчивости, так и последующего развития течения с разрушением поверхности раздела, приводящим к образованию пальцев. Изменение основных уравнений путем использования обобщенного уравнения фильтрации Бринкмана позволяет устранить аномальный характер эволюции коротковолновых возмущений, что открывает возможность исследовать задачи, которые не являлись корректными в рамках приближения Дарси.

Работа выполнена при поддержке гранта Российского научного фонда № 21-11-00126.

Список литературы

Лапук Б.Б. Теоретические основы разработки месторождений природных газов. М.: Институт компьютерных исследований, 2002. 296 с.
Кутырев Е.Ф., Шкандратов В.В., Белоусов Ю.В. Некоторые результаты физического моделирования процессов газообмена в пластовой системе нефть–нагнетаемая вода // Георесурсы. 2005. № 5. С. 33–36.
Tsypkin G.G., Shargatov V.A. Influence of capillary pressure gradient on connectivity of flow through a porous medium // Int. J. Heat and Mass Transfer. 2018. V. 127. P. 1053–1063.
Tsypkin G.G., Il’ichev A.T. Gravitational stability of the water-vapor phase transition interface in geothermal systems // Transp. Porous Media. 2004. V. 55. P. 183–199.
Il’ichev A.T., Tsypkin G.G. Catastrophic transition to instability of evaporation front in a porous medium // Eur. J. Mech. B/Fluids. 2008. V. 27. № 6. P. 665–677.
Shargatov V.A., Il’ichev A.T., Tsypkin G.G. Dynamics and stability of moving fronts of water evaporation in a porous medium // Int. J. Heat and Mass Transfer. 2015. V. 83. P. 552–561.
Tsypkin G.G., Il’ichev A.T. Superheating of water and morphological instability of the boiling front moving in the low-permeability rock // Int. J. Heat and Mass Transfer. 2021. V. 167. 120820.
Цыпкин Г.Г. Неустойчивость легкой жидкости над тяжелой при движении поверхности раздела в пористой среде // Изв. РАН. МЖГ. 2020. № 2. С. 70–76.
Brinkman H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles // Appl. Sci. Res. 1947. V. A1. P. 27–34.
Beavers G.S., Joseph D.D. Boundary conditions at a naturally permeable wall // J. Fluid Mech. 1967. V. 30. P. 197–207.
Ochoa-Tapia J.A., Whitaker S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid – I. Theoretical development // Int. J. Heat Mass Transfer. 1995. V. 38. P. 2635–2646.
Valdes-Parada F.J., Ochoa-Tapia J.A., Alvarez-Ramirez J. On the effective viscosity for the Darcy–Brinkman equation // Physica A. 2007. V. 385. P. 69–79.
Nield D.A. Modelling high speed flow of a compressible fluid in a saturated porous medium // Transp. Porous Media. 1994. V. 14. P. 85–88.
Nield D.A. The Beavers–Joseph boundary condition and related matters: a historical and critical note // Transp. Porous Media. 2009. V. 78. P. 537–540.
Tsiberkin K. Effect of inertial terms on fluid–porous medium flow coupling // Transp. Porous Media. 2018. V. 121. P. 109–210.
Fernandez J., Kurowski P., Petitjeans P., Meiburg E. Density-driven unstable flows of miscible fluids in a Hele-Shaw cell // J. Fluid Mech. 2002. V. 451. P. 239–260.
Lyubimova T.P., Lyubimov D.V., Baydina D.T. et al. Instability of plane-parallel flow of incompressible liquid over a saturated porous medium // Phys. Rev. 2016. V. 94. 013104.
Ильичев А.Т., Шаргатов В.А. Динамика фронтов испарения воды // ЖВММФ. 2013. Т. 53. № 9. С. 1531–1553.
Shargatov V.A., Gorkunov S.V., Il’ichev A.T. Dynamics of front-like water evaporation phase transition interfaces // Commun. in Nonlinear Sci. Numer. Simul. 2019. V. 67. P. 223–236.
Соболева Е.Б. Начало конвекции Рэлея-Тейлора в пористой среде // Изв. РАН. МЖГ. 2021. № 2. С. 52–62.
Soboleva E.B. Density-driven convection in an inhomogeneous geothermal reservoir // Int. J. Heat and Mass Transfer. 2018. V. 127. P. 784–798.
Khanukaeva D.Yu., Filippov A.N., Yadav P.K. et al. Creeping flow of micropolar fluid through a swarm of cylindrical cells with porous layer (membrane) // J. Mol. Liq. 2019. V. 294. 111558.
Журавлева Е.Н., Пухначев В.В. Задача о деформации вязкого слоя // Доклады РАН. 2020. Т. 490. № 1. С. 66–69.
Tsypkin G.G., Woods A.W. Vapour extraction from a water saturated geothermal reservoir // J. Fluid Mech. 2004. V. 506. P. 315–330.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал