1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2022

Известия РАН. Механика жидкости и газа, 2022, № 3, стр. 3-16

КОНТИНУАЛЬНОЕ МОДЕЛИРОВАНИЕ СОРТИРОВКИ КЛЕТОК В ПЛОСКОМ СЛОЕ С УЧЕТОМ ВОЗМОЖНОГО РАСХОЖДЕНИЯ ГРАНИЦ ОБЛАСТЕЙ, ЗАНЯТЫХ КЛЕТКАМИ ДВУХ РАЗНЫХ ТИПОВ

С. А. Логвенков a, b, *, А. А. Штейн b, **

a Национальный исследовательский университет “Высшая школа экономики”
Москва, Россия

b МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия

* E-mail: logv@bk.ru
** E-mail: stein.msu@bk.ru

Поступила в редакцию 07.11.2021
После доработки 21.12.2021
Принята к публикации 21.12.2021

Полный текст (PDF)

Аннотация

В агрегатах, образованных клетками разных типов, наблюдается явление их сортировки: в результате клеточных взаимодействий формируются структуры, в которых клетки одного типа могут образовывать компактную массу, окруженную клетками другого типа. Физические механизмы, лежащие в основе процесса сортировки, до сих пор остаются предметом обсуждения. Нами была ранее предложена континуальная модель биологической сплошной среды, образованной двумя активно взаимодействующими клеточными фазами и жидкостью. На основе этой модели была рассмотрена модельная задача о перераспределении клеток двух типов, заполняющих бесконечный плоский слой, в предположении, что континуумы, моделирующие две клеточные популяции, ограничены общей внешней границей. В предлагаемой работе поставлена и исследована аналогичная задача с учетом возможного относительного перемещения поверхностей, ограничивающих клетки разных типов. Такая постановка позволяет описывать образование и распространение фронтов, разделяющих области, различающиеся концентрациями клеточных фаз. Изучено поведение решений в зависимости от безразмерных параметров, характеризующих активные межклеточные взаимодействия. Численно проанализировано участие этих механизмов в формировании новых клеточных структур. Показано, что в широком диапазоне параметров клетки с более сильными стягивающими активными взаимодействиями стремятся занять центральную область, вытесняя на периферию клетки, обладающие более слабыми стягивающими взаимодействиями. Новая постановка физически более адекватна и позволяет расширить диапазон параметров, в котором достигается стабильный результат.

Ключевые слова: клеточные системы, активные среды, биологическое формообразование

Формирование полей механических напряжений – необходимое условие нормального развития зародышей животных [1–3]. Важнейшим фактором возникновения и эволюции полей механических напряжений в биологических средах являются активные механические взаимодействия клеток между собой и с внеклеточными составляющими биологической среды. Активные механические напряжения играют существенную роль в управлении движением клеток, в частности эмбриональных на ранней стадии развития, что приводит к формированию структур, которые в дальнейшем трансформируются в ткани и органы.

С активными межклеточными взаимодействиями связано явление сортировки клеток в клеточных агрегатах, полученных перемешиванием клеток разных тканей. При сортировке происходит пространственное разделение клеток разных типов. Например, при перемешивании клеток двух разных эмбриональных тканей позвоночных может наблюдаться формирование клеточной структуры, характеризуемой образованием компактной массы клеток одного типа, окруженной слоем клеток другого типа. Наблюдаются и более сложные случаи пространственного разделения клеток [4–7]. Физические процессы, лежащие в основе процесса сортировки клеток, до сих пор остаются предметом обсуждения.

Первые результаты решения задачи о сортировке двух разных типов клеток были получены с использованием дискретных моделей. В их числе модели Поттса [8–11], в которых эволюция клеточной системы рассматривается как результат случайного процесса, направленного на минимизацию энергии, учитывающей различные механизмы взаимодействия между соседними клетками. В другой группе работ [12–15] дискретное моделирование осуществлялось на основе представления клеток многоугольниками.

Недостатком моделей первого типа является отсутствие ясного физического смысла у рассматриваемого случайного процесса изменения конфигурации системы. Кроме того, в рамках этих моделей нет возможности формулировать постановки задач с граничными условиями на силы и перемещения, поскольку силовые взаимодействия учитываются только через изменение энергии. Возможность применения моделей второй группы ограничена тем, что рассматривается равновесие сил, действующих только в поверхностном слое клетки. Описание других моделей, использующих близкие подходы и страдающих сходными дефектами, можно найти в [6, 7, 16–18].

Примеры континуального моделирования сортировки клеток немногочисленны. По большей части, описание клеточной динамики ограничивается постулированием диффузионных уравнений для объемных концентраций клеток [19, 20]. При этом потоки компонентов определяются соотношениями, учитывающими помимо эффективной диффузии, соответствующей случайным клеточным блужданиям, также активную нелокальную составляющую, которая интерпретируется как проявление активных взаимодействий, связанных с межклеточной адгезией (сцеплением поверхностей клеток посредством специализированных молекул). Используемые соотношения обосновываются рассмотрением баланса адгезионных сил, действующих на клетки; при этом напряжения в среде не вводятся и влияние напряжений в самих клетках на соседние клетки не рассматривается.

В работах [21, 22] предложено более корректное с точки зрения механики описание движения клеток: клеточные среды рассматриваются как две идеальные жидкости с одинаковым давлением, пропорциональным сумме плотностей клеток. В результате для этих плотностей получается система двух уравнений параболического типа с нелинейным коэффициентом диффузии. При решении задач в рамках упомянутых редуцированных континуальных моделей, в конце концов сводящихся к диффузионным, в [19, 21, 22] используется условие периодичности на границах рассматриваемой фиксированной области, которое не имеет отчетливого биологического смысла. Использование граничных условий, традиционных для задач механики, оказывается невозможным в рамках диффузионного приближения, поскольку при этом игнорируется связь потоков с параметрами, характеризующими развиваемые клетками усилия и напряженное состояние среды.

Общий подход к моделированию процессов в механически активных клеточных средах, основанный на применении методов механики многофазных сред, предложен в наших работах и наиболее полно сформулирован в [23]. В отличие от всех вышеупомянутых работ, рассмотрение основано на непосредственном учете реальных механизмов взаимодействий, действующих в клеточных системах. В рамках такого подхода в работе [24] разработана модель биологической среды, образованной клетками различных типов. В модели учитываются активные взаимодействия как между клетками внутри одной клеточной популяции, так и между клетками разных популяций. Допускается как локальная, так и нелокальная зависимость активных напряжений от характеризующих среду параметров. В [24] решена модельная задача об эволюции первоначально однородной смеси клеток двух типов в бесконечном плоском слое. На этом примере было показано, что разработанная модель способна описать явление сортировки как результат различий в значениях параметров, определяющих клеточную активность.

Задача о сортировке клеток в плоском слое решалась в [24] в предположении, что обе клеточные фазы в процессе разделения заполняют всю область решения. В настоящей работе аналогичная задача решена и исследована с учетом возможности независимого перемещения поверхностей, ограничивающих области, занятые клетками разных типов. Такая принципиально новая постановка, потребовавшая сформулировать условия на поверхностях разрыва, позволила описать формирование и распространение фронтов, разделяющих области, различающиеся концентрациями в них клеточных фаз. Результаты сравниваются с полученными в [24]. Показано, что новая, физически более адекватная, постановка позволяет расширить диапазон параметров, дающих стабильное решение.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим эволюцию плотностей двух типов клеток, заполняющих в начальный момент времени бесконечный плоский слой, окруженный жидкостью с нулевым давлением. Считается, что в последующие моменты времени слой остается плоским; при этом его толщина может меняться.

Будет использована разработанная в [24] континуальная модель биологической сплошной многофазной среды, образованной двумя активно взаимодействующими типами клеток, которые различаются параметрами зависимостей, управляющих их активным поведением – развитием активных напряжений и активными перемещениями клеток друг относительно друга. Помимо двух клеточных фаз, модель включает в себя внеклеточную жидкость и дополнительные фазы, посредством которых описываются активные силовые взаимодействия между клетками. Дополнительные фазы – обобщенное понятие; они могут отождествляться, например, с псевдоподиями (активными выпячиваниями клеточной мембраны), содержащими сократительные элементы цитоскелета (клеточного скелета) или с единой механически напряженной сетью, составленной мембранами контактирующих клеток и выстилающими их поверхностными сократительными структурами. Объемы, занимаемые дополнительными фазами, в сравнении с объемами основных фаз считаются пренебрежимо малыми. Тем самым предполагается выполнение условия ${{\phi }_{1}} + {{\phi }_{2}} + {{\phi }_{w}} = 1$. Здесь ${{\phi }_{1}}$, ${{\phi }_{2}}$ и ${{\phi }_{w}}$ – относительные объемные концентрации первой и второй клеточных фаз и жидкости соответственно. Истинные плотности фаз считаются совпадающими поэтому объемные концентрации совпадают с массовыми. Перемещения клеток характеризуются тензорами скоростей деформаций фаз, которые зависят как от активных, так и от пассивных напряжений.

Далее предполагается присутствие, вообще говоря, трех дополнительных фаз. Две из них обеспечивают активные взаимодействия между клетками одного типа, т.е. принадлежащими только к первой или только ко второй клеточной фазе. Третья дополнительная фаза обеспечивает перекрестные активные взаимодействия между клетками разных фаз.

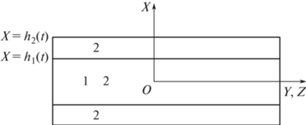
Введем декартову систему координат с осями $Oy$ и $Oz$, лежащими в средней плоскости слоя и осью $Ox$, направленной перпендикулярно этой плоскости (рис. 1). Следуя работе [24], будем искать решение задачи о перераспределении объемных концентраций клеток и жидкости в слое в виде зависимости всех неизвестных от времени $t$ и только поперечной координаты $x$. Полагаем, что скорости всех фаз имеют единственную отличную от нуля компоненту, направленную по оси $Ox$. Это допущение физически соответствует слою с шириной в направлениях осей $Oy$ и $Oz$, много большей его толщины в направлении оси $Ox$, компоненты смещения которого в плоскости $Oyz$ на удаленной границе равны нулю, тогда как в направлении оси $Ox$ на этой границе имеет место свободное проскальзывание. У всех тензоров напряжений смешанные компоненты считаются равными нулю. Будем отмечать компоненты векторов и тензоров в направлениях $y$ и $z$ соответствующим буквенным индексом, заменяя повторяющийся индекс у компонент тензоров однократным. У компонент векторов и тензоров в направлении $x$ индекс опускается.

Рис. 1.

Схема плоского слоя, образованного клетками 1-го и 2-го типов, с разошедшимися границами фаз в момент времени t.

Оценка коэффициента межфазного вязкого трения между клеточными фазами и жидкостью позволяет пренебречь в уравнениях импульсов изменением гидростатического давления во внеклеточной жидкости $p$ [24], поэтому в дальнейшем оно считается пространственно-однородным. Тогда уравнения для клеточных фаз можно решать отдельно от уравнений, описывающих движение жидкости. В дальнейшем будем полагать p = 0.

Имея в виду рассматриваемые далее в настоящей работе задачи, будем предполагать, что активные стягивающие силы действуют только между клетками, принадлежащими к одной фазе, а между клетками двух разных фаз отсутствуют. Таким образом, в межфазной активной силе будем учитывать только расталкивающую компоненту. Система уравнений имеет следующий вид:

(1.1)
$\frac{{\partial {{\phi }_{1}}}}{{\partial t}} + \frac{{\partial {{\phi }_{1}}{{{v}}_{1}}}}{{\partial x}} = 0,\quad \frac{{\partial {{\phi }_{2}}}}{{\partial t}} + \frac{{\partial {{\phi }_{2}}{{{v}}_{2}}}}{{\partial x}} = 0,\quad {{\phi }_{1}} + {{\phi }_{2}} + {{\phi }_{w}} = 1$
(1.2)
$\begin{gathered} \frac{\partial }{{\partial x}}({{\phi }_{1}}{{\sigma }^{{(1)}}} + {{\tau }^{{(1)}}} + {{\tau }^{{(12)}}}) + {{\phi }_{2}}{{p}_{1}}\frac{\partial }{{\partial x}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - \\ - \;{{\phi }_{1}}{{p}_{2}}\frac{\partial }{{\partial x}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) + {{k}_{{12}}}{{\phi }_{1}}{{\phi }_{2}}({{{v}}_{2}} - {{{v}}_{1}}) = 0 \\ \end{gathered} $
(1.3)
$\begin{gathered} \frac{\partial }{{\partial x}}({{\phi }_{2}}{{\sigma }^{{(2)}}} + {{\tau }^{{(2)}}} + {{\tau }^{{(12)}}}) + {{\phi }_{1}}{{p}_{2}}\frac{\partial }{{\partial x}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - \\ - \;{{\phi }_{2}}{{p}_{1}}\frac{\partial }{{\partial x}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) + {{k}_{{12}}}{{\phi }_{1}}{{\phi }_{2}}({{{v}}_{1}} - {{{v}}_{2}}) = 0 \\ \end{gathered} $
(1.4)
${{p}_{1}} = - \frac{1}{3}{{I}_{1}}({{\sigma }^{{(1)}}}),\quad {{p}_{2}} = - \frac{1}{3}{{I}_{1}}({{\sigma }^{{(2)}}})$
(1.5)
${{\tau }^{{(1)}}} = - {{\Pi }_{1}} + {{m}_{1}}\frac{3}{{4\pi R_{s}^{4}}} \cdot {{\phi }_{1}}\int\limits_S {{{\phi }_{1}}} \cdot {{x}^{2}}ds,\quad {{\tau }^{{(2)}}} = - {{\Pi }_{2}} + {{m}_{2}}\frac{3}{{4\pi R_{s}^{4}}} \cdot {{\phi }_{2}}\int\limits_S {{{\phi }_{2}}} \cdot {{x}^{2}}ds$
(1.6)
$\tau _{\alpha }^{{(1)}} = - {{\Pi }_{1}} + {{m}_{1}}\frac{3}{{4\pi R_{s}^{4}}} \cdot {{\phi }_{1}}\int\limits_S {{{\phi }_{1}}} \cdot r_{\alpha }^{2}ds,\quad \tau _{\alpha }^{{(2)}} = - {{\Pi }_{2}} + {{m}_{2}}\frac{3}{{4\pi R_{s}^{4}}} \cdot {{\phi }_{2}}\int\limits_S {{{\phi }_{2}}} \cdot r_{\alpha }^{2}ds$
(1.7)
${{\Pi }_{1}} = {{E}_{1}}\frac{{\phi _{1}^{{2\theta }}}}{{1 - {{\phi }_{1}} - {{\phi }_{2}}}},\quad {{\Pi }_{2}} = {{E}_{2}}\frac{{\phi _{2}^{{2\theta }}}}{{1 - {{\phi }_{1}} - {{\phi }_{2}}}},\quad \tau _{{}}^{{(12)}} = \tau _{\alpha }^{{(12)}} = - {{\Pi }_{{12}}} = - {{E}_{{12}}}\frac{{{{{\left( {{{\phi }_{1}}{{\phi }_{2}}} \right)}}^{\theta }}}}{{1 - {{\phi }_{1}} - {{\phi }_{2}}}}$
(1.8)
${{e}^{{(1)}}} = \frac{1}{{2{{\mu }_{1}}}}({{\sigma }^{{(1)}}} - {{\phi }_{2}}{{\sigma }^{{(2)}}}) - \frac{1}{{2{{\mu }_{{11}}}}}{{\tau }^{{(1)}}} - \frac{1}{{2{{\mu }_{{12}}}}}{{\tau }^{{(12)}}}$
(1.9)
${{e}^{{(2)}}} = \frac{1}{{2{{\mu }_{2}}}}({{\sigma }^{{(2)}}} - {{\phi }_{1}}{{\sigma }^{{(1)}}}) - \frac{1}{{2{{\mu }_{{22}}}}}{{\tau }^{{(2)}}} - \frac{1}{{2{{\mu }_{{21}}}}}{{\tau }^{{(12)}}}$
(1.10)
$\frac{1}{{2{{\mu }_{1}}}}(\sigma _{\alpha }^{{(1)}} - {{\phi }_{2}}\sigma _{\alpha }^{{(2)}}) - \frac{1}{{2{{\mu }_{{11}}}}}\tau _{\alpha }^{{(1)}} - \frac{1}{{2{{\mu }_{{12}}}}}\tau _{\alpha }^{{(12)}} = 0$
(1.11)
$\frac{1}{{2{{\mu }_{2}}}}(\sigma _{\alpha }^{{(2)}} - {{\phi }_{1}}\sigma _{\alpha }^{{(1)}}) - \frac{1}{{2{{\mu }_{{22}}}}}\tau _{\alpha }^{{(2)}} - \frac{1}{{2{{\mu }_{{21}}}}}\tau _{\alpha }^{{(12)}} = 0$
(1.12)
$e_{{}}^{{(1)}} = \frac{{\partial {{{v}}_{1}}}}{{\partial x}},\quad e_{{}}^{{(2)}} = \frac{{\partial {{{v}}_{2}}}}{{\partial x}}$

Здесь ${{{v}}_{1}}$ и ${{{v}}_{2}}$ – компоненты векторов скорости клеточных фаз; ${{\sigma }^{{(1)}}}$ и ${{\sigma }^{{(2)}}}$ – тензоры напряжений в клеточных фазах; тензоры ${{\tau }^{{(1)}}}$ и ${{\tau }^{{(2)}}}$ – характеризуют напряжения в дополнительных фазах, обеспечивающих активные межклеточные взаимодействия между клетками только первой и только второй клеточных фаз соответственно; тензор напряжений ${{\tau }^{{(12)}}}$ описывает активное взаимодействие клеток, принадлежащих к разным фазам; ${{e}^{{(1)}}}$ и ${{e}^{{(2)}}}$ – компоненты тензоров скоростей деформаций клеточных фаз; ${{p}_{1}}$ и ${{p}_{2}}$ – давления в первой и второй клеточных фазах соответственно; для первого инварианта любого тензора второго ранга T принято обозначение ${{I}_{1}}(T)$; индекс α принимает значения y и z; ${{r}_{y}} \equiv y$, ${{r}_{z}} \equiv z$.

Безразмерный параметр $\theta $, присутствующий в выражениях для “расталкивающих” активных напряжений (1.7) отвечает за быстроту их затухания при понижении концентраций клеточных фаз. В работе [24] он полагался равным единице. Однако расчеты (см. далее разд. 4) показывают, что в рамках рассматриваемой постановки задачи такой выбор может приводить к некоторым нефизичным следствиям. Для их исключения далее подбираем значение $\theta > 1$.

Уравнения неразрывности для клеточных фаз (1.1) написаны с учетом отсутствия в среде клеточных делений, гибели клеток и массообмена между клеточной фазой и внеклеточной жидкостью. Истинные плотности фаз считаются постоянными и равными между собой. Уравнения баланса импульса для клеточных фаз (1.2) и (1.3) по оси Ox, в пренебрежении инерционными эффектами, учитывают силы их взаимодействия с дополнительными фазами (второе и третье слагаемые), а также силы межфазного взаимодействия между двумя клеточными фазами и этих фаз с межклеточной жидкостью [24]. Уравнения баланса импульса по осям Oy и Oz выполнены тождественно. В слое присутствуют клеточные и активные напряжения, параллельные слою, которые могут быть рассчитаны по уравнениям системы (1.1)–(1.12), содержащим компоненты с индексом $\alpha $.

Уравнения (1.5)–(1.7) имеют смысл определяющих соотношений для активных напряжений в дополнительных фазах и учитывают как хаотическую активность клеток, характеризуемую соответствующими давлениями, проявляющимися в отталкивании клеток, так и развиваемые ими стягивающие усилия, направленно реагирующие на неоднородность их микроокружения. Интегрирование в соотношениях (1.5), (1.6) выполняется по сферической поверхности S некоторого фиксированного для данной среды радиуса ${{R}_{s}}$ (радиуса дальнодействия) с центром в рассматриваемой точке. Для точек, находящихся на расстоянии, меньшем ${{R}_{s}}$ от поверхности, ограничивающей рассматриваемый объем среды, интегрирование ведется по той части поверхности сферы, которая лежит внутри этого объема.

В дальнейшем, при решении рассматриваемой ниже задачи появляется область, где присутствует лишь клеточная фаза 2. В этой области ${{\phi }_{1}} = 0$, ${{\sigma }^{{(1)}}} = {{\tau }^{{(1)}}} = {{\tau }^{{(12)}}} = 0$, и те уравнения системы (1.1)–(1.12), которые относятся к фазе 1, выполняются тождественно.

Соотношения (1.8)–(1.11) представляют собой выражения для компонент тензоров скоростей деформаций основных фаз. Учитывается, что компоненты этих тензоров, ориентированные по осям y и z, равны нулю в силу сделанных выше предположений о виде решения. В общем случае тензор скоростей деформаций в клеточной среде учитывает как деформацию клеток, так и их переупаковку [25]. В настоящей работе предполагается, что деформация основных фаз определяется только переупаковками, что правомерно для достаточно рыхлых тканей. Система дополняется кинематическими соотношениями (1.12) для отличных от нуля компонент тензоров скоростей деформации клеточных фаз.

Все входящие в систему уравнений (1.1)–(1.12) коэффициенты положительны. Система (1.1)–(1.12) отличается от уравнений для плоского слоя, рассмотренных и подробно мотивированных в [24], только отличающимся от единицы показателем степени $\theta $. Однако постановки задач в [24] и в настоящей работе принципиально различаются принятыми граничными условиями.

2. НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯ

Пусть в начальный момент времени клетки двух разных типов заполняют бесконечный плоский слой толщиной $2{{h}_{0}}$, окруженный жидкостью, в которой давление равно нулю. Постановка задачи теперь учитывает возможность независимого перемещения границ, ограничивающих области, занятые клетками каждого типа. Координаты $x = {{h}_{1}}(t)$ и $x = {{h}_{2}}(t)$ задают положение в момент времени t границ первой и второй клеточных фаз соответственно (рис. 1). Распределение концентраций клеток обеих фаз считается симметричным по толщине слоя, поэтому задача решается на отрезках $\left[ {0;\;{{h}_{1}}(t)} \right]$ для первой и $\left[ {0;\;{{h}_{2}}(t)} \right]$ для второй фазы.

Из условий симметрии следует, что при $x = 0$

(2.1)
${{{v}}_{1}} = {{{v}}_{2}} = 0$

Дальнейшие рассуждения будут проведены для случая ${{h}_{1}}(t) < {{h}_{2}}(t)$, когда центральная область $\left[ { - {{h}_{1}}(t),\;{{h}_{1}}(t)} \right]$ занята двумя типами клеток, а внешняя, представленная на рисунке отрезками $\left[ {{{h}_{1}}(t),\;{{h}_{2}}(t)} \right]$ и симметричным ему $\left[ { - {{h}_{2}}(t), - {{h}_{1}}(t)} \right]$ – только клетками второго типа. В случае ${{h}_{1}}(t) > {{h}_{2}}(t)$ рассуждения будут аналогичными. Какая из фаз замыкает в себе другую, определяется соотношением между числовыми параметрами, характеризующими каждую фазу и в конечном счете устанавливается в процессе численного решения. В дальнейшем (разд. 4) эти параметры выбраны таким образом, что выполняется именно неравенство ${{h}_{1}}(t) < {{h}_{2}}(t)$. Там же поясняется физический смысл такого выбора. Будем рассматривать случай равенства нулю внешней силы на внешней границе.

Давление в жидкости p, как уже упоминалось, считается пространственно-однородным. В рассматриваемой задаче будем полагать, что жидкость может свободно перетекать через границу слоя (т.е. области, занятой клетками) и, таким образом, давление p определяется давлением во внешней среде. В расчетах будем считать его равным нулю. Однако при написании граничных условий, имея в виду их дальнейшее использование, рассмотрим общий случай, когда давление может отличаться от нуля.

Будем считать, что в начальный момент времени $t = 0$ внешние границы фаз совпадают: ${{h}_{1}}(0)$ = h2(0). Полагаем, что в этот момент внешняя сила, действующая на каждую из клеточных фаз, сводится к давлению окружающей среды, распределенному между фазами пропорционально их концентрациям:

(2.2)
$\phi _{1}^{{}}{{\sigma }^{{(1)}}} + {{\tau }^{{(1)}}} + {{\tau }^{{(12)}}} = - \phi _{1}^{{}}p,\quad \phi _{2}^{{}}{{\sigma }^{{(2)}}} + {{\tau }^{{(2)}}} + {{\tau }^{{(12)}}} = - \phi _{2}^{{}}p$

В дальнейшем, после формирования границы между двухфазной и однофазной клеточными средами, второе условие (2.2) (для второй фазы) сохраняется. Для первой фазы межфазовая граница теперь внешняя, и условие на ней должно учитывать силовое воздействие второй фазы. Для второй фазы эта граница является поверхностью разрыва, на которой необходимо сформулировать дополнительные условия. Обозначим скорость перемещения поверхности разрыва для второй фазы (равную скорости перемещения внешней границы первой) ${v}{\text{*}}$. Тогда из условия сохранения массы следует

(2.3)
$\left[ {{{\phi }_{2}}({{{v}}_{2}} - {v}*)} \right] = 0$

Квадратные скобки здесь и далее обозначают разность между значениями любой величины Z по разные стороны поверхности разрыва: $[Z] = {{Z}^{ + }} - {{Z}^{ - }}$. Верхний индекс “минус” указывает на принадлежность к области 12 совместного присутствия обеих фаз (рис. 1), а индекс “плюс” на принадлежность к области 2 (где присутствует только вторая фаза).

Прежде чем формулировать второе условие на поверхности разрыва для второй фазы и условие на этой границе для первой, необходимо принять гипотезу о виде межфазной силы, действующей на этой границе. Присутствие такой силы определяется силовым взаимодействием частиц первой фазы в зоне 12 с частицами второй фазы в зоне 2. Поскольку средние напряжения в частицах разных фаз не совпадают, необходимо принять выражение для среднего давления на поверхности контакта частиц p*. Будем поступать в соответствии с методологией, развитой в работе [24]. Полагая, что средний размер частицы каждой фазы пропорционален ее концентрации, а распределение давления в клеточных фазах линейно, получаем аналогично [24] для p* максимально простое выражение

(2.4)
$p* = \frac{{p_{1}^{ - }\phi _{2}^{ + } + p_{2}^{ + }\phi _{1}^{ - }}}{{\phi _{1}^{ - } + \phi _{2}^{ + }}}$

Полагая, что в среднем площадь контакта между фазами на рассматриваемой границе пропорциональна концентрациям соответствующих фаз (второй в области 2 и первой в области 12), получаем для среднего макроскопического межфазного давления $p{\text{**}}$, отнесенного ко всей межфазной поверхности в единице объема среды, выражение

(2.5)
$p{\text{**}} = \phi _{1}^{ - }\phi _{2}^{ + }p* = \phi _{1}^{ - }\phi _{2}^{ + }\frac{{p_{1}^{ - }\phi _{2}^{ + } + p_{2}^{ + }\phi _{1}^{ - }}}{{\phi _{1}^{ - } + \phi _{2}^{ + }}}$

Полагая, что сила давления жидкости, приходящаяся на вторую фазу с каждой стороны поверхности разрыва, пропорциональна концентрациям второй и жидкой фаз с соответствующих сторон, получаем еще одно условие на разрыве для второй фазы

(2.6)
$[\phi _{2}^{{}}{{\sigma }^{{(2)}}} + {{\tau }^{{(2)}}} + {{\tau }^{{(12)}}}] = - p{\text{**}} + (\phi _{2}^{ - }\phi _{w}^{ + } - \phi _{2}^{ + }\phi _{w}^{ - })p$

Считая, что площадь контакта между первой фазой на той же поверхности (внешней для этой фазы границе) и внешней для нее жидкостью также пропорциональна их соответствующим концентрациям, получаем условие для первой фазы при $x = {{h}_{1}}(t)$

(2.7)
$\phi _{1}^{{}}{{\sigma }^{{(1)}}} + {{\tau }^{{(1)}}} + {{\tau }^{{(12)}}} = - p{\text{**}} - \phi _{1}^{{}}\phi _{w}^{ + }p$

Соотношения (2.6) и (2.7) для описания межфазной силы, действующей на поверхности разрыва, основаны на тех же физических допущениях, что были использованы при получении выражения для объемной межфазной силы, присутствующей в уравнениях (1.2) и (1.3) [24].

Перемещение границ $x = {{h}_{1}}(t)$ и $x = {{h}_{2}}(t)$ определяется движением клеток соответствующих фаз, поэтому на этих границах выполнены условия ${v}* = {{\dot {h}}_{1}} = {{{v}}_{1}}$ при $x = {{h}_{1}}(t)$ и ${{\dot {h}}_{2}} = {{{v}}_{2}}$ при $x = {{h}_{2}}(t)$ (точкой обозначено дифференцирование по времени).

Граничные условия для ${{\phi }_{1}}$ при x = 0 и $x = {{h}_{1}}(t)$и ${{\phi }_{2}}$ при $x = 0$ и $x = {{h}_{2}}(t)$ не ставятся, так как x = 0 и $x = {{h}_{1}}(t)$ являются характеристиками для первого уравнения (1.1), а x = 0 и $x = {{h}_{2}}(t)$ – для второго.

В качестве начальных условий при t = 0 будем задавать начальное положение внешней границы (общее для обеих клеточных фаз) ${{h}_{1}}(0) = {{h}_{2}}(0) = {{h}_{0}}$ и начальные распределения концентраций фаз ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}}(x)$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}}(x)$.

В каждый момент времени при известных текущих расположениях внешних границ и распределениях концентраций фаз система уравнений для определения скоростей фаз и напряжений в них имеет четвертый порядок. При t = 0, когда поверхность разрыва еще не сформировалась, граничных условий четыре. Они определяются соотношениями (2.1) и (2.2). В дальнейшем с учетом присутствия поверхности разрыва для второй фазы, расположение которой в этот момент известно (совпадает с внешней границей первой фазы), необходимо шесть граничных условий. К их числу относятся оба равенства (2.1), второе соотношение (2.2), (2.3), а также (2.6) и (2.7) с учетом (2.5). По известному распределению скоростей клеточных фаз ${{{v}}_{1}}$ и ${{{v}}_{2}}$ из уравнений неразрывности (1.1) могут быть найдены скорости изменения фазовых концентраций ${{\phi }_{1}}$ и ${{\phi }_{2}}$. Если распределения концентраций первоначально непрерывны, они остаются непрерывными и в дальнейшем, в том числе и при прохождении поверхности разрыва по частицам второй фазы: рвется лишь скорость изменения концентрации ${{\phi }_{2}}$. В силу условия (2.3) на этой поверхности остается непрерывной и скорость второй фазы ${{{v}}_{2}}$. Таким образом, при $x = {{h}_{1}}$ скорость и концентрация второй фазы претерпевают слабый разрыв, тогда как разрыв напряжения в этой фазе ${{\sigma }_{2}}$ оказывается сильным, что видно, например, из условия (2.6).

3. ЧИСЛЕННОЕ РЕШЕНИЕ

Преобразуем систему уравнений (1.1)–(1.12). Для этого выразим напряжения в клеточных фазах $\sigma _{{}}^{{(1)}}$ и $\sigma _{{}}^{{(2)}}$ из уравнений (1.8), (1.9) и подставим их в уравнения импульсов (1.2) и (1.3). Компоненты тензоров скоростей деформаций заменим с помощью кинематических соотношений (1.12). Добавив уравнения (1.1), получим полную систему для нахождения ${{\phi }_{1}}$, ${{\phi }_{2}}$ и ${{{v}}_{1}}$, ${{{v}}_{2}}$.

Введем безразмерные величины:

$t* = t\frac{E}{\mu },\quad x* = \frac{x}{{{{h}_{0}}}},\quad R_{s}^{*} = \frac{{{{R}_{s}}}}{{{{h}_{0}}}},\quad h_{k}^{*} = \frac{{{{h}_{k}}}}{{{{h}_{0}}}},\quad \sigma _{{}}^{{(k)*}} = \frac{{\sigma _{{}}^{{(k)}}}}{E},\quad \sigma _{\alpha }^{{(k)*}} = \frac{{\sigma _{\alpha }^{{(k)}}}}{E},\quad \tau _{{}}^{{(k)*}} = \frac{{\tau _{{}}^{{(k)}}}}{E},\quad \tau _{\alpha }^{{(k)*}} = \frac{{\tau _{\alpha }^{{(k)}}}}{E},$
$\tau _{{}}^{{(12)*}} = \frac{{\tau _{{}}^{{(12)}}}}{E},\quad \tau _{\alpha }^{{(12)*}} = \frac{{\tau _{\alpha }^{{(12)}}}}{E},\quad {{{v}}^{{(k)*}}} = {{{v}}^{{(k)}}}\frac{\mu }{{E{{h}_{0}}}},\quad \Pi _{k}^{*} = \frac{{{{\Pi }_{k}}}}{E},\quad \Pi _{{12}}^{*} = \frac{{{{\Pi }_{{12}}}}}{E},\quad E_{k}^{*} = \frac{{{{E}_{k}}}}{E},\quad E_{{12}}^{*} = \frac{{{{E}_{{12}}}}}{E},$
$\mu _{k}^{*} = \frac{{{{\mu }_{k}}}}{\mu },\quad \mu _{{kn}}^{*} = \frac{{{{\mu }_{{kn}}}}}{\mu },\quad m_{k}^{*} = \frac{{{{m}_{k}}}}{E},\quad k_{{12}}^{*} = \frac{{{{k}_{{12}}}h_{0}^{2}}}{\mu }(k = 1,\;2;n = 1,\;2;\alpha = y,\;z)$

Здесь E и $\mu $ – некоторые характерные значения соответствующих групп коэффициентов. В дальнейшем звездочку при безразмерных параметрах будем опускать.

Реализация численного метода решения полученной системы на каждом шаге по времени начинается с решения уравнений для ${{{v}}_{1}}$ и ${{{v}}_{2}}$, при этом значения ${{\phi }_{1}}$ и ${{\phi }_{2}}$ берутся с предыдущего временного шага. Затем при найденных скоростях решаются уравнения (1.1), позволяющие найти ${{\phi }_{1}}$ и ${{\phi }_{2}}$.

На каждом шаге сначала находятся значения ${{{v}}_{1}}$ и ${{{v}}_{2}}$ на отрезке $\left[ {0;{{h}_{1}}(t)} \right]$ (на этом отрезке присутствуют обе клеточные фазы), после чего ${{{v}}_{2}}$ продолжается на отрезок $\left[ {{{h}_{1}}(t);{{h}_{2}}(t)} \right]$, на котором присутствует только вторая клеточная фаза.

При расчете скоростей на отрезке $\left[ {0;{{h}_{1}}(t)} \right]$ вводится безразмерная координата ${{\xi }_{1}} = x{\text{/}}{{h}_{1}}(t)$, что позволяет перейти от решения уравнений с подвижной верхней границей к решению уравнений на отрезке [0; 1].

Система уравнений для безразмерных неизвестных ${{{v}}_{1}}$ и ${{{v}}_{2}}$ имеет следующий вид:

(3.1)
$\begin{gathered} \frac{\partial }{{\partial {{\xi }_{1}}}}\left( {2{{\mu }_{1}}\frac{{{{\phi }_{1}}}}{\Delta } \cdot \frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }_{1}}}} + 2{{\mu }_{2}}\frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta } \cdot \frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right) + \;\frac{{2{{\mu }_{1}}}}{{3\Delta }}\left( {\phi _{1}^{2}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - {{\phi }_{2}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right)} \right) \cdot \frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }_{1}}}} + \\ + \;\frac{{2{{\mu }_{2}}}}{{3\Delta }}\left( {{{\phi }_{1}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - \phi _{2}^{2}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right)} \right) \cdot \frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}} + \;{{k}_{{12}}}{{\phi }_{1}}{{\phi }_{2}}h_{1}^{2}({{{v}}_{2}} - {{{v}}_{1}}) = - {{h}_{1}}\left( {\Phi + \frac{{\partial {{\Sigma }_{1}}}}{{\partial {{\xi }_{1}}}}} \right) \\ \end{gathered} $
$\begin{gathered} \frac{\partial }{{\partial {{\xi }_{1}}}}\left( {2{{\mu }_{1}}\frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta } \cdot \frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }_{1}}}} + 2{{\mu }_{2}}\frac{{{{\phi }_{2}}}}{\Delta } \cdot \frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right) + \frac{{2{{\mu }_{1}}}}{{3\Delta }}\left( {{{\phi }_{2}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - \phi _{1}^{2}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right)} \right) \cdot \frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }_{1}}}} + \\ + \;\frac{{2{{\mu }_{2}}}}{{3\Delta }}\left( {\phi _{2}^{2}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - {{\phi }_{1}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right)} \right)\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}} + {{k}_{{12}}}{{\phi }_{1}}{{\phi }_{2}}h_{1}^{2}({{{v}}_{1}} - {{{v}}_{2}}) = - {{h}_{1}}\left( { - \Phi + \frac{{\partial {{\Sigma }_{2}}}}{{\partial {{\xi }_{1}}}}} \right) \\ \end{gathered} $

Здесь $\Delta = 1 - {{\phi }_{1}}{{\phi }_{2}}$,

$\begin{gathered} \Phi = \frac{1}{{3\Delta }}\left( {\left( {\phi _{1}^{2}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - {{\phi }_{2}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right)} \right)} \right.\left( {\frac{{{{\mu }_{1}}}}{{{{\mu }_{{11}}}}}I({{\tau }^{{(1)}}}) + \frac{{{{\mu }_{1}}}}{{{{\mu }_{{12}}}}}I({{\tau }^{{(12)}}})} \right) + \\ \left. { + \;\left( {{{\phi }_{1}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{2}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right) - \phi _{2}^{2}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {\frac{{{{\phi }_{1}}}}{{{{\phi }_{1}} + {{\phi }_{2}}}}} \right)} \right)\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}}I({{\tau }^{{(2)}}}) + \frac{{{{\mu }_{2}}}}{{{{\mu }_{{21}}}}}I({{\tau }^{{(12)}}})} \right)} \right), \\ \end{gathered} $
${{\Sigma }_{1}} = \left( {\frac{{{{\phi }_{1}}}}{\Delta } \cdot \frac{{{{\mu }_{1}}}}{{{{\mu }_{{11}}}}} + 1} \right){{\tau }^{{(1)}}} + \frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}}{{\tau }^{{(2)}}} + \left( {\frac{{{{\phi }_{1}}}}{\Delta } \cdot \frac{{{{\mu }_{1}}}}{{{{\mu }_{{12}}}}} + \frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{2}}}}{{{{\mu }_{{21}}}}} + 1} \right){{\tau }^{{(12)}}},$
${{\Sigma }_{2}} = \frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{1}}}}{{{{\mu }_{{11}}}}}{{\tau }^{{(1)}}} + \left( {\frac{{{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}} + 1} \right){{\tau }^{{(2)}}} + \left( {\frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{1}}}}{{{{\mu }_{{12}}}}} + \frac{{{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{2}}}}{{{{\mu }_{{21}}}}} + 1} \right){{\tau }^{{(12)}}}$

В качестве граничных условий при решении системы (3.1) используется равенство ${{{v}}_{1}} = {{{v}}_{2}} = 0$ при ${{\xi }_{1}} = 0$, а при ${{\xi }_{1}} = 1$ – соотношения (2.6) и (2.7).

Условие (2.7) при ${{\xi }_{1}} = 1$ после подстановки в него выражений для $\sigma _{{}}^{{(1)}}$ и $\sigma _{{}}^{{(2)}}$, полученных из (1.8) и (1.9), с учетом выражения для межфазного давления p** (2.5) и равенства нулю гидростатического давления принимает следующий вид (верхний индекс “–”, указывающий на принадлежность к области 12 совместного присутствия обеих фаз опущен):

(3.2)
$\begin{gathered} 2{{\mu }_{1}}\frac{{{{\phi }_{1}}}}{\Delta }\left( {1 - \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}} \right)\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }_{1}}}} + 2{{\mu }_{2}}\frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta }\left( {1 - \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}} \right)\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}} + \\ + \;{{h}_{1}}\left( {\frac{{{{\phi }_{1}}}}{\Delta } \cdot \frac{{{{\mu }_{1}}}}{{{{\mu }_{{11}}}}}\left( {{{\tau }^{{(1)}}} - \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(1)}}})} \right)} \right. + {{\tau }^{{(1)}}} + \frac{{{{\phi }_{1}}{{\phi }_{2}}}}{\Delta }.\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}}\left( {{{\tau }^{{(2)}}} - \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(2)}}})} \right) + \\ + \;\frac{{{{\phi }_{1}}}}{\Delta }\left( {\frac{{{{\mu }_{1}}}}{{{{\mu }_{{12}}}}} + {{\phi }_{2}} \cdot \frac{{{{\mu }_{2}}}}{{{{\mu }_{{21}}}}}} \right)\left( {{{\tau }^{{(12)}}} - \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(12)}}})} \right) + {{\tau }^{{(12)}}} - \\ \left. { - \;\frac{1}{3}\frac{{{{{(\phi _{1}^{{}})}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}\left( {\phi _{2}^{ + }\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}}I({{\tau }^{{(2) + }}}) + 2\frac{{{{\mu }_{2}}}}{{{{h}_{1}}}}{{{\left. {\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right|}}^{ + }}} \right)} \right) = 0 \\ \end{gathered} $

Поскольку ${{\tau }^{{(12)}}} = 0$ в области $x \in \left[ {{{h}_{1}}(t);{{h}_{2}}(t)} \right]$, то из уравнения импульсов (1.3) и второго условия (2.2) следует, что в этой области выполнено уравнение

(3.3)
${{\phi }_{2}}{{\sigma }^{{(2)}}} + {{\tau }^{{(2)}}} = 0$

После подстановки в (3.3) выражения для $\sigma _{{}}^{{(2)}}$ получаем соотношение

(3.4)
$2{{\mu }_{2}}\phi _{2}^{{}}\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}} + {{h}_{1}}\left( {\phi _{2}^{{}}\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}} + 1} \right){{\tau }^{{(2)}}} = 0$

Уравнение (3.4) позволяет исключить ${{\left. {\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right|}^{ + }}$ из граничного условия (3.2).

Из условий (2.6) и (3.3) следует, что $\phi _{2}^{ - }{{\sigma }^{{{{{(2)}}^{ - }}}}} + {{\tau }^{{(2) - }}} + {{\tau }^{{(12) - }}} = p{\text{**}}$ при ${{\xi }_{1}} = 1$. После подстановки выражений для $\sigma _{{}}^{{(1)}}$ и $\sigma _{{}}^{{(2)}}$ из (1.8) и (1.9) и выражения для межфазного давления p** (2.5) получаем второе граничное условие при ${{\xi }_{1}} = 1$ для решения уравнений (3.1) в следующем виде:

(3.5)
$\begin{gathered} 2{{\mu }_{1}}\frac{{{{\phi }_{1}}}}{\Delta }\left( {{{\phi }_{2}} + \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}} \right)\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }_{1}}}} + 2{{\mu }_{2}}\frac{{{{\phi }_{2}}}}{\Delta }\left( {1 + \frac{1}{3}{{\phi }_{1}}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}} \right)\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}} + \\ + \;{{h}_{1}}\left( {\frac{{{{\phi }_{1}}}}{\Delta } \cdot \frac{{{{\mu }_{1}}}}{{{{\mu }_{{11}}}}}\left( {{{\phi }_{2}}{{\tau }^{{(1)}}} + \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(1)}}})} \right)} \right. + \frac{{{{\phi }_{2}}}}{\Delta } \cdot \frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}}\left( {{{\tau }^{{(2)}}} + \frac{1}{3}{{\phi }_{1}}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(2)}}})} \right) + \\ + \;{{\tau }^{{(2)}}} + \frac{{{{\phi }_{1}}}}{\Delta }\frac{{{{\mu }_{1}}}}{{{{\mu }_{{12}}}}}\left( {{{\phi }_{2}}{{\tau }^{{(12)}}} + \frac{1}{3}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(12)}}})} \right) + \frac{{{{\phi }_{2}}}}{\Delta }\frac{{{{\mu }_{2}}}}{{{{\mu }_{{21}}}}}\left( {{{\tau }^{{(12)}}} + \frac{1}{3}{{\phi }_{1}}\frac{{{{{(\phi _{2}^{ + })}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}I({{\tau }^{{(12)}}})} \right) + \\ \left. { + \;{{\tau }^{{(12)}}} + \frac{1}{3}\frac{{{{{(\phi _{1}^{{}})}}^{2}}}}{{{{\phi }_{1}} + \phi _{2}^{ + }}}\left( {\phi _{2}^{ + }\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}}I({{\tau }^{{(2) + }}}) + 2\frac{{{{\mu }_{2}}}}{{{{h}_{1}}}}{{{\left. {\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right|}}^{ + }}} \right)} \right) = 0 \\ \end{gathered} $
где величина ${{\left. {\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right|}^{ + }}$ исключается с помощью (3.4).

В результате решения системы (3.1) при соответствующих граничных условиях находится скорость клеток первой фазы во всей области, которую они занимают. Скорость клеток второй фазы подлежит определению дополнительно на отрезке $\left[ {{{h}_{1}}(t);{{h}_{2}}(t)} \right]$. В этой области будем использовать интеграл уравнения импульсов для второй клеточной фазы (3.3) и перейдем к безразмерной координате ${{\xi }_{2}} = x{\text{/}}{{h}_{2}}(t)$. После подстановки выражения для ${{\sigma }^{{(2)}}}$ уравнение (3.3) принимает аналогичный (3.4) вид:

(3.6)
$2{{\mu }_{2}}{{\phi }_{2}}\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{2}}}} + {{h}_{2}}\left( {{{\phi }_{2}}\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}} + 1} \right){{\tau }^{{(2)}}} = 0$

Интегрирование уравнения (3.6) выполняется на отрезке ${{\xi }_{2}} \in \left[ {{{h}_{1}}(t){\text{/}}{{h}_{2}}(t);\;1} \right]$. В качестве граничного условия при ${{\xi }_{2}} = {{h}_{1}}(t){\text{/}}{{h}_{2}}(t)$ используется значение ${v}_{2}^{ + }$, полученное из условия на разрыве (2.3), которое включает в себя ${v}_{2}^{ - }$, полученное из рассмотренного выше решения для области совместного присутствия двух клеточных фаз.

Вычисление интегралов, присутствующих в выражениях для активных напряжений, выполнено путем разложения подынтегральной функции в ряд по формуле Тейлора второго порядка точности и с помощью пятиточечной квадратуры Гаусса [26], при этом учитывалось различие пределов интегрирования для внутренних и граничных точек среды, т.е. точек, удаленных от границы слоя на расстояние, не превышающее радиус дальнодействия.

Разностная схема для решения системы (3.1), полученная интегро-интерполяционным методом [27], монотонна и имеет первый порядок аппроксимации по ${{\xi }_{1}}$. Монотонность достигается использованием направленных разностей при аппроксимации $\partial {{{v}}_{1}}{\text{/}}\partial {{\xi }_{1}}$ и $\partial {{{v}}_{2}}{\text{/}}\partial {{\xi }_{1}}$ в зависимости от знаков стоящих при них коэффициентов. Полученная система разностных уравнений решалась методом матричной прогонки. Уравнение (3.6) решалось методом Эйлера.

Полученные значения ${{{v}}_{1}}({{\xi }_{1}})$ и ${{{v}}_{2}}({{\xi }_{2}})$ используются далее при решении уравнений для ${{\phi }_{1}}$ и ${{\phi }_{2}}$.

(3.7)
$\begin{gathered} \frac{{\partial {{\phi }_{1}}}}{{\partial t}} + \frac{1}{{{{h}_{1}}}}\frac{\partial }{{\partial {{\xi }_{1}}}}\left( {{{\phi }_{1}}\left( {{{{v}}_{1}} - \frac{{d{{h}_{1}}}}{{dt}}{{\xi }_{1}}} \right)} \right) + \frac{1}{{{{h}_{1}}}}\frac{{d{{h}_{1}}}}{{dt}}{{\phi }_{1}} = 0 \\ \frac{{\partial {{\phi }_{2}}}}{{\partial t}} + \frac{1}{{{{h}_{2}}}}\frac{\partial }{{\partial {{\xi }_{2}}}}\left( {{{\phi }_{2}}\left( {{{{v}}_{2}} - \frac{{d{{h}_{2}}}}{{dt}}{{\xi }_{2}}} \right)} \right) + \frac{1}{{{{h}_{2}}}}\frac{{d{{h}_{2}}}}{{dt}}{{\phi }_{2}} = 0 \\ \end{gathered} $

Эти уравнения решаются по отдельности. Численное решение уравнений (3.7) было выполнено с использованием TVD схемы Хартена с ограничителем minmod [28, 29].

Уравнения (3.1), (3.5) и (3.7) дополняются уравнениями ${{\dot {h}}_{1}} = {{{v}}_{1}}$ при ${{\xi }_{1}} = 1$ и ${{\dot {h}}_{2}} = {{{v}}_{2}}$ при ${{\xi }_{2}} = 1$, которые описывают изменение толщины клеточных фаз. Эти уравнения решаются методом Эйлера.

При решении задач используется разбиение отрезков $[0;\;{{h}_{1}}]$ и $[0;\;{{h}_{2}}]$ на одинаковое число частей. При переходе от одного разбиения к другому (т.е. при переходе от координаты ${{\xi }_{1}}$ к координате ${{\xi }_{2}}$) используется пересчет соответствующих величин с использованием линейной интерполяции.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Будем исследовать эволюцию плотностей двух типов клеток, для которых активные стягивающие взаимодействия внутри фаз доминируют над межфазными активными стягивающими взаимодействиями, так что последними можно пренебречь. При этом будем считать, что активные взаимодействия внутри первой клеточной фазы превышают таковые внутри второй клеточной фазы (${{m}_{1}} > {{m}_{2}}$). В настоящее время отсутствуют экспериментальные данные, позволяющие получить оценки числовых значений коэффициентов. Поэтому свойства системы будут исследованы в зависимости от значений безразмерных параметров. В последующих расчетах приняты значения безразмерных параметров, характеризующих напряжения, развивающиеся в результате активных межклеточных взаимодействий, такие же, как в [24]: ${{m}_{1}} = 12$, ${{m}_{2}} = 6$. Активное взаимодействие клеточных фаз одна с другой сводится только к расталкивающей силе. Для остальных безразмерных параметров используются два набора числовых значений, близкие к принятым в [24]. Набор 1: ${{\mu }_{1}} = {{\mu }_{2}} = 1$, ${{\mu }_{{12}}} = {{\mu }_{{21}}} = 0.5$, ${{E}_{1}} = 0.33$, $E_{2}^{{}} = 0.33$, $E_{{12}}^{{}} = 0.167$, ${{k}_{{12}}} = 0.3$, ${{R}_{s}}$ = = 0.01, ${{\phi }_{{10}}}(x) = {{\phi }_{{20}}}(x) = 0.4$. Набор 2 отличается от набора 1 значениями параметров, характеризующих расталкивающую активность клеток: ${{E}_{1}} = 0.33$, $E_{2}^{{}} = 0.12$, $E_{{12}}^{{}} = 0.06$. Значение показателя степени $\theta $, присутствующего в зависимостях для активных давлений, будет в дальнейшем выбираться в соответствии с данными расчетов.

Будем сравнивать численные решения двух задач, описывающих перераспределение клеток в бесконечном плоском слое, различающихся граничными условиями. В обеих постановках внешние границы клеточных фаз подвижны, но в одном случае для обеих фаз эти границы совпадают (как в [24]), а в другом движутся независимо в соответствии с условиями, сформулированными выше (разд. 2).

На рис. 2 представлены результаты расчетов эволюции пространственно-однородных начальных распределений ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}}$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}}$ при значениях параметров из набора 1 и $\theta = 1$ [24]. Пунктирные кривые соответствуют задаче с общей границей, а сплошные – задаче с двумя независимо движущимися границами. На рис. 2а показаны распределения плотностей клеточных фаз ${{\phi }_{1}}$ и ${{\phi }_{2}}$ в момент времени $t = 1.48$. Рисунок 2б демонстрирует эволюцию границ клеточных фаз в задачах с одной общей границей (пунктир) и в задаче с двумя независимо движущимися границами (сплошные кривые). Обрыв сплошной линии 1 на рис. 2а соответствует границе области, занятой фазой: ${{\phi }_{1}} \equiv 0$ при бо́льших значениях координаты $x$. Здесь и на последующих графиках видно незначительное падение концентраций фаз в узких (порядка нескольких радиусов дальнодействия) зонах вблизи границ, которое имеет место вследствие уменьшения активной стягивающей силы из-за сокращения области интегрирования в соотношении (1.5). Этот мелкомасштабный модельный эффект несуществен для исследуемого процесса сортировки.

Рис. 2.

Решения задач о перераспределении клеток в плоском слое при начальных условиях ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}}$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}}$ в момент времени $t = 1.48$. Используются значения параметров из набора 1 и $\theta = 1$. (а) Распределения концентраций клеток в задаче с общей границей (пунктирные кривые) и двумя независимыми границами (сплошные кривые): 1 и 2 для ${{\phi }_{1}}$ и ${{\phi }_{2}}$ соответственно. (б) Эволюция границ клеточных фаз. Представлены зависимости от времени безразмерных координат границ: пунктирная кривая – $h{\text{/}}{{h}_{0}}$ ($h = {{h}_{1}} = {{h}_{2}}$) в задаче с общей границей, сплошные кривые 1 и 2 – ${{h}_{1}}{\text{/}}{{h}_{0}}$ и ${{h}_{2}}{\text{/}}{{h}_{0}}$ в задаче с независимо движущимися границами.

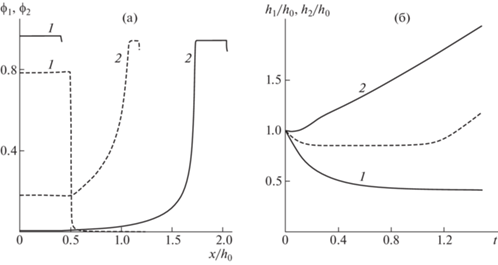
Из рис. 2 видно, что в рамках обеих постановок задач удается описать тенденцию к разделению клеточных фаз: фаза 1, в которой активные стягивающие взаимодействия между клетками сильнее, стремится занять центральную область, а фаза 2 – периферийную. При независимо перемещающихся границах формируется поверхность разрыва, ограничивающая область вне которой фаза 1 полностью отсутствует, при общей границе разрыва нет, но имеется узкая переходная зона, в которой ${{\phi }_{1}}$ падает до очень малых значений. Что касается ${{\phi }_{2}}$, то в этой зоне она становится очень малой, а по выходе из нее постепенно повышается, вблизи внешней границы выходя на плато. Сортировка клеток, описываемая решением задачи с двумя независимо перемещающимися границами, происходит быстрее сортировки, описываемой решением задачи с одной общей границей в силу отсутствия скрепления клеток разных фаз на внешней границе. Это видно из того, что концентрация клеток второй фазы ${{\phi }_{2}}$, расположенных во внутренней области $\left[ {0;{{h}_{1}}} \right]$, значительно ниже для решений первой задачи по сравнению со значениями ${{\phi }_{2}}$ в той же области, полученными во второй задаче, а плато ${{\phi }_{2}}$ вблизи внешней границы слоя заметно шире.

В обоих случаях наблюдается широкая переходная зона роста ${{\phi }_{2}}$, в которой имеет место низкая концентрация всех клеток. К этому не слишком физичному обстоятельству в задаче с независимо перемещающимися границами добавляется еще одна не согласующаяся с реальными процессами особенность: граница оказавшейся снаружи фазы демонстрирует постоянное движение наружу, естественно, сопровождающееся разрастанием зоны разрежения.

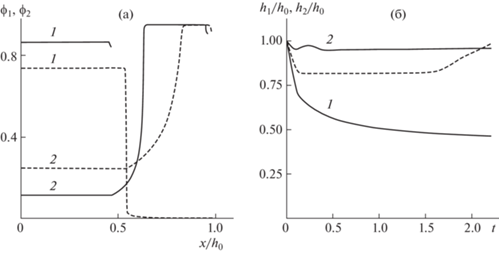
Оба указанных модельных эффекта связаны с доминированием при $\theta = 1$ активных сил расталкивания над активными стягивающими силами. Картина существенно меняется при $\theta > 1$. На рис. 3 показаны результаты расчетов для обеих постановок задач при тех же значениях параметров, что на рис. 2, с единственным отличием: $\theta = 1.8$. Распределения фазовых плотностей даны при $t = 2.2$. Теперь переходная область в задаче с независимо движущимися границами фаз становится значительно уже, тогда как в задаче с общей границей ее заметного сужения не происходит. Соответственно, в задаче с независимыми границами картина перемещения границ претерпевает радикальное изменение: более нет заметного расширения слоя, тогда как в задаче с общей границей картина перемещения границы практически не изменяется. Что касается сортировки клеточных фаз и ускорения этого процесса при учете расхождения границ, то тут никаких существенных изменений не происходит.

Рис. 3.

Решения задач о перераспределении клеток в плоском слое при начальных условиях ${{\phi }_{1}}(0,\;x) = {{\phi }_{{10}}}$ и ${{\phi }_{2}}(0,\;x) = {{\phi }_{{20}}}$ в момент времени $t = 2.2$. Используются значения параметров из набора 1; $\theta = 1.8$. (а) Распределения плотностей фаз; (б) эволюция их границ. Обозначения на рисунках а и б совпадают с обозначениями на рисунках 2а и 2б соответственно.

Выполненные многочисленные численные эксперименты показали, что имеются области параметров, в которых эволюция распределений плотностей клеточных фаз для двух постановок задачи может различаться значительно. При этом для разделяющихся границ распределения плотностей качественно сохраняют ту же форму, что и в расчетах, представленных выше, тогда как в случае общей границы поведение решений оказывается существенно иным. Таким образом, допущение разделения границ ведет к повышению устойчивости результата. Покажем это на конкретном примере.

Изменим параметры, определяющие расталкивающую активность клеток, приняв набор параметров 2 и $\theta = 1.2$. На рис. 4а представлены распределения концентраций клеточных фаз в случае, когда на начальные пространственно-однородные распределения (те же, что и в примерах, рассмотренных выше) наложены гармонические возмущения малой амплитуды: ϕ1(0, x) = = ${{\phi }_{{10}}} + 0.001\cos (15.5\pi x)$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}} - 0.001\cos (15.5\pi x)$. Эволюция этих начальных распределений клеток в задаче с общей границей приводит к формированию слоистой структуры, в которой чередуются области с различным соотношением между плотностями клеточных фаз. Использование малых случайных возмущений начальных пространственно-однородных распределений ${{\phi }_{1}}(0,\;x) = {{\phi }_{{10}}} + 0,001\;{\text{random}}(x)$ и ${{\phi }_{2}}(0,\;x) = {{\phi }_{{20}}} - 0,001\;{\text{random}}(x)$ (функция ${\text{random}}(x)$ генерирует равномерно распределенную на отрезке [–1, 1] случайную величину при каждом значении x) приводит к колебательному характеру концентраций клеток со случайным распределением амплитуд и “периодов”. С другой стороны, в задаче с разделяющимися границами возмущения (и синусоидальные, и случайные) затухают с формированием распределений, представленных сплошными кривыми на рис. 4б.

Рис. 4.

(а) Распределения плотностей клеточных фаз по толщине слоя в момент времени $t = 5$ при значениях параметров из набора 2 и $\theta = 1.2$: (а) в задаче с одной внешней границей с начальными распределениями ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}} + 0.001\cos (15.5\pi x)$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}} - 0.001\cos (15.5\pi x)$ (пунктирная кривая – ${{\phi }_{1}}$ и сплошная – ${{\phi }_{2}}$); (б) в задачах с одной клеточной границей (пунктирные кривые) и с раздельными границами (сплошные кривые) при начальных распределениях ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}}$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}}$ (1 и 2 для ${{\phi }_{1}}$ и ${{\phi }_{2}}$ соответственно).

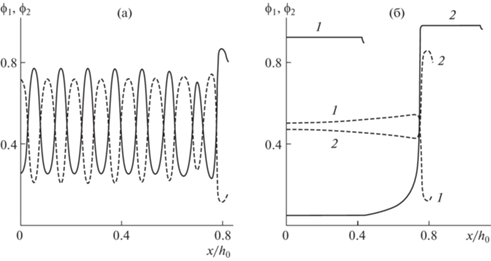
На рис. 4б представлены также распределения концентраций клеточных фаз в задаче с общей внешней границей при невозмущенных начальных условиях ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}}$ и ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}}$. Решение дает в этом случае распределения, качественно отличающиеся от ожидаемых: максимум ${{\phi }_{1}}$ и минимум ${{\phi }_{2}}$ достигаются на некоторой близкой к внешней границе поверхности. Дальнейшая эволюция приводит лишь к закреплению этого паттерна, и сортировка не происходит.

Может показаться странной получающаяся при вычислениях стабильность такого поведения, если принять во внимание неустойчивость относительно малых возмущений, показанную на рис. 4а. Однако специально проведенные расчеты показали, что скорость развития возмущений значительно уменьшается с их амплитудой, и при достаточно малых амплитудах они на обследуемом временном интервале не успевают развиться.

ЗАКЛЮЧЕНИЕ

В работе предложена новая постановка задачи о трансформации клеточной системы, составленной клетками разных типов, в рамках подхода, основанного на представлении такой системы многофазной сплошной средой. В отличие от постановки, рассмотренной ранее, допускается независимое перемещение границ, ограничивающих каждую клеточную фазу. Таким образом, оказывается возможным описывать образование и перемещение фронтов, разделяющих области с различными объемными концентрациями клеток разных типов. Сформулированы условия на таких разрывах. Численно решена и исследована модельная задача об эволюции первоначально однородной смеси клеток двух типов, заполняющей бесконечный плоский слой в предположении, что внешние границы каждой клеточной фазы перемещаются независимо. Проанализировано влияние различных параметров, характеризующих активные межклеточные воздействия, на формирование клеточных структур. В широком диапазоне определяющих параметров модель описывает известное явление клеточной сортировки: клетки с более сильными стягивающими активными взаимодействиями стремятся занять центральную область, вытесняя на периферию клетки, у которых эти взаимодействия слабее. Результаты сравнивались с решением аналогичной задачи, в которой внешние границы фаз остаются принудительно совпадающими. Новая постановка физически более адекватна и дает возможность расширить диапазон параметров, в котором получается качественно тот же результат. Методология, развитая в работе, может быть применена к широкому классу задач, описывающих поведение смесей клеток с различными моделями активности.

Работа поддержана РФФИ (проект № 20-01-00329) и Госпрограммой АААА-А19-119012990119-3.

Список литературы

  1. Beloussov L.V., Dorfman J.G., Cherdantzev V.G. Mechanical stresses and morphological patterns in amphibian embryos // J. Embr. Exp. Morphol. 1975. V. 34. P. 559–574.

  2. Keller R., Davidson L.A., Shook D.R. How we are shaped: The biomechanics of gastrulation // Differentiation. 2003. V. 71. P. 171–205.

  3. Mammoto T., Ingber D.E. Mechanical control of tissue and organ development // Development. 2010. V. 137. № 9. P. 1407–1420.

  4. Steinberg M.S., Wiseman L.L. Do morphogenetic tissue rearrangements require active cell movements? // J. Cell Biol. 1972. V. 55. P. 606–615.

  5. Foty R.A., Steinberg M.S. Cadherin-mediated cell-cell adhesion and tissue segregation in relation to malignancy // Int. J. Dev. Biol. 2004. V. 48. P. 397–409.

  6. Mehes E., Viscek T. Segregation mechanisms of tissue cells: from experimental data to models // Complex Adapt. Syst. Model. 2013. V. 1. P. 4.

  7. Mehes E., Viscek T. Collective motion of cells: from experiments to models // Integr. Biol. 2014. V. 6. № 9. P. 831–854.

  8. Graner F., Glazier J.A. Simulation of biological cell sorting using a two-dimensional extended Potts model // Phys. Rev. Lett. 1992. V. 69. P. 2013–2016.

  9. Glazier J.A., Graner F. Simulation of the differential adhesion driven rearrangement of biological cells // Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1993. V. 47. P. 2128–2154.

  10. Krieg M., Arboleda-Estudillo Y., Puech P. H., Kafer J., Graner F., Muller D.J., Heisenberg C.P. Tensile forces govern germ-layer organization in zebrafish // Nat. Cell Biol. 2008. V. 10. P. 429–436.

  11. Zhang Y., Thomas G.L., Swat M., Shirinifard A., Glazier J.A. Computer simulations of cell sorting due to differential adhesion // PLoS One. 2011. V. 6. P. e24999.

  12. Brodland G.W., Chen H.H. The mechanics of heterotypic cell aggregates: insights from computer simulations // J. Biomech. Eng. 2000. V. 122. P. 402–407.

  13. Brodland G.W. The Differential Interfacial Tension Hypothesis (DITH): a comprehensive theory for the self-rearrangement of embryonic cells and tissues // J. Biomech. Eng. 2002. V. 124. P. 188–197.

  14. Fletcher A.G., Osborne J.M., Maini P.K., Gavaghan D.J. Implementing vertex dynamics models of cell populations in biology within a consistent computational framework // Prog. Biophys. Mol. Biol. 2013. V. 113. P. 299–326.

  15. Katsunuma S., Honda H., Shinoda T., Ishimoto Y., Miyata T., Kiyonari H., Abe T., Nibu K., Takai Y., Togashi H. Synergistic action of nectins and cadherins generates the mosaic cellular pattern of the olfactory epithelium // J. Cell Biol. 2016. V. 212. P. 561–575.

  16. Tanaka S. Simulation Frameworks for Morphogenetic Problems // Computation. 2015. V. 3. P. 197–221.

  17. Osborne J.M., Fletcher A.G., Pitt-Francis J.M., Maini P.K., Gavaghan D.J. Comparing individual-based approaches to modelling the self-organization of multicellular tissues // PLoS Comput. Biol. 2017. V. 13. P. e1005387.

  18. Camley B.A., Rappel W.J. Physical models of collective cell motility: from cell to tissue // J. Phys. D Appl. Phys. 2017. V. 50. P. 113002.

  19. Armstrong N.J., Painter K.J., Sherratt J.A. A continuum approach to modelling cell-cell adhesion // J Theor. Biol. 2006. V. 243. P. 98–113.

  20. Painter K.J., Bloomfield J.M., Sherratt J.A., Gerisch A. A nonlocal model for contact attraction and repulsion in heterogeneous cell populations // Bull. Math. Biol. 2015. V. 77. P. 1132–1165.

  21. Murakawa H., Togashi H. Continuous models for cell-cell adhesion// J. Theor. Biol. 2015. V. 374. P. 1–12.

  22. Carrillo J.A., Murakawa H., Sato M., Togashi H., Trush O. A population dynamics model of cell-cell adhesion incorporating population pressure and density saturation // J. Theor. Biol. 2019. V. 474. P. 14–24.

  23. Stein A.A., Logvenkov S.A., Volodyaev I.V. Continuum modeling of mechano-dependent reactions in tissues composed of mechanically active cells // BioSystems. 2018. V. 173. P. 225–234.

  24. Логвенков С.А., Штейн А.А. Континуальное моделирование биологической среды, составленной активно взаимодействующими клетками двух разных типов // Изв. РАН. МЖГ. 2020. № 6. С. 3–16.

  25. Белоусов Л.В., Логвенков С.А., Штейн А.А. Математическая модель активной биологической сплошной среды с учетом деформаций и переупаковки клеток // Изв. РАН. МЖГ. 2015. № 1. С. 3–14.

  26. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. 831 с.

  27. Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.

  28. Harten A. High resolution schemes for hyperbolic conservation laws // J. Comput. Phys. 1983. V. 49. № 3. P. 357–393.

  29. Чирков Д.В., Черный С.Г. Сравнение точности и сходимости некоторых TVD-схем // Вычислительные технологии. 2000. Т. 5. № 5. С. 86–107.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал