Известия РАН. Механика жидкости и газа, 2022, № 3, стр. 88-101

ЛИНЕЙНЫЕ ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ, ПОРОЖДЕННЫЕ ЛОКАЛИЗОВАННЫМИ ВО ВРЕМЕНИ И ПРОСТРАНСТВЕ ИСТОЧНИКАМИ В УПРУГОМ ОСНОВАНИИ

С. Ю. Доброхотов^a, *, Х. Х. Ильясов^a, **, О. Л. Толстова^b, c, ***

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^b Московский физико-технический институт
Долгопрудный, Россия

^c Национальный исследовательский московский государственный строительный университет
Москва, Россия

^* E-mail: s.dobrokhotov@gmail.com
^** E-mail: hisam.ilyasov@gmail.com
^*** E-mail: olgall1@rambler.ru

Поступила в редакцию 02.11.2021
После доработки 21.12.2021
Принята к публикации 21.12.2021

EDN: GLPTRQ
DOI: 10.31857/S0568528122030045

Полный текст (PDF)

Аннотация

На основе совместного решения уравнений теории волн в жидкости и упругости решена задача о возбуждении волн в жидком слое, лежащем на упругом полупространстве. Источник возбуждения специального вида, локализованный во времени и пространстве, располагается в упругой среде. С помощью разложения решения по собственным волнам дифференциального оператора получены интегральные представления для возвышения свободной поверхности жидкости в дальней зоне. Для случая длинных волн получены аналитические формулы для смещения поверхности жидкости. Проведен анализ влияния параметров источника на свойства порождаемых им волн.

Ключевые слова: волны цунами, слой жидкости, упругое полупространство, задача Коши, разложение по собственным волнам, локализованный во времени и пространстве источник .

В статье рассматривается задача о возбуждении волн на поверхности слоя жидкости, расположенного на упругом основании. Предполагается, что источник возбуждения располагается внутри упругого полупространства. В предыдущей работе [1] был рассмотрен случай, когда источник действует мгновенно – постановка задачи включала однородную систему уравнений и соответствующие краевые условия с локализованными начальными условиями. Там же были описаны различные подходы к решению данной задачи и приведена соответствующая библиография. Отметим, что исследуются решения совместной системы уравнений теории упругости в упругом полупространстве и теории волн в жидкости, которые связаны на границе раздела соответствующими граничными условиями (используется модель Г.С. Подъяпольского [2]).

Волновые процессы в рассматриваемой системе складываются из волн (мод), которые в предельных случаях соответствуют продольным и поперечным волнам внутри упругого основания, поверхностным волнам Рэлея и поверхностным волнам на воде. При этом внутренние моды и мода Рэлея имеют компоненты и на поверхности жидкости, а водяная мода имеет компоненты, распространяющиеся внутри упругого полупространства и на границе раздела. В начальный момент времени и при малых временах все эти моды оказывают влияние на возмущение свободной поверхности жидкости, но скорости распространения, соответствующие этим модам, сильно отличаются от скорости распространения водяной моды. Волны, соответствующие предельным упругим модам, распространяются значительно быстрее “водяной моды” (например, скорость упругих волн в базальте 22 680 км/ч – продольной и 12 600 км/ч – поперечной, а волны возвышения слоя воды глубиной 4 км – 700 км/ч). Поэтому через сравнительно небольшое время на поверхности воды остается водяная мода, и вопросы, касающиеся связанной с ней эволюции свободной поверхности, можно изучать отдельно, что и делается в данной работе. Предполагаем, что действие источника распределено по времени, поэтому рассматриваем в отличие от задачи [1] неоднородную систему уравнений с теми же, что и в ранее рассмотренной задаче, граничными условиями. Принцип Дюгамеля позволяет свести задачу к рассмотренной в [1] и воспользоваться полученными формулами, с дополнительным интегралом по времени. Считая действие источника непродолжительным [3, 4], представим решение в виде двух слагаемых – одно описывает распространяющиеся волны, а другое – волны, локализованные вокруг источника. Волны 2-го типа довольно быстро затухают, а 1-го представляют большой интерес и аналогично [1] мы можем их представить как волны, возбуждаемые “эквивалентным” мгновенным источником. Соображения, близкие к использованным в [1], приводят к эффективным формулам, и основной результат настоящей работы представлен в относительно простой интегральной формуле для решения.

1. УРАВНЕНИЯ И ГРАНИЧНЫЕ УСЛОВИЯ

Постановка задачи близка к постановке [3, 4], приведем ее для полноты изложения. Идеальная незавихренная жидкость описывается потенциалом перемещений $\Psi (x,z,t)$, деформации упругого полупространства – вектором смещений $U(x,z,t) = ({{u}_{1}},{{u}_{2}},{{u}_{3}})$, где $x \in {{R}^{2}}$ – горизонтальные, $z$ – вертикальная координаты. Плоскость z = 0 совпадает с невозмущенной поверхностью жидкости, а граница раздела слоев задается уравнением $z = - D$. $U$ и $\Psi $ определяются из следующей системы уравнений и граничных условий (в упругой среде – уравнения Ламе, в жидком слое – уравнение Лапласа)

${{U}_{{tt}}} = c_{t}^{2}{{\nabla }^{2}}U + (c_{l}^{2} - c_{t}^{2})\nabla {\text{div}}U + \frac{{{{\partial }^{2}}f}}{{\partial {{t}^{2}}}}(t,x,z),\quad z < - D$

${{\nabla }^{2}}\Psi = 0\quad - D < z < 0$

на невозмущенной поверхности жидкости $z = 0$

$\frac{1}{{\mathbf{g}}}{{\Psi }_{{tt}}} + {{\Psi }_{z}} = 0$

на границе раздела $z = - D$

$\frac{{\partial {{u}_{i}}}}{{\partial z}} + \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{i}}}} = 0,\quad i = 1,\;2$

$(c_{l}^{2} - c_{t}^{2})\left( {\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{u}_{2}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{u}_{3}}}}{{\partial z}}} \right) + 2c_{t}^{2}\frac{{\partial {{u}_{3}}}}{{\partial z}} = \rho \frac{{{{\partial }^{2}}\Psi }}{{\partial {{t}^{2}}}} + (\rho - 1){{u}_{3}},\quad \frac{{\partial \Psi }}{{\partial z}} = {{u}_{3}}$

(1.1)

${\text{и}}\quad U \to 0\quad {\text{при}}\quad z \to \infty $

Здесь $c = {{c}_{l}}{\text{/}}{{c}_{t}}$ – отношение скоростей продольных и поперечных волн в упругой среде, $\rho = {{\rho }_{w}}{\text{/}}{{\rho }_{e}}$ – отношение плотностей жидкости и упругой среды. Функция $f(t,x,z)$ описывает локализованные в пространстве и времени перемещения внутри упругого полупространства. Приведем приблизительные значения физических параметров задачи. Имеем $g \approx 0.01$ км/с², ${{\rho }_{w}} \approx 1024$ кг/м³ и для базальта (гранита) соответственно – ${{c}_{l}} \approx 22\,680$ км/ч (19 800 км/ч), ${{c}_{t}} \approx 12\,600$ км/ч (10 080 км/ч), ${{\rho }_{e}} \approx 3000$ кг/м³ (2600 кг/м³). Также мы будем предполагать, что глубина бассейна находится в пределах 2–5 км; тогда скорость распространения длинных волн в слое жидкости ${v}$ находится в пределах 700–720 км/ч. Таким образом, $\rho \approx 1{\text{/}}3$, ${v}{\text{/}}{{c}_{l}} \approx 0.035$, ${v}{\text{/}}{{c}_{t}} \approx 0.063$, и отношение скоростей поперечных и продольных волн в упругой среде c = ${{c}_{t}}{\text{/}}{{c}_{l}} \approx 1{\text{/}}\sqrt 3 $. К этим параметрам следует добавить характеристики начальных возмущений и размеры области, в которой изучаются решения.

Наиболее интересный объект с точки зрения приложений к волнам на воде – это превышение свободной поверхности $\eta $; если решения U, $\Psi $ приведенной выше системы получены, то функция $\eta $ восстанавливается по формуле

(1.2)

$\eta = {{\left. { - \frac{1}{{\mathbf{g}}}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{t}^{2}}}}} \right|}_{{z = 0}}} \equiv {{\left. {\frac{{\partial \Psi }}{{\partial z}}} \right|}_{{z = 0}}}$

Система (1.1) имеет нестандартную с точки зрения уравнений в частных производных форму. Однако мы можем использовать общие результаты из теории операторов и уравнений с частными производными, если представить систему в виде стандартной задачи Коши

(1.3)

$\frac{{{{\partial }^{2}}\Upsilon }}{{\partial {{t}^{2}}}} = \hat {L}\Upsilon + \frac{{{{\partial }^{2}}F}}{{\partial {{t}^{2}}}}(t,x,z),\quad \Upsilon {{|}_{{t = 0}}} = {{\Upsilon }_{0}}(x,z),\quad {{\left. {{{\Upsilon }_{t}}} \right|}_{{t = 0}}} = {{\Upsilon }_{1}}(x,z)$

где $\hat {L} = L\left( {i\frac{\partial }{{\partial x}},\frac{\partial }{{\partial z}}} \right)$ – матричный дифференциальный оператор по переменным (x, z), формулы для него приведены в [5]. Соответствующее физическое пространство, в котором заданы неизвестные функции $\Upsilon $ и функции ${{\Upsilon }_{0}}$, ${{\Upsilon }_{1}}$ (см. [5, 6]), задается следующим образом: оно состоит из упругого полупространства $z < - D(x)$ и двух плоскостей $z = 0$ и $z = - D$. Вектор-функция $\Upsilon = ({{u}_{1}},{{u}_{2}},{{u}_{3}},{{\psi }_{W}},{{\psi }_{H}}{{)}^{{\text{т}}}}$ состоит из пяти компонент, три из которых $U = ({{u}_{1}},{{u}_{2}},{{u}_{3}}{{)}^{{\text{т}}}}$ зависят от $x$, $z$, $t$, а две $\psi (x,t) = ({{\psi }_{W}},{{\psi }_{D}}{{)}^{{\text{т}}}}$, ${{\psi }_{W}} = {{\left. {\Psi (x,z,t)} \right|}_{{z = 0}}}$, ${{\psi }_{D}} = {{\left. {\Psi (x,z,t)} \right|}_{{z = - D}}}$ – зависят только от $x$, $t$. Здесь и ниже индекс ${\text{T}}$ означает транспонирование. Удобная энергетическая норма в пространстве решений в случае $D = {\text{const}}$ определяется скалярным произведением вида

$({{\Upsilon }^{1}},{{\Upsilon }^{2}}) = \int\limits_{\mathbb{R}_{x}^{2}} {\left( {\int\limits_{ - \infty }^{ - D} {\langle {{{\bar {U}}}^{1}},{{U}^{2}}\rangle } dz} \right)dx} + \rho \int\limits_{\mathbb{R}_{p}^{2}} {\left\langle {\bar {\tilde {\psi }}(p,t),R(p)\tilde {\psi }(p,t)} \right\rangle } dp$

$R = \left( {\begin{array}{*{20}{c}} {\left| p \right|\coth \left( {\left| p \right|D} \right)}&{ - \left| p \right|{\text{/}}\sinh \left( {\left| p \right|D} \right)} \\ {\left| p \right|{\text{/}}\sinh \left( {\left| p \right|D} \right)}&{ - \left| p \right|\coth \left( {\left| p \right|D} \right)} \end{array}} \right)$

Здесь и ниже $\left\langle { \cdot , \cdot } \right\rangle $ означает евклидово вещественное произведение соответствующих векторов, тильда – преобразование Фурье по горизонтальным переменным (${{x}_{1}}$, ${{x}_{2}}$), двойственные переменные обозначаются (${{p}_{1}}$, ${{p}_{2}}$) и черта – комплексное сопряжение.

Исследование существования и единственности решения задачи Коши для жидкости произвольной (включая случай переменной) глубины проведено в [5, 6]). Ниже рассматривается задача Коши с нулевыми начальными условиями

(1.4)

${{\left. U \right|}_{{t = 0}}} = 0,\quad {{\left. {\frac{{\partial U}}{{\partial t}}} \right|}_{{t = 0}}} = 0,\quad {{\left. {{{\psi }_{{W,D}}}} \right|}_{{t = 0}}} = 0,\quad {{\left. {\frac{{\partial {{\psi }_{{W,D}}}}}{{\partial t}}} \right|}_{{t = 0}}} = 0$

Предполагаем, что правая часть $\frac{{{{\partial }^{2}}F}}{{\partial {{t}^{2}}}}$ определяет локализованное в полупрострнстве и во времени возмущение перемещений. Считаем что у F не обращается в ноль только упругая компонента – вектор функция (возбуждения перемещений) $f(t,x,z)$, которая быстро убывает при отдалении от точки (x = 0, ${{z}_{0}}$), ${{z}_{0}} < 0$. Кроме того считаем, что $f(0,x,z) = \partial f(0,x,z){\text{/}}\partial t = 0$ и $f(t,x,z)$ при больших t выходит на функцию ${{F}_{\infty }}(x,z)$. Более того, для получения эффективных формул для решения полагаем, что вектор-функция $F(t,x,z)$ имеет вид

(1.5)

$f(t,x,z) = {\mathbf{a}}G(t)e(z)V(x){{e}^{{ - {\kern 1pt} {\kern 1pt} \frac{{{{{(z - {{z}_{0}})}}^{2}}}}{{2b_{3}^{2}}}}}},\quad V(x) = \frac{1}{{{{{(1 + {{{({{x}_{1}}{\text{/}}{{b}_{1}})}}^{2}} + {{{({{x}_{2}}{\text{/}}{{b}_{2}})}}^{2}})}}^{{3/2}}}}}$

где a – постоянный трехмерный вектор-столбец амплитуд с компонентами (${{a}_{1}}$, ${{a}_{2}}$, ${{a}_{{v}}}$), ${\mathbf{e}}(z)$ – гладкая срезающая функция, равная единице при $z < - D - 2\delta $ и принимающая нулевые значения при $z > - D - \delta $ (в окончательном ответе она роли не играет и вводится для математической строгости). Параметры ${{a}_{1}}$, ${{a}_{2}}$, ${{a}_{{v}}}$, ${{b}_{1}}$, ${{b}_{2}}$, ${{b}_{3}}$ – размерные константы (км), характеризующие амплитуды перемещений и их размер в источнике. Относительно безразмерной функции $G(t)$ будем предполагать, что $G = {{G}_{0}}(\lambda t)$, где ${{G}_{0}}(\tau )$ – гладкая функция на полупрямой $[0,\;\infty )$, выходящая на некоторую константу ${{C}_{0}}$, быстрее чем $1{\text{/}}{{\tau }^{\kappa }}$, $\kappa > 1$, когда $\tau \to \infty $, ${{G}_{0}}(\tau ) = 0$, ${{G}_{{0\tau }}}(\tau ) = 0$ при $t \leqslant 0$. Последние условия означают, что ${{G}_{0}}(0) = 0$, ${{G}_{{0\tau }}}(0) = 0$. Положительная вещественная величина $\lambda $ характеризует время выхода 1/λ функции $G(t)$ на ${{G}_{0}}$ и имеет размерность 1/с. Если ${{C}_{0}} \ne 0$, то без уменьшения общности можно считать, что ${{C}_{0}} = 1$ (включить ${{C}_{0}}$ в a). В этом случае для функции

(1.6)

$G(t) = \lambda {{G}_{0}}(\lambda t)$

в пределе $\lambda \to \infty $ имеем $G(t) \to \delta (t - 0)$. Равенство ${{C}_{0}} = 1$ означает, что вектор смещений в упругом основании выходит на V и в конечном итоге имеются остаточные смещения, и остаточные смещения отсутствуют, если ${{C}_{0}} = 0$. В окончательных формулах по существу присутствует производная $\partial G{\text{/}}\partial t$, поэтому нам удобно представить функцию ${{G}_{0}}(\tau )$ в виде

(1.7)

${{G}_{0}} = \int\limits_0^\tau g (\tau )d\tau \Leftrightarrow g = \frac{{\partial {{G}_{0}}}}{{\partial \tau }},\quad {{G}_{0}}(0) = 0$

Как и в [3, 4], приведем два примера функции g.

(а) $g(\tau ) = {{e}^{{ - \tau }}}P(\tau )$, где $P(\tau ) = \sum\nolimits_{k = 1}^n {\frac{{{{P}_{k}}}}{{k!}}} {{\tau }^{k}}$ – полином степени $n$ с коэффициентами ${{P}_{k}}$ такими, что ${{P}_{0}}$ = 0 and $\sum\nolimits_{k = 1}^n {{{P}_{k}}} = 1$.

(б) $g(\tau ) = a{{e}^{{ - \tau }}}(\sin (\alpha \tau + \phi ) - {\text{sin}}\phi )$, где $\alpha > 0$ и $\phi $ – вещественные параметры и a = (α² + 1)/ /$(\alpha {\text{cos}}\phi - {{\alpha }^{2}}{\text{sin}}\phi )$.

Здесь ${{G}_{0}} \to 1,$ когда $\tau \to \infty $. Примеры, когда ${{C}_{0}} = 0$, обсудим позже.

2. РЕШЕНИЕ В ВИДЕ ИНТЕГРАЛА ДЮГАМЕЛЯ

Решение задачи (1.3), (1.4) можно записать в виде интеграла Дюгамеля, переместив правую часть $\frac{{{{\partial }^{2}}F}}{{\partial {{t}^{2}}}}$ в начальные данные, заданные в момент времени $\tau $.

С помощью интеграла Дюгамеля решение $\Upsilon $ выражается через решение $W(t,\tau ,x,z)$ задачи

(2.1)

${{W}_{{tt}}} = \hat {L},\quad {{\left. W \right|}_{{t = \tau }}} = \frac{{\partial F}}{{\partial t}}(\tau ,x,z),\quad {{\left. {{{W}_{\tau }}} \right|}_{{t = \tau }}} = 0$

по формуле

(2.2)

$\Upsilon = \int\limits_0^t W (t,\tau ,x,z)d\tau $

Решение задачи (2.1), основанное на преобразовании Фурье по горизонтальным переменным, последующего разложения по собственным функциям (по различным модам) и обобщенным собственным функциям оператора $\hat {L}$, записанного в Фурье-представлении, получено в [1, 7]. В этих работах приведены аргументы, объясняющие, что локализованный источник порождает различные волны (моды), переходящие в пределе в продольные и поперечные внутренные упругие волны, поверхностные упругие волны Рэлея и водяные поверхностные волны. При этом скорость упругих волн существенно больше, чем скорость водяных волн и спустя какое-то время в ограниченной, но большой окрестности точки расположения источника, остаются только водяные поверхностные волны. Для таких волн получены формулы, которые можно применить для описания соответствующей функции $\eta $, с учетом отсутствия второй производной по времени. Учитывая представление правой части в виде (1.5), получим

(2.3)

$\begin{gathered} \eta = - \frac{1}{{4\pi }}\int\limits_0^t {\left[ {\sum\limits_ \pm {\int\limits_{\mathbb{R}_{p}^{2}} {{{e}^{{i(\langle p,x\rangle \pm (t - \xi )\omega (|p|))}}}} } \times } \right.} \\ \times \;\left. {\frac{{\partial {{C}_{W}}}}{{\partial t}}(p,\xi )\frac{{i{{\omega }^{4}}\left( {{\text{|}}p{\text{|}}} \right)A}}{{2c_{t}^{2}\cosh ({\text{|}}p{\text{|}}D)({{\omega }^{2}}\left( {{\text{|}}p{\text{|}}} \right) - g\left| p \right|\tanh ({\text{|}}p{\text{|}}D))}}dp} \right]d\xi \\ \end{gathered} $

(2.4)

$\begin{gathered} A = \left( {\frac{{{{p}^{2}}(k_{t}^{2} + {{p}^{2}})}}{{2{{k}_{t}}}} + \frac{{{{{(k_{t}^{2} + {{p}^{2}})}}^{2}}(k_{l}^{2} + {{p}^{2}})}}{{8k_{l}^{3}}} - \frac{{{{p}^{2}}(k_{t}^{2} + {{p}^{2}})}}{{{{k}_{l}}}}} \right. + \\ + \;{{\left. {\frac{{\rho {{\omega }^{4}}\left| p \right|\tanh \left( {\left| p \right|D} \right)}}{{4c_{t}^{4}{{{({{\omega }^{2}} - g\left| p \right|\tanh \left( {\left| p \right|D} \right))}}^{2}}}}\left( {{{g}^{2}} - 2g\frac{{{{\omega }^{2}}}}{{\left| p \right|}}\tanh \left( {\left| p \right|D} \right) + \frac{{{{\omega }^{4}}}}{{{{p}^{2}}}}} \right)} \right)}^{{ - 1/2}}} \\ \end{gathered} $

Здесь частота $\omega \left( {\left| p \right|} \right)$ определяется из сложного дисперсионного соотношения (см. (3.1) в [1]), и ${{C}_{W}}(p,\tau )$ – коэффициент разложения функции $\frac{{\partial F}}{{\partial t}}(\tau ,x,z)$ по собственным функциям оператора $\tilde {L}$, соответствующий в пределе водяной моде. В [1, 7, 8] показано, что функция $\omega \left( {\left| p \right|} \right)$ может быть приблизительно представлена в виде

(2.5)

${{\omega }^{2}} \approx g\left( {1 - \frac{{g\rho }}{{g + 2c_{t}^{2}\left| p \right|}}} \right)\left| p \right|\tanh \left( {D\left| p \right|} \right)$

Также из формул, полученных в этих работах, следует, что при выборе правой части в виде (1.4), коэффициент ${{C}_{W}}$ примет вид

(2.6)

$\begin{gathered} {{C}_{W}} = \lambda g(\lambda \tau ){{C}_{0}},\quad {{C}_{0}} = - iA{{b}_{1}}{{b}_{2}}{{e}^{{ - |p|b(\varphi )}}} \times \\ \times \;\left( {(i{{k}_{t}}\left\langle {p,a} \right\rangle - {{p}^{2}}{{a}_{{v}}}){{e}^{{{{k}_{t}}({{z}_{0}} + D)}}}{{f}_{t}} + \frac{{k_{t}^{2} + {{p}^{2}}}}{{2{{k}_{l}}}}\left( { - i\left\langle {p,a} \right\rangle + {{k}_{l}}{{a}_{{v}}}} \right){{e}^{{{{k}_{l}}({{z}_{0}} + D)}}}{{f}_{l}}} \right) \\ \end{gathered} $

$b(\varphi ) = \sqrt {b_{1}^{2}\mathop {\cos }\nolimits^2 \psi + b_{2}^{2}\mathop {\sin }\nolimits^2 \psi } ,\quad \left\langle {p,a} \right\rangle = {{p}_{1}}{{a}_{1}} + {{p}_{2}}{{a}_{2}}$

${{f}_{{t,l}}} \approx {{b}_{3}}\sqrt {2\pi } {{e}^{{\frac{{b_{3}^{2}k_{{t,l}}^{2}}}{2}}}}e({{z}_{0}} + b_{3}^{2}{{k}_{{t,l}}})\quad {{k}_{t}} = \sqrt {{{p}^{2}} - \lambda {\text{/}}c_{t}^{2}} ,\quad {{k}_{l}} = \sqrt {{{p}^{2}} - \lambda {\text{/}}c_{l}^{2}} $

Поменяем интеграл по времени в формуле (2.3) с интегралом по p и представим его в виде суммы

(2.7)

$\int\limits_9^t {{{e}^{{ \mp i\xi \omega (|p|)}}}} \frac{{\partial G}}{{\partial t}}(\xi )d\xi = \int\limits_0^\infty {{{e}^{{ \mp i\xi \omega (|p|)}}}} \frac{{\partial G}}{{\partial t}}(\xi )d\xi - \int\limits_\tau ^\infty {{{e}^{{ \mp i\tau \omega (|p|)}}}} \frac{{\partial G}}{{\partial t}}(\xi )d\xi $

В [3, 4] было показано, что второе слагаемое с интегралами в правой части последнего равенства быстро убывает при больших $\tau $ и определяет быстро осциллирующие и быстро затухающие волны в воде в области, расположенной над источником. Первое слагаемое, содержащее не зависящие от $\tau $ интегралы от $t$ c учетом соответствующих множителей ${{e}^{{i(\langle p,x\rangle \pm t\omega (|p|))}}}$, описывает распространяющиеся волны и именно оно представляет основной интерес. Соответствующие интегралы можно переписать в виде

(2.8)

$\int\limits_0^\infty {{{e}^{{ - i\frac{{\omega (|p|)}}{\lambda }}}}} g(\tau )d\tau = \sqrt {2\pi } {{\tilde {g}}^{ + }}\left( {\frac{{\omega \left( {\left| p \right|} \right)}}{\lambda }} \right)$

$\int\limits_0^\infty {{{e}^{{i\frac{{\tau \omega (|p|)}}{\lambda }}}}} g(\tau )d\tau = \sqrt {2\pi } {{\tilde {g}}^{ - }}\left( {\frac{{\omega \left( {\left| p \right|} \right)}}{\lambda }} \right),\quad {{\tilde {g}}^{ + }} = {{\bar {\tilde {g}}}^{ - }} = \tilde {g}$

где $\tilde {g} = {{\tilde {g}}^{ + }}({v})$ – преобразование Фурье функции g и черта означает комплексное сопряжение.

Для примера (a) имеем

(2.9)

$\sqrt {2\pi } \tilde {g} = \sum\limits_{k = 1}^n {\frac{{{{P}_{k}}}}{{{{{(1 + i{v})}}^{{k + 1}}}}}} = {{\left. {\gamma P\left( { - \mathop \gamma \limits^2 \mathop {\frac{\partial }{{\partial \gamma }}}\limits^1 } \right)\left( {\frac{\gamma }{{{{\gamma }^{2}} + {{{v}}^{2}}}} - i\frac{{v}}{{{{\gamma }^{2}} + {{\zeta }^{2}}}}} \right)} \right|}_{{\gamma = 1}}}$

и для примера (б)

(2.10)

$\sqrt {2\pi } \tilde {g} = a\left( {\frac{{\alpha ((1 + i{v})\cos (\phi ) - \alpha {\text{sin}}\phi )}}{{(1 + i{v})({{\alpha }^{2}} + {{{(1 + i{v})}}^{2}})}}} \right)$

Сохраняя теперь в (2.3) при временах $t \gg 1{\text{/}}\lambda $ только распространяющиеся волны, эту формулу можно переписать в виде

(2.11)

$\eta \approx - \frac{1}{{4\pi }}\sum\limits_ \pm {\int\limits_{\mathbb{R}_{p}^{2}} {{{e}^{{i(\langle p,x\rangle \pm t\omega (|p|))}}}} } \frac{{i\sqrt {2\pi } {{{\tilde {g}}}^{ \pm }}(p){{C}_{0}}(p){{\omega }^{4}}\left( {\left| p \right|} \right)A}}{{2c_{t}^{2}\cosh \left( {\left| p \right|D} \right)({{\omega }^{2}}\left( {\left| p \right|} \right) - g\left| p \right|\tanh \left( {\left| p \right|D} \right))}}dp$

Из (2.11) видно, что изменение во времени действия источника сводится к появлению множителей ${{\tilde {g}}^{ \pm }}(p$), что можно интерпретировать как замену протяженного во времени источника на некоторый мгновенный эквивалентный источник, см. [3, 4].

Теперь подставим в (2.11) выражения для функции V и проведем ее упрощения аналогичные [1, 7, 8] с помощью программы Mathematica. Получим

(2.12)

$\eta \approx \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}{\mathbf{g}}}}{{4\sqrt {2\pi } c_{t}^{2}}}{\text{Re}}\left[ {\sum\limits_ \pm {\int\limits_{\mathbb{R}_{p}^{2}} {\frac{{{{e}^{{i\left( {\langle p,x\rangle \pm t\omega (|p|)} \right){{e}^{{ - |p|{\mathbf{b}}(\varphi )}}}}}}{{{(1 - {\mathbf{\rho }} + 2\left| p \right|c_{t}^{2}{\text{/}}{\mathbf{g}})}}^{2}}\sinh \left( {D\left| p \right|} \right)}}{{{{p}^{2}}(1 + 2\left| p \right|c_{t}^{2}{\text{/}}{\mathbf{g}})({\mathbf{\rho }}{{{\cosh }}^{2}}\left( {D\left| p \right|} \right) + \tanh \left( {D\left| p \right|} \right))}}} } Qdp} \right]$

$Q = - \frac{{{{e}^{{|p|({{z}_{0}} + D)}}}{{e}^{{\frac{{b_{3}^{2}{{p}^{2}}}}{2}}}}\sqrt {2\pi } {{{\tilde {g}}}^{ \pm }}(p){{\omega }^{2}}\left( {\left| p \right|} \right)}}{{\left| p \right|2c_{t}^{2}c_{l}^{2}}}({{a}_{{v}}}\left| p \right|(c_{l}^{2} - R) + i\left\langle {p,a} \right\rangle (c_{t}^{2} + R)){\mathbf{e}}({{z}_{0}} + b_{3}^{2}\left| p \right|)$

где $R = (c_{l}^{2} - c_{t}^{2})\left| p \right|(D + b_{3}^{2}\left| p \right| + {{z}_{0}})$.

Изучим этот интеграл при больших $\left| x \right|$. Пусть $\varphi $ – полярный угол вектора x, $\psi $ – полярный угол вектора p, $\left\langle {p,x} \right\rangle = \left| x \right|\rho \cos (\psi - \varphi )$, $\varrho = \left| p \right|$. Перейдем в интегрировании по переменным $p$ к полярным координатам ($\varrho $, $\psi $) и учтем, что точка $x$ находится достаточно далеко от начала координат, т.е. от горизонтального местоположения источника. Тогда по углу $\psi $ можно применить метод стационарной фазы, что даст слагаемые ${{e}^{{i( \pm |x|\varrho - t\omega (\varrho ))}}}$. Так как $\partial \omega {\text{/}}\partial \varrho > 0$, то в силу соображений, использованных при вычислении асимптотик быстро меняющихся интегралов [9], при $t > 0$ слагаемое с $ - \left| x \right|\varrho - t\omega (\varrho )$ вносит вклад в асимптотику $O({{\left| x \right|}^{{ - 2}}})$ и им можно пренебречь. В результате получим $\eta \approx {{\eta }_{F}}$ (в приближении дального поля)

$\begin{gathered} {{\eta }_{F}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}{\mathbf{g}}}}{{4\pi c_{l}^{2}\sqrt {\left| x \right|} }}{\text{Re}}\left[ {\int\limits_0^\infty {\frac{{{{e}^{{i(|x|\varrho - t\omega (\rho ) - \pi /4)}}}{{e}^{{ - \varrho ({\mathbf{b}}(\varphi ) - {{z}_{0}} - D)}}}\sqrt \varrho \mathop {\tanh }\nolimits^2 (D\varrho )}}{{\cosh (D\varrho )({\mathbf{\rho }} + \tanh (D\varrho ){\text{/}}{{{\cosh }}^{2}}(D\varrho )}}} } \right. \times \\ \times \;\left. {{{e}^{{\frac{{b_{3}^{2}{{\rho }^{2}}}}{2}}}}\sqrt {2\pi } {{{\tilde {g}}}^{ - }}\left( {\frac{{\omega (\varrho )}}{\lambda }} \right)({{a}_{{v}}}({{c}^{2}} - R) + i{{a}_{h}}(\varphi )(1 + R))e({{z}_{0}} + b_{3}^{2}\varrho ))} \right]d\varrho \\ \end{gathered} $

где $R = ({{c}^{2}} - 1)\varrho (D + b_{3}^{2}\varrho + {{z}_{0}})$, $c = {{c}_{{\text{l}}}}{\text{/}}{{c}_{t}},{{a}_{h}}(\varphi ) = {{a}_{1}}\cos \varphi + {{a}_{2}}\sin \varphi $. Срезающая функция $e({{z}_{0}} + b_{3}^{2}\varrho )$ дает лишь сходимость интеграла, ответ от ее выбора практически не зависит. Хотя она предполагается финитной, но ее можно выбрать быстро убывающей при положительных $z$, например, в виде $e(y) = 1{\text{/}}(1 + \exp ((y{\text{/}}{{b}_{3}} + {{2)}^{3}})$.

Рассмотрим теперь длинноволновое приближение. Считая $\left| {pD} \right|$ достаточно малым и b_j + $\left| {{{z}_{0}}} \right| \gg D$, $\sinh (D\varrho ) \approx D\varrho $, ${{\cosh }^{2}}(D\varrho ) \approx 1$, можем написать $\omega \approx \tilde {\omega } = \left| p \right|\sqrt {gD} \sqrt {1 - \frac{{g\rho }}{{g + 2c_{t}^{2}\left| p \right|}}} $ и $\eta \approx {{\eta }_{L}}$, где

(2.13)

$\begin{gathered} {{\eta }_{L}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}{\mathbf{g}}{{D}^{2}}}}{{4\pi c_{l}^{2}\sqrt {\left| x \right|} }}{\text{Re}}\left[ {\int\limits_0^\infty {{{\varrho }^{{5/2}}}} {{e}^{{i(|x|\varrho - t\tilde {\omega }(\varrho ) - \pi /4)}}}\frac{{{{e}^{{ - \varrho L}}}{{e}^{{\frac{{b_{3}^{2}{{\varrho }^{2}}}}{2}}}}}}{{(\rho + D\varrho )}}\sqrt {2\pi } {{{\tilde {g}}}^{ - }}\left( {\frac{{\tilde {\omega }(\rho )}}{\lambda }} \right) \times } \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \times \;({{a}_{{v}}}({{c}^{2}} - R) + i{{a}_{h}}(\varphi )(1 + R))e({{z}_{0}} + b_{3}^{2}\varrho )d\varrho } \right] \\ \end{gathered} $

$R = - ({{c}^{2}} - 1)\varrho (h - b_{3}^{2}\varrho ),\quad h = - {{z}_{0}} - D,\quad L = b(\varphi ) - {{z}_{0}} - D$

Величина h характеризует глубину (считая от границы раздела вода–упругое основание) залегания источника. Сравнение (2.13) с выражениями из [17] показывает, что параметр $L$ в ${{e}^{{ - \varrho L}}}$ играет роль, аналогичную характеристическому размеру в потенциальной модели, и с ростом глубины залегания источника длина порождаемых волн увеличивается. Однако из-за знаменателя $\rho + D\varrho $ в (2.13) говорить о прямом соответствии L характеристическому размеру нельзя.

Дальнейшие упрощения сводятся к следующему. Во-первых, можно одновременно отбросить экспоненту ${{e}^{{\frac{{b_{3}^{2}{{\varrho }^{2}}}}{2}}}}$, $b_{3}^{2}\varrho $ в множителе $R$, а также срезающую функцию. Кроме того, учитывая наличие в интеграле множителя ${{\rho }^{{5/2}}}$, быстрое стремление к 0 подынтегральной функции и существенное изменения подынтегральной функции лишь при очень малых $\varrho $, частоту $\tilde {\omega }$ (дисперсионное соотношение) можно заменить на $\omega = C\varrho $, $C = \sqrt {gD} $. В результате приходим к следующей формуле

(2.14)

$\begin{gathered} {{\eta }_{L}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}g{{D}^{2}}}}{{4\pi c_{l}^{2}\sqrt {\left| x \right|} }}{\text{Re}}\left[ {\int\limits_0^\infty {{{\varrho }^{{5/2}}}} } \right.{{e}^{{i((|x| - tC)\varrho - \pi /4)}}}\frac{{{{e}^{{ - \varrho L}}}}}{{(\rho + D\varrho )}}\sqrt {2\pi } {{{\tilde {g}}}^{ - }}\left( {\frac{{C\rho }}{\lambda }} \right) \times \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} \times ({{a}_{{v}}}({{c}^{2}} - R) + i{{a}_{h}}(\varphi )(1 + R))d\varrho } \right],\quad R \approx - \varrho ({{c}^{2}} - 1)h \\ \end{gathered} $

Для случая (a), когда $g = {{e}^{{ - \tau }}}\tau $

$\sqrt {2\pi } {{\tilde {g}}^{ - }}({v}) = \frac{1}{{{{{(1 - i{v})}}^{2}}}}$

при $g = {{e}^{{ - \tau }}}\left( {\beta \tau + \frac{{1 - \beta }}{2}{{\tau }^{2}}} \right)$

$\sqrt {2\pi } \tilde {g}({v}) = \frac{\beta }{{{{{(1 - i{v})}}^{2}}}} + \frac{{1 - \beta }}{{{{{(1 - i{v})}}^{3}}}}$

Здесь $\beta $ – вещественный безразмерный параметр.

Тогда (2.14) сводится к вычислению интегралов вида

(2.15)

${{I}_{{km}}} = {{I}_{{km}}}(y,L,\rho ,D,q) = \frac{1}{{2\pi }}\int\limits_0^\infty {{{\varrho }^{{k + 1/2}}}} \frac{{{{e}^{{(iy - L)\varrho }}}}}{{{{{(1 - iq\varrho )}}^{m}}(\rho + D\varrho )}}d\varrho ,\quad q = \frac{C}{\lambda }$

где $y = \left| x \right| - tC$, числа k принимают значения 2, 3, а $m$ – значения $2,\;3,\; \ldots $ в зависимости от функции $g$. Параметры $L$, $D$ принимают размерные значения и мы считаем, что они находятся в пределах $L = 10{\kern 1pt} - {\kern 1pt} 50$ км, $D = 2{\kern 1pt} - {\kern 1pt} 5$ км, кроме того $\rho = 0.3{\kern 1pt} - {\kern 1pt} 0.35$. Далее, считая что $C = 500{\kern 1pt} - {\kern 1pt} 800$ км/ч и $1{\text{/}}\lambda = 0{\kern 1pt} - {\kern 1pt} 20$ с, получим $q = 0{\kern 1pt} - {\kern 1pt} 4.5$. Интегралы (2.15) вычисляются точно и выражаются через функцию ошибок ${\text{Erf}}$ комплексного аргумента. Так, для $g = {{e}^{{ - \tau }}}\tau $ выражение (2.14) представляется как

(2.16)

${{\hat {\eta }}_{L}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}g{{D}^{2}}}}{{2c_{l}^{2}\sqrt {\left| x \right|} }}{\text{Re}}[{{e}^{{ - i\pi /4}}}(({{a}_{{v}}}{{c}^{2}} + i{{a}_{h}}(\varphi )){{{\text{I}}}_{{22}}} + ({{c}^{2}} - 1)h\left( {{{a}_{{v}}} - i{{a}_{h}}(\varphi )} \right){{{\text{I}}}_{{32}}})]$

$\begin{gathered} {{I}_{{22}}} = - \frac{{i\rho }}{{4{{\theta }^{{3/2}}}\sqrt \xi {{q}^{4}}{{{(q - i\theta )}}^{2}}}}(2i\sqrt \xi {{q}^{4}}{{e}^{{\xi /\theta }}}(1 - {\text{erf}}(\sqrt {\xi {\text{/}}\theta } )) + \\ + \;{{\theta }^{{3/2}}}\sqrt { - iq\xi } {{e}^{{\frac{{i\xi }}{q}}}}(2\theta \xi + 5{{q}^{2}} - 3i\theta q + 2i\xi q)(i + {\text{erfi}}(\sqrt { - i\xi {\text{/q}}} )) - \\ - \;2i\sqrt {\theta {\text{/}}\pi } q(q - i\theta )(\theta \xi + {{q}^{2}} - i\theta q)) \\ \end{gathered} $

$\begin{gathered} {{I}_{{32}}} = - \frac{{i\rho }}{{4{{\theta }^{{5/2}}}{{\xi }^{{3/2}}}{{q}^{5}}{{{(q - i\theta )}}^{2}}}}(2i{{\xi }^{{3/2}}}{{q}^{5}}{{e}^{{\xi /\theta }}}({\text{erf}}(\sqrt {\xi {\text{/}}\theta } ) - 1) + \\ + \;{{\theta }^{{5/2}}}{{\xi }^{{3/2}}}\sqrt { - iq} {{e}^{{\frac{{i\xi }}{q}}}}{\text{erfi}}(\sqrt { - i\xi {\text{/}}q} )( - 2i\theta \xi - 7i{{q}^{2}} - 5\theta q + 2\xi q) + \\ + \;({{\theta }^{{5/2}}}{{\xi }^{{3/2}}}\sqrt { - iq} {{e}^{{\frac{{i\xi }}{q}}}}(2\theta \xi + 7{{q}^{2}} - 5i\theta q + 2i\xi q) + \\ + \;i\sqrt {\theta {\text{/}}\pi } q(q - i\theta )(2i{{\theta }^{2}}{{\xi }^{2}} - {{q}^{3}}(\theta - 2\xi ) + i\theta {{q}^{2}}(\theta + 2\xi ) + 4{{\theta }^{2}}\xi q))) \\ \end{gathered} $

где ${\text{Erfi}}(z) = {\text{Erf}}(iz){\text{/}}i$, $\xi = L - iy$, $\theta = D{\text{/}}\rho $.

В случае (б) $g(\tau ) = a{{r}^{{ - \tau }}}(\sin (\alpha \tau + \phi ) - \sin \phi )$

$\sqrt {2\pi } {{\tilde {g}}^{ - }}({v}) = a\alpha \frac{{(1 - i{v})\cos (\phi ) - \alpha \sin (\phi )}}{{(1 - i{v})({{\alpha }^{2}} + {{{(1 - i{v})}}^{2}})}},$

и (2.14)) сводится к вычислению интегралов

${{I}_{{k,m}}} = \frac{1}{{2\pi }}\int\limits_0^\infty {{{\varrho }^{{k + 1/2}}}} \frac{{{{e}^{{(iy - L)\varrho }}}}}{{(\rho + D\varrho )(1 - iq\varrho {{)}^{m}}({{\alpha }^{2}} + {{{(1 - i{v})}}^{2}})}}d\varrho ,\quad k = 2,3\quad m = 0,1$

Как и в случае (a), указанные интегралы вычисляются точно через функцию ошибок комплексного аргумента, но из-за громоздкости эти формулы не приводятся.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

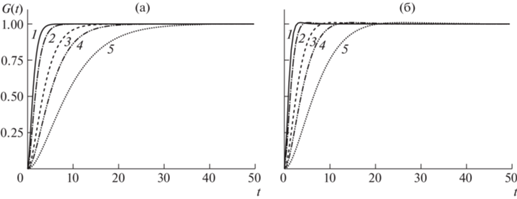
Влияние длительности воздействия и вида источника на волновые профили. Рассмотрим осесимметричный источник, действующий в вертикальном направлении (${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = b$, ${{a}_{h}} = 0$). Рисунок 1 (а) и (б) демонстрирует зависимость времени для двух типов источников: $g(\tau ) = \tau {{e}^{{ - \tau }}}$ и $\hat {g}(\tau ) = a{{e}^{{ - \lambda \tau }}}(\sin (\alpha \lambda \tau + \phi )$ – sinϕ) для $\alpha = 0.3$. Параметр $\lambda $ принимает следующие значения 1.5, 1.0, 0.5, 0.35, 0.2 (с уменьшением $\lambda $ возрастает время воздействия – кривые сдвигаются вправо). Оба источника относятся к типу с остаточными деформациями, т.е. по окончании действия перемещения в упругой среде отличны от нуля. Параметр $\alpha $ выбран таким образом, чтобы смещения в эпицентре происходили поступательно и временные зависимости обоих источников были похожими.

Рис. 1.

Зависимость источников от времени $g(\tau ) = \lambda \tau {{e}^{{ - \lambda \tau }}}$ (а) и $\hat {g}(\tau ) = a{{e}^{{ - \lambda \tau }}}(\sin (\alpha \lambda \tau + \phi ) - \sin \phi )$ (б) для $\alpha = 0.3$: 1–5 –$\lambda = $ $1.5$, $1.0$, $0.5$, $0.35$, 0.2.

На рис. 2 показаны вычисленные по формуле (2.11) возвышения поверхности жидкости от расстояния (волновые профили) для источника, зависящего от времени как $g(\tau ) = \lambda \tau {{e}^{{ - \lambda \tau }}}$. Данные для расчета: $b = 2$ км, $H = 5$ км; глубина залегания источника $z = 43$ км. Для верхнего ряда кривых безразмерное время наблюдения t₀ = 60 (что соответствует 22.6 мин от начала воздействия источника), для нижнего ряда кривых время наблюдения ${{t}_{0}} = 150$ (56.5 мин от начала действия источника). Для удобства сравнения зависимости отнормированы таким образом, чтобы максимальное возвышение жидкости (амплитуда головного гребня) была единичной.

Рис. 2.

Поведение волновых профилей в зависимости от длительности действия источника, зависящего от времени как $\lambda \tau {{e}^{{ - \lambda \tau }}}$, глубина залегания ${{z}_{0}} = 43$ км. (а, б) – ${{t}_{0}} = 60$ ($ \approx {\kern 1pt} 23$ мин), (в, г) – ${{t}_{0}} = 150$ ($ \approx {\kern 1pt} 57$ мин). (а, в): 1–3 – $\lambda = $ $0.5$, 0.35, $0.2$. (б, г): 1–3 – $\lambda = $ $1.5$, 1.0, $0.5$.

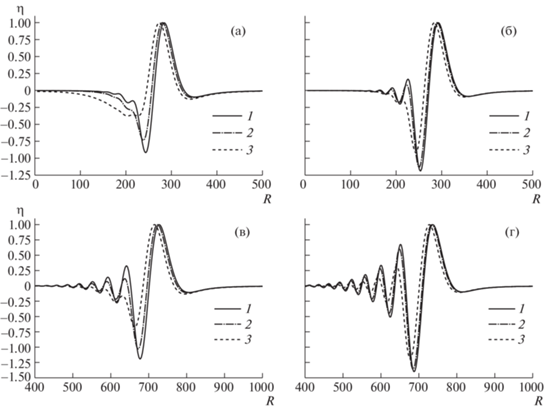
Как видно из рисунков, увеличение длительности действия источника приводит к незначительному росту времени выхода волн на максимум. При этом сами скорости волн не претерпевают заметных изменений – сдвиг во времени (по расстоянию) головных гребней от разных возмущений с расстоянием практически не меняется. Изменение длительности воздействия почти не влияет на ширину головных гребней, но при этом существенно сказывается на дисперсионных эффектах при распространении волн. Чем дольше по времени действует источник, тем на больших расстояниях происходит проявление дисперсии: уменьшается количество гребней и впадин, следующих за головными, снижается их амплитуда.

Волновые профили на рис. 3 получены по формуле (2.11) для источника, зависящего от времени как $\hat {g}(\tau ) = a{{e}^{{ - \lambda \tau }}}(\sin (\alpha \lambda \tau + \phi ) - \sin \phi )$ источника при $\alpha = 0.3$ (в этом случае перемещения среды в эпицентре происходят без колебаний – так же, как и для зависимости источника от времени g(τ) = $\lambda \tau {{e}^{{ - \lambda \tau }}}$). Сравнение рис. 2 и 3 показывает, что, несмотря на близкие по виду зависимости возмущений от времени, дисперсионные эффекты при воздействии источника с временной зависимостью $\hat {g}(\tau )$ развиваются существенно быстрее, чем у источника с зависимостью $g(\tau )$. При этом протяженность головных гребней для обоих видов возмущений почти одинакова. Точно так же, как и в предыдущем случае возмущения, увеличение времени воздействия приводит к небольшому запаздыванию головных гребней, но без изменения скорости распространения самих волн.

Рис. 3.

Влияние длительности воздействия источника, зависящего от времени как $a{{e}^{{ - \lambda \tau }}}(\sin (\alpha \lambda \tau + \phi ) - \sin \phi )$, $\alpha = 0.3$; (а, б) – ${{t}_{0}} = 60$, (в, г) – ${{t}_{0}} = 150$. (а, в): 1–3 – $\lambda = $ 0.5, $0.35$, $0.2$. (б, г): 1–3 – $\lambda = $ $1.5$, $1.0$, $0.5$. Глубина залегания источника ${{z}_{0}} = 43$ км.

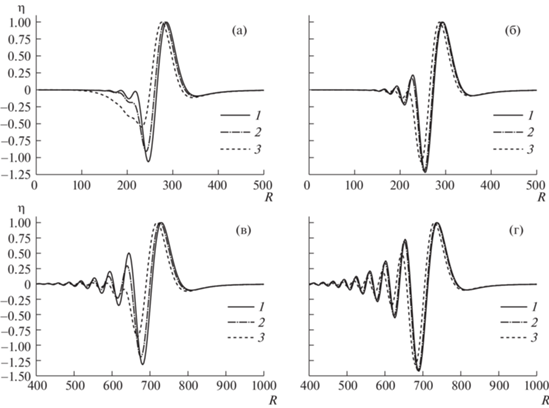
Влияние глубины залегания источника на профили волн. Приведенные на рис. 4 волновые профили вычислены для зависимости источника от времени $g(\tau )$, расположенного на глубине ${{z}_{0}} = 83$ км. Сравнение рис. 2 и 4 показывает, что увеличение глубины расположения источника приводит к возрастанию ширины головного гребня (аналогично поведению, связанному с ростом размеров источника в потенциальной модели). Точно таким же образом глубина залегания влияет на дисперсионные эффекты при распространении волн, в данном случае они практически не наблюдаются. Время действия источника, также как и в случае ${{z}_{0}} = 43$ км, приводит к изменению времени прихода головного гребня – чем длиннее во времени возмущение, тем позже приходит головной гребень.

Рис. 4.

Поведение волновых профилей в зависимости от длительности действия источника, зависящего от времени как $\lambda \tau {{e}^{{ - \lambda \tau }}}$, ${{z}_{0}} = 83$ км. (а, б) – ${{t}_{0}} = 60$, (в, г) – ${{t}_{0}} = 150$. (а, в): 1–3 – $\lambda = $ 0.5, $0.35$, $\lambda = 0.2$. (б, г): 1–3 – $\lambda = $ 1.5, $1.0$, $0.5$.

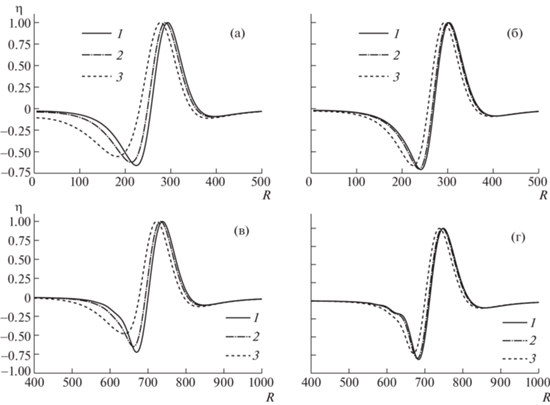
Рисунок 5 демонстрирует волновые профили, вычисленные для источника с временной зависимостью $\hat {g}(\tau )$ для $\lambda = 0.3$ – смещения в эпицентре носят поступательный характер. На графиках (в, г) рисунка на восходящих ветвях головной впадины наблюдаются небольшие колебания, более явные, чем на рис. 4, – свидетельство того, что дисперсионные эффекты для возмущения с $\hat {g}(\tau )$ проявляются сильнее. Из сравнения рис. 4 и 5 следует, что функциональный вид временной зависимости возмущения не оказывает существенного влияния на ширину головного гребня – она в обоих случаях практически одинакова.

На рис. 6 показано влияние глубины залегания источника, зависящего от времени как $\lambda \tau {{e}^{{ - \lambda \tau }}}$, на волновые профили. Время наблюдения ${{t}_{0}} = 60$ выбрано таким образом, чтобы влияние дисперсионных эффектов было незначительным. Как видно из зависимостей, с ростом глубины залегания источника длина волны растет – происходит увеличение протяженности головного гребня и головной впадины. В случае малого времени воздействия источника (в, г) и небольшой глубины залегания ${{z}_{0}} = $ 43 км, на кривых существенно проявляются дисперсионные эффекты, которые с ростом ${{z}_{0}}$ становятся незаметными. Аналогичным образом на волновых профилях сказывается увеличение размера источника в поршневой модели, что подтверждает выводы, сделанные при анализе выражения (2.13).

Рис. 5.

Влияние длительности воздействия источника, зависящего от времени как $a{{e}^{{ - \lambda \tau }}}(\sin (\alpha \lambda \tau + \phi ) - \sin \phi )$, $\alpha = 0.3$; ${{t}_{0}} = 60$ – (а, б), ${{t}_{0}} = 150$ – (в, г). (а, в): 1–3 – $\lambda = $ 0.5, 0.35, 0.2. (б, г): 1–3 – $\lambda = $ $1.5$, 1.0, 0.5. Глубина залегания источника ${{z}_{0}} = 83$ км.

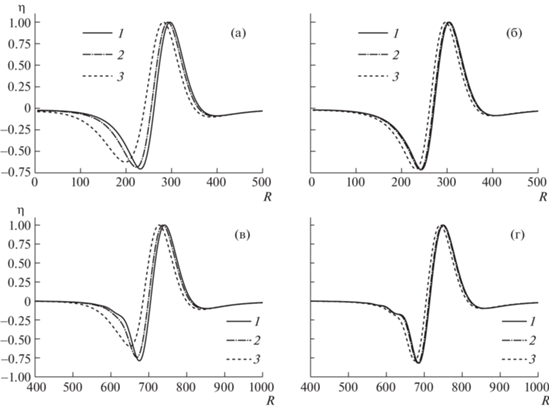
Рис. 6.

Влияние глубины залегания источника, зависящего от времени как $\lambda \tau {{e}^{{ - \lambda \tau }}}$, ${{t}_{0}} = 60$, (а–г) – $\lambda = $ $0.2$, 0.35, $0.5$, $1.5$; глубина залегания: 1–3 – ${{z}_{0}} = $ $43$, $63$, $83$ км.

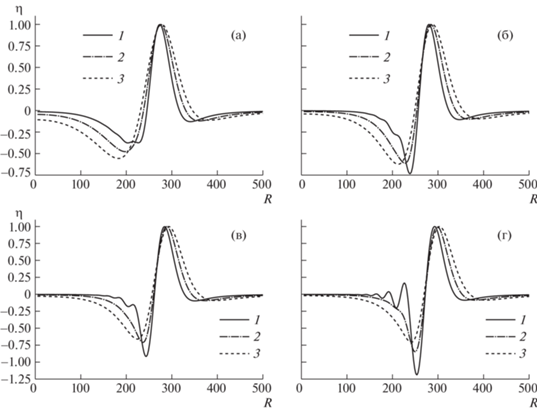
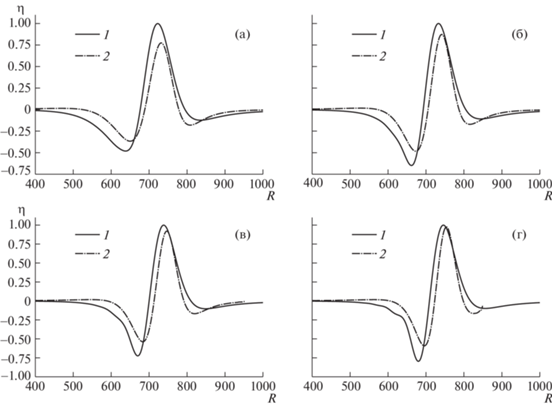
Сравнение волновых профилей, рассчитанных по интегральным формулам и явным аналитическим зависимостям. На рис. 7 показаны волновые профили, вычисленные по явным аналитическим формулам и по интегральным представлениям (2.16). Как следует из графиков, явные аналитические зависимости немного уменьшают (около 9%) амплитуду головного гребня и более существенно (до 25%) занижает амплитуду головной впадины. При этом положение головного гребня аналитические и аналитико-численные представления дают весьма близкое, что позволяет использовать явные аналитические засисимости в моделях для оперативного прогнозирования развития цунами.

Рис. 7.

Поведение волновых профилей в зависимости от длительности действия источника, зависящего от времени как $\tau {{e}^{{ - \tau }}}$, глубина залегания ${{z}_{0}} = 83$ км, (а–г): $\lambda = $ $0.2$, $0.35$, $0.5$, $1.0$ Линия 1 – получена по (2.11), 2 – по (2.16).

ЗАКЛЮЧЕНИЕ

На основе разложения решения задачи о возбуждении гравитационных волн в слое жидкости, покоящемся на упругом основании, локализованным в пространстве и во времени источником в упругой среде по собственным волнам (модам), получены эффективные интегральные формулы для определения возвышения поверхности жидкости. В результате упрощения указанных интегральных представлений с помощью системы Mathematica выведены явные аналитические формулы для решения в случае длинных волн. Полученные аналитические формулы позволяют значительно сократить время прогнозирования распространения волн цунами.

Выполнены расчеты зависимостей возвышения поверхности жидкости от расстояния, т.н. волновых профилей, для двух типов зависимостей поведения источника от времени при различных параметрах источника. Показано, что длительность и форма временной зависимости источника оказывают существенное влияние на проявление дисперсионных эффектов при распространении волн. При этом ширина головного гребня волны не зависит значительным образом от времени действия источника, а определяется в основном глубиной его залегания.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант 17-01-00644, номер госзадания АААА-А20-120011690131-7.

Список литературы

Доброхотов С.Ю., Ильясов Х.Х., Толстова О.Л. Простые решения линейной задачи о возбуждении длинных волн на поверхности. жидкости источником в упругом основании // Изв. РАН. МТТ. 2020. № 4. С. 126–139.
Подъяпольский Г.С. Возбуждение цунами землетрясением. //Методы расчета возникновения и распространения цунами. М.: Наука, 1978. С. 30–87.
Dobrokhotov S.Yu., Nazaikinskii V.E., Tirozzi B. Asymptotic solutions of 2D wave equations with variable velocity and localized right-hand side // Russ. J. Math. Phys. 2010. V. 17. № 1. P. 66–76.
Dobrokhotov S., Minenkov D., Nazaikinskii V., Tirozzi B. Functions of Noncommuting Operators in an Asymtotic Problem for 2D Wave Equation with Variable Velocity and Localized Right-hand Size // Oper. Theory: Adv. Appl. 2013. V. 228. P. 95–125.
Доброхотов С.Ю., Толстова О.Л., Чудинович И.Ю. Волны в жидкости на упругом основании. Теорема существования и точные решения // Матем. заметки. 1993. Т. 54. № 3. С. 33–55.
Гринив Р.О., Доброхотов С.Ю., Шкаликов А.А. Операторная модель задачи о колебаниях жидкости на упругом основании //Матем. заметки. 2000. Т. 68. № 1. С. 57–70.
Доброхотов С.Ю., Ильясов Х.Х., Секерж-Зенькович С.Я., Толстова О.Л. Простые решения задачи о волнах на поверхности жидкости в рамках линейной гидроупругой модели // ДАН. 2019. Т. 18. № 4. С. 370–375.
Dobrokhotov S.Yu., Tolstova O.L., Sekerzh-Zenkovich S.Ya., Vargas C.A. Influence of the elastic base of a basin on the propagation of waves on the water surface //Russ. J. Math. Phys. 2018. V. 25. № 4. P. 459–469.
Федорюк М.В. Асимптотика, Интегралы и ряды. М.: Наука, 1987. 544 с.
Пелиновский Е.Н. Гидродинамика волн цунами. Нижний Новгород: ИПФ РАН, 1996. 276 с.
Kanamori H. Mechanism of tsunami earthquakes // Phys. Earth Planet. Inter. 1972. V. 6. № 5. P. 349–359.
Yamashita T., Sato R. Generation of tsunami by a fault model // J. Phys. Earth. 1974. № 22. P. 415–440.
Sabatier P.C. On water waves produced by ground motions // J. Fluid Mech. 1983. V. 126. P. 27–58.
Гусяков В.К., Чубаров Л.Б. Численное моделирование возбуждения и распространения цунами в прибрежной зоне // Изв. АН СССР. Физика Земли. 1987. № 11. С. 53–64.
Фрагела А.К. К задаче о движении идеальной жидкости в неограниченном упругом бассейне // Дифф. уравнения. 1989. Т. 25. № 8. С. 1417–1426.
Зволинский Н.В., Карпов И.И., Никитин И.С., Секерж-Зенькович С.Я. Возбуждение волн цунами и Рэлея гармоническим двумерным центром вращения // Изв. РАН. Физика Земли. 1994. № 9. С. 29–33.
Sekerzh-Zen’kovich S.Ya. Analytical Study of a Potential Model of Tsunami with a Simple Source of Piston Type. 1. Exact Solution. Creation of Tsunami // Russ. J. Math. Phys. 2012. V. 19. № 3. P. 385–393.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал