Известия РАН. Механика жидкости и газа, 2022, № 3, стр. 65-78

ГИДРОУПРУГИЕ ВОЛНЫ В КАНАЛЕ, ПОКРЫТОМ ЛЬДОМ С ЛИНЕЙНО МЕНЯЮЩЕЙСЯ ТОЛЩИНОЙ

Е. А. Батяев^a, *, Т. И. Хабахпашева^a, **

^a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

^* E-mail: john@hydro.nsc.ru
^** E-mail: tkhab@ngs.ru

Поступила в редакцию 17.11.2021
После доработки 21.11.2021
Принята к публикации 21.11.2021

EDN: VFEWQY
DOI: 10.31857/S0568528122030033

Аннотация

Построено и исследовано решение задачи об изгибно-гравитационных волнах в канале, покрытом льдом, толщина которого линейно меняется от одной стенки канала до другой. Канал имеет прямоугольное сечение. Предполагается, что толщина ледовой пластины мала по сравнению с глубиной канала, а ее края приморожены к стенкам канала. Прогиб ледового покрова описывается в рамках линейной теории упругих пластин, течение жидкости подо льдом полагается потенциальным. Задача решается методом разложения по модам колебаний балки, толщина которой меняется линейно по ширине канала. Определены дисперсионные соотношения, профили изгибно-гравитационных волн поперек канала и распределения удлинений в ледовом покрове. Найдены групповые и фазовые скорости гидроупругих волн. Исследована зависимость гидроупругих характеристик от линейного коэффициента, определяющего неравномерность толщины льда. Проведено сравнение полученных результатов с результатами для однородного ледового покрова.

Ключевые слова: изгибно-гравитационные волны, канал, ледовый покров, линейная толщина льда, упругая пластина, деформации, максимальные удлинения

Задача о распространении изгибно-гравитационных волн в ледовых покровах рек и каналов активно исследуется последние десятилетия в связи с освоением северных территорий и возможностью длительного использования северного морского пути. Использование замерзших рек в качестве транспортных путей является обычной и естественной практикой для развития северных регионов. Сохранение целостности ледового покрова является важной проблемой при перемещении грузов и людей. В этой связи возникает множество задач по исследованию условий сохранения и разрушения ледового покрова, в том числе проблемы, вызываемые бегущими волнами или движением нагрузки. Рассматриваемый в настоящей работе канал прямоугольного сечения является простейшей моделью русла реки. Кроме того, большинство экспериментальных ледовых бассейнов имеет прямоугольное сечение [1–3], и аналитическое исследование изгибно-гравитационных волн в канале конечной ширины имеет важное значение для интерпретации экспериментальных результатов.

Обычно в задачах о взаимодействии жидкости с ледовым покровом последний моделируется тонкой упругой пластиной. Подробный обзор работ и новые результаты в этой области содержатся в [4–7]. В работах [5, 6] показано, что наличие стенок канала приводит к бесконечному (счетному) множеству дисперсионных кривых и критических скоростей для распространяющихся в канале гидроупругих волн. Критические скорости важны при исследовании задач о движении нагрузки в канале [8–11]. Так, при движении нагрузки со скоростью ниже первой критической основной прогиб ледовой пластины формируется в окрестности нагрузки, а при движении со сверхкритической скоростью образуется система гидроупругих волн, распространяющихся от нагрузки. Число волн в этой системе конечно и зависит от соотношения скорости движения нагрузки с критическими скоростями изгибно-гравитационных волн в канале.

В [5, 6] решение связанной задачи гидроупругости о бегущих волнах в канале строилось методом нормальных мод, в [9–11] для определения прогиба ледовой пластины при движении нагрузки применялось преобразование Фурье вдоль канала. В работе [7] решение получено путем разложения потенциала скорости и четвертой производной прогиба льда в ряд по косинусам с неизвестными коэффициентами. Для получения значений прогиба ледовой пластины ряды интегрируются, что добавляет к тригонометрическим функциям четыре полиномиальных члена с соответствующими константами, которые определяются из конкретных условий закрепления пластины к стенкам канала.

Почти во всех предыдущих работах по волнам в ледовом покрове и по движению нагрузки по льду или в непосредственной близости от него толщина льда полагалась постоянной [4–27]. Известны только несколько работ с кусочно-постоянными по толщине плавающими пластинами [28, 29]. Кроме того, слабо-неоднородная плавающая пластина рассматривалась в [30]. В этой работе уравнения линейной теории плавающих пластин с помощью вариационного принципа были сведены к упрощенной форме, в которой отсутствует вертикальная координата. Это удалось сделать за счет предположения о малости изменения толщины льда и глубины жидкости. Однако в природных условиях ледовый покров является существенно неоднородным. В силу разных причин он может оказаться у одного берега реки толще, чем у другого. В настоящей работе рассматривается случай ледового покрова, толщина которого меняется по линейному закону. Плотность льда при этом считается постоянной. Задача решается методом нормальных мод, описывающих свободные цилиндрические колебания пластины с линейно изменяющейся толщиной.

Для предлагаемого подхода к решению рассматриваемой задачи принципиальным является аналитическое представление форм свободных колебаний пластины с линейно изменяющейся толщиной. В предыдущих работах, в которых использовался метод нормальных мод, рассматривались только пластины постоянной или кусочно-постоянной толщины [5, 6, 9–11, 29, 31], при этом формы свободных колебаний пластины выражались через тригонометрические и экспоненциальные функции. В работе [32] говорится, что “существует очень мало уравнений вибрирующих пластин с переменным поперечным сечением, для которых можно получить точные решения. Такие точные решения доступны только для определенных форм пластин и граничных условий”. Так, колебания клиновидной пластины с линейно меняющейся толщиной исследовались в книге Тимошенко [33] приближенными методами через представление решения в виде степенных рядов по параметру неравномерности толщины. Коэффициентами этого ряда являются функции, определяемые из системы дифференциальных уравнений. Эти функции, в свою очередь, также ищутся в виде рядов с разделением переменных. В [34] разработан аналитический подход для свободных колебаний опертой пластины с одним изменением толщины в форме ступени. В [35] построены аналитические решения для свободных колебаний свободно-закрепленной пластины с кусочно-постоянной толщиной.

В работе [36] уравнения статического равновесия изгибных колебаний балки переменного сечения записаны в виде системы самосопряженных дифференциальных уравнений второго порядка. Показано, что они могут быть сведены к уравнениям Бесселя. В работе [32] основные дифференциальные уравнения для свободных колебаний изгибаемых пластин с переменным распределением массы и жесткости устанавливаются и сводятся к уравнениям Бесселя или уравнению Эйлера путем выбора для них подходящих выражений, в виде степенных или экспоненциальных функций по длине пластины. Полученные в [32] общие решения, в виде функций Бесселя, использованы в настоящей работе. Подобные функции для исследования свободных колебаний пластин с линейно меняющейся толщиной были использованы также в работе [37]. В работе [38] эти функции определяются с помощью метода пристрелки. Вибрации кусочно-однородных балок рассматривались в [31], где была показана ортогональность мод свободных колебаний балки с весовым множителем. Эта ортогональность используется и в настоящей работе.

Целью работы является исследование особенностей гидроупругих характеристик линейной задачи о распространении изгибно-гравитационных волн в канале конечной глубины, заполненном идеальной несжимаемой жидкостью, с ледовым покровом при линейном изменении толщины льда поперек канала.

1. ПОСТАНОВКА ЗАДАЧИ

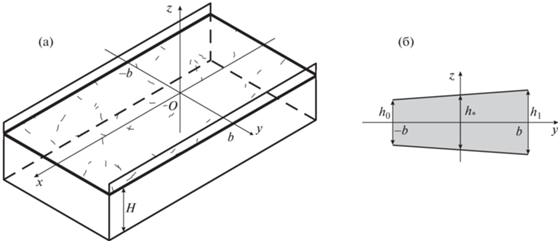
Рассматривается задача о распространении гидроупругих волн в ледовом покрове канала бесконечной длины, заполненного жидкостью. Ширина канала $2b$, глубина H. Схема исследуемой задачи и направления координатных осей показаны на рис. 1а. Канал заполнен идеальной несжимаемой жидкостью плотности ${{\rho }_{l}}$. Жидкость покрыта сверху ледовой пластиной, толщина которой меняется по линейному закону в поперечном сечении

(1.1)

${{h}_{i}}(y) = {{h}_{*}}\left( {1 + \alpha \times y{\text{/}}b} \right)\quad ( - b \leqslant y \leqslant b)$

где ${{h}_{*}}$ – средняя толщина льда, $\alpha $ – параметр утолщения льда, ${{h}_{0}} = {{h}_{*}}(1 - \alpha )$, ${{h}_{1}} = {{h}_{*}}(1 + \alpha )$. Схема поперечного сечения ледового покрова и используемые обозначения размеров приведены на рис. 1б. Толщина ледового покрова значительно меньше глубины канала ${{h}_{*}} \ll H$. Ледовый покров моделируется тонкой однородной упругой пластиной плотности ${{\rho }_{i}}$ и переменной цилиндрической жесткости

(1.2)

$D(y) = \frac{{Eh_{i}^{3}(y)}}{{12(1 - {{\nu }^{2}})}}$

где $E$ – модуль упругости Юнга, $\nu $ – коэффициент Пуассона льда. Края ледового покрова полагаются примороженными к стенкам канала.

Рис. 1.

Схема прямоугольного канала (a) и поперечное сечение ледового покрова (б).

Задача формулируется в рамках линейной теории гидроупругих волн. Предполагается, что изгибно-гравитационная волна распространяется с частотой $\omega $ в отрицательном направлении оси Ox. За амплитуду волны $A$ принимается максимум прогиба ледовой пластины в поперечном сечении. Прогиб срединной поверхности ледового покрова $w(x,y,t)$ под действием гидродинамической нагрузки описывается линейным уравнением изгиба пластины [33]

(1.3)

$\frac{{\partial {{Q}_{x}}}}{{\partial x}} + \frac{{\partial {{Q}_{y}}}}{{\partial y}} - {{h}_{i}}(y){{\rho }_{i}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + p(x,y,t) = 0\quad (z = 0)$

где ${{Q}_{x}}$, ${{Q}_{y}}$ – перерезывающие силы

${{Q}_{x}} = \frac{{\partial {{M}_{x}}}}{{\partial x}} + \frac{{\partial {{M}_{{xy}}}}}{{\partial y}},\quad {{Q}_{y}} = \frac{{\partial {{M}_{{xy}}}}}{{\partial x}} + \frac{{\partial {{M}_{y}}}}{{\partial y}}$

${{M}_{x}}$, ${{M}_{y}}$, ${{M}_{{xy}}}$ – изгибающие и крутящий моменты упругих сил

$\begin{gathered} {{M}_{x}} = - D\left( {\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \nu \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}}} \right), \\ {{M}_{y}} = - D\left( {\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \nu \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}} \right),\quad {{M}_{{xy}}} = - (1 - \nu )D\frac{{{{\partial }^{2}}w}}{{\partial x\partial y}}\quad \\ \end{gathered} $

Краевые условия для прогиба, в случае жесткого закрепления упругой пластины по берегам канала, имеют вид

(1.4)

$w = 0,\quad \frac{{\partial w}}{{\partial y}} = 0\quad (y = \pm b)$

Гидродинамическое давление p определяется линеаризованным уравнением Бернулли

(1.5)

$\frac{p}{{{{\rho }_{l}}}} = - \frac{{\partial \varphi }}{{\partial t}} - g \cdot w\quad (z = 0)$

где $g$ – ускорение свободного падения. Течение жидкости в канале описывается потенциалом скоростей $\varphi (x,y,z,t)$, удовлетворяющим уравнению Лапласа

(1.6)

$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 0\quad ( - \infty < x < \infty , - b < y < b, - H < z < 0)$

и краевым условиям

(1.7)

$\frac{{\partial \varphi }}{{\partial y}} = 0\quad (y = \pm b),\quad \frac{{\partial \varphi }}{{\partial z}} = 0\quad (z = - H),\quad \frac{{\partial \varphi }}{{\partial z}} = \frac{{\partial w}}{{\partial t}}\quad (z = 0)$

Далее используются безразмерные переменные с сохранением обозначений. В качестве масштаба длины принимается половина ширины канала $b$, отношение 1/ω – масштаб времени, амплитуда $A$ – масштаб перемещений ледового покрова, ${{\rho }_{l}}gA$ – масштаб давления, $Ab\omega $ – масштаб потенциала скоростей. Безразмерная глубина канала обозначается как $h$ ($h = H{\text{/}}b$), размеры поперечного сечения канала будут: $ - 1 \leqslant y \leqslant 1$, $ - h \leqslant z \leqslant 0$. В безразмерных переменных уравнение (1.3) с учетом (1.5) примет вид

(1.8)

$\begin{gathered} (1 + \alpha \cdot y)\beta \left[ {{{{(1 + \alpha \cdot y)}}^{2}}\left( {\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + 2\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{2}}\partial {{y}^{2}}}} + \frac{{{{\partial }^{4}}w}}{{\partial {{y}^{4}}}}} \right)} \right. + \\ + \;6\alpha (1 + \alpha \cdot y)\left( {\frac{{{{\partial }^{3}}w}}{{\partial {{x}^{2}}\partial y}} + \frac{{{{\partial }^{3}}w}}{{\partial {{y}^{3}}}}} \right) + \left. {6{{\alpha }^{2}}\left( {\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \nu \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}} \right) + \frac{{\delta \gamma }}{\beta }\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}} \right] = - \gamma \frac{{\partial \varphi }}{{\partial t}} - w \\ \end{gathered} $

где $\beta = {{D}_{*}}{\text{/}}{{\rho }_{l}}g{{b}^{4}}$, $\gamma = b{{\omega }^{2}}{\text{/}}g$, $\delta = {{h}_{*}}{{\rho }_{i}}{\text{/}}b{{\rho }_{l}}$, ${{D}_{*}} = Eh_{*}^{3}{\text{/}}12(1 - {{\nu }^{2}})$. Остальные соотношения в безразмерных переменных сохранят свою форму.

Решение задачи (1.8), (1.4), (1.6), (1.7) ищется в виде бегущей волны

(1.9)

$w(x,y,t) = {\text{Re}}[F(y){{e}^{{i(\kappa x + t)}}}]$

где $\kappa $ – безразмерное волновое число ($\kappa = kb$, $k$ – размерное волновое число), $F(y)$ – амплитудная функция прогиба пластины. В связи с линейностью рассматриваемой задачи на функцию $F(y)$ налагается условие нормировки: $\mathop {\max }\limits_{ - 1 < y < 1} \left| {F(y)} \right| = 1$. Из-за неравномерной толщины пластины точки, в которых достигается максимум $F(y)$, определятся только после решения задачи. Для бегущих волн $\kappa $ – действительное и положительное число, при этом размерная длина волны равна $2\pi {\text{/}}k = 2\pi b{\text{/}}\kappa $. Отметим, что решения (1.9) с комплексными $\kappa $ и $F(y)$, если они существуют, не удовлетворяют условию ограниченности, так как соответствуют волнам, которые растут либо при $x \to - \infty $, либо при $x \to \infty $.

Потенциал скорости, соответствующий гидроупругой волне (1.9) и граничным условиям (1.7), может быть представлен в виде

(1.10)

$\varphi (x,y,z,t) = {\text{Re}}[i\Phi (y,z){{e}^{{i(\kappa x + t)}}}]$

где $\Phi (y,z)$ – комплексный потенциал скорости, который удовлетворяет уравнению Гельмгольца

${{\Phi }_{{yy}}} + {{\Phi }_{{zz}}} = {{\kappa }^{2}}\Phi \quad ( - 1 < y < 1, - h < z < 0)$

и краевым условиям

(1.11)

${{\Phi }_{y}} = 0\quad (y = \pm 1),\quad {{\Phi }_{z}} = 0\quad (z = - h),\quad {{\Phi }_{z}} = F\quad (z = 0)$

Подстановка выражений (1.9)–(1.10) в уравнение упругой пластины (1.8) дает

(1.12)

$\begin{gathered} \,\,\,\,\,\,\beta (1 + \alpha y)\left[ {{{{(1 + \alpha y)}}^{2}}F{\kern 1pt} {\text{''''}} + 6\alpha (1 + \alpha y)F{\kern 1pt} {\text{'''}} + 6{{\alpha }^{2}}F{\kern 1pt} {\text{''}} + {{{(1 + \alpha y)}}^{2}}{{\kappa }^{4}}F{{ - }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { - \;2{{\kappa }^{2}}({{{(1 + \alpha y)}}^{2}}F{\kern 1pt} {\text{''}} + 3\alpha (1 + \alpha y)F{\kern 1pt} {\text{'}}) - 6{{\alpha }^{2}}\nu {{\kappa }^{2}}F - \frac{{\delta \gamma }}{\beta }F} \right] = \gamma \Phi (y,0) - F \\ \end{gathered} $

условия жестко закрепленных краев пластины приобретают вид

$F = 0,\quad F{\kern 1pt} ' = 0\quad (y = \pm 1)$

Штрих обозначает производную по переменной y.

Таким образом, для известных инерционно-упругих характеристик ледового покрова и параметров канала требуется определить формы волн $F(y)$ с максимальной амплитудой, равной 1, соответствующие им дисперсионные соотношения, групповые и фазовые скорости, а также напряжения и деформации в ледовом покрове.

2. ГИДРОУПРУГИЕ ВОЛНЫ В КАНАЛЕ

Прогиб ледовой пластины ищется в виде разложения

(2.1)

$F(y) = \sum\limits_{n = 1}^\infty {{{a}_{n}}} {{\psi }_{n}}(y)$

где коэффициенты ${{a}_{n}}$ подлежат определению, а функции ${{\psi }_{n}}$ являются решениями задачи о собственных колебаниях упругой неоднородной балки с жестко закрепленными концами [33]

(2.2)

$\frac{{{{d}^{2}}}}{{d{{y}^{2}}}}\left[ {D(y)\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}}} \right] = {{\rho }_{i}}{{h}_{i}}(y){{\Omega }^{2}}\psi $

(2.3)

$\psi ( \pm 1) = 0,\quad \psi {\text{'}}( \pm 1) = 0$

где $\Omega $ – собственная частота. Для рассматриваемого случая линейно изменяющейся толщины льда (1.1)–(1.2) уравнение (2.2) принимает вид

(2.4)

${{(1 + \alpha y)}^{2}}\psi {\text{''''}} + 6\alpha (1 + \alpha y)\psi {\text{'''}} + 6{{\alpha }^{2}}\psi {\text{''}} = {{\theta }^{4}}\psi $

где $\theta = {{\rho }_{i}}{{h}_{*}}{{\Omega }^{2}}{\text{/}}{{D}_{*}}$. Так же как в [32, 37], уравнение (2.4) решается введением дифференциального оператора

$\Delta = \frac{1}{{1 + \alpha y}}\frac{d}{{dy}}\left[ {{{{(1 + \alpha y)}}^{2}}\frac{d}{{dy}}} \right]$

с помощью которого уравнение (2.4) представляется в виде разложения

$(\Delta + {{\theta }^{2}})(\Delta - {{\theta }^{2}})\psi (y) = 0$

решением которого являются функции

${{\psi }_{n}}(y) = \frac{1}{\xi }\left[ {{{A}_{n}}{{J}_{1}}({{\eta }_{n}}\xi ) + {{B}_{n}}{{Y}_{1}}({{\eta }_{n}}\xi ) + {{C}_{n}}{{I}_{1}}({{\eta }_{n}}\xi ) + {{D}_{n}}{{K}_{1}}({{\eta }_{n}}\xi )} \right]\quad (n = 1,\;2,\; \ldots )$

где ${{\eta }_{n}} = 2{{\theta }_{n}}{\text{/}}\alpha $, $\xi = \sqrt {1 + \alpha y} $, ${{J}_{1}}$, ${{Y}_{1}}$, ${{I}_{1}}$, ${{K}_{1}}$ – функции Бесселя. Коэффициенты ${{A}_{n}}$, ${{B}_{n}}$, ${{C}_{n}}$, ${{D}_{n}}$ определяются краевыми условиями (2.3), которые принимают вид

$\begin{array}{*{20}{c}} {{{J}_{1}}({{\eta }_{n}}{{\xi }_{ \pm }}){{A}_{n}} + {{Y}_{1}}({{\eta }_{n}}{{\xi }_{ \pm }}){{B}_{n}} + {{I}_{1}}({{\eta }_{n}}{{\xi }_{ \pm }}){{C}_{n}} + {{K}_{1}}({{\eta }_{n}}{{\xi }_{ \pm }}){{D}_{n}} = 0} \\ {{{J}_{0}}({{\eta }_{n}}{{\xi }_{ \pm }}){{A}_{n}} + {{Y}_{0}}({{\eta }_{n}}{{\xi }_{ \pm }}){{B}_{n}} + {{I}_{0}}({{\eta }_{n}}{{\xi }_{ \pm }}){{C}_{n}} - {{K}_{0}}({{\eta }_{n}}{{\xi }_{ \pm }}){{D}_{n}} = 0} \end{array}$

где ${{\xi }_{ \pm }} = \sqrt {1 \pm \alpha } $. Условием существования нетривиального решения данной однородной системы алгебраических уравнений является равенство нулю определителя соответствующей матрицы. Корнями данного уравнения являются числа ${{\eta }_{n}}$, через которые выражаются ${{\theta }_{n}} = \alpha {{\eta }_{n}}{\text{/}}2$. Функции ${{\psi }_{n}}(y)$ образуют ортогональную в обобщенном смысле систему, нормированную следующим образом

(2.5)

$\int\limits_{ - 1}^1 {(1 + \alpha y)} {{\psi }_{n}}(y){{\psi }_{m}}(y)dy = {{\delta }_{{nm}}}$

где ${{\delta }_{{nm}}} = 0$ при $n \ne m$ и ${{\delta }_{{nn}}} = 1$.

Из третьего краевого условия (1.11) при $z = 0$ следует, что потенциал можно искать в виде разложения

(2.6)

$\Phi (y,z) = \sum\limits_{n = 1}^\infty {{{a}_{n}}} {{\Phi }_{n}}(y,z)$

в котором функции ${{\Phi }_{n}}(y,z)$ являются решениями задач

$\frac{{{{\partial }^{2}}{{\Phi }_{n}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{\Phi }_{n}}}}{{\partial {{z}^{2}}}} = {{\kappa }^{2}}{{\Phi }_{n}}$

(2.7)

$\frac{{\partial {{\Phi }_{n}}}}{{\partial y}} = 0\quad (y = \pm 1),\quad \frac{{\partial {{\Phi }_{n}}}}{{\partial z}} = 0\quad (z = - h),\quad \frac{{\partial {{\Phi }_{n}}}}{{\partial z}} = {{\psi }_{n}}\quad (z = 0)$

Функции ${{\Phi }_{n}}(y,z)$ ищем в виде разложения в ряд Фурье по координате $y$

${{\Phi }_{n}}(y,z) = \frac{1}{2}\Phi _{{n0}}^{c}(z) + \sum\limits_{k = 1}^\infty {\Phi _{{nk}}^{c}} (z)\cos (\pi ky) + \sum\limits_{l = 1}^\infty {\Phi _{{nl}}^{s}} (z)\sin [(\pi l - \pi {\text{/}}2)y]$

Такое представление позволяет сразу удовлетворить первому условию из (2.7). Аналогичным рядом Фурье представляем ${{\psi }_{n}}(y)$

${{\psi }_{n}}(y) = \frac{1}{2}\psi _{{n0}}^{c} + \sum\limits_{k = 1}^\infty \psi _{{nk}}^{c}\cos (\pi ky) + \sum\limits_{l = 1}^\infty \psi _{{nl}}^{s}\sin [(\pi l - \pi {\text{/}}2)y]$

где коэффициенты вычисляются по формулам

$\begin{gathered} \psi _{{nk}}^{c} = \int\limits_{ - 1}^1 {{{\psi }_{n}}} (y)\cos (\pi ky)dy\quad (k = 0,\;1,\;2\; \ldots ), \\ \psi _{{nl}}^{s} = \int\limits_{ - 1}^1 {{{\psi }_{n}}} (y)\sin [(\pi l - \pi {\text{/}}2)y]dy\quad (l = 1,\;2\; \ldots ) \\ \end{gathered} $

Функции $\Phi _{{nk}}^{c}(z)$, $\Phi _{{nl}}^{s}(z)$ являются решениями задач

(2.8)

$\frac{{{{d}^{2}}\Phi _{{nk}}^{c}}}{{d{{z}^{2}}}} = [{{\kappa }^{2}} + {{(\pi k)}^{2}}]\Phi _{{nk}}^{c}\quad \frac{{{{d}^{2}}\Phi _{{nl}}^{s}}}{{d{{z}^{2}}}} = [{{\kappa }^{2}} + {{(\pi l - \pi {\text{/}}2)}^{2}}]\Phi _{{nl}}^{s}$

(2.9)

$\frac{{d\Phi _{{nk}}^{c}}}{{dz}} = \frac{{d\Phi _{{nl}}^{s}}}{{dz}} = 0\quad (z = - h),\quad \frac{{d\Phi _{{nk}}^{c}}}{{dz}} = \psi _{{nk}}^{c},\quad \frac{{d\Phi _{{nl}}^{s}}}{{dz}} = \psi _{{nl}}^{s}\quad (z = 0)$

Решения задач (2.8)–(2.9) имеют вид

$\Phi _{{nk}}^{c} = \frac{{\psi _{{nk}}^{c}}}{{\mu _{k}^{c}}}\frac{{{\text{ch}}\mu _{k}^{c}(z + h)}}{{{\text{sh}}\mu _{k}^{c}h}},\quad \Phi _{{nl}}^{s} = \frac{{\psi _{{nl}}^{s}}}{{\mu _{l}^{s}}}\frac{{{\text{ch}}\mu _{l}^{s}(z + h)}}{{{\text{sh}}\mu _{l}^{s}h}}$

$\mu _{k}^{c} = \sqrt {{{\kappa }^{2}} + {{{(\pi k)}}^{2}}} \quad \mu _{l}^{s} = \sqrt {{{\kappa }^{2}} + {{{(\pi l - \pi {\text{/}}2)}}^{2}}} $

Подставляя разложения для прогиба (2.1) и потенциала (2.6) в уравнение для упругих колебаний пластины (1.12), получим

$\begin{gathered} \sum\limits_{n = 1}^\infty {{{a}_{n}}} \left\{ {\beta (1 + \alpha y)\theta _{n}^{4}{{\psi }_{n}} + {{\kappa }^{4}}\beta {{{(1 + \alpha y)}}^{3}}{{\psi }_{n}} - 2{{\kappa }^{2}}\beta ({{{(1 + \alpha y)}}^{3}}\psi _{n}^{{''}} + 3\alpha {{{(1 + \alpha y)}}^{2}}\psi _{n}^{'}) - } \right. \\ \left. { - \;{{\kappa }^{2}}6{{\alpha }^{2}}\nu \beta (1 + \alpha y){{\psi }_{n}} - \delta \gamma (1 + \alpha y){{\psi }_{n}} - \gamma {{\Phi }_{n}}(y,0) + {{\psi }_{n}}} \right\} = 0 \\ \end{gathered} $

Умножая это уравнение на ${{\psi }_{m}}(y)$ ($m = 1,\;2,\; \ldots $) и интегрируя по $y \in [ - 1,\; + {\kern 1pt} 1]$, с учетом условия (2.5) получим выражения

(2.10)

$\sum\limits_{n = 1}^\infty {{{a}_{n}}} \left\{ {\beta {{D}_{n}} \cdot {{\delta }_{{nm}}} + {{\kappa }^{4}}\beta \cdot {{K}_{{nm}}} + 2{{\kappa }^{2}}\beta \cdot {{S}_{{nm}}} - \delta \gamma \cdot {{\delta }_{{nm}}} + M_{{nm}}^{{(1)}} - \gamma M_{{nm}}^{{(2)}}} \right\} = 0$

где

${{D}_{n}} = \theta _{n}^{4} - \nu {{\kappa }^{2}}6{{\alpha }^{2}},\quad {{K}_{{nm}}} = \int\limits_{ - 1}^1 {{{{(1 + \alpha y)}}^{3}}} {{\psi }_{n}}{{\psi }_{m}}dy,\quad {{S}_{{nm}}} = \int\limits_{ - 1}^1 {{{{(1 + \alpha y)}}^{3}}} \psi _{n}^{'}\psi _{m}^{'}dy$

$M_{{nm}}^{{(1)}} = \int\limits_{ - 1}^1 {{{\psi }_{n}}} {{\psi }_{m}}dy,\quad M_{{nm}}^{{(2)}} = \int\limits_{ - 1}^1 {{{\Phi }_{n}}} (y,0){{\psi }_{m}}dy$

Приводя в (2.10) подобные слагаемые с величиной $\gamma $, содержащей частоту гидроупругих колебаний $\omega $, представим полученную систему линейных уравнений для коэффициентов ${{a}_{n}}$ в разложении прогиба пластины (2.1) в матричном виде

(2.11)

$\{ \beta [D + {{\kappa }^{4}}K + 2{{\kappa }^{2}}S] + {{M}_{{\text{1}}}} - \gamma \left[ {\delta I + {{M}_{{\text{2}}}}} \right]\} a = 0$

где все матрицы $D = {\text{diag}}\{ {{D}_{n}}\} $, $K = \{ {{K}_{{nm}}}\} $, $S = \{ {{S}_{{nm}}}\} $, ${{M}_{1}} = \left\{ {M_{{nm}}^{{(1)}}} \right\}$, ${{M}_{2}} = \left\{ {M_{{nm}}^{{(2)}}} \right\}$ являются симметричными, I – единичная матрица. Для существования нетривиального решения полученной системы уравнений необходимо обращение в ноль определителя матрицы в фигурных скобках

(2.12)

$\det \{ [D + {{\kappa }^{4}}K + 2{{\kappa }^{2}}S] + {{M}_{{\text{1}}}} - \gamma \left[ {\delta I + {{M}_{{\text{2}}}}} \right]\} = 0$

которое определяет дисперсионные соотношения для гидроупругих волн $\omega = \sqrt {\gamma g{\text{/}}b} = {{\omega }_{n}}(\kappa )$. Каждому корню ${{\gamma }_{n}}$, а значит каждой частоте ${{\omega }_{n}}$, соответствует вектор a_n из (2.11), который определяет форму колебаний ${{F}_{n}}(y)$ в разложении (2.1). Компоненты a_n нормируются так, что абсолютное максимальное значение функции ${{F}_{n}}(y)$ равно единице. Характеристики ледового покрова и размеры канала входят в коэффициенты всех матриц и параметры $\beta $, $\delta $.

3. ДЕФОРМАЦИИ В ЛЕДОВОМ ПОКРОВЕ

Деформации в ледовом покрове описываются в рамках линейной теории в предположении, что значения $w_{x}^{2} + w_{y}^{2}$ малы, и напряжения в пластине пропорциональны удлинениям. Отметим, что лед достаточно хрупкий материал, поэтому предельные напряжения в ледовой пластине, приводящие к ее расколу, достигаются раньше, чем деформации пластины выходят за рамки линейной теории.

Так как решение задачи ищется в виде бегущих вдоль канала волн, то оно является периодической функцией относительно фазы $\theta (x,t) = \kappa x + t$ и представляется в виде

$w(x,y,t) = F(y)\cos \theta $

Абсолютный максимум удлинений в волне является функцией безразмерных параметров $\alpha $, $\beta $, $\gamma $, $\delta $, $\kappa $, $h$ и вычисляется по формуле

(3.1)

${{\varepsilon }_{{ABS}}} = \mathop {\max }\limits_{ - 1 \leqslant y \leqslant 1} \left[ {{{\varepsilon }_{{\max }}}(y)} \right]$

где

(3.2)

${{\varepsilon }_{{\max }}} = \mathop {\max }\limits_{0 \leqslant \theta \leqslant 2\pi } \varepsilon (y,\theta )$

В качестве масштаба удлинений выбирается величина ${{h}_{*}}A{\text{/}}2{{b}^{2}}$.

Поле удлинений в ледовой пластине описывается через тензор деформаций [5, 39]

${{T}_{\varepsilon }} = - \zeta \left[ {\begin{array}{*{20}{c}} {{{w}_{{xx}}}}&{{{w}_{{xy}}}} \\ {{{w}_{{xy}}}}&{{{w}_{{yy}}}} \end{array}} \right]$

где $\zeta $ – безразмерная переменная, изменяющаяся по толщине льда, $ - (1 + \alpha y) \leqslant \zeta \leqslant (1 + \alpha y)$. Чтобы оценить максимальное удлинение в точке (x, y) ледового покрова в момент времени $t$, нужно определить главные удлинения и найти их максимум. В рамках линейной теории максимальные напряжения и удлинения достигаются на поверхности льда, при $\left| \zeta \right| = 1 + \alpha y$.

Главные удлинения $\varepsilon $ определяются через собственные значения тензора ${{T}_{\varepsilon }}$ по формуле

(3.3)

${{\varepsilon }^{{(1,2)}}}(y,\theta ) = \frac{\zeta }{2}[ - a\cos \theta \pm \sqrt {({{b}^{2}} - {{c}^{2}}){\text{co}}{{{\text{s}}}^{2}}\theta + {{c}^{2}}} ]$

где введены обозначения

$a(y) = F{\kern 1pt} {\text{''}}(y) - {{\kappa }^{2}}F(y),\quad b(y) = F{\kern 1pt} {\text{''}}(y) + {{\kappa }^{2}}F(y),\quad c(y) = 2\kappa F{\kern 1pt} {\text{'}}(y)$

Функции (3.3) являются гладкими по переменной $\theta $, поэтому максимум (3.2) достигается в точке экстремума из условия

(3.4)

$\frac{{d\varepsilon }}{{d\theta }} = \frac{\zeta }{2}\left[ {a \mp \frac{{({{b}^{2}} - {{c}^{2}}){\text{cos}}\theta }}{{\sqrt {({{b}^{2}} - {{c}^{2}}){\text{co}}{{{\text{s}}}^{2}}\theta + {{c}^{2}}} }}} \right]{\text{sin}}\theta = 0$

Решение уравнения (3.4) определяет максимальные по длине волны главные удлинения в виде

$\varepsilon _{{\max }}^{{(1)}} = \frac{{1 + \alpha y}}{2}\left( {\left| a \right| + \left| b \right|} \right),\quad \varepsilon _{{\max }}^{{(2)}} = \frac{{1 + \alpha y}}{2}\left| c \right|\sqrt {\frac{{{{b}^{2}} - {{c}^{2}} - {{a}^{2}}}}{{{{b}^{2}} - {{c}^{2}}}}} $

Нетрудно показать, что ${{\varepsilon }_{{\max }}}$ имеет вид

${{\varepsilon }_{{\max }}} = \left\{ \begin{gathered} \varepsilon _{{\max }}^{{(1)}}\quad {\text{при}}\quad {{c}^{2}} - {{b}^{2}}\leqslant \left| {ab} \right| \hfill \\ \varepsilon _{{\max }}^{{(2)}}\quad {\text{при}}\quad {{c}^{2}} - {{b}^{2}} \geqslant \left| {ab} \right| \hfill \\ \end{gathered} \right.$

Отметим, что фактически

$\varepsilon _{{\max }}^{{(1)}} = (1 + \alpha y)\max \left\{ {\left| {F{\kern 1pt} {\text{''}}} \right|,{{\kappa }^{2}}\left| F \right|} \right\}$

т.е. соответствует максимальным поперечным $\left| {{{w}_{{yy}}}} \right|$ или продольным $\left| {{{w}_{{xx}}}} \right|$ удлинениям относительно оси канала. Значение $\varepsilon _{{\max }}^{{(2)}}$ отвечает максимальным удлинениям, которые не являются ни продольными, ни поперечными, образуя ненулевой угол с осью канала.

4. ЧИСЛЕННЫЙ АЛГОРИТМ И РЕЗУЛЬТАТЫ РАСЧЕТОВ

Вычисления линейных гидроупругих волн в канале выполнены для пресноводного льда с плотностью ${{\rho }_{i}} = 917$ кг/м³, модулем Юнга $E = 4.2 \times {{10}^{9}}$ Н/м² и коэффициентом Пуассона $\nu $ = 0.3. Полагалось, что средняя толщина неравномерного ледового покрова ${{h}_{*}} = 0.1$ м, ширина канала $2b = 20$ м, глубина канала H = 2 м. Параметр утолщения льда $\alpha $ изменялся от 0.05 до 0.95. Сравнение полученных результатов расчета проводилось с результатами работы [5], где рассматривался ледовый покров постоянной толщины, а остальные характеристики льда и размеры канала совпадали с указанными выше. Ниже представлены результаты расчетов для волн, длина которых больше 6 м ($0 < k < 1$ м^–1), а период больше 0.3 с ($0 < \omega < 20$ с^–1).

Решение системы алгебраических уравнений (2.11) строилось методом редукции. Количество мод ${{\psi }_{n}}(y)$ в разложении форм прогиба поперечного сечения (2.1) менялось от 10 до 30. Расчеты показали, что в рассматриваемых диапазонах волновых чисел k и частот $\omega $, использование 20 мод достаточно для получения дисперсионных соотношений, распределения упругих деформаций и удлинений с высокой степенью точности.

На рис. 2 линиями представлены первые четыре формы гидроупругих колебаний ${{F}_{n}}(y)$ неравномерной ледовой пластины для разных значений $\alpha $ и маркерами для однородной ледовой пластины толщины 0.1 м при $k = 0.2$ м^–1.

Рис. 2.

Формы гидроупругих волн ледового покрова неравномерной толщины: а–г – первая–четвертая формы; 1–4 для $\alpha = 0.05,\;0.5,\;0.75,\;0.95$; маркеры – формы ледового покрова равномерной толщины из [5].

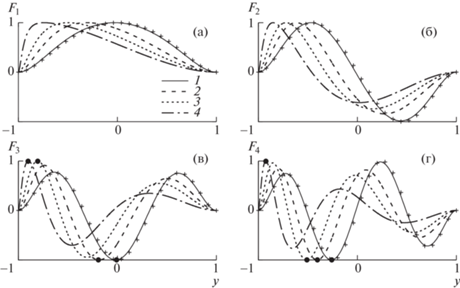
Видно хорошее совпадение форм однородного по толщине льда и неоднородного при малом $\alpha $. С увеличением $\alpha $ наибольший изгиб форм смещается влево к тонкому краю льда при $y = - 1$, а вблизи более толстого края при $y = 1$ изгиб форм значительно уменьшается. Максимумы абсолютных значений форм прогиба для разных $\alpha $ достигаются в точках экстремума ${{F}_{n}}(y)$. С ростом $\alpha $ максимумы смещаются к тонкому краю пластины, причем это смещение может происходить со сменой локального экстремума близкого к центру пластины, на экстремум, находящийся ближе к тонкому краю. На рис. 2,в,г указанные максимумы форм отмечены точками. Видно, что при небольших $\alpha $ максимумы находятся в нижней точке перегиба ${{F}_{n}}(y)$ (для ${{F}_{3}}$ при $\alpha = 0.05,0.5$, для ${{F}_{4}}$ при $\alpha = 0.05,0.5,0.75$), а с увеличением $\alpha $ переходят на верхнюю точку перегиба вблизи тонкого края пластины.

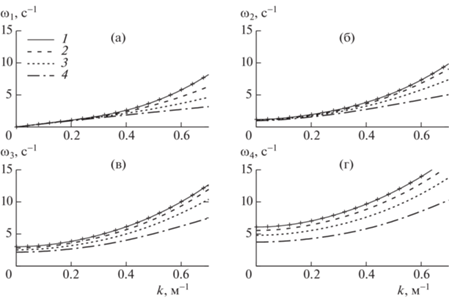
Дисперсионные соотношения, связывающие частоту изгибно-гравитационной волны $\omega $ и волновое число k, определялись из характеристического уравнения (2.12). Для этого вычислялись значения определителя при фиксированных $\kappa = kb$, $0 < k < 1$ м^–1 и разных $\gamma = {{\omega }^{2}}b{\text{/}}g$ с приращением $\Delta \gamma = 0.1$. Определялись интервалы, где определитель меняет знак, и методом деления отрезка пополам определялись корни ${{\gamma }_{n}}$ уравнения с точностью до 10^–12. Далее определялись соответствующие значения ${{\omega }_{n}}(k)$ для каждой формы ${{F}_{n}}$.

На рис. 3 линиями представлены дисперсионные кривые ${{\omega }_{n}}(k)$ для первых четырех форм ${{F}_{n}}$ неравномерной ледовой пластины при разных значениях $\alpha $ и маркерами для однородной ледовой пластины толщины 0.1 м. Видно, что частоты уменьшаются с увеличением параметра утолщения льда $\alpha $ для всех форм, причем в значительной степени для больших $k$, т.е для коротких волн.

Рис. 3.

Дисперсионные кривые гидроупругих волн: а–г – первая–четвертая формы; 1–4 – неравномерный лед при $\alpha = 0.05,0.5,0.75,0.95$; маркеры – ледовый покров равномерной толщины [5].

На рис. 4 приведены дисперсионные кривые для первых четырех форм неравномерного ледового покрова маркерами при $\alpha = 0.5$ и ${{h}_{*}} = 0.1$ м, что соответствует толщинам $h( - 1) = {{h}_{0}} = 0.05$ м и $h(1) = {{h}_{1}} = 0.15$ м на краях пластины. Также показаны дисперсионные кривые для равномерного льда толщиной 0.05, 0.1 и 0.15 м.

Рис. 4.

Дисперсионные кривые гидроупругих волн: а–г – первая–четвертая формы; 1–3 – ледовый покров равномерной толщины 0.05, 0.1, 0.15 м; маркеры – неравномерный лед при $\alpha = 0.5$, ${{h}_{*}} = 0.1$ м.

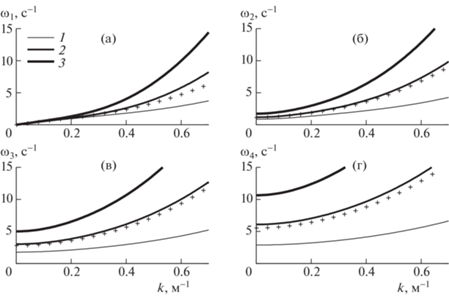
Сравнивая кривые на рис. 3, 4 , можно отметить, что при увеличении параметра утолщения льда $\alpha $, ${{\omega }_{n}}(k)$ уменьшаются для всех форм гидроупругих волн так же, как это происходит при уменьшении толщины однородного льда.

На рис. 5 и рис. 6 представлены распределения фазовых скоростей $c(k) = \omega (k){\text{/}}k$ и групповых скоростей ${{c}_{g}}(k) = d\omega (k){\text{/}}dk$ гидроупругих волн для первых четырех форм: линиями – для неравномерной ледовой пластины при разных значениях $\alpha $ и маркерами для однородной ледовой пластины толщины 0.1 м [5]. Отметим понижение значений $c(k)$ и ${{c}_{g}}(k)$ с ростом параметра $\alpha $.

Рис. 5.

Фазовые скорости гидроупругих волн: а–г – первая–четвертая формы; 1–4 – неравномерный лед при $\alpha = 0.05$, 0.5, 0.75, 0.95; маркеры – ледовый покров равномерной толщины [5].

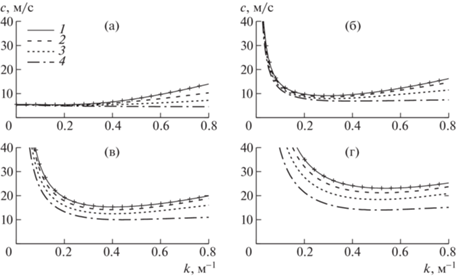
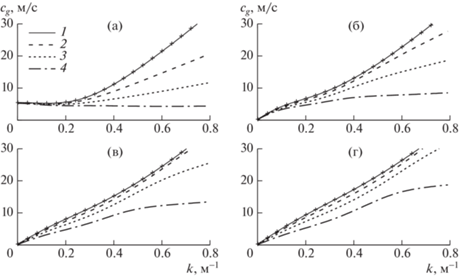
Рис. 6.

Групповые скорости гидроупругих волн: а–г – первая–четвертая формы; 1–4 – неравномерный лед при $\alpha = 0.05$, 0.5, 0.75, 0.95; маркеры – ледовый покров равномерной толщины [5].

На рис. 7 показаны распределения безразмерных удлинений ${{\varepsilon }_{{\max }}}(y)$ гидроупругих волн для первых четырех форм неравномерной ледовой пластины при $\alpha = 0.25$, для волновых чисел $k = 0.2,\;0.5,\;0.8$, 1 м^–1. Сплошные участки кривых соответствуют поперечным удлинениям $\varepsilon _{{\max }}^{{(1)}} = (1 + \alpha y)\left| {F''} \right|$, точечные линии – продольным удлинениям $\varepsilon _{{\max }}^{{(1)}} = (1 + \alpha y){{\kappa }^{2}}\left| F \right|$, пунктирные – комбинированным $\varepsilon _{{\max }}^{{(2)}}$. При используемых в расчетах размерах канала и толщины льда масштаб удлинений равен 0.0005.

Рис. 7.

Распределение максимальных удлинений ледового покрова поперек канала при $\alpha = 0.25$: а–г – первая-четвертая формы; 1–4 – $k = 0.2$, 0.5, 0.8, 1 м^–1; сплошные линии – поперечные удлинения, маркеры – продольные, пунктирные – комбинированные.

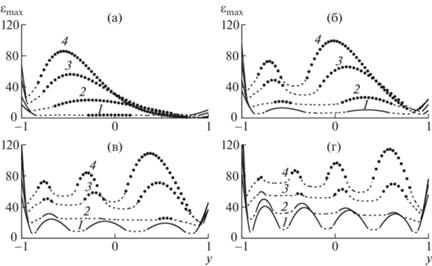
Видно, что при малых k абсолютные максимумы удлинений соответствуют поперечным удлинениям и для всех форм колебаний достигаются на кромке более тонкого (левого) края пластины $y = - 1$. Это показывает, что наиболее вероятен отрыв ледового покрова от левого берега. С ростом k продольные удлинения (точечные линии) внутри канала растут быстрее, чем поперечные, и при некотором значении k именно продольные удлинения внутри пластины становятся абсолютно максимальными и остаются такими при дальнейшем увеличении k (см. рис. 7а,б). Этот эффект наблюдается при всех рассмотренных в вычислениях значениях $\alpha $. Сначала он проявляется только для первой формы колебаний пластины (для $\alpha = 0.25$ это происходит при $k = 0.65$ м^–1), потом, с ростом k, возникает на второй форме (при $k = 0.93$ м^–1) и так далее для других форм. Отметим, что для старших форм внутренние максимумы с ростом k смещаются к правому, более толстому краю. Кроме того, комбинированные удлинения $\varepsilon _{{\max }}^{{(2)}}$ при всех рассмотренных значениях $\alpha $ никогда не становятся абсолютно максимальными.

На рис. 8 представлены распределения безразмерной величины ${{\varepsilon }_{{ABS}}}$ (3.1) от k для четырех форм гидроупругих колебаний ледового покрова при разных значениях параметра $\alpha $. Линиями на кривых обозначены поперечные удлинения $\varepsilon _{{\max }}^{{(1)}} = (1 + \alpha y)\left| {F{\kern 1pt} {\text{''}}} \right|$, точечными маркерами – продольные удлинения $\varepsilon _{{\max }}^{{(1)}} = (1 + \alpha y){{\kappa }^{2}}\left| F \right|$.

Рис. 8.

Абсолютные максимальные удлинения ледового покрова: а–г – первая–четвертая формы колебаний; 1–4 – $\alpha = 0.05$, 0.25, 0.5, 0.75; линии соответствуют случаю максимальных поперечных удлинений, маркеры – для продольных удлинений.

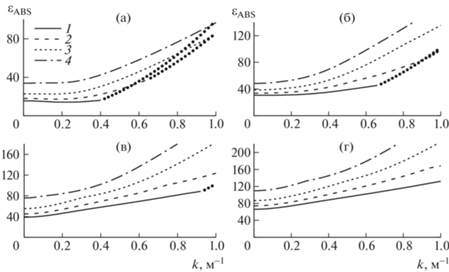
Видно, что с ростом $\alpha $ значения ${{\varepsilon }_{{{\text{ABS}}}}}$ увеличиваются для каждой формы. При фиксированном значении $\alpha $, чем выше номер формы, тем больше удлинения ${{\varepsilon }_{{{\text{ABS}}}}}$. Общий характер поведения всех кривых ${{\varepsilon }_{{{\text{ABS}}}}}$ в зависимости от $k$ является одинаковым:

• сначала (при малых $k$) располагается участок, соответствующий максимальным поперечным удлинениям $\varepsilon _{{\max }}^{{(1)}} = (1 + \alpha y)\left| {F{\kern 1pt} {\text{''}}} \right|$, на более тонком краю ледовой пластины ($y = - 1$), при которых могут развиваться трещины в ледовом покрове вдоль этого берега канала, т.е. происходит отрыв льда от берега;

• при некотором k начинают доминировать продольные удлинения пластины $\varepsilon _{{\max }}^{{(1)}}$ = $(1 + \alpha y){{\kappa }^{2}}\left| F \right|$ внутри канала ($\left| y \right| < 1$), что наблюдается в виде резких изломов кривых на рис. 8. Тогда трещины будут появляться поперек канала.

Наиболее отчетливо это видно для первых трех форм при $\alpha = 0.05$. Для $\alpha > 0.05$ и старших форм, характер кривых ${{\varepsilon }_{{ABS}}}$ остается аналогичным, однако участок максимальных поперечных удлинений (линии) длинее, и продольные удлинения становятся максимальными при $k > 1$ м^–1.

ЗАКЛЮЧЕНИЕ

Исследованы гидроупругие характеристики изгибно-гравитационных волн, распространяющихся по каналу, покрытому примороженным к берегам ледовым покровом с линейно изменяющейся поперек канала толщиной. Получены формы колебаний ледовой пластины и распределение максимальных удлинений. Определены дисперсионные кривые, получены фазовые и групповые скорости бегущих волн.

Проведено сравнение полученных данных с аналогичными результатами для задачи с жестко закрепленными (примороженными) кромками однородной ледовой пластины [5]. Показана сходимость результатов для пластины линейной толщины к результатам для однородной пластины при уменьшении коэффициента утолщения льда $\alpha $.

Исследовано влияние неоднородности толщины пластины на частоты, фазовые и групповые скорости гидроупругих колебаний. При увеличении значения параметра утолщения пластины происходит уменьшение частот и скоростей для всех форм колебаний, как у однородной пластины с уменьшением толщины.

Показано, что для длинных волн наиболее вероятное разрушение пластины соответствует поперечным удлинениям на тонком краю пластины, что может привести к отрыву льда от соответствующего берега. Для коротких волн максимальными становятся продольные напряжения внутри пластины, локализованные ближе к толстому краю. Это может привести к растрескиванию пластины в поперечном направлении. Такой характер изменения распределения максимальных напряжений по пластине является особенностью гидроупругого поведения ледовой пластины с неравномерным по толщине ледовым покровом.

Работа выполнена при поддержке совместного проекта TUBITAK и РФФИ 20-58-46009.

Список литературы

Добродеев А.А., Сазонов К.Е. Модельный эксперимент по определению ледовой нагрузки на морские инженерные сооружения // Труды Крыловского государственного научного центра. 2019. Т. 2. № 388. С. 24–40.
Крупина Н.А., Лихоманов В.А., Максимова П.В., Николаев П.М., Савицкая А.В., Свистунов И.А., Чернов А.В. Итоги работы большого ледового бассейна ААНИИ // Проблемы Арктики и Антарктики. 2015. № 1 (103). С. 101–110.
Pogorelova A.V., Zemlyak V.L., Kozin V.M. Body motion in liquid under ice plate with snow cover // Appl. Ocean Res. 2019. V.84. P. 32–37.
Squire V.A., Hosking R., Kerr A., Langhorne P.J. Moving loads on ice plates. Dordrecht: Kluwer, 1996. 244 p.
Korobkin A.A., Khabakhpasheva T.I., Papin A.A. Waves propagating along a channel with ice cover // Eur J Mech B Fluids. 2014. V. 47. P. 166–175.
Батяев Е.A., Хабахпашева Т.И. Гидроупругие волны в канале со свободным ледовым покровом // Изв. РАН. МЖГ. 2015. № 6. С. 71–88.
Ren K., Wu G.X., Li Z.F. Hydroelastic waves propagating in an ice-covered channel // J. Fluid Mech. 2020. V. 886. A18.
Козин В.М. Резонансный метод разрушения ледяного покрова. Изобретения и эксперименты. М.: Акад. естествознания, 2007. 355 с.
Shishmarev K.A., Khabakhpasheva T.I., Korobkin A.A. The response of ice cover to a load moving along a frozen channel // Appl. Ocean Res. 2016. V. 59. P. 313–326.
Khabakhpasheva T.I., Shishmarev K.A., Korobkin A.A. Large-time response of ice cover to a load moving along a frozen channel // Appl. Ocean Res. 2019. V. 86. P. 154–165.
Shishmarev K.A., Khabakhpasheva T.I., Korobkin A.A. Ice response to an underwater body moving in a frozen channel // Appl. Ocean Res. 2019. V. 91. P. 101877.
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат, 1967. 215 с.
Hosking R.J., Sneyd A.D., Waugh D.W. Viscoelastic response of a floating ice plate to a steadily moving load // J. Fluid Mech. 1988. V. 196. P. 409–430.
Părău E.I., Dias F. Nonlinear effects in the response of a floating ice plate to a moving load // J. Fluid Mech. 2002. V. 460. P. 281–305.
Bonnefoy F., Meylan M.H., Ferrant P. Nonlinear higher-order spectral solution for a two-dimensional moving load on ice // J. Fluid Mech. 2009. V. 621. P. 215–242.
Plotnikov P.I., Toland J.F. Modelling nonlinear hydroelastic waves // Phil. Trans. R. Soc. A. 2011. V. 369. P. 2942–2956.
Погорелова А.В. Особенности волнового сопротивления СВПА при нестационарном движении по ледяному покрову // ПМТФ. 2008. Т. 49. № 1. С. 89–99.
Meylan M.H., Sturova I.V. Time-dependent motion of a two-dimensional floating elastic plate // J Fluids Struct. 2009. V. 25. № 3. P. 445–460.
Погорелова А.В., Козин В.М., Матюшина А.А. Исследование напряженно-деформированного состояния ледяного покрова при взлете и посадке на него самолета // ПМТФ. 2015. Т. 56. № 5. С. 214–221.
Brocklehurst P., Korobkin A.A., Părău E.I. Interaction of hydro-elastic waves with a vertical wall // J Eng Math. 2010. V. 68. P. 215–231.
Sturova I.V., Tkacheva L.A. Movement of external load over free surface of fluid in the ice channel // J Phys Conf Ser. 2019. V. 1268. № 1 P. 012066.
Stepanyants Y.A., Sturova I.V. Waves on a compressed floating ice plate caused by motion of a dipole in water // J. Fluid Mech. 2021. V. 907. P. A7.
Ткачева Л.А. Колебания цилиндра в жидкости под ледяным покровом вблизи вертикальной стенки // Изв. РАН. МЖГ. 2020. № 3. С. 12–25.
Марченко А.В. Изгибно-гравитационные волны // Тр. ИОФАН. 1999. Т. 56. С. 65–111.
Савин А.А., Савин А.С. Пространственная задача о возмущении ледяного покрова движущимся в жидкости диполем // Изв. РАН. МЖГ. 2015. № 5. С. 16–23.
Ильичев А.Т., Савин А.С. Процесс установления системы плоских волн на ледовом покрове над диполем, равномерно движущимся в толще идеальной жидкости // ТМФ. 2017. Т. 193. № 3. С. 455–465.
Il’ichev A. Physical parameters of envelope solitary waves at a water-ice interface // AIP Conf. Proc. 2018. V. 1982. P. 20036.
Khabakhpasheva T.I., Korobkin A.A. Hydroelastic behaviour of compound floating plate in waves // J Eng Math. 2002. V. 44. № 1. P. 21–40.
Стурова И.В. Нестационарное поведение упругой составной балки, плавающей на мелководье // ПМТФ. 2009. Т. 50. № 4. С. 54–65.
Porter D., Porter R. Approximations to wave scattering by an ice sheet of variable thickness over undulating bed topography // J. Fluid Mech. 2004. V. 509. P. 145–179.
Korobkin A.A., Khabakhpasheva T.I., Malenica S. Maximum stress of stiff elastic plate in uniform flow and due to jet impact // Phys. Fluids. 2017. V. 29. № 7. P. 072105.
Li Q.S. Vibration analysis of flexural-shear plates with varying cross-section // Int J Solids Struct. 2000. V. 37. № 9. P. 1339–1360.
Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. М.: Наука, 1966. 636 с.
Chopra I. Vibration of stepped thickness plates // Int. J. Mech. Sci. 1974, V. 16. № 6. P. 337–344.
Guo S.J., Keane A.J., Moshrefi-Torbat M. Vibration of stepped thickness plates // J. Sound Vib. 1997. V. 204. № 4. P. 645–657.
Li Q.S., Cao H., Li G. Static and dynamic analysis of straight bars with variable cross-section // Comput Struct. 1996. V. 59. № 6. P. 1185–1191.
Taha M.H., Abohadima S. Mathematical model for vibrations of non-uniform flexural beams // Eng Mech. 2008. V. 15. № 1. P. 3–11.
Nesterov S.V., Baydulov V.G. Transverse oscillations of a cantilever rod of rectangular cross section and variable thickness // J. Phys. Conf. Ser. 2019. V. 1301. P. 012023.
Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. М.: Высшая школа, 1984. 472 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал