Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 38-50

УСТОЙЧИВОСТЬ АДВЕКТИВНОГО ТЕЧЕНИЯ ВО ВРАЩАЮЩЕМСЯ ГОРИЗОНТАЛЬНОМ ТЕПЛОИЗОЛИРОВАННОМ СНИЗУ СЛОЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ С ТВЕРДЫМИ ГРАНИЦАМИ ПРИ МАЛОМ ЧИСЛЕ ПРАНДТЛЯ

К. Г. Шварц^*

Пермский государственный национальный исследовательский университет
Пермь, Россия

Поступила в редакцию 29.06.2021
После доработки 15.09.2021
Принята к публикации 21.09.2021

EDN: YGNMBY
DOI: 10.31857/S0568528122020086

Аннотация

Исследуется устойчивость адвективного течения в плоском вращающемся горизонтальном слое несжимаемой жидкости с твердыми границами. На верхней границе слоя задано линейное распределение температуры, нижняя граница теплоизолированная. Адвективное течение, возникшее за счет горизонтальной конвекции, описывается аналитически в виде нового точного решения уравнений Навье–Стокса в приближении Буссинеска. При малом значении числа Прандтля в рамках линейной теории исследуется устойчивость адвективного течения на нормальные возмущения для широкого диапазона числа Тейлора. Определяются наиболее опасные моды, строятся нейтральные кривые. В рамках нелинейной постановки задачи изучается влияние вращения на структуру конечно-амплитудных возмущений в надкритической области вблизи минимумов нейтральных кривых.

Ключевые слова: горизонтальная конвекция, адвективные течения, точное решение, нормальные возмущения, устойчивость, конечно-амплитудные возмущения

Под воздействием продольного градиента температуры в горизонтальном слое жидкости возникает адвективное течение [1]. Его специфика состоит в отсутствии вертикальной компоненты скорости, вектор скорости в потоке ориентирован перпендикулярно силе плавучести, которая является основной причиной движения. В случае, когда температура на одной или обеих горизонтальных границах слоя является линейной функцией ($T = Ax$, где $x$ – продольная координата, $A$ – постоянный горизонтальный температурный градиент на границах слоя), течение описывается аналитическим выражением, которое является точным решением уравнений Навье–Стокса [2, 3]. При наличии твердых границ, на которых задано условие прилипания, возникает течение Остроумова–Бириха [4]. Устойчивость такого течения исследована в [5], в частности, при малых числах Прандтля неустойчивость обусловлена гидродинамическим механизмом (неподвижные вихри на границе встречных потоков). Обзор устойчивости других подобных течений представлен в [6].

Адвективное течение в горизонтальном слое жидкости с теплоизолированной нижней границей описано аналитически в [7]. В этом случае кубический профиль скорости остается неизменным, а в профиле температуры отсутствуют зоны потенциально неустойчивой стратификации, тем самым исключаются моды неустойчивости рэлеевской природы. Линейный анализ устойчивости, проведенный в [7], показал, что опасные гидродинамические моды возникают при малых числах Прандтля ($Pr$) от 0.015 до 0.27.

В монографии [8] представлено точное решение уравнений Навье–Стокса в приближении Буссинеска, описывающее адвективное течение, возникающее во вращающемся горизонтальном слое жидкости с твердыми границами и линейной температурой на обеих границах слоя. Имеются две горизонтальные компоненты скорости, профили которых являются антисимметричными относительно вертикальной оси $z$. Они описывают движение жидкости типа спирали Экмана, поле же температуры описывает два тепловых потока, двигающихся вдоль слоя. С ростом числа Тейлора (Ta) вблизи твердых границ образуются пограничные слои скорости и температуры, в которых градиент давления балансируется с силами вязкости и силами Кориолиса.

Устойчивость такого течения изучена в работе [9] для большого диапазона Ta. Было показано, что при малых значениях $Pr$ с ростом числа Тейлора наиболее опасные моды неустойчивости меняются. При малых значениях Ta в слое с твердыми границами снижается устойчивость адвективного течения, а затем, начиная с некоторого порогового значения, стабилизирует его. Этот же факт был зафиксирован в горизонтальном слое жидкости со свободной верхней границей при исследовании устойчивости адвективного течения [10], а также при численных расчетах во вращающихся круглых кюветах [11–14].

В данной работе исследуется устойчивость адвективного течения во вращающемся горизонтальном слое жидкости с твердыми границами при теплоизолированной нижней границе.

1. АДВЕКТИВНОЕ ТЕЧЕНИЕ

Рассмотрим бесконечный горизонтальный слой несжимаемой жидкости шириной $2h$ с твердыми границами, вращающийся с постоянной угловой скоростью ${\mathbf{\Omega }} = {{\Omega }_{0}}{{{\mathbf{i}}}_{{\mathbf{z}}}}$, где ${{{\mathbf{i}}}_{{\mathbf{z}}}}$ – орт-вектор вертикальной оси $z$. Направление оси вращения совпадает с вертикальной осью координат $Oz$. На обеих границах задано условие прилипания, поток замкнутый, на верхней границе приложен постоянный горизонтальный градиент температуры $T$, нижняя граница теплоизолированная. Движение жидкости описывается уравнениями конвекции в приближении Буссинеска [15] в декартовой системе координат $Oxyz$ ($z$ – вертикальная координата, $x$, $y$ – горизонтальные координаты). Выбрав в качестве единиц измерения длины, времени, скорости, температуры и давления $h$, ${{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} \nu }} \right. \kern-0em} \nu }$, ${{g{\kern 1pt} \beta A{{h}^{3}}} \mathord{\left/ {\vphantom {{g{\kern 1pt} \beta A{{h}^{3}}} \nu }} \right. \kern-0em} \nu }$, $Ah$, ${{\rho }_{0}}g\beta A{{h}^{3}}$ (где $\nu $ – кинематическая вязкость, $\beta $ – коэффициент теплового расширения, g – ускорение свободного падения, ${{\rho }_{0}}$ – средняя плотность), получим исходные уравнения в безразмерном виде

$\begin{gathered} \frac{{\partial {{\upsilon }_{x}}}}{{\partial t}} + Gr\left( {{{\upsilon }_{x}}\frac{{\partial {{\upsilon }_{x}}}}{{\partial x}} + {{\upsilon }_{y}}\frac{{\partial {{\upsilon }_{x}}}}{{\partial y}} + {{\upsilon }_{z}}\frac{{\partial {{\upsilon }_{x}}}}{{\partial z}}} \right) - \sqrt {Ta} \cdot {{\upsilon }_{y}} = - \frac{{\partial p}}{{\partial x}} + \Delta {{\upsilon }_{x}} \\ \frac{{\partial {{\upsilon }_{y}}}}{{\partial t}} + Gr\left( {{{\upsilon }_{x}}\frac{{\partial {{\upsilon }_{y}}}}{{\partial x}} + {{\upsilon }_{y}}\frac{{\partial {{\upsilon }_{y}}}}{{\partial y}} + {{\upsilon }_{z}}\frac{{\partial {{\upsilon }_{y}}}}{{\partial z}}} \right) + \sqrt {Ta} \cdot {{\upsilon }_{x}} = - \frac{{\partial p}}{{\partial y}} + \Delta {{\upsilon }_{y}} \\ \end{gathered} $

(1.1)

$\frac{{\partial {{\upsilon }_{z}}}}{{\partial t}} + Gr\left( {{{\upsilon }_{x}}\frac{{\partial {{\upsilon }_{z}}}}{{\partial x}} + {{\upsilon }_{y}}\frac{{\partial {{\upsilon }_{z}}}}{{\partial y}} + {{\upsilon }_{z}}\frac{{\partial {{\upsilon }_{z}}}}{{\partial z}}} \right) = - \frac{{\partial p}}{{\partial z}} + \Delta {{\upsilon }_{z}} + T$

$\begin{gathered} \frac{{\partial {{\upsilon }_{x}}}}{{\partial x}} + \frac{{\partial {{\upsilon }_{y}}}}{{\partial y}} + \frac{{\partial {{\upsilon }_{z}}}}{{\partial z}} = 0 \\ \frac{{\partial T}}{{\partial t}} + Gr\left( {{{\upsilon }_{x}}\frac{{\partial T}}{{\partial x}} + {{\upsilon }_{y}}\frac{{\partial T}}{{\partial y}} + {{\upsilon }_{z}}\frac{{\partial T}}{{\partial z}}} \right) = \frac{1}{{Pr}}\Delta T \\ \end{gathered} $

где $\,{\mathbf{\upsilon }}\left( {x,\,y,\,z,\,t} \right) = \left( {{{\upsilon }_{x}},\,{{\upsilon }_{y}},\,{{\upsilon }_{z}}} \right)$ – вектор скорости, p – конвективная добавка к гидростатическому давлению, соответствующему средним значениям температуры и плотности [1, 16], Gr = ${{g\beta A{{h}^{4}}} \mathord{\left/ {\vphantom {{g\beta A{{h}^{4}}} {{{\nu }^{2}}}}} \right. \kern-0em} {{{\nu }^{2}}}}$ – число Грасгофа, $Ta = {{({{2{{\Omega }_{0}}{{h}^{2}}} \mathord{\left/ {\vphantom {{2{{\Omega }_{0}}{{h}^{2}}} \nu }} \right. \kern-0em} \nu })}^{2}}$ – число Тейлора, $Pr = {\nu \mathord{\left/ {\vphantom {\nu \chi }} \right. \kern-0em} \chi }$ – число Прандтля, χ – коэффициент температуропроводности, оператор Лапласа $\Delta = {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{x}^{2}} + }}} \right. \kern-0em} {\partial {{x}^{2}} + }}{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}} + }}} \right. \kern-0em} {\partial {{y}^{2}} + }}{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}$. Граничные условия в безразмерном виде имеют вид:

(1.2)

$\begin{gathered} z = - 1:\;\;\frac{{\partial T}}{{\partial z}} = 0,\;\;{\mathbf{\upsilon }} = 0;\quad z = 1:\;\;T = x,\;\;{\mathbf{\upsilon }} = 0 \\ \int\limits_{ - 1}^1 {{{\upsilon }_{x}}dz} = 0,\quad \int\limits_{ - 1}^1 {{{\upsilon }_{y}}dz} = 0 \\ \end{gathered} $

Краевая задача (1.1), (1.2) имеет аналитическое решение [8]:

(1.3)

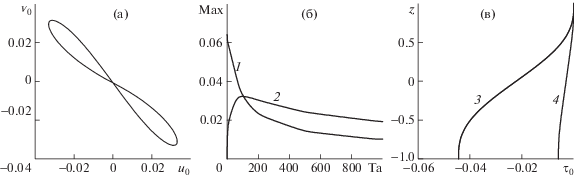
$\begin{gathered} {{u}_{0}}\left( z \right) = \frac{1}{{\sqrt {Ta} }}\operatorname{Im} {{f}_{1}}\left( z \right),\quad {{\upsilon }_{0}}\left( z \right) = \frac{1}{{\sqrt {Ta} }}\left( {z - \operatorname{Re} {{f}_{1}}\left( z \right)} \right),\quad {{w}_{0}}\left( z \right) \equiv 0 \\ {{T}_{0}} = x + GrPr{{\tau }_{0}}\left( z \right),\quad {{\tau }_{0}}(z) = \frac{1}{{\sqrt {Ta} }}[{{\upsilon }_{0}}(z) - \upsilon _{0}^{'}( - 1)(z - 1)] \\ {{f}_{1}}\left( z \right) = \frac{{{\text{sh}}\left( {\mu z} \right)}}{{{\text{sh}}\left( \mu \right)}},\quad \mu = \sqrt[4]{{\frac{{Ta}}{4}}}\left( {1 + i} \right),\quad i = \sqrt { - 1} \\ \end{gathered} $

где ${{u}_{0}}\left( z \right)$, ${{\upsilon }_{0}}\left( z \right)$ и ${{w}_{0}}\left( z \right)$ – компоненты вектора скорости, Re – действительная часть комплексного значения, $\operatorname{Im} $ – мнимая часть комплексного значения, ${{T}_{0}}$ – температура.

Профили компонент скорости ${{u}_{0}}(z)$, ${{\upsilon }_{0}}(z)$ во вращающемся слое являются антисимметричными относительно оси $z$. Они описывают движение спирального типа, что иллюстрирует годограф вектора скорости на рис. 1а. На рис. 1б представлен график зависимости максимумов горизонтальных компонент скорости от числа Тейлора. Максимум первой компоненты скорости ${{u}_{0}}(z)$ монотонно убывает с увеличением числа Тейлора пропорционально ${1 \mathord{\left/ {\vphantom {1 {\sqrt {Ta} }}} \right. \kern-0em} {\sqrt {Ta} }}$. При отсутствии вращения ${{\upsilon }_{0}}\left( z \right) \equiv 0$, вторая компонента скорости возникает при наличии вращения, когда $Ta > 0$. Ее максимум начинает возрастать в диапазоне $0 \leqslant Ta \leqslant 98.4$, оставаясь при этом меньше максимума первой компоненты скорости ${{u}_{0}}$. Таким образом, под действием силы Кориолиса течение Остроумова-Бириха [2–4] начинает перестраиваться. При $Ta > 98.4$ максимум первой и максимум второй горизонтальной компоненты скорости выравниваются и теперь они оба монотонно убывают по корневому закону. На рис. 1в представлены графики ${{\tau }_{0}}(z)$ при $Ta = 0.1$ и $Ta = {{10}^{3}}$. Профили температуры не обладают симметрией. С ростом числа Тейлора максимум ${{\tau }_{0}}(z)$ по модулю монотонно убывает.

Рис. 1.

Годограф вектора скорости при ${\text{Ta}} = 100$ (а), зависимость максимумов компонент скорости ${{u}_{0}}(z)$ и ${{\upsilon }_{0}}(z)$ от числа Тейлора: 1 − max u₀, 2 − max v₀ (б), графики ${{\tau }_{0}}(z)$ при ${\text{Ta}} = 0.1$(3) и ${\text{Ta}} = {{10}^{3}}$(4) (в).

2. ЛИНЕЙНАЯ ТЕОРИЯ

Для исследования устойчивости адвективного течения (1.3) применим метод малых возмущений [5]

(2.1)

${\mathbf{v}} = {{{\mathbf{v}}}_{0}} + V,\quad {{{\mathbf{v}}}_{0}} = \left( {{{u}_{0}},{{\upsilon }_{0}},0} \right),\quad V = \left( {U,V,W} \right),\quad T = {{T}_{0}} + \theta ,\quad P = {{p}_{0}} + P{\kern 1pt} '$

Здесь $V$, $\theta $, $P{\kern 1pt} '$ – малые возмущения. Подставив возмущенные поля скорости, температуры и давления (2.1) в исходную систему (1.1) и граничные условия (1.2), получим следующую задачу:

(2.2)

$\begin{gathered} \frac{{\partial V}}{{\partial t}} + Gr\left[ {\left( {V\nabla } \right)V + \left( {V\nabla } \right){{v}_{0}} + \left( {{{v}_{0}}\nabla } \right)V} \right] + \sqrt {Ta} {\text{ }}\left( {{\kern 1pt} {{i}_{z}} \times V} \right) = - P{\kern 1pt} ' + \Delta V + \theta {\kern 1pt} {{i}_{z}}, \\ {{i}_{z}} = \left( {0{\text{,0,1}}} \right)\quad {\text{div}}V = 0 \\ \end{gathered} $

(2.3)

$\begin{gathered} \frac{{\partial \theta }}{{\partial t}} + Gr\left[ {V\nabla \theta + V\nabla {{T}_{0}} + {{v}_{0}}\nabla \theta } \right] = \frac{1}{{\Pr }}\Delta \theta \\ z = - 1:\;\;U = V = W = 0,\quad \frac{{\partial \theta }}{{\partial z}} = 0 \\ \end{gathered} $

(2.4)

$z = 1:\;\;U = V = W = 0,\quad \theta = 0$

В рамках линейной теории устойчивости в уравнениях (2.2)–(2.4) пренебрегаем малыми квадратичными по возмущениям $V$ и $\theta $ слагаемыми. Полученная система линейных уравнений имеет решения в виде нормальных возмущений, пропорциональных ${\text{exp}}\left( {\lambda t + {{k}_{x}}x + {{k}_{y}}y} \right)$, где $\lambda = {{\lambda }_{1}} + i{{\lambda }_{2}}$, – декремент, определяющий временной ход возмущений. Вещественные коэффициенты ${{k}_{x}}$ и ${{k}_{y}}$ – это компоненты волнового вектора вдоль осей $Ox$ и $Oy$. Следуя [1, 5], будем изучать два предельных случая. Это пространственные винтовые периодические возмущения в виде валов с осью, параллельной оси $Ox$, которые при отсутствии вращения превращаются в плоские, и пространственные спиральные периодические по y возмущения в виде валов с осью, перпендикулярной к оси $Ox$ при $Pr = 0.1$. Числа Тейлора рассматриваются в диапазоне от 0 до 10⁵.

Случай винтовых возмущений. Уравнения возмущений выводятся из линеаризованной системы (2.2)–(2.4) в предположении, что производная по $y$ от всех функций равна нулю (${{k}_{y}} = 0$). Имеются все три компоненты вектора возмущения скорости и возмущение температуры, которые являются функциями времени $t$ и двух пространственных координат x и z. Учитывая, что дивергенция возмущений скорости равна нулю, введем функцию тока возмущений $\psi \left( {t{\text{,}}x{\text{,}}z} \right)$ и вихря возмущения скорости $\phi \left( {t{\text{,}}x{\text{,}}z} \right)$

$U = - \frac{{\partial \psi }}{{\partial z}},\quad W = \frac{{\partial \psi }}{{\partial x}},\quad \phi = \frac{{\partial U}}{{\partial z}} - \frac{{\partial W}}{{\partial x}} = - \Delta \psi ,\quad \Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}$

Рассмотрим нормальные возмущения вида

$\phi = \left[ {{{\phi }_{1}}\left( {t,z} \right) + i{{\phi }_{2}}\left( {t,z} \right)} \right]\exp \left( {i{{k}_{x}}x} \right),\quad \psi = \left[ {{{\psi }_{1}}\left( {t,z} \right) + i{{\psi }_{2}}\left( {t,z} \right)} \right]\exp \left( {i{{k}_{x}}x} \right)$

$V = \left[ {{{v}_{1}}\left( {t,z} \right) + i{{v}_{2}}\left( {t,z} \right)} \right]\exp \left( {i{{k}_{y}}y} \right),\quad \vartheta = \left[ {{{\vartheta }_{1}}\left( {t,z} \right) + i{{\vartheta }_{2}}\left( {t,z} \right)} \right]\exp \left( {i{{k}_{x}}x} \right)$

В результате задача сведется к решению системы линейных уравнений в частных производных по времени $t$ и переменной $z$, описанной в [8], с граничными условиями

(2.5)

$z = - 1:\;\;{{\psi }_{\alpha }} = \frac{{\partial {{\psi }_{\alpha }}}}{{\partial z}} = {{v}_{\alpha }} = \frac{{\partial {{\vartheta }_{\alpha }}}}{{\partial z}} = 0,\quad (\alpha = 1,2)$

(2.6)

$z = 1:\;\;{{\psi }_{\alpha }} = \frac{{\partial {{\psi }_{\alpha }}}}{{\partial z}} = {{v}_{\alpha }} = {{\vartheta }_{\alpha }} = 0,\quad (\alpha = 1,2)$

В качестве начальных возмущений функции тока, второй компоненты скорости и аддитивной компоненты поля температуры берем функцию ${{\sin }^{2}}\left( {\pi z} \right)$, удовлетворяющую граничным условиям (2.5), (2.6).

Полученная начально-краевая задача решается по численной методике, описанной в [8]. При построении нейтральной кривой, описывающей зависимость критического числа Грасгофа от волнового числа, для каждого выбранного значения ${{k}_{x}}$ требуется найти такое число Грасгофа, при котором действительная часть декремента возмущений $\lambda = {{\lambda }_{1}} + i{{\lambda }_{2}}$ равна нулю. Иными словами, решается задача о поиске корня ${{\lambda }_{1}} = 0$ для неявной функции ${{\lambda }_{1}}$ (k_x, Gr, Ta). Эта функция строится дискретно по точкам с помощью многократного решения эволюционной задачи методом сеток. Для нахождения действительной части декремента возмущений ${{\lambda }_{1}}$ прослеживалась эволюция во времени максимумов по модулю неизвестных. В силу линейности задачи устойчивости в качестве аппроксимации зависимости амплитуд по времени использовалась экспоненциальная формула $C\exp \left( {{{\lambda }_{1}}t} \right)$. Неизвестные ${{\lambda }_{1}}$ и $C$ определяются методом наименьших квадратов [17] по ходу вычислений уравнений системы методом сеток. Нулевое значение декремента возмущений уточняется методом половинного деления [17]. Характер поведения возмущений от времени существенно зависит от всех параметров задачи; в области неустойчивости все возмущения нарастают, а в области устойчивости затухают.

Расчеты показали, что в рассмотренном диапазоне чисел Тейлора сохраняется колебательный характер неустойчивости. С ростом $Ta$ наблюдались четыре наиболее опасные моды (рис. 2а,б,в), сменяющие друг друга. Мода I (рис. 2а) при отсутствии вращения ($Ta = 0$) описана в [7]. При $Ta \ne 0$ она наиболее опасна в интервале $0 < Ta < 33$. В указанном диапазоне числа Тейлора адвективное течение резко стабилизируется. С ростом Ta возрастает критическое число Грасгофа ($G{{r}_{k}}$), волновое число ${{k}_{x}}$ растет от $1.26$ до $1.56$. Отметим, что, как и в [7], инкремент возмущений ${{\lambda }_{2}} > 8$ и он становится больше с увеличением числа Тейлора. На рис. 2г представлены характерные для данной моды нейтральные кривые при $Ta = 1$ и $Ta = 10$. При меньшем значении числа Тейлора критическое число Грасгофа становится меньше, также как и волновое число.

Рис. 2.

Зависимость критического числа Грасгофа (${\text{G}}{{{\text{r}}}_{k}}$) от числа Тейлора (${\text{Ta}}$) для первой (I), второй (II) (а), третьей (III) (б) и четвертой (IV) моды неустойчивости (в) на винтовые возмущения; нейтральные кривые зависимости числа Грасгофа от волнового числа ${{k}_{x}}$ при (г) – $Ta = 1,10$ (1–2); (д) – $Ta = 100,200$ (3–4); (е) – $Ta = 400,500$ (5–6) и (ж) – $Ta = 1000$.

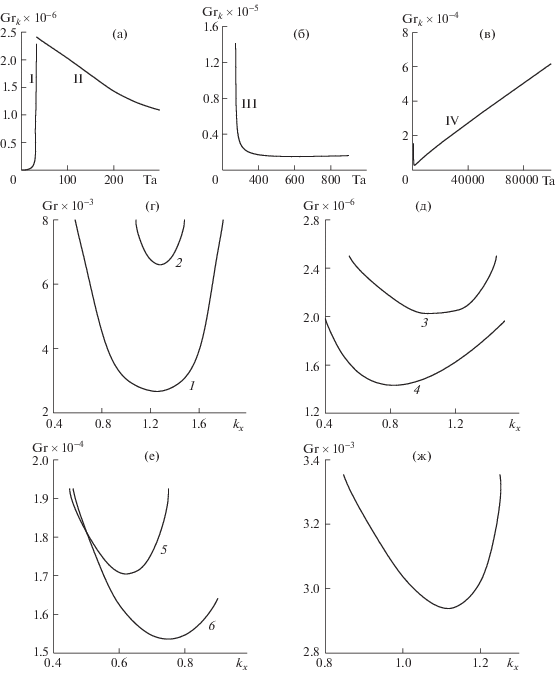
Вторая мода (рис. 2а) развивается в интервале $32.6 \leqslant Ta < 270$. С ростом числа Тейлора волновое число ${{k}_{x}}$ уменьшается от ${\text{1}}{\text{.27}}$ до ${\text{0}}{\text{.82}}$, адвективное течение становится менее устойчивым, так как критическое число Грасгофа уменьшается от 2411836.9 до 1224076.9. На рис. 2д представлены нейтральные кривые при $Ta = 100$ и $Ta = 200$. При меньшем значении числа Тейлора критическое число Грасгофа, также как и волновое число, больше.

Третья мода (рис. 2б) является наиболее опасной при $270 \leqslant Ta \leqslant 715$. С ростом числа Тейлора волновое число ${{k}_{x}}$ увеличивается от 0.07 до 0.91, критическое число Грасгофа уменьшается от 138434.5 до 15270.3, таким образом, здесь течение дестабилизируется. На рис. 2е представлены нейтральные кривые при $Ta = 400$ и $Ta = 500$. С ростом значений числа Тейлора убывает критическое число Грасгофа, волновое число увеличивается.

Четвертая мода (рис. 2в) находится в интервале $715 < Ta \leqslant {{10}^{5}}$. С ростом числа Тейлора волновое число ${{k}_{x}}$ увеличивается от 0.27 до 8.2, $G{{r}_{k}}$ уменьшается до ${\text{2715}}{\text{.2 }}$ при $Ta = 1300$, это значение является минимальным на всем интервале от 0 до 10⁵. При $Ta > 1300$ критическое число Грасгофа монотонно возрастает с ростом числа Тейлора до ${\text{61646}}{\text{.2}}$ при $Ta = {{10}^{5}}$. На рис. 2ж представлена нейтральная кривая при $Ta = 1000$.

Случай спиральных возмущений. Уравнения спиральных возмущений выводятся из системы (2.2)–(2.4) в предположении, что производные в ней по $x$ от всех функций равны нулю (${{k}_{x}} = 0$). Имеются три компоненты вектора возмущения скорости, а также возмущения температуры, которые являются функциями времени $t$ и двух пространственных переменных $y$, $z$. Аналогично предыдущему случаю введем функцию тока возмущений $\psi \left( {t{\text{,}}y{\text{,}}z} \right)$ и вихря возмущения скорости $\varphi $(t, y, z):

$V = - \frac{{\partial \psi }}{{\partial z}},\quad W = \frac{{\partial \psi }}{{\partial {\text{y}}}},\quad \varphi = \frac{{\partial V}}{{\partial z}} - \frac{{\partial W}}{{\partial y}} = - \Delta \psi ,\quad \Delta = \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}$

Рассмотрим нормальные возмущения вида:

$\varphi = \left[ {{{\varphi }_{1}}\left( {t{\text{,}}z} \right) + i{{\varphi }_{2}}\left( {t{\text{,}}z} \right)} \right]\exp \left( {i{{k}_{{\text{y}}}}y} \right),\quad \psi = \left[ {{{\psi }_{1}}\left( {t{\text{,}}z} \right) + i{{\psi }_{2}}\left( {t{\text{,}}z} \right)} \right]\exp \left( {i{{k}_{y}}y} \right)$

$U = \left[ {{{u}_{1}}\left( {t{\text{,}}z} \right) + i{{u}_{2}}\left( {t{\text{,}}z} \right)} \right]\exp \left( {i{{k}_{y}}y} \right),\quad \theta = \left[ {{{\theta }_{1}}\left( {t{\text{,}}z} \right) + i{{\theta }_{2}}\left( {t{\text{,}}z} \right)} \right]\exp \left( {i{{k}_{y}}y} \right)$

В результате задача сведется к решению системы линейных уравнений в частных производных по времени $t$ и переменной $z$ [8] с граничными условиями:

(2.7)

$z = - 1:\;\;{{\psi }_{\alpha }} = \frac{{\partial {{\psi }_{\alpha }}}}{{\partial z}} = {{u}_{\alpha }} = \frac{{\partial {{\theta }_{\alpha }}}}{{\partial z}} = 0,\quad (\alpha = 1,2)$

(2.8)

$z = 1:\;\;{{\psi }_{\alpha }} = \frac{{\partial {{\psi }_{\alpha }}}}{{\partial z}} = {{u}_{\alpha }} = {{\theta }_{\alpha }} = 0,\quad (\alpha = 1,2)$

Полученная начально-краевая задача решается по вычислительной схеме аналогично случаю винтовых возмущений. В качестве начальных возмущений для неизвестных возьмем снова функцию ${{\sin }^{2}}\left( {\pi z} \right)$, удовлетворяющую граничным условиям (2.7), (2.8).

Расчеты показали, что в рассмотренном диапазоне чисел Тейлора сохраняется колебательный характер неустойчивости. С ростом Ta наблюдались две наиболее опасные моды (рис. 3а,б), сменяющие друг друга. Мода I (рис. 3a) наиболее опасна на интервале $0 < Ta < 95$. При $0 < Ta \leqslant 10$ критическое число Грасгофа уменьшается до 1163.9 с увеличением числа Тейлора, тем самым делая адвективное течение менее устойчивым во вращающемся слое жидкости, $G{{r}_{k}} = {\text{1163}}{\text{.9 }}$ является минимальным для всех чисел Тейлора на всем рассматриваемом интервале от 0 до 10⁵. При $10 < Ta < 95$ критическое число Грасгофа растет с увеличением числа Тейлора и достигает значения ${\text{11931}}{\text{.3}}$ при $Ta = 93$. Волновое число ${{k}_{y}}$ монотонно возрастает с ростом числа Тейлора от 0.34 до 0.64 при $0 < Ta \leqslant 20$, а затем убывает от ${\text{0}}{\text{.64}}$ до ${\text{0}}{\text{.2}}$ при $20 \leqslant Ta \leqslant 93$. На рис. 3в представлены характерные нейтральные кривые при $Ta = 10$ и $Ta = 30$.

Рис. 3.

Зависимость критического числа Грасгофа ($G{{r}_{k}}$) от числа Тейлора ($Ta$) для первой (а) и второй моды неустойчивости (б) на спиральные возмущения; нейтральные кривые зависимости числа Грасгофа от волнового числа ${{k}_{y}}$: Ta = 10 (а), 30 (б), 1000 (в), 2000 (г).

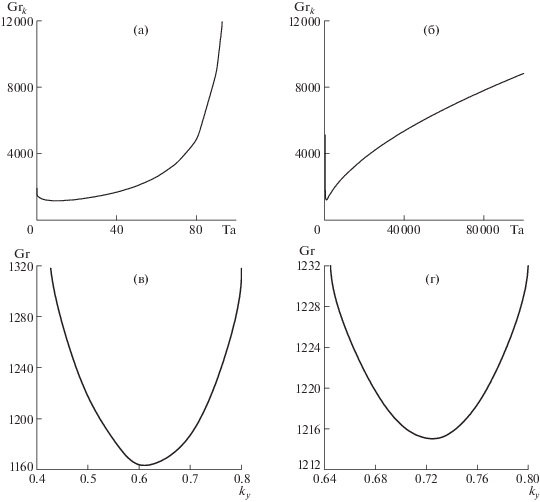
При $93 < Ta < 400$ адвективное течение устойчиво на спиральные возмущения при любых значениях числа Грасгофа.

Вторая мода (рис. 3б) находится в интервале $400 \leqslant Ta \leqslant {{10}^{5}}$. При $400 \leqslant Ta \leqslant 923$ критическое число Грасгофа уменьшается от ${\text{5126}}{\text{.6}}$ до ${\text{1202}}{\text{.4}}$ с увеличением числа Тейлора. Происходит дестабилизация адвективного течения на данном интервале, $G{{r}_{k}} = {\text{1202}}{\text{.4 }}$ является локальным минимумом на рассматриваемом интервале. При $923 < Ta < {{10}^{5}}$ критическое число Грасгофа растет с увеличением числа Тейлора и достигает значения ${\text{8833}}{\text{.6}}$ при максимальном значении числа Тейлора. Большое число Тейлора можно связать с большой угловой скоростью вращения при фиксированной вязкости жидкости и фиксированной толщине слоя. Тогда справедливо утверждение, что быстрое вращение стабилизирует течение. Волновое число ${{k}_{y}}$ монотонно возрастает с ростом числа Тейлора от 0.7 до 1.67. В качестве примера на рис. 3г представлены нейтральные кривые при $Ta = 1000$ и $Ta = 2000$.

3. КОНЕЧНО-АМПЛИТУДНЫЕ ВОЗМУЩЕНИЯ

Поведение возмущений конечной амплитуды в надкритической области исследуется на основе нелинейной системы уравнений (2.2)–(2.4).

Случай винтовых возмущений. Для винтовых периодических по $x$ возмущений система имеет вид

$\frac{{\partial \phi }}{{\partial t}} + Gr\left[ { - \frac{{\partial \psi }}{{\partial z}}\frac{{\partial \phi }}{{\partial x}} + \frac{{\partial \psi }}{{\partial x}}\frac{{\partial \phi }}{{\partial z}} + {{u}_{0}}\left( z \right)\frac{{\partial \phi }}{{\partial x}} + u_{0}^{{''}}\left( z \right)\frac{{\partial \psi }}{{\partial x}}} \right] - \sqrt {Ta} \frac{{\partial \upsilon }}{{\partial z}} = \Delta \phi - \frac{{\partial \theta }}{{\partial x}}\quad \Delta \psi + \phi = 0$

(3.1)

$\frac{{\partial \upsilon }}{{\partial t}} + Gr\left[ { - \frac{{\partial \psi }}{{\partial z}}\frac{{\partial \upsilon }}{{\partial x}} + \frac{{\partial \psi }}{{\partial x}}\frac{{\partial \upsilon }}{{\partial z}} + {{u}_{{\text{0}}}}\left( z \right)\frac{{\partial \upsilon }}{{\partial x}} + \upsilon _{0}^{'}\left( z \right)\frac{{\partial \psi }}{{\partial x}}} \right] - \sqrt {Ta} \frac{{\partial \psi }}{{\partial x}} = \Delta \upsilon $

$\frac{{\partial \theta }}{{\partial t}} + Gr\left[ { - \frac{{\partial \psi }}{{\partial z}}\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \psi }}{{\partial x}}\frac{{\partial \theta }}{{\partial z}} + {{u}_{{\text{0}}}}\left( z \right)\frac{{\partial \theta }}{{\partial x}} - \frac{{\partial \psi }}{{\partial z}} + Ra\theta _{0}^{'}\left( z \right)\frac{{\partial \psi }}{{\partial x}}} \right] = \frac{1}{{\Pr }}\Delta \theta $

(3.2)

$z = - 1:\;\;\frac{{\partial \psi }}{{\partial z}} = 0,\quad \psi = 0,\quad \frac{{\partial \theta }}{{\partial z}} = 0$

(3.3)

$z = 1:\;\;\frac{{\partial \psi }}{{\partial z}} = 0,\quad \psi = 0,\quad \theta = 0$

(3.4)

$\psi \left( {t,0,z} \right) = \psi \left( {t,L,z} \right),\quad \phi \left( {t,0,z} \right) = \phi \left( {t,L,z} \right),\quad \upsilon \left( {t,0,z} \right) = \upsilon \left( {t,L,z} \right),\quad \theta \left( {t,0,z} \right) = \theta \left( {t,L,z} \right)$

где $L$ – длина волны возмущений, оператор Лапласа $\Delta = {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{x}^{2}} + }}} \right. \kern-0em} {\partial {{x}^{2}} + }}{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}$, $\psi \left( {t,x,z} \right)$, $\phi $(t, x, z), $\upsilon \left( {t,x,z} \right)$, $\theta $(t, x, z) – конечно-амплитудные возмущения функции тока, вихря скорости, второй компоненты скорости и температуры.

Нелинейная двумерная задача (3.1)–(3.4) решалась численно методом сеток [18]. В рамках двухполевого метода [19] использовалась явная конечно-разностная схема. Уравнение Пуассона для функции тока решалось методом последовательной верхней релаксации. Основные расчеты проводились на сетке 101 × 200.

Функции тока и вихря скорости описывают проекцию движения конечно-амплитудных возмущений на плоскость $xOz$. Вторая y-я компонента скорости описывает проекцию движения конечно-амплитудных возмущений на плоскость $yOz$ или $xOy$. Положительное значение возмущения скорости $\upsilon \left( {t,x,z} \right)$ описывает движение вглубь, а отрицательное – движение в противоположном направлении, перпендикулярное плоскости $xOz$.

Расчеты показали, что при всех рассматриваемых значениях числа Тейлора возмущения представляют собой систему бегущих винтообразных вихрей, возникающих в областях с неустойчивой температурной стратификацией. Однако для разных мод картина конечно-амплитудных возмущений имеет некоторые отличия.

На рис. 4а,б,в представлены изотермы конечно-амплитудных возмущений температуры $\theta $(t, x, z), изолинии возмущений функции тока ψ(t, x, z) и скорости $\upsilon \left( {t,x,z} \right)$ при $Ta = 10$ для числа Грасгофа $Gr = 10{\kern 1pt} {\kern 1pt} 000$ выше критического. Поперек слоя возникают движущиеся вдоль слоя чередующиеся холодные и теплые пятна. Проекция движения, описанная функцией возмущения функции тока вблизи порога устойчивости, представляет собой две цепочки вращающихся, соответственно, против и по часовой стрелке вихрей, локализованных в верхней и нижней половине слоя и движущихся в противоположных направлениях вдоль слоя. Одновременно y-я компонента возмущения скорости описывает в центре слоя вращение против и по часовой стрелке попарно движущихся вдоль оси $Ox$ вихрей в плоскости $xOy$.

Рис. 4.

Изолинии конечно-амплитудных возмущений температуры $\theta \left( {t,x,z} \right)$ (а, г), функции тока $\psi \left( {t,x,z} \right)$ (б, д) и второй компоненты скорости $\upsilon \left( {t,x,z} \right)$ (в, е): $Ta = 10$, $Gr = 10{\kern 1pt} {\kern 1pt} 000$, ${{k}_{x}} = 1.28$ (а–в); $Ta = 1000$, $Gr = 4000$, ${{k}_{x}} = 1.12$ (г–е).

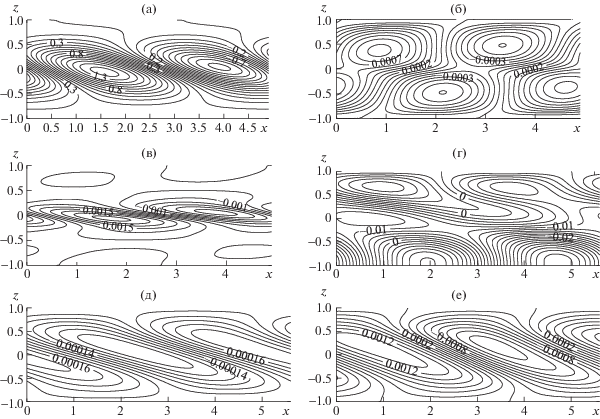
При $Ta = 500$ и $Gr = 20{\kern 1pt} {\kern 1pt} 000$ (рис. 5a–5c) чередующиеся тепловые пятна, движущиеся вдоль оси абсцисс, локализуются в нижней половине слоя и имеют форму, близкую к полуокружности. Проекция движения адвективного течения на плоскость $xOz$, описанная $\psi \left( {t,x,z} \right)$, представляет собой последовательность вращающихся поперек слоя против и по часовой стрелке вихрей и движущихся вдоль него. Одновременно y-я компонента возмущения скорости описывает в центре слоя вращение против и по часовой стрелке попарно движущихся вдоль оси $Ox$ вихрей в плоскости $xOy$.

Рис. 5.

Изолинии конечно-амплитудных возмущений $\theta \left( {t,x,z} \right)$ (а, г) и функции тока $\psi \left( {t,x,z} \right)$ (б) и $\psi \left( {t,x,z} \right) \times {{10}^{5}}$ (д), второй компоненты скорости $\upsilon \left( {t,x,z} \right)$ (в, е): $Ta = 500$, $Gr = 20{\kern 1pt} {\kern 1pt} 000$, ${{k}_{x}} = 0.75$ (а–в); $Ta = {{10}^{5}}$, $Gr = 70{\kern 1pt} {\kern 1pt} 000$, ${{k}_{x}} = 5.2$ (г–е).

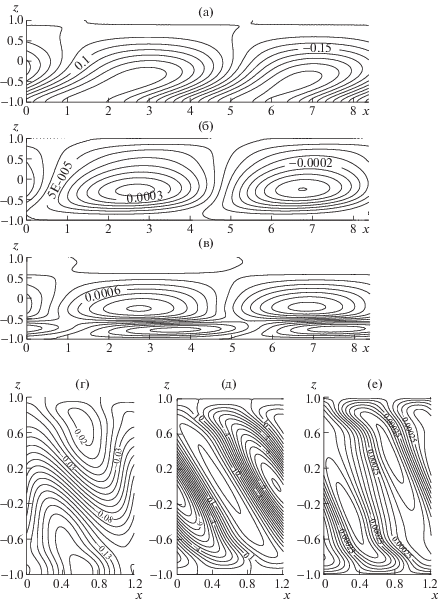
При $Ta = 1000$ и $Gr = 4000$ (рис. 4г,д,е) две цепочки движущихся вдоль слоя чередующихся теплых и холодных пятен находятся вблизи границ слоя. Причем в силу теплоизоляции нижней границы вращающегося слоя жидкости нижние тепловые пятна имеют форму, близкую к полуокружности. Проекция, описанная функцией тока, представляет собой последовательность движущихся вдоль и вращающихся поперек слоя пары вихрей. Одновременно $\upsilon \left( {t,x,z} \right)$ описывает вращение против и по часовой стрелке последовательности движущихся вдоль оси $Ox$ вихрей в плоскости $xOy$. При $Ta = {{10}^{5}}$ и $Gr = 70{\kern 1pt} {\kern 1pt} 000$ (рис. 5г–5е) структура конечно-амплитудных возмущений аналогична предыдущему случаю. Однако вторая компонента скорости описывает вихревое движение жидкости под углом к плоскости $xOy$.

Случай спиральных возмущений. Для пространственных периодических по $y$ возмущений система имеет вид

(3.5)

$\begin{gathered} \frac{{\partial \Phi }}{{\partial t}} + Gr\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial \Phi }}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \Phi }}{{\partial z}} + {{v}_{0}}(z)\frac{{\partial \Phi }}{{\partial y}} + v_{0}^{{''}}(z)\frac{{\partial \Psi }}{{\partial y}}} \right] - \sqrt {Ta} \frac{{\partial u}}{{\partial z}} = \Delta \Phi - \frac{{\partial \theta }}{{\partial y}} \\ \Delta \Psi + \Phi = 0 \\ \frac{{\partial U}}{{\partial t}} + Gr\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial U}}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial U}}{{\partial z}} + {{v}_{0}}(z)\frac{{\partial U}}{{\partial y}} + u_{0}^{'}(z)\frac{{\partial \Psi }}{{\partial y}}} \right] + \sqrt {Ta} \frac{{\partial \Psi }}{{\partial z}} = \Delta U \\ \end{gathered} $

$\frac{{\partial \theta }}{{\partial t}} + Gr\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial \theta }}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \theta }}{{\partial z}} + {{v}_{0}}(z)\frac{{\partial \theta }}{{\partial y}} + u + Ra\theta _{0}^{'}(z)\frac{{\partial \Psi }}{{\partial y}}} \right] = \frac{1}{{\Pr }}\Delta \theta $

(3.6)

$z = - 1:\;\;\frac{{\partial \Psi }}{{\partial {\text{z}}}} = 0,\quad \Psi = 0,\quad U = 0,\quad \frac{{\partial \theta }}{{\partial z}} = 0$

(3.7)

$z = 1:\;\;\frac{{\partial \Psi }}{{\partial {\text{z}}}} = 0,\quad \Psi = 0,\quad U = 0,\quad \theta = 0$

(3.8)

$\Psi \left( {t,0,z} \right) = \Psi \left( {t,L,z} \right){\text{,}}\Phi \left( {t,0,z} \right) = \Phi \left( {t,L,z} \right),\quad U\left( {t,0,z} \right) = U\left( {t,L,z} \right),\quad \theta \left( {t,0,z} \right) = \theta \left( {t,L,z} \right)$

где оператор Лапласа $\Delta = {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}} + }}} \right. \kern-0em} {\partial {{y}^{2}} + }}{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}$. Имеются все три компоненты возмущений скорости, которые зависят от времени $t$ и двух пространственных координат $y$ и $z$. $\Psi \left( {t,y{\text{,}}z} \right)$ – конечно-амплитудные возмущения функции тока, описывающие проекцию возмущений скорости на плоскость $yOz$, $U\left( {t,y,z} \right)$ – конечно-амплитудные возмущения первой компоненты скорости, описывающие проекцию возмущений скорости на плоскость $xOz$ или $xOy$, $\Phi \left( {t,y,z} \right)$, $\theta \left( {t,y,z} \right)$ – конечно-амплитудные возмущения вихря скорости и температуры.

Нелинейная двумерная задача (3.5)–(3.8) решалась численно методом сеток, аналогично задачи (3.1)–(3.4). Основные расчеты проводились на сетке $101 \times 200$. Расчеты показали, что аналогично случаю винтовых возмущений, при всех рассматриваемых значениях числа Тейлора в областях с неустойчивой температурной стратификацией возникает система разнообразных бегущих винтообразных вихрей. Для разных мод картина конечно-амплитудных возмущений имеет некоторые отличия.

На рис. 6а,б,в представлены изотермы возмущений температуры $\theta \left( {t,y,z} \right)$, изолинии возмущений функции тока $\Psi \left( {t,y{\text{,}}z} \right)$ и компоненты скорости $U\left( {t,y,z} \right)$ при $Ta = 10$ для числа Грасгофа $Gr = 2000$ выше критического. В середине вдоль слоя движется холодное пятно. Проекция движения, описанная функцией возмущения функции тока вблизи порога устойчивости, представляет собой цепочку вращающихся в разном направлении вихрей, занимающих весь слой, движущихся вдоль оси $Oy$. Одновременно x-я компонента возмущения скорости описывает в центре слоя вращение против и по часовой стрелке попарно движущихся вдоль оси $Oy$ вихрей в плоскости $xOy$.

Рис. 6.

Изолинии конечно-амплитудных возмущений температуры $\theta \left( {t,y,z} \right)$ (а–г), функции тока $\Psi \left( {t,y,z} \right) \times {{10}^{6}}$ (б) и $\Psi \left( {t,y,z} \right)$ (д), первой компоненты скорости $U\left( {t,y,z} \right) \times {{10}^{5}}$ (в) и $U\left( {t,y,z} \right)$ (е): $Ta = 10$, $Gr = 2000$, ${{k}_{y}} = 0.6$ (а–в); $Ta = 1000$, $Gr = 2500$, ${{k}_{y}} = 0.72$ (г–е).

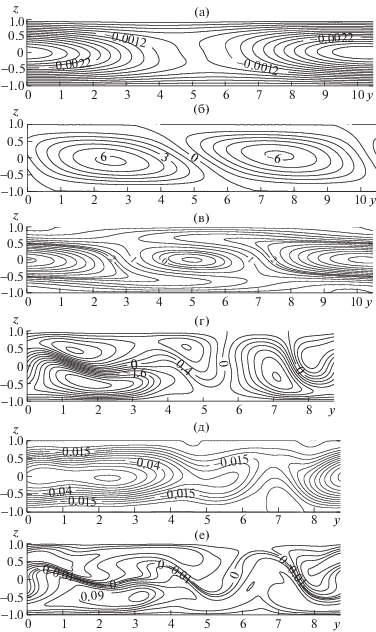
Для второй моды в качестве примера, иллюстрирующего поведения конечно-амплитудных возмущений, рассматривается случай, близкий к наименее устойчивой ситуации при $Ta = 1000$ и $Gr = 2500$ (рис. 6г,д,е). Поперек слоя формируется теплое и холодное пятно сложной конфигурации, которые движутся вдоль слоя. Одновременно там образуется перемещающийся вихрь, который вращается против часовой стрелки. Отметим, что с ростом числа Тейлора конфигурация движения усложняется, поперек слоя образуется пара спиралевидных вихрей. Что касается изолиний возмущения первой компоненты скорости, то можно заметить, что они описывают вращение жидкости поперек слоя в плоскости $xOz$.

ЗАКЛЮЧЕНИЕ

Представленное новое точное решение уравнений Навье–Стокса, записанное в приближении Обербека–Буссинеска и описывающее адвективное течение несжимаемой жидкости во вращающемся горизонтальном слое с твердыми границами и условием теплоизоляции на нижней границе, меняет свой профиль с ростом числа Тейлора. С увеличением $Ta$ течение перестраивается, что влияет на его устойчивость.

Под воздействием вращения обогащается картина устойчивости адвективного течения по сравнению с результатами работы [7], полученными при отсутствии вращения. В рамках линейной теории устойчивости показано, что на всем рассматриваемом диапазоне числа Тейлора для значений числа Грасгофа выше критического развивается колебательная неустойчивость. С ростом Ta последовательно меняются наиболее опасные колебательные моды. Винтовые возмущения дестабилизируют течение при $32.6 \leqslant Ta \leqslant 1300$, а спиральные возмущения делают течение менее устойчивым при $0 \leqslant Ta \leqslant 10$ и $400 \leqslant Ta \leqslant 923$. Спиральные возмущения являются более опасными, минимальное критическое число Грасгофа $G{{r}_{k}} = {\text{1163}}{\text{.9}}$ достигается при $Ta = 10$. При условии теплоизоляции на нижней границе слоя адвективное течение более устойчиво на нормальные возмущения, чем в случае, когда на нижней границе задано линейное распределение температуры [20].

Поведение конечно-амплитудных возмущений, возникающих в слое жидкости при значениях числа Грасгофа выше критического, исследовано конечно-разностным методом сеток на основе нелинейной задачи. За порогом устойчивости возникают нестационарные периодические конечно-амплитудные возмущения скорости и температуры в виде системы пространственных вихрей и температурных пятен.

Список литературы

Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений. М.: Наука, 1989. 320 с.
Остроумов Г.А. Свободная конвекция в условиях внутренней задачи. М.: Гостехтеориздат, 1952. 286 с. [Ostroumov G.A. Free convection under the condition of the internal problem. NASA TM, 1958].
Андреев В.К. Решения Бириха уравнений конвекции и некоторые его обобщения. Препринт СО РАН. ИВМ. № 1–10. Красноярск, 2010.
Бирих Р.В. О термокапиллярной конвекции в горизонтальном слое жидкости // ПМТФ. 1966. № 3. С. 69–72. [Birikh R.V. Thermocapillary convection in a horizontal layer of liquid // Journal of Applied Mechanics and Technical Physics. May 1966. V. 7. Issue 3. P. 43–44].
Gershuni G.Z., Laure P., Myznikov V.M., Roux B., Zhukhovitsky E.M. On the stability of plane-parallel advective flows in long horizontal layers // Microgravity Q. 1992. V. 2. № 3. P. 141–151.
Андреев В.К., Бекежанова В.Б. Устойчивость неизотермических жидкостей (обзор) // ПМТФ. 2013. № 2. С. 3–20. [Andreev V.K., Bekezhanova V.B. Stability of Non-Isothermal Fluids (Review) // Journal of Applied Mechanics and Technical Physics. 2013. № 2. Р. 171–184].
Hart J. A note on the stability of low-Prandtle-number Hadley circulations // J. Fluid Mech. 1983. V. 132. P. 271–281.
Аристов С.Н., Шварц К.Г. Вихревые течения адвективной природы во вращающемся слое жидкости. Перм. ун-т. Пермь, 2006. 155 с.
Чикулаев Д.Г., Шварц К.Г. Влияние вращения на устойчивость адвективного течения в горизонтальном слое жидкости с твердыми границами при малых числах Прандтля // Изв. РАН. МЖГ. 2015. № 2. С. 48–56 [Chikulaev D.G. and Shvarts K.G. Effect of Rotation on the Stability of Advective Flow in a Horizontal Liquid Layer with Solid Boundaries at Small Prandtl Numbers // Fluid Dynamics. 2015. V. 50. № 2. P. 215–222].
Shvarts K.G., Boudlal A. Effect of rotation on stability of advective flow in horizontal liquid layer with a free upper boundary // Journal of Physics: Conference Series. 2010. V. 216. № 1. 012005.
Han-Ming Li, Wan-Yuan Shi, Ermakov Michael K. Thermocapillary flow instabilities of medium Prandtl number liquid in rotating annular pools // International Journal of Thermal Sciences. October 2017. V. 120. P. 233–243. https://doi.org/10.1016/j.ijthermalsci.2017.06.016
Cheng-Zhi, Zhu Lan Peng The effect of rotation on the thermal-solutal capillary-buoyancy flow in a shallow annular pool with various capillary ratios // International Journal of Thermal Sciences. May 2020. V. 152. Article 119482. https://doi.org/10.1016/j.ijheatmasstransfer.2020.119482
Dong-Ming Mo, Sen Zhang, Li Zhang, Deng-Fang Ruan, You-Rong Li. Effect of Heat Dissipation on Thermocapillary Convection of Low Prandtl Number Fluid in the Annular Pool Heated from Inner Cylinder // Microgravity Science and Technology. Published online: 29 April 2020. V. 32. P. 661–672. https://doi.org/10.1007/s12217-020-09788-x
C.Z. Zhu, J.J. Yu, Y.R. Li, L. Peng. A numerical study on the thermal capillary-buoyancy convection of a binary mixture driven by rotation and surface-tension gradient in a shallow annular pool // International Journal of Heat and Mass Transfer. 2021. V. 171. P. 121035. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121035
Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972. 392 с.
Boussinesq J. Theorie analytique de la chaleut. T. 2. Paris, Gaufhier-Villars, 1903. 625 p.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. СПб.: Изд-во “Лань”, 2008. 400 с.
Шварц К.Г. Конечно-амплитудные пространственные возмущения адвективного течения во вращающемся горизонтальном слое жидкости // Вычислительные технологии. 2001. Т. 6. Спец. вып. Ч. 2. Тр. Междунар. конф. RDAMM-2001. С. 702–707.
Тарунин Е.Л. Вычислительный эксперимент в задачах свободной конвекции. Иркутск: Изд-во Иркут. ун-та, 1990. 225 с.
Шварц К.Г. Влияние вращения на устойчивость адвективного течения в горизонтальном слое жидкости при малом значении числа Прандтля // Известия РАН. Механика жидкости и газа. 2005. № 2. С. 29–38.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал