Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 3-13

1. УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ОСЕСИММЕТРИЧНОМ СЛУЧАЕ

Рассмотрим осесимметричные течения. Ось симметрии выберем за ось $z$, а расстояние до оси обозначим через $\rho $. Составляющие скорости обозначим, соответственно, $u,\;{v}$. Уравнения движения имеют вид

Первое уравнение – уравнение неразрывности (${\text{div}}{\mathbf{u}} = 0$), а второе условие – отсутствие завихренности (${\text{rot}}{\mathbf{u}} = 0$). Последнее условие является необходимым и достаточным условием потенциальности поля течения. Компоненты вектора скорости течения с осевой симметрией выражаются в виде

Потенциал скоростей $\xi $ удовлетворяет соотношению

которое является уравнением Лапласа в цилиндрических координатах. Отметим, что функция ξ является гармонической функцией декартовых координат.

Согласно первому уравнению, выражение – $\rho {v}dz + \rho ud\rho $ является точным дифференциалом функции. Получаем

В случае осесимметричного движения жидкости по меридианным плоскостям ($\eta = {\text{сonst}}$) равенства $\zeta (\rho ,z) = {\text{const}}$ представляют поверхности, образованные вращением линий тока вокруг оси Oz. Функция тока сохраняет постоянное значение на каждой линии тока и будет оставаться постоянной на поверхности, получаемой вращением данной линии тока вокруг оси симметрии. Отметим, что функция тока зависит от выбора системы координат и характера движения. Функция тока $\zeta $ удовлетворяет уравнению

Уравнение (1.4) не является уравнением Лапласа, а функция $\zeta $ не является гармонической в декартовых координатах.

Задача определения в некоторой области D функции, удовлетворяющей уравнению Лапласа, по известным значениям нормальной производной функции $\xi $ на поверхности S называется задачей Неймана. Для областей D с достаточно гладкой границей гармоническая в D функция $\xi $, удовлетворяющая граничному условию $\tfrac{{\partial \xi }}{{\partial n}} = 0$ и условию на бесконечности, если D содержит бесконечную точку, всегда существует и определяется с точностью до действительной постоянной.

Из соотношений (1.2) и (1.3) следует, что функция тока и потенциал связаны соотношениями

Уравнения осесимметричных течений во многом аналогичны уравнениям плоских движений. Векторные линии поля скоростей совпадают с линиями $\zeta (z,\rho ) = {\text{const}}$ и, как в двумерном случае, являются линиями тока. Из уравнений следует, что линии $\xi (z,\rho ) = {\text{const}}z$ и $\zeta (x,\rho ) = {\text{const}}$ ортогональны.

Если потенциал скоростей известен, то функция тока в осесимметричном случае находится по известным формулам.

2. ПРОСТРАНСТВЕННЫЕ (ОСЕСИММЕТРИЧНЫЕ) ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

Система уравнений (1.1) является системой уравнений эллиптического типа с особенностью на оси вращения. Отображения обладают основными свойствами квазиконформных отображений [6].

Аналогично плоской задаче, построим аналоги степеней функции комплексного переменного для осесимметричного случая. Для квазиконформных отображений введем понятие квазианалитических функций. Обозначим эту функцию $w(Z) = {{Z}^{{(n)}}}(\alpha ,Z,{{Z}_{0}})$ и назовем ее формальной степенью (см. [8]). Квазианалитическая функция подобна аналитической функции $\alpha {{(z - {{z}_{0}})}^{n}}$, где n – положительное или отрицательное число. Функция ведет себя, как $\alpha {{(z - {{z}_{0}})}^{n}}$ при $z \to {{z}_{0}}$ и равна $O({{\left| z \right|}^{n}})$ на бесконечности. Применяя принцип подобия ([8]), можно убедиться в том, что эти свойства однозначно определяют функции Z⁽ⁿ⁾.

С помощью формальных степеней можно найти аналитические выражения для произвольных квазианалитических функций по аналогии с результатами плоской теории функций. Построим гармонические полиномы произвольной степени и подберем сопряженные к ней функции ([6]). Для любой гармонической функции ξ двух переменных в цилиндрической системе координат можно найти сопряженную функцию ζ такую, что $\xi ,\zeta $ удовлетворяют системе уравнений (1.6). Запишем наши преобразования в виде формальных степеней

Отрицательные формальные степени получаются дифференцированием функции $Z_{{}}^{{ - 1}}$ по переменной ${\text{ z}}$. В результате имеем

Здесь r² = z² + ρ², ρ² = x² + y².

Рассмотрим квазианалитическую функцию $w = f(Z)$ голоморфную в области Z, за исключением точки $Z = \infty $, в которой функция имеет полюс первого порядка. Разложим эту функцию в ряд Лорана такого вида

Здесь формальные Z^k – степени – функции, удовлетворяющие уравнению Лапласа в цилиндрической системе координат, ${{\alpha }_{k}}$ – действительные величины. Величины Z^k – (2.1), (2.2) – функции, зависящие от $z,\rho $. Ряд сходится в любой точке области (${{\alpha }_{1}} > 0$). В дальнейшем формула (2.3) для представления квазикомплексного потенциала будет использована при получении результатов течений около осесимметричных тел, тел конечного и полубесконечного размера, в каналах.

Для стационарного течения потенциал скоростей позволяет вычислить линии тока, которые идентичны с траекториями частиц, которые используются при визуализации течения. В системе координат, связанной с линиями тока, решение определяется для каждой линии тока. Таким образом, произвольная твердая стенка является линией тока. Если разбить течение на трубки тока, то можно, используя непроницаемость боковой поверхности, рассматривать независимо движения вдоль выделенного объема жидкости.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Форму обтекаемых тел вращения можно определить наложением на однородный поток, параллельный оси Оz, потока от системы источников (стоков), диполей, а также – непрерывных их распределений.

Зададим течение с комплексным квазипотенциалом

Рассмотрим случай, когда формальные степени имеют вид $Z_{{}}^{1} = z + i{{\rho }^{2}}{\text{/}}2,$ $Z_{{}}^{{ - 1}} = ( - z + i{{\rho }^{2}}){\text{/}}{{r}^{3}}$, а величины $\alpha ,\;\beta $ – положительные постоянные. Если выбрать α = 1, $\beta = 1{\text{/}}2$, то в результате получим потенциал и функцию тока течения около сферы, которые имеют вид ([7])

Ось симметрии $\rho = 0$ является линией тока и осью симметрии течения. Функция тока течения обращается в нуль на оси $\rho = 0$ и на сфере радиуса r = R. Напомним, что ${{r}^{2}} = {{z}^{2}} + {{\rho }^{2}},$ ${{\rho }^{2}} = {{x}^{2}} + {{y}^{2}}$, ${{R}^{3}} = q{\text{/}}2\pi {{u}_{\infty }}$. Здесь q – мощность источника или стока, которая определяется как секундный объемный расход жидкости сквозь замкнутый контур, охватывающий источник или сток. Картину обтекания сферы можно рассматривать как наложение на однородный поток, движущийся с постоянной скоростью на бесконечности, на дублет – поток от источника и стока, помещенных в одной точке.

Численный алгоритм построения и визуализации осесимметричных течений идеальной жидкости в многосвязных областях реализован на языке “Fortran”. Наглядное представление о картине течения жидкости дают линии тока. В случае осесимметричного течения линии тока определяются системой дифференциальных уравнений

В каждый момент времени через каждую регулярную (неособую) точку в непрерывном векторном поле проходит только одна траектория. Исключение составляют особые точки (в частности, точки торможения), через которые проходит бесчисленное множество линий тока, либо ни одной. Особые точки можно определить как точки, в которых скорость обращается в нуль (все составляющие скорости или две из трех в пространственном случае). Единственное решение можно найти в том случае, если поверхность тока не является характеристической.

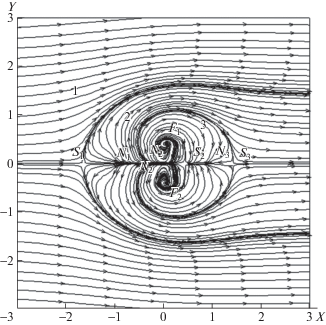
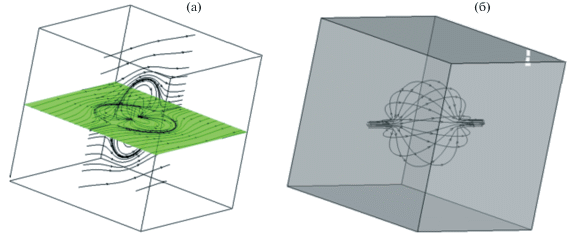
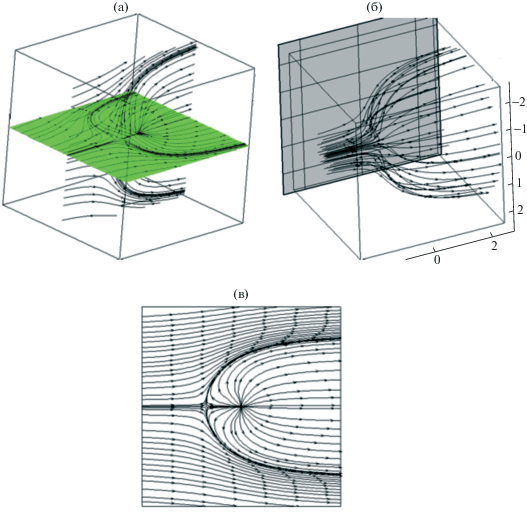
На рис. 1 приведена общая картина течения около сферы в виде картины линий тока. На рис. 1а приведена картина линий тока в двух перпендикулярных плоскостях XZ и YZ. Поверхность сферы – характеристическая, поэтому, отступив на некоторую малую величину и проинтегрировав уравнения линий тока, получим картину, близкую к “предельным” линиям тока. На рис. 1б приведены линии тока, которые получены заданием предельных линий тока вблизи оси симметрии $\rho = 0$ на некотором малом расстоянии ε от r = R.

В плоском случае “предельные” линии тока (сепаратрисы) делят плоскость на области с одинаковым поведением траекторий. В осесимметричном случае особые точки можно соединить сепаратрисными поверхностями, которые получатся вращением вокруг оси симметрии двумерных сепаратрис. В области течения можно выделить внешнюю безвихревую часть течения (рис. 1а). Вторая область – область течения внутри сферы, образуемая диполем с интенсивностью (моментом) q. Отметим, что область течения – неодносвязная. Вихревые линии тока во внутренней области окружены замкнутой поверхностью тока, которые отделяет внутренние вихревые линии от внешней окружающей жидкости. Если заменить поверхность тока, отделяющую течение внутри сферы от внешнего течения, твердой поверхностью, то при отсутствии трения ничего не изменится.

Во внешней области получаем картину обтекания сферы радиуса R плоскопараллельным потоком идеальной несжимаемой жидкости, имеющей на бесконечности скорость |u_∞|.

Если заменить точечный диполь системой источников интенсивностей $ \pm q$, расположенных в точках $ \pm a$ оси $x$, то получим течение с комплексным потенциалом

Здесь

На рис. 2 приведена картина течения в случае, когда источник интенсивности (момента) q и сток такой же обильности помещены на оси в точках $z = \pm a,$ $a = 3$. Суммарная интенсивность истоков и стоков равна нулю.

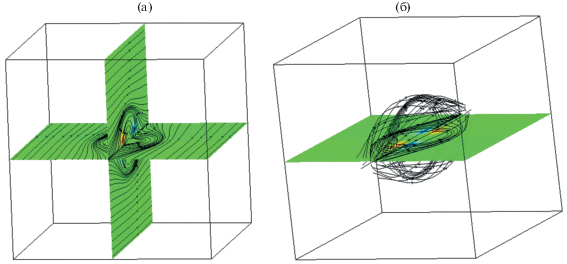
В этом случае задача сводится к задаче обтекания геометрии неизвестной формы. В результате получим картину осесимметричного течения, потенциал и функция тока которого в безразмерном виде задаются формулами

Здесь ${{q}_{1}}$ = 0.5, а ${{u}_{\infty }} = 1$ как и в дальнейшем.

На рис. 2а показаны линии тока в двух плоскостях XY и YZ. На рис. 2б приведены предельные линии тока, которые задают форму обтекаемого тела вращения.

На рис. 3а показана картина течения, полученная наложением двух потенциальных полей $\xi = {{\xi }_{1}} + {{\xi }_{2}}$, которые – ${{\xi }_{1}}$ и ${{\xi }_{2}}$ – определяются формулами, приведенными ниже. Потенциал скорости течения в безразмерной форме определяется следующим образом

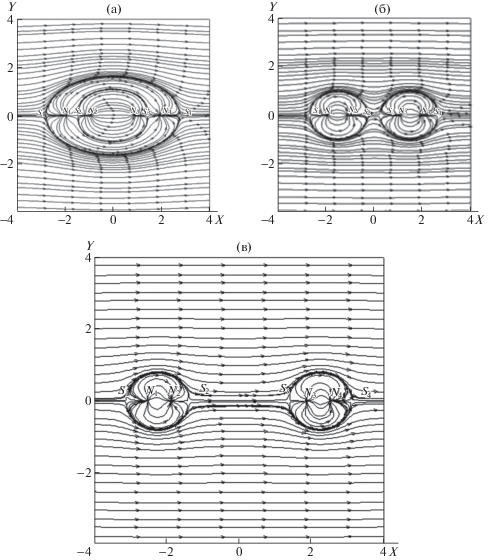
На рис. 3 приведены линии тока при различных расположениях источников и стоков, которые соответствуют параметрам, приведенным в описании рис. 3. Отметим, что многосвязная область (рис. 3а) распадается на две области конечного размера, связанные между собой (рис. 3в)).

В зависимости от мощности источников, их расположения реализуется качественно различный характер пространственных течений. Поля течений топологически отличаются друг от друга. Топологические свойства структур определяются числом и типом особенностей, траекториями, соединяющими особые точки. Особые точки, которые приведены на рис. 3, являются особенностями нескольких видов. Ими являются хорошо известные особые точки, как и в двумерном случае: узел (${{N}_{i}}$), седло (${{S}_{k}}$), фокус (${{F}_{n}}$) и др. Количество узловых точек (узлы, полуузлы, фокусы или те и другие) связано с числом седловых точек (седло, полуседло), причем разность зависит от топологии рассматриваемой области [9]. Особые точки появляются и взаимодействуют друг с другом. Узел появляется вместе с седловой точкой. Комбинации узловой, седловой точек приводят к различным формам течения. В случае обтекания тел конечных размеров число узловых точек ${{N}_{i}}$ превышает число седловых точек ${{S}_{k}}$ на две единицы $R = 2$: $\Sigma {{N}_{i}} - \Sigma {{S}_{k}} \geqslant R$. Если рассматривать течение на плоскости с препятствием, то $R = 0$. В нелинейном случае особенности в пространственном случае намного сложнее, чем в двумерном случае, и подробно обсуждаются в работе [10].

На рис. 4 приведены линии тока в случае наложения трех потенциальных полей $\xi = {{\xi }_{1}} + {{\xi }_{2}} + {{\xi }_{3}}$ при различных расположениях источников и стоков, задаваемых потенциалами, где

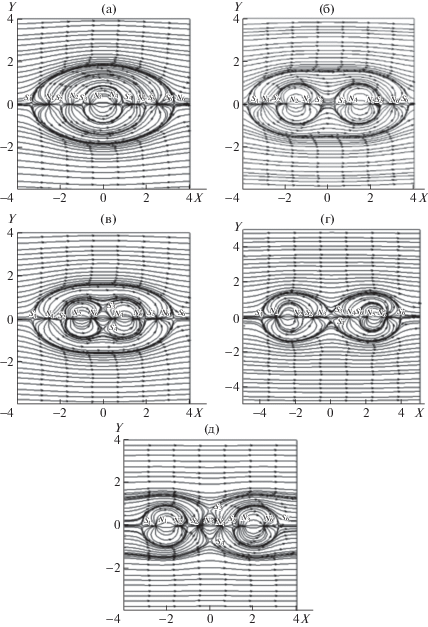
Качественный характер формирования, расщепления и взаимодействия особых точек в зависимости от определяющих параметров приведен на рис. 4.

Отметим, что в случае, приведенном на рис. 4д, картина течения полностью перестраивается топологически. Течение около тела конечного размера переходит в течение в канале.

На рис. 5 приведены линии тока в случае, когда в однородный поступательный поток внесен одиночный источник мощности q. Это приводит к обтеканию полубесконечного тела вращения. Случай можно рассматривать как частный случай обтекания источника и стока, когда сток удаляется в бесконечность. Потенциал и функция тока известны и имеют вид

На рис. 5а приведена общая картина течения около полубесконечного тела вращения в виде картины линий тока в двух перпендикулярных плоскостях. На рис. 5б приведены “предельные” линии тока, которые задают форму обтекаемого тела и получены при нахождении линий тока вблизи оси симметрии $\rho = 0$ на некотором малом расстоянии $\varepsilon $ от оси симметрии. На рис. 5в приведены линии тока в полуплоскости, проведенной через ось симметрии.

На рис. 6 приведены картины линий тока около полубесконечного тела вращения с дополнительными источниками и стоками, внесенными в поле вдоль оси симметрии. Потенциал известен и имеет вид

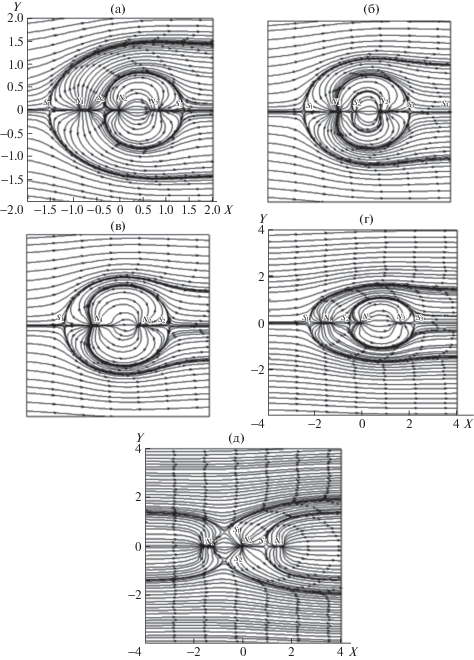
На рис. 6а по сравнению с рис. 6б можно заметить появление на оси дополнительной узловой точки. При сравнении рис. 6б и рис. 6в видим появление дополнительной сепаратрисы (рис. 6б). На рис. 6г в дальней части следа внутри появляется горловина, которая уходит на бесконечность. На рис. 6д представлено осесимметричное течение несжимаемой жидкости сквозь канал, поверхность которого является поверхностью вращения. Форма поверхности канала находится по заданному закону изменения скорости вдоль оси канала.

На рис. 7 приведены результаты численных экспериментов, в которых за счет введения дублета, в поле течения появляется новая особая точка – пространственный фокус. Рисунок 7 соответствует потенциалу скоростей следующего вида

Во внешней области течения можно выделить потенциальную часть течения – (1). Вторая и третья области (2, 3) на рис. 7 – это области течения внутри 1-й области. В области 3 находятся вихревые линии, которые окружены замкнутой поверхностью тока, отделяющие внутренние вихревые линии от окружающей жидкости области 2.

Известно, что динамическая система структурно устойчива в некоторой области на плоскости в случае, когда число точек равновесия и предельных циклов конечно и все они являются гиперболическими [10]. Равновесие называется гиперболическим, если собственные значения линеаризованной матрицы не лежат на мнимой оси. В этом случае имеется три топологических класса гиперболического равновесия на плоскости. Ими являются устойчивые узлы, седла и неустойчивые узлы. Седла имеют одномерное устойчивое и неустойчивое множество, называемое сепаратрисами. Если сепаратрисы седел не связывают два различных седла или возвращаются в то же седло, то в этом случае система является структурно устойчивой.

В идеальной жидкости можно, не нарушая картину течения, поверхности тока заменить твердыми стенками, непроницаемыми для других частиц. Картина течения в отсутствие сил трения не изменится. В ряде задач проектирования возможно выбрать направление течения в трубке тока в одном направлении, а вдоль другой трубки тока – в противоположном, и использовать принцип “отвердевания”. Уравнения движения (1.1) инвариантны по отношению к изменению направления движения. Так как течение происходит в отсутствие сил трения, то этот подход позволяет построить решения в сложных системах, которые удовлетворяют закону сохранения массы.

Отметим, что полученные результаты относятся к тому разделу гидродинамики, в которой пренебрегают вязкостью. Расхождение между результатами гидродинамики и действительностью возникает вследствие пренебрежения трением и появлением пограничного слоя [11]. Хотя реальные жидкости не удовлетворяет таким условиям, на практике для многих встречающихся течений жидкости законы сохранения массы выполняются с хорошей точностью.

ЗАКЛЮЧЕНИЕ

Рассмотрена обратная задача проектирования, которая состоит в определении свойств течения неизвестной формы по характеристикам поля течения.

Построены псевдоаналитические полиномы произвольной степени и подобраны сопряженные к ней функции. Найдены аналоги степеней комплексного переменного. Это позволяет рассматривать квазиконформные отображения осесимметрических областей, которые обладают основными свойствами конформных отображений. Изучаются различные случаи задания квазикомплексного потенциала. Разработанная программа позволяет рассматривать пространственные (осесимметричные) течения при различных заданиях источников и стоков. Использование системы координат, связанной с течением, позволяет рассматривать такие задачи, в которых использование обычных численных методов затруднено. В системе координат, связанной с линиями тока, метод позволяет построить решение в многосвязных областях.

Работа выполнена в рамках госконтракта Института автоматизации проектирования РАН.