Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 87-95

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим течение в окрестности особой точки с позиций молекулярно-кинетической теории газов. На рис. 1 схематически представлено движение молекулярных потоков в кнудсеновском слое в окрестности носика обтекаемого клина. В двух произвольных точках геометрического пространства 0XY построена декартова система координат $0{{\xi }_{x}}{{\xi }_{y}}$ пространства молекулярных скоростей ${\mathbf{\xi }}$. Из носика клина проведены линии, являющиеся траекториями молекулярных потоков, пришедших из окрестности носика. Уточним: рассматривается электрически нейтральная среда при отсутствии гравитационных сил.

Рис. 1.

Схема распределения молекулярных потоков в кнудсеновском слое. 0XY и $0{{\xi }_{x}}{{\xi }_{y}}$ – системы координат в геометрическом пространстве и в пространстве молекулярных скоростей. G – область молекулярных потоков, сформировавшихся в газовой среде перед носиком клина. S – область молекулярных потоков, отраженных поверхностью клина.

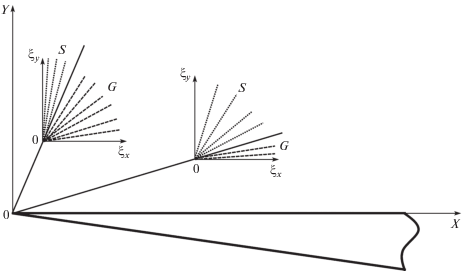
Указанные линии делят пространство молекулярных скоростей на две области, условно обозначенные G и S. В области G присутствуют молекулярные потоки, сформировавшиеся в газовой среде перед носиком клина. В области S – потоки, отраженные поверхностью клина. На линии, разделяющей эти области, имеют место две различные функции распределения молекул по скоростям, а сама линия является линией разрыва функции распределения в пространстве молекулярных скоростей.

Из общих физических соображений понятно, что разрыв функции распределения вдоль траектории невозможен, что учтено при постановке данной задачи. Разрыв возникает между соседними, сколь угодно близкими траекториями, где имеет место разрыв первого рода. Если положение линии (в общем случае – поверхности) разрыва определено, то вычисление моментов функции распределения (макропараметров газа) осуществляется стандартными методами вычислительной математики.

Описанное течение характерно для обтекания поверхностей свободномолекулярным потоком, которое в значительной степени реализуется в кнудсеновском слое. В частности, такого рода разрывы возникают всегда при взаимодействии газа с поверхностью в условиях теплового и динамического неравновесия. Специально отметим, что в условиях сильно неравновесных течений для описания такого процесса взаимодействия используют модели молекулярно кинетической теории газов, даже в достаточно плотных средах. К моделям такого рода относится и используемое в данной работе модельное кинетическое уравнение многоатомных газов.

Математическую модель обтекания тонкой пластины целесообразно строить в полярных системах координат как в геометрическом, так и скоростном пространствах. Спецификой решаемой задачи является то, что полярные углы геометрической и скоростной системы координат взаимосвязаны. Такая связь не характерна для кинетических уравнений, в которых геометрическое и скоростное пространства независимы. Для решения данной задачи эта взаимосвязь необходима для выделения линии разрыва.

Система координат геометрического пространства 0rθ показана на рис. 2. Полюс системы совмещен с особой точкой, т.е. носиком пластины. Сама пластина изображена утолщенной линией. Дополнительно нанесены оси 0X и 0Y прямоугольной декартовой системы, используемые для иллюстрации результатов. В пространстве молекулярных скоростей полюс системы координат 0ξψ соответствует ξ = 0. На рис. 3 изображен первый квадрант этой системы.

Рис. 2.

Полярная система координат 0rθ геометрического пространства. Пластина изображена утолщенной линией. Дополнительно нанесены оси декартовой системы 0XY.

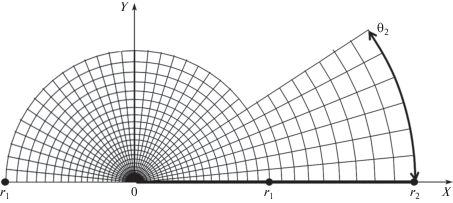
Рис. 3.

Первый квадрант полярной системы координат 0ξψ пространства молекулярных скоростей ξ. Дополнительно нанесены оси декартовой системы 0ξ_xξ_y.

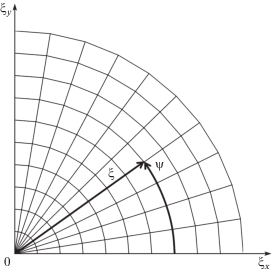
Решение кинетического уравнения будет строиться вдоль траектории молекулярного потока $\xi \in \left( {0{\text{,}}\;{{\xi }_{{{\text{max}}}}}} \right)$, $\psi = {\text{const}}$. Это позволит выделить линии разрыва функции распределения, для которых $\psi = \theta $.

Модельное кинетическое уравнение релаксационного типа, записанное вдоль траектории молекулярного потока, имеет вид:

Здесь $f$ – одночастичная функция распределения молекул по скоростям; ${{f}^{ + }}$ – функция распределения, моделирующая интеграл обратных столкновений; $\tau $ – характерное время релаксации. Символом $d{\text{/}}dt$ обозначена лагранжева производная.

Специфика кинетических уравнений релаксационного типа заключается в следующем. После элементарных преобразований приходим к выражению

Моменты времени t₀ и t₁ соответствуют начальной и конечной точкам траектории молекулярного потока на интервале времени $\tau $.

Отметим, что характерное время релаксации $\tau $ близко к среднему времени свободного пробега молекулы ${{\tau }_{c}}$. В области сильнонеравновесных течений, когда существенное изменение параметров газа происходит на интервале ${{\tau }_{c}}$, зависимость (1.2) имеет характер сильного допущения. Тем не менее, если шаг вычислительной сетки $\Delta t \ll \tau $, модель (1.1) вполне адекватно описывает реальное течение.

Это утверждение не относится к BGK-модели [18], в которой f  ⁺ соответствует локально максвелловской функции распределения и, следовательно, неравновесные напряжения (девиатор напряжений) и тепловые потоки релаксируют одновременно, что противоречит известным физическим законам. В частности, в одноатомных газах тепловые потоки релаксируют в полтора раза медленнее напряжений. Еще более худший результат дает эллипсоидальная модель [19], в которой напряжения релаксируют медленнее тепловых потоков. В настоящей работе для двухатомного газа используется модель [17], переходящая в S-модель [5] в случае одноатомного газа, и лишенная указанных недостатков.

Свободные параметры модели [17]

– s в аппроксимации ${\mu \mathord{\left/ {\vphantom {\mu {{{\mu }_{\infty }}}}} \right. \kern-0em} {{{\mu }_{\infty }}}} = {{\left( {{{{{T}_{t}}} \mathord{\left/ {\vphantom {{{{T}_{t}}} {{{T}_{\infty }}}}} \right. \kern-0em} {{{T}_{\infty }}}}} \right)}^{s}}$, где μ – коэффициент вязкости, T_t – температура поступательных степеней свободы молекул;

– $Z = Z\left( {{{{{T}_{r}}} \mathord{\left/ {\vphantom {{{{T}_{r}}} {{{T}_{t}}}}} \right. \kern-0em} {{{T}_{t}}}}} \right)$, здесь T_r – температура вращательных степеней свободы молекул.

Обратная величина параметра Z представляет долю неупругих межмолекулярных столкновений к общему числу столкновений.

2. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ ЗАДАЧИ

Модельное кинетическое уравнение [17] записано для двух функций распределения:

f_t – функция распределения молекул по скоростям при поступательном движении; f_r – функция распределения молекул по вращательным энергиям. Характерное время релаксации соответствует времени релаксации напряжений τ_p.

Адаптация f_t и f_r к условиям решаемой задачи аналогична, поэтому обозначим обе функции общим символом f, как это записано в (1.1). Время релаксации ${{\tau = {{\tau }_{p}} = \mu } \mathord{\left/ {\vphantom {{\tau = {{\tau }_{p}} = \mu } {\left( {\rho R{{T}_{t}}} \right)}}} \right. \kern-0em} {\left( {\rho R{{T}_{t}}} \right)}}$, где ρ – плотность, R – удельная газовая постоянная.

После формального интегрирования (1.1) на интервале от t₀ до t₁ и в предположении стационарного течения приходим к выражению:

Эта интегральная форма дифференциально-интегрального уравнения (1.1) отличается от классического интегрального уравнения [3] тем, что в ней не учтено рассеивание на интервале (t₀, t₁) молекул, образовавшихся в результате обратных столкновений. Однако на интервалах времени меньших среднего времени свободного пробега молекулы, на которых релаксационные уравнения физически адекватны, изменение функции распределения в результате как прямых, так и обратных столкновений достаточно мало. Изменение статистики вновь образовавшихся молекул, описываемой ${{f}^{ + }}$, на таком интервале времени представляет собой величину второго порядка малости. Можно ожидать, что на мелких геометрических расчетных сетках, соответствующих малому интервалу времени, погрешность (2.1) не будет превышать погрешности самой физико-математической модели, положенной в основу кинетических уравнений релаксационного типа.

Подынтегральные функции (2.1) на интервале $\Delta t = {{t}_{1}} - t{}_{0}$ аппроксимировались линейной зависимостью, а интеграл по времени заменялся интегралом по пространству на интервале $\Delta l = \Delta t\xi $. Полученная дискретная форма (2.1) имеет вид

В особой точке пространства скоростей (ξ = 0) при условии стационарного течения из (1.1) следует f₁ = $f_{1}^{ + }$.

Решение (2.2) вдоль траектории молекулярного потока связано с интерполяцией значений f₀ и τ_p0 на геометрической сетке (рис. 2). В данной работе использована линейная интерполяция. Для молекулярных скоростей, лежащих в разных квадрантах пространства скоростей, требуются различные геометрические схемы решения, что усложняет программный код, но позволяет выделять линии разрыва функции распределения в первом и во втором квадрантах. В третьем и четвертом квадрантах линии разрыва отсутствуют по естественным причинам.

В качестве характерных величин или единиц измерения в безразмерных выражениях использованы параметры невозмущенного потока: ρ_∞, T_∞, p_∞= ρ_∞RT_∞ (единица напряжения), $\sqrt {R{{T}_{\infty }}} $ (единица скорости), τ_∞ = μ_∞/p_∞ (единица времени), ${{\lambda }_{\infty }} = {{\tau }_{\infty }}\sqrt {R{{T}_{\infty }}} $ (длина свободного пробега молекулы или единица длины).

В геометрическом пространстве (рис. 2) использовалась расчетная сетка с переменным шагом по r. В полюсе $\Delta r = {\text{0}}{\text{.1}}{{\lambda }_{\infty }}$, на периферии вычислительной области $\Delta r = {{\lambda }_{\infty }}$. Протяженность сетки ${{r}_{1}} = 5{{\lambda }_{\infty }}$. Максимальная протяженность сетки ${{r}_{2}} = 100{{\lambda }_{\infty }}$.

Шаг полярного угла $\Delta \theta $ принимался постоянным и был определен соотношением ${{r}_{2}}\Delta \theta = {{\lambda }_{\infty }}$. Раствор полярного угла θ₂ = 30°.

Сетка пространства скоростей строилась с постоянным шагом по переменным ξ и ψ: $\Delta \xi = 0.1\sqrt {R{{T}_{\infty }}} $, $\Delta \psi = 0.5\Delta \theta $. Граница скоростной сетки ${{\xi }_{{\max }}} = 20\sqrt {R{{T}_{\infty }}} $. Такие параметры скоростной сетки позволили выполнять законы сохранения до 7-го знака. При вычислении макропараметров использовалась аппроксимация f полиномом второй степени.

Граничные условия задачи поставлены следующим образом. На дуге радиуса r₁ в интервале угла θ от θ₂ до π и на радиусе с полярным углом θ₂ в интервале от r₁ до r₂ приняты условия невозмущенного потока. Здесь функция распределения молекул по скоростям является максвелловой функцией с параметрами невозмущенного потока. На радиусе с полярным углом θ = π выставлены граничные условия симметрии, т.е. $f({{\xi }_{y}} < 0) = f({{\xi }_{y}} > 0)$. На нижней по потоку границе (дуга с радиусом r₂) приняты граничные условия Неймана, а именно – вторые производные по координате X всех макропараметров приравнены нулю. По значениям этих макропараметров восстановлены аппроксимирующие функции вида

Здесь p_ij – девиатор напряжений, φ_i и ω_i – тепловые потоки, обусловленные поступательным и вращательным движением молекул, c_i – тепловая скорость молекул.

На поверхности пластины принимался диффузный закон взаимодействия молекул газа с поверхность: концентрация отраженных молекул определялась условиями непротекания, групповая скорость отраженных молекул относительно пластины принималась равной нулю, температура отраженных молекул считалась равной температуре пластины.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Расчеты проводились для течения, исследованного экспериментально в [6]. Число Маха принималось M_∞ = 10.15. Температура пластины T_w = 2.16 T_∞. Рассматривалось течение двухатомного газа. Свободные параметры модели: s = 0.72, Z = 1.3(1 + 0.75 T_r/T_t).

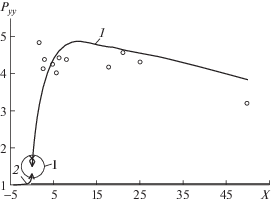
На рис. 4 показано распределение нормального напряжения P_yy на линии y=0 вдоль координаты 0X декартовой системы координат или координаты r при θ = 0 полярной системы. На поверхности пластины расчетные данные удовлетворительно согласуются с экспериментальными. Перед носиком пластины (кривая 2) газ достаточно сильно возмущен, что не учитывается в ряде цитированных работ.

Рис. 4.

Распределение нормального напряжения P_yy на линии y = 0. Кружками отмечены экспериментальные данные [6], 1 и 2 – расчетная кривая. Крестик соответствует значению P_yy в особой точке, т.е. на носике пластины. Область I увеличена на рис. 5.

На носике пластины, в особой точке течения, имеет место разрыв, подробно показанный на рис. 5. Обращает на себя внимание характер разрыва в особой точке, левая окрестность которой принадлежит набегающему потоку, а правая – поверхности пластины. Значение P_yy в самой особой точке существенно превышает значения в обеих ее окрестностях.

Рис. 5.

Увеличенное изображение области I рис. 4.

Этот факт имеет простое объяснение даже при упрощенном рассмотрении. Будем считать, что концентрация молекул (интеграл функции распределения по пространству скоростей) в областях геометрических пространств, непосредственно прилегающих к особой точке, равна единице. Декартова система координат $0{{\xi }_{x}}{{\xi }_{y}}$ соответствует рис. 3, на котором показан первый квадрант системы.

В условиях гиперзвукового течения в левой (согласно рис. 4) окрестности особой точки почти все молекулы будут сосредоточены в 1-м и 4-м квадрантах пространства скоростей, так как только незначительное количество молекул движется против потока газа. Концентрации молекул в каждом из этих квадрантов (интегралы функции распределения по соответствующим квадрантам) будет составлять примерно по 0.5, а в квадрантах 2 и 3 – примерно 0.

В правой окрестности особой точки квадранты 3 и 4 заполнены так же, как и в левой. Это обусловлено тем, что они содержат молекулы, пришедшие из той же области течения, расположенной выше пластины. В квадрантах 1 и 2 содержатся отраженные поверхностью молекулы. Если пренебречь различием температур поверхности и газа, то суммарная концентрация в квадрантах 1 и 2 должна соответствовать суммарной концентрации квадрантов 3 и 4, т.е. 0.5. При диффузном законе отражения концентрация в квадрантах 1 и 2 будет составлять по 0.25.

В особой точке концентрация молекул в квадрантах 3 и 4 составляет 0 и 0.5, как и в окрестностях этой точки. Квадрант 1 содержит молекулы набегающего потока. Их концентрация принята нами 0.5. Квадрант 2 наполнен отраженными молекулами с концентрацией 0.25. Суммарная концентрация молекул в особой точке составляет 1.25, т.е. на четверть превосходит концентрацию молекул в ее окрестностях.

Этот модельный эффект возникает в точке, разделяющей газовую среду и твердую поверхность при достаточно больших числах Маха и при любых числах Кнудсена. В реальных условиях такой точки не существует. Взаимодействие набегающего потока с твердой поверхностью происходит в области конечного размера.

Здесь анализировалась концентрация молекул, момент нулевого порядка. Очевидно, аналогичные выкладки справедливы и для моментов более высоких порядков. Графики, представленные на рис. 4 и рис. 5, демонстрируют описанный эффект для момента второго порядка, P_yy.

При решении задачи обтекания острой кромки с использованием гидродинамических уравнений в достаточно широкой области, охватывающей особую точку, наблюдается осцилляция решения [16]. При использовании кинетического подхода по описанной методике разрыв решения возникает только в особой точке. В остальной области течения решение является гладким.

Если рассматривать область течения, расположенную выше (y > 0) особой точки на сколь угодно малом расстоянии от последней, то разрыв не будет наблюдаться. Все точки этой области принадлежат газовой среде и, следовательно, не являются граничными токами газообразной и твердой сред.

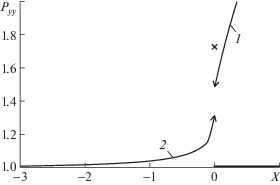
На рис. 6 показано распределение P_yy вдоль оси 0X (r при θ = 0) при значении координаты $y = 0.1{{\lambda }_{\infty }}$. Распределение является гладкой кривой. Между участками 1 и 2 разрыв отсутствует. Это характерно только для моментов функции распределения. Разрыв функции распределения между соседними траекториями в пространстве скоростей наблюдается на протяжении нескольких длин свободного пробега молекулы.

Рис. 6.

Распределение нормального напряжения P_yy на линии $y = 0.1{{\lambda }_{\infty }}$, 1 и 2 – участки расчетной кривой.

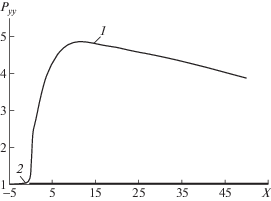
На рис. 7 показано сглаживание разрыва функции распределения вдоль линии разрыва по мере удаления от носика пластины. Анализируется значение интеграла

Рис. 7.

Изменение интегралов f функции распределения областей G и S, вычисленных на линии разрыва. Полярный угол линии разрыва θ = π/8.

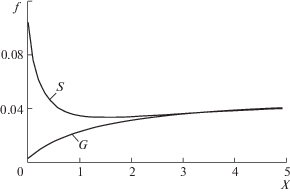
Полярный угол линии разрыва составлял θ = π/8. Интеграл f вычислялся для молекулярных потоков, принадлежащих областям G и S согласно рис. 1. Различие в значениях интегралов становится несущественным при r ≈ 3λ_∞. При меньших удалениях от особой точки различие в этих “неполных” моментах функции распределения достаточно велико.

ЗАКЛЮЧЕНИЕ

Предложенный метод решения модельного кинетического уравнения позволяет явным образом выделять поверхности разрыва в пространстве молекулярных скоростей. В пределах кнудсеновского слоя такие разрывы играют существенную роль.

Проведенные расчеты показывают, что даже при гиперзвуковом обтекании абсолютно острой кромки имеет место значительное возмущение потока перед кромкой.

Показано, что значение макропараметров газа в особой точке, разделяющей набегающий поток и носовую часть кромки, не является некоторым осредненным значением параметров в окрестности этой точки. В особой точке значение макропараметра значительно выходит за пределы интервала значений, определенных в окрестностях этой точки. Этот факт необходимо учитывать при разработке физико-математических моделей, направленных на описание динамики газа в окрестностях острой кромки.

Также необходимо учитывать, что разрыв значений макропараметров возникает только на линии тока, проходящей через особую точку. На других линиях тока, сколь угодно близких к указанной выше, разрывов не возникает. Имеет место гладкое решение.

Результаты проведенного исследования могут быть полезны при разработке математических моделей течения динамически неравновесных сред.

Работа выполнена в рамках государственного задания Минобрнауки России, номер темы FSFF-2020-0013.