Известия РАН. Механика жидкости и газа, 2022, № 1, стр. 47-56

ЗАДАЧА КОШИ–ПУАССОНА ДЛЯ ЖИДКОСТИ С ЛЕДЯНЫМ ПОКРОВОМ ПРИ НАЛИЧИИ СДВИГОВОГО ТЕЧЕНИЯ (ДВУМЕРНЫЙ СЛУЧАЙ)

И. В. Стурова^a, *

^a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 17.05.2021
После доработки 21.09.2021
Принята к публикации 21.09.2021

EDN: MZUUTG
DOI: 10.31857/S0568528122010108

Аннотация

В линейной постановке решена двумерная нестационарная задача об эволюции начального возмущения в жидкости, на поверхности которой плавает ледяной покров. В невозмущенном состоянии продольная скорость жидкости линейно меняется с глубиной. Ледяной покров моделируется тонкой упругой пластиной с учетом сжимающих усилий. Построено интегральное представление решения, описывающее поведение ледяного покрова. Получены асимптотики этого решения при больших временах, позволяющие описывать дальние поля возмущений как вблизи, так и вдали от волнового фронта.

Ключевые слова: плавающая упругая пластина, изгибно-гравитационные волны, сжимающие усилия, сдвиговые течения, эволюция начального возмущения

Исследование нестационарного движения тяжелой жидкости, возникающего благодаря действию в начальный момент времени импульсного давления или нарушению вида горизонтальной равновесной поверхности жидкости (так называемая задача Коши–Пуассона), является одной из классических задач волновой гидродинамики, которая довольно подробно изучена для случая однородной несжимаемой жидкости, когда ее верхняя граница является свободной, и жидкость в начальный момент покоится (см., например, [1, 2]).

В последние годы активно исследуются более сложные постановки этой задачи. Исследование трехмерного случая для осесимметричного начального возмущения, создаваемого на поверхности жидкости под ледяным покровом без учета сжимающих усилий, выполнено в [3]. В исходном состоянии жидкость покоится и ее глубина бесконечна. Начальное возмущение вызвано распределенным импульсным давлением или вертикальным смещением ледяного покрова. В трехмерном случае задача Коши–Пуассона для жидкости со сдвиговым течением и при наличии поверхностного натяжения на свободной поверхности изучена в работах [4, 5]. В невозмущенном состоянии линейное сдвиговое течение задано только для одной компоненты горизонтальной скорости жидкости. В [4] исследована эволюция осесимметричного начального возвышения свободной поверхности, а в [5] – действие внешнего давления. Экспериментальное подтверждение полученных теоретических результатов представлено в [6].

В данной работе в линейной постановке рассмотрена двумерная задача о поведении потока с вертикальным сдвигом скорости однородной идеальной несжимаемой жидкости, на поверхности которой плавает сплошной упругий ледяной покров с учетом продольного сжатия. В начальный момент времени верхняя граница жидкости отклоняется от невозмущенного горизонтального положения. Построено интегральное представление решения, описывающее поведение ледяного покрова. Получены асимптотики этого решения, позволяющие оценить дальние поля возмущений как вблизи, так и вдали от волнового фронта.

1. ПОСТАНОВКА ЗАДАЧИ

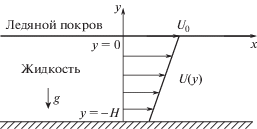
В невозмущенном состоянии слой однородной невязкой несжимаемой жидкости постоянной глубины $H$ имеет продольную скорость $U(y) = {{U}_{0}} + \alpha y$. Система декартовых координат $x$, $y$ введена так, что ось $x$ совпадает с невозмущенной горизонтальной верхней границей жидкости, а ось $y$ направлена вертикально вверх. На поверхности потока жидкости плывет сплошной ледяной покров, который моделируется тонкой упругой пластиной постоянной толщины и плотности. Предполагается, что в упругой пластине существуют продольные сжимающие усилия и во все моменты времени $t$ жидкость находится в контакте с пластиной. Схема течения приведена на рис. 1.

Рис. 1.

Схема течения в невозмущенном состоянии.

Вывод основных уравнений движения жидкости и ледяного покрова выполняется аналогично [7]. При наличии линейного сдвига продольной скорости основного течения горизонтальную $u(x,y,t)$ и вертикальную ${v}(x,y,t)$ компоненты скорости возмущенного течения можно представить в виде [8]

$u(x,y,t) = U(y) + \partial \varphi {\text{/}}\partial x,\quad {v}(x,y,t) = \partial \varphi {\text{/}}\partial y$

где функция $\varphi (x,y,t)$ удовлетворяет уравнению Лапласа

(1.1)

${{\partial }^{2}}\varphi {\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}\varphi {\text{/}}\partial {{y}^{2}} = 0\quad \left( {\left| x \right| < \infty , - H \leqslant y \leqslant 0} \right)$

и условию непротекания на дне

(1.2)

$\partial \varphi {\text{/}}\partial y = 0\quad (y = - H)$

Кинематическое и динамическое условия на верхней границе жидкости ($y = 0$) имеют вид

(1.3)

$\frac{{\partial w}}{{\partial t}} + {{U}_{0}}\frac{{\partial w}}{{\partial x}} = \frac{{\partial \varphi }}{{\partial y}}$

(1.4)

$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + Q\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + M\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = {{p}_{s}}$

Здесь $w(x,t)$ – вертикальный прогиб ледяного покрова, его цилиндрическая жесткость равна $D = E{{h}^{3}}{\text{/}}[12(1 - {{\nu }^{2}})]$, $M = {{\rho }_{1}}h$; $E$, ${{\rho }_{1}}$, $h$, $\nu $ – модуль Юнга, плотность, толщина и коэффициент Пуассона пластины; $Q$ – продольное напряжение (сжатие при положительных и растяжение при отрицательных значениях); ${{p}_{s}}$ – давление, действующее со стороны жидкости на ледяной покров. Первое слагаемое в динамическом условии (1.4) описывает упругие свойства ледяного покрова, второе слагаемое представляет сжимающее или растягивающее напряжение в нем, а третье – его инерционные свойства.

Использем уравнения Эйлера в форме Громеко для описания течения весомой жидкости (см., например, [9])

$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \nabla \left( {\frac{{{{{\mathbf{u}}}^{2}}}}{2} + \frac{p}{\rho } + gy} \right) = {\mathbf{u}} \times {\text{rot}}{\mathbf{u}},\quad {\mathbf{u}} = (u,{v})$

где p(x, y, t) – гидродинамическое давление. Пренебрегая членами второго порядка малости, получим следующее уравнение для определения ${{p}_{s}}$ = p(x, 0, t)

$\frac{\partial }{{\partial x}}\left( {\frac{{\partial \varphi }}{{\partial t}} + {{U}_{0}}\frac{{\partial \varphi }}{{\partial x}} + \frac{{{{p}_{s}}}}{\rho } + gw} \right) = - \alpha \frac{{\partial \varphi }}{{\partial y}}\quad (y = 0)$

где $\rho $ – плотность жидкости, $g$ – ускорение свободного падения. После подстановки этого соотношения в (1.4) динамическое условие примет вид

(1.5)

$\frac{\partial }{{\partial x}}\left( {D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + Q\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \rho \frac{{\partial \varphi }}{{\partial t}} + \rho {{U}_{0}}\frac{{\partial \varphi }}{{\partial x}} + \rho gw} \right) + \alpha \rho \frac{{\partial \varphi }}{{\partial y}} = 0\quad (y = 0)$

При этом сделано предположение, что упругая восстанавливающая сила в ледяном покрове существенно больше, чем инерционная сила, и слагаемым с коэффициентом $M$ в (1.4) можно пренебречь. Начальные условия равны

(1.6)

$w(x,0) = {{w}_{0}}(x),\quad \varphi (x,y,0) = {{\left. {\partial w{\text{/}}\partial t} \right|}_{{t = 0}}} = 0$

Далее для простоты предполагается, что функция ${{w}_{0}}(x)$ является четной.

Для решения задачи (1.1)–(1.3), (1.5), (1.6) используется преобразование Фурье

$\Phi (k,y,t) = \int\limits_{ - \infty }^\infty \varphi (x,y,t)exp( - ikx)dx$

$W(k,t) = \int\limits_{ - \infty }^\infty w (x,t)exp( - ikx)dx$

Из уравнения Лапласа (1.1) и граничного условия на дне (1.2) получим

$\Phi (k,y,t) = G(k,t){\text{ch}}[k(y + H)]$

где $G(k,t)$ – неизвестная функция. Из кинематического условия (1.3) имеем

(1.7)

$\dot {W} + ik{{U}_{0}}W = kG{\text{sh}}(kH)$

где точкой сверху обозначена производная по времени t. Согласно динамическому условию (1.5)

(1.8)

$(i\dot {G} - k{{U}_{0}}G){\text{ch}}(kH) + \alpha G{\text{sh}}(kH) + i\left( {\frac{{{{k}^{4}}D}}{\rho } - \frac{{{{k}^{2}}Q}}{\rho } + g} \right)W = 0$

Исключая функцию $G(k,t)$ из (1.7), (1.8), получим обыкновенное дифференциальное уравнение для функции $W(k,t)$

(1.9)

$\ddot {W} + A(k)\dot {W} + B(k)W = 0$

с начальными условиями

(1.10)

$W(k,0) = {{W}_{0}}(k),\quad \dot {W}(k,0) = 0$

Здесь

$A(k) = i\left[ {2k{{U}_{0}} - \alpha {\text{th}}(kH)} \right],\quad B(k) = k\left[ {\left( {\frac{D}{\rho }{{k}^{4}} - \frac{Q}{\rho }{{k}^{2}} + \alpha {{U}_{0}} + g} \right){\text{th}}(kH) - U_{0}^{2}k} \right]$

${{W}_{0}}(k) = 2\int\limits_0^\infty {{{w}_{0}}} (x)cos(kx)dx$

Представленные ниже расчеты выполнены для функции

${{w}_{0}}(x) = acos(bx)exp( - c{{x}^{2}})$

преобразование Фурье для которой равно

${{W}_{0}}(k) = \frac{a}{2}\sqrt {\frac{\pi }{c}} \left\{ {exp\left[ { - \frac{{{{{(k + b)}}^{2}}}}{{4c}}} \right] + exp\left[ { - \frac{{{{{(k - b)}}^{2}}}}{{4c}}} \right]} \right\}$

Решение уравнения (1.9) с начальными условиями (1.10) имеет вид

$W(k,t) = {{W}_{0}}(k)exp[i\gamma (k)t]\left\{ {cos\left[ {\sigma (k)t} \right] - \frac{{i\gamma (k)}}{{\sigma (k)}}sin\left[ {\sigma (k)t} \right]} \right\}$

где

$\gamma (k) = \frac{\alpha }{2}{\text{th}}(kH) - k{{U}_{0}}$

$\sigma (k) = \sqrt {k{\text{th}}(kH)\left( {\frac{D}{\rho }{{k}^{4}} - \frac{Q}{\rho }{{k}^{2}} + g} \right) + \frac{{{{\alpha }^{2}}}}{4}{\text{t}}{{{\text{h}}}^{2}}(kH)} $

После выполнения обратного преобразования Фурье

$w(x,t) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty W (k,t)exp(ikx)dk$

введения безразмерных переменных

$x{\text{'}} = \frac{x}{H},\quad t{\text{'}} = t\sqrt {\frac{g}{H}} ,\quad w{\text{'}} = \frac{w}{a},\quad D{\text{'}} = \frac{D}{{\rho g{{H}^{4}}}},\quad Q{\text{'}} = \frac{Q}{{\rho g{{H}^{2}}}},\quad \alpha {\text{'}} = \frac{\alpha }{2}\sqrt {\frac{H}{g}} $

$U_{0}^{'} = \frac{{{{U}_{0}}}}{{\sqrt {gH} }},\quad W_{0}^{'} = \frac{{{{W}_{0}}}}{{aH}},\quad b{\text{'}} = Hb,\quad c{\text{'}} = {{H}^{2}}c$

и перехода в подвижную систему координат $X = x{\text{'}} - U_{0}^{'}t{\text{'}}$ получим (далее штрихи опускаются)

(1.11)

$w(X,t) = \frac{1}{{2\pi }}\int\limits_0^\infty {{{W}_{0}}} (k)\left\{ {{{C}_{ - }}(k)cos[{{\sigma }_{ + }}(k)t + kX] + {{C}_{ + }}(k)cos[{{\sigma }_{ - }}(k)t - kX]} \right\}dk$

где

${{C}_{ \pm }}(k) = 1 \pm (\alpha {\text{th}}k - k{{U}_{0}}){\text{/}}S(k),{{\sigma }_{ \pm }}(k) = S(k) \pm \alpha {\text{th}}k$

(1.12)

$S(k) = \sqrt {k{\text{th}}k(1 + D{{k}^{4}} - Q{{k}^{2}}) + {{{(\alpha {\text{th}}k)}}^{2}}} $

При $D = Q = {{U}_{0}} = \alpha = 0$ полученное решение совпадает с решением двумерной задачи Коши–Пуассона для первоначально покоящейся жидкости и обычной свободной поверхности (см., например, [1]). При $D = 0$, $Q = - T$ ($T > 0$) полученное решение является решением двумерной задачи Коши–Пуассона для свободной поверхности с учетом коэффициента поверхностного натяжения $T$. Трехмерный вариант этой задачи рассмотрен в [4].

Соотношение (1.12) накладывает ограничение на величину сжимающего усилия $Q$, так как для существования вещественного значения функции $S(k)$ необходимо, чтобы подкоренное выражение было неотрицательным. Это условие гарантирует устойчивость плавающей упругой пластины. При отсутствии сдвигового течения ($\alpha = 0$) имеет место хорошо известное ограничение на сжимающее усилие $Q \leqslant {{Q}_{ * }} \equiv 2\sqrt D $ (см., например, [10]). При $\alpha \ne 0$ для определения ${{Q}_{ * }}$ необходимо решить систему уравнений

$F({{k}_{ * }}) = {{\left. {dF{\text{/}}dk} \right|}_{{k = {{k}_{ * }}}}} = 0$

где

$F(k) = k(1 + D{{k}^{4}} - Q{{k}^{2}}) + {{\alpha }^{2}}{\text{th}}k$

Для решения этой системы уравнений можно определить зависимость ${{k}_{ * }}(\alpha )$ при заданном значении $D$ из уравнения

$2(D{{k}^{4}} - 1) + {{\alpha }^{2}}(1 - 3{\text{th}}k{\text{/}}k - {\text{t}}{{{\text{h}}}^{2}}k) = 0$

и затем определить значение ${{Q}_{ * }}(\alpha )$ из соотношения

${{Q}_{ * }} = {{[{{k}_{ * }} + Dk_{ * }^{5} + {{\alpha }^{2}}{\text{th}}{{k}_{ * }}]} \mathord{\left/ {\vphantom {{[{{k}_{ * }} + Dk_{ * }^{5} + {{\alpha }^{2}}{\text{th}}{{k}_{ * }}]} {k_{ * }^{3}}}} \right. \kern-0em} {k_{ * }^{3}}}$

2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Использованы следующие параметры ледяного покрова и жидкости

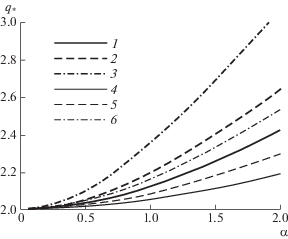
$E = 5 \times {{10}^{9}}\;{\text{Па}},\quad \nu = 0.3,\quad \rho = 1025\;{\text{кг/}}{{{\text{м}}}^{3}}$

На рис. 2 приведены зависимости ${{q}_{ * }} \equiv {{Q}_{ * }}{\text{/}}\sqrt D $ от безразмерного параметра $\alpha $ при различных глубинах жидкости $H = 20$ м и $H = 50$ м соответственно и толщинах льда $h = 10,\;20,\;50$ см. Видно, что при наличии сдвигового течения с увеличением толщины ледяного покрова и уменьшением глубины жидкости существенно возрастает диапазон допустимых значений параметра сжатия.

Рис. 2.

Зависимость ${{q}_{ * }}$ от безразмерного параметра сдвига $\alpha $ при различных глубине жидкости $H$ и толщине льда $h$: 1–3 – $H = 20$ м; 4–6 – $H = 50$ м; 1, 4 – $h = 10$ см; 2, 5 – $h = 20$ см; 3, 6 – $h = 50$ см.

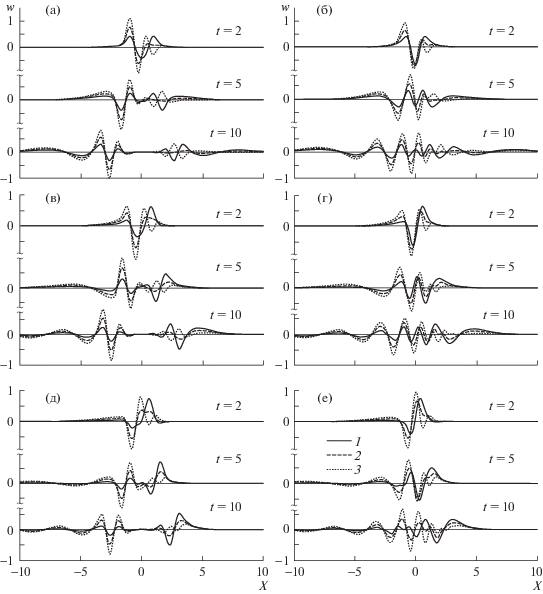
Представленные ниже расчеты выполнены для толщины ледяного покрова $h = 20$ см и глубины жидкости $H = 50$ м. На рис. 3 показаны прогибы ледяного покрова $w(X,t)$ для моментов времени $t = 2,\;5,\;10$ при различных значениях параметров сдвига, сжатия и скорости ${{U}_{0}} = 0,\;0.5,\;1$. Для бессдвигового потока ($\alpha = 0$) безразмерный параметр сжатия $q \equiv Q{\text{/}}\sqrt D = 0,\;1.9$, для сдвиговых потоков при $\alpha = 0.5,\;1$ использованы параметры сжатия $q = 0,\;2$. Численное интегрирование (1.11) выполнено для параметров начального возвышения $b = 3$, $c = 2$. При отсутствии сдвигового течения ($\alpha = 0$) и ${{U}_{0}} = 0$ волновые возмущения симметричны относительно эпицентра начального возмущения. В остальных случаях волновые движения являются несимметричными. Область значений продольной координаты X, охваченной волновым движением, больше при $X < 0$ и с увеличением скорости ${{U}_{0}}$ также в этой области возрастают амплитуды волновых возмущений. Влияние параметра сжатия более всего проявляется в области малых значений $\left| X \right|$. При $q = 0$ с ростом времени в окрестности $\left| X \right| \approx 0$ волновые возмущения практически исчезают. Однако при $q \ne 0$ волновые движения в этой области довольно значительные.

Рис. 3.

Вертикальные прогибы ледяного покрова в моменты времени $t = 2,\;5,\;10$: а–е – (α, q) = (0, 0); (0, 1.9); $(0.5,0);(0.5,2);(1,0);(1,2)$. Кривые 1–3 соответствуют ${{U}_{0}} = 0,\;0.5,\;1$.

Используя асимптотические оценки интеграла в (1.11), можно получить приближенные решения для волнового движения при больших временах. Для задачи Коши–Пуассона в случае первоначально покоящейся жидкости с обычной свободной поверхностью асимптотические решения получены, например, в [11]. В данной работе аналогичным образом выведены асимптотики решения в окрестности волновых фронтов для рассматриваемой задачи.

Используем метод стационарной фазы для оценки интеграла в (1.11) при $t \to \infty $. Фазовые функции первого и второго слагаемых в подынтегральном выражении равны соответственно

${{\Psi }_{1}}(k,V,t) = t{{\Lambda }_{1}}(k,V),\quad {{\Psi }_{2}}(k,V,t) = t{{\Lambda }_{2}}(k,V)$

где

${{\Lambda }_{1}}(k,V) = S(k) + \alpha {\text{th}}k + kV,\quad {{\Lambda }_{2}}(k,V) = S(k) - \alpha {\text{th}}k - kV,\quad V = X{\text{/}}t$

Стационарные точки должны удовлетворять уравнениям

(2.1)

$\frac{{\partial {{\Lambda }_{1}}}}{{\partial k}} = {{\Omega }_{ + }}(k) + V = 0,\quad \frac{{\partial {{\Lambda }_{2}}}}{{\partial k}} = {{\Omega }_{ - }}(k) - V = 0,\quad {{\Omega }_{ \pm }} = \frac{{dS}}{{dk}} \pm \alpha (1 - {\text{t}}{{{\text{h}}}^{2}}k)$

где

$\frac{{dS}}{{dk}} = \frac{{0.5}}{{S(k)}}\{ k(1 + D{{k}^{4}} - Q{{k}^{2}})(1 - {\text{t}}{{{\text{h}}}^{2}}k) + {\text{th}}k[1 + 5D{{k}^{4}} - 3Q{{k}^{2}} + 2{{\alpha }^{2}}(1 - {\text{t}}{{{\text{h}}}^{2}}k)]\} $

На рис. 4 представлены зависимости функций ${{\Omega }_{ \pm }}(k)$ при $\alpha = 0.5$ для двух значений параметра сжатия $q = 0$ и $q = 2$. Значения ${{\Omega }_{ \pm }}(0)$ не зависят от параметра сжатия $q$ и равны

(2.2)

${{\Omega }_{ \pm }}(0) = \sqrt {1 + {{\alpha }^{2}}} \pm \alpha $

Рис. 4.

Зависимости функций ${{\Omega }_{ + }}(k)$ (кривые 1, 3) и ${{\Omega }_{ - }}(k)$ (кривые 2, 4) при $\alpha = 0.5$: 1, 2 – $q = 0$; 3, 4 – $q = 2$.

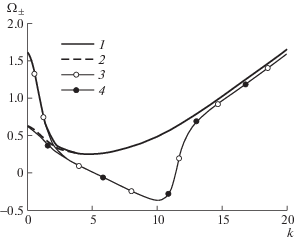
С ростом $\alpha $ значение ${{\Omega }_{ + }}(0)$ стремится к $2\alpha $, а значение ${{\Omega }_{ - }}(0)$ – к нулю. Кривые, соответствующие ${{\Omega }_{ + }}(k)$ и ${{\Omega }_{ - }}(k)$, сливаются при достаточно больших значениях волнового числа $k$.

Далее для получения асимптотических выражений ограничимся только областью относительно малых значений волнового числа $0 \leqslant k < K$. При $q = 0$ выбрано значение $K = 4.8$, соответствующее минимуму функций ${{\Omega }_{ \pm }}(k)$, а для $q = 2$ – значение $K = 5.1$, при котором эти функции еще являются положительными. С учетом введенных ограничений на диапазон значений волнового числа $k$ уравнение $\partial {{\Lambda }_{1}}{\text{/}}\partial k = 0$ в (2.1) не имеет действительных корней при $V > 0$, а уравнение $\partial {{\Lambda }_{2}}{\text{/}}\partial k = 0$ не имеет действительных корней при $V < 0$. Следовательно, для описания волнового движения вниз по потоку $(X < 0)$ при больших временах следует учитывать только первое слагаемое в подынтегральном выражении (1.11), а для волнового движения вверх по потоку $(X > 0)$ – только второе слагаемое.

Согласно методу стационарной фазы справедливы асимптотики: при $X < 0$

(2.3)

$w(X,t) \approx \frac{{{{W}_{0}}({{k}_{1}}){{C}_{ - }}({{k}_{1}})}}{{\sqrt {2\pi t{{{\left| {\tfrac{{d{{\Omega }_{ + }}}}{{dk}}} \right|}}_{{k = {{k}_{1}}}}}} }}cos\left\{ {\left[ {S({{k}_{1}}) + \alpha {\text{th}}{{k}_{1}}} \right]t - {{k}_{1}}\left| X \right| - \frac{\pi }{4}} \right\}$

при $X > 0$

(2.4)

$w(X,t) \approx \frac{{{{W}_{0}}({{k}_{2}}){{C}_{ + }}({{k}_{2}})}}{{\sqrt {2\pi t{{{\left| {\tfrac{{d{{\Omega }_{ - }}}}{{dk}}} \right|}}_{{k = {{k}_{2}}}}}} }}cos\left\{ {\left[ {S({{k}_{2}}) - \alpha {\text{th}}{{k}_{2}}} \right]t - {{k}_{2}}X - \frac{\pi }{4}} \right\}$

где ${{k}_{1}}$ и ${{k}_{2}}$ являются корнями первого и второго уравнений в (2.1) соответственно.

Эти асимптотики становятся непригодными при $V \to {{V}_{ - }}$ для $X > 0$ и $\left| V \right| \to {{V}_{ + }}$ для $X < 0$, т.е. вблизи волновых фронтов ${{V}_{ \pm }} = {{\Omega }_{ \pm }}(0)$. Следует отметить, что согласно (2.2) положение волновых фронтов $\left| {X_{f}^{ \pm }} \right| = {{V}_{ \pm }}t$ зависит только от параметра сдвига $\alpha $ и не зависит от свойств ледяного покрова.

Локальные асимптотики в окрестности волновых фронтов выписываются отдельно для областей справа и слева от фронта. При $X < 0$ прогибы ледяного покрова справа от фронта описываются соотношением

(2.5)

$w(X,t) \approx \frac{{{{W}_{0}}({{k}_{1}})}}{{\sqrt 2 {{t}^{{1/3}}}}}\frac{{Z_{1}^{{1/4}}}}{{\left| {\tfrac{{d{{\Omega }_{ + }}}}{{dk}}} \right|_{{k = {{k}_{1}}}}^{{1/2}}}}{{C}_{ - }}({{k}_{1}}){\text{Ai}}( - {{Z}_{1}}{{t}^{{2/3}}})$

где

${{Z}_{1}} = {{\left\{ {\frac{3}{2}\left[ {{{\sigma }_{ + }}({{k}_{1}}) - \left| V \right|{{k}_{1}}} \right]} \right\}}^{{2/3}}}$

а при $X > 0$ слева от фронта

(2.6)

$w(X,t) \approx \frac{{{{W}_{0}}({{k}_{2}})}}{{\sqrt 2 {{t}^{{1/3}}}}}\frac{{Z_{2}^{{1/4}}}}{{\left| {\tfrac{{d{{\Omega }_{ - }}}}{{dk}}} \right|_{{k = {{k}_{2}}}}^{{1/2}}}}{{C}_{ + }}({{k}_{2}}){\text{Ai}}( - {{Z}_{2}}{{t}^{{2/3}}})$

где

${{Z}_{2}} = {{\left\{ {\frac{3}{2}\left[ {{{\sigma }_{ - }}({{k}_{2}}) - V{{k}_{2}}} \right]} \right\}}^{{2/3}}}$

${\text{Ai}}(z)$ – функция Эйри (см., например, [12]). В отличие от формул (2.3), (2.4), полученных обычным методом стационарной фазы, вертикальные прогибы, описываемые соотношениями (2.5), (2.6), ограничены в окрестности волнового фронта.

Для нахождения локальной асимптотики в окрестности волнового фронта слева при $X < 0$ и справа при $X > 0$ вводится новая переменная $z = - ik$. Стационарная точка ${{z}_{1}}$ для $X < 0$ определяется как наименьшее положительное решение уравнения

$d{{\Upsilon }_{ + }}{\text{/}}dz = \left| V \right|$

а стационарная точка ${{z}_{2}}$ для $X > 0$ как решение уравнения

$d{{\Upsilon }_{ - }}{\text{/}}dz = V$

где

${{\Upsilon }_{ \pm }} = \bar {S}(z) \pm \alpha {\text{tg}}z,\quad \bar {S}(z) = \sqrt {z{\text{tg}}z(1 + D{{z}^{4}} + Q{{z}^{2}}) + {{{(\alpha {\text{tg}}z)}}^{2}}} $

При $X < 0$ прогиб ледяного покрова слева от волнового фронта описывается соотношением

(2.7)

$w(X,t) \approx \frac{{{{W}_{0}}({{z}_{1}})}}{{\sqrt 2 {{t}^{{1/3}}}}}\frac{{\mathop {\bar {Z}}\nolimits_1^{1/4} }}{{\left| {\tfrac{{{{d}^{2}}{{\Upsilon }_{ + }}}}{{d{{z}^{2}}}}} \right|_{{z = {{z}_{1}}}}^{{1/2}}}}{{C}_{ - }}{\text{(}}i{{z}_{{\text{1}}}}{\text{)Ai}}({{\bar {Z}}_{1}}{{t}^{{2/3}}})$

где

${{\bar {Z}}_{1}} = {{\left\{ {\frac{3}{2}\left[ {{{\Upsilon }_{ + }}({{z}_{1}}) - \left| V \right|{{z}_{1}}} \right]} \right\}}^{{2/3}}}$

а при $X > 0$ справа от волнового фронта

(2.8)

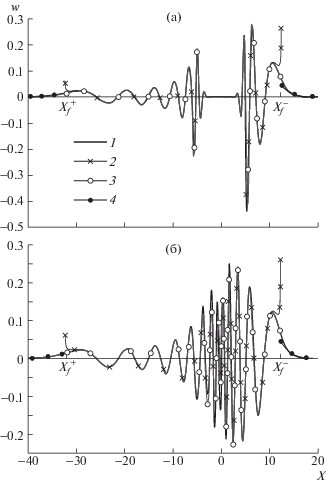
$w(X,t) \approx \frac{{{{W}_{0}}({{z}_{2}})}}{{\sqrt 2 {{t}^{{1/3}}}}}\frac{{\bar {Z}_{2}^{{1/4}}}}{{\left| {\tfrac{{{{d}^{2}}{{\Upsilon }_{ - }}}}{{d{{z}^{2}}}}} \right|_{{z = {{z}_{2}}}}^{{1/2}}}}{{C}_{ + }}{\text{(}}i{{z}_{{\text{2}}}}{\text{)Ai}}({{\bar {Z}}_{2}}{{t}^{{2/3}}})$

где

${{\bar {Z}}_{2}} = {{\left\{ {\frac{3}{2}\left[ {{{\Upsilon }_{ - }}({{z}_{2}}) - V{{z}_{2}}} \right]} \right\}}^{{2/3}}}$

На рис. 5а,б представлено сопоставление различных приближений с результатами численного интегрирования (1.11) при ${{U}_{0}} = 0$, $\alpha = 0.5$, $t = 20$, $q = 0,\;2$. Видно, что асимптотики (2.5)–(2.8) хорошо описывают поведение ледяного покрова, а приближение (2.3), (2.4) применимо только вдали от волнового фронта.

Рис. 5.

Вертикальные прогибы ледяного покрова при ${{U}_{0}} = 0$, $\alpha = 0.5$, $t = 20$: а, б – $q = 0,\;2$; 1 – численное интегрирование (1.11); 2 – приближение стационарной фазы (2.3), (2.4); 3 – асимптотики (2.5), (2.6); 4 – асимптотики (2.7), (2.8). Положение волновых фронтов указано значениями $X_{f}^{ \pm }$.

ЗАКЛЮЧЕНИЕ

Построено решение задачи об эволюции начального возвышения верхней границы жидкости при наличии плавающего ледяного покрова и линейного сдвигового потока. Для ледяного покрова учитываются его упругие свойства и сжимающие усилия. Показано, что при наличии сдвигового потока с увеличением толщины ледяного покрова и уменьшением глубины жидкости существенно возрастает диапазон допустимых значений параметра сжатия.

С помощью метода стационарной фазы получено асимптотическое решение, описывающее динамику вертикальных смещений ледяного покрова при больших временах. Для уточнения асимптотического решения используется обобщенный метод стационарной фазы, позволяющий с помощью функции Эйри получить равномерную асимптотику по продольной переменной. Показано, что построенные равномерные асимптотики хорошо описывают поведение ледяного покрова в окрестности волнового фронта.

В подвижной системе координат положение волнового фронта не зависит от свойств ледяного покрова и определяется только значением параметра сдвига. При наличии сдвигового течения и/или продольной скорости основного потока волновые возмущения становятся несимметричными относительно эпицентра начального возмущения. Влияние сжатия ледяного покрова проявляется более всего в области малых значений продольной координаты. Представляет интерес исследование задачи Коши–Пуассона в трехмерном случае для неравномерно сжатого ледяного покрова.

Список литературы

Wehausen J.V., Laitone E.V. Surface waves. Handbuch der Physik. 1960. V. 9. P. 446–778.
Сретенский Л.Н. Теория волновых движений жидкости. М.: Наука. 1977. 816 с.
Maiti P., Mandal B.N. Water waves generated due to initial axisymmetric disturbances in water with an ice-cover // Arch. Appl. Mech. 2005. V. 74. № 9. P. 629–636. https://doi.org/10.1007/s00419-005-0384-7
Ellingsen S.Å. Initial surface disturbance on a shear current: the Cauchy-Poisson problem with a twist // Phys. Fluids. 2014. V. 26. № 8. P. 082104. https://doi.org/10.1063/1.4891640
Li Y., Ellingsen S.Å. Initial value problems for water waves in the presence of a shear current// Proc. 25th Intern. Ocean and Polar Eng. Conf. 2015. V. 3. P. 543–549.
Smeltzer B.K., Æsøy E., Ellingsen S.Å. Observation of surface wave patterns modified by sub-surface shear currents// J. Fluid Mech. 2019. V. 873. P. 508–530. https://doi.org/10.1017/jfm.2019.424
Das S., Kar P., Sahoo T., Meylan M.H. Flexural-gravity wave motion in the presence of shear current: Wave blocking and negative energy waves// Phys. Fluids. 2018. V. 30. № 10. P. 106606. https://doi.org/10.1063/1.5052228
Maissa P., Rousseaux G., Stepanyants Y. Negative energy waves in a shear flow with a linear profile// Eur. J. Mech. B/ Fluids. 2016. V. 56. P. 192–199. https://doi.org/10.1016/j.euromechflu.2016.01.003
Черкесов Л.В. Основы динамики несжимаемой жидкости. Киев: Наук. Думка, 1984. 168 с.
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат, 1967. 215 с.
Коробкин А.А., Стурова И.В. Плоская задача Коши–Пуассона для бассейна с плавно меняющимся дном. Примеры численных расчетов // ПМТФ. 1990. № 3. С. 54–60.
Абрамовиц М., Стиган И. Справочник по специальным функциям с формулами, графиками и таблицами. М., Наука, 1979. 832 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал